Abstract
The subcarrier domain of multicarrier continuous-variable quantum key distribution (CVQKD) is defined. In a multicarrier CVQKD scheme, the information is granulated into Gaussian subcarrier CVs and the physical Gaussian link is divided into Gaussian sub-channels. The subcarrier domain injects physical attributes to the description of the subcarrier transmission. We prove that the subcarrier domain is a natural representation of the subcarrier-level transmission in a multicarrier CVQKD scheme. We also extend the subcarrier domain to a multiple-access multicarrier CVQKD setting. We demonstrate the results through the adaptive multicarrier quadrature-division (AMQD) CVQKD scheme and the AMQD-MQA (multiuser quadrature allocation) multiple-access multicarrier scheme. The subcarrier domain representation provides a general apparatus that can be utilized for an arbitrary multicarrier CVQKD scenario.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The continuous-variable quantum key distribution protocols allow for the parties to establish an unconditionally secure communication over the traditional telecommunication networks [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. In comparison to discrete-variable (DV) QKD, the CVQKD schemes do not require single-photon devices, a fact that allows us to implement in practice by standard devices [21,22,23,24,25,26,27,28,29,30,31]. Despite the several attractive benefits of CVQKD [1,2,3, 9,10,11,12,13,14], these protocols still require significant performance improvements to be comparable with that of the traditional telecommunications [32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49]. For this purpose, the multicarrier CVQKD has been defined through the adaptive multicarrier quadrature division (AMQD) modulation [5]. In a multicarrier CVQKD system, the Gaussian input CVs are granulated into subcarrier Gaussian CVs via the inverse Fourier transform, which are decoded by the receiver by the unitary CVQFT (continuous-variable quantum Fourier transform) operation [5]. Precisely, the multicarrier transmission divides the physical Gaussian link into several Gaussian sub-channels, where each sub-channel is dedicated for the conveying of a Gaussian subcarrier CV. In particular, the multicarrier transmission injects several benefits to CVQKD, such as improved secret key rates, higher tolerable excess noise, and enhanced transmission distances [5, 6, 8, 9, 29,30,31, 50,51,52,53,54,55,56,57]. Specifically, the benefits of the multicarrier CVQKD modulation has been extended to a multiple-access CVQKD through the AMQD-MQA (multiuser quadrature allocation) scheme [8], in which the simultaneous reliable transmission of the legal users is handled through the sophisticated allocation mechanism of the Gaussian subcarriers. The SVD-assisted (singular value decomposition) AMQD injects further extra degrees of freedom into the transmission [29, 52], which can also be exploited in a multiple-access multicarrier CVQKD.
The achievable secret key rates in a multicarrier CVQKD setting have been rigorously derived in [6]. These secret key rates also confirm the multimode bounds determined in [43] (see the results on fundamental rate-loss scaling in quantum optical communications in [43]). For further information on the bounds of private quantum communications, we suggest [44].
Here, we provide a natural representation of the subcarrier CV transmission and show that it also allows us to utilize the physical attributes into the sub-channel modeling. The angular domain representation is a useful tool in traditional telecommunications to model the physical signal propagation through a communication channel. The angular domain representation is aimed at revealing and verifying the connections of the physical layer and the mathematical channel model in different scenarios, avoiding the use of an inaccurate channel representation [58,59,60]. Here, we show that similar benefits can be brought up to multicarrier CVQKD. We define the subcarrier domain representation for multicarrier CVQKD. The subcarrier domain utilizes the phase-space angles of the Gaussian subcarrier CV to construct the model of a Gaussian sub-channel and to build an appropriate statistical model of subcarrier transmission. The subcarrier domain is an adequate application for multicarrier CVQKD since it is a natural representation of the CVQFT operation. The key behind the subcarrier domain representation is the Fourier operation, which has a central role in a multicarrier CVQKD setting since this operation makes possible the construction of Gaussian subcarrier CVs from the single-carriers and Gaussian sub-channels from the physical Gaussian link.
Particularly, the CVQFT transformation not just opens the door for the characterization of the subcarrier domain of a Gaussian sub-channel but also provides us a framework to study the effects of psychical layer transmission in an experimental multicarrier CVQKD scenario. The subcarrier domain utilizes physical attributes such as the phase space angle into the description of the transmission. Thus, the subcarrier domain representation takes into account not just the theoretical model but also the physical level of the subcarrier transmission. Since the subcarrier domain is a natural representation of a multicarrier CVQKD transmission, it allows us to extend it to a multiple-access multicarrier CVQKD setting. Furthermore, the subcarrier domain model provides a general framework for any experiential multicarrier CVQKD.
The novel contributions of our manuscript are as follows:
- 1.
We define the subcarrier domain of multicarrier continuous-variable quantum key distribution.
- 2.
The subcarrier domain injects physical attributes to the description of the subcarrier transmission.
- 3.
We prove that the subcarrier domain is a natural representation of the subcarrier-level transmission in a multicarrier CVQKD scheme.
- 4.
We extend the subcarrier domain to a multiple-access multicarrier CVQKD setting. We demonstrate the results through the adaptive multicarrier quadrature-division (AMQD) CVQKD scheme and the AMQD-MQA (multiuser quadrature allocation) multiple-access multicarrier scheme.
- 5.
The subcarrier domain representation provides a general apparatus that can be utilized for an arbitrary multicarrier CVQKD scenario. The framework is particularly convenient for experimental multicarrier CVQKD scenarios.
This paper is organized as follows. In Sect. 2, some preliminaries are briefly summarized. Section 3 discusses the subcarrier domain representation for multicarrier CVQKD. Section 4 extends the subcarrier domain for multiple-access multiuser CVQKD. Finally, Sect. 5 concludes the results. Supplemental information is included in the Appendix.
3 Subcarrier Domain of Multicarrier CVQKD
Proposition 1
(Subcarrier domain representation of multicarrier transmission.) For the i-th Gaussian sub-channel \({ {{\mathcal {N}}}}_{i} \), the subcarrier domain representation is \({{{\mathcal {R}}}}_{\phi _{i} } \left( T_{i} \left( { {{\mathcal {N}}}}_{i} \right) \right) =UT_{i} \left( { {{\mathcal {N}}}}_{i} \right) U\), where U is the CVQFT operator.
Proof
The proofs throughout assume l Gaussian sub-channels for the multicarrier transmission. The angles of the \({\left| \phi _{i} \right\rangle } \) transmitted and the \({\left| \phi '_{i} \right\rangle } \) received subcarrier CVs in the phase space \({{{\mathcal {S}}}}\) are denoted by \(\theta _{i}^{\mathrm{*}} \in \left[ 0,2\pi \right] \), and \(\theta _{i} \in \left[ 0,2\pi \right] \), respectively.
Specifically, first, we express \(F\left( {\mathbf {T}}\left( {\mathcal {N}} \right) \right) \) as
from which \(F\left( T_{i} \left( {{{\mathcal {N}}}}_{i} \right) \right) \) is yielded as
Next, we recall the attributes of a multicarrier CVQKD transmission from [5]. In particular, assuming l Gaussian sub-channels, the output \({\mathbf {y}}\) is precisely as follows:
where
The l columns of the \(l\times l\) unitary matrix F formulate basis vectors, which are referred to as the domain \({{\mathcal R}}_{\phi _{i} } \), from which the subcarrier domain representation \({{{\mathcal {R}}}}_{\phi _{i} } \left( T_{i} \left( {{\mathcal {N}}}_{i} \right) \right) \) of \(T_{i} \left( {{{\mathcal {N}}}}_{i} \right) \) is defined as
Thus, (3) can be rewritten as
where \({{{\mathbf {y}}}^{{{{\mathcal {R}}}_{\phi }}}}\) is referred to as the subcarrier domain representation of \({\mathbf {y}}\).
Particularly, from (5) follows that \({{{\mathcal {R}}}}_{\phi _{i} } \left( T_{i} \left( {{{\mathcal {N}}}}_{i} \right) \right) \) can be expressed as
where U is an \(l\times l\) unitary matrix as
where F refers to the CVQFT operator which for l subcarriers can be expressed by an \(l\times l\) matrix, as
thus,
To conclude, the results in (1) and (2) can be rewritten as
thus
Specifically, an arbitrary distributed \({{{\mathcal {R}}}_{\phi }}\left( {\mathbf {T}}\left( {\mathcal {N}} \right) \right) \) can be approximated via an averaging over the following statistics:
by theory.
Since the unitary U operation does not change the distribution of \({{{\mathcal {S}}}}\left( {\mathbf {T}}\left( {{\mathcal {N}}}\right) \right) \), an arbitrarily distributed \({\mathbf {T}}\left( {{{\mathcal {N}}}}\right) \) can be approximated via an averaging over the statistics of
\(\square \)
Theorem 1
(Subcarrier domain of a Gaussian sub-channel). The \({{\mathcal R}}_{\phi _{i} } \) subcarrier domain representation of \({{{\mathcal {N}}}}_{i} \), \(i=0\ldots l-1\), is \({{{\mathcal {R}}}}_{\phi _{i} } \left( T_{i} \left( {{{\mathcal {N}}}}_{i} \right) \right) =\sum _{k}\mathrm{A} \left( {{{\mathcal {N}}}}_{i} \right) b\left( {k/ l} \right) ^{\dag } b\left( \cos \theta _{i} \right) b\left( \cos \theta _{i}^{\mathrm{*}} \right) ^{\dag } b\left( {i /l} \right) \), \(k=0\ldots l-1\), where \(b\left( \cdot \right) \) is an orthonormal basis vector of \({{{\mathcal {R}}}}_{\phi _{i} } \), \(\theta _{i}^{\mathrm{*}} \) and \(\theta _{i} \) are the phase-space angles of \({\left| \phi _{i} \right\rangle } \) and \({\left| \phi '_{i} \right\rangle } \), \(\mathrm{A} \left( {{{\mathcal {N}}}}_{i} \right) =x_{i} \), where \(x_{i} \) is a real variable, \(x_{i} \ge 0\).
Proof
The b basis vectors of \({{{\mathcal {R}}}}_{\phi _{i} } \) are evaluated as follows. Let \(\theta _{i}^{\mathrm{*}} \in \left[ 0,2\pi \right] \) refer to the angle of the i-th noise-free input Gaussian subcarrier CV \({\left| \phi _{i} \right\rangle } \) in \({{{\mathcal {S}}}}\). The angle of the i-th noisy subcarrier CV \(\left| {{\phi _{i}^{\prime }}} \right\rangle \) is referred to as \(\theta _{i} \in \left[ 0,2\pi \right] \), \(\theta _{i} \ne \theta _{i}^{\mathrm{*}} \).
In particular, for the subcarrier domain representation, the scaled CVQFT operation defines the \(b\left( \cdot \right) \) basis at l Gaussian sub-channels as an \(l\times 1\) matrix:
while for the input angle \(\theta _{i}^{{*}} \) also defines an \(l\times 1\) matrix as
Precisely, the difference of the cos functions of the i-th \(\theta _{i}^{\mathrm{*}} \) transmitted and the \(\theta _{i} \) received angles is defined as
Let \(b\left( \cos \theta _{i} \right) \) and \(b\left( \cos \theta _{i}^{\mathrm{*}} \right) \) be the basis vectors of \(\cos \theta _{i} ,\cos \theta _{i}^{\mathrm{*}} \) [58,59,60], then for the \(\Omega _{i} =\theta _{i} -\theta _{i}^{\mathrm{*}} \) angle
and
where [58]
In particular, using (20), after some calculations, the result in (18) can be rewritten as
Specifically, by expressing (20) via the formula of
one can find that for \(l\rightarrow \infty \), \(f\left( \tau _{i} \right) \) can be rewritten as [58]
The function \(\left| f\left( \tau _{i} \right) \right| \) for different values of \(\tau _{i} \) is depicted in Fig. 1. The function picks up the \(\left| f\left( \tau _{i} \right) \right| =1\) maximum at \(\tau _{i} =0\), with a period \(r=1\). For l sub-channels, a period yields l values.
Next, we utilize function \(f\left( \cdot \right) \) to derive the \({{{\mathcal {R}}}}_{\phi _{i} } \) subcarrier domain representation of \({{{\mathcal {N}}}}_{i} \). Function \(f\left( \tau _{i} \right) \) at a given \(\theta _{i} \) formulates a plot
where from the \(r=1\) periodicity of \(f\left( \cdot \right) \) follows that the main loops are obtained at
The plot \(\left| f\left( \tau _{i} \right) \right| \) as a function of \(\cos \theta _{i} \) is depicted in Fig. 2, for \(\theta _{i}^{\text {*}}={\pi }/{2}\;\), \(l=2\).
From the bases \(b\left( \cdot \right) \) of (15) and (16), the Fourier bases \(b\left( {\textstyle \frac{k}{l}} \right) \) and \(b\left( {\textstyle \frac{i}{l}} \right) \), \(i,k=0,\ldots , l-1\), is defined as follows.
The set \(\mathrm{S}_{b} \) of the \({{{\mathcal {R}}}}_{\phi } \) orthonormal basis over the \({{{\mathcal {C}}}}^{l} \) complex space of the \({{{\mathcal {R}}}}_{\phi } \) subcarrier domain representation can be defined as
and \(b\left( {\textstyle \frac{k}{l}} \right) \) is an \(l\times 1\) matrix as
and
while the \(b\left( {\textstyle \frac{i}{l}} \right) \)\(l\times 1\) matrix is precisely as
Precisely, using the orthonormal basis of (26), the result in (20) can be rewritten as
Specifically, the expression of (30) allows us to redefine the plot of (24) to express \(b\left( {\textstyle \frac{k}{l}} \right) \) as follows:
and thus the maximum values are obtained at
Particularly, at a given l, evaluating f at \(k=1,\ldots ,l-1\) yields the following values [58]:
and
In particular, the \(\mathrm{A} \left( {{{\mathcal {N}}}}_{i} \right) \) parameter is called the virtual gain of the \({{{\mathcal {N}}}}_{i} \) sub-channel transmittance coefficient, and without loss of generality, it is defined as
where \(x_{i} \) is a real variable, \(x_{i} \ge 0\).
From (15), (16), and (35), \({\mathbf {T}}\left( {{{\mathcal {N}}}}\right) \) can be expressed as
By exploiting the properties of the Fourier transform [58,59,60], for a given \(\cos \theta _{i}^{\mathrm{*}} \) and \(\cos \theta _{i} \), \({{{\mathcal {R}}}}_{\phi } \left( {\mathbf {T}}\left( {{{\mathcal {N}}}}\right) \right) \) can be rewritten as
Specifically, in (37), for the representation of term \(b{{\left( \cos \theta _{i}^{\text {*}} \right) }^{\dagger }}b\left( {i}/{l}\; \right) \) [58], set \(S^{{{\mathcal R}}_{\phi _{i} } } \) can be defined for the \({{\mathcal R}}_{\phi _{i} } \) domain of \({{{\mathcal {N}}}}_{i} \) as
The set \(S^{{{{\mathcal {R}}}}_{\phi } } \) in the subcarrier domain representation for \(\theta _{i}^{\text {*}}={\pi }/{2}\;\), \(l=2\) and \(k=0,\ldots , l-1\), is illustrated by the dashed area in Fig. 3. The \(b\left( 0\right) ,b\left( {\textstyle \frac{1}{l}} \right) ,\ldots ,b\left( {\textstyle \frac{l-k}{l}} \right) \) basis vectors of \({{{\mathcal {R}}}}_{\phi } \) for \(l=2\) are also depicted, evaluated via (31).
Putting the pieces together, from (37), \({{{\mathcal {R}}}}_{\phi _{i} } \left( T_{i} \left( {{{\mathcal {N}}}}_{i} \right) \right) \) of a given Gaussian sub-channel \({{\mathcal {N}}}_{i} \) is yielded as
\(\square \)
The set \(S^{{{{\mathcal {R}}}}_{\phi } } \) (dashed areas) for \(\theta _{i}^{\text {*}}={\pi }/{2}\;\), \(l=2\) Gaussian sub-channels and \(k=0,\ldots l-1\). The curves (red, green) depict the basis vectors \(b\left( 0\right) ,b\left( {\textstyle \frac{1}{l}} \right) \) of \({{{\mathcal {R}}}}_{\phi } \)
3.1 Statistics of Subcarrier Domain Sub-channel Transmission
Theorem 2
(Transmittance of the Gaussian sub-channels). For arbitrary \(\theta _{i}^{\mathrm{*}} \), the magnitude \(\left| {{{\mathcal {R}}}}_{\phi _{i} } \left( T_{i} \left( {{{\mathcal {N}}}}_{i} \right) \right) \right| \) of \({{{\mathcal {R}}}}_{\phi _{i} } \left( T_{i} \left( {{\mathcal {N}}}_{i} \right) \right) \) of a given \({{{\mathcal {N}}}}_{i} \) is maximized in the asymptotic limit of \(\cos \Omega _{i} \rightarrow 1\), where \(\Omega _{i} =\theta _{i} -\theta _{i}^{\mathrm{*}} \). Averaging over the statistics \({{{\mathcal {S}}}}\left( {{{\mathcal {R}}}}_{\phi } \left( {\mathbf {T}}\left( {{{\mathcal {N}}}}\right) \right) \right) \in {{{\mathcal {C}}}{{\mathcal {N}}}}\left( 0,\sigma _{{\mathbf {T}}\left( {{{\mathcal {N}}}}\right) }^{2} \right) \), \(rank\left( {{\mathcal S}}\left( {{{\mathcal {R}}}}_{\phi } \left( {\mathbf {T}}\left( {{{\mathcal {N}}}}\right) \right) \right) \right) =\min \left( \left| S_{i} \right| ,\left| S_{k} \right| \right) \), where the cardinality of sets \(S_{i} ,S_{k} \) identifies the number of non-zero rows and columns of \({{{\mathcal {R}}}}_{\phi _{i} } \left( {\mathbf {T}}\left( {{{\mathcal {N}}}}\right) \right) \).
Proof
First, we recall \({{{\mathcal {R}}}}_{\phi _{i} } \left( T_{i} \left( {{{\mathcal {N}}}}_{i} \right) \right) \) from (39) and express \(\left| {{{\mathcal {R}}}}_{\phi _{i} } \left( T_{i} \left( {{{\mathcal {N}}}}_{i} \right) \right) \right| \) as
For a given \(\theta _{i}^{\mathrm{*}} \), the values of angle \(\theta _{i} \) has the following statistical impacts on (40).
Without loss of generality, let parameters i and k be fixed as
where \(C>0\) is a real variable.
Particularly, for the \({{{\mathcal {N}}}}_{i} \) sub-channels, the \(\left| {{{\mathcal {R}}}}_{\phi _{i} } \left( T_{i} \left( {{{\mathcal {N}}}}_{i} \right) \right) \right| \) magnitudes formulate a set
Let
and let s be the number of sub-channels for which \(\left| {{{\mathcal {R}}}}_{\phi _{i} } \left( T_{i} \left( {{{\mathcal {N}}}}_{i} \right) \right) \right| \approx 0\).
Specifically, for \(\partial \), let determine \(\Omega _{i} \) the value of k as
Let us define a \({{{\mathcal {G}}}}_{0} \) initial subset with \(\left| {{{\mathcal {G}}}}_{0} \right| =s_{0} \), as
where
In this setting, as \(\cos \Omega _{i} \rightarrow 1\), the cardinality of \({{{\mathcal {G}}}}\) increases,
while as \(\cos \Omega _{i} \rightarrow -1\), the cardinality of \({{{\mathcal {G}}}}\) decreases, thus
In particular, as (48) holds, the range of k expands from C to the full domain of \(k=\left[ 0,2C\right] \), and \(\left| {{{\mathcal {R}}}}_{\phi _{i} } \left( T_{i} \left( {{{\mathcal {N}}}}_{i} \right) \right) \right| \) decreases, thus
where a is an average which around the \(\left| {{\mathcal R}}_{\phi _{i} } \left( T_{i} \left( {{{\mathcal {N}}}}_{i} \right) \right) \right| \) coefficients stochastically moves [58,59,60].
The impact of \(\cos \Omega _{i} \rightarrow -1\) on \(\left| {{\mathcal R}}_{\phi _{i} } \left( T_{i} \left( {{{\mathcal {N}}}}_{i} \right) \right) \right| \) is depicted in Fig. 4 for \(i,k=\left\{ C,C\right\} \), \(i=C=0.5l\). The maximum transmittance is normalized to unit for \(k=0.5C\). Statistically, the convergence of \(\cos \Omega _{i} \rightarrow -1\) improves the range of k and decreases the sub-channel transmittance (see (44)).
The impact of \(\cos \Omega _{i} \rightarrow -1\) on \(\left| {{{\mathcal {R}}}}_{\phi _{i} } \left( T_{i} \left( {{{\mathcal {N}}}}_{i} \right) \right) \right| \) for a fixed \(i=C=0.5l\) on a sub-channel \({{{\mathcal {N}}}}_{i} \). The parameter range changes to \(i,k=\left\{ C,\left[ 0,2C\right] \right\} ,C=0.5l\), from \(i,k=\left\{ C,C\right\} \). For \(\cos \Omega _{i} \rightarrow 1\), the transmittance picks up the maximum at \(k=C=0.5l\) (red) in a narrow range of \(k\approx C\). Statistically, as \(\cos \Omega _{i} \rightarrow -1\), the transmittance significantly decreases, moving stochastically around an average a (dashed grey line) within the full range \(k=\left[ 0,2C\right] \)
Particularly, the degrees of freedom in \({{{\mathcal {R}}}}_{\phi } \left( {\mathbf {T}}\left( {{{\mathcal {N}}}}\right) \right) \) can be evaluated through the rank of \({{{\mathcal {R}}}}_{\phi } \left( {\mathbf {T}}\left( {{{\mathcal {N}}}}\right) \right) \).
Let us identify the number of non-zero rows and columns of \({{{\mathcal {R}}}}_{\phi _{i} } \left( {\mathbf {T}}\left( {{\mathcal {N}}}\right) \right) \) via \(\left| S_{i} \right| \) and \(\left| S_{k} \right| \), of sets \(S_{i} ,S_{k} \), respectively. By averaging [58,59,60] over the statistics of
thus the rank of \({{{\mathcal {S}}}}\left( {{{\mathcal {R}}}}_{\phi } \left( {\mathbf {T}}\left( {{{\mathcal {N}}}}\right) \right) \right) \) without loss of generality is expressed as
for an arbitrary distribution, by theory [58].
The rank in (51) basically changes in function of the number l of \({{{\mathcal {N}}}}_{i} \) Gaussian sub-channels utilized for the multicarrier transmission since the increasing l results in more non-zero elements in \({{{\mathcal {S}}}}\left( {{{\mathcal {R}}}}_{\phi } \left( {\mathbf {T}}\left( {{\mathcal {N}}}\right) \right) \right) \) [58,59,60]. On the other hand, the rank in (51) also changes in function of \(\theta _{i} \). Specifically, as \(\cos \Omega _{i} \rightarrow 1\), the matrix \({{{\mathcal {S}}}}\left( {{{\mathcal {R}}}}_{\phi } \left( {\mathbf {T}}\left( {{{\mathcal {N}}}}\right) \right) \right) \) will have significantly decreased number of non-zero entries (see (47)), while for \(\cos \Omega _{i} \rightarrow -1\), the rank increases because the number of non-zero entries in (51) increases [58] (see (48)).
These statements can be directly extended to the diversity, since the \(\text {div}\left( \cdot \right) \) diversity function of \({{{\mathcal {S}}}}\left( {{{\mathcal {R}}}}_{\phi } \left( {\mathbf {T}}\left( {{{\mathcal {N}}}}\right) \right) \right) \) is evaluated via the number of non-zero entries in \({{\mathcal S}}\left( {{{\mathcal {R}}}}_{\phi } \left( {\mathbf {T}}\left( {{{\mathcal {N}}}}\right) \right) \right) \),
where \(E_{i,k} \) identifies an \(\left( i,k\right) \) entry of \({{{\mathcal {S}}}}\left( {{{\mathcal {R}}}}_{\phi } \left( {\mathbf {T}}\left( {{{\mathcal {N}}}}\right) \right) \right) \). Precisely, from (52) follows that \(\text {div}\left( {{{\mathcal {S}}}}\left( {{{\mathcal {R}}}}_{\phi } \left( {\mathbf {T}}\left( {{\mathcal {N}}}\right) \right) \right) \right) \) increases with the number l of Gaussian sub-channels. \(\square \)
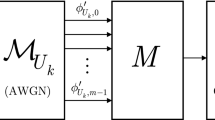
4 Subcarrier Domain of Multiuser Multicarrier CVQKD
Lemma 1
(Subcarrier domain of multiple-access multicarrier CVQKD). The \({{{\mathcal {R}}}}_{\phi } \left( {\mathbf {T}}\left( {{\mathcal {N}}}\right) \right) \) of \({\mathbf {T}}\left( {{{\mathcal {N}}}}\right) \) in a \(K_{in} ,K_{out} \) multiuser setting is \({{{\mathcal {R}}}}_{\phi }^{K_{in} ,K_{out} } \left( {\mathbf {T}}\left( {{\mathcal {N}}}\right) \right) =U_{K_{out} } {\mathbf {T}}\left( {{\mathcal {N}}}\right) U_{K_{out} } \), where \(U_{K_{out} } \) is a \(K_{out} \times K_{out} \) unitary \(U_{K_{out} } ={\textstyle \frac{1}{\sqrt{K_{out} } }} e^{{\textstyle \frac{-\mathrm{i}2\pi ik}{K_{out} }} } \), \(i,k=0,\ldots ,K_{out} -1\).
Proof
Let \(K_{in} ,K_{out} \) be the number of transmitter and receiver users in a multiple access multicarrier CVQKD [8], and let \({\mathbf {Z}}\) be the \(K_{in} \) dimensional input of the \(K_{in} \) users. The Gaussian CV subcarriers formulate the \(K_{in} \) dimensional vector
where \(U_{K_{in} } \) stands for the inverse CVQFT unitary operation.
The \(U_{K_{in} } \) and \(U_{K_{out} } \), \(K_{in} \times K_{in} \), \(K_{out} \times K_{out} \) unitary matrices at l Gaussian sub-channels are as
and
which unitary is the CVQFT operation (For further details, see the properties of the multicarrier CVQKD modulation [5, 6, 8, 9].).
Specifically, the output \({\mathbf {Y}}\) in a \(K_{in} ,K_{out} \) setting is then yielded as
thus without loss of generality
Particularly, by rewriting (37), \({{\mathcal R}}_{\phi }^{K_{in} ,K_{out} } \left( {\mathbf {T}}\left( {{\mathcal {N}}}\right) \right) \) can be expressed as
where the basis vectors are precisely as
and
thus
and
Without loss of generality, the function f from (20) can be rewritten as
with
such that
and
The maximum values of \(f^{K_{out} } \left( {\textstyle \frac{k}{l}} \right) \) are obtained at
The subcarrier domain representation \({{{\mathcal {R}}}}_{\phi }^{K_{in} ,K_{out} } \left( T_{i} \left( {{{\mathcal {N}}}}_{i} \right) \right) \) via \(\left| f^{K_{out} } \left( \tau _{i} \right) \right| \) for \(K_{out} >l\), at \(\theta _{i}^{\text {*}}={\pi }/{2}\;\), \(l=2\) is shown in Fig. 5.
The sets \(\mathrm{S}_{b_{K_{in} } } \), \(\mathrm{S}_{b_{K_{out} } } \) of the \(b_{K_{in} } \), \(b_{K_{out} } \) orthonormal bases of a \(K_{in} ,K_{out} \) setting are as
and
\(\square \)
5 Conclusions
We defined the subcarrier domain for multicarrier CVQKD. In a multicarrier CVQKD protocol, the characterization of the subcarrier domain of a Gaussian sub-channel is provided by the unitary CVQFT transformation, which has a central role in multicarrier CVQKD. The subcarrier domain injects physical attributes to the mathematical model of the Gaussian sub-channels. It provides a natural representation of multicarrier CVQKD and allows us to extend it to a multiple-access multicarrier CVQKD setting. The subcarrier domain representation is a general framework that can be utilized for an arbitrary multicarrier CVQKD scenario. The subcarrier domain also offers an apparatus to formulate the psychical model of the sub-channel transmission, which is particularly convenient for an experimental multicarrier CVQKD scenario.
References
Pirandola, S., Mancini, S., Lloyd, S., Braunstein, S.L.: Continuous-variable quantum cryptography using two-way quantum communication. Nat. Phys. 4, 726–730 (2008)
Grosshans, F., Cerf, N.J., Wenger, J., Tualle-Brouri, R., Grangier, P.: Virtual entanglement and reconciliation protocols for quantum cryptography with continuous variables. Quant. Inf. Comput. 3, 535–552 (2003)
Navascues, M., Acin, A.: Security bounds for continuous variables quantum key distribution. Phys. Rev. Lett. 94, 020505 (2005)
Gyongyosi, L., Imre, S., Nguyen, H.V.: A survey on quantum channel capacities. IEEE Commun. Surv. Tutor. 99, 1 (2018). https://doi.org/10.1109/COMST.2017.2786748
Gyongyosi, L., Imre, S.: Adaptive multicarrier quadrature division modulation for long-distance continuous-variable quantum key distribution, Proc. SPIE 9123, Quantum Information and Computation XII, 912307; https://doi.org/10.1117/12.2050095. From Conference Volume 9123, Quantum Information and Computation XII, Baltimore, Maryland, USA (2014)
Gyongyosi, L., Imre, S.: Secret key rate proof of multicarrier continuous-variable quantum key distribution. Int. J. Commun. Syst. 32(4), e3865 (2018). https://doi.org/10.1002/dac.3865
Gyongyosi, L., Imre, S.: Diversity Space of Multicarrier Continuous-Variable Quantum Key Distribution. Int. J. Commun. Syst. (2019). https://doi.org/10.1002/dac.4003
Gyongyosi, L., Imre, S.: Multiple Access Multicarrier Continuous-Variable Quantum Key Distribution, Chaos, Solitons and Fractals. Elsevier. https://doi.org/10.1016/j.chaos.2018.07.006,ISSN: 0960-0779, (2018)
Gyongyosi, L., Imre, S.: Gaussian quadrature inference for multicarrier continuous-variable quantum key distribution. In: Gyongyosi, L., Imre, S. (eds.) Quantum Studies: Mathematics and Foundations. Springer, New York (2019). https://doi.org/10.1007/s40509-019-00183-9
Pirandola, S., Garcia-Patron, R., Braunstein, S.L., Lloyd, S.: Direct and reverse secret-key capacities of a quantum channel. Phys. Rev. Lett. 102, 050503 (2009)
Pirandola, S., Serafini, A., Lloyd, S.: Correlation matrices of two-mode Bosonic systems. Phys. Rev. A 79, 052327 (2009)
Pirandola, S., Braunstein, S.L., Lloyd, S.: Characterization of collective Gaussian attacks and security of coherent-state quantum cryptography. Phys. Rev. Lett. 101, 200504 (2008)
Weedbrook, C., Pirandola, S., Lloyd, S., Ralph, T.: Quantum cryptography approaching the classical limit. Phys. Rev. Lett. 105, 110501 (2010)
Weedbrook, C., Pirandola, S., Garcia-Patron, R., Cerf, N.J., Ralph, T., Shapiro, J., Lloyd, S.: Gaussian quantum information. Rev. Mod. Phys. 84, 621 (2012)
Gyongyosi, L., Imre, S.: Geometrical Analysis of Physically Allowed Quantum Cloning Transformations for Quantum Cryptography, Information Sciences, pp. 1–23. Elsevier, Amsterdam (2014). https://doi.org/10.1016/j.ins.2014.07.010
Jouguet, P., Kunz-Jacques, S., Leverrier, A., Grangier, P., Diamanti, E.: Experimental demonstration of long-distance continuous-variable quantum key distribution, arXiv:1210.6216v1, (2012)
Navascues, M., Grosshans, F., Acin, A.: Optimality of Gaussian attacks in continuous-variable quantum cryptography. Phys. Rev. Lett. 97, 190502 (2006)
Garcia-Patron, R., Cerf, N.J.: Unconditional optimality of Gaussian attacks against continuous-variable quantum key distribution. Phys. Rev. Lett. 97, 190503 (2006)
Grosshans, F.: Collective attacks and unconditional security in continuous variable quantum key distribution. Phys. Rev. Lett. 94, 020504 (2005)
Adcock, M.R.A., Hoyer, P., Sanders, B.C.: Limitations on continuous-variable quantum algorithms with Fourier transforms. New J. Phys. 11, 103035 (2009)
Lloyd, S.: Capacity of the noisy quantum channel. Phys. Rev. A 55, 1613–1622 (1997)
Lloyd, S., Shapiro, J.H., Wong, F.N.C., Kumar, P., Shahriar, S.M., Yuen, H.P.: Infrastructure for the quantum Internet. ACM SIGCOMM Comput. Commun. Rev. 34, 9–20 (2004)
Lloyd, S., Mohseni, M., Rebentrost, P.: Quantum algorithms for supervised and unsupervised machine learning. arXiv:1307.0411 (2013)
Lloyd, S., Mohseni, M., Rebentrost, P.: Quantum principal component analysis. Nat. Phys. 10, 631 (2014)
Muralidharan, S., Kim, J., Lutkenhaus, N., Lukin, M.D., Jiang, L.: Ultrafast and fault-tolerant quantum communication across long distances. Phys. Rev. Lett. 112, 250501 (2014)
Kiktenko, E.O., Pozhar, N.O., Anufriev, M.N., Trushechkin, A.S., Yunusov, R.R., Kurochkin, Y.V., Lvovsky, A.I., Fedorov, A.K.: Quantum-secured blockchain. Quantum. Sci. Technol. 3, 035004 (2018)
Gyongyosi, L., Imre, S.: Decentralized base-graph routing for the quantum internet. Phys. Rev. A (2018). https://doi.org/10.1103/PhysRevA.98.022310
Van Meter, R.: Quantum Networking. Wiley, ISBN 1118648927, 9781118648926 (2014)
Gyongyosi, L., Imre, S.: Singular layer transmission for continuous-variable quantum key distribution, IEEE Photonics Conference (IPC) 2014. IEEE (2014). https://doi.org/10.1109/IPCon.2014.6995246
Gyongyosi, L., Imre, S.: Proc. SPIE 9377, Advances in Photonics of Quantum Computing, Memory, and Communication VIII, 937711, https://doi.org/10.1117/12.2076532(2015)
Gyongyosi, L., Imre, S.: Gaussian Quadrature Inference for Multicarrier Continuous-Variable Quantum Key Distribution, SPIE Quantum Information and Computation XIV,17–21. Baltimore, Maryland, USA (2016)
Imre, S., Balazs, F.: Quantum Computing and Communications—An Engineering Approach, Wiley, ISBN 0-470-86902-X, p. 283 (2005)
Petz, D.: Quantum Information Theory and Quantum Statistics, vol. Hiv, p. 6. Springer, Heidelberg (2008)
Gyongyosi, L., Imre, S.: Long-distance Continuous-Variable Quantum Key Distribution with Advanced Reconciliation of a Gaussian Modulation. Proceedings of SPIE Photonics West OPTO 2013, (2013)
Pirandola, S.: Capacities of repeater-assisted quantum communications, arXiv:1601.00966 (2016)
Pirandola, S.: End-to-end capacities of a quantum communication network. Commun. Phys. 2, 51 (2019)
Gyongyosi, L., Imre, S.: Entanglement-gradient routing for quantum networks. Sci. Rep. Nat. (2017). https://doi.org/10.1038/s41598-017-14394-w
Gyongyosi, L., Imre, S.: Entanglement availability differentiation service for the quantum internet. Sci. Rep. Nat. (2018). https://doi.org/10.1038/s41598-018-28801-3
Biamonte, J., et al.: Quantum machine learning. Nature 549, 195–202 (2017)
Laudenbach, F., Pacher, C., Fred Fung, C.-H., Poppe, A., Peev, M., Schrenk, B., Hentschel, M., Walther, P., Hubel, H.: Continuous-variable quantum key distribution with Gaussian modulation-The theory of practical implementations. Adv. Quantum Technol. 1800011, (2018)
Shor, P.W.: Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 52, R2493–R2496 (1995)
Kimble, H.J.: The quantum internet. Nature 453, 1023–1030 (2008). https://doi.org/10.1038/nature07127
Pirandola, S., Laurenza, R., Ottaviani, C., Banchi, L.: Fundamental limits of repeaterless quantum communications. Nat. Commun. 8, 15043 (2017). https://doi.org/10.1038/ncomms15043
Pirandola, S., Braunstein, S.L., Laurenza, R., Ottaviani, C., Cope, T.P.W., Spedalieri, G., Banchi, L.: Theory of channel simulation and bounds for private communication. Quantum Sci. Technol. 3, 035009 (2018). https://doi.org/10.1088/2058-9565/aac394
Laurenza, R., Pirandola, S.: General bounds for sender-receiver capacities in multipoint quantum communications. Phys. Rev. A 96, 032318 (2017)
Bacsardi, L.: On the way to quantum-based satellite communication. IEEE Commun. Mag. 51(08), 50–55 (2013)
Gyongyosi, L., Imre, S.: Low-dimensional reconciliation for continuous-variable quantum key distribution. Appl. Sci. (2018). https://doi.org/10.3390/app8010087,ISSN 2076-3417
Shieh, W., Djordjevic, I.: OFDM for Optical Communications. Elsevier, ISBN (eBook): 9780080952062, ISBN (Hardcover): 9780123748799 (2010)
Imre, S., Gyongyosi, L.: Advanced Quantum Communications—An Engineering Approach. Wiley-IEEE Press (New Jersey, USA), ISBN-10: 1118002369, ISBN-13: 978-11180023 (2012)
Gyongyosi, L., Imre, S.: Proceedings Volume 8997, Advances in Photonics of Quantum Computing, Memory, and Communication VII; 89970C; https://doi.org/10.1117/12.2038532(2014)
Gyongyosi, L.: Diversity Extraction for Multicarrier Continuous-Variable Quantum Key Distribution. In Proceedings of the 2016 24th European Signal Processing Conference (EUSIPCO 2016) (2016)
Gyongyosi, L., Imre, S.: Eigenchannel decomposition for continuous-variable quantum key distribution. In: Proceedings Volume 9377, Advances in Photonics of Quantum Computing, Memory, and Communication VIII; 937711, https://doi.org/10.1117/12.2076532 (2015)
Zhao, W., Liao, Q., Huang, D., et al.: Performance analysis of the satellite-to-ground continuous-variable quantum key distribution with orthogonal frequency division multiplexed modulation. Quant. Inf. Proc. 18, 39 (2019). https://doi.org/10.1007/s11128-018-2147-8
Zhang, H., Mao, Y., Huang, D., Li, J., Zhang, L., Guo, Y.: Security analysis of orthogonal-frequency-division-multiplexing-based continuous-variable quantum key distribution with imperfect modulation. Phys. Rev. A 97, 052328 (2018)
Gyongyosi, L.: Singular value decomposition assisted multicarrier continuous-variable quantum key distribution. Theor. Comput. Sci. (2019). https://doi.org/10.1016/j.tcs.2019.07.029
Gyongyosi, L., Imre, S.: Secret key rates of free-space optical continuous-variable quantum key distribution. Int. J. Commun. Syst. (2019). https://doi.org/10.1002/dac.4152
Gyongyosi, L., Imre, S.: Statistical quadrature evolution by inference for multicarrier continuous-variable quantum key distribution. In: Quantum Studies: Mathematics and Foundations. Springer, New York (2019). https://doi.org/10.1007/s40509-019-00202-9
Tse, D., Viswanath, P.: Fundamentals of Wireless Communication, Cambridge University Press, ISBN-13: 978-0521845274, ISBN-10: 0521845270 (2005)
Middlet, D.: An Introduction to Statistical Communication Theory: An IEEE Press Classic Reissue, Hardcover, IEEE, ISBN-10: 0780311787, ISBN-13: 978-0780311787 (1960)
Kay, S.: Fundamentals of Statistical Signal Processing, Volumes I–III, Prentice Hall, ISBN-13: 978-0133457117, ISBN-10: 0133457117 (2013)
Acknowledgements
Open access funding provided by Budapest University of Technology and Economics (BME). The research reported in this paper has been supported by the National Research, Development and Innovation Fund (TUDFO/51757/2019-ITM, Thematic Excellence Program). This work was partially supported by the National Research Development and Innovation Office of Hungary (Project No. 2017-1.2.1-NKP-2017-00001), by the Hungarian Scientific Research Fund-OTKA K-112125 and in part by the BME Artificial Intelligence FIKP grant of EMMI (BME FIKP-MI/SC).
Funding
No relevant funding.
Author information
Authors and Affiliations
Contributions
LGY designed the protocol and wrote the manuscript. LGY and SI analyzed the results. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
We have no competing financial interests.
Research Involving Human Participants
This work did not involve any active collection of human data.
Additional information
Communicated by Alessandro Giuliani.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Multicarrier CVQKD
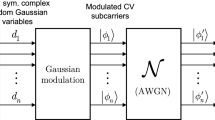
First we summarize the basic notations of AMQD [5]. The following description assumes a single user, and the use of n Gaussian sub-channels \({{{\mathcal {N}}}}_{i} \) for the transmission of the subcarriers, from which only l sub-channels will carry valuable information.
In the single-carrier modulation scheme, the j-th input single-carrier state \({\left| \varphi _{j} \right\rangle } ={\left| x_{j} +\mathrm{i}p_{j} \right\rangle } \) is a Gaussian state in the phase space \({{{\mathcal {S}}}}\), with i.i.d. Gaussian random position and momentum quadratures \(x_{j} \in {{\mathcal {N}}}\left( 0,\sigma _{\omega _{0} }^{2} \right) \), \(p_{j} \in {{\mathcal {N}}}\left( 0,\sigma _{\omega _{0} }^{2} \right) \), where \(\sigma _{\omega _{0} }^{2} \) is the modulation variance of the quadratures. (For simplicity, \(\sigma _{\omega _{0} }^{2} \) is referred to as the single-carrier modulation variance, throughout.) Particularly, this Gaussian single-carrier is transmitted through a Gaussian quantum channel \({{{\mathcal {N}}}}\). In the multicarrier scenario, the information is carried by Gaussian subcarrier CVs, \({\left| \phi _{i} \right\rangle } ={\left| x_{i} +\mathrm{i}p_{i} \right\rangle } \), \(x_{i} \in {{\mathcal {N}}}\left( 0,\sigma _{\omega }^{2} \right) \), \(p_{i} \in {{\mathcal {N}}}\left( 0,\sigma _{\omega }^{2} \right) \), where \(\sigma _{\omega }^{2} \) is the modulation variance of the subcarrier quadratures, which are transmitted through a noisy Gaussian sub-channel \({{{\mathcal {N}}}}_{i} \). Each \({{{\mathcal {N}}}}_{i} \) Gaussian sub-channel is dedicated for the transmission of one Gaussian subcarrier CV from the n subcarrier CVs. (Note: index i refers to the subcarriers, while index j to the single-carriers throughout the manuscript.) The single-carrier state \({\left| \varphi _{j} \right\rangle } \) in the phase space \({{{\mathcal {S}}}}\) can be modeled as a zero-mean, circular symmetric complex Gaussian random variable \(z_{j} \in {{{\mathcal {C}}}{{\mathcal {N}}}}\left( 0,\sigma _{\omega _{z_{j} } }^{2} \right) \), with variance \(\sigma _{\omega _{z_{j} } }^{2} ={{\mathbb {E}}}\left[ \left| z_{j} \right| ^{2} \right] \), and with i.i.d. real and imaginary zero-mean Gaussian random components \(\text {Re}\left( z_{j} \right) \in {{\mathcal {N}}}\left( 0,\sigma _{\omega _{0} }^{2} \right) \), \(\text {Im}\left( z_{j} \right) \in {{\mathcal {N}}}\left( 0,\sigma _{\omega _{0} }^{2} \right) \).
In the multicarrier CVQKD scenario, let n be the number of Alice’s input single-carrier Gaussian states. The n input coherent states are modeled by an n-dimensional, zero-mean, circular symmetric complex random Gaussian vector
where each \(z_{j} \) can be modeled as a zero-mean, circular symmetric complex Gaussian random variable
Specifically, the real and imaginary variables (i.e., the position and momentum quadratures) formulate n-dimensional real Gaussian random vectors, \({\mathbf {x}}={{\left( {{x}_{1}},\ldots , {{x}_{n}} \right) }^{T}}\) and \({\mathbf {p}}={{\left( {{p}_{1}},\ldots , {{p}_{n}} \right) }^{T}}\), with zero-mean Gaussian random variables with densities \(f(x_{j})\) and \(f(p_{j})\) as
where \({{{\mathbf {K}}}_{{\mathbf {z}}}}\) is the \(n\times n\) Hermitian covariance matrix of \({\mathbf {z}}\):
while \({{{\mathbf {z}}}^{\dagger }}\) is the adjoint of \({\mathbf {z}}\).
For vector \({\mathbf {z}}\),
holds, and
for any \(\gamma \in \left[ 0,2\pi \right] \). The density of \({\mathbf {z}}\) is as follows (if \({{{\mathbf {K}}}_{{\mathbf {z}}}}\) is invertible):
A n-dimensional Gaussian random vector is expressed as \({\mathbf {x}}={{\mathbf {A}}}{{\mathbf {s}}}\), where \({\mathbf {A}}\) is an (invertible) linear transform from \({{\mathbb {R}}}^{n} \) to \({{\mathbb {R}}}^{n} \), and \({\mathbf {s}}\) is an n-dimensional standard Gaussian random vector \({{\mathcal {N}}}\left( 0,1\right) _{n} \). This vector is characterized by its covariance matrix \({{{\mathbf {K}}}_{{\mathbf {x}}}}={\mathbb {E}}\left[ {\mathbf {x}}{{{\mathbf {x}}}^{T}} \right] ={\mathbf {A}}{{{\mathbf {A}}}^{T}} \), and has density
The Fourier transformation \(F\left( \cdot \right) \) of the n-dimensional Gaussian random vector \({\mathbf {v}}=\left( v_{1}, \ldots , v_{n} \right) ^{T} \) results in the n-dimensional Gaussian random vector \({\mathbf {m}}={{\left( {{m}_{1}},\ldots , {{m}_{n}} \right) }^{T}}\), as:
In the first step of AMQD, Alice applies the inverse FFT (fast Fourier transform) operation to vector \({\mathbf {z}}\) (see (A.1)), which results in an n-dimensional zero-mean, circular symmetric complex Gaussian random vector \({\mathbf {d}}\), \({\mathbf {d}}\in {{\mathcal {C}}}{{\mathcal {N}}}\left( 0,{{{\mathbf {K}}}_{{\mathbf {d}}}} \right) \), \({\mathbf {d}}={{\left( {{d}_{1}},\ldots , {{d}_{n}} \right) }^{T}}\), as
where
where \(\sigma _{\omega _{d_{i} } }^{2} ={{\mathbb {E}}}\left[ \left| d_{i} \right| ^{2} \right] \) and the position and momentum quadratures of \({\left| \phi _{i} \right\rangle } \) are i.i.d. Gaussian random variables
where \({{{\mathbf {K}}}_{{\mathbf {d}}}}={\mathbb {E}}\left[ {\mathbf {d}}{{{\mathbf {d}}}^{\dagger }} \right] \), \({\mathbb {E}}\left[ {\mathbf {d}} \right] ={\mathbb {E}}\left[ {{e}^{i\gamma }}{\mathbf {d}} \right] ={\mathbb {E}}{{e}^{i\gamma }}\left[ {\mathbf {d}} \right] \), and \({\mathbb {E}}\left[ {\mathbf {d}}{{{\mathbf {d}}}^{T}} \right] ={\mathbb {E}}\left[ {{e}^{i\gamma }}{\mathbf {d}}{{\left( {{e}^{i\gamma }}{\mathbf {d}} \right) }^{T}} \right] ={\mathbb {E}}{{e}^{i2\gamma }}\left[ {\mathbf {d}}{{{\mathbf {d}}}^{T}} \right] \), for any \(\gamma \in \left[ 0,2\pi \right] \).
The \({\mathbf {T}}\left( {\mathcal {N}} \right) \) transmittance vector of \({{{\mathcal {N}}}}\) in the multicarrier transmission is
where
is a complex variable, which quantifies the position and momentum quadrature transmission (i.e., gain) of the i-th Gaussian sub-channel \({{{\mathcal {N}}}}_{i} \), in the phase space \({{{\mathcal {S}}}}\), with real and imaginary parts
and
Particularly, the \(T_{i} \left( {{{\mathcal {N}}}}_{i} \right) \) variable has the squared magnitude of
where
The Fourier-transformed transmittance of the i-th sub-channel \({{{\mathcal {N}}}}_{i} \) (resulted from CVQFT operation at Bob) is denoted by
The n-dimensional zero-mean, circular symmetric complex Gaussian noise vector \(\Delta \in {{{\mathcal {C}}}{{\mathcal {N}}}}\left( 0,\sigma _{\Delta }^{2} \right) _{n} \) of the quantum channel \({{{\mathcal {N}}}}\), is evaluated as
where
with independent, zero-mean Gaussian random components
and
with variance \(\sigma _{{{{\mathcal {N}}}}_{i} }^{2} \), for each \(\Delta _{i} \) of a Gaussian sub-channel \({{{\mathcal {N}}}}_{i} \), which identifies the Gaussian noise of the i-th sub-channel \({{{\mathcal {N}}}}_{i} \) on the quadrature components in the phase space \({{{\mathcal {S}}}}\).
The CVQFT-transformed noise vector can be rewritten as
with independent components \(F\left( \Delta _{x_{i} } \right) \in {{\mathcal {N}}}\left( 0,\sigma _{F\left( {{{\mathcal {N}}}}_{i} \right) }^{2} \right) \) and \(F\left( \Delta _{p_{i} } \right) \in {{\mathcal {N}}}\left( 0,\sigma _{F\left( {{{\mathcal {N}}}}_{i} \right) }^{2} \right) \) on the quadratures, for each \(F\left( \Delta _{i} \right) \). It also defines an n-dimensional zero-mean, circular symmetric complex Gaussian random vector \(F\left( \Delta \right) \in {{{\mathcal {C}}}{{\mathcal {N}}}}\left( 0,{\mathbf {K}}_{F\left( \Delta \right) } \right) \) with a covariance matrix
where \({\mathbf {K}}_{F\left( \Delta \right) } ={\mathbf {K}}_{\Delta } \), by theory. At a constant subcarrier modulation variance \(\sigma _{\omega _{i} }^{2} \) for the n Gaussian subcarrier CVs, the corresponding relation is
where \(\sigma _{\omega _{i} }^{2} \) is the modulation variance of the quadratures of the subcarrier \({\left| \phi _{i} \right\rangle } \) transmitted by sub-channel \({{{\mathcal {N}}}}_{i} \). Assuming l good Gaussian sub-channels from the n with constant quadrature modulation variance \(\sigma _{\omega _{i} }^{2} \), where \(\sigma _{\omega _{i} }^{2} =0\) for the i-th unused sub-channel,
In particular, from the relation of (A.27), for the transmittance parameters the following relation follows at a given modulation variance \(\sigma _{\omega _{0} }^{2} \), precisely,
where \(\left| T\left( {{{\mathcal {N}}}}\right) \right| ^{2} \) is the transmittance of \({{{\mathcal {N}}}}\) in a single-carrier scenario, and
For the method of the determination of these l Gaussian sub-channels, see [5]. Alice’s i-th Gaussian subcarrier is expressed as
1.2 A.2 Abbreviations
- AMQD :
-
Adaptive Multicarrier Quadrature Division
- AWGN :
-
Additive White Gaussian Noise
- CV :
-
Continuous-Variable
- CVQFT :
-
Continuous-Variable Quantum Fourier Transform
- DV :
-
Discrete-Variable
- FFT :
-
Fast Fourier Transform
- IFFT :
-
Inverse Fast Fourier Transform
- MQA :
-
Multiuser Quadrature Allocation
- QKD :
-
Quantum Key Distribution
- SNR :
-
Signal-to-Noise Ratio
- SVD :
-
Singular Value Decomposition
1.3 A.3 Notations
The notations of the manuscript are summarized in Table 1.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Gyongyosi, L., Imre, S. Subcarrier Domain of Multicarrier Continuous-Variable Quantum Key Distribution. J Stat Phys 177, 960–983 (2019). https://doi.org/10.1007/s10955-019-02404-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-019-02404-2