On the Use of Monotonicity-Preserving Interpolatory Techniques in Multilevel Schemes for Balance Laws

Abstract

Cost-effective multilevel techniques for homogeneous hyperbolic conservation laws are very successful in reducing the computational cost associated to high resolution shock capturing numerical schemes. Because they do not involve any special data structure, and do not induce savings in memory requirements, they are easily implemented on existing codes and are recommended for 1D and 2D simulations when intensive testing is required. The multilevel technique can also be applied to balance laws, but in this case, numerical errors may be induced by the technique. We present a series of numerical tests that point out that the use of monotonicity-preserving interpolatory techniques eliminates the numerical errors observed when using the usual 4-point centered Lagrange interpolation, and leads to a more robust multilevel code for balance laws, while maintaining the efficiency rates observed for hyperbolic conservation laws.

1 Introduction

Hyperbolic systems of balance laws often require a rather specialized numerical treatment in order to guarantee both a correct handling of shocks (existing and/or forming) and the preservation of at least certain steady states. In the last decades, there has been a lot of activity in this field, and nowadays there is a number of numerical schemes that combine High Resolution Shock Capturing (HRSC) features for shock computations, using techniques inherited from hyperbolic conservation laws [30, 32, 35], with the so called well balancing (WB) properties, that is, the ability to preserve numerically (at least certain) steady states [9, 11, 14, 15, 28, 37], that trace back to the work of Bermúdez and Vázquez [6] where the C-property (that owns numerical methods able to preserve the water at rest steady-state in shallow water flows), was introduced. These numerical schemes tend to be quite expensive and very often the numerical simulations involve spatial meshes with a large number of points. Hence, it is only natural to consider numerical techniques to lower their computational cost.

Adaptive Mesh Refinement (AMR) techniques for Hyperbolic Conservation Laws [4, 5] have been adapted to the case of balance laws (see e.g., [21, 23, 26]). In these works, it was recognized that it is necessary to introduce also a “well balanced” interpolation/projection operators in the fine/coarse transfer of information between grids, in order to avoid numerical errors when using the full multi-level technique to compute numerical solutions which are near water-at-rest solutions of the shallow water equations. AMR techniques are very effective in reducing the cost of a WB numerical scheme on fine meshes, but their implementation may become a hard task for non-experts, especially for parallel or GPU codes [4, 19].

On the other hand, the so-called cost-effective multilevel technique designed originally by Harten [29] for hyperbolic conservation laws, and further developed in [16] (in the context of finite difference schemes) and [7] in the context of finite-volume schemes, may provide a relatively simple mechanism to lower the cost of computing the numerical solution of a system of balance laws with a given (WB) scheme, since it does not involve the use of any specific data structure. The goal of this technique is to compute the numerical solution of the PDE on a grid with the required resolution (this has to be decided by the user “a priori”) at a much lower cost than what would be required by a direct computation, by replacing the numerical method by a much cheaper interpolatory technique at selected locations inside a recursive multilevel algorithm. Its efficiency in numerical simulations for conservation laws has been demonstrated in many papers (see e.g., [7, 10, 34]) although we do mention that, as observed in [36], a significant reduction of the cost is obtained only for costly numerical schemes, or a large number of resolution levels, while the savings in cost are nearly negligible when simpler (e.g., TVD) schemes and/or a small number of resolution levels are considered. Since there are no memory savings, the technique is recommended for 1D and 2D simulations when intensive testing is required.

It is the purpose of this work to expose some numerical deficiencies observed when applying the cost-effective multilevel technique to balance laws. We show that, when applying the technique to WB numerical schemes for shallow water flows, numerical errors may appear in the multilevel computation of the solution. We propose an alternative, based on exploiting the properties of the interpolatory technique used in the multilevel algorithm, that recovers the excellent performance obtained when applying this technique to hyperbolic conservation laws, even when including source terms that do not require the specialized numerical treatment needed to maintain the WB property, as in [8, 17].

To keep the description of the main ideas in this paper as simple as possible, we consider the case of hyperbolic balance laws in one dimension, which can be written in the general form

$$\begin{aligned} U_t+ F(U)_x= S(x, U). \end{aligned}$$

(1)

Most well-balanced schemes can be written in the form (assuming a method of lines discretization of the system):

$$\begin{aligned} \partial _{t} U+\frac{F_{i+1/2}-F_{i-1/2}}{\Delta x} =\mathcal {B}_i, \end{aligned}$$

(2)

where $F_{i+1/2}$ is a numerical flux consistent with the physical flux F(U) in (1). The term $\mathcal {B}_i$ is not a simple pointwise evaluation of the source term in (4), but the result of a complex (and often fairly costly) process that takes into account an upwind decentering of the source term. High-order numerical schemes for balance laws combine HRSC techniques for the numerical flux functions, with a specialized numerical definition of the ${{\mathcal {B}}}_i$ term. This leads to sophisticated, and computationally expensive, numerical schemes.

The time discretization process in (2) leads to expressions of the form

$$\begin{aligned} U_i^{n+1}=U_i^n + \Delta t {{\mathcal {D}}}_i^n, \end{aligned}$$

(3)

where $U_i^n$ can be considered as an approximation to either the point-values or the cell-averages of the solution on a given grid ${{\mathcal {G}}}=\{x_i\}_{i=1}^N$, $\Delta t$ is the time step and ${{\mathcal {D}}}_i^n$ is an extended numerical divergence which is the core of the numerical scheme (see e.g., [6, 9, 11, 14, 22, 28, 33, 37]).

Notice that (3) has the same formal expression as the numerical schemes for balance laws considered in [16], where the computation of the numerical divergence on the required (fine) grid is carried out using a multilevel strategy within Harten’s Multiresolution (MR) Framework. Hence, it is only natural to consider the use of the cost-effective multilevel computation of the numerical divergence, as in [16], to lower the computational cost of a (finite-difference) WB numerical scheme on a given mesh.

However, our numerical experiments for the shallow water equations reveal that a direct application of the cost-effective multilevel technique may lead to numerical errors. Our analysis points out a relatively simple solution to reduce/avoid unwanted oscillatory behavior, which is particularly dangerous in the numerical simulation of shallow water flows.

The paper is organized as follows: in Sect. 2, we review the shallow water equations and some relevant features to be taken into account in their numerical simulation. In Sect. 3, we briefly review the general framework for interpolatory multiresolution of Harten, since it is the basic framework used in the paper. Section 3.2 is devoted to the shape-preserving interpolatory technique used in the paper to improve the performance of the multilevel method, that is described, in turn, in Sect. 4. Numerical experiments are included in Sect. 5, and some conclusions are summarized in Sect. 6.

2 The Shallow Water Equations

The shallow water equations form a hyperbolic system of balance laws that approximately describes various geophysical flows. For simplicity in the description, we shall consider shallow water equations with source terms due to topography in the 1D case, i.e.,

$$\left\{\begin{aligned} \begin{aligned} & h_t+ (h v)_x =0,\\& (h v)_t+ \left( h v^2+\frac{gh^2}{2}\right) _x =-gh z_x, \end{aligned} \end{aligned}\right.$$

(4)

where z(x, t) describes the bottom topography, h is the water height, v is the velocity of the fluid, and $g=9.81\, \textrm{m} \cdot \textrm{s}^{-2}$ is the gravitational acceleration. Notice that they take the form (1) with

$$\begin{aligned} U= \begin{bmatrix} h&hv \end{bmatrix}^{\text {T}}\!,\ F(U)=\begin{bmatrix} hv&hv^2+\frac{gh^2}{2} \end{bmatrix}^{\text {T}}\!,\ S(x, U)=\begin{bmatrix} 0&-ghz_x \end{bmatrix}^{\text {T}}\!. \end{aligned}$$

The so-called water at rest solution, where $h+z=$ constant and $v=0$ is physically relevant because it is often necessary to compute solutions that represent a small perturbation of a steady state. In the standard literature a scheme is called well balanced if it preserves exactly (to machine accuracy) at least the water at rest steady state. Finding well-balanced schemes or numerical schemes that preserve the water at rest steady state is both important and non-trivial, and much research has been devoted to this issue in recent times. We refer the interested reader to e.g., [6, 9, 11, 14, 28, 37] and references therein.

In the numerical experiments in this paper, we use a one-step, second order, finite difference well-balanced scheme based on a flux limiting technique which hybridizes an extension of the Lax-Wendroff numerical flux with a first order monotone counterpart. The scheme is described and analyzed in [22] for scalar balance laws and in [33] for (4) and its 2D extension. The reader is referred to these papers for specific details on the scheme and its properties. Its fully discrete version takes the form

$$\begin{aligned} U_{i}^{n+1} = U_i^n- \frac{\Delta t}{\Delta x}( {F}_{i+1/2}-F_{i-1/2})+\Delta t \mathcal {B}_{i}, \end{aligned}$$

(5)

where it should be emphasized that $\mathcal {B}_{i}$ is not the evaluation of the source term at a grid point, but is the outcome of a rather sophisticated numerical technique that guarantees that (5) is a well-balanced scheme.

Notice that (5) takes the form (3), with

$$\begin{aligned} \mathcal {D}_i^n:= \frac{F_{i+1/2}-F_{i-1/2}}{\Delta x} - \mathcal {B}_i^n \end{aligned}$$

as the extended divergence. Hence, the cost-effective multilevel technique in [16] could, in principle, be applied in order to reduce the number of costly computations of the quantities ${{\mathcal {D}}}_i^n$ on the given grid.

The multilevel technique developed in [16] is briefly reviewed in Sect. 4. Since the strategy is based on using Harten’s Framework for multiresolution, we provide next a brief description of the essential features of this framework, for the sake of completeness and ease of reference.

3 Harten’s Framework for Multiresolution: Interpolatory MR Transformations

Harten’s framework for Multiresolution provides a versatile set of tools to obtain linear, as well as nonlinear, multiresolution representations of discrete data-sets. A distinctive characteristic of Harten’s approach is that the discrete data at different resolution levels in a specific setting are assumed to come from a particular discretization procedure, acting on an appropriate functional space, which is “naturally” linked to a hierarchy of nested meshes¹$({\chi }^{l})_{l=0}^L$ covering a fixed spatial domain.

Assuming that $N_l$ is the dimension of the discrete data attached to ${\chi }^{l}$, where $N_L<N_{L-1}< \cdots < N_0$, an MR representation of a discrete data set, $v^0\in \mathbb {R}^{N_0}$, is an equivalent representation (in $\mathbb {R}^{N_0}$) which consists in a coarse representation of this data set, $v^0 \in \mathbb {R}^{N_0}$, together with a sequence of details, $d^\ell$, that can be understood as an “essential” (non-redundant) difference in information between consecutive resolution levels, i.e.,

$$\begin{aligned} v^0 \equiv M v^0 = \left( v^L, d^L, d^{L-1}, \cdots , d^1\right) . \end{aligned}$$

(6)

We refer the interested reader to [2, 7, 29] for a complete description of the framework and some applications. Here, we only describe the interpolatory MR framework, which is the one used in [16] and in this paper, because the data in (5) can be interpreted as approximations of the point-values of the true solution of (1).

In one dimension, the simplest setting relies on a hierarchy of nested meshes obtained by dyadic refinement/coarsening of a closed interval. In this case, it is usual to assume that $x_{i} \in \chi ^{l} \iff x_{2^{l}i} \in \chi ^{0}$, which is the finest grid. Then, if $v^{0}_{i}=u(x^0_i)$ are the point values of a function u on $\chi ^{0}$, the discrete values at the l-th resolution level

$$\begin{aligned} v^{l}_{i}=v^{0}_{2^li}, \quad i=0,\cdots ,N_l=\frac {N_0}{2^l}, \qquad i \in N_l \end{aligned}$$

(7)

correspond to the point-values of u on the $\chi ^l$ grid. Clearly, $v^{l}_i = v^{l-1}_{2i}, \; i \in N_l$.

Now, if $\mathcal {I}[\cdot ,v]$ denotes an interpolatory technique on discrete data, v, attached to a given spatial mesh $\chi$, we can easily design decomposition/reconstruction (or analysis/synthesis) algorithms that relate a set of discrete data $v^ {l-1}$ attached to the grid $\chi ^{l-1}$ with its coarser version, $v^l$, at the next (coarser) resolution level, $\chi ^l$, by means of a set of details, which are simply interpolation errors. The decomposition step can be described as follows:

$$\begin{aligned} \text {decomposition} \ \chi ^{l-1} \rightarrow \chi ^l, \quad \left\{ \begin{array}{ll} v^{l}_{i}= v^{l-1}_{2i}, &{} \text {if } x_{i}\in \chi ^{l},\\ d_i^{l}=v^{l-1}_{i}-\mathcal {I}\left[ x_{i};\,v^{l}\right], &{} \text {if } x_{i}\in \chi ^{l-1}\backslash \chi ^{l}. \end{array} \right. \end{aligned}$$

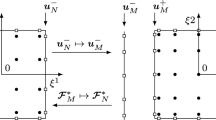
Notice that the discrete data at level $l-1$ is split in two sets, a discrete version of the same data at the next (coarser) level $v^{l}$, and a set of details, $d^l$, which are just interpolation errors at odd locations of the finer grid (see Fig. 1). The reconstruction step

$$\begin{aligned} \text {reconstruction} \ \chi ^l \rightarrow \chi ^{l-1}, \quad {v}^{l-1}_{i} = \left\{ \begin{array}{ll} v^{l}_{i/2}, &{} \text {if } x_{i}\in \chi ^{l},\\ \mathcal {I}\left[ x_{i};\,v^{l}\right] + d_i^{l}, &{} \text {if } x_{i}\in \chi ^{l-1}\backslash \chi ^{l} \end{array} \right. \end{aligned}$$

recovers the data on the finest grid from the information contained in $v^l, d^l$.

Fig. 1

Transfer of information between consecutive resolution levels

The sets $\{v^{l-1}\}$ and $\{v^{l}, d^l\}$ are algebraically equivalent, and have the same cardinality. Hence, by repeatedly applying the decomposition step from the finest to the coarsest resolution level, we get

i.e., a one to one correspondence between the data at the finest resolution level and its MR representation

$$\begin{aligned} v^0 \quad \leftrightarrow \quad M v^0=\left( v^L,d^L,\cdots ,d^1\right) . \end{aligned}$$

The stability of M is directly related to the properties of the interpolatory technique ${\mathcal {I}}$ used to define M. In particular, it depends on the convergence properties of the associated subdivision scheme, an issue which will be briefly described in Sect. 3.3.

In Harten’s interpolatory multiresolution, the details are simply interpolation errors. If $v^l_i=u(x_i^l)$, with u a piecewise smooth function, their size can be estimated using the interpolation error formulas of the interpolatory technique ${\mathcal {I}}$, which is usually based on piecewise polynomial interpolation. We describe next the interpolatory techniques to be used in this paper. For simplicity in the description, we shall assume that the nested grid hierarchy covers the closed interval, so that $\chi ^l=\{x^l_i\}_{i=0}^{N_l}$.

3.1 Centered Piecewise-Polynomial Interpolation

Interpolatory techniques based on piecewise polynomial Lagrange interpolation with a centered stencil are used in the multilevel schemes described in [7, 16]. In these references, $\mathcal {I}[x,v]=P_i(x)$ for $x \in [x_i,x_{i+1}]$, $x_i \in \chi ^{l}$, where $P_i(x)$ is the unique polynomial of degree $r=2s-1$ satisfying $P_i(x_{i+l})=v_{i+l}$ for $l= -(s-1),\cdots , s$.

The Decomposition/Reconstruction algorithms stated in the previous section only require the computation of ${{\mathcal {I}}}(x_i,v^l)$, for $x_i \in \chi ^{l-1}\backslash \chi ^l$, which amounts to computing $P_i(x_{i+1/2})$, where $x_{i+1/2}=(x_i+ x_{i+1})/2$ is the midpoint of the interval $[x_i,x_{i+1}]$. This can easily be accomplished by expressing $P_i$ in the Lagrange basis associated to its interpolatory stencil. For $s=1$ (2-point interpolation), we easily get

$$\begin{aligned} P_i^1 ( x_{i+1/2}) = \frac{1}{2} (v_i+ v_{i+1}), \end{aligned}$$

(8)

while for $s=2$, we get

$$\begin{aligned} P_i^2 ( x_{i+1/2}) = -\frac{1}{16} v^l_{i-1}+\frac{9}{16} v^l_i +\frac{9}{16} v^l_{i+1} - \frac{1}{16} v^l_{i+2}. \end{aligned}$$

(9)

Then, the two-level Decomposition/Reconstruction algorithms take the form of linear filters and the multiresolution transformation M in (6) acts as a linear operator on any set of given data.

Notice that if $v_i^0= u(x_i^0)$, with u a piecewise smooth function, the behavior of detail coefficients $d_i^{l}$ is determined from well-known error formulas for Lagrange interpolation. In regions of smoothness, the detail coefficients in the above algorithm behave as $d_i^l= O(\Delta x^{2s}_{l})$, where $\Delta x_{l}$ is the mesh size in $\chi ^l$ grid, if u is smooth in the convex hull of the stencil of points used in the interpolatory polynomial $P_i^s$, while $d_i^l =O(1)$ if there is a discontinuity in the function in this same set. Hence, a discontinuity in the function located within two mesh points will have $2s-1$ O(1) detail coefficients associated to it. It should also be mentioned that discontinuities in the first or second derivative of u also lower the order of the approximation error in Lagrange interpolation.

These observations justify the fact that the detail coefficients in a multiresolution representation of a data set can be used to determine the regions of smoothness of the underlying function whose point values are attached to the data set. Large detail coefficients can be associated to non-smooth regions, while small detail coefficients are linked to small interpolation errors, and thus to smooth regions. Obviously, using the size of the detail coefficients to determine smoothness regions requires setting a threshold parameter, which will depend on the context and the chosen application. We will return to this issue in Sect. 4.

3.2 Shape Preserving Interpolation

The interpolatory technique described in the previous section does not preserve monotonicity in the original data unless $s=1$, (i.e., piecewise linear interpolation of the data) is used. Linear interpolation, however, is too crude for applications and other interpolatory techniques which are higher order accurate on smooth data, but still non-oscillatory, are often required.

In this paper, we shall consider an interpolatory technique based on cubic Hermite interpolants, where the derivative values are first order approximations to the real derivatives in regions of smoothness, but undergo a limiting procedure that avoids oscillations and keeps the monotonicity properties of the original data. This technique is implemented in the pchip function in MATLAB and can be described as follows: $\mathcal {I}[x,v]=P_i(x)$ for $x \in [x_i,x_{i+1}]$, $x_i \in \chi ^{l}$, where

$$\begin{aligned} P_{i}(x)=c_1 \,+\,c_2 \, (x-x_i) \,+ \,c_3\,(x-x_i)^2 \,+\, c_4\, (x-x_{i})^{2}\,(x-x_{i+1}) \end{aligned}$$

(10)

is the unique polynomial satisfying $P_i(x_{i+l})=v_{i+l}$, $l=0,1$ and $P'(x_{i+l})=\dot{v}_{i+l}$, $l=0,1$ for given values $\dot{v}_i$. It is easy to see that

$$\left\{\begin{aligned} \begin{array}{lcl} c_{1}:= v_{i}, &{} &{} c_{2}:= P[x_i,x_i]=P'(x_i)=\dot{v}_{i}, \\ c_{3}:= P[x_i,x_i,x_{i+1}] = \displaystyle \frac{m_i-\dot{v}_{i}}{h}, &{} &{} c_{4}:= P[x_i,x_i,x_{i+1},x_{i+1}]= \displaystyle \frac{\dot{v}_{i+1}+\dot{v}_{i}-2\,m_{i}}{h^{2}}, \end{array} \end{aligned}\right.$$

(11)

where $m_i=(v_{i+1}-v_{i})/ h$. In the PCHIP interpolation method, the values $\dot{v}_i$ are computed using Brodlie’s formula

$$\begin{aligned} \dot{v}_{i}= H(m_{i-1},m_i) =\left\{ \begin{array}{ll} \displaystyle \frac{2\,m_{i-1}\,m_{i}}{m_{i}+m_{i-1}}, &{} m_{i}\,m_{i-1} > 0, \\ 0, &{} m_{i}\,m_{i-1} \leqslant 0, \end{array} \right. \end{aligned}$$

(12)

where H is a limited harmonic mean. The resulting piecewise cubic Hermite interpolant is monotonicity-preserving [25] and third order accurate on smooth regions wherever the interpolation data are monotone (see e.g., [18]).

This technique is obviously nonlinear, and so would be the associated multiresolution transformation associated to it. However, we notice that the value $P_i(x_{i+1/2})$ is easily computed in terms of the forward differences of the given data, $\nabla v_i=v_{i+1}-v_i$ as follows:

$$\begin{aligned} P_i(x_{i+1/2})= {v_i} + \frac{1}{2} \nabla v_i + \frac{1}{8} \left( H(\nabla v_{i-1},\nabla v_i)- H(\nabla v_{i},\nabla v_{i+1}) \right) , \end{aligned}$$

(13)

hence its computational cost is similar to that of the centered technique described in the previous section with $s=2$.

3.3 Interpolatory Subdivision Refinement

Assume that $\chi ^l \subset \chi ^{l-1}$ are two nested grids with a refinement factor of 2. If $v^{l}$ are known data associated to the grid $\chi ^l$, then the interpolatory technique $\mathcal {I}[x,v^l]$ serves to generate new data associated to the grid $\chi ^{l-1}$ as follows:

$$\begin{aligned} {\hat{v}}^{l-1}_i = \mathcal {I}[x_i, v^l] \qquad \text { for } x_i \in \chi ^{l-1}. \end{aligned}$$

Since $\mathcal {I}[x,v^l]$ is an interpolatory function, we have

$$\begin{aligned} {\hat{v}}^{l-1}_{2i} = v^l_{i} \quad \text { for } x_i \in \chi ^l, \end{aligned}$$

hence the values on a given mesh are just copied at the same location on higher resolution levels. On the other hand, new values on $\chi ^l$ are generated at mesh points $x_i \in \chi ^{l-1}\backslash \chi ^l$ according to the rules specified by the interpolation technique.

When this process is recursively applied, sequences of values on denser meshes are obtained, and, if the process converges, a continuous function is obtained in the limit (the interested reader is referred to e.g., [24] for further details on this issue). Since the initial values are retained at each resolution level, the name interpolatory refinement is completely justified.

The subdivision schemes associated to the centered Lagrange piecewise polynomial techniques described in Sect. 3.1 were originally described and analyzed by Deslauriers-Dubuc [20]. They are in fact linear operators between spaces of bounded sequences and their convergence properties schemes are well known, as it is that they do not preserve the shape properties of the original data to be refined. The subdivision scheme associated to the PCHIP interpolatory reconstruction is nonlinear. Its convergence and stability properties were studied in [3].

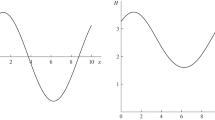
In Fig. 2, we show the result of the recursive subdivision processes associated to the interpolatory techniques described in the previous subsections, applied to a point value discretization of the function

$$\begin{aligned} f(x)= \left\{ \begin{array}{ll} 0.5\sin (\uppi x), &{} 0 \leqslant x < \frac{2}{3}, \\ -0.5\sin (\uppi x), &{} \frac{2}{3} \leqslant x \leqslant 1 \end{array} \right. \end{aligned}$$

(14)

on an initial mesh of 11 equally spaced points in the interval [0, 1]. It can be easily observed that the subdivision processes associated to (8) and (13) preserve the monotonicity properties of the initial data, while Gibbs-type numerical oscillations are clearly visible around the discontinuity in the function when (9) is applied. In addition, the limiting function obtained from (8) is only continuous, while the limiting functions obtained from the use of (9) and (13) are at least $C^1$. These considerations will be relevant when discussing the application of the cost-effective multilevel technique in the contest of balance laws in the next two sections.

Fig. 2

Recursive subdivision with 6 resolution levels, starting from an initial discretization of (14) with 11 points (left) and 21 points (right). Deslauriers-Dubuc subdivision with $s=1,2$ and PCHIP subdivision

4 The Cost-Effective Multilevel Scheme in the Context of Balance Laws

As observed in Sect. 2, the well-balanced discretization of the shallow water system proposed in [33] takes the form

$$\begin{aligned} U^{n+1}_i = U^n_i - \Delta t \mathcal {D}_i^n, \end{aligned}$$

(15)

where the extended divergence $\mathcal {D}_i^n$ takes into account the (complex) source term evaluation. The multilevel scheme developed in [16] has two main ingredients.

• Step 1 A flagging process (analysis), where grid-points are separated into two groups:

  • smooth locations: the solution (at time levels n and $n+1$) is assumed to be smooth at a neighborhood of the grid point;

  • non-smooth location: a discontinuity/singularity is suspected in the vicinity of the grid point.

• Step 2 A multilevel computation of the numerical divergence (synthesis). This process is closely related to the interpolatory subdivision refinement processes described in the previous section. It is carried out as follows: the numerical divergence is computed at each grid-point on the coarsest grid in the nested grid hierarchy by applying the (costly) prescription of the chosen numerical scheme. Then, at each resolution level, from coarse to fine, the subdivision rule is applied at locations flagged as “smooth”, while at “non-smooth” locations, a direct computation using the (costly) prescription is performed. Notice that direct computations of ${{\mathcal {D}}}_i^n$ at any resolution level must use the data $U^n_i$ at the finest resolution level, which is always available, since the technique involves no memory savings.

The flagging process is a key point of the algorithm. From (15), it is clear that the smoothness region of the (discrete) data $U^n$ and $U^{n+1}$ determine the smoothness regions of ${{\mathcal {D}}}^n$. The observations in the previous section allow us to extract the information of the smoothness regions of $U^n$ from the analysis of the detail coefficients in its MR representation, $MU^n$. Since $U^n$ is the only data available at the beginning of the time step, the determination of the smoothness regions of $U^{n+1}$ is “estimated” taking into account “Harten’s heuristics”, i.e., the loss of smoothness in the solution of the balance laws is due to either movement of existing discontinuities or compression leading to shock formation.

In [16], the process to determine the flag vector $(b^{l}_{i})_{l,i}$, whose value (either 0 or 1) identifies those spatial locations where non-smooth behavior in both $U^n$ and $U^{n+1}$ is suspected, takes into account “Harten’s heuristics” and it is based on a problem-dependent threshold $\varepsilon$ that specifies the level below which the user considers that the size of the details corresponds to that of interpolation errors on smooth regions, for the target solution.

The flagging process is as follows: for each level and location, the following two tests are applied

$$\left\{\begin{aligned} \text {if } |d_{i}^{l}|\geqslant & {} \, \varepsilon \Rightarrow b_{i-k}^{l}=1,\quad k=-2,\cdots ,2, \nonumber \\ \text {if } |d_{i}^{l}|\geqslant & {} \, 2^{r}\varepsilon \quad \text {and} \quad l>0 \Rightarrow b_{2i-k}^{l-1}=1, \quad k=-1,0,1, \end{aligned}\right.$$

(16)

where r is the accuracy of the polynomial interpolatory technique used in the MR transformation.

The first test identifies large interpolation errors, associated to regions where non-smooth behavior is suspected. The value of the flag vector is set to one at the detected location and a “safety region” around it, which takes into account the number of points in the interpolatory stencil of the chosen technique. Harten’s heuristics is then used to argue that, at the next time step ($t_{n+1}$), the locations associated to non-smooth behavior may have moved, but at a rate which is controlled by the CFL number of the scheme. Additional neighbors are also marked to account for signal movement, since they might correspond to non-smooth locations of $U^{n+1}$.

The second test seeks to identify non-smooth behavior across scales, possibly due to compression leading to shock formation. It derives from the observation that, since $\Delta x_{l+1}= 2 \Delta x^l$, smooth behavior in the underlying function, together with the accuracy of the interpolatory technique, implies that if $d^{l}_{i}=O(\Delta x_l^r)$ then $d^{l-1}_{2i}=O(\Delta x_{l-1}^r)=d^{l-1}_{2i-1}$. Hence, if at a given location/resolution level the detail coefficients are “too large”, according to the threshold and the accuracy of the interpolatory technique, non-smooth behavior might have not been detected at the next higher resolution level and it is consequently marked at the appropriate locations.

Then, if a certain spatial location has associated a zero flag value, according to the above considerations, it must be situated in a region of smoothness of both $U^n$ and $U^{n+1}$. Notice that, if M is a linear operator, applying it to the discrete data (in the finest resolution grid) in (15), we obtain

$$\begin{aligned} M U^{n+1} = M U^n - \Delta t M {{\mathcal {D}}}^n, \end{aligned}$$

(17)

thus, if the scale coefficients associated to a particular scale/location in $M U^n$ and $MU^{n+1}$ are small and, in view of (17), the detail coefficients associated to this spatial location in $M \mathcal {D}^n$ should also be small, indicating that, at this particular location, the value of $\mathcal {D}^n$ could be associated to that of a smooth function and it can be accurately recovered by recursive interpolation from lower resolution data.

The multilevel evaluation of the numerical divergence in Step 2 is carried as specified below.

• (i) For all points $x_i^L \in \chi ^L$, ${{\mathcal {D}}}^n$ is computed using the prescription of the chosen numerical scheme (using values of $U^n$ a the finest resolution level).

• (ii) Assuming we know the values of ${{\mathcal {D}}}^n$ on the $\chi ^{l+1}$ grid, we proceed from $l=L-1$ to $l=0$ recursively as follows:

  • (a) if $b_i^l =1$ compute ${{\mathcal {D}}}^n_i$ by using the prescription of the chosen numerical scheme;

  • (b) if $b_i^l =0$ compute ${{\mathcal {D}}}^n_i$ using a convenient subdivision refinement rule, using the known values of ${{\mathcal {D}}}^n$ on $\chi ^{l+1}$.

In [16], the same interpolation operator was used for the smoothness analysis of the detail coefficients (the 4-point centered piecewise polynomial interpolatory technique described in Sect. 3.1 ). It is worth remarking that the technique has been successfully applied to compute solutions of hyperbolic equations and systems with different types of source terms, and to the shallow water system when flows near steady states are not involved [7, 17], but we shall see that its numerical behavior is not as robust when applying the technique to compute solutions of shallow water flow near stationary solutions.

Since there is no specific requirement in the design principle of the multilevel technique to use the same interpolatory reconstruction in the multiresolution transform of the available data $U^n$ and, in the recursive refinement used in the multilevel computation of the extended divergence, we propose to use the monotone, shape preserving, interpolatory technique described in Sect. 3.2 for the multilevel computation of the extended numerical divergence. This technique is third order accurate, and we shall see that it leads to an accurate representation of the solution on smooth regions of the flow, and a robust representation of solutions near steady states.

As mentioned previously, the cost-effective technique is particularly useful in those situations where intensive testing is required, for example when a new scheme is being designed and undergoes intensive testing on very fine meshes, or when varying certain parameters/conditions in a controlled environment (see e.g., [1]).

4.1 Efficiency and Quality

We recall that the objective of the multilevel technique is to carry out the computation of the numerical divergence at all points of a given grid, which has been identified as appropriate by the end user, in a (hopefully) much cheaper way than by a direct computation using the chosen (very expensive) numerical scheme. Thus, the efficiency of the multilevel algorithm can be measured by comparing the percentage of numerical divergences that are being computed directly (expensive computation) or interpolated (cheap computation) per time step. However, as in [16], we shall measure directly the CPU gain, $\theta$, for the global simulation (at the prescribed final time) by considering $t_{F}(i)$ and $t_{mr}(i)$ as the CPU times at iteration i for the fixed-mesh simulation on the finest mesh considered in the multilevel structure, and the multilevel algorithm, respectively. Then, $\theta$ is defined as

$$ \theta =\frac{\sum _{i} t_{F}(i)}{\sum _{i} t_{mr}(i)}.$$

(18)

To address the issue of the quality of the outcome of the multilevel technique, let $U^{n}_0$ denote the solution obtained by a direct computation on the desired mesh, $U^n_{0,m}$ be the finest-mesh solution obtained from the multilevel computation of the numerical divergence by considering the desired grid as the finest mesh in a nested sequence of grids covering the computational domain, and $U^n_{\text {ref}}$ the values of a reference solution, which could be either the exact solution on the desired mesh, or the restriction to this mesh of a solution obtained with a reliable numerical scheme on a much finer mesh. Notice that we can write

$$\begin{aligned} \Vert U^n_{0,m}- U^n_{\text {ref}}\Vert \leqslant \Vert U^n_{0,m}-U^n_{0}\Vert + \Vert U^n_{0}-U^n_{\text {ref}}\Vert \end{aligned}$$

(19)

for any $\Vert \cdot \Vert$ denotes an appropriate (discrete) norm.

The difference between $U^n_0$ and $U^n_{\text {ref}}$ depends usually on the accuracy of the chosen numerical scheme and its resolution power. The difference between $U^n_0$ and $U^n_{0,m}$ is the result of a delicate interplay between the accuracy, and the properties, of the interpolatory techniques used in the construction of the flag vector and in the refinement by subdivision of the numerical divergence. In [16], taking $\varepsilon$ of the order of the desired accuracy for the computed solution led to an estimate of the type

$$\begin{aligned} \Vert U^n_{0,m}- U^n_{\text {ref}}\Vert \leqslant C \varepsilon , \end{aligned}$$

(20)

i.e., by choosing $\varepsilon$ as the target accuracy of the fine-mesh simulation we obtained a numerical solution computed by the cost-effective technique of the same quality as that of the direct simulation.

In the next section, we explore to which extent this observation still holds for balance laws. In fact, it turns out that the interplay between the accuracy and the properties of the interpolatory techniques used in the multilevel technique, combined with specific difficulties arising in the numerical approximation of balance laws near steady states, may be the source of numerical pathologies in the computed numerical solutions of certain shallow water flows.

5 Numerical Experiments

In this section, we carry out a series of numerical experiments on several standard test problems in shallow water flow in one dimension in order to evaluate the performance of the cost-effective multilevel technique in the context of balance laws. The examples considered in this section are physically significant, standard test problems in the specialized literature. We include also a numerical simulation of a 2D test problem to show that the robustness of the technique is maintained in 2D. The extension of the technique to 2D is carried out as in [16].

We consider the following acronyms for the interpolatory techniques described in this paper.

• Mo2, monotone linear interpolation, second order accurate on smooth regions, Eq. (8).

• NMo4, non-monotone and fourth order accurate, Eq. (9).

• Mo3, the pchip interpolatory technique, Eq. (13), which is monotone and third order accurate on smooth monotone data.

Taking into account (17), which only holds for linear MR transformations, the linear interpolatory techniques, Mo2 or NMo4 will be used in Step 1, the flagging step. In the numerical tests, we perform a careful comparison of the results obtained when using the three different interpolatory techniques in Step 2, the multilevel interpolation of the extended divergence.

For the numerical experiments in one dimension, we always consider $N_L = 50$, so that the finest mesh in the nested grid structure has $N_0= 2^L N_L$ points in the computational domain. Our goal is to examine the quality of the solution obtained with the multilevel technique, and its relation to the threshold parameter $\varepsilon$ and the interpolatory technique used in Step 2. For this,

• (i) We measure $\Vert U^n_{0,m} - U^n_{\text {ref}} \Vert _1$, the discrete $\mathcal {L}^{1}$-norm of the difference between the multilevel solution and a reference solution. As in [16], we consider a representative variable of the system (in this case, h, the water height) on the finest mesh to measure the difference between discrete data sets.²

• (ii) Additionally, we display the free surface of the numerical solution and compare it to that of the reference solution. The purpose is to visualize the type of numerical errors that occur when using the different alternatives proposed in this paper.

In all cases, the reference solution is the exact solution, when it is available, or the numerical solution computed with the scheme in [33] on a mesh with 12 800 equally spaced points covering the computational domain.

In addition, we measure the efficiency of the multilevel technique by computing $\theta$ in (18).

All numerical tests were carried out using a PC Intel Core i5 1.7 Ghz with 4 GB of RAM, and implemented in the C language.

5.1 Test A: Dam-Break Problem

Our first test involves a rapidly varying flow over a discontinuous bottom topography, see [38] for details. The initial conditions are null discharge and the following values for the initial water height, which simulate a dam break at $t=0$,

$$\begin{aligned} h(x,0)=\left\{ \begin{array}{ll} 20-z(x), &{} x \leqslant 750 \text { m} \\ 15-z(x), &{} \text { otherwise,} \end{array} \right. \end{aligned}$$

(21)

where $0\leqslant x \leqslant 1\,500$. The bottom topography is given by a square function, $z(x)=8$ if $|x-750|\leqslant 1\,500/8$, and $z(x)=0$ otherwise. The numerical simulations are run up to $t=15$ s.

We first examine the influence of the threshold parameter $\varepsilon$ in the overall computation. Recall that this parameter is used to determine the flag vector, which in turn determines the number of costly evaluations of the numerical divergence in the overall computation. For this, we consider the Mo2 interpolatory technique in the determination of the flag vector and also in the numerical computation of the extended numerical divergence on a fine mesh with $N_0=6\,400$ points, i.e., $L=7$. In Fig. 3 we show the computed solution with $\varepsilon = 10^{-2}$ (left plot) and $\varepsilon = 10^{-4}$ (right plot), together with the non-zero locations of the flag vector at each resolution level, shown below the plots. Notice that points at the coarsest level are always marked.

The numerical solution obtained for $\varepsilon = 10^{-4}$ displays the correct behavior of the numerical solution, and the flag vector correctly identifies all non-smooth regions of the solution. On the other hand, the value $\varepsilon = 10^{-2}$ seems to be too crude for this example, with the Mo2 interpolatory technique. Figure 3 clearly shows that the value of $\varepsilon$ is most important in determining the quality of the numerical approximation obtained with the multilevel technique.

Fig. 3

Test A ($N_L=50$, $L=7$, $N_0=6\,400$). Interpolatory technique used in the flagging step and in the evaluation of the numerical divergence is Mo2. Numerical solution and non-zero locations of the flag vector at $t=15$. Left: $\varepsilon =10^{-2}$. Right: $\varepsilon =10^{-4}$

In the next set of numerical experiments, we consider $\varepsilon =10^{-3}$ (an intermediate value) and run the numerical simulation on three different “fine” meshes, i.e., for three different values of L: $L=3$, i.e., $N_0= 400$, $L=5$, $N_0= 1\,600$, and $L=7$, $N_0=6\,400$. In Fig. 4 we consider Mo2 in the flagging step, and NMo4 in Fig. 5. The plots show the numerical solutions obtained by using the multilevel technique with the different interpolatory techniques in Step 2. Our goal now is to examine the effect of the monotonicity properties of the interpolatory technique used in the numerical computation of the numerical divergence during the time evolution of the numerical simulation.

Fig. 4

Test A ($t=15$ s, $N_L=50$, $L=7$, $\varepsilon =10^{-3}$). Flagging step with Mo2. TOP: computed free surface and non-zero locations of the flag vector at $t= 15$. Interpolatory technique in the evaluation of the numerical divergence: Left: Mo2. Middle: NMo4. Right: Mo3. Bottom: enlarged views of the computed free surface with different interpolatory techniques in the multilevel computation of the numerical divergence

Fig. 5

Test A ($t=15$ s, $N_L=50$, $L=7$, $\varepsilon =10^{-3}$). Flagging step with NMo4. Interpolatory technique in the evaluation of the numerical divergence: top and bottom plots as in Fig. 4

Figures 4 and 5 show that the combination of NMo4 in Step 1 with Mo3 in Step 2 produces the best results, avoiding overshoots or excessive diffusion around non-smooth regions or large gradients, and maintaining a flat profile in the region between the rarefaction wave and the shock, a region which is notoriously hard to compute.

We examine next the ${{\mathcal {L}}}^1$ error in (20) for various values of $\varepsilon$ and the different options considered in Figs. 4 and 5. As observed before, $\varepsilon = 10^{-2}$ and Mo2 in Steps 1 and 2 of the multilevel computation leads to large errors (Table 1), which are not observed when NMo4 is used in the flagging step (Table 2). Except for this case, we see that (20) holds true and, in fact, the error tends to be one order of magnitude smaller than the value of $\varepsilon$.

Table 1 Test A: $\Vert U^n_{0,m}- U^n_{\text {ref}}\Vert _1$ at $t_n=15$ s for the specifications in Fig. 4 and various values of $\varepsilon$

Table 2 Test A: $\Vert U^n_{0,m}- U^n_{\text {ref}}\Vert _1$ at $t_n=15$ s for the specifications in Fig. 5 and various values of $\varepsilon$

Finally, we estimate the gain in the multilevel simulation, with respect to the direct computation on the finest mesh, by computing $\theta$ in (18). In Table 3, Mo2 is used in the flagging step, while NMo4 is used instead to compile the results of Table 4. It is worth observing that the gain is similar in all cases, and it depends on the size of the finest mesh. This coincides with the observations made in [16, 36], in the sense that the multilevel technique leads to significant savings in computational time when considering very costly numerical schemes on fine meshes.

Table 3 CPU gain for Test A, $t=15$ s with $N_L=50$, $N_0=400$ ($L=3)$, 1 600 ($L=5)$, 6 400 ($L=7$). Flagging step by Mo2 and different interpolatory techniques in the multilevel evaluation of the numerical divergence

Table 4 CPU gain for Test A. Data as in Table 3, but NMo4 in the flagging step

5.2 Test B: Steady Flow and the C-Property

This test was proposed in the workshop on dam-break wave simulation [27] to check the preservation of water-at-rest solutions by numerical schemes. The solution is the steady state $h+z=12$, $v=0$, and the initial conditions can be found in e.g., [27, 33]. When a well-balanced scheme is applied to this test problem, the steady state is maintained on the discrete mesh up to machine accuracy.

We check whether this property is maintained by running the multilevel scheme up to $T=200$ on discrete grids of $N_0=400, 1\,600, 6\,400$ points ($N_L=50$, $L=3,5,7$). In this case, we check the ${{\mathcal {L}}}^\infty$ error of the water surface versus the true solution, i.e., $\max _{1 \leqslant i \leqslant N_0} \mid (h+z)_i - 12\mid$ and compile the results in Tables 5 and 6. Notice that the bottom topography is composed of straight lines and, hence, this test is specially well suited for the Mo2 interpolatory technique. Nevertheless, it is worth noticing that using Mo3 in the multilevel computation of the numerical divergence always leads to smaller errors than when NMo4 is used in Step 2 of the multilevel technique.

Table 5 Test B: $\max _{1 \leqslant i \leqslant N_0} \mid (h+z)_i - 12\mid$ at $t=200$ s with $N_L=50$, $N_0=400$ ($L=3)$, 1 600 ($L=5)$, 6 400 ($L=7$). Flagging step by Mo2 and different interpolatory techniques in the multilevel evaluation of the numerical divergence

Table 6 $\mathcal {L}^{\infty }$-error for Test B. Data as in Table 5, but NMo4 in the flagging step

In Fig. 6, we display the bottom topography and the non-zero locations of the flag vector at each resolution level, when using Mo2 (left plot) and NMo4 (right plot) in Step 1 of the multilevel technique and, in Fig. 7 we show an enlarged view of the water surface, which shows that the errors when using NMo4 are one order of magnitude larger that when using Mo3. In both figures $\varepsilon =10^{-3}$. It is worth mentioning that the max-error between the true and the computed solution is $3.55 \times 10^{-15}$ on the coarsest mesh, i.e., round off error as expected, since a well-balanced scheme is being used.

Table 7 shows the savings in CPU of the multilevel computation with respect to the fine mesh computation for this experiment and $\varepsilon = 10^{-3}$, for $L=3$ and $L=7$, just to show that, the computational savings are similar to those in the previous example and increase with the size of the underlying fine mesh.

Fig. 6

Test B ($T=200$ s, $N_L=50$, $L=7$, $\varepsilon =10^{-3}$). Non-zero locations of flag vector. Flagging step with left: Mo2, right: NMo4

Fig. 7

Test B: zoom of the numerical solution computed with the multilevel scheme. Velocity (left) and deviation of the free surface from the steady state (right). $L=7, \varepsilon =10^{-3}$. Flagging step with Mo2

Table 7 CPU gain for Test B, $t=200$ s with $N_L=50$, $N_0=400$ ($L=3)$, 6 400 ($L=7$), $\varepsilon =10^{-3}$. Flagging step by Mo2 and different interpolatory techniques in the multilevel evaluation of the numerical divergence

5.3 Test C: Quasi Stationary Flow Over Smooth Topography

This test was proposed by LeVeque in [31] in order to evaluate the capability of a scheme to accurately compute small perturbations of a water-at-rest solution over a variable topography and it involves an initial perturbation of a water-at-rest steady state as the initial condition which generates two waves that move apart from each other and towards the boundaries of the domain. If the magnitude of the perturbation of the height is $10^{-3}$, then the perturbation of each of the two generated waves is $5 \times 10^{-4}$. A highly resolved numerical solution can be obtained with a WB high resolution scheme on a sufficiently fine mesh. We refer the reader to [12] for some examples of the type of numerical oscillations observed when even the approximate C-property is not satisfied. We refer to [31, 33] for details on the initial conditions and bottom topography.

Fig. 8

Test C ($t=0.7$ s, $\varepsilon =10^{-4}$). Free surface and enlarged view. Flagging step with Mo2. Top: $L=3$, $N_0=400$. Bottom: $L=7$, $N_0=6\,400$

In Fig. 8, we show the numerical solution computed with the WB scheme of [33] on a fixed grid of $N_0= 400$ mesh points (top), and on a fixed grid of $N_0=6\,400$ mesh points (bottom), together with the numerical solutions obtained by the multilevel technique (Mo2 in the flagging step) with the three different interpolatory reconstructions in Step 2. It is easily seen that the essential features of the solution (water height, spatial location of perturbation) are already observed on the 400-point mesh, but the fine details of the structure of the solution, visible on the 6 400-point mesh, are not observable on the 400-point mesh. It is worth noticing that a sufficiently accurate interpolatory technique is needed in order to obtain a well resolved numerical solution on the 6 400-point mesh. The enlarged plots show the type of numerical deficiencies observed when using Mo2 in Step 2.

In Tables 8 and 9 we display the ${{\mathcal {L}}}^1$ errors (for the h variable) with respect to a reference solution, obtained by a direct computation of the WB scheme on a mesh with 12 800 points. The errors are always smaller than $\varepsilon$, however, for Mo2 and $\varepsilon =10^{-3}$ they are of the order of the perturbation, while for NMo4 and Mo3 they are always smaller (one order of magnitude at least) of the perturbation of the free surface, leading to an accurate, well resolved, numerical approximation.

Table 8 Test C: $\Vert U^n_{0,m}- U^n_{\text {ref}}\Vert _1$ at $t=0.7$ s with $N_L=50$, $N_0=400$ ($L=3$), 1 600 ($L=5$), 6 400 ($L=7$). Flagging with Mo2 and various values of $\varepsilon$

Table 9 $\Vert U^n_{0,m}- U^n_{\text {ref}}\Vert _1$ for Test C. Data as in Table 8, but NMo4 in the flagging step

As in the previous examples, the computational gain shown in Table 10 indicates that the type of interpolatory technique, among the three considered in this paper, is not relevant in terms of efficiency.

Table 10 Quasi-stationary flow over smooth topography. CPU gain ($\theta$ in (18)). $t=0.7$ s, $N_L=50$, $\varepsilon =10^{-4}$

5.4 Test D: Circular Dam-Break Problem for 2D Shallow Water Flow

We consider next a simulation in 2D in order to illustrate the behavior of a straightforward, tensor-product, 2D extension of the multilevel technique. The test problem is described in [13, 33]. The domain is the square $[0,2]\times [0,2]$ and the topography is given by the function:

$$\begin{aligned} z(x,y)=\left\{ \begin{array}{ll} \frac{1}{8}\left( \cos \big(2\uppi \big(x-\frac{1}{2}\big)\big)+1\right) (\cos (2\uppi y)+1), &{} \text {if } \big(x-\frac{3}{2}\big)^{2} + (y-1)^{2} \leqslant \frac{1}{4}, \\ 0, &{}\text {otherwise.} \end{array}\right. \end{aligned}$$

The initial conditions are $v_1 = v_2 = 0$ and

$$\begin{aligned} h(x,y)=\displaystyle \left\{ \begin{array}{lcl} 1.1-z(x,y), &{} \quad &{} \text {if } (x-1.25)^{2}+(y-1)^{2}\leqslant (0.1)^{2}, \\ 0.6-z(x,y), &{} \quad &{} \text {otherwise}. \end{array}\right. \end{aligned}$$

We apply the multilevel technique with $N_L=50$, $L=3$, $\varepsilon =10^{-2}$ and show the results in Fig. 9. These can be directly compared with those obtained in [33] (with the well-balanced scheme on a fixed mesh). In Fig. 10 we examine the behavior of the different interpolatory techniques in the evaluation of the numerical divergence. As in the 1D tests, it can be clearly observed that the use of Mo3 leads to superior results.

Fig. 9

2D Circular dam break problem. Free surface for $t=0.15$ s, $N_L=50$, $L=3$, $\varepsilon =10^{-2}$. Flagging with NMo4. Interpolatory technique in the evaluation of the numerical divergence Mo3. Left: global view. Right: longitudinal section at $y = 1$

Fig. 10

Longitudinal section at $y=1$ of the 2D circular dam break test. $t=0.15$ s, $N_L=50$, $L=3$, $\varepsilon =10^{-2}$. Flagging with NMo4. Top: left: free surface; right: first component of discharge. Bottom: enlarged views

6 Conclusions

To evaluate the performance of the cost-effective multilevel techniques described in [16] in the context of balance laws, we have performed a series of numerical experiments comparing the usual technique, based on centered, 4-point, piecewise polynomial interpolation, with a monotone cubic interpolant that is used in the pchip function in Matlab. The results show that the combination of high (third order) accuracy and monotonicity in the pchip function leads to a multilevel technique which is more robust, and less prone to the numerical perturbations induced by the usual, non-monotone, interpolation procedure used in the multilevel computation of the extended numerical divergence of the scheme.

In addition, our 1D experiments show that the cost of using the nonlinear monotone interpolatory technique has no significant effect on the efficiency of the multilevel technique, with efficiency rates that depend on the number of points of the finest mesh of the simulation, and that are comparable to those observed for similar problems in the context of homogeneous conservation laws. We have also carried out a 2D simulation to show that monotone interpolatory techniques are less prone to the numerical errors induced by the multilevel technique in [16]. The efficiency of the 2D simulation is not reported in this paper, but, as in the 1D examples, it is expected to be similar to that of the examples reported in [16].

The application to other hyperbolic problems of multilevel schemes relying on monotonicity-preserving reconstructions is a possible future research topic.