Radon Measure Solutions to Riemann Problems for Isentropic Compressible Euler Equations of Polytropic Gases

Abstract

We solve the Riemann problems for isentropic compressible Euler equations of polytropic gases in the class of Radon measures, and the solutions admit the concentration of mass. It is found that under the requirement of satisfying the over-compressing entropy condition:  (i)  there is a unique delta shock solution, corresponding to the case that has two strong classical Lax shocks; (ii) for the initial data that the classical Riemann solution contains a shock wave and a rarefaction wave, or two shocks with one being weak, there are infinitely many solutions, each consists of a delta shock and a rarefaction wave; (iii) there are no delta shocks for the case that the classical entropy weak solutions consist only of rarefaction waves. These solutions are self-similar. Furthermore, for the generalized Riemann problem with mass concentrated initially at the discontinuous point of initial data, there always exists a unique delta shock for at least a short time. It could be prolonged to a global solution. Not all the solutions are self-similar due to the initial velocity of the concentrated point-mass (particle). Whether the delta shock solutions constructed satisfy the over-compressing entropy condition is clarified. This is the first result on the construction of singular measure solutions to the compressible Euler system of polytropic gases, that is strictly hyperbolic, and whose characteristics are both genuinely nonlinear. We also discuss possible physical interpretations and applications of these new solutions.

Appendix A Wave Curves and Classical Riemann Solutions of Riemann Problems

In this appendix, we recall some fundamental results on wave curves and entropy weak solutions to Riemann problems for system (1), with the initial conditions

$$\begin{aligned} (u, \rho )|_{t=0}=\left\{ \begin{aligned} (u_1, \rho _1),&\quad \text {if}~x<0, \\ (u_2, \rho _2),&\quad \text {if}~x>0. \\ \end{aligned} \right. \end{aligned}$$

(A1)

The complete analysis and results could be found in [7, Chapter 2]. It is well known that (1) has two real eigenvalues

$$\begin{aligned} \lambda _{1}=u-c, \ \ \ \lambda _{2}=u+c, \end{aligned}$$

(A2)

when $\rho >0,$ where $c=( p'(\rho ))^{\frac{1}{2}}.$ So it is strictly hyperbolic for polytropic gases without vacuum. The associated right eigenvectors are

$$\begin{aligned} \mathbf{r }_{1}=\begin{pmatrix}-\rho ,&c\end{pmatrix}^{\top }, \mathbf{r }_{2}=\begin{pmatrix}\rho ,&c \end{pmatrix}^{\top }. \end{aligned}$$

Moreover, $\nabla _{(u,\rho )}\lambda _{i}\cdot \mathbf{r }_{i}\ne 0$ if $p''(\rho )>0, i=1, 2.$ Hence, both the characteristics are genuinely nonlinear for non-vacuum polytropic gases with $\gamma >1$.

For the shock wave curves in the $(u,\rho )$-plane, with $\sigma$ being the speed of shocks, considering the Rankine-Hugoniot conditions

$$\begin{aligned} \sigma [\rho ]=[\rho u],\qquad \sigma [\rho u]=[\rho u^{2}+p(\rho )], \end{aligned}$$

(A3)

which yield

$$\begin{aligned} u-u_{1}=\pm \sqrt{\frac{(\rho -\rho _{1})(p-p_{1})}{\rho \rho _{1}}}. \end{aligned}$$

(A4)

According to the Lax condition, or equivalently, density increases across shock front [44, Section 18.B, p.349], for 1-shocks, we have $\rho >\rho _{1}.$ Since $\sigma <0,$ the first equation in (A3) implies that $u<u_{1}.$ Thus,

$$\begin{aligned} S_{1}\doteq \left\{ (u,\rho )~\bigg{|}~ u-u_{1}=-\sqrt{\frac{(\rho -\rho _{1})(p-p_{1})}{\rho \rho _{1}}}, \ \ \ \rho >\rho _{1}\right\} . \end{aligned}$$

(A5)

Similar analysis shows that

$$\begin{aligned} S_{2}\doteq \left\{ (u,\rho )~\bigg{|}~ u-u_{1}=-\sqrt{\frac{(\rho -\rho _{1})(p-p_{1})}{\rho \rho _{1}}}, \ \ \ \rho <\rho _{1}\right\} . \end{aligned}$$

(A6)

Fig. A1

Wave curves of Riemann problem (1), (A1) in the $(u,\rho )$-plane

For the rarefaction wave curves, set $\xi \doteq \frac{x}{t}.$ Then system (1) is reduced to the ordinary differential equations

$$\begin{aligned} \left\{ \begin{aligned}&(u-\xi )\rho _{\xi }+\rho u_{\xi }=0,\\&p'(\rho )\rho _{\xi }+\rho (u-\xi )u_{\xi }=0,\\ \end{aligned} \right. \end{aligned}$$

(A7)

which implies that

$$\begin{aligned} \xi =\lambda _{1}=u-c \quad \text {or} \quad \xi =\lambda _{2}=u+c. \end{aligned}$$

(A8)

For 1-waves, from the first equation in (A7), we have

$$\begin{aligned} \frac{\mathrm {d} u}{\mathrm {d} \rho }=-\frac{c}{\rho }<0. \end{aligned}$$

(A9)

Integrating both sides of (A9) gives

$$\begin{aligned} R_{1}\doteq \left\{ (u,\rho )~|~ u-u_{1}=-\int _{\rho _{1}}^{\rho }\frac{\sqrt{p'(s)}}{s}\mathrm {d} s, \ \ \ \rho <\rho _{1}\right\} . \end{aligned}$$

(A10)

Similarly, the 2-rarefaction wave curve is

$$\begin{aligned} R_{2}\doteq \left\{ (u,\rho )~|~ u-u_{1}=\int _{\rho _{1}}^{\rho }\frac{\sqrt{p'(s)}}{s}\mathrm {d} s, \ \ \ \rho >\rho _{1}\right\} . \end{aligned}$$

(A11)

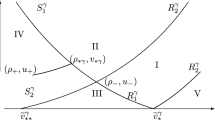
For the Riemann problem (1), (A1) with given left state $(u_{1}, \rho _{1})$, if the right state $(u_{2}, \rho _{2})$ lies on any of the above four curves, then $(u_{1}, \rho _{1})$ and $(u_{2}, \rho _{2})$ can be connected by a single shock wave or rarefaction wave as indicated by the name of the wave curves above. If $(u_{2}, \rho _{2})$ lies in one of the four open regions $\mathrm {I},\ \mathrm {II},\ \mathrm {III},$ or $\mathrm {IV}$ as depicted in Fig. A1, then the solution contains two waves. To be more specific, it is $R_1+R_2$ (two rarefaction waves) if $(u_2,\rho _2)\in \mathrm {I}$; $R_1+S_2$ (a rarefaction wave followed by a shock) if $(u_2,\rho _2)\in \mathrm {II}$; $S_1+R_2$ (a shock followed by a rarefaction wave) if $(u_2,\rho _2)\in \mathrm {III}$; and $S_1+S_2$ (two shocks) if $(u_2,\rho _2)\in \mathrm {IV}$. States in region $\mathrm {V}$ can only be connected to $(u_1,\rho _1)$ by a vacuum lying in the middle of 1- and 2-rarefaction waves.

In Sect. 4.1, for the proof of Theorem 1, we utilized the inverse rarefaction wave curves. $R_1^{*}(U_1)$ is exactly the curve given by

$$\begin{aligned} \left\{ (u,\rho )~|~u-u_{1}=-\int _{\rho _{1}}^{\rho }\frac{\sqrt{p'(s)}}{s}\mathrm {d} s, \ \ \ \rho >\rho _{1}\right\} , \end{aligned}$$

(A12)

which consists of left state U that could be connected to the right state $U_1$ by a 1-rarefaction wave. Similarly, U on the curve

$$\begin{aligned} R_2^{*}(U_1)\doteq \left\{ (u,\rho )~|~ u-u_{1}=\int _{\rho _{1}}^{\rho }\frac{\sqrt{p'(s)}}{s}\mathrm {d} s, \ \ \ \rho <\rho _{1}\right\} \end{aligned}$$

(A13)

could be connected from right by a 2-rarefaction wave to the right state $U_1$.