Quinpi: Integrating Conservation Laws with CWENO Implicit Methods

Abstract

Many interesting applications of hyperbolic systems of equations are stiff, and require the time step to satisfy restrictive stability conditions. One way to avoid small time steps is to use implicit time integration. Implicit integration is quite straightforward for first-order schemes. High order schemes instead also need to control spurious oscillations, which requires limiting in space and time also in the linear case. We propose a framework to simplify considerably the application of high order non-oscillatory schemes through the introduction of a low order implicit predictor, which is used both to set up the nonlinear weights of a standard high order space reconstruction, and to achieve limiting in time. In this preliminary work, we concentrate on the case of a third-order scheme, based on diagonally implicit Runge Kutta ($\mathsf {DIRK}$) integration in time and central weighted essentially non-oscillatory ($\mathsf {CWENO}$) reconstruction in space. The numerical tests involve linear and nonlinear scalar conservation laws.

1 Introduction

Hyperbolic systems of conservation laws in one dimension can be written in the form

$$\begin{aligned} u_t+f(u)_x=0, \end{aligned}$$

(1)

where u(x, t) is the unknown solution, and f(u) is the flux function. The system is hyperbolic provided the Jacobian of f, J(f), has real eigenvalues and a complete set of eigenvectors.

These systems model propagation phenomena, where initial and boundary data travel and interact along the eigenvectors of the system, with finite speed. The eigenvalues of J(f), which depend on the solution itself when the flux is a nonlinear function of u, are the propagation speeds of the system. The size of the eigenvalues can span different orders of magnitude in many applications, and this fact introduces difficulties in the numerical integration of hyperbolic systems of PDE’s.

In this paper, we will consider the method of lines (MOL), which is a very popular approach in the integration of hyperbolic systems. See for instance the textbook [32], and the classic review [39], but other approaches are also effective, as in [18]. In our case, we introduce a grid in the computational domain of points $x_j$. Here for simplicity we will consider a uniform grid, so all points are separated by a distance $h=x_{j}-x_{j-1}$. The computational domain $\varOmega$ is thus covered with a mesh of cells $\varOmega _j=[x_j-\nicefrac {1}{2}\,h,x_j+\nicefrac {1}{2}\,h]$, such that $\cup _j \varOmega _j=\varOmega$. Introducing the cell averages of the exact solution $\overline{u}(t)_j=\tfrac{1}{h} \int _{\varOmega _j}\!u(x,t)\, \mathrm {d}x$, the hyperbolic system (1) can be written as

$$\begin{aligned} \frac{\mathrm {d}{\overline{u}_j}}{\mathrm {d}{t}} = -\frac{1}{h}\left[ f \left(u \left (x_j+\tfrac{1}{2} h,t\right ) \right) - f \left(u \left(x_j-\tfrac{1}{2} h,t \right) \right)\right] , \end{aligned}$$

(2)

which gives the exact evolution of the cell averages in terms of the difference of the fluxes at the cells interfaces. To transform this relation in a numerical scheme, one introduces reconstruction algorithms, $\mathcal {R}$, whose task is to estimate the value of the solution at the cell interfaces from cell averages, and numerical fluxes $\mathcal {F}$, which estimate the flux at the cell interfaces. Thus, the structure of a numerical scheme in the method of lines approach can be written as follows.

• i) Define a reconstruction algorithm $\mathcal {R}(\{\overline{u}\})$ such that the exact solution u at time t is approximated with $u(x,t) = \sum _j R_j(x; t)\chi _j(x)$, where $\chi _j$ is the characteristic function of the interval $\varOmega _j$, and $R_j$ is the restriction of $\mathcal {R}$ to the interval $\varOmega _j$. Typically, $R_j$ is a polynomial of degree $d_j$, which changes in time because it is defined starting from the time-dependent cell averages. In this paper, we will assume that $d_j\equiv d$ is constant.

• ii) Compute the boundary extrapolated data (BED) at the cell interfaces $u^+_{j+\nicefrac 12}=R_{j+1}(x_j+\tfrac{h}{2})$ and $u^-_{j+\nicefrac 12}=R_{j}(x_j+\tfrac{h}{2})$. Recall that the two BED’s computed at the same interface are different, with $u^+_{j+\nicefrac 12}-u^-_{j+\nicefrac 12}=\mathcal {O}(h^{d+1})$ when the flow is smooth enough.

• iii) Choose a smooth enough numerical flux function $\mathcal {F}(a,b)$ such that $\mathcal {F}(a,a)=f(a)$, with the stability property that $\mathcal {F}$ be an increasing function of the first argument and a decreasing function of the second argument.

• iv) Then the solution of the PDE is approximated by the solution of the system of ODE’s

  $$\begin{aligned} \frac{\mathrm {d}{\overline{u}_j}}{\mathrm {d}{t}} = - \frac{1}{h}\left( \mathcal {F}_{j+\nicefrac 12}-\mathcal {F}_{j-\nicefrac 12}\right) \end{aligned}$$

  (3)

  with $\mathcal {F}_{j+\nicefrac 12}=\mathcal {F}(u^-_{j+\nicefrac 12},u^+_{j+\nicefrac 12})$.

It is well known that for explicit schemes the time step ${\Delta } t$ must satisfy the CFL condition, namely $\lambda = {\Delta } t/h\leqslant c/\max _u|f'(u)|$, for a constant $c,\,1\geqslant c>0$, the Courant number. Thus the numerical speed $1/\lambda$ must be faster than all the waves present in the system. Since the error in the numerical solution depends on the difference between the numerical and the actual speed, it follows that in explicit schemes the waves which are better approximated are the fastest waves.

Several systems of hyperbolic conservation laws are characterized by waves with very different speeds, and in many applications the phenomenon of interest travels with slow speeds, while the fastest waves which impose the CFL condition do not need to be accurately represented. Low Mach problems in gas dynamics and kinetic problems close to equilibrium provide good examples.

Low Mach problems arise in gas dynamics when the flow is close to incompressibility. In these cases the actual speed of the gas is much slower than the acoustic waves, and if one is interested in the movement of the gas, accuracy in the propagation of sound is irrelevant. A huge literature has developed for these problems, here we mention just a few pioneering works, [13, 14] and some more recent developments [1, 7, 15, 16, 41].

A second example in which fast velocities constrain the CFL condition, but the signals carried by them do not need to be accurately represented, occurs in kinetic problems, especially close to equilibrium. In kinetic problems the typical evolution equation has the form

$$\begin{aligned} f_t + v \cdot \nabla _x f= Q(f,f), \end{aligned}$$

(4)

where $f=f(x,t,v)$ is the distribution function for particles located at x, with velocity v at time t, and Q(f, f) is the collision term, accounting for the interaction between particles during which the microscopic speeds v are modified. When the flow is close to equilibrium, the relevant phenomena travel with macroscopic speeds which have magnitude of order $\int \!\!v \,f(x,t,v) \mathrm {d}v$ and $[\int \!\!v^2 \,f(x,t,v) \mathrm {d}v]^{\nicefrac 12}$. Still, the CFL condition is based on the fastest microscopic speeds, which are typically much larger. Several attempts have been proposed to go around this restriction, see the review [17], and [33]. Note that the microscopic speeds appear in the convective term only, and convection is linear in kinetic problems. Thus it is feasible to integrate these equations with implicit schemes, taking advantage of the linearity of the convective terms, as in [36]. As we will see, Quinpi schemes are linear on linear problems. We expect, therefore, that their application will be particularly effective on kinetic problems.

The structure of the convective term of kinetic problems is exploited also by semi-Lagrangian schemes, as in [6, 25], and the papers of the same series. Semi-Lagrangian schemes track characteristics, and therefore they are explicit, while satisfying automatically stability conditions. However, they need to interpolate the solution on the grid, because the foot of the characteristic, from which the solution is carried up to the next time level, typically does not coincide with a grid point. Enforcing a non-oscillatory interpolation will then widen the stencil. Moreover, especially when the problem is stiff, characteristics may cross the boundary of the domain, before hitting the surface of known data. This makes the construction of semi-Lagrangian schemes for problems on bounded domains quite tricky. On other applications of semi-Lagrangian schemes, see also [8].

Another setting in which convection is linear, and therefore more amenable to implicit integration, arises with relaxation systems of the form proposed in [29]. Relaxation leads to systems of PDE’s which have a kinetic form with linear transport, as in (4). Besides kinetic problems, diffusive relaxation leads to fast relaxation microscopic speeds, which again prompts the need for implicit time integration.

In this paper, we will propose numerical schemes for the implicit integration in time of hyperbolic systems of equations. This is a preliminary work. For the time being, we will focus on third-order implicit schemes for scalar conservation laws. As noted in [3], there are three levels of nonlinearity in high order implicit methods for conservation laws, which make implicit integration particularly challenging. The first level consists in the nonlinearity of the flux function, which is due to the physical structure of the model, and therefore is unavoidable. The other sources of nonlinearity are due to the need to prevent spurious oscillations, arising with high order numerical schemes. Even in the explicit case, non-oscillatory high order schemes must use nonlinear reconstructions. As is well known, nonlinear reconstructions in space are needed even in implicit schemes. Moreover, high order time integrators are typically based on a polynomial approximation of the time derivative. Thus, a nonlinear limiting is needed also in the time reconstruction of the derivative. These problems have been addressed by several authors. We mention work on second-order schemes in [20, 21], where limiters are applied in space and time simultaneously and TVD estimates are derived. An interesting discussion on TVD bounds in space and time can be found in [22], and in the classic paper [27]. See also [24]. A fully nonlinear third-order implicit scheme, which is limited in both space and time simultaneously can be found in [3].

The next section, Sect. 2, contains a discussion of revisited TVD bounds which are at the basis of our approach, and a summary of the choices leading to the final scheme. Section 3 is the main part of the work, and it offers a complete discussion of the bricks composing the proposed Quinpi algorithm. Next, Sect. 4 documents the properties of the scheme with a selection of numerical tests for scalar equations. We end with conclusions and a plan for future work in Sect. 5.

2 Motivation

To study TVD conditions for implicit schemes, we consider the linear advection equation $u_t+au_x=0$ with $a>0$ and the upwind scheme. In this section, $u_j^n$ is the numerical approximation to the exact solution, at one of the space-time grid points, namely, $u_j^n\simeq u(x_j,t^n)$, with $x_j\in \varOmega$, is a grid point in the space mesh, and $t^n=n\Delta t$, $\Delta t$ being the time step. The mesh ratio is $\lambda =\Delta t/h$.

In the explicit case, we have

$$\begin{aligned} u_j^{n+1}=u_j^n -\lambda a(u_j^n-u_{j-1}^n) \end{aligned}$$

and the total variation of $u^{n+1}$ is

$$\begin{aligned} \text{ TV }(u^{n+1})&= \sum _j\left| (1-\lambda a)(u^n_j-u^n_{j-1}) +\lambda a(u_{j-1}^n-u_{j-2}^n)\right| \\&\leqslant |1-\lambda a| \sum _j\left| u^n_j-u^n_{j-1}\right| +|\lambda a|\sum _j\left| u^n_{j-1}-u^n_{j-2}\right| . \end{aligned}$$

Then, using the fact that $a>0$, periodic boundary conditions, or compact support of the solution, and the CFL condition, one has that $\text{ TV }(u^{n+1})\leqslant \text{ TV }(u^n)$.

For the implicit upwind scheme instead, we start from

$$\begin{aligned} u_j^n= u_j^{n+1}+\lambda a(u_j^{n+1}-u_{j-1}^{n+1}). \end{aligned}$$

Now

$$\begin{aligned} \text{ TV }(u^{n})&= \sum _j\left| (1+\lambda a)(u^{n+1}_j-u^{n+1}_{j-1}) -\lambda a(u_{j-1}^{n+1}-u_{j-2}^{n+1})\right| \\&\geqslant |1+\lambda a| \sum _j\left| u^{n+1}_j-u^{n+1}_{j-1}\right| -|\lambda a|\sum _j\left| u^{n+1}_{j-1}-u^{n+1}_{j-2}\right| . \end{aligned}$$

Since $a>0$, and applying again periodic boundary conditions, we find $\text{ TV }(u^{n+1})\leqslant \text{ TV }(u^n), \ \forall \lambda$. Thus, the implicit upwind scheme is not only unconditionally stable, but it is also unconditionally total variation non-increasing.

We now consider the explicit Euler scheme with second-order space differencing, using a piecewise limited reconstruction. The numerical solution now is

$$\begin{aligned} u_j^{n+1}=u_j^n -\lambda a\left( 1-\tfrac{1}{2}\varPhi (\theta _{j-1})\right) \left( u_j^n-u_{j-1}^n\right) -\tfrac{1}{2} \lambda a\varPhi (\theta _j) \left( u_{j+1}^n-u_{j}^n\right) , \end{aligned}$$

where $\varPhi (\theta )$ is the limiter, and the quantity $\theta _j=\tfrac{u_j-u_{j-1}}{u_{j+1}-u_{j}}$, so that the limited slope is $\sigma _j=\varPhi (\theta _j)(u_{j+1}-u_{j})$.

To prove under what conditions the scheme is TVD, following Harten [26], and Sweby [40], one rewrites this scheme as

$$\begin{aligned} u_j^{n+1}=u_j^n -C_{j-1}\left( u_j^n-u_{j-1}^n\right) \end{aligned}$$

with

$$\begin{aligned} C_{j-1}=\lambda a\left[ 1-\tfrac{1}{2} \left( \varPhi (\theta _{j-1})-\frac{\varPhi (\theta _{j})}{\theta _{j}}\right) \right] . \end{aligned}$$

Computing the total variation of the scheme above, one finds that the scheme is TVD provided

$$\begin{aligned} C_j \geqslant 0, \qquad \text{ and }\quad 1-C_j\geqslant 0. \end{aligned}$$

Since $a>0$, the first condition holds provided

$$\begin{aligned} \alpha _j = 1-\tfrac{1}{2} \left( \varPhi (\theta _{j-1})-\frac{\varPhi (\theta _{j})}{\theta _{j}}\right) \geqslant 0. \end{aligned}$$

From this, one recovers the familiar restrictions in the choice of the limiter function, namely $0\leqslant \tfrac{\varPhi (\theta )}{\theta }\leqslant 2$ and $0\leqslant \varPhi (\theta )\leqslant 2$, see also LeVeque [32]. With these bounds, one has $0\leqslant \alpha _j\leqslant 2$, and the second condition on $C_{j}$ is satisfied provided a slightly restricted CFL holds, namely, $\lambda \leqslant 1/(2a)$.

How do these estimates change in the implicit case? Now we have

$$\begin{aligned} u_j^n= u_j^{n+1}+\lambda a\left( 1-\tfrac{1}{2}\varPhi (\theta _{j-1})\right) \left( u_j^{n+1}-u_{j-1}^{n+1}\right) +\tfrac{1}{2} \lambda a\varPhi (\theta _j) \left( u_{j+1}^{n+1}-u_{j}^{n+1}\right) , \end{aligned}$$

and introducing the same quantity $C_j$ we saw before, this expression can be rewrited as

$$\begin{aligned} u_j^n= u_j^{n+1}+C_{j-1}\left( u_j^{n+1}-u_{j-1}^{n+1}\right) . \end{aligned}$$

The total variation of this scheme is

$$\begin{aligned} \text{ TV }(u^{n})&= \sum _j\left| (1+C_{j-1})(u^{n+1}_j-u^{n+1}_{j-1}) -C_{j-2}(u_{j-1}^{n+1}-u_{j-2}^{n+1})\right| \\&\geqslant \sum _j|1+C_{j-1}| \left| u^{n+1}_j-u^{n+1}_{j-1}\right| -\sum _j|C_{j-2}|\left| u^{n+1}_{j-1}-u^{n+1}_{j-2}\right| , \end{aligned}$$

where we have used the inverse triangle inequality. Applying periodic boundary conditions, and assuming that

$$\begin{aligned} C_j \geqslant 0, \qquad \text{ and }\quad 1+C_j\geqslant 0, \end{aligned}$$

one finds that the scheme is TVD. The important point for the development in this work is that the first condition gives exactly the same restrictions on the choice of the limiter function we find in the explicit case. The second condition instead is always satisfied. This means that the implicit scheme with piecewise linear reconstruction in space is TVD for all $\lambda$, provided the limiter function satisfies the usual bounds holding for explicit schemes.

The limiter is subject also to accuracy constraints. We achieve second-order accuracy if the limited slope is a first-order approximation of the exact slope. Namely, if U(x) is a smooth function with cell averages $\overline{u}_j$, second-order accuracy requires that

$$\begin{aligned} U(x_{j+\nicefrac 12})-\left( \overline{u}_j+\tfrac{1}{2} \sigma _j\right) =\mathcal {O}(h)^2. \end{aligned}$$

Substituting the limited slope and expanding around $U(x_j)=u_j$, one finds

$$\begin{aligned} U(x_{j+\nicefrac 12})-u^-_{j+\nicefrac 12}=\tfrac{h}{2}(1-\varPhi (1))+\mathcal {O}(h)^2. \end{aligned}$$

As in the explicit case, we see that second-order accuracy requires $\varPhi (1)=1$, together with at least Lipshitz continuity for $\varPhi$. This means that $\varPhi$ and $\theta$ can be computed using auxiliary functions that must be at least first order approximations of the unknown function $u(x,t^{n+1})$. For these reasons, in this work we will get as follows.

• Build implicit schemes for stiff hyperbolic systems with unconditional stability, based on diagonally implicit Runge Kutta ($\mathsf {DIRK}$) schemes.

• Prevent spurious oscillations in space using exactly the same techniques for space limiting we are familiar with. In fact, as pointed out in [24], Runge Kutta schemes can be seen as combinations of Euler steps. This is true also in the implicit case. We will strive to ensure that each implicit Euler step composing the whole Runge Kutta step prevents spurious oscillations. In other words, we will rewrite the PDE as a system of ODE’s in the cell averages, with a non-oscillatory right-hand side.

• The nonlinearities in the space reconstruction will be tackled using first-order predictors, that can be computed without limiting, because, as we have recalled, they are unconditionally TVD. They allow to compute each $\mathsf {DIRK}$ stage by solving a system which is nonlinear only because of the nonlinear flux function, and, at the same time, they will constitute a low order non-oscillatory approximation of the solution in its own right.

• As is known, this is not enough to prevent spurious oscillations, when high order space reconstructions are coupled with high order time integrators. A high order Runge Kutta scheme can be viewed as a polynomial reconstruction in time through natural continuous extensions [35, 42]. Not surprisingly, limiting is needed also in time, as pointed out in [20] and more recently [3]. Unlike these authors, however, we limit the solution in time applying the limiter directly on the computed solution, blending the accurate solution with the low order predictor, without coupling space and time limiting.

We will name the resulting schemes Quinpi, for central weighted essentially non-oscillatory ($\mathsf {CWENO}$) implicit. In this paper, we will introduce only third-order Quinpi schemes. We plan to extend the construction to include higher-order schemes, BDF extensions and applications in future works.

3 Quinpi Finite Volume Scheme

This section is devoted to the description of the implicit numerical solution of a one-dimensional scalar conservation law of the form (1) with the Quinpi approach. As pointed out in Sect. 1, we focus on the finite volume framework employing the method of lines, which leads to the system of ODEs (3) for the evolution of the approximate cell averages.

In the following subsections, we will initially describe the space reconstruction for a function u(x), with limiters based on a predicted solution p(x), where p should be at least a first-order approximation of u. We will concentrate on the third order $\mathsf {CWENO}$ reconstruction [34]. For the general $\mathsf {CWENO}$ algorithm, see [10]. More details, improvements and extensions can be found in [9, 11, 12, 19, 31, 37]. Other non-oscillatory reconstructions can also be used, such as $\mathsf {WENO}$, see the classic review [39]. and its extensions as [4].

Next, we will consider the integration in time, with a $\mathsf {DIRK3}$ scheme, describing the interweaving of predictor and time advancement of the solution. Finally, we will introduce the limiting in time, which consists in a nonlinear blending between the predicted and the high order solution, and the conservative correction that is needed at the end of the time step.

3.1 Space Approximation: the $\mathsf {CWENO}$ Reconstruction Procedure

The $\mathsf {CWENO}$ schemes are a class of high-order numerical methods to reconstruct accurate and non-oscillatory point values of a function u starting from the knowledge of its cell averages. The main characteristic of $\mathsf {CWENO}$ reconstructions is that they are uniformly accurate within the entire cell, [10].

For the purpose of this work, here we briefly recall the definition of the $\mathsf {CWENO}$ reconstruction procedure restricting the presentation to the one-dimensional third-order scalar case on a uniform mesh. In order to reconstruct a function u at some $x\in \varOmega$ and at a fixed time t, we consider as given data the cell averages $\overline{u}_j$ of u at time t over the cells $\varOmega _j$ of a grid, which is a uniform discretization of $\varOmega$.

A third-order $\mathsf {CWENO}$ reconstruction is characterized by the use of an optimal polynomial of degree 2 and two linear polynomials. Let $P_{j,L}^{(1)}$ and $P_{j,R}^{(1)}$ be the linear polynomials

$$ \left\{ {\begin{array}{*{20}c} P_{j,L}^{(1)}&= \overline{u}_j + \frac{\overline{u}_j-\overline{u}_{j-1}}{h} (x-x_j), \\ P_{j,R}^{(1)}&= \overline{u}_j + \frac{\overline{u}_{j+1}-\overline{u}_{j}}{h} (x-x_j), \\ \end{array} } \right.$$

(5)

and let us write the optimal polynomial of degree 2 as

$$\begin{aligned} {\left\{ \begin{array}{ll} P_j^{(2)}(x)= a + b(x-x_j) + c(x-x_j)^{2},\\ \qquad a= \frac{-\overline{u}_{j+1} +26\overline{u}_j -\overline{u}_{j-1}}{24},\\ \qquad b= \frac{\overline{u}_{j+1} -\overline{u}_{j-1}}{2h},\\ \qquad c= \frac{\overline{u}_{j+1} -2\overline{u}_j +\overline{u}_{j-1}}{2h^2}. \end{array}\right. } \end{aligned}$$

(6)

All polynomials $P_{j,L}^{(1)}$, $P_{j,R}^{(1)}$ and $P_j^{(2)}$ interpolate the data in the sense of cell averages. We also introduce the second degree polynomial $P_{j,0}$ defined as

$$\begin{aligned} {\left\{ \begin{array}{ll} P_{j,0}(x)= \frac{1}{C_0} \left( P_j^{(2)}(x) - C_L P_{j,L}^{(1)} - C_R P_{j,R}^{(1)} \right) = A + B(x-x_j) + C(x-x_j^2), \\ \qquad A= \frac{a}{C_0} - \frac{C_L+C_R}{C_0} \overline{u}_j, \\ \qquad B= \frac{(1-2C_R)\overline{u}_{j+1} -(2C_L-2C_R)\overline{u}_j +(2C_L-1)\overline{u}_{j-1}}{2C_0h}, \\ \qquad C= \frac{c}{C_0}, \end{array}\right. } \end{aligned}$$

(7)

where $C_0, C_L, C_R \in (0,1)$ with $C_0+C_L+C_R = 1$ are the linear or optimal coefficients. Note that this polynomial reproduces the underlying data with second order accuracy.

The Jiang-Shu smoothness indicators [28] of the polynomials related to the cell $\varOmega _j$ are defined by

$$\begin{aligned} I[P^{(r)}] := \sum _{i=1}^r h^{2i-1} \int _{\varOmega _j} \left( \frac{\mathrm {d}^i}{\mathrm {d}x^i} P^{(r)}(x)\right) ^2 \mathrm {d}x. \end{aligned}$$

(8)

Then, in our case, they reduce to

$$\begin{aligned} \begin{aligned} I_{j,L} = (\overline{u}_j -\overline{u}_{j-1})^2, \quad I_{j,R} = (\overline{u}_{j+1} -\overline{u}_{j})^2, \quad I_{j,0} = b^2 h^2 + \frac{52}{3} c^2 h^4. \end{aligned} \end{aligned}$$

(9)

From these, the nonlinear weights are defined as

$$\begin{aligned} \tilde{\omega }_{j,k} = \frac{C_{k}}{(\epsilon _x+I_{j,k})^\tau }, \quad \omega _{j,k} = \frac{\tilde{\omega }_{j,k}}{\tilde{\omega }_{j,0}+\tilde{\omega }_{j,L}+\tilde{\omega }_{j,R}}, \quad k = 0,L,R. \end{aligned}$$

(10)

Following [11, 12, 31], we will always set $\epsilon _x=h^2$ and $\tau =2$. The reconstruction polynomial $P_{j,\text {rec}}$ is

$$\begin{aligned} P_{j,\text {rec}}(x) = \omega _{j,0} P_{j,0}(x) + \omega _{j,L} P_{j,L}^{(1)}(x) + \omega _{j,R} P_{j,R}^{(1)}(x). \end{aligned}$$

(11)

Note that if $\omega _{j,k}=C_k$, $k=0,L,R$, then the reconstructed polynomial $P_{j,\text {rec}}$ coincides with the optimal polynomial $P_j^{(2)}$, and the reconstruction is third order accurate in the whole cell.

If the nonlinear weights satisfy

$$\begin{aligned} C_k-\omega _{j,k}=\mathcal {O}(h), \end{aligned}$$

(12)

then $\mathsf {CWENO}$ boosts the accuracy of the reconstruction polynomial $P_{\textsf {rec}}$ to the highest possible accuracy, 3 in this case. This occurs when the stencil containing the data is smooth.

Once the reconstruction is known, we can compute the boundary extrapolated data as

$$\begin{aligned} u^-_{j+\nicefrac 12}= P_{j,\text {rec}}(x_{j+\nicefrac 12}), \qquad u^+_{j+\nicefrac 12}= P_{j+1,\text {rec}}(x_{j+\nicefrac 12}). \end{aligned}$$

(13)

In Quinpi methods, we suppose we are given a predictor p(x) alongside the solution u(x), where the predictor is at least a first-order approximation of the solution. We compute the smoothness indicators (8) using the predictor. Thus, the weights $\omega _{j,k}$ depend only on the predictor. In this fashion, the boundary extrapolated data (13) are linear functions of the solution u with coefficients that are not constant across the grid.

3.2 Time Approximation: Diagonally Implicit Runge-Kutta ($\mathsf {DIRK}$)

The space reconstruction algorithm allows to compute boundary extrapolated data of the solution u of the conservation law (1) at each cell interface. Next we pick a consistent and monotone numerical flux function $\mathcal {F}$. For example, in this work, we will apply the Lax Friedrichs numerical flux

$$\begin{aligned} \mathcal {F}(u^-,u^+) = \frac{1}{2} \left( f(u^{+}) + f(u^{-}) - \alpha (u^{+} - u^{-}) \right) \end{aligned}$$

(14)

with $\alpha = \max _u|f'(u)|$.

This completely defines the system of ODE’s (3). This system needs to be approximated in time by means of a time integration scheme. Here, we focus on $\mathsf {DIRK}$ methods, with s stages and general Butcher tableau

$$\begin{aligned} \begin{array}{c|cccc} c_1 &{} a_{11} &{} 0 &{} \dots &{} 0 \\ c_2 &{} a_{21} &{} a_{22} &{} \dots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} &{} \vdots \\ c_s &{} a_{s1} &{} a_{s2} &{} \dots &{} a_{ss} \\ \hline &{}&{}&{}&{}\\ &{} b_1 &{} b_2 &{} \dots &{} b_s \end{array} \end{aligned}$$

(15)

having the property $a_{k,\ell }=0$, for each $k<\ell$.

Discretization of (3) with a $\mathsf {DIRK}$ method leads to the fully discrete scheme

$$\begin{aligned} \overline{u}_j^{n+1} = \overline{u}_j^{n} - \frac{\Delta t}{h} \sum _{k=1}^s b_k \left[ \mathcal {F}_{j+\frac{1}{2}}^{(k)} - \mathcal {F}_{j-\frac{1}{2}}^{(k)} \right] , \quad n\geqslant 0, \ j=1,\cdots ,N, \end{aligned}$$

(16)

where we recall that h is the mesh spacing, $\Delta t$ is the time step, and $\overline{u}_j^n \approx \overline{u}_j(t^n)$. Finally, $\mathcal {F}_{j+\frac{1}{2}}^{(k)}=\mathcal {F}(u_{j+\frac{1}{2}}^{-,(k)},u_{j-\frac{1}{2}}^{+,(k)})$, where the boundary extrapolated data $u_{j+\frac{1}{2}}^{-,(k)}$, $u_{j-\frac{1}{2}}^{+,(k)}$, are reconstructions at the cell boundaries of the stage values

$$\begin{aligned} \overline{u}_j^{(k)} = \overline{u}_j^n - \frac{\Delta t}{h} \sum _{\ell =1}^{k} a_{k,\ell } \left[ \mathcal {F}_{j+\frac{1}{2}}^{(\ell )} - \mathcal {F}_{j-\frac{1}{2}}^{(\ell )} \right] , \quad k=1,\cdots ,s, \end{aligned}$$

(17)

which are approximations at times $t^{(k)} = t^n + c_k\Delta t$. We point out that $\mathcal {F}_{j+\frac{1}{2}}^{(k)}$ depends on the k-th stage value, and thus the computation of each stage is implicit but independent from the following ones.

The $\mathsf {DIRK}$ scheme used in this work is

$$\begin{aligned} \begin{array}{c|ccc} \lambda &{} \lambda &{} 0 &{} 0 \\ \frac{1+\lambda }{2} &{} \frac{1-\lambda }{2} &{} \lambda &{} 0 \\ 1 &{} -\frac{3}{2} \lambda ^2 + 4\lambda - \frac{1}{4} &{} \frac{3}{2}\lambda ^2-5\lambda +\frac{5}{4} &{} \lambda \\ \hline &{}&{}&{}\\ &{} -\frac{3}{2} \lambda ^2 + 4\lambda - \frac{1}{4} &{} \frac{3}{2}\lambda ^2-5\lambda +\frac{5}{4} &{} \lambda \end{array} \end{aligned}$$

(18)

with $\lambda =0.435\,866\,521\,5$, see [2].

The fully discrete set of Eqs. (16), (17) has two sources of nonlinearity when solved with high-order schemes: one arises from the physics of the system (1) when the flux function f is nonlinear, and cannot be avoided; the other one arises from the computation of the boundary extrapolated data using a high order $\mathsf {CWENO}$ or $\mathsf {WENO}$ reconstruction, which is nonlinear even for linear problems. Therefore, even for a linear PDE, the resolution of (16), (17) requires a nonlinear solver. Typically, one uses Newton’s algorithm, which requires the computation of the Jacobian of the scheme, which depends on the nonlinear weights (10) and on the oscillation indicators (8), (9), resulting in a prohibitive computational cost.

In the next subsection, we propose a way to circumvent the nonlinearity with a high-order reconstruction procedure relying on a predictor.

3.3 Third-Order Quinpi Approach

A prototype of an implicit scheme for $\mathsf {WENO}$ reconstructions based on a predictor was developed by Gottlieb et al. [23]. The method relies on the idea of a predictor-corrector approach to avoid the nonlinearity of the reconstruction. The solution of an explicit scheme is used as predictor to compute the nonlinear weights of $\mathsf {WENO}$ within the high-order implicit scheme, which is used as corrector.

In [23] the approximation with the explicit predictor is computed in a single time step, namely, without performing several steps within the whole time step. On the contrary, in the Quinpi approach, the nonlinearity arising from the nonlinear weights of $\mathsf {CWENO}$ is circumvented by computing an approximation of the solution at each intermediate time $t^{(k)} = t^n + c_k \Delta t$ with an implicit, but linear, low-order scheme, with which the nonlinear weights of $\mathsf {CWENO}$ are predicted at each stage.

Once the weights are known, a correction of order 3 is obtained by employing a $\mathsf {DIRK}$ method of order three coupled with the third-order $\mathsf {CWENO}$ space reconstruction, with the weights computed from the predictor.

In this way, the complete scheme is linear with respect to the space reconstruction. In this context, by linear we mean that, for a linear conservation law, the solution can be advanced by a time step solving a sequence of s narrow-banded linear systems. However, the scheme overall is nonlinear with respect to its initial data because the entries of the linear systems’ matrices depend nonlinearly on the predicted solution through (10) and (9). When f(u) is not linear, the systems become nonlinear but only through the flux function.

Clearly, an implicit predictor is more expensive to compute than the explicit predictor proposed in [23]. But using an implicit predictor has a double advantage. First, the predictor itself is stable, and this allows to have a reliable prediction of the weights, even for high Courant numbers. Second, at the end of the time step, the predictor itself is a reliable, stable and non-oscillatory low order solution, with which we will blend the high order solution to obtain the time limiting required by high order time integrators.

3.3.1 First-Order Predictor: Composite Implicit Euler

We solve (14),  (16), (17), within the time step $\Delta t$ using an s stages composite backward Euler scheme in time, where s is the number of stages in the $\mathsf {DIRK}$ scheme (15). In other words, we apply the backward Euler scheme s times in each time step. The k-th substep advances the solution from $t^n+\tilde{c}_{k-1} \Delta t$ to $t^n+\tilde{c}_{k} \Delta t$, with $\tilde{c}_0=0$, where the coefficients $\tilde{c}_k$, $k=1,\cdots ,s$, are the ordered abscissae of the $\mathsf {DIRK}$ (15). Overall, this is equivalent to implementing a $\mathsf {DIRK}$ scheme with Butcher tableau given by

$$\begin{aligned} \begin{array}{c|cccc} \tilde{c}_1 &{} \tilde{c}_1 &{} 0 &{} \dots &{} 0 \\ \tilde{c}_2 &{} \tilde{c}_1 &{} \tilde{c}_2-\tilde{c}_1 &{} \dots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} &{} \vdots \\ \tilde{c}_s &{} \tilde{c}_1 &{} \tilde{c}_2-\tilde{c}_1 &{} \dots &{} \tilde{c}_s-\tilde{c}_{s-1} \\ \hline &{}&{}&{}&{}\\ &{} \tilde{c}_1 &{} \tilde{c}_2-\tilde{c}_1 &{} \dots &{} \tilde{c}_s-\tilde{c}_{s-1} \end{array} \end{aligned}$$

(19)

In space, we use piecewise constant reconstructions from the cell averages. At the final stage, we thus obtain a first-order stable non-oscillatory approximation of the solution at the time step $t^{n+1}$, which we will call $u^{\mathsf {IE}, n+1}$. A similar low order composite backward Euler scheme is also employed in the third-order scheme of Arbogast et al. [3].

The resulting scheme also provides first-order approximations $\overline{u}_j^{\mathsf {IE},(k)}$ of the solution at the intermediate times $t^{(k)}=t^n + \tilde{c}_k \Delta t$, for $k=1,\cdots ,s$. At each stage therefore one needs to solve the nonlinear system

$$\begin{aligned} \begin{aligned} G_j(\overline{U}^{\mathsf {IE},(k)}) :=&\frac{\theta _k \Delta t}{h} \left[ \frac{1}{2} f(\overline{u}_{j+1}^{\mathsf {IE},(k)}) - \frac{1}{2} f(\overline{u}_{j-1}^{\mathsf {IE},(k)}) - \frac{\alpha }{2} \overline{u}_{j+1}^{\mathsf {IE},(k)} \right. \\&\left. + \left( \alpha + \frac{h}{\theta _k \Delta t} \right) \overline{u}_j^{\mathsf {IE},(k)} - \frac{\alpha }{2} \overline{u}_{j+1}^{\mathsf {IE},(k)} \right] - \overline{u}_j^{\mathsf {IE},(k-1)} = 0, \end{aligned} \end{aligned}$$

(20)

where $\theta _k:=\tilde{c}_{k}-\tilde{c}_{k-1}$, $\overline{U}^{\mathsf {IE},(k)}:=\{\overline{u}_j^{\mathsf {IE},(k)}\}_j$ and $\overline{u}_j^{\mathsf {IE},(0)}:=\overline{u}_j^{n}$. We use Newton’s method. Note that the system is nonlinear only through the flux function.

3.3.2 $\mathsf {CWENO}$ Third-Order Correction

Once the low order predictions $\overline{u}_j^{\mathsf {IE},(k)}$ are known at all times $t^{(k)} = t^n+\tilde{c}_k\Delta t$, we correct the accuracy of the solution by solving (14), (16), (17) using the third-order $\mathsf {DIRK}$ (18) in time and the third-order $\mathsf {CWENO}$ reconstruction in space, with the weights $\omega _j^{(k)}$ at the k-th stage computed through the predictor $\overline{u}_j^{\mathsf {IE},(k)}$. Thus the boundary extrapolated data will be given by

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{j+\frac{1}{2}}^{-,(k)}= P_{j,\text {rec}}(x_{j+\frac{1}{2}}) = \sum _{\ell =-1}^1 W_{j,\ell }^{-} \overline{u}_{j+\ell }^{(k)}, \\ u_{j+\frac{1}{2}}^{+,(k)}= P_{j+1,\text {rec}}(x_{j+\frac{1}{2}}) = \sum _{\ell =-1}^1 W_{j,\ell }^{+} \overline{u}_{j+1+\ell }^{(k)}, \end{array}\right. } \end{aligned}$$

(21)

where the weights $W_j^{\pm }$ depend only on $\overline{u}_j^{\mathsf {IE},(k)}$ and are constant with respect to $\overline{u}^k$. Finally, from (14), (16), (17), at each stage, we solve the system

$$\begin{aligned} G_j(\overline{U}^{(k)}):=&\overline{u}_j^{(k)}- \overline{u}_j^n \\&+ \frac{a_{k,k}\Delta t}{h} \left[ \mathcal {F}_{j+1/2}^{(k)}-\mathcal {F}_{j-1/2}^{(k)} \right] + \frac{\Delta t}{h} \sum _{\ell =1}^{k-1} a_{k,\ell } [\mathcal {F}_{j+1/2}^{(\ell )}-\mathcal {F}_{j-1/2}^{(\ell )}] = 0. \end{aligned}$$

We observe that the nonlinearity of $G_j$ is only due to the flux function, and not to the $\mathsf {CWENO}$ reconstruction, which uses the predictor $\overline{u}_j^{\mathsf {IE},(k)}$ to compute the nonlinear weights.

In the following, the numerical solution obtained applying the $\mathsf {DIRK}$3 scheme, with the third-order $\mathsf {CWENO}$ reconstruction exploiting the $u^\mathsf {IE}$ predictor will be called $\mathsf {D3P1}$ scheme.

3.3.3 Nonlinear Blending in Time

The solution $u^{\mathsf {D3P1}}$ obtained with the $\mathsf {D3P1}$ scheme is third-order accurate, and has control over spurious oscillations, thanks to the limited space reconstruction described above. However, this solution may still exhibit oscillations, because it is not limited in time. We discuss in this section the definition of the time-limited solution.

It is easy to associate a continuous extension (CE) to a Runge-Kutta scheme. For example, when the abscissae $c_k$, $k=1,\cdots ,s$, are distinct, following [35] one can construct a polynomial P(t) such that $P(t^n)=u^n$ and $P^\prime (t^n+c_k\Delta t)=K_k$, where the $K_k$’s are the RK fluxes of the Runge-Kutta scheme and $u^n$ is the solution at time $t^n$. The polynomial P(t) is such that $P(t^n+\Delta t)=u^{n+1}$ and it provides a way to interpolate the numerical solution at any point $t^n+\gamma \Delta t$ for $\gamma \in (0,1)$. If, for a particular Runge-Kutta scheme, a natural continuous extension in the sense of [42] exists, one could use that, but for this work we do not require the extensions to be natural, since we use them only as a device to assess the smoothness of the solution in the time step.

In our case, the CE of the $\mathsf {DIRK}$3 scheme we are using defines a polynomial extension of degree 3 in the sense of [35], which will be called $P^{(3)}_t$. Instead, we name $P^{(1)}_t$ the polynomial extension underlying the composite implicit Euler (19).

We define the limited in time solution $u^B(t)$ in a $\mathsf {CWENO}$ fashion as

$$\begin{aligned} u^{B}_j(t)=\frac{\omega _j^{H,n}}{C_H} \left( P^{(3)}_t(t)-C_L P^{(1)}_t(t)\right) +\omega _j^{L,n}P^{(1)}_t(t), \quad t\in [t^n,t^{n+1}] \end{aligned}$$

(22)

with $\omega _j^{H,n}+\omega _j^{L,n}=1$. In this and in all subsequent equations, H and L stand for high and low order quantities, respectively. The coefficients $C_L$ and $C_H$ are such that $C_L, C_H\in (0,1)$ with $C_L+C_H=1$. We observe that, by a property of the CE polynomials, at time $t^{n+1}$ we have

$$\begin{aligned} u^{B,n+1}_j=\frac{\omega _j^{H,n}}{C_H} \left( u_j^{\mathsf {D3P1},n+1}-C_Lu_j^{\mathsf {IE},n+1}\right) +\omega _j^{L,n}u_j^{\mathsf {IE},n+1}. \end{aligned}$$

(23)

Equation (23) describes a nonlinear blending between the low order solution $u^{\mathsf {IE}}$ and the high order solution $u^{\mathsf {D3P1}}$ at time $t^{n+1}$. We notice that if $\omega _j^{H,n}=C_H$, and consequently $\omega _j^{L,n}=C_L$, then $u^{B,n+1}_j=u_j^{\mathsf {D3P1},n+1}$ and the blending selects the solution of the high order scheme. Instead, if $\omega _j^{L,n}=1$, $u^{B,n+1}_j=u_j^{\mathsf {IE},n+1}$ and the blending selects the solution of the low order scheme.

The weights $\omega ^L$ and $\omega ^H$ must be thus designed in order to privilege the high order solution when it is not oscillatory, and the low order solution otherwise. In the following we discuss their definition, which is also carried out as in $\mathsf {CWENO}$ and relies on suitable regularity indicators. In fact, we define

$$\begin{aligned} \omega _j^{\ell ,n}=\frac{\tilde{\omega }_j^{\ell ,n}}{\tilde{\omega }_j^{L,n} +\tilde{\omega }_j^{H,n}}, \quad \ell =L,H, \end{aligned}$$

(24)

where

$$\begin{aligned} \tilde{\omega }_j^{L,n}= \frac{C_L}{\epsilon _t^2} \end{aligned}$$

(25)

is the constant weight associated to the first-order non-oscillatory solution $u^\mathsf {IE}$ in the time interval $[t^n,t^{n+1}]$, and

$$\begin{aligned} \tilde{\omega }_j^{H,n}= \frac{C_H}{(\epsilon _t + I_j^3)^2} \end{aligned}$$

(26)

is the weight associated to the $\mathsf {D3P1}$ approximation in the j-th cell in the time interval $[t^n,t^{n+1}]$. Here, $\epsilon _t=\Delta t^\tau$, and we always take $\tau =2$ if not otherwise stated. The $I_j^3$ is a smoothness indicator  that measures the regularity of the $\mathsf {D3P1}$ solution. We define $I_j^3$ as the contribution of two terms

$$\begin{aligned} I_j^3= I_j^t + I_j^{x,-} + I_j^{x,+}, \end{aligned}$$

(27)

where $I_j^t$ and $I_j^{x,\pm }$ are smoothness indicators designed in order to detect discontinuity in time and space, respectively, over the cell j. The definition of $I_j^t$ relies on the CE polynomial $P_t^{(3)}$. In fact, at each cell, the CE polynomial changes, and we will have different CE’s, and each CE will provide local information on the smoothness of the $\mathsf {DIRK}$ advancement in time. We measure the regularity of $P_t^{(3)}$ by the Jiang-Shu smoothness indicator, namely

$$\begin{aligned} I_j^t= \sum _{\ell =1}^3 (\Delta t)^{2\ell -1}\int _{t^n}^{t^{n+1}} \left( \frac{\mathrm {d}^\ell }{\mathrm {d}t^\ell } P^{(3)}_t(t)\right) ^2 \mathrm {d}t. \end{aligned}$$

Instead, the definition of $I_j^{x,\pm }$ draws inspiration from [3], and for the $\mathsf {DIRK3}$ method (18) we have

$$\begin{aligned} I_j^{x,+}&= (\overline{u}_{j+1}^{\mathsf {D3P1},n}-\overline{u}_{j}^{\mathsf {D3P1},n})^2 + \sum _{k=1}^2 (\overline{u}_{j+1}^{\mathsf {D3P1},(k)}-\overline{u}_{j}^{\mathsf {D3P1},(k)})^2 + (\overline{u}_{j+1}^{\mathsf {D3P1},n+1}-\overline{u}_{j}^{\mathsf {D3P1},n+1})^{2}, \\ I_j^{x,-}&= (\overline{u}_{j-1}^{\mathsf {D3P1},n}-\overline{u}_{j}^{\mathsf {D3P1},n})^2 + \sum _{k=1}^2 (\overline{u}_{j-1}^{\mathsf {D3P1},(k)}-\overline{u}_{j}^{\mathsf {D3P1},(k)})^2 + (\overline{u}_{j-1}^{\mathsf {D3P1},n+1}-\overline{u}_{j}^{\mathsf {D3P1},n+1})^2 \end{aligned}$$

with $\overline{u}_{j}^{\mathsf {D3P1},(k)}$ being the approximation at the k-th stage.

Finally, we point out that the coefficients $C_L$ and $C_H$ must be carefully chosen. In fact, since the time-limited solution (22) blends a first-order accurate solution with a third-order accurate one, according to [38] we must choose $C_L=\Delta t^2$ in order to obtain a third-order time limited solution.

3.3.4 Conservative Correction

The two solutions $u^{\mathsf {IE}}$ and $u^{\mathsf {D3P1}}$ are obtained with conservative schemes, and thus conserve mass. However, the blending (23) itself is not conservative, because it occurs at the cell level, instead of at interfaces.

It is possible therefore that at the $j+\nicefrac 12$ interface a mass loss (or gain) is observed. More precisely, the low order predictor can be written as

$$\begin{aligned} u^{\mathsf {IE},n+1}_j=\overline{u}_j^n-\frac{\Delta t}{h}\left( \mathcal {F}_{j+1/2}^{\mathsf {IE}}-\mathcal {F}_{j-1/2}^{\mathsf {IE}} \right) , \end{aligned}$$

(28)

while the high order corrector is

$$\begin{aligned} u^{\mathsf {D3P1},n+1}_j=\overline{u}_j^n-\frac{\Delta t}{h}\left( \mathcal {F}_{j+1/2}^{\mathsf {D3P1}}-\mathcal {F}_{j-1/2}^{\mathsf {D3P1}} \right) . \end{aligned}$$

(29)

The blended solution therefore is

$$\begin{aligned} u^{B,n+1}_j=\overline{u}_j^n-\frac{\Delta t}{h}\left[ \frac{\omega _j^{H,n}}{C_H}\Delta \mathcal {F}_{j}^{\mathsf {D3P1}}+ \left( \omega _j^L- \frac{C_L}{C_H}\omega _j^H\right) \Delta \mathcal {F}_{j}^{\mathsf {IE}} \right] . \end{aligned}$$

(30)

Since the blending is cell-centered, while the fluxes are based on the interfaces, we expect that through the $j+\nicefrac 12$ interface there will be a mass loss (or gain) given by

$$\begin{aligned} \mu _{j+\nicefrac 12}^{n+1}= \frac{\Delta t}{C_Hh} \left( (\omega _j^{H,n}-\omega _{j+1}^{H,n})\mathcal {F}_{j+1/2}^{\mathsf {D3P1}} + \left( C_H(\omega _j^{L,n}-\omega _{j+1}^{L,n}) - C_L (\omega _j^{H,n}-\omega _{j+1}^{H,n})\right) \mathcal {F}_{j+1/2}^{\mathsf {IE}} \right) . \end{aligned}$$

(31)

Thus we redistribute the mass lost through the $j+1/2$ interface among the j-th and $(j+1)$-th cell, obtaining the limited in time, limited in space Quinpi3 solution, which will be called $\mathsf {Q3P1}$ solution. The redistribution is done proportionally to the high order nonlinear weight, so that

$$\begin{aligned} u_j^{\mathsf {Q3P1},n+1}=u_j^{B,n+1}+\frac{\omega _j^H}{\omega _j^H+\omega _{j+1}^H} \mu _{j+\nicefrac 12} + \frac{\omega _{j}^H}{\omega _j^H+\omega _{j-1}^H} \mu _{j-\nicefrac 12}. \end{aligned}$$

(32)

This is the updated solution at time $t^{n+1}$. The resulting scheme is conservative with numerical flux

$$\begin{aligned} \mathcal {F}_{j+1/2}^{\mathsf {Q3P1}} =&\frac{1}{C_H}\frac{2\omega _j^{H}\omega _{j+1}^{H}}{\omega _j^{H}+\omega _{j+1}^{H}} \mathcal {F}_{j+1/2}^{\mathsf {D3P1}} \\&+ \frac{1}{C_H} \left( C_H \frac{\omega _j^L\omega _{j+1}^H+\omega _j^H\omega _{j+1}^L}{\omega _j^H+\omega _{j+1}^H} - C_L\frac{2\omega _j^H\omega _{j+1}^H}{\omega _j^H+\omega _{j+1}^H}\right) \mathcal {F}_{j+1/2}^{\mathsf {IE}} . \end{aligned}$$

Introducing the “reduced mass” of the high order weights

$$\begin{aligned} \tilde{\omega }^H_{j+\nicefrac 12} = \frac{2\omega _j^{H}\omega _{j+1}^{H}}{\omega _j^{H}+\omega _{j+1}^{H}}, \end{aligned}$$

we can rewrite the conservative flux as

$$\begin{aligned} \mathcal {F}_{j+1/2}^{\mathsf {Q3P1}} =&\frac{\tilde{\omega }^H_{j+\nicefrac 12}}{C_H} \left[ \mathcal {F}_{j+1/2}^{\mathsf {D3P1}} + \left( \frac{C_H}{2}\left( \frac{\omega _j^L}{\omega _j^H}+ \frac{\omega _{j+1}^L}{\omega _{j+1}^H}\right) -C_L\right) \mathcal {F}_{j+1/2}^{\mathsf {IE}} \right] . \end{aligned}$$

From the formula, it is apparent that the high order flux of the interface contributes significantly to the time-limited flux only when the cells on both sides are detected as smooth. Moreover, it is also clear that $C_L$ must be infinitesimal.

In [5] an analogous conservative correction is employed to ensure the conservation property at interfaces between grid patches in an adaptive mesh refinement (AMR) algorithm. Other approaches are possible, in particular we refer to [30] which avoids a cell-centered blending by means of flux-based Runge-Kutta. Similar techniques are used in [3].

4 Numerical Simulations

The purpose of the tests appearing in this section is to study the accuracy of the Quinpi scheme proposed in this work, and to verify their smaller dissipation compared to the first-order predictor $\mathsf {IE}$ and their improved non-oscillatory properties compared to the non-limited in time corrector $\mathsf {D3P1}$. Thus we will consider the standard tests which are commonly used in the literature on high order methods for conservation laws: linear advection of non-smooth waves, shock formation and interaction in Burgers’ equation and the Buckley-Leverett non-convex equation. Furthermore, on one of the tests with singularities, see Fig. 7, we also demonstrate the need of the conservative correction discussed in the previous section.

As mentioned in the description of the scheme, when solving nonlinear conservation laws the solution of nonlinear systems is required both for the prediction and the correction steps. To this end, we employ Newton’s method. The initial guess to start the iteration leading to $\overline{u}^{\mathsf {IE},(k)}$ is chosen as $\overline{u}^{\mathsf {IE},(k-1)}$, $k=2,3$. For the first stage, $k=1$, we use the high order solution emerging from the previous time step. The initial guess to compute the stages $\overline{u}^{(k)}$ of the corrector is the corresponding values $\overline{u}^{\mathsf {IE},(k)}$ of the predictor, for each $k=1,2,3$. The stopping criteria are based on the relative error between two successive approximations and on the norm of the residual. We use a given tolerance $\Delta t^3$, according to the global error of the scheme.

4.1 Convergence Test

We test the numerical convergence rate of the third-order Quinpi introduced in Sect. 3 on the nonlinear Burgers’ equation

$$\begin{aligned} u_t + \left( \frac{u}{2} \right) ^2_x = 0 \end{aligned}$$

(33)

with the initial condition

$$\begin{aligned} u_0(x) = 0.5 - 0.25\sin (\uppi x) \end{aligned}$$

(34)

on $\varOmega = [0,2]$ with the periodic domain, and up to the final time $t=1$, i.e., before the shock appears. The numerical errors, in both $L^1$ and $L^\infty$ norms, and convergence rates are showed in Table 1 for different CFL numbers.

Table 1 Orders of convergence of the Quinpi scheme $\mathsf {Q3P1}$

In the nonlinear blending in time between the low-order solution, i.e., the composite implicit Euler ($\mathsf {IE}$), and the high-order solution, i.e., $\mathsf {D3P1}$, we use $C_{L} = \Delta t^2$ and $C_{H} = 1-\Delta t^2$ as linear weights. We observe third-order convergence in both norms. In particular, we point out that with large CFL numbers our method reaches smaller errors and faster convergence with respect to the results in [3] for the same grid.

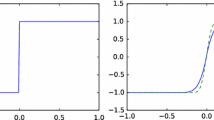
On the same smooth problem, we also test the convergence rate of the low-order predictor $\mathsf {IE}$ and the high-order corrector $\mathsf {D3P1}$, separately. The convergence tests are shown in Fig. 1. Clearly, with $\mathsf {IE}$ we observe first-order accuracy. Instead, $\mathsf {D3P1}$ achieves the optimal third-order accuracy, as expected.

Fig. 1

Convergence test of the predictor scheme $\mathsf {IE}$, left panel, and of the corrector scheme $\mathsf {D3P1}$, right panel, for different CFL numbers

4.2 Linear Transport

We consider the linear scalar conservation law

$$\begin{aligned} u_t+u_x=0 \end{aligned}$$

(35)

on the periodic domain in space $\varOmega =[-1,1]$, and evolve the initial profile $u_0(x)$ for one period, i.e., up to the final time $t=2$. As the initial condition we consider the non-smooth profiles

$$\begin{aligned} u_0(x) = \sin (\uppi x) + {\left\{ \begin{array}{ll} 3, &{} -0.4 \leqslant x \leqslant 0.4,\\ 0, &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$

(36a)

$$\begin{aligned} u_0(x) = {\left\{ \begin{array}{ll} 1, &{} -0.25 \leqslant x \leqslant 0.25,\\ 0, &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(36b)

This problem is used to investigate the properties of a scheme to transport non-smooth data with minimal dissipation, dispersion and oscillation effects.

Fig. 2

Linear transport equation (35) with the initial condition (36a) on 400 cells at time $t=2$. The markers are used to distinguish the schemes, and are drawn one out of 10 cells

Figure 2 shows the numerical solutions of the linear transport problem with the initial profile (36a) computed with the predictor $\mathsf {IE}$ and with the corrector methods with no time limiting, i.e., $\mathsf {D3P1}$  and with blending in time, i.e., $\mathsf {Q3P1}$. We consider two different CFL numbers. All the solutions are computed on a grid of 400 cells. We observe that the low-order predictor is very diffusive, whereas the corrector $\mathsf {D3P1}$ is oscillating across the discontinuities, in particular with CFL number 5. The corrector $\mathsf {Q3P1}$  obtained after nonlinear blending of the $\mathsf {IE}$ and $\mathsf {D3P1}$ solutions, is much less diffusive than $\mathsf {IE}$ and does not produce spurious oscillations, even with large CFL number.

Fig. 3

Linear transport equation (35) with the initial condition (36b) with $\Delta t=5h$ at time $t=2$. The solutions in the left panel are computed on 400 cells. The right panel shows the solutions obtained with the $\mathsf {Q3P1}$ method on different grids. The markers are used to distinguish the schemes, and are drawn one out of 10 cells on the left and 15 cells on the right

In Fig. 3 we provide the numerical solutions of the linear transport problem with the initial double-step profile (36b) with a zoom on the top part of the non-smooth region of the solution. The simulations are performed with $\Delta t= 5h$. In the left panel, we compare the three methods on a grid of 400 cells. We observe that the novel method $\mathsf {Q3P1}$ introduced in this work presents less oscillations than $\mathsf {D3P1}$ close to discontinuities, and it is less dissipative than $\mathsf {IE}$. The right panel shows the approximation provided by $\mathsf {Q3P1}$ on different grids. As we expect, on finer grids the frequency of the oscillations increases, whereas the amplitude slightly decreases.

4.3 Burgers’ Equation

We investigate the behavior of the schemes on the nonlinear Burgers’ equation (33) for different initial conditions.

4.3.1 Smooth Profile: Shock Formation

As in [3], we consider the smooth initial condition (34) on the periodic domain $\varOmega =[0,2]$, and up to the final time $t=2$, i.e., after shock formation.

Fig. 4

Burgers’ equation (33) with the initial condition (34) on $N=256$ cells at time $t=2$. The markers are used to distinguish the schemes, and are drawn each 5 cells

The results in Fig. 4 are obtained with 256 cells with two values of the CFL number. In both cases the $\mathsf {Q3P1}$ scheme is slightly more diffusive than its non-blended version $\mathsf {D3P1}$, and exhibits a much lower dissipation than the first-order predictor $\mathsf {IE}$. For $\Delta t = 3h$, all schemes do not produce large oscillations near the discontinuity, and the solutions of $\mathsf {Q3P1}$ and $\mathsf {D3P1}$ are very close. We appreciate the difference when $\Delta t = 5h$. In fact, the $\mathsf {Q3P1}$ scheme reduces the oscillations created by $\mathsf {D3P1}$, while maintaining a very high resolution.

Fig. 5

Numerical solution of the Burgers’ equation (33) with initial condition (34) on $N=256$ cells at time $t=2$ obtained with the space-time non-limited scheme

On this test, we show also the numerical approximation provided by the space-time non-limited scheme, cf. Fig. 5. The setup of the simulation is as in Fig. 4, i.e., we consider 256 cells with CFL numbers 3 and 5. Compared to Fig. 4, we observe the importance of the limiting technique to avoid the very large spurious oscillations appearing also at moderate CFL numbers.

4.3.2 Non-smooth Profile

We test the Burgers’ equation on the discontinuous initial condition (36b), on the periodic domain $\varOmega =[-1,1]$, and up to the final time $t=0.5$.

Fig. 6

Burgers’ equation (33) with the initial condition (36b) on 400 cells at time $t=0.5$. The markers are used to distinguish the schemes, and are drawn every 8 cells

The numerical solutions are shown in Fig. 6 with 400 cells, with $\Delta t=3h$ and $\Delta t=5h$. The nonlinear Burgers’ equation develops a rarefaction and a moving shock. Again, we observe the ability of the new implicit scheme $\mathsf {Q3P1}$ of increasing the accuracy on smooth zones compared to $\mathsf {IE}$, and, at the same time, reducing the spurious oscillations across the shock.

Fig. 7

Right plot: numerical solutions of $\mathsf {Q3P1}$, with and without conservative correction, on the Burgers’ equation (33) with the initial condition (36b) using 400 cells at time $t=5$ and with $\Delta t=5h$. The markers are used to distinguish the schemes, and are drawn every 8 cells. Left plot: deviation in time of the total mass of the numerical solution from the exact total mass

On this particular test, we provide a numerical evidence of the need and of the effectiveness of the conservative correction introduced after the nonlinear blending in time between the predictor scheme $\mathsf {IE}$ and the third-order corrector $\mathsf {D3P1}$. In the right panel of Fig. 7 we show the solutions provided by the Quinpi scheme $\mathsf {Q3P1}$ with and without the conservative correction, using 400 cells and $\Delta t=5h$. Instead, in the left panel of Fig. 7 we show the behavior in time of the deviation of the mass of the numerical solution from the mass of the initial condition. We observe that, without correction, the $\mathsf {Q3P1}$ scheme does not capture the correct shock location because of the mass lost. The conservative correction allows to predict the shock at the correct location and the mass is conserved at all time.

Fig. 8

Numerical solution of Burgers’ equation (33) with the initial condition (36b) on 400 cells with $\Delta t=5h$. The solution is limited according to the weights computed with an explicit first-order predictor, unlike the Quinpi approach which is characterized by implicit predictors

Finally, in Fig. 8 we show the numerical approximations obtained limiting the third-order scheme with an explicit first-order predictor as in  [23], on a grid of 400 cells with $\Delta t=5h$. The solutions are shown at two different times, and we observe that the use of an explicit predictor is not enough to prevent spurious oscillations in the high order scheme, at relatively high CFL numbers. At this CFL, the explicit predictor is already unstable, and thus the information it would provide on where to limit the solution is not reliable.

4.3.3 Shock Interaction

We consider Burgers’ equation with smooth initial condition

$$\begin{aligned} u_0(x) = 0.2 -\sin (\uppi x) + \sin (2 \uppi x) \end{aligned}$$

(37)

on the periodic domain $\varOmega =[-1,1]$, and with $\Delta t = 5h$. This test allows to compare the behavior of the schemes on both shock formation and shock interaction. In fact, the exact solution is characterized by the formation of two shocks which collide at a larger time, developing a single discontinuity.

Fig. 9

Burgers’ equation (33) with the initial condition (37) on 256 cells with $\Delta t=5h$ at three different times. The markers are used to distinguish the schemes, and are drawn each 10 cells

In Fig. 9 we show the numerical solutions at three snapshots: at $t=\frac{1}{2\uppi }$, when the two shocks occur, at $t=0.6$, which is slightly before the interaction of the two shocks, and finally at $t=1$, shortly after the shock interaction. It is clear that $\mathsf {Q3P1}$ does not produce spurious oscillations, and its profile has a higher resolution with respect to $\mathsf {IE}$.

4.4 Buckley-Leverett Equation

We also show results on a non-convex problem, such as the Buckley-Leverett equation

$$\begin{aligned} u_t + \left( \frac{u^2}{u^2+\frac{1}{3}(1-u)^2} \right) _x = 0, \end{aligned}$$

(38)

which is characterized by a non-convex flux function. We consider the same setup as in [3]. Therefore, the initial profile is the step function

$$\begin{aligned} u_0(x) = {\left\{ \begin{array}{ll} 0.5, &{} -0.25 \leqslant x \leqslant 0.25,\\ 0, &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(39)

on the periodic domain $\varOmega =[0,1]$, and up to the final time $t=0.085$.

Fig. 10

Buckley-Leverett equation (38) with the initial condition (39) on 100 cells at time $t=0.085$

In Fig. 10 we show the results on a grid of 100 cells with $\Delta t = 1.1h$ and $\Delta t = 4.4h$. For this particular example, we set $\epsilon _t=\Delta t^3$ in the nonlinear blending in time. The results produced by the three schemes are very similar when the CFL is small. With large CFL, instead, we observe that $\mathsf {Q3P1}$ improves $\mathsf {D3P1}$ avoiding the spurious overshoots. However, we note that on this particular test the $\mathsf {Q3P1}$ and $\mathsf {IE}$ solutions almost coincide, in fact, the $\mathsf {IE}$ profile is hidden by $\mathsf {Q3P1}$. Here the time limiting is dominating, probably because of the structure of the initial data.

4.5 Computational Complexity

The implicit method proposed in this paper is clearly more expensive compared to a corresponding explicit scheme, for a fixed number of time steps. But the benefit of an implicit scheme is to permit to use a larger CFL number, and thus a smaller number of time steps. This may result in more efficient computations for stiff problems.

When integrating a system of hyperbolic equations with a numerical scheme, one chooses the time step as

$$\begin{aligned} \Delta t = \min \left( \Delta t_{\mathrm {acc}}, \Delta t_{\mathrm{stab}}\right) , \end{aligned}$$

where $\Delta t_{\mathrm{acc}}$ is fixed by accuracy constraints, and $\Delta t_{\mathrm{stab}}$ is due to the CFL stability condition with

$$\begin{aligned} \Delta t_{\mathrm{stab}} \leqslant c\frac{ h}{||f'(u)||_S}, \end{aligned}$$

where $||f'(u)||_S$ is the spectral norm of the Jacobian of the flux. When $||f'(u)||_S \gg 1$, the stability constraint is more demanding than accuracy, and implicit schemes may become convenient.

On scalar conservation laws, $\Delta t_{\mathrm{acc}}$ and $\Delta t_{\mathrm{stab}}$ have the same size, because there is only one propagation speed. Implicit integrators become of interest when there are fast waves one is not interested in, which however determine $\Delta t_{\mathrm{stab}}$, while the phenomena one would like to resolve accurately are linked to slow waves, which then determine $\Delta t_{\mathrm{acc}}$. In this case one is willing to tolerate a deterioration of the error on the fast waves, preserving accuracy on the slow waves. This is the case for instance for many solvers for low Mach or low Froude flows.

In a scalar problem, this improvement is not apparent. However, we can estimate the computational cost for a single time step of the explicit third-order SSP Runge-Kutta scheme and of the $\mathsf {Q3P1}$ scheme. The ratio between these two costs will tell as at what CFL the implicit scheme becomes competitive.

In Table 2 we report the results obtained on the linear equation on $[-1,1]$ and on Burgers’ equation on [0, 2] with the initial condition (37). The results are obtained on a quadcore Intel Core i7-6600U with clock speed 2.60 GHz.

Table 2 CPU time for each step of the SSP-RK3 explicit scheme and of the $\mathsf {Q3P1}$ implicit scheme on linear and nonlinear problems

As expected, a step of the implicit scheme is more expensive than a step of the explicit one. But several things can be noted. First of all, we expect that the implicit scheme should be faster on linear problems. In this case, in fact, no Newton iteration is needed, thanks to the linearity of the predictor. This is confirmed by our data. Moreover, both the explicit and the implicit schemes should have a computational cost scaling as N, and this is true for $\mathsf {Q3P1}$. Apparently the computational cost scales more favorably for the explicit scheme, but this can be due to more efficient memory operations whose analysis goes beyond the purpose of this work.

The complexity of the implicit scheme increases on a nonlinear problem. In fact, the $\mathsf {Q3P1}$ scheme requires approximately six Newton’s iterations each time step. However, the number of iterations remains bounded, and, most important, it does not depend on N. The computational cost increases slightly for the non-smooth problem: in this case, in fact, the initial guess of the first Newton’s method is given by the solution obtained at the previous time step, which may not be accurate in the presence of shocks.

In any case, it is clear that the $\mathsf {Q3P1}$ scheme becomes faster for CFL numbers larger than 5 or 6 in the nonlinear case, and even before in the linear case. Since stiff problems, such as low Mach, can have CFLs of order hundreads and even more, it is to be expected that the implicit scheme can be convenient in many applications.

In Fig. 11 we show the total number of iterations required for Newton’s method in each time step as a function of time in solving Burgers’ equation with the smooth (37) and non-smooth (36b) initial profiles up to $t=0.5$ and with three different Courant numbers. We recall that a nonlinear system must be solved at each predictor step, and at each Runge Kutta stage. Thus a total of 6 nonlinear systems of algebraic equations must be solved at each time step of a third-order scheme.

The top panels of Fig. 11 are obtained with 400 cells, whereas the bottom panels are with 800 cells.

Fig. 11

Total number of iterations in each time step required for the convergence of Newton’s method when solving Burgers’ equation up to $t=0.5$, with the initial condition (37) (blue lines) and (36b) (red lines). Three different values of the Courant number are considered

For the smooth initial condition, we observe that the number of iterations is not larger than 2 for each Newton’s application as long as the solution remains smooth. Instead, the number of iterations slightly increases when the solution becomes discontinuous. In fact, each Newton’s method is converging with maximum 3 iterations. For the double-step initial condition, the number of iterations is larger, but no more than 3 iterations are needed on average for each Newton’s solution.

But the most important point is that the number of iterations of Newton’s method is independent of the number of cells and of the CFL. Thus the implicit method becomes more and more convenient as the stiffness of the method increases.

5 Conclusions

In this work, we have proposed a new approach to the integration of hyperbolic conservation laws with high order implicit schemes. The main characteristic of this framework is to use low order implicit predictors with a double purpose. First, the predictor is used to determine the nonlinear weights in a $\mathsf {CWENO}$ or $\mathsf {WENO}$ high order space reconstruction. In this fashion, one greatly simplifies the differentiation of the $\mathsf {WENO}$ weights when computing the Jacobian of the numerical fluxes. Second, the predictor is used as low order approximation of the solution and is blended with the high order solution to achieve limiting also in time.

The resulting scheme is linear with respect to the solution at the new time level on linear equations, unlike most, if not all, high order implicit schemes available. The non-linearity of the scheme is linked only to the nonlinearity of the flux. This does not mean that the coefficients appearing in the scheme are constant. It means that the nonlinearities in the limiting in space and time of the scheme involve only the predictor, which is already known when the high order solution is evolved in time.

We expect the new scheme to have applications in many stiff problems, as low Mach gas dynamics or kinetic problems. In these cases, one is not interested in the accuracy of the fast waves which determine the stiffness of the system, but would like to use a time step tailored to preserve the accuracy of the slow material waves.

Future work will involve the application of the Quinpi approach to stiff gas dynamics, the exploration of this new framework with BDF time integration, and extensions to a higher order.