Preventing Pressure Oscillations Does Not Fix Local Linear Stability Issues of Entropy-Based Split-Form High-Order Schemes

Abstract

Recently, it was discovered that the entropy-conserving/dissipative high-order split-form discontinuous Galerkin discretizations have robustness issues when trying to solve the simple density wave propagation example for the compressible Euler equations. The issue is related to missing local linear stability, i.e., the stability of the discretization towards perturbations added to a stable base flow. This is strongly related to an anti-diffusion mechanism, that is inherent in entropy-conserving two-point fluxes, which are a key ingredient for the high-order discontinuous Galerkin extension. In this paper, we investigate if pressure equilibrium preservation is a remedy to these recently found local linear stability issues of entropy-conservative/dissipative high-order split-form discontinuous Galerkin methods for the compressible Euler equations. Pressure equilibrium preservation describes the property of a discretization to keep pressure and velocity constant for pure density wave propagation. We present the full theoretical derivation, analysis, and show corresponding numerical results to underline our findings. In addition, we characterize numerical fluxes for the Euler equations that are entropy-conservative, kinetic-energy-preserving, pressure-equilibrium-preserving, and have a density flux that does not depend on the pressure. The source code to reproduce all numerical experiments presented in this article is available online (https://doi.org/10.5281/zenodo.4054366).

Introduction

In recent years, discontinuous Galerkin (DG) spectral collocation methods with summation-by-parts (SBP) property have gained a lot of traction in the high-order community [4, 5, 11, 30, 31, 45,46,47], due to the possibility to construct entropy-conservative/dissipative [7, 10, 27, 32, 50, 51] and/or kinetic-energy-preserving (KEP) [22, 26, 33, 34] discretizations. Such discretizations are currently successful, as they provide strongly increased robustness for the approximation of highly non-linear problems [14, 24, 41], in some cases even outperform DG discretization with polynomial de-aliasing [53]. A key building block in these novel high-order collocation discretizations is a special two-point flux formulation of the volume terms introduced by LeFloch et al. for central finite differences in periodic domains [27], Fisher et al.  for SBP finite differences in bounded domains [10], and by Carpenter et al.  for discontinuous spectral collocation schemes [2, 3].

Unsurprisingly, the choice of (symmetric) two-point flux function used in the novel volume term formulation is a key ingredient and determines the properties of the resulting high-order discretization. It is a somewhat surprising result that properties of the two-point fluxes used in simple low-order finite volume formulations directly translate to the high-order volume integral terms in this formulation. When using an entropy-conserving (EC) two-point finite volume flux, the corresponding two-point flux volume integral term of the DG scheme is EC as well [10, 27]. The same is for instance true for kinetic energy preservation [14, 33]; as we will show in this paper, it also holds for pressure equilibrium preservation. We note that the simple arithmetic mean two-point flux function recovers exactly the original nodal DG operator, while other choices of two-point flux functions may result in non-linear split-form DG operators, even for linear advection problems.

Unfortunately, it was recently discovered that the novel EC/dissipative (and many other split-form) DG schemes can have stability issues [13]. While the DG discretization is equipped with a provably discrete entropy inequality, it turns out that the schemes might struggle to retain local linear stability, i.e., the linear stability of the non-linear operator when linearized around a base-flow. Investigations of the spectrum of the linearized high-order operators revealed modes with spurious exponential growth, attributed to anti-diffusion of EC two-point fluxes. A particular striking example is given in [13] for the compressible Euler equations with a simple density wave

$$\begin{aligned} \begin{pmatrix} \rho (x,t) \\ v(x,t) \\ p(x,t) \end{pmatrix} = \begin{pmatrix} 1 + 0.98 \sin (2\,\uppi \,(x-v\,t))\\ 0.1\\ 20 \end{pmatrix}, \end{aligned}$$

(1)

where the density $\rho$ is variable, but the velocity v and pressure p are constant. Such a density wave (1) is a simple and smooth exact solution to the compressible Euler equations with perfect gas law, when equipped with appropriate (e.g.,  periodic) boundary conditions. Surprisingly, the EC/dissipative DG schemes and other split-form variants fundamentally struggle for this simple problem. It turns out that the linearized spectrum shows spurious modes with exponential growth, that may cause fatal crashing of the simulation.

In another recent paper, Shima et al.  [44] investigated the capability of their KEP two-point flux to retain what they call pressure equilibrium. Consider the compressible Euler equations with an ideal gas law,

$$\begin{aligned} \partial _t \underbrace{\begin{pmatrix} \rho \\ \rho v \\ \rho e \end{pmatrix}}_{= u} + \partial _x \underbrace{\begin{pmatrix} \rho v \\ \rho v^2 + p \\ (\rho e + p) v \end{pmatrix}}_{= f(u)} = 0, \end{aligned}$$

(2)

where $\rho e$ is the total energy, $\rho \varepsilon$ the internal energy, $\rho v^2 / 2$ the kinetic energy, and

$$\begin{aligned} p = (\gamma - 1) \rho \varepsilon , \quad \rho \varepsilon = \rho e - \frac{1}{2} \rho v^2. \end{aligned}$$

(3)

Pressure equilibrium is precisely the case, when the velocity v and the pressure p are both constant, e.g., the density-wave (1). We get from the evolution of the compressible Euler equations the evolution equations of the velocity

$$\begin{aligned} \rho \partial _t v = \partial _t (\rho v) - v \partial _t \rho = - \partial _x (\rho \,v^2) - \partial _x p+ v\,\partial _x (\rho \,v), \end{aligned}$$

(4)

and of the pressure

$$\begin{aligned} \begin{aligned} \frac{1}{\gamma - 1} \partial _t p&= \partial _t (\rho e) - \frac{1}{2} \partial _t (\rho v^2) = - \partial _x ( (\rho e + p) v) - \frac{1}{2} v \partial _t (\rho v) - \frac{1}{2} v \rho \partial _t v \\&= - \frac{\gamma }{\gamma - 1} \partial _x (p v) - \frac{1}{2} \partial _x (\rho v^3) + \frac{1}{2} v \partial _x (\rho v^2 + p) - \frac{1}{2} v \rho \partial _t v. \end{aligned} \end{aligned}$$

(5)

It follows that for constant velocity and pressure, the time derivatives $\partial _t v = 0$ and $\partial _t p =0$, hence the coined term pressure equilibrium. Shima et al.  [44] found exponential spurious growth for a similar density-wave test case when using their KEP two-point flux [26]. When they modified the two-point flux to discretely preserve pressure equilibrium, they could demonstrate numerically that the novel scheme robustly solves the density-wave, even for very long simulation times.

In summary, the starting point of this paper are the works [13, 44] and we view the current work as a direct continuation of the analysis and discussion presented therein. This brings us directly to the research questions we are addressing in the current paper.

• (RQ1) Is it possible to construct two-point flux functions that are not only KEP and PEP as the one proposed by Shima et al.  [44], but also EC according to Tadmor’s condition [50, 51]?

• (RQ2) Is pressure equilibrium preservation a remedy for the local linear stability issues of the EC/dissipative DG framework reported in [13]?

• (RQ3) Are there entropies, such that the EC two-point fluxes and corresponding EC volume integral terms are locally linearly stable?

The remainder of the paper is organized as follows: in the next section, Sect. 2, we investigate research question (RQ1) and discuss the construction and existence of EC, KEP, and PEP two-point flux functions. In Sect. 3, we investigate research questions (RQ2) and (RQ3) and discuss the impact of pressure equilibrium preservation on local linear stability. As a by-product, we show that the PEP property of the two-point flux function carries over to the high-order split-form DG scheme in Appendix A. In the final Sect. 4, we summarize our results and collect the answers to the research questions.

On the Construction of EC, KEP, and PEP Two-Point Fluxes

Structure Preservation Properties

The first goal of this subsection is to collect and define the properties of the compressible Euler equations we want to preserve with our discretization. For the definition of two-point fluxes, it suffices to concentrate on semi-discrete finite volume methods of the form

$$\begin{aligned} \partial _t u_i + \frac{1}{{\Delta } x} \left( \underbrace{f^{{\mathrm {num}}}(u_{i+1}, u_{i})}_{= f^{{\mathrm {num}}}_+} - \underbrace{f^{{\mathrm {num}}}(u_{i}, u_{i-1})}_{= f^{{\mathrm {num}}}_-} \right) = 0. \end{aligned}$$

(6)

In what follows, we drop the subscript $+$ for the numerical flux function for convenience and assume an interface at location i and $i+1$ if not stated otherwise.

Definition 1

(Entropy-conservation [50, 51]) A numerical flux $f^{{\mathrm {num}}}$ and the corresponding finite volume method is EC if

$$\begin{aligned}{}[\![w]\!] \cdot f^{{\mathrm {num}}}- [\![\psi ]\!] = 0, \end{aligned}$$

(7)

where $w = U'$ are the entropy variables, $\psi$ is the flux potential, and $[\![w]\!] := w_{i+1} - w_i$ denotes the jump operator.

Unless stated otherwise, we will use the entropy

$$\begin{aligned} U = \frac{- \rho \,s}{\gamma - 1}, \quad s = \log \frac{p}{\rho ^\gamma } \end{aligned}$$

(8)

of the compressible Euler equation (2), with associated entropy variables

$$\begin{aligned} w = \left( \frac{\gamma }{\gamma - 1} - \frac{\log ({p}/{\rho ^\gamma })}{\gamma - 1} - \frac{\rho v^2}{2 p}, \frac{\rho v}{p}, - \frac{\rho }{p} \right) , \end{aligned}$$

(9)

and flux potential $\psi = \rho v$.

Definition 2

(Kinetic energy preservation [22, 26, 33, 34]) A numerical flux $f^{{\mathrm {num}}}= (f^{{\mathrm {num}}}_\rho , f^{{\mathrm {num}}}_{\rho v}, f^{{\mathrm {num}}}_{\rho e})$ and the corresponding finite volume method is KEP if

$$\begin{aligned} f^{{\mathrm {num}}}_{\rho v} = \{\!\{v\}\!\} f^{{\mathrm {num}}}_{\rho } + \{\!\{p\}\!\}, \end{aligned}$$

(10)

where $\{\!\{p\}\!\}:= (p_i + p_{i+1})/2$ denotes the arithmetic mean.

Definition 3

(Pressure equilibrium preservation) A numerical flux $f^{{\mathrm {num}}}= (f^{{\mathrm {num}}}_\rho , f^{{\mathrm {num}}}_{\rho v}, f^{{\mathrm {num}}}_{\rho e})$ and the corresponding finite volume method is PEP if

$$\left\{\begin{aligned} \begin{aligned} f^{{\mathrm {num}}}_{\rho v}&= v f^{{\mathrm {num}}}_{\rho } + {\mathrm {const}}(p, v), \\ f^{{\mathrm {num}}}_{\rho e}&= \frac{1}{2} v^2 f^{{\mathrm {num}}}_\rho + {\mathrm {const}}(p, v), \end{aligned} \end{aligned} \right.$$

(11)

whenever the velocity v and the pressure p are constant throughout the domain.

We motivate our definition of PEP fluxes with the following

Lemma 1

Pressure equilibrium, i.e., $p \equiv {\mathrm {const}}$, $v \equiv {\mathrm {const}}$, is preserved by (6) if and only if $f^{{\mathrm {num}}}$ is PEP.

Proof

The semidiscrete evolution equation for the velocity is

$$\begin{aligned} \rho \partial _t v = \partial _t \rho v - v \partial _t \rho = - \frac{1}{{\Delta } x} \left( f^{{\mathrm {num}}}_{\rho v, +} - f^{{\mathrm {num}}}_{\rho v, -} - v \left( f^{{\mathrm {num}}}_{\rho , +} - f^{{\mathrm {num}}}_{\rho , -} \right) \right) . \end{aligned}$$

(12)

Similarly, for $\partial _t v = 0$, the pressure evolves according to

$$\begin{aligned} \frac{1}{\gamma - 1} \partial _t p = \partial _t \rho \varepsilon = \partial _t \rho e - \frac{1}{2} v^2 \partial _t \rho = - \frac{1}{{\Delta } x} \left( f^{{\mathrm {num}}}_{\rho e, +} - f^{{\mathrm {num}}}_{\rho e, -} - \frac{1}{2} v^2 \left( f^{{\mathrm {num}}}_{\rho , +} - f^{{\mathrm {num}}}_{\rho , -} \right) \right) . \end{aligned}$$

(13)

Thus, $\partial _t v = 0$ and $\partial _t p = 0$ if and only if (11) is satisfied.

We are ready to formulate the central theorem of this work and to give the answer to the first research question (RQ1) in the following

Theorem 1

The numerical flux of Ranocha [33, 34],

$$\left\{\begin{aligned} \begin{aligned} f^{{\mathrm {num}}}_{\rho }&= \{\!\{\rho \}\!\}_{{\mathrm {log}}} \{\!\{v\}\!\}, \\ f^{{\mathrm {num}}}_{\rho v}&= \{\!\{\rho \}\!\}_{{\mathrm {log}}} \{\!\{v\}\!\}^2 + \{\!\{p\}\!\}, \\ f^{{\mathrm {num}}}_{\rho e}&= \frac{1}{2} \{\!\{\rho \}\!\}_{{\mathrm {log}}} \{\!\{v\}\!\} (\!(v \cdot v)\!) + \frac{1}{\gamma - 1} \{\!\{\rho \}\!\}_{{\mathrm {log}}} \{\!\{{\rho }/{p}\}\!\}_{{\mathrm {log}}}^{-1} \{\!\{v\}\!\} + (\!(p \cdot v)\!), \end{aligned} \end{aligned} \right.$$

(14)

with logarithmic mean

$$\begin{aligned} \{\!\{\rho \}\!\}_{{\mathrm {log}}} := \frac{[\![\rho ]\!]}{[\![\log \rho ]\!]}, \end{aligned}$$

(15)

and product mean

$$\begin{aligned} (\!(a \cdot b)\!) := \frac{a_+ b_- + a_- b_+}{2} = 2 \{\!\{a\}\!\} \{\!\{b\}\!\} - \{\!\{a b\}\!\}, \end{aligned}$$

(16)

for the compressible Euler equation (2) is EC, KEP, PEP, and has a density flux $f^{{\mathrm {num}}}_{\rho }$ that does not depend on the pressure. Moreover, it is the only numerical flux with these properties for $v \equiv {\mathrm {const}}$.

Remark 1

The motivation for the last property, i.e., that the density flux does not depend on pressure such as, e.g., in the EC flux by Ismail and Roe [21], is due to the discussion presented in [8, 32], where positivity failure could be identified for certain setups with large pressure jumps and constant densities.

Remark 2

The numerical flux (14) can also be derived by reversing the role of energy and entropy in the compressible Euler equations [32, Section 5]. Indeed, the flux (66) of [32] is the same as (14) developed in [33, Theorem 7.8]. This numerical flux is essentially uniquely defined by its properties, cf.  Remark 4.

Proof of Theorem 1

We first investigate the necessary conditions for EC and PEP and get the following

Lemma 2

For $p \equiv {\mathrm {const}}$, $v \equiv {\mathrm {const}}$, an EC numerical flux that is also KEP or PEP satisfies

$$\begin{aligned} f^{{\mathrm {num}}}_{\rho e} = \frac{1}{2} v^2 f^{{\mathrm {num}}}_{\rho } + \frac{\gamma }{\gamma - 1} \frac{p}{\{\!\{\rho \}\!\}_{{\mathrm {log}}}} f^{{\mathrm {num}}}_{\rho }. \end{aligned}$$

(17)

Proof

For $p \equiv {\mathrm {const}}$, $v \equiv {\mathrm {const}}$, the left-hand side of (7) reduces to

$$\begin{aligned}{}[\![w]\!] \cdot f^{{\mathrm {num}}}- [\![\psi ]\!] = \left( \frac{\gamma }{\gamma - 1} [\![\log \rho ]\!] - \frac{v^2}{2 p} [\![\rho ]\!] \right) f^{{\mathrm {num}}}_{\rho } + \frac{v}{p} [\![\rho ]\!] f^{{\mathrm {num}}}_{\rho v} - \frac{1}{p} [\![\rho ]\!] f^{{\mathrm {num}}}_{\rho e} - v [\![\rho ]\!]. \end{aligned}$$

(18)

Inserting $f^{{\mathrm {num}}}_{\rho v} = v f^{{\mathrm {num}}}_{\rho } + p$ from the KEP (10) or PEP (11) property and using the discrete chain rule

$$\begin{aligned}{}[\![\log \rho ]\!] = \frac{[\![\rho ]\!]}{\{\!\{\rho \}\!\}_{{\mathrm {log}}}} \end{aligned}$$

(19)

results in

$$\begin{aligned}&\left( \frac{\gamma }{\gamma - 1} \frac{[\![\rho ]\!]}{\{\!\{\rho \}\!\}_{{\mathrm {log}}}} - \frac{v^2}{2 p} [\![\rho ]\!] \right) f^{{\mathrm {num}}}_{\rho } + \frac{v^2}{p} [\![\rho ]\!] f^{{\mathrm {num}}}_{\rho } + v [\![\rho ]\!] - \frac{1}{p} [\![\rho ]\!] f^{{\mathrm {num}}}_{\rho e} - v [\![\rho ]\!] \nonumber \\&\quad = \frac{\gamma }{\gamma - 1} \frac{[\![\rho ]\!]}{\{\!\{\rho \}\!\}_{{\mathrm {log}}}} f^{{\mathrm {num}}}_{\rho } + \frac{v^2}{2 p} [\![\rho ]\!] f^{{\mathrm {num}}}_{\rho } - \frac{1}{p} [\![\rho ]\!] f^{{\mathrm {num}}}_{\rho e}. \end{aligned}$$

(20)

This expression has to vanish for arbitrary values of $\rho _\pm$ for an EC flux, resulting in (17).

Lemma 3

For $p \equiv {\mathrm {const}}$, $v \equiv {\mathrm {const}}$, an EC and PEP numerical flux must be of the form

$$\left\{\begin{aligned} \begin{aligned} f^{{\mathrm {num}}}_{\rho }&= \{\!\{\rho \}\!\}_{{\mathrm {log}}} v, \\ f^{{\mathrm {num}}}_{\rho v}&= \{\!\{\rho \}\!\}_{{\mathrm {log}}} v^2 + p, \\ f^{{\mathrm {num}}}_{\rho e}&= \frac{1}{2} \{\!\{\rho \}\!\}_{{\mathrm {log}}} v^3 + \frac{\gamma }{\gamma - 1} p v. \end{aligned} \end{aligned} \right.$$

(21)

Proof

Comparing (11) and (17),

$$\begin{aligned} \frac{\gamma }{\gamma - 1} \frac{p}{\{\!\{\rho \}\!\}_{{\mathrm {log}}}} f^{{\mathrm {num}}}_{\rho } \end{aligned}$$

(22)

must be independent of $\rho _\pm$. Hence, $f^{{\mathrm {num}}}_{\rho }$ must be of the form $f^{{\mathrm {num}}}_{\rho } = \{\!\{\rho \}\!\}_{{\mathrm {log}}} v$ for $p \equiv {\mathrm {const}}, v \equiv {\mathrm {const}}$. Inserting the PEP property (11) for $f^{{\mathrm {num}}}_{\rho v}$ results in the final form (21).

Lemma 4

For $v \equiv {\mathrm {const}}$, an EC and PEP numerical flux for which the density flux does not depend on the pressure must be of the form

$$\left\{\begin{aligned} \begin{aligned} f^{{\mathrm {num}}}_{\rho }&= \{\!\{\rho \}\!\}_{{\mathrm {log}}} v,\\ f^{{\mathrm {num}}}_{\rho v}&= \{\!\{\rho \}\!\}_{{\mathrm {log}}} v^2 + \varphi (\rho _\pm , p_\pm ),\\ f^{{\mathrm {num}}}_{\rho e}&= \frac{1}{2} \{\!\{\rho \}\!\}_{{\mathrm {log}}} v^3 + \frac{1}{\gamma - 1} \{\!\{\rho \}\!\}_{{\mathrm {log}}} \{\!\{{\rho }/{p}\}\!\}_{{\mathrm {log}}}^{-1} v + \varphi (\rho _\pm , p_\pm ) v, \end{aligned} \end{aligned} \right.$$

(23)

where $\varphi (\rho _\pm , p_\pm )$ is some kind of mean value depending on $\rho _\pm , p_\pm$ such that $\forall \rho _\pm , p > 0:\varphi (\rho _+, \rho _-, p, p) = p$.

Proof

Because of Lemma 3, the general form of dependencies on $\rho$ for $p \equiv {\mathrm {const}}$ is already determined. The remaining degrees of freedom for non-constant pressure p can be described by two functions $\varphi _{1,2}$, resulting in the numerical fluxes

$$\left\{\begin{aligned} \begin{aligned} f^{{\mathrm {num}}}_{\rho }&= \{\!\{\rho \}\!\}_{{\mathrm {log}}} v,\\ f^{{\mathrm {num}}}_{\rho v}&= \{\!\{\rho \}\!\}_{{\mathrm {log}}} v^2 + \varphi _1(\rho _\pm , p_\pm ),\\ f^{{\mathrm {num}}}_{\rho e}&= \frac{1}{2} \{\!\{\rho \}\!\}_{{\mathrm {log}}} v^3 + \frac{\gamma }{\gamma - 1} \varphi _2(\rho _\pm , p_\pm ) v, \end{aligned} \end{aligned} \right.$$

(24)

where $\varphi _{1,2}$ depend on $\rho _\pm , p_\pm$ such that

$$\begin{aligned} \forall p, \rho _\pm > 0\!:\quad \varphi _{1,2}(\rho _+, \rho _-, p, p) = p. \end{aligned}$$

(25)

Inserting this form of the numerical flux in the left-hand side of (7) for $v \equiv {\mathrm {const}}$ results in

$$\begin{aligned} \begin{aligned}{}[\![w]\!] \cdot f^{{\mathrm {num}}}- [\![\psi ]\!]&= \left( [\![\log \rho ]\!] + \frac{1}{\gamma - 1} [\![\log \frac{\rho }{p}]\!] - \frac{v^2}{2} [\![\frac{\rho }{p}]\!] \right) f^{{\mathrm {num}}}_{\rho }\\&\quad + v [\![\frac{\rho }{p}]\!] f^{{\mathrm {num}}}_{\rho v} - [\![\frac{\rho }{p}]\!] f^{{\mathrm {num}}}_{\rho e} - v [\![\rho ]\!] \\&= v [\![\rho ]\!] + \frac{v}{\gamma - 1} \frac{[\![{\rho }/{p}]\!]}{\{\!\{{\rho }/{p}\}\!\}_{{\mathrm {log}}}} \{\!\{\rho \}\!\}_{{\mathrm {log}}} - \frac{v^3}{2} [\![\frac{\rho }{p}]\!] \{\!\{\rho \}\!\}_{{\mathrm {log}}} + v^3 [\![\frac{\rho }{p}]\!] \{\!\{\rho \}\!\}_{{\mathrm {log}}} \\&\quad + v [\![\frac{\rho }{p}]\!] \varphi _1 - \frac{v^3}{2} [\![\frac{\rho }{p}]\!] \{\!\{\rho \}\!\}_{{\mathrm {log}}} - \frac{\gamma }{\gamma - 1} v [\![\frac{\rho }{p}]\!] \varphi _2 - v [\![\rho ]\!] \\&= \frac{v}{\gamma - 1} \frac{\{\!\{\rho \}\!\}_{{\mathrm {log}}}}{\{\!\{{\rho }/{p}\}\!\}_{{\mathrm {log}}}} [\![\frac{\rho }{p}]\!] + v [\![\frac{\rho }{p}]\!] \varphi _1 - \frac{\gamma }{\gamma - 1} v [\![\frac{\rho }{p}]\!] \varphi _2. \end{aligned} \end{aligned}$$

(26)

Since this has to vanish for arbitrary $\rho _\pm , p_\pm , v$,

$$\begin{aligned} \varphi _2 = \frac{1}{\gamma } \frac{\{\!\{\rho \}\!\}_{{\mathrm {log}}}}{\{\!\{{\rho }/{p}\}\!\}_{{\mathrm {log}}}} + \frac{\gamma - 1}{\gamma } \varphi _1. \end{aligned}$$

(27)

Having established the lemmata above, we are prepared to prove Theorem 1.

Proof of Theorem 1

The KEP (10) property is satisfied by construction. Moreover, the numerical flux for the total energy satisfies the PEP property (11), since it can be written as

$$\begin{aligned} \begin{aligned} f^{{\mathrm {num}}}_{\rho e}&= \frac{1}{2} \{\!\{\rho \}\!\}_{{\mathrm {log}}} \{\!\{v\}\!\} (\!(v \cdot v)\!) + \frac{1}{\gamma - 1} \{\!\{{1}/{p}\}\!\}_{{\mathrm {log}}}^{-1} \{\!\{v\}\!\} + (\!(p \cdot v)\!)\\&\quad + \frac{1}{\gamma - 1} \left( \{\!\{\rho \}\!\}_{{\mathrm {log}}} \{\!\{{\rho }/{p}\}\!\}_{{\mathrm {log}}}^{-1} - \{\!\{{1}/{p}\}\!\}_{{\mathrm {log}}}^{-1} \right) \{\!\{v\}\!\}, \end{aligned} \end{aligned}$$

(28)

where

$$\begin{aligned} \frac{1}{\gamma - 1} \left( \{\!\{\rho \}\!\}_{{\mathrm {log}}} \{\!\{{\rho }/{p}\}\!\}_{{\mathrm {log}}}^{-1} - \{\!\{{1}/{p}\}\!\}_{{\mathrm {log}}}^{-1} \right) \{\!\{v\}\!\} = 0, \end{aligned}$$

(29)

whenever p is constant. Finally, the flux is EC as shown in [33, 34]. It is the only numerical flux with all these properties for $v \equiv {\mathrm {const}}$, since the KEP property (10) requires the pressure mean in (23) to be $\varphi = \{\!\{p\}\!\}$.

Remark 3

The pressure mean in the momentum flux is determined uniquely by the KEP property (10), resulting in a pressure mean depending on the density in the energy flux. As required by the PEP property (11), this dependency occurs only for non-constant pressure. However, such a mixed dependency on $\rho$ and p of an approximation to the pressure is necessary for EC and PEP fluxes because of Lemma 4.

We have obtained a complete characterization of numerical fluxes for the compressible Euler equations that are EC, KEP, PEP, and have a density flux $f^{{\mathrm {num}}}_\rho$ that does not depend on the pressure for $v \equiv {\mathrm {const}}$ in Theorem 1. The analogous characterization for $p \equiv {\mathrm {const}}$ is a bit more involved and leaves a degree of freedom.

Lemma 5

For fixed $p \equiv {\mathrm {const}}$, a (symmetric) EC, KEP, and PEP numerical flux must be of the form

$$\left\{\begin{aligned} \begin{aligned} f^{{\mathrm {num}}}_{\rho }&= \{\!\{\rho \}\!\}_{{\mathrm {log}}} \{\!\{v\}\!\} + \chi (\rho _\pm , v_\pm ), \\ f^{{\mathrm {num}}}_{\rho v}&= \{\!\{\rho \}\!\}_{{\mathrm {log}}} \{\!\{v\}\!\}^2 + p + \{\!\{v\}\!\} \chi (\rho _\pm , v_\pm ), \\ f^{{\mathrm {num}}}_{\rho e}&= \frac{1}{2} \{\!\{\rho \}\!\}_{{\mathrm {log}}} \{\!\{v\}\!\} (\!(v \cdot v)\!) + \frac{\gamma }{\gamma - 1} p \{\!\{v\}\!\} \\&\quad +\left( \frac{1}{2} (\!(v \cdot v)\!) + \frac{\gamma }{\gamma - 1} \frac{p}{\{\!\{\rho \}\!\}_{{\mathrm {log}}}} \right) \chi (\rho _\pm , v_\pm ), \end{aligned} \end{aligned} \right.$$

(30)

where $\chi$ is a function depending on $\rho _\pm , v_\pm$ (symmetrically with respect to ±) such that $\forall \rho _\pm , v :\chi (\rho _+, \rho _-, v, v) = 0$.

Proof

Because of consistency, every numerical flux can be written as the sum of a given numerical flux and a perturbation $\chi$ that is consistent with zero. Using (14) as baseline flux for fixed $p \equiv {\mathrm {const}}$, every numerical flux can be written as

$$\left\{\begin{aligned} \begin{aligned} f^{{\mathrm {num}}}_{\rho }&= \{\!\{\rho \}\!\}_{{\mathrm {log}}} \{\!\{v\}\!\} + \chi _{\rho }(\rho _\pm , v_\pm ), \\ f^{{\mathrm {num}}}_{\rho v}&= \{\!\{\rho \}\!\}_{{\mathrm {log}}} \{\!\{v\}\!\}^2 + p + \chi _{\rho v}(\rho _\pm , v_\pm ), \\ f^{{\mathrm {num}}}_{\rho e}&= \frac{1}{2} \{\!\{\rho \}\!\}_{{\mathrm {log}}} \{\!\{v\}\!\} (\!(v \cdot v)\!) + \frac{\gamma }{\gamma - 1} p \{\!\{v\}\!\} + \chi _{\rho e}(\rho _\pm , v_\pm ), \end{aligned} \end{aligned} \right.$$

(31)

where $\forall \rho , v :\chi _{\rho }(\rho , \rho , v, v) = \chi _{\rho v}(\rho , \rho , v, v) = \chi _{\rho e}(\rho , \rho , v, v) = 0$. Kinetic energy preservation (10) requires $\chi _{\rho v} = \{\!\{v\}\!\} \chi _{\rho }$. Since the chosen baseline numerical flux (14) is EC, requiring entropy conservation for the perturbed numerical flux yields

$$\begin{aligned} \begin{aligned} 0&= [\![w]\!] \cdot f^{{\mathrm {num}}}- [\![\psi ]\!] = \left( \frac{\gamma }{\gamma - 1} [\![\log \rho ]\!] - \frac{1}{2 p} [\![\rho v^2]\!] \right) \chi _{\rho } + \frac{1}{p} [\![\rho v]\!] \{\!\{v\}\!\} \chi _{\rho } - \frac{1}{p} [\![\rho ]\!] \chi _{\rho e} \\&= \left( \frac{\gamma }{\gamma - 1} \frac{[\![\rho ]\!]}{\{\!\{\rho \}\!\}_{{\mathrm {log}}}} - \frac{1}{2 p} \{\!\{v^2\}\!\} [\![\rho ]\!] + \frac{1}{p} \{\!\{v\}\!\}^2 [\![\rho ]\!] \right) \chi _{\rho } - \frac{1}{p} [\![\rho ]\!] \chi _{\rho e} \\&= \left( \frac{1}{2 p} (\!(v \cdot v)\!) [\![\rho ]\!] + \frac{\gamma }{\gamma - 1} \frac{[\![\rho ]\!]}{\{\!\{\rho \}\!\}_{{\mathrm {log}}}} \right) \chi _{\rho } - \frac{1}{p} [\![\rho ]\!] \chi _{\rho e}. \end{aligned} \end{aligned}$$

(32)

Hence,

$$\begin{aligned} \chi _{\rho e}(\rho _\pm , v_\pm ) = \left( \frac{1}{2} (\!(v \cdot v)\!) + \frac{\gamma }{\gamma - 1} \frac{p}{\{\!\{\rho \}\!\}_{{\mathrm {log}}}} \right) \chi _{\rho }(\rho _\pm , v_\pm ). \end{aligned}$$

(33)

Pressure equilibrium preservation (11) requires $\chi _{\rho e} = \frac{1}{2} v^2 \chi _\rho + {\mathrm {const}}(p, v)$ for $v \equiv {\mathrm {const}}$. The first term $\frac{1}{2} (\!(v \cdot v)\!) \chi _{\rho }$ satisfies this requirement. However, the second term $\frac{\gamma }{\gamma - 1} \frac{p}{\{\!\{\rho \}\!\}_{{\mathrm {log}}}} \chi _{\rho }$ fits if and only if $\forall \rho _\pm , v :\chi (\rho _+, \rho _-, v, v) = 0$.

Remark 4

Extending the numerical flux (30) developed for fixed pressure $p \equiv {\mathrm {const}}$ to general variable pressures results in a pressure-dependent density flux unless the perturbation vanishes, i.e., $\chi = 0$. Thus, the numerical flux (14) is also unique for general velocities v in the class of continuous numerical fluxes with the properties given in Theorem 1.

Proof

Using the ansatz (31) for a general pressure p yields

$$\left\{\begin{aligned} \begin{aligned} f^{{\mathrm {num}}}_{\rho }&= \{\!\{\rho \}\!\}_{{\mathrm {log}}} \{\!\{v\}\!\} + \chi _{\rho }(\rho _\pm , v_\pm ), \\ f^{{\mathrm {num}}}_{\rho v}&= \{\!\{\rho \}\!\}_{{\mathrm {log}}} \{\!\{v\}\!\}^2 + \{\!\{p\}\!\} + \chi _{\rho v}(\rho _\pm , v_\pm , p_\pm ), \\ f^{{\mathrm {num}}}_{\rho e}&= \frac{1}{2} \{\!\{\rho \}\!\}_{{\mathrm {log}}} \{\!\{v\}\!\} (\!(v \cdot v)\!) + \frac{1}{\gamma - 1} \{\!\{\rho \}\!\}_{{\mathrm {log}}} \{\!\{{\rho }/{p}\}\!\}_{{\mathrm {log}}}^{-1} \{\!\{v\}\!\} + (\!(p \cdot v)\!) \\&\quad + \chi _{\rho e}(\rho _\pm , v_\pm , p_\pm ), \end{aligned} \end{aligned} \right.$$

(34)

where $\forall \rho , v, p :\chi _{\rho }(\rho , \rho , v, v) = \chi _{\rho v}(\rho , \rho , v, v, p, p) = \chi _{\rho e}(\rho , \rho , v, v, p, p) = 0$. Kinetic energy preservation (10) requires again $\chi _{\rho v} = \{\!\{v\}\!\} \chi _{\rho }$. Requiring entropy conservation additionally yields

$$\begin{aligned} 0&= [\![w]\!] \cdot f^{{\mathrm {num}}}- [\![\psi ]\!] = \left( [\![\log \rho ]\!] + \frac{1}{\gamma - 1} [\![\log {\rho }/{p}]\!] - \frac{1}{2} [\![{\rho v^2}/{p}]\!] \right) \chi _{\rho } \nonumber \\&\quad + [\![{\rho v}/{p}]\!] \{\!\{v\}\!\} \chi _{\rho } - [\![{\rho }/{p}]\!] \chi _{\rho e} \nonumber \\&= \left( \frac{[\![\rho ]\!]}{\{\!\{\rho \}\!\}_{{\mathrm {log}}}} + \frac{1}{\gamma - 1} \frac{[\![{\rho }/{p}]\!]}{\{\!\{{\rho }/{p}\}\!\}_{{\mathrm {log}}}} - \frac{1}{2} \{\!\{v^2\}\!\} [\![{\rho }/{p}]\!] + [\![{\rho }/{p}]\!] \{\!\{v\}\!\}^2 \right) \chi _{\rho } - [\![{\rho }/{p}]\!] \chi _{\rho e}. \end{aligned}$$

(35)

For arbitrary $\rho _\pm , v_\pm$, choosing $p_\pm$ such that $[\![{\rho }/{p}]\!] = 0$ requires $\chi _{\rho } = 0$. Hence, the perturbation $\chi$ must vanish if the density flux does not depend on the pressure.

The KEP and PEP Two-Point Flux of Shima et al.

Shima et al.  [44] introduced a modification to their KEP flux [26] and constructed a KEP flux with the PEP property,

$$\left\{\begin{aligned} \begin{aligned} f^{{\mathrm {num}}}_{\rho }&= \{\!\{\rho \}\!\} \{\!\{v\}\!\}, \\ f^{{\mathrm {num}}}_{\rho v}&= \{\!\{\rho \}\!\} \{\!\{v\}\!\}^2 + \{\!\{p\}\!\}, \\ f^{{\mathrm {num}}}_{\rho e}&= \frac{1}{2} \{\!\{\rho \}\!\} \{\!\{v\}\!\} (\!(v \cdot v)\!) + \frac{1}{\gamma - 1} \{\!\{p\}\!\} \{\!\{v\}\!\} + (\!(p \cdot v)\!). \end{aligned} \end{aligned}\right.$$

(36)

We note that the density flux and the general structure of the momentum and energy fluxes is very closely related to Ranocha’s two-point flux (14), except for the EC property, because Shima et al.  used the arithmetic mean in the density flux instead of the logarithmic mean. Although the numerical flux (36) is not EC, it has four desirable properties, namely KEP, PEP, and a pressure-independent density flux. As we realize later in Sect. 3, the fourth desirable property is the arithmetic mean of the density in the density flux function, as it enhances robustness for the density wave propagation.

In their paper, Shima et al.  demonstrated numerically very good robustness of their novel KEP and PEP discretization, even for highly non-linear problems such as underresolved turbulence. Hence, an interesting question is whether there is an entropy function for the compressible Euler equations such that the two-point flux function of Shima et al.  with the arithmetic mean happens to be an EC flux. This would be a possible explanation of the improved numerical robustness of this flux for non-linear problems. To partially answer this question, we consider next the family of entropy functions introduced by Harten [15].

Harten [15] discovered the family of entropy functions for the Euler equation (2)

$$\begin{aligned} U = -\rho h(s), \qquad s = \log \frac{p}{\rho ^\gamma }, \end{aligned}$$

(37)

where h is a sufficiently smooth function satisfying

$$\begin{aligned} \frac{h''(s)}{h'(s)} < \frac{1}{\gamma } \end{aligned}$$

(38)

to ensure convexity of the entropy function U, Eq. (37). In particular, Harten discovered the one-parameter family

$$\begin{aligned} U = -\rho h(s), \qquad h(s) = \frac{\gamma + \alpha }{\gamma - 1} {\mathrm {e}}^{s / (\gamma + \alpha )} = \frac{\gamma + \alpha }{\gamma - 1} (p / \rho ^\gamma )^{1 / (\gamma + \alpha )}, \qquad \alpha > 0. \end{aligned}$$

(39)

Up to now, we considered the entropy (8) given by $h(s) \propto s$ above, since it is the only convex entropy (37) which symmetrizes the compressible Navier-Stokes equations with heat flux [19]. Nevertheless, it is interesting to know whether there are other entropies (37) of the compressible Euler equation (2) that result in a corresponding EC numerical density flux $f^{{\mathrm {num}}}_{\rho }$, where the mean value of the density is arithmetic.

Following the approach used in Sect. 2.2, we will make use of the entropy variables

$$\begin{aligned} w = \frac{(\gamma - 1) h'(s)}{p} \left( - \frac{1}{2} \rho v^2 - \frac{p}{\gamma - 1} \left( \frac{h(s)}{h'(s)} - \gamma \right) , \rho v, - \rho \right) , \end{aligned}$$

(40)

and the flux potential

$$\begin{aligned} \psi = (\gamma - 1) h'(s) \rho v, \end{aligned}$$

(41)

associated with the entropy (37). Lemma 2 is a special case of

Lemma 6

For $p \equiv {\mathrm {const}}$, $v \equiv {\mathrm {const}}$, an EC numerical flux for the entropy (37) that is also KEP or PEP satisfies

$$\begin{aligned} f^{{\mathrm {num}}}_{\rho e} = \frac{1}{2} v^2 f^{{\mathrm {num}}}_{\rho } + \frac{p}{\gamma - 1} \frac{[\![\gamma h' - h]\!]}{[\![\rho h']\!]} f^{{\mathrm {num}}}_{\rho }. \end{aligned}$$

(42)

Proof

For $p \equiv {\mathrm {const}}$, $v \equiv {\mathrm {const}}$, the left-hand side of (7) reduces to

$$\begin{aligned}{}[\![w]\!] \cdot f^{{\mathrm {num}}}- [\![\psi ]\!]= & {} \left( - \frac{1}{2} v^2 \frac{\gamma - 1}{p} [\![\rho h']\!] - [\![h]\!] + \gamma [\![h']\!] \right) f^{{\mathrm {num}}}_{\rho }\nonumber \\&+ v \frac{\gamma - 1}{p} [\![\rho h']\!] f^{{\mathrm {num}}}_{\rho v} - \frac{\gamma - 1}{p} [\![\rho h']\!] f^{{\mathrm {num}}}_{\rho e} - (\gamma - 1) v [\![\rho h']\!]. \end{aligned}$$

(43)

This term vanishes if and only if

$$\begin{aligned} 0= & {} - \frac{1}{2} v^2 [\![\rho h']\!] f^{{\mathrm {num}}}_{\rho } - \frac{1}{\gamma - 1} p [\![h]\!] f^{{\mathrm {num}}}_{\rho } + \frac{\gamma }{\gamma - 1} p [\![h']\!] f^{{\mathrm {num}}}_{\rho }+ v [\![\rho h']\!] f^{{\mathrm {num}}}_{\rho v} \nonumber \\&- [\![\rho h']\!] f^{{\mathrm {num}}}_{\rho e} - p v [\![\rho h']\!]. \end{aligned}$$

(44)

Inserting $f^{{\mathrm {num}}}_{\rho v} = v f^{{\mathrm {num}}}_{\rho } + p$ from the KEP (10) or PEP (11) property results in

$$\begin{aligned} 0 = \frac{1}{2} v^2 [\![\rho h']\!] f^{{\mathrm {num}}}_{\rho } - \frac{1}{\gamma - 1} p [\![h]\!] f^{{\mathrm {num}}}_{\rho } + \frac{\gamma }{\gamma - 1} p [\![h']\!] f^{{\mathrm {num}}}_{\rho } - [\![\rho h']\!] f^{{\mathrm {num}}}_{\rho e}. \end{aligned}$$

(45)

This expression has to vanish for arbitrary values of $\rho _\pm$ for an EC flux, resulting in (42).

Comparing (11) and (42), a PEP flux that is also EC for (37) must contain an average of the density proportional to

$$\begin{aligned} \frac{ [\![\rho h']\!] }{ [\![\gamma h' - h]\!] }. \end{aligned}$$

(46)

In general, (46) is not the arithmetic mean of $\rho _\pm$. It becomes the linear mean proportional to $\{\!\{\rho \}\!\}$ for $p \equiv {\mathrm {const}}$ for the choice of h as in (39) with $\alpha = - 2 \gamma$. However, in this case, the resulting U is not convex anymore. Hence, entropy-conservative and pressure equilibrium preserving numerical fluxes for the compressible Euler equations have to use nonlinear means of the density and we have demonstrated that the two-point flux of Shima et al.  is not related to one of Harten’s entropies.

Corollary 1

There is no Harten entropy pair for the compressible Euler equations such that a corresponding EC two-point flux with the KEP and PEP property uses the arithmetic mean of the density in the density flux.

So far, we have not found any evidence, that there is another strictly convex entropy pair for which the EC flux with KEP and PEP might have an arithmetic mean and thus have the conjecture, that there is none.

Finally, it is interesting to see whether the arithmetic mean can be used in the density flux of an EC flux if the additional constraints are relaxed by not requiring the KEP/PEP property anymore. Considering again the family of entropies (37), we consider the case $v \equiv {\mathrm {const}}$, $h'(s) \rho / p \equiv {\mathrm {const}}$. Inserting the entropy variables (40) into the EC condition (7) results in

$$\begin{aligned} 0 = [\![w]\!] \cdot f^{{\mathrm {num}}}- [\![\psi ]\!] = - [\![h(s) - \gamma h'(s)]\!] f^{{\mathrm {num}}}_{\rho } - (\gamma - 1) [\![h'(s) \rho v]\!]. \end{aligned}$$

(47)

Hence, the density flux must again contain an average of the density proportional to (46), but for the case of $h'(s) \rho p \equiv {\mathrm {const}}$ instead of the case $p \equiv {\mathrm {const}}$ discussed above. For a given entropy such as (8) or (39), it is easy to solve $h'(s_+) \rho _+ / p_+ = h'(s_-) \rho _- / p_-$ for $\rho _+$ and pick values of $p_\pm , \rho _-$ such that (47) is not satisfied by $f^{{\mathrm {num}}}_{\rho } = \{\!\{\rho \}\!\} v$. Hence, we arrive at

Corollary 2

There is no Harten entropy pair for the compressible Euler equations such that a corresponding EC two-point flux uses the arithmetic mean of density in the density flux.

Remark 5

We refer to an entropy pair if the entropy function is strictly convex (resulting in an invertible transformation from the conserved variables to the entropy variables). Linear functionals of the conserved variables are of course non-strictly convex and can be combined with a density flux using the arithmetic mean.

On Local Linear Stability of EC Schemes with the PEP Property

In this section, we consider the (local) linear stability [13] of high-order discretizations based on two-point fluxes. The extension to high-order accuracy is relatively straight forward when assuming the SBP property. Several classes of numerical methods can be formulated via (periodic) SBP operators, including finite difference [25, 48], finite volume [28, 29], continuous Galerkin [17, 18], DG [12], and flux reconstruction methods [39]. A brief review how to formulate these methods in the SBP framework with application to structure-preserving numerical methods can be found in [38]. Further details and background information about SBP methods can be found, e.g., in the review articles [9, 49].

Building upon earlier works such as [27, 46], Fisher and Carpenter [10] created conservative high-order semi-discretizations of hyperbolic conservation laws using a special class of two-point numerical fluxes. The final extension to general symmetric numerical fluxes was obtained in [7, 14, 32] and will be recalled briefly below.

Numerical Investigation of the Robustness of the Split-Form DG Scheme

In this part, we consider the split-form DG approximation with the numerical fluxes discussed above and apply them to solve a simple density wave problem. In particular, we compare the results when using a central flux with arithmetic means, Ranocha’s two-point flux function (14) that is EC, KEP and PEP, and the two-point flux by Shima et al.  (36) that is KEP and PEP.

Following [13], we consider the two-dimensional compressible Euler equations with the initial condition

$$\begin{aligned} \rho = 1 + 0.98 \sin (2\uppi (x_1 + x_2)), \quad v_1 = 0.1, \quad v_2 = 0.2, \quad p = 20, \quad x \in [-1, 1]^2, \end{aligned}$$

(48)

and fully periodic boundary conditions. We use the split-form DG methods with spectral collocation on Legendre-Gauss-Lobatto nodes, with a polynomial degree of $N = 5$ on a grid with $4 \times 4$ elements implemented in the open source code Trixi.jl [42, 43]. The semi-discretizations are integrated in time using the fourth-order, five-stage, low-storage Runge-Kutta method of [23] with a relative CFL number $\mathtt {cfl} = 0.05$, which then gets additionally scaled by the choice of polynomial degree N, as is common for DG. This ensures a negligible impact of the time integrator on the numerical solution.

Remark 6

The numerical methods applied in this article are written in Julia [1]. The plots are created using Matplotlib [20]. The source code necessary to reproduce all results shown in this article is available online [36]. We use the numerically stable evaluation of the logarithmic mean proposed in [21] in Trixi.jl.

The simulation with the pure central approximation with the arithmetic mean flux is stable for all times for the density wave (48). We emphasize that we use the central flux for both, the split-form volume integral and the surface integral fluxes—so there is no added numerical dissipation. This shows that in principle, the problem is very well resolved by the chosen DG discretization. We can further numerically confirm, that the modification of Shima et al.  [44] gives a high-order split-form DG discretization, that is able to robustly run this test case for very long integration times ($t > 100$, corresponding to more than 935 000 time steps). Hence, at first, it seems that the added PEP property indeed solves the robustness issue. However, in accordance with the findings of [13] for other EC fluxes, the high-order DG discretization with Ranocha’s EC flux (14) crashes because of negative density already at $t \approx 0.55$. We note that Ranocha’s flux is KEP and PEP, i.e., it preserves the pressure equilibrium by construction and there are no fluctuations in velocity and pressure!

Following these numerical results, we can already answer our second research question and state, that, unfortunately, the answer to (RQ2) is no, the PEP property is not a remedy for the stability issues of the EC fluxes, as the simple density wave problem still crashes after very short simulation times. Note that these findings are not sensitive to the choice of the $\mathtt {cfl}$ number or the time integration method.

However, it is interesting that the Shima et al.  flux can indeed robustly run the density wave test case. Because of the PEP property, both the flux (36) of Shima et al.  and the flux (14) of Ranocha reduce the density wave (1) for the compressible Euler equations to four linear advection equations. The main difference between the Shima et al.  flux and Ranocha’s flux are the mean values of the density used in the density flux: the former uses the arithmetic mean to approximate the linear advection, and the latter uses the logarithmic mean to discretize the linear advection.

Stability for Linear Advection: Investigation of the Impact of the Choice of the Mean Value

In this subsection, we focus on how the choice of the mean values in a split-form approximation of the linear advection equation influences the stability. For this purpose, we consider periodic high-order SBP discretizations of the linear advection equation. We use

Definition 4

A periodic SBP operator consisting of a derivative matrix D approximating the first derivative as $D u \approx \partial _x u$, and a mass matrix M approximating the $L^2$ scalar product via $u^{\rm{T}} M v \approx \int u v$, such that

$$\begin{aligned} M D + D^{\rm{T}} M = 0. \end{aligned}$$

(49)

Given an SBP operator D with symmetric mass matrix M and a symmetric two-point numerical flux $f^{{\mathrm {num}}}$ for the hyperbolic conservation law

$$\begin{aligned} \partial _t u + \partial _x f(u) = 0, \end{aligned}$$

(50)

the semi-discretization

$$\begin{aligned} \partial _t u_i + \sum _{l} 2 D_{i,l} f^{{\mathrm {num}}}(u_i, u_l) = 0 \end{aligned}$$

(51)

is a conservative approximation of (50) with at least the same order of accuracy as the SBP operator [7, 10, 32]. Moreover, the semi-discretization conserves the entropy U of (50) if the numerical flux is entropy-conservative for that entropy U [10].

Following [13], we compute the spectrum of a semi-discretization (51) of the linear advection equation

$$\left\{ \begin{aligned} \begin{aligned} \partial _t u(t, x) + \partial _x u(t, x) = 0,\\ u(0, x) = 2 + 1.9 \sin (\uppi x) \end{aligned} \end{aligned}\right.$$

(52)

in a periodic domain $x \in [0, 2]$. The scheme (51) is implemented in Julia [1] and the Jacobian of the semi-discretization is computed via forward-mode automatic differentiation (AD) [40]. Note that AD is not necessary if a linear numerical flux is used for this linear PDE. However, we are also interested in nonlinear numerical fluxes, involving, e.g., the logarithmic mean. For nonlinear discretizations, it is not as trivial to compute the Jacobian and AD becomes a valuable tool.

We note that if the numerical flux is chosen as the arithmetic mean, $f^{{\mathrm {num}}}= \{\!\{u\}\!\}$, the semi-discretization is linear and skew-symmetric (with respect to the scalar product induced by the mass matrix M). This semi-discretization conserves the $L^2$ entropy $U(u) = u^2 / 2$. Hence, as expected, all eigenvalues are purely imaginary in our numerical test.

In contrast, choosing the numerical flux as the logarithmic mean $f^{{\mathrm {num}}}= \{\!\{u\}\!\}_{{\mathrm {log}}}$ results in a nonlinear semi-discretization, which conserves the entropy $U(u) = u \log u - u$ with entropy flux $F(u) = u \log u - u$. Indeed, the corresponding entropy variables are $w(u) = U'(u) = \log (u)$ and the flux potential is $\psi (u) = u$. Hence, the associated entropy-conservative numerical flux is $f^{{\mathrm {num}}}(u) = [\![\psi (u)]\!] / [\![w(u)]\!] = [\![u]\!] / [\![\log u]\!] = \{\!\{u\}\!\}_{{\mathrm {log}}}$. The resulting spectra of the Jacobian of the semi-discretization with logarithmic mean values are shown in Fig. 1 for different choices of SBP operators.

Fig. 1

Spectra of nonlinear semi-discretizations (51) using different variants of SBP operators and the logarithmic mean as numerical flux

Clearly, all of the spectra have eigenvalues with positive real part (of order unity) that do not converge to zero under grid refinement. In particular, these eigenvalues with positive real part occur for all choices of semi-discretizations. We checked that the occurrence of eigenvalues with positive real parts does not depend on the parity of the number of nodes/elements or the polynomial degree. For the investigation of spectra based on discretizations with other mean value choices, we refer to Appendix B. All other mean values tested give discretizations where the spectra have significant positive real parts.

This nicely suggests that the reason for the stability issues of the high-order split-form DG scheme with the EC flux of Ranocha for the simple density wave example is due to the logarithmic mean of the density in the density flux. Even with the PEP property, which guarantees that pressure and velocity stay constant throughout the simulation, the discretization of the density evolution is unstable when using the logarithmic mean, while the discretization with the flux of Shima et al.  is based on an arithmetic mean of the density and hence runs the example robustly. It remains to discuss however, if the Shima et al.  flux is locally linearly stable as defined in [13], i.e., if the spectrum of the linearized operator is stable towards perturbations.

Investigation of Local Linear Stability

We want to dig deeper and analyze the respective spectra of the Jacobians of the different DG semi-discretizations for the two-dimensional compressible Euler equations. We observed in Sect. 3.1 that the EC scheme immediately crashes, whereas the central scheme and the scheme powered by the Shima et al.  flux run for very long times ($t > 100$) without any problems.

For the linearization, we use the initial condition as the linearization state and compute the Jacobians approximately with a central finite difference approach in our simulation framework Trixi.jl [42]. The resulting spectra for the central flux with arithmetic means, the flux by Shima et al., and Ranocha’s EC flux are shown in Fig. 2. As in Sect. 3.1, we use the same numerical flux for the volume terms and the surface terms without any further dissipation.

Fig. 2

Spectra of split-form DG semi-discretizations of the compressible Euler equations in two space dimensions with linearization state (48). The DG methods use polynomials of degree $N = 5$ and a uniform grid of $4 \times 4$ elements in the domain $[-1, 1]^2$ with periodic boundary conditions. The same numerical flux is used for both the volume terms and at surfaces

As expected, the central flux results in a spectra that is almost purely imaginary, with only small deviations of the eigenvalues from the imaginary axis that are within machine accuracy when considering the approximation of the Jacobian via finite differences and the conditioning of the associated eigenvector matrix for this problem.

Remark 7

We would like to stress that eigenvalues of nonlinear right-hand sides in an ODE $u'(t) = g(u(t))$ do not necessarily predict the global behavior of solutions. For example, an energy-conserving ODE with purely positive and negative eigenvalues is discussed in [35, 37]. However, eigenvalues of the linearized Jacobian predict the local behavior of the solution, e.g., the temporal development of initial perturbations. In fluid dynamics, it is well known that there are many flow states that are physically unstable, i.e., flow states such as shear layers where added initial perturbations grow exponentially in time, until they start to behave nonlinearly and transition to turbulence. In the considered case of density propagation discussed in this section, we do not expect to find significant signs of exponential growth, as also indicated by the almost imaginary spectrum obtained for the central flux. In particular, the compressible Euler equations are reduced to linear advection equations and hence this particular flow state is physically stable with respect to density perturbations.

As anticipated following the numerical investigations in Sect. 3.1, the EC, KEP, and PEP flux (14) of Ranocha yields eigenvalues with clearly positive real parts of order unity, which do not vanish under grid refinement, but shift to higher imaginary values (see [13] for a more detailed discussion on this effect). This underlines our conclusion to research question (RQ2), that the PEP property does not fix the local linear stability issue of the EC split-form DG scheme.

Surprisingly, the spectrum with the KEP and PEP flux (36) of Shima et al.  [44] shows similar issues—it clearly has eigenvalues with positive real parts. This discretization is not locally linearly stable neither. However, as observed in Sect. 3.1, the discretization could robustly handle the density wave example (we made sure to test very long times $t > 100$ as well).

It is important to point out that the density wave example is a specific test case particular well suited to the Shima et al.  powered discretization where it works perfectly fine, as it preserves the pressure and velocity as constants down to machine precision and hence reduces to the central scheme in this particular case. The spectrum clearly shows that adding just a small perturbation to this state may lead to spurious exponential growth—hence it is not locally linearly stable. The spectrum with the central flux is (almost) purely imaginary and has no growth of any modes. Constant pressure and velocity within machine precision accuracy cause very small perturbations in the range of $10^{-15}$. Hence, it would take a really (really) long simulation run time until these machine accuracy fluctuations grow. Furthermore, at this very small perturbation scale, the artificial dissipation of the time integration is effective and the $\mathtt {cfl}$ would have to be drastically reduced.

We thus need a feasible setup to further assess the robustness of the DG split-form with the Shima et al.  flux: we make a simulation that investigates the growth of medium scale perturbations added to the initial conditions (see [13] for additional details). We start with the same setup as above and compute the eigenvector ${\tilde{u}}_0$ associated with the biggest real eigenvalue of the semi-discretization using the numerical flux (36) of Shima et al.  [44]. The numerically computed eigenvector is purely real valued. Note that this eigenvector can always be chosen to be real-valued since the Jacobian and its corresponding eigenvalue are both real-valued. We normalize the eigenvector such that $\Vert {\tilde{u}}_0 \Vert _\infty = 1$ and use the perturbed initial condition $u_0 + 10^{-3} {\tilde{u}}_0$, where $u_0$ is the original initial condition given by (48). Thus, the perturbation scale is now $10^{-3}$, instead of $10^{-15}$. Furthermore, the shape of the perturbation corresponds to the eigenmode of the spectrum. Thus, we are able to compare the growth of the fluctuations from the simulation, to the one predicted by the spectra using the real part of the eigenvalue as the growth rate.

To get the evolution of the perturbation, we subtract in each Runge-Kutta stage the semi-discretization applied to the unperturbed initial condition from the resulting semi-discretization of the perturbed initial state. We perform these numerical experiments using the flux (36) of Shima et al.  [44] as surface flux for the DG scheme, and in addition also using the dissipative HLL flux [16] as surface flux, while both discretizations use the Shima et al.  flux for the split-form volume integral.

Fig. 3

Evolution of an eigenvector perturbation of the initial condition (48). The DG methods use polynomials of degree $N = 5$ and a uniform grid of $4 \times 4$ elements in the domain $[-1, 1]^2$ with periodic boundary conditions and the numerical flux of Shima et al.  [44]

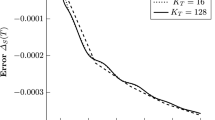
The resulting discrete $l^\infty$ error of the perturbations in the conserved variables is visualized in Fig. 3. Clearly, the fluctuations grow exponentially with a rate perfectly matching that of the real part of the eigenvalue. The simulation terminates at $t \approx 4.6$ because of negative densities for the case without surface dissipation and at $t \approx 9$ if the HLL flux is used. Clearly, the dissipative HLL flux reduces the growth of the fluctuations but only quantitatively, not qualitatively. Surface dissipation can not guarantee to control errors stemming from badly discretized split-form volume integrals. Consequently, in this case, the error still spuriously grows exponentially in time and finally results in unphysical solutions, which underlines the local stability issues of the Shima et al.  flux and hence confirms the statement in [13], that many split-form discretizations have these problems.

Fig. 4

Evolution of a random perturbation of the initial condition (48). The DG methods use polynomials of degree $N = 5$ and a uniform grid of $4 \times 4$ elements in the domain $[-1, 1]^2$ with periodic boundary conditions and the numerical flux of Shima et al.  [44]

We also considered a random perturbation of the initial condition, where each conserved variable is perturbed randomly at each point with a uniform distribution that is symmetric around zero. Such an approach is also used to estimate the Lyapunov exponent of a dynamical system [52]. The resulting errors of the fluctuation simulation are visualized in Fig. 4. Without adding dissipation, the error grows approximately exponentially with a rate governed by the maximal real eigenvalue. When surface dissipation in form of an HLL flux is added, the perturbation grows slowly at first but shows the same exponential growth governed by the largest real eigenvalue later.

EC and Local Linear Stability

Combining the results from our numerical investigations with Corollary 1 or Corollary 2 gives at least a partial answer to our third research question (RQ3): there are no Harten entropies for the compressible Euler equations such that the associated EC two-point fluxes result in locally linearly stable schemes.

Summary and Discussion

In this paper, we investigate the answers to the three research questions.

• (RQ1) Are there EC two-point fluxes for the compressible Euler equations with the KEP and PEP property?

• (RQ2) Does the PEP property remedy the local linear stability issues of high-order split-form DG schemes?

• (RQ3) Are there entropies, such that the EC two-point fluxes and corresponding EC volume integral terms are locally linearly stable?

We first stress and clarify, as discussed in detail in [13], the final goal is not to construct a discretization that is entropy-conservative. However, the entropy-conservative volume terms in the high-order split-form DG discretization are the key to achieve provably discrete entropy-dissipation. And while it is possible (and common) to introduce dissipation through the surface integrals by proper choice of entropy-dissipative/stable two-point fluxes as surface fluxes, it was also observed here and in [13] that surface type dissipation alone is not enough to fix the issue stemming from the volume terms. Consequently, the answers that we found for our research questions not only underline the worrisome findings in [13], but even strengthen them.

Collecting the answers to our research questions, we found in Sect. 2 that the answer to the first research question (RQ1) is yes. It turns out that the flux developed in [33, 34] is indeed EC, KEP, and PEP. It is interesting to note, that this is also the only available choice for the compressible Euler equations with ideal gas law.

Unfortunately, we could show that the answer to the research question (RQ2) is no, as discussed in Sect. 3. The additional property of PEP does not fix the stability issue for the simple density wave propagation when using the EC scheme. We demonstrated that the issue is the logarithmic mean of the density, which is necessary in the density flux. This is in contrast to the two-point flux proposed by Shima et al.  [44], which is KEP and PEP and can robustly run the density wave example as it uses the arithmetic mean of density in the density flux. However, this discretization is again not locally linearly stable as shown by computing the spectra and performing simulations to analyze the growth of perturbations.

The worrisome answer to the third research question (RQ3) is no, at least if we consider the family of entropies introduced by Harten. We could prove that it is not possible to find a Harten entropy for the compressible Euler equation, such that the density flux is based on the arithmetic mean of the density. Our investigations of the linear advection equation clearly show that without arithmetic mean, the discretizations are not locally linearly stable. Thus, all corresponding EC split-form schemes for the compressible Euler equation will have local linear stability issues for the simple density wave propagation.

Appendices

Appendix A The PEP Property for High-Order Schemes

Extending Lemma 1, the PEP property (11) of a numerical flux $f^{{\mathrm {num}}}$ extends directly to a high-order semi-discretization (51).

Lemma A.1

A pressure equilibrium $p \equiv {\mathrm {const}}, v \equiv {\mathrm {const}}$ is preserved by any general linear method applied to the semi-discretization (51) if the numerical flux $f^{{\mathrm {num}}}$ is PEP.

Proof

It suffices to consider linear combinations of numerical solutions as well as the addition of the semidiscrete operator to a numerical solution. Linear combinations preserve a pressure equilibrium, since $\rho$, $\rho v$, and $\rho e = \rho v^2 / 2 + p / (\gamma - 1)$ are linear in $\rho$. Given $\alpha \in {\mathbb {R}}$, the scaled addition of the semidiscrete operator to a solution preserves the pressure equilibrium, since

$$\left\{\begin{aligned} \begin{aligned}&\rho :\rho _i + \alpha \sum _l D_{i,l} f^{{\mathrm {num}}}_{\rho }(u_i, u_l), \\&\rho v :(\rho v)_i + \alpha \sum _l D_{i,l} f^{{\mathrm {num}}}_{\rho v}(u_i, u_l) = \rho _i v + \alpha \sum _l D_{i,l} \left( v f^{{\mathrm {num}}}_{\rho }(u_i, u_l) + {\mathrm {const}}(p, v) \right) \\&\quad = \left( \rho _i + \alpha \sum _l D_{i,l} f^{{\mathrm {num}}}_{\rho }(u_i, u_l) \right) v, \\&\rho e :(\rho e)_i + \alpha \sum _l D_{i,l} f^{{\mathrm {num}}}_{\rho e}(u_i, u_l) = \frac{1}{2} \rho _i v^2 + \frac{1}{\gamma - 1} p\\&\qquad + \alpha \sum _l D_{i,l} \left( \frac{1}{2} v^2 f^{{\mathrm {num}}}_{\rho }(u_i, u_l) + {\mathrm {const}}(p, v) \right) \\&\quad = \frac{1}{2} \left( \rho _i + \alpha \sum _l D_{i,l} f^{{\mathrm {num}}}_{\rho }(u_i, u_l) \right) v^2 + \frac{1}{\gamma - 1} p. \end{aligned} \end{aligned}\right.$$

(A1)

Here, we used $\sum _l D_{i,l} = 0$, which is a necessary condition for a consistent derivative operator D.

Appendix B Stability Investigation of Alternative Mean Values

The logarithmic mean value is not the only mean value that is problematic for the stability. To demonstrate this, we show spectra of second-order central finite difference methods of the form (51), where the numerical flux is chosen as any of the different mean values studied in [6], namely

• the centroidal mean $f^{{\mathrm {num}}}(u_-, u_+) = 2 (u_-^2 + u_- u_+ + u_+^2) / 3 (u_- + u_+)$,

• the arithmetic mean $f^{{\mathrm {num}}}(u_-, u_+) = (u_- + u_+) / 2$,

• the Heronian mean $f^{{\mathrm {num}}}(u_-, u_+) = (u_- + \sqrt{u_- u_+} + u_+) / 3$,

• the logarithmic mean $f^{{\mathrm {num}}}(u_-, u_+) = (u_+ - u_-) / (\log u_+ - \log u_-)$,

• the geometric mean $f^{{\mathrm {num}}}(u_-, u_+) = \sqrt{u_- u_+}$,

• and the harmonic mean $f^{{\mathrm {num}}}(u_-, u_+) = 2 u_- u_+ / (u_- + u_+)$.

This list is ordered in descending order of the size of the mean values [6].

The resulting spectra are shown in Fig. 5. Clearly, all mean values except the arithmetic mean result in eigenvalues with positive real parts. The size of the maximal real part of the spectrum increases for mean values that deviate more from the arithmetic mean value.

Fig. 5

Spectra of nonlinear semi-discretizations (51) using second-order central finite difference methods and different mean values as numerical flux