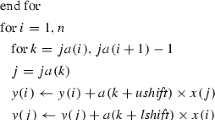p-Multilevel Preconditioners for HHO Discretizations of the Stokes Equations with Static Condensation

Abstract

We propose a p-multilevel preconditioner for hybrid high-order (HHO) discretizations of the Stokes equation, numerically assess its performance on two variants of the method, and compare with a classical discontinuous Galerkin scheme. An efficient implementation is proposed where coarse level operators are inherited using $L^2$-orthogonal projections defined over mesh faces and the restriction of the fine grid operators is performed recursively and matrix-free. Both h- and k-dependency are investigated tackling two- and three-dimensional problems on standard meshes and graded meshes. For the two HHO formulations, featuring discontinuous or hybrid pressure, we study how the combination of p-coarsening and static condensation influences the V-cycle iteration. In particular, two different static condensation procedures are considered for the discontinuous pressure HHO variant, resulting in global linear systems with a different number of unknowns and matrix non-zero entries. Interestingly, we show that the efficiency of the solution strategy might be impacted by static condensation options in the case of graded meshes.

1 Introduction

In this work we develop and numerically validate p-multigrid solution strategies for nonconforming polytopal discretizations of the Stokes equations, governing the creeping flow of incompressible fluids.

For the sake of simplicity, we focus on a Newtonian fluid with uniform density and unit kinematic viscosity. Given a polygonal or polyhedral domain $\varOmega \subset {\mathbb {R}}^d$, $d\in \{2,3\}$, with boundary $\partial\varOmega$, the Stokes problem consists in finding the velocity field ${\varvec{u}}: \varOmega \rightarrow {\mathbb {R}}^d$ and the pressure field $p: \varOmega \rightarrow {\mathbb {R}}$, such that

$$\begin{aligned} -{\Delta {\varvec{u}}} + {\nabla p}&= {\varvec{f}}&\quad&\text {in }\varOmega , \end{aligned}$$

(1a)

$$\begin{aligned} {\nabla \cdot {\varvec{u}}}&= 0&\quad&\text {in }\varOmega , \end{aligned}$$

(1b)

$$\begin{aligned} {\varvec{u}}&= {\varvec{g}}_{\mathrm{D}}&\quad&\text {on }\partial \varOmega _{\mathrm{D}}, \end{aligned}$$

(1c)

$$\begin{aligned} - {\varvec{n}}\cdot \nabla {\varvec{u}}+ p {\varvec{n}}&= {\varvec{g}}_{\mathrm{N}}&\quad&\text {on }\partial \varOmega _{\mathrm{N}}, \end{aligned}$$

(1d)

where ${\varvec{n}}$ denotes the unit vector normal to $\partial \varOmega$ pointing out of $\varOmega$, ${\varvec{g}}_{\mathrm{D}}$ and ${\varvec{g}}_{\mathrm{N}}$ denote, respectively, the prescribed velocity on the Dirichlet boundary $\partial \varOmega _{\mathrm{D}}\subset \partial \varOmega$ and the prescribed traction on the Neumann boundary $\partial \varOmega _{\mathrm{N}}{:}=\partial \varOmega \setminus \partial \varOmega _{\mathrm{D}}$, while ${\varvec{f}}:\varOmega \rightarrow {\mathbb {R}}^d$ is a given body force. For the sake of simplicity, it is assumed in what follows that both $\partial \varOmega _{\mathrm{D}}$ and $\partial \varOmega _{\mathrm{N}}$ have non-zero $(d-1)$-dimensional Hausdorff measure (otherwise, additional closure conditions are needed).

Our focus is on new generation discretization methods for problem (1) that support general polytopal meshes and high-order: hybrid high-order (HHO) and discontinuous Galerkin (DG) methods.

HHO discretizations of the Stokes equations have been originally considered in [2] and later extended in [38] to incorporate robust handling of large irrotational body forces. Other extensions include their application to the Brinkman problem, considered in [18], Stokes equations [20, 35, 36]; see also [32, Chapters 8 and 9] for further details. In this work, we consider two HHO schemes that are novel variations of existing schemes with improved features. The first scheme, based on a hybrid approximation of the velocity along with a discontinuous approximation of the pressure, is a variation of the one considered in [32, Chapter 8] including two choices for the polynomial degree of the element velocity unknowns in the spirit of [30] (see also [32, Section 5.1]). The second scheme, inspired by the hybridizable discontinuous Galerkin (HDG) method of [52], see also [47], hinges on hybrid approximations of both the velocity and the pressure and includes, with respect to the above reference, a different treatment of viscous terms that results in improved orders of convergence. In both cases, the Dirichlet condition on the velocity is enforced weakly in the spirit of [20].

Since the pioneering works [23,24,25,26,27] dating back to the late 1980s, DG methods have gained significant popularity in computational fluid mechanics, boosted by the 1997 landmark papers [9, 10] on the treatment of viscous terms. The extension of DG methods to general polyhedral meshes was systematically considered in [33, 34]. Crucially, this extension paved the way to adaptive mesh coarsening by agglomeration, a strategy proposed in [14] and exploited in [13, 15] in practical CFD applications to provide high-order accurate geometry representation with arbitrarily coarse meshes. More recent developments, including hp-versions and the support of meshes with small faces, can be found in [3, 5]; see also the recent monograph [21]. Our focus is on an equal-order approximation with stabilized pressure-velocity coupling in the spirit of [28] and a treatment of the viscous term based on the Bassi-Rebay 2 (BR2) method of [10]. Related works include [11, 31]; see also [34, Chapter 6] and references therein.

p-Multilevel solvers, extending the original ideas of [53] on spectral element multigrid, are well suited for both HHO and DG methods because the process of building coarse level operators based on polynomial degree reduction is straightforward and inexpensive. The purpose of applying iterative solvers to coarse problems is twofold: on the one hand, a coarser operator translates into a global sparse matrix of smaller size with fewer non-zero entries, resulting in cheaper matrix-vector products; on the other hand, coarse level iterations are best suited to smooth out the low-frequency components of the error, that are hardly damped by fine level iterations. In the context of DG discretizations, p-multilevel solvers have been fruitfully utilized in practical applications, see, e.g., [12, 42, 43, 48, 54]. h-, p- and hp-multigrid solvers for DG discretizations of elliptic problems have been considered in [4], where uniform convergence with respect to the number of levels for the W-cycle iteration has been proved, and in [19]. Multigrid solvers for HDG discretizations of scalar elliptic problems were considered in [29] and, more recently, in [41, 46], where a comparison with DG is carried out. p-Multivel solvers for HDG methods with application to compressible flow simulations have been recently considered in [44]. Preconditioners for DG and HDG discretizations of the Stokes problem have been considered in [1, 7, 17, 22, 45, 51], respectively. Finally, an h-multigrid method for HHO discretizations of scalar diffusion problems has been recently proposed in [39]. The main novelty consists, in this case, in the use of the local potential reconstruction in the prolongation operator. Notice that h-multilevel solvers for HHO face a fundamental difficulty linked to the fact that face coarsening is required to damp high frequencies; see again [39] for further details on this subject and [16] for an extension of HHO to more general faces.

In this work we propose and numerically assess p-multilevel solution strategies for HHO discretizations of the Stokes equations. We specifically investigate how the combination of p-coarsening and static condensation influences the performance of the V-cycle iteration. To this end, we compare different static condensation strategies. In order to preserve computational efficiency, statically condensed coarse level operators are inherited using local $L^2$-orthogonal projections defined over mesh faces. Restriction of fine grid operators is performed recursively and matrix-free, relying on $L^2$-orthogonal basis functions to further reduce the computational burden. Performance assessment is based on accuracy and efficiency of p-multilevel solvers considering DG discretizations as a reference for comparison. High-order accurate solutions approximating smooth analytical velocity and pressure fields are computed over standard and severely graded h-refined mesh sequences in both two and three space dimensions. Interestingly, the static condensation strategy plays a crucial role in case of graded meshes.

The rest of this work is organized as follows. In Sect. 2 we state the HHO and DG schemes considered in the numerical tests. The p-multilevel strategy is discussed in Sect. 3 and computational aspects are discussed in Sect. 4. Section 5 contains an extensive panel of numerical results that enable one to assess and compare several solution strategies. Finally, some conclusions are drawn in Sect. 8.

2 Three Nonconforming Methods for the Stokes Problem

In this section we describe two HHO and one DG methods for the approximation of problem (1) that will be used to assess the performance of the p-multilevel preconditioner. In order to lay the ground for future works on the full nonlinear Navier-Stokes equations, the corresponding discrete problems are formulated in terms of the annihilation of residuals.

2.1 Discrete Setting

We consider meshes of the domain $\varOmega$ corresponding to couples ${\mathcal {M}}_h:=({\mathcal {T}}_h,{\mathcal {F}}_h)$, where ${\mathcal {T}}_h$ is a finite collection of polygonal (if $d=2$) or polyhedral (if $d=3$) elements such that $h:=\max _{T\in {\mathcal {T}}_h}h_T>0$ with $h_T$ denoting the diameter of T, while ${\mathcal {F}}_h$ is a finite collection of line segments (if $d=2$) or polygonal faces (if $d=3$). For the sake of brevity, in what follows the term “face” will be used in both two and three space dimensions. It is assumed henceforth that the mesh ${\mathcal {M}}_h$ matches the geometrical requirements detailed in [32, Definition 1.4]. This covers, essentially, any reasonable partition of $\varOmega$ into polyhedral sets, not necessarily convex. For each mesh element $T \in {\mathcal {T}}_h$, the faces contained in the element boundary $\partial T$ are collected in the set ${\mathcal {F}}_T$, and, for each mesh face $F \in {\mathcal {F}}_h$, ${\mathcal {T}}_F$ is the set containing the one or two mesh elements sharing F. We define three disjoint subsets of the set ${\mathcal {F}}_T$: the set of Dirichlet boundary faces ${\mathcal {F}}_T^{\mathrm{D}}:=\{F \in {\mathcal {F}}_T: F \subset \partial \Omega _{\mathrm{D}}\}$; the set of Neumann boundary faces ${\mathcal {F}}_T^{\mathrm{N}}:=\{F \in {\mathcal {F}}_T: F \subset \partial \Omega _{\mathrm{N}}\}$; the set of internal faces ${\mathcal {F}}_T^\mathrm{i}:={\mathcal {F}}_T\setminus \big ({\mathcal {F}}_T^{\mathrm{D}}\cup {\mathcal {F}}_T^{\mathrm{N}}\big )$. For future use, we also let ${\mathcal {F}}_T^{\mathrm{i},{\mathrm{D}}}:={\mathcal {F}}_T^\mathrm{i}\cup {\mathcal {F}}_T^{\mathrm{D}}$. For all $T\in {\mathcal {T}}_h$ and all $F\in {\mathcal {F}}_T$, ${\varvec{n}}_{TF}$ denotes the unit vector normal to F pointing out of T.

HHO methods hinge on local polynomial spaces on mesh elements and faces. For given integers $\ell \geqslant 0$ and $n\geqslant 1$, we denote by ${\mathbb {P}}_{n}^{\ell }$ the space of n-variate polynomials of total degree $\leqslant \ell$ (in short, of degree $\ell$). For X mesh element or face, we denote by ${\mathcal {P}}^{\ell }(X)$ the space spanned by the restriction to X of functions in ${\mathbb {P}}_d^\ell$. When X is a mesh face, the resulting space is isomorphic to ${\mathbb {P}}_{d-1}^\ell$ (see [32, Proposition 1.23]). At the global level, we will need the broken polynomial space

$$\begin{aligned} {\mathcal {P}}^{\ell }({\mathcal {T}}_h){:}=\left\{ q\in L^2(\Omega): q_{|T}\in {\mathcal {P}}^{\ell }(T)\text { for all }T\in {\mathcal {T}}_h\right\} . \end{aligned}$$

Let again X denote a mesh element or face. The local $L^2$-orthogonal projector $\pi _X^\ell :L^2(X)\rightarrow {\mathcal {P}}^{\ell }(X)$ is such that, for all $q\in L^2(X)$,

$$\begin{aligned} \int _X ( q - \pi _X^\ell q ) r = 0,\quad \forall r\in {\mathcal {P}}^{\ell }(X). \end{aligned}$$

Notice that, above and in what follows, we omit the measure from integrals as it can always be inferred from the context. The $L^2$-orthogonal projector on ${\mathcal {P}}^{\ell }(X)^d$, obtained applying $\pi _X^\ell$ component-wise, is denoted by $\varvec{\pi }_X^\ell$.

2.2 Local Reconstructions and Face Residuals

The HHO discretizations of the Stokes problem considered in this work hinge on velocity reconstructions devised at the element level and obtained assembling diffusive potential reconstructions component-wise. In what follows, we let a mesh element $T\in {\mathcal {T}}_h$ be fixed, denote by $k\geqslant 0$ the degree of polynomials attached to mesh faces, and by $k'\in \{k,k+1\}$ the degree of polynomials attached to mesh elements.

2.2.1 Scalar Potential Reconstruction

The velocity reconstruction is obtained leveraging, for each component, the scalar potential reconstruction originally introduced in [37] in the context of scalar diffusion problems (see also [30] and [32, Section 5.1] for its generalization to the case of different polynomial degrees on elements and faces). Define the local scalar HHO space.

$$\begin{aligned} {\underline{V}}_T^{k',k} {:}=\left\{ {\underline{v}}_T = \left( v_T, (v_F)_{F \in {\mathcal {F}}_T} \right): v_T \in {\mathcal {P}}^{k'}(T) \,\,\text {and} \,\, v_F \in {\mathcal {P}}^{k}(F) \text { for all }F \in {\mathcal {F}}_T \right\} . \end{aligned}$$

(2)

The scalar potential reconstruction operator ${\mathfrak {p}}_T^{k+1}$: ${\underline{V}}_T^{k',k} \rightarrow {\mathcal {P}}^{k+1}(T)$ maps a vector of polynomials of ${\underline{V}}_T^{k',k}$ onto a polynomial of degree $(k+1)$ over T as follows: given ${\underline{v}}_{T} \in {\underline{V}}_T^{k',k}$, ${\mathfrak {p}}_T^{k+1}{\underline{v}}_T$ is the unique polynomial in ${\mathcal {P}}^{k+1}(T)$ satisfying

$$\begin{aligned} \begin{aligned} \int _T \nabla {\mathfrak {p}}_T^{k+1} {\underline{v}}_T \cdot \nabla {w_T}&= \int _T \nabla {v_T} \cdot \nabla {w_T} \\&\quad + \sum _{F \in {\mathcal {F}}_T} \int _F \left( {v_F} - {v_T}\right) \, \nabla {w_T} \cdot {\varvec{n}}_{TF}, \quad \forall w_T \in {\mathcal {P}}^{k +1}(T), \\ \int _T {\mathfrak {p}}_T^{k+1} {\underline{v}}_T&= \int _T {v_T}. \end{aligned} \end{aligned}$$

Computing ${\mathfrak {p}}_T^{k+1}$ for each $T\in {\mathcal {T}}_h$ requires to solve a small linear system. This is an embarrassingly parallel task that can fully benefit from parallel architectures.

2.2.2 Velocity Reconstruction

Define, in analogy with (2), the following vector-valued HHO space for the velocity:

$$\begin{aligned} {\underline{\varvec{V}}}_T^{k',k} {:}=\left\{ {\underline{\varvec{v}}}_T = \big ({\varvec{v}}_T, ({\varvec{v}}_F)_{F \in {\mathcal {F}}_T} \big ) : {{\varvec{v}}}_T \in {\mathcal {P}}^{k'}(T)^d \text { and }{\varvec{v}}_F \in {\mathcal {P}}^{k}(F)^d \text { for all }F \in {\mathcal {F}}_T \right\} . \end{aligned}$$

The velocity reconstruction ${\mathfrak {p}}_T^{k+1}$: ${\underline{\varvec{V}}}_T^{k',k} \rightarrow {\mathcal {P}}^{k+1}(T)^d$ is obtained setting

$$\begin{aligned} {\mathfrak {p}}_T^{k+1} {\underline{\varvec{v}}}_T {:}=\big ({\mathfrak {p}}_T^{k+1} {\underline{v}}_{T,i}\big )_{i=1,\cdots ,d}, \end{aligned}$$

where for all $i=1,\cdots ,d$, ${\underline{v}}_{T,i}\in {\underline{V}}_T^{k',k}$ is obtained gathering the ith components of the polynomials in ${\underline{\varvec{v}}}_T$, i.e., ${\underline{v}}_{T,i}{:}=\big (v_{T,i}, (v_{F,i})_{F\in {\mathcal {F}}_T}\big )$ if ${\varvec{v}}_T=(v_{T,i})_{i=1,\cdots ,d}$ and ${\varvec{v}}_F=(v_{F,i})_{i=1,\cdots ,d}$ for all $F\in {\mathcal {F}}_T$.

2.2.3 Face Residuals

Let $T\in {\mathcal {T}}_h$ and $F\in {\mathcal {F}}_T$. The stabilization bilinear form for the HHO discretization of the viscous term in the momentum equation (1a) hinges on the face residual ${\mathfrak {R}}_{TF}^k : {\underline{\varvec{V}}}_T^{k',k} \rightarrow {\mathcal {P}}^{\max (k',k)}(F)^d$ such that, for all ${\underline{\varvec{v}}}_T\in {\underline{\varvec{V}}}_T^{k',k}$,

$$\begin{aligned} {\mathfrak {R}}_T^{k',k} {\underline{\varvec{v}}}_T {:}=\big ( {\mathfrak {R}}_{TF}^{k',k} {\underline{v}}_{T,i} \big )_{i=1,\cdots ,d}, \end{aligned}$$

where the scalar face residual ${\tau}_{TF}^{k',k}:{\underline{V}}_T^{k',k}\rightarrow {\mathcal {P}}^{\max (k',k)}(F)$ is such that, for all ${\underline{v}}_T\in {\underline{V}}_T^{k',k}$,

$$\begin{aligned} {\tau}_{TF}^{k',k} {\underline{v}}_T {:}=\pi ^k_F \big (v_F - {\mathfrak {p}}_T^{k+1} {\underline{v}}_T \big ) - \pi ^{k'}_T \big (v_T - {\mathfrak {p}}_T^{k+1} {\underline{v}}_T \big ). \end{aligned}$$

2.3 HHO Schemes

We consider two HHO schemes based, respectively, on discontinuous and hybrid approximations of the pressure. In both cases, the Dirichlet boundary condition is enforced weakly, considering a symmetric variation of the method discussed in [18].

2.3.1 An HHO Scheme with Discontinuous Pressure

Let again $k\geqslant 0$ and $k'\in \{k,k+1\}$ denote the polynomial degrees of the face and element unknowns, respectively, and let a mesh element $T\in {\mathcal {T}}_h$ be fixed. Given $(\underline{{\varvec{u}}}_T, p_T) \in {\underline{\varvec{V}}}_T^{k',k}\times {\mathcal {P}}^{k}(T)$, the local residuals $r^{\mathrm{mnt}}_{\mathrm{{I}},T}(({\underline{{\varvec{u}}}}_T,p_T);\cdot ):{\underline{\varvec{V}}}_T^{k',k}\rightarrow {\mathbb {R}}$ of the discrete momentum conservation equation and $r^{\mathrm{cnt}}_{\mathrm{{I}},T}({\underline{{\varvec{u}}}}_T;\cdot ):{\mathcal {P}}^{k}(T)\rightarrow {\mathbb {R}}$ of the discrete mass conservation equation are such that, respectively: for all ${\underline{\varvec{v}}}_T\in {\underline{\varvec{V}}}_T^{k',k}$ and all $q_T\in {\mathcal {P}}^{k}(T)$,

$$\begin{aligned} r^{\mathrm{mnt}}_{\mathrm{{I}},T}(({\underline{{\varvec{u}}}}_T,p_T);{\underline{\varvec{v}}}_T)&{:}=\int _T \nabla {\mathfrak {p}}_T^{k+1} \underline{{\varvec{u}}}_{T} : \nabla {\mathfrak {p}}_T^{k+1} {\underline{\varvec{v}}}_{T} + \sum _{F \in {\mathcal {F}}_T} \frac{1}{h_F} \int _F {\mathfrak {R}}_{TF}^k \underline{{\varvec{u}}}_T \, \cdot \, {\mathfrak {R}}_{TF}^k {\underline{\varvec{v}}}_T \nonumber \\& - \sum _{F \in {\mathcal {F}}_T^{\mathrm{D}}} \int _F \left[ \bigl ( {\varvec{n}}_{TF} \cdot \nabla {\mathfrak {p}}_T^{k+1} \underline{{\varvec{u}}}_{T} \bigr ) \cdot {\varvec{v}}_F + {\varvec{u}}_F \cdot \bigl ( {\varvec{n}}_{TF} \cdot \nabla {\mathfrak {p}}_T^{k+1} {\underline{\varvec{v}}}_{T}\bigr ) \right] \nonumber \\&\quad +\sum _{F \in {\mathcal {F}}_T^{\mathrm{D}}} \frac{\eta }{h_F} \int _F {\varvec{u}}_F \cdot {\varvec{v}}_{F}\nonumber - \int _T p_T \, (\nabla \cdot {\varvec{v}}_T) - \sum _{F \in {\mathcal {F}}_T} \int _F p_T \, ({\varvec{v}}_F - {\varvec{v}}_T) \cdot {\varvec{n}}_{TF} \nonumber \\&\quad + \sum _{F \in {\mathcal {F}}_T^{\mathrm{D}}} \int _F p_T \, ({\varvec{v}}_F \cdot {\varvec{n}}_{TF}) \nonumber - \sum _{F \in {\mathcal {F}}_T^{\mathrm{D}}} \int _F {\varvec{g}}_{\mathrm{D}}\cdot \left( {\varvec{n}}_{TF} \cdot \nabla {\mathfrak {p}}_T^{k+1} {\underline{\varvec{v}}}_{T} + \frac{\eta }{h_F} {\varvec{v}}_{F} \right) \nonumber \\&\quad - \sum _{F \in {\mathcal {F}}_T^{\mathrm{N}}} \int _F {\varvec{g}}_{\mathrm{N}}\cdot {\varvec{v}}_F - \int _{T} {\varvec{f}} \cdot {\varvec{v}}_T,\end{aligned}$$

(3a)

$$\begin {aligned} r^{\mathrm{cnt}}_{\mathrm{{I}},T}({\underline{{\varvec{u}}}}_T;q_T)&{:}=- \int _T (\nabla \cdot {\varvec{u}}_T) \, q_T - \sum _{F \in {\mathcal {F}}_T} \int _F ({\varvec{u}}_F - {\varvec{u}}_T) \cdot {\varvec{n}}_{TF} \, q_T \nonumber \\&\quad + \sum _{F \in {\mathcal {F}}_T^{\mathrm{D}}} \int _F ({\varvec{u}}_F \cdot {\varvec{n}}_{TF}) \, q_T \nonumber - \sum _{F \in {\mathcal {F}}_T^{\mathrm{D}}} \int _F {\varvec{g}}_{\mathrm{D}}\cdot {\varvec{n}}_{TF} \, q_T. \end{aligned}$$

(3b)

In the expression of $r^{\mathrm{mnt}}_{\mathrm{{I}},T}(({\underline{{\varvec{u}}}}_T,p_T);\cdot )$, $\eta >0$ is a user-dependent parameter that has to be taken large enough to ensure coercivity. The penalty term where the parameter $\eta$ appears, along with the consistency terms in the second line and the term involving the boundary datum ${\varvec{g}}_{\mathrm{D}}$ in the fifth line, are responsible for the weak enforcement of the Dirichlet boundary condition for the velocity. In the numerical tests provided below, $\eta$ is taken equal to 3.

Define the global vector HHO space

$$\begin{aligned}&{\underline{\varvec{V}}}_h^{k',k}{:}=\left\{ {\underline{\varvec{v}}}_h = \big ( ({\varvec{v}}_T)_{T\in {\mathcal {T}}_h} , ({\varvec{v}}_F)_{F \in {\mathcal {F}}_h} \big ) \right. \left. : {{\varvec{v}}}_T \in {\mathcal {P}}^{k'}(T)^d \text { for all }T\in {\mathcal {T}}_h\text { and }{\varvec{v}}_F \in {\mathcal {P}}^{k}(F)^d \text { for all }F \in {\mathcal {F}}_h\right\} . \end{aligned}$$

For all ${\underline{\varvec{v}}}_h\in {\underline{\varvec{V}}}_h^{k',k}$ and all $T\in {\mathcal {T}}_h$, we denote by ${\underline{\varvec{v}}}_T\in {\underline{\varvec{V}}}_T^{k',k}$ the restriction of ${\underline{\varvec{v}}}_h$ to T. The global residuals $r_{\mathrm{{I}},h}^{\mathrm{mnt}}\left( ({\underline{{\varvec{u}}}}_h,p_h);\cdot \right):{\underline{\varvec{V}}}_h^{k',k}\rightarrow {\mathbb {R}}$ and $r^{\mathrm{cnt}}_{\mathrm{{I}},h}({\underline{{\varvec{u}}}}_h;\cdot):{\mathcal {P}}^{k}({\mathcal {T}}_h)\rightarrow {\mathbb {R}}$ are obtained by element-by-element assembly, i.e., for all ${\underline{\varvec{v}}}_h\in {\underline{\varvec{V}}}_h^{k',k}$ and all $q_h\in {\mathcal {P}}^{k}({\mathcal {T}}_h)$,

$$\begin{aligned} r_{\mathrm{{I}},h}^{\mathrm{mnt}}\left( ({\underline{{\varvec{u}}}}_h,p_h);{\underline{\varvec{v}}}_h\right) {:}=\sum _{T\in {\mathcal {T}}_h} r^{\mathrm{mnt}}_{\mathrm{{I}},T}\left( ({\underline{{\varvec{u}}}}_T,p_T);{\underline{\varvec{v}}}_T\right) ,\quad r_{\mathrm{{I}},h}^{\mathrm{cnt}}({\underline{{\varvec{u}}}}_h;q_h) {:}=\sum _{T\in {\mathcal {T}}_h} r^{\mathrm{cnt}}_{\mathrm{{I}},T}({\underline{{\varvec{u}}}}_T;q_{h|T}). \end{aligned}$$

(4)

Scheme I

(HHO-dp: HHO scheme with discontinuous pressure) Find $({\underline{{\varvec{u}}}}_h,p_h)\in {\underline{\varvec{V}}}_h^{k',k}\times {\mathcal {P}}^{k}({\mathcal {T}}_h)$ such that

$$\left\{\begin{aligned} \begin{aligned} &r_{\mathrm{{I}},h}^{\mathrm{mnt}}\left( ({\underline{{\varvec{u}}}}_h,p_h);{\underline{\varvec{v}}}_h\right)&= 0,&\quad&\forall {\underline{\varvec{v}}}_h\in {\underline{\varvec{V}}}_h^{k',k}, \\ &r_{\mathrm{{I}},h}^{\mathrm{cnt}}({\underline{{\varvec{u}}}}_h;q_h)= 0,&\quad&\forall q_h\in {\mathcal {P}}^{k}({\mathcal {T}}_h). \end{aligned} \end{aligned}\right.$$

(5)

2.3.2 An HHO Scheme with Hybrid Pressure

An interesting variation of Scheme I is obtained combining the HHO discretization of the viscous term with $k'=k+1$ with a hybrid approximation of the pressure inspired by [52]. Let $T\in {\mathcal {T}}_h$. Given $(\underline{{\varvec{u}}}_T, {\underline{p}}_T)\in {\underline{\varvec{V}}}_T^{k+1,k}\times {\underline{V}}_T^{k,k}$, the local residuals $r^{\mathrm{mnt}}_{\mathrm{{II}},T} (({\underline{{\varvec{u}}}}_T,{\underline{p}}_T);\cdot ):{\underline{\varvec{V}}}_T^{k+1,k}\rightarrow {\mathbb {R}}$ of the discrete momentum and $r^{\mathrm{cnt}}_{\mathrm{{II}},T}({\underline{{\varvec{u}}}}_T;\cdot ):{\underline{V}}^{k,k}_T\rightarrow {\mathbb {R}}$ of the discrete mass conservation equations for the HHO scheme with hybrid pressure are such that, for all ${\underline{\varvec{v}}}_T\in {\underline{\varvec{V}}}_T^{k+1,k}$ and all $\underline{q}_T\in {\underline{V}}_T^{k,k}$,

$$\begin{aligned} r^{\mathrm{mnt}}_{\mathrm{{II}},T} (({\underline{{\varvec{u}}}}_T,{\underline{p}}_T);{\underline{\varvec{v}}}_T)&{:}=\int _T \nabla {\mathfrak {p}}_T^{k+1} \underline{{\varvec{u}}}_{T} : \nabla {\mathfrak {p}}_T^{k+1} {\underline{\varvec{v}}}_{T} + \sum _{F \in {\mathcal {F}}_T} \frac{1}{h_F} \int _F {\mathfrak {R}}_{TF}^k {\underline{\varvec{v}}}_T \, \cdot \, {\mathfrak {R}}_{TF}^k {\underline{\varvec{v}}}_T\\&\quad- \sum _{F \in {\mathcal {F}}_T^{\mathrm{D}}} \int _F \left[ \bigl ( {\varvec{n}}_{TF} \cdot \nabla {\mathfrak {p}}_T^{k+1} \underline{{\varvec{u}}}_{T} \bigr ) \cdot {\varvec{v}}_F + {\varvec{u}}_F \cdot \bigl ( {\varvec{n}}_{TF} \cdot \nabla {\mathfrak {p}}_T^{k+1} {\underline{\varvec{v}}}_{T}\bigr ) \right] \\&\quad +\sum _{F \in {\mathcal {F}}_T^{\mathrm{D}}} \frac{\eta }{h_F} \int _F {\varvec{u}}_F \cdot {\varvec{v}}_{F}- \int _T p_{T} \, (\nabla \cdot {\varvec{v}}_T) + \boxed { \displaystyle \sum _{F \in {\mathcal {F}}_T} \int _F p_F \, ({\varvec{v}}_T - {\varvec{v}}_F) \cdot {\varvec{n}}_{TF} } \\&\quad + \sum _{F \in {\mathcal {F}}_T^{\mathrm{D}}} \int _F p_F \, ({\varvec{v}}_F \cdot {\varvec{n}}_{TF})- \sum _{F \in {\mathcal {F}}_T^{\mathrm{D}}} \int _F {\varvec{g}}_{\mathrm{D}}\cdot \left( {\varvec{n}}_{TF} \cdot \nabla {\mathfrak {p}}_T^{k+1} {\underline{\varvec{v}}}_{T} + \frac{\eta }{h_F} {\varvec{v}}_{F} \right) \\&\quad - \sum _{F \in {\mathcal {F}}_T^{\mathrm{N}}} \int _F {\varvec{g}}_{\mathrm{N}}\cdot {\varvec{v}}_F - \int _{T} {\varvec{f}} \cdot {\varvec{v}}_T, \\ r^{\mathrm{cnt}}_{\mathrm{{II}},T}({\underline{{\varvec{u}}}}_T;\underline{q}_T)&{:}=- \int _T (\nabla \cdot {{\varvec{u}}}_T) \, q_T + \boxed { \displaystyle \sum _{F \in {\mathcal {F}}_T} \int _F ( {\varvec{u}}_T - {\varvec{u}}_F ) \cdot {\varvec{n}}_{TF} \, q_F } \\&\quad\, + \sum _{F \in {\mathcal {F}}_T^{\mathrm{D}}} \int _F ({\varvec{u}}_F \cdot {\varvec{n}}_{TF}) \, q_F - \sum _{F \in {\mathcal {F}}_T^{\mathrm{D}}} \int _F {\varvec{g}}_{\mathrm{D}}\cdot {\varvec{n}}_{TF} \, q_F. \end{aligned}$$

As before, $\eta >0$ is a penalty parameter that has to be taken large enough to ensure coercivity. The boxed terms are the ones that distinguish the local residuals on the momentum and mass conservation equations for the HHO scheme with hybrid pressure from Scheme I with $k'=k+1$.

Define the global scalar HHO space

$$\begin{aligned}&{\underline{V}}_h^{k,k}{:}=\left\{ \underline{q}_h=\big ((q_T)_{T\in {\mathcal {T}}_h}, (q_F)_{F\in {\mathcal {F}}_h}\big )\,\ \right. \left. :\, q_T\in {\mathcal {P}}^{k}(T) \text { for all }T\in {\mathcal {T}}_h\text { and }q_F\in {\mathcal {P}}^{k}(F) \text { for all }F\in {\mathcal {F}}_h\right\} . \end{aligned}$$

The global residuals $r^{\mathrm{mnt}}_{\mathrm{{II}},h}(({\underline{{\varvec{u}}}}_h,{\underline{p}}_h);\cdot ):{\underline{\varvec{V}}}^{k+1,k}_h\rightarrow {\mathbb {R}}$ and $r^{\mathrm{cnt}}_{\mathrm{{II}},h}({\underline{{\varvec{u}}}}_h;\cdot ):{\underline{V}}^{k,k}_h\rightarrow {\mathbb {R}}$ are obtained by element-by-element assembly of the local residuals.

Scheme II

(HHO-hp: HHO scheme with hybrid pressure) Find $({\underline{{\varvec{u}}}}_h,{\underline{p}}_h)\in {\underline{\varvec{V}}}_h^{k+1,k}\times {\underline{V}}^{k,k}_h$ such that

$$\left\{\begin{aligned} \begin{aligned} &r_{\mathrm{{II}},h}^{\mathrm{mnt}}(({\underline{{\varvec{u}}}}_h,{\underline{p}}_h);{\underline{\varvec{v}}}_h)= 0,&\quad&\forall {\underline{\varvec{v}}}_h\in {\underline{\varvec{V}}}_h^{k+1,k}, \\ &r_{\mathrm{{II}},h}^{\mathrm{cnt}}({\underline{{\varvec{u}}}}_h;\underline{q}_h)= 0,&\quad&\forall \underline{q}_h\in {\underline{V}}_h^{k,k}. \end{aligned} \end{aligned}\right.$$

(7)

The HHO method (7) yields a velocity approximation that is pointwise divergence free (as can be checked adapting the argument of [52, Proposition 1]). As compared with the HDG method proposed in [52], the h-convergence rates for velocity and pressure are improved by one order. A key point consists in using an HHO discretization of the viscous term (cf. the discussion in [30] and also [32, Section 5.1.6]) with element unknowns for the velocity one degree higher than face unknowns. Notice that seeking the velocity in the space ${\underline{\varvec{V}}}_T^{k+1,k}$ as opposed to ${\underline{\varvec{V}}}_T^{k,k}$ does not alter the number of globally coupled unknowns, as all velocity degrees of freedom attached to the mesh elements can be removed from the global linear system by static condensation procedures similar to the ones discussed in Sect. 4.1.2.

2.4 DG Scheme

The third approximation of the Stokes problem is based on discontinuous approximations of both the velocity and the pressure. Specifically, we use the BR2 formulation for the vector Laplace operator (see [10] and also [34, Section 5.3.2]) together with a stabilized equal order pressure-velocity coupling. Fix a polynomial degree $k\geqslant 1$ and let $T\in {\mathcal {T}}_h$. We define the local discrete gradient ${\varvec{\mathfrak {G}}}_T^k : H^1({\mathcal {T}}_h)^d \rightarrow {\mathcal {P}}^{k}(T)^{d\times d}$ such that, for all ${\varvec{v}}\in H^1({\mathcal {T}}_h)^d$,

$$\begin{aligned} \int _T {\varvec{\mathfrak {G}}}_T^k({\varvec{v}}) : \varvec{\tau } = \int _T \nabla {\varvec{v}}_{|T} : \varvec{\tau } - \sum _{F \in {\mathcal {F}}_T^{\mathrm{i},{\mathrm{D}}}} \frac{1}{2} \int _F \left( {\varvec{n}}_{TF} \otimes \llbracket {\varvec{v}} \rrbracket _{TF} \right) : \varvec{\tau }, \quad \forall \varvec{\tau } \in {\mathcal {P}}^{k}(T)^{d \times d}, \end{aligned}$$

where, for any $F\in {\mathcal {F}}_T^{\mathrm{i},{\mathrm{D}}}$, the jump of ${\varvec{v}}$ across F is defined as

$$\begin{aligned} \llbracket {\varvec{v}} \rrbracket _{TF} {:}={\left\{ \begin{array}{ll} {\varvec{v}}_{|T} - {\varvec{v}}_{|T'} &{} \text {if }F\in {\mathcal {F}}_T^\mathrm{i}\cap {\mathcal {F}}_{T'}^\mathrm{i}\text { with} T,T'\in {\mathcal {T}}_h, T\ne T',\\ 2({\varvec{v}}_T - {\varvec{g}}_{\mathrm{D}}) &{} \text {if }F\in {\mathcal {F}}_T^{\mathrm{D}}. \end{array}\right. } \end{aligned}$$

Introducing, for all $F\in {\mathcal {F}}_T^{\mathrm{i},{\mathrm{D}}}$, the jump lifting operator $\varvec{\mathfrak {L}}_{FT}^k: L^2(F)^d \rightarrow {\mathcal {P}}^{k}(T)^{d \times d}$ such that, for all $\varvec{\varphi }\in L^2(F)^d$ and all $\varvec{\tau }\in {\mathcal {P}}^{k}(T)^{d\times d}$,

$$\begin{aligned} \int _T \varvec{\mathfrak {L}}_{FT}^k (\varvec{\varphi }) : \varvec{\tau } = \frac{1}{2} \int _F \left( {\varvec{n}}_{TF} \otimes \varvec{\varphi } \right) : \varvec{\tau }, \end{aligned}$$

it holds, for all ${\varvec{v}}\in H^1({\mathcal {T}}_h)^d$,

$$\begin{aligned} {\varvec{\mathfrak {G}}}_T^k({\varvec{v}}) = \nabla {\varvec{v}}_{|T} - \sum _{F\in {\mathcal {F}}_T^{\mathrm{i},{\mathrm{D}}}} \varvec{\mathfrak {L}}_{FT}^k(\llbracket {\varvec{v}} \rrbracket _{TF}). \end{aligned}$$

Given $({\varvec{u}}_h, p_h) \in {\mathcal {P}}^{k}({\mathcal {T}}_h)^d\times {\mathcal {P}}^{k}({\mathcal {T}}_h)$, the local residuals $r^{\mathrm{mnt}}_{\mathrm{{III}},T}(({\varvec{u}}_h,p_h);\cdot ):{\mathcal {P}}^{k}(T)^d\rightarrow {\mathbb {R}}$ of the discrete momentum equation and $r^{\mathrm{cnt}}_{\mathrm{{III}},T}(({\varvec{u}}_h,p_h);\cdot ):{\mathcal {P}}^{k}(T)\rightarrow {\mathbb {R}}$ of the discrete mass equation are such that, for all ${\varvec{v}}_T\in {\mathcal {P}}^{k}(T)^d$ and all $q_T\in {\mathcal {P}}^{k}(T)$,

$$\begin{aligned} r^{\mathrm{mnt}}_{\mathrm{{III}},T}(({\varvec{u}}_h,p_h);{\varvec{v}}_T)&{:}=\int _T {\varvec{\mathfrak {G}}}_T^k({\varvec{u}}_h) : \nabla {\varvec{v}}_T - \sum _{F \in {\mathcal {F}}_T^{\mathrm{i},{\mathrm{D}}}} \int _F \left[ {\varvec{n}}_{TF} \cdot \{ \nabla {\varvec{u}}_T - \eta _F \varvec{\mathfrak {L}}_{FT}^k(\llbracket {\varvec{u}}_h \rrbracket _{TF}) \}_F \right] \cdot {\varvec{v}}_T \\&\,\,- \int _T p_T \, (\nabla \cdot {\varvec{v}}_T) + \sum _{F \in {\mathcal {F}}_T^{\mathrm{i},{\mathrm{D}}}} \int _F \{ p_h \}_F \, ({\varvec{v}}_T \cdot {\varvec{n}}_{TF})\\&\,\,- \int _{T} {\varvec{f}} \cdot {\varvec{v}}_T - \sum _{F \in {\mathcal {F}}_T^{\mathrm{N}}} \int _F {\varvec{g}}_{\mathrm{N}}\cdot {\varvec{v}}_T, \\ r^{\mathrm{cnt}}_{\mathrm{{III}},T}(({\varvec{u}}_h,p_h);q_T)&{:}=\int _T {\varvec{u}}_T \cdot \nabla q_T - \sum _{F \in {\mathcal {F}}_T^{\mathrm{i},{\mathrm{D}}}} \int _F \{ {\varvec{u}}_h \}_F \cdot {\varvec{n}}_{TF} \, q_T + \sum _{F \in {\mathcal {F}}_T^\mathrm{i}} h_F \int _F \llbracket p_h \rrbracket _{TF} \, q_T, \end{aligned}$$

where, for all $\varphi \in H^1({\mathcal {T}}_h)$ and all $F\in {\mathcal {F}}_h$,

$$\begin{aligned} \{ \varphi \}_F {:}={\left\{ \begin{array}{ll} \frac{1}{2}\left( \varphi _{|T} + \varphi _{|T'}\right) &{} \text {if }F\in {\mathcal {F}}_T^\mathrm{i}\cap {\mathcal {F}}_{T'}^\mathrm{i}\text { with }T,T'\in {\mathcal {T}}_h, T\ne T', \\ \varphi _{|F} &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

with the understanding that the average operator acts componentwise when applied to vector and tensor functions, and

$$\begin{aligned} \eta _F > {\left\{ \begin{array}{ll} \max \big ({{\,{\mathrm{card}}\,}}({\mathcal {F}}_T), {{\,{\mathrm{card}}\,}}({\mathcal {F}}_{T'})\big ) &{} \text {if } F\in {\mathcal {F}}_T^\mathrm{i}\cap {\mathcal {F}}_{T'}^\mathrm{i}\text { with }T,T'\in {\mathcal {T}}_h, T\ne T',\\ {{\,{\mathrm{card}}\,}}({\mathcal {F}}_T) &{} \text {if }F \in {\mathcal {F}}_T^{\mathrm{D}}. \end{array}\right. } \end{aligned}$$

In the numerical tests provided below, the stabilization parameter is taken equal to 2 (this value, while below the theoretical threshold, leads to invertible systems on all the considered meshes and experimentally delivers the smallest errors). The global residuals $r^{\mathrm{mnt}}_{\mathrm{{\mathrm{{III}}}},h}(({\varvec{u}}_h,p_h);\cdot):{\mathcal {P}}^{k}({\mathcal {T}}_h)^d\rightarrow {\mathbb {R}}$ and $r^{\mathrm{cnt}}_{\mathrm{{III}},h}(({\varvec{u}}_h,p_h);\cdot ):{\mathcal {P}}^{k}({\mathcal {T}}_h)\rightarrow {\mathbb {R}}$ are obtained by element-by-element assembly of local residuals.

Scheme III

(DG: DG scheme) Find $({\varvec{u}}_h,p_h)\in {\mathcal {P}}^{k}({\mathcal {T}}_h)^d\times {\mathcal {P}}^{k}({\mathcal {T}}_h)$ such that

$$\begin{aligned} \begin{aligned} r_{\mathrm{{III}},h}^{\mathrm{mnt}}\big ( ({\varvec{u}}_h,{p}_h);{\varvec{v}}_h\big )&= \sum _{T \in {\mathcal {T}}_h} r_{\mathrm{{III}},T}^{\mathrm{mnt}}\big ( ({\varvec{u}}_h,{p}_h);{\varvec{v}}_h{}_{|T}\big ) = 0,&\quad&\forall {\varvec{v}}_h\in {\mathcal {P}}^{k}({\mathcal {T}}_h)^d, \\ r_{\mathrm{{III}},h}^{\mathrm{cnt}}\big (({\varvec{u}}_h,p_h);q_h)&= \sum _{T \in {\mathcal {T}}_h} r_{\mathrm{{III}},T}^{\mathrm{cnt}}\big (({\varvec{u}}_h,p_h);q_h{}_{|T}) = 0,&\quad&\forall q_h\in {\mathcal {P}}^{k}({\mathcal {T}}_h). \end{aligned} \end{aligned}$$

3 p-Multilevel Solution Strategy

We consider L coarse problems, indexed as $\ell =1,\cdots ,L$. Given a polynomial degree $k\geqslant 0$ (for Schemes I, II) or $k\geqslant 1$ (for Scheme III), we set

$$\begin{aligned} k_0\,:=k, \end{aligned}$$

the reference polynomial degree on the fine level, and denote by $k_\ell$ the polynomial degree at level $\ell$. Coarsening is achieved taking $k_{\ell +1}< k_\ell$. The notation for the three schemes discussed in Sect. 2 is summarized in Table 1. Notice that, for the sake of simplicity, we only consider the equal-order version of Scheme I, where both element and face velocity unknowns have the same polynomial degree.

Table 1 Notation for the p-multilevel solver. We only consider the equal-order version of Scheme I, where both element and face velocity unknowns have the same polynomial degree

3.1 Intergrid Transfer Operators

Denoting by $X\in {\mathcal {T}}_h\cup {\mathcal {F}}_h$ a mesh element or face, the prolongation operator ${\mathcal {I}}_{\ell +1}^{\ell ,X}: {\mathcal {P}}^{k_{\ell +1}}(X) \rightarrow {\mathcal {P}}^{k_\ell }(X)$ from level $\ell +1$ to level $\ell$ is the injection ${\mathcal {P}}^{k_{\ell +1}}(X)\hookrightarrow {\mathcal {P}}^{k}(X)$. The prolongation operator ${\mathcal {I}}^0_\ell$ from level $\ell$ to level 0 can be recursively defined by the composition of one level prolongation operators:

$$\begin{aligned} {\mathcal {I}}_\ell ^0 = {\mathcal {I}}^0_1 \, {\mathcal {I}}^1_2 \, \cdots \, {\mathcal {I}}_\ell ^{\ell -1}. \end{aligned}$$

The restriction operator ${\mathcal {I}}_{\ell ,X}^{\ell +1}: {\mathcal {P}}^{k_\ell }(X) {\rightarrow } {\mathcal {P}}^{k_{\ell +1}}(X)$ from level $\ell$ to level $\ell +1$ is simply taken equal to the $L^2$-orthogonal projector on ${\mathcal {P}}^{k_{\ell +1}}(X)$, that is, for all $w_{X,\ell } \in {\mathcal {P}}^{k_\ell }(X)$, we set

$$\begin{aligned} {\mathcal {I}}_{\ell ,X}^{\ell +1} w_{X,\ell } :=\pi _{X}^{\ell +1} w_{X,\ell }. \end{aligned}$$

(9)

The restriction operator ${\mathcal {I}}^\ell _0$ from level 0 to level $\ell$ is again obtained by the following composition:

$$\begin{aligned} {\mathcal {I}}^\ell _0 = {\mathcal {I}}^\ell _{\ell -1} \, \cdots \,{\mathcal {I}}^2_1 \,{\mathcal {I}}^1_0. \end{aligned}$$

It can be checked that ${\mathcal {I}}_{\ell ,X}^{\ell +1}$ is the transpose of ${\mathcal {I}}_{\ell +1}^{\ell ,X}$ with respect to the $L^2(X)$-inner product. When applied to vector-valued functions, intergrid transfer operators act component-wise and are denoted using boldface font by ${\varvec{\mathcal {I}}}_{\ell +1}^{\ell ,X}$, ${\varvec{\mathcal {I}}}_{\ell ,X}^{\ell +1}$. The global restriction operator $\underline{{\varvec{\mathcal {I}}}}^{\ell +1}_{\ell } : {\underline{\varvec{V}}}_h^{k_\ell ',k_\ell }\rightarrow {\underline{\varvec{V}}}_h^{k_{\ell +1}',k_{\ell +1}}$ for HHO spaces is defined using the following setting: for all ${\underline{\varvec{v}}}_{h,\ell }\in {\underline{\varvec{V}}}_h^{k_\ell ',k_\ell }$,

$$\begin{aligned} \underline{{\varvec{\mathcal {I}}}}^{\ell +1}_{\ell } {\underline{\varvec{v}}}_{h,\ell } {:}=\big ( ({\varvec{\mathcal {I}}}_{\ell ,T}^{\ell +1} {\varvec{v}}_{T,\ell })_{T\in {\mathcal {T}}_h}, ({\varvec{\mathcal {I}}}_{\ell ,F}^{\ell +1} {\varvec{v}}_{F,\ell })_{F\in {\mathcal {F}}_h} \big ), \end{aligned}$$

while the global restriction operator for DG spaces ${{\varvec{\mathcal {I}}}}^{\ell +1}_{\ell } : {\mathcal {P}}^{k_\ell }({\mathcal {T}}_h)^d\rightarrow {\mathcal {P}}^{k_{\ell +1}}({\mathcal {T}}_h)^d$ is obtained patching the following element restriction operators: for all ${{\varvec{v}}}_{h,\ell }\in {\mathcal {P}}^{k_\ell }({\mathcal {T}}_h)^d$,

$$\begin{aligned} \big ({{\varvec{\mathcal {I}}}}^{\ell +1}_{\ell } {{\varvec{v}}}_{h,\ell }\big )_{|T} {:}={\varvec{\mathcal {I}}}_{\ell ,T}^{\ell +1} ({\varvec{v}}_{h,\ell })_{|T}, \quad \forall T\in {\mathcal {T}}_h. \end{aligned}$$

3.2 Inherited Multilevel Operators

For any $\ell =1,\cdots ,L$, set, for the sake of brevity,

$$\begin{aligned} {\varvec{W}}_{\mathrm{{I}},h}^\ell {:}={\underline{\varvec{V}}}^{k_\ell ,k_\ell }_h \times {\mathcal {P}}^{k_\ell }({\mathcal {T}}_h),\quad {\varvec{W}}_{\mathrm{{II}},h}^\ell {:}={\underline{\varvec{V}}}^{k_\ell +1,k_\ell }_h \times {\underline{V}}^{k_\ell ,k_\ell }_h,\quad {\varvec{W}}_{\mathrm{{III}},h}^\ell {:}={\mathcal {P}}^{k_\ell }({\mathcal {T}}_h)^d \times {\mathcal {P}}^{k_\ell }({\mathcal {T}}_h). \end{aligned}$$

The coarse residuals for the momentum and mass continuity equations for the schemes of Sect. 2 corresponding to a velocity-pressure couple at level $\ell$ are obtained evaluating the corresponding fine residuals defined in Sect. 2.3 at the prolongation of the given function, i.e., for $\ell =1,\cdots ,L$,

• Scheme I (HHO-dp)

  Given $({\underline{{\varvec{u}}}}_{h,\ell }, p_{h,\ell } ) \in {\varvec{W}}_{\mathrm{{I}},h}^\ell$, $r_{\mathrm{{I}},\ell }\big (({\underline{{\varvec{u}}}}_{h,\ell }, p_{h,\ell } ); \cdot \big):{\varvec{W}}_{\mathrm{{I}},h}^\ell \rightarrow {\mathbb {R}}$ is such that, for all $({\underline{\varvec{v}}}_{h,\ell }, q_{h,\ell } ) \in {\varvec{W}}_{\mathrm{{I}},h}^\ell$,

  $$\begin{aligned}&\; \; r_{\mathrm{{I}},\ell }&\big (({\underline{{\varvec{u}}}}_{h,\ell }, p_{h,\ell } ); ({\underline{\varvec{v}}}_{h,\ell }, q_{h,\ell }) \big )&{:}={r}^{\mathrm{mnt}}_{\mathrm{{I}},\ell }\big (({\underline{{\varvec{u}}}}_{h,\ell },p_{h,\ell });{\underline{\varvec{v}}}_{h,\ell }\big ) + r^{\mathrm{cnt}}_{\mathrm{{I}},\ell } ({\underline{{\varvec{u}}}}_{h,\ell };q_{h,\ell }) \nonumber \\&\text {with}&{r}^{\mathrm{mnt}}_{\mathrm{{I}},\ell }\big (({\underline{{\varvec{u}}}}_{h,\ell },p_{h,\ell });{\underline{\varvec{v}}}_{h,\ell }\big )&{:}={r}^{\mathrm{mnt}}_{\mathrm{{I}},h}\big ( (\underline{{\varvec{\mathcal {I}}}}_\ell ^0{\underline{{\varvec{u}}}}_{h,\ell }, \mathcal {I}_\ell ^0 p_{h,\ell });\underline{{\varvec{\mathcal {I}}}}_\ell ^0{\underline{\varvec{v}}}_{h,\ell } \big ) \; \nonumber \\&\text {and}&r^{\mathrm{cnt}}_{\mathrm{{I}},\ell } ({\underline{{\varvec{u}}}}_{h,\ell };q_{h,\ell })&{:}=r^{\mathrm{cnt}}_{\mathrm{{I}},h} (\underline{{\varvec{\mathcal {I}}}}_\ell ^0{\underline{{\varvec{u}}}}_{h,\ell };\mathcal {I}_\ell ^0 q_{h,\ell }). \end{aligned}$$

  (10)

• Scheme II (HHO-hp)

  Given $({\underline{{\varvec{u}}}}_{h,\ell },{\underline{p}}_{h,\ell }) \in {\varvec{W}}_{\mathrm{{II}},h}^\ell$, $r_{\mathrm{{II}},\ell }\big (({\underline{{\varvec{u}}}}_{h,\ell },{\underline{p}}_{h,\ell });\cdot \big ):{\varvec{W}}_{\mathrm{{II}},h}^\ell \rightarrow {\mathbb {R}}$ is such that, for all $({\underline{\varvec{v}}}_{h,\ell },\underline{q}_{h,\ell }) \in {\varvec{W}}_{\mathrm{{II}},h}^\ell$,

  $$\begin{aligned}&\;\; r_{\mathrm{{II}},\ell }&\big (({\underline{{\varvec{u}}}}_{h,\ell },{\underline{p}}_{h,\ell }); ({\underline{\varvec{v}}}_{h,\ell },\underline{q}_{h,\ell })\big )&{:}={r}^{\mathrm{mnt}}_{\mathrm{{II}},\ell }\big (({\underline{{\varvec{u}}}}_{h,\ell },{\underline{p}}_{h,\ell });{\underline{\varvec{v}}}_{h,\ell }\big ) + r^{\mathrm{cnt}}_{\mathrm{{II}},\ell } ({\underline{{\varvec{u}}}}_{h,\ell };\underline{q}_{h,\ell }) \; \nonumber \\&\text { with }&{r}^{\mathrm{mnt}}_{\mathrm{{II}},\ell }\big (({\underline{{\varvec{u}}}}_{h,\ell },{\underline{p}}_{h,\ell });{\underline{\varvec{v}}}_{h,\ell }\big )&{:}={r}^{\mathrm{mnt}}_{\mathrm{{II}},h}\big ((\underline{{\varvec{\mathcal {I}}}}_\ell ^0{\underline{{\varvec{u}}}}_{h,\ell }, \underline{\mathcal {I}}_\ell ^0 {\underline{p}}_{h,\ell });\underline{{\varvec{\mathcal {I}}}}_\ell ^0{\underline{\varvec{v}}}_{h,\ell }\big ) \; \nonumber \\&\text { and }&r^{\mathrm{cnt}}_{\mathrm{{II}},\ell } ({\underline{{\varvec{u}}}}_{h,\ell };\underline{q}_{h,\ell })&{:}=r^{\mathrm{cnt}}_{\mathrm{{II}},h} (\underline{{\varvec{\mathcal {I}}}}_\ell ^0{\underline{{\varvec{u}}}}_{h,\ell };\underline{\mathcal {I}}_\ell ^0 \underline{q}_{h,\ell }). \end{aligned}$$

  (11)

• Scheme III (DG)

  Given $({{\varvec{u}}}_{h,\ell } , p_{h,\ell }) \in {\varvec{W}}_{\mathrm{{III}},h}^\ell$, $r_{\mathrm{{III}},\ell }\big (({{\varvec{u}}}_{h,\ell } , p_{h,\ell });\cdot \big ):{\varvec{W}}_{\mathrm{{III}},h}^\ell \rightarrow {\mathbb {R}}$ is such that, for all $({{\varvec{v}}}_{h,\ell } , q_{h,\ell }) \in {\varvec{W}}_{\mathrm{{III}},h}^\ell$,

  $$\begin{aligned}&\; r_{\mathrm{{III}},\ell }&\big (({{\varvec{u}}}_{h,\ell } , p_{h,\ell });({{\varvec{v}}}_{h,\ell } , q_{h,\ell })\big )&{:}={r}^{\mathrm{mnt}}_{\mathrm{{III}},\ell }\big (({{\varvec{u}}}_{h,\ell },p_{h,\ell });{{\varvec{v}}}_{h,\ell } \big ) + r^{\mathrm{cnt}}_{\mathrm{{III}},\ell } \big (({{\varvec{u}}}_{h,\ell }, p_{h,\ell });q_{h,\ell } \big ) \nonumber \\&\text { with }&{r}^{\mathrm{mnt}}_{\mathrm{{III}},\ell }\big (({{\varvec{u}}}_{h,\ell },p_{h,\ell });{{\varvec{v}}}_{h,\ell } \big )&{:}={r}^{\mathrm{mnt}}_{\mathrm{{III}},h}\big (({{\varvec{\mathcal {I}}}}_\ell ^0{{\varvec{u}}}_{h,\ell }, {\mathcal {I}}_\ell ^0 p_{h,\ell });{{\varvec{\mathcal {I}}}}_\ell ^0{{\varvec{v}}}_{h,\ell }\big ) \; \nonumber \\&\text { and }&r^{\mathrm{cnt}}_{\mathrm{{III}},\ell } \big (({{\varvec{u}}}_{h,\ell }, p_{h,\ell });q_{h,\ell } \big )&{:}=r^{\mathrm{cnt}}_{\mathrm{{III}},h} \big (({{\varvec{\mathcal {I}}}}_\ell ^0{{\varvec{u}}}_{h,\ell }, {\mathcal {I}}_\ell ^0 p_{h,\ell });{\mathcal {I}}_\ell ^0q_{h,\ell } \big ). \end{aligned}$$

  (12)

Fix $\bullet \in \{\mathrm{I},\mathrm{II},\mathrm{\mathrm{{III}}}\}$, $\ell =0,\cdots ,L$, and denote by $(\cdot ,\cdot )$ an inner product in ${\varvec{W}}_{\bullet ,h}^\ell$. Let ${\varvec{A}}_{h,\ell }:{\varvec{W}}_{\bullet ,h}^\ell \rightarrow {\varvec{W}}_{\bullet ,h}^\ell$ be the operator corresponding to the linear part of the residual $r_{\bullet ,\ell }$, i.e., for all ${\varvec{w}}_{h,\ell }\in {\varvec{W}}_{\bullet ,h}^\ell$, $({\varvec{A}}_{h,\ell }{\varvec{w}}_{h,\ell },{\varvec{z}}_{h,\ell }) = r_{\bullet ,\ell }({\varvec{w}}_{h,\ell };{\varvec{z}}_{h,\ell }) - r_{\bullet ,\ell }(\varvec{0};{\varvec{z}}_{h,\ell })$ for all ${\varvec{z}}_{h,\ell }\in {\varvec{W}}_{\bullet ,h}^\ell$. Letting ${\varvec{b}}_{h,\ell }\in {\varvec{W}}_{\bullet ,h}^\ell$ denote the Riesz representation of the affine part of the residual such that $({\varvec{b}}_{h,\ell },{\varvec{z}}_{h,\ell }) = r_{\bullet ,\ell }(\varvec{0};{\varvec{z}}_{h,\ell })$ for all ${\varvec{z}}_{h,\ell }\in {\varvec{W}}_{\bullet ,h}^\ell$, the global problem at level $\ell$ reads as follows: find ${\varvec{w}}_{h,\ell }\in {\varvec{W}}_{\bullet ,h}^\ell$ such that

$$\begin{aligned} {\varvec{A}}_{h,\ell } {\varvec{w}}_{h,\ell } = {\varvec{b}}_{h,\ell }. \end{aligned}$$

Besides the formal definition given above, coarse level operators can be efficiently inherited from the fine operators relying on the restriction and prolongation operators. This computationally efficient strategy, also known as Galerkin projection, is detailed in Sect. 4.2 focusing on Scheme I.

3.3 Multilevel V-Cycle Iteration

The approximate solution $\overline{{\varvec{w}}}_{h,\ell }$ to the global problem at level $\ell < L$ can be improved by means of one V-cycle iteration, as described in the following algorithm:

where ${\varvec{d}}_{h,\ell +1}$ is the restriction of the defect and ${\varvec{c}}_{h,\ell +1}$ is the coarse grid correction. All applications of prolongation and restriction operators involved in the multilevel V-cycle iteration are performed matrix-free, that is, without assembling the global sparse matrices associated to the operators ${\varvec{\mathcal {I}}}_{\ell }^{\ell +1},{\varvec{\mathcal {I}}}^{\ell }_{\ell +1}$.

In the pre- and post-smoothing steps, a few iterations of the generalized minimal residual (GMRES) method preconditioned with an incomplete lower-upper (ILU) factorization are performed in order to reduce the error ${\varvec{e}}_{h,\ell } = {\varvec{w}}_{h,\ell } - \overline{{\varvec{w}}}_{h,\ell }$. Indeed, the components of the error associated with the highest-order basis functions at level $\ell$ are expected to be damped very fast, while the components of the error associated with lower-order basis functions are smoothed at a later stage when the recursion reaches coarser levels.

In the numerical tests of Sect. 5 we consider one V-cycle iteration as a preconditioner for the FGMRES (flexible GMRES) iteration applied to solve the global problem ${\varvec{A}}_{h,0} {\varvec{w}}_{h,0} = {\varvec{b}}_{h,0}$. We employ the solver and preconditioner framework provided by the PETSc library [8].

4 Computational Aspects

In what follows, we discuss some computational aspects focusing, for the sake of simplicity, on the Scheme I (HHO with discontinuous pressure). Algebraic objects are denoted using sans serif font, with boldface distinguishing matrices from vectors.

4.1 Static Condensation

4.1.1 Algebraic Expression for the Local Residuals

We assume that local bases for each polynomial space attached to mesh elements and faces have been fixed, so that bases for the global approximations spaces for the velocity and the pressure can be obtained by taking the Cartesian product of the latter. Possible choices of local bases are discussed in [32, Appendix B.1]. In the numerical tests of Sect. 5, polynomial spaces over mesh elements are spanned by orthonormalized modal bases defined in the physical frame for both DG and HHO discretizations. For HHO discretizations, the polynomial spaces over mesh faces are spanned by orthogonal bases defined in the reference frame. Accordingly, the algebraic counterpart of restriction and prolongation operators are unit diagonal rectangular matrices, and their action on vectors is implemented matrix-free as inexpensive vector shrink and expansion operations, respectively. Similarly, the Galerking projection is implemented as a sub-block extraction; see Sect. 4.2 for further details.

The unknowns for a mesh element $T\in {\mathcal {T}}_h$ correspond to the coefficients of the expansions of the velocity and pressure in the selected local bases. Assuming that the velocity unknowns are ordered so that element velocities come first and boundary velocities next, these coefficients are collected in the following vectors:

$$\begin{aligned} \underline{\textsf { U}}_T=\begin{bmatrix} \textsf {U}_T \\ \textsf {U}_{\partial T} \end{bmatrix} \text { and }\textsf {P}_T, \end{aligned}$$

where the block partition of the vector $\underline{\textsf { U}}_T$ is the one naturally induced by the selected ordering of velocity unknowns.

The local matrices corresponding to the HHO discretization of the viscous term (first four terms in the right-hand side of (3a)) and of the pressure-velocity coupling (first three terms of the right-hand side of (3b)) are

$$\begin{aligned} {\mathbf {\mathsf{{A}}}}_T = \begin{bmatrix} {\mathbf {\mathsf{{A}}}}_{T T} &{} {\mathbf {\mathsf{{A}}}}_{T \partial T} \\ {\mathbf {\mathsf{{A}}}}_{\partial T T} &{} {\mathbf {\mathsf{{A}}}}_{\partial T \partial T} \end{bmatrix},\quad {\mathbf {\mathsf{{B}}}}_T = \begin{bmatrix} {\mathbf {\mathsf{{B}}}}_{T T}&{\mathbf {\mathsf{{B}}}}_{T \partial T} \end{bmatrix}, \end{aligned}$$

where again the block partition is the one induced by the ordering of velocity unknowns. Details on the construction of the matrix ${\mathbf {\mathsf{{A}}}}_T$ can be found in [32, Appendix B.2].

Remark 1

(Block structure) Denoting by N the number of faces of T, the block structure of the matrix ${\mathbf {\mathsf{{A}}}}_T$ can be further detailed as follows:

$$\begin{aligned} {\mathbf {\mathsf{{A}}}}_T = \left[ \begin{array}{c|ccc} {\mathbf {\mathsf{{A}}}}_{T T} &{} {\mathbf {\mathsf{{A}}}}_{T F_1} &{} \cdots &{} {\mathbf {\mathsf{{A}}}}_{T F_N} \\ \hline {\mathbf {\mathsf{{A}}}}_{F_1 T} &{} {\mathbf {\mathsf{{A}}}}_{F_1 F_1} &{} \cdots &{} {\mathbf {\mathsf{{A}}}}_{F_1 F_N} \\ \vdots &{} \vdots &{} &{} \vdots \\ {\mathbf {\mathsf{{A}}}}_{F_N T} &{} {\mathbf {\mathsf{{A}}}}_{F_N F_1} &{} \cdots &{} {\mathbf {\mathsf{{A}}}}_{F_N F_N} \end{array}\right] . \end{aligned}$$

(13)

Assume that the velocity unknowns attached to T and its faces are ordered by component. Since the viscous term is modeled in (1a) applying the Laplace operator to each velocity component, each block in the decomposition (13) is itself block-diagonal and is efficiently constructed starting from the corresponding matrix for the scalar Laplace operator.

Introducing the vector representations $\underline{\textsf { R}}_{\mathrm{{I}},T}^{\mathrm{mnt}}=\begin{bmatrix}\textsf {R}_{\mathrm{{I}},T}^{\mathrm{mnt}}\\ \textsf {R}_{\mathrm{{I}},\partial T}^{\mathrm{mnt}}\end{bmatrix}$ and $\textsf {R}_{\mathrm{{I}},T}^{\mathrm{cnt}}$ of the residual linear forms defined by (3), $\textsf {G}_{\partial T}$ of the terms involving the boundary data corresponding to the last two terms in the right-hand side of (3a), $\textsf {F}_T$ of the term involving the volumetric body force in (3a), and $\widehat{\textsf {G}}_{\partial T}$ of the last term in the right-hand side of (3b), it holds

$$\begin{aligned} \begin{bmatrix} \textsf {R}^{\mathrm{mnt}}_{\mathrm{{I}},T} \\ \textsf {R}^{\mathrm{mnt}}_{\mathrm{{I}}, \partial T} \\ \textsf {R}^{{\mathrm{cnt}}}_{\mathrm{{I}},T} \end{bmatrix} = \begin{bmatrix} {\mathbf {\mathsf{{A}}}}_{T T} &{} {\mathbf {\mathsf{{A}}}}_{T\partial T} &{} {\mathbf {\mathsf{{B}}}}_{T T}^\intercal \\ {\mathbf {\mathsf{{A}}}}_{\partial T T} &{} {\mathbf {\mathsf{{A}}}}_{\partial T \partial T} &{} {\mathbf {\mathsf{{B}}}}_{T\partial T}^\intercal \\ {\mathbf {\mathsf{{B}}}}_{T T} &{} {\mathbf {\mathsf{{B}}}}_{T \partial T} &{} {\mathbf {\mathsf{{0}}}} \end{bmatrix} \begin{bmatrix} \textsf {U}_T \\ \textsf {U}_{\partial T} \\ \textsf {P}_T \end{bmatrix} - \begin{bmatrix} \textsf {F}_T \\ \textsf {G}_{\partial T} \\ \widehat{\textsf {G}}_{\partial T} \end{bmatrix}. \end{aligned}$$

(14)

4.1.2 Static Condensation Strategies

The discrete problem (5) is obtained enforcing that the global residuals are zero, which requires the solution of a global linear system. The size of this linear system can be reduced by statically condensing the element velocity unknowns and, possibly, the pressure unknowns corresponding to high-order modes inside each element. In what follows, we discuss two possible static condensations procedures leading to global systems with different features.

• ● HHO–dp v–cond: Static condensation of velocity element unknowns

The first static condensation procedure hinges on the observation that, given a mesh element $T\in {\mathcal {T}}_h$, the velocity unknowns collected in $\textsf {U}_T$ are not directly coupled with unknowns attached to mesh elements other than T. As a result, enforcing that the residuals in the left-hand side of (14) are zero, $\textsf {U}_T$ can be locally eliminated by expressing it in terms of $\textsf {U}_{\partial T}$ and $\textsf {P}_T$ by computing the Schur complement

$$\begin{aligned} {\mathbf {\mathsf{{S}}}}_T^{\texttt {v}} = \begin{bmatrix} {\mathbf {\mathsf{{S}}}}_{\partial T\partial T}^{\texttt {v}} &{} {\mathbf {\mathsf{{S}}}}_{\partial T T}^{\texttt {v}} \\ {\mathbf {\mathsf{{S}}}}_{T\partial T}^{\texttt {v}} &{} {\mathbf {\mathsf{{S}}}}_{T T}^{\texttt {v}} \\ \end{bmatrix} {:}=\begin{bmatrix} {\mathbf {\mathsf{{A}}}}_{\partial T \partial T} &{} {\mathbf {\mathsf{{B}}}}_{T\partial T}^\intercal \\ {\mathbf {\mathsf{{B}}}}_{T \partial T} &{} {\mathbf {\mathsf{{0}}}} \end{bmatrix} - \begin{bmatrix} {\mathbf {\mathsf{{A}}}}_{\partial T T} \\ {\mathbf {\mathsf{{B}}}}_{T T} \end{bmatrix}{\mathbf {\mathsf{{A}}}}_{TT}^{-1}\begin{bmatrix} {\mathbf {\mathsf{{A}}}}_{T\partial T}&{\mathbf {\mathsf{{B}}}}_{T T}^\intercal \end{bmatrix} \end{aligned}$$

(15)

of the block ${\mathbf {\mathsf{{A}}}}_{TT}$ in the matrix in the right-hand side of (14). With this static condensation strategy, the zero residual condition translates into

$$\begin{aligned} {\mathbf {\mathsf{{S}}}}_T^{\texttt {v}}\begin{bmatrix} \textsf {U}_{\partial T} \\ \textsf {P}_T \end{bmatrix} = \begin{bmatrix} \textsf {G}_{\partial T} \\ \widehat{\textsf {G}}_{\partial T} \end{bmatrix} - \begin{bmatrix} {\mathbf {\mathsf{{A}}}}_{\partial T T} \\ {\mathbf {\mathsf{{B}}}}_{TT} \end{bmatrix} {\mathbf {\mathsf{{A}}}}_{TT}^{-1}\textsf {F}_T. \end{aligned}$$

• ● HHO–dp v&p–cond: Static condensation of velocity element unknowns and high-order pressure modes

The second static condensation strategy was originally suggested in [2] in the framework of HHO methods and later detailed in [38, Section 6] (this strategy is similar to the one discussed in [49] in the context of hybridizable DG methods). Assume that the basis for the pressure inside each mesh element $T\in {\mathcal {T}}_h$ is selected so that the first degree of freedom corresponds to the mean value of the pressure inside T and the remaining basis functions are $L^2$-orthogonal to the first (this condition typically requires the use of modal bases). Let now a mesh element $T\in {\mathcal {T}}_h$ be fixed. The above choice for the pressure basis induces the following partitions of the pressure unknowns and of the pressure-velocity coupling matrix:

$$\begin{aligned} \textsf {P}_T = \begin{bmatrix} \overline{\textsf {P}}_T \\ \widetilde{\textsf {P}}_T \end{bmatrix},\quad {\mathbf {\mathsf{{B}}}}_T = \begin{bmatrix} \overline{{\mathbf {\mathsf{{B}}}}}_{T T} &{} \overline{{\mathbf {\mathsf{{B}}}}}_{T \partial T} \\ \widetilde{{\mathbf {\mathsf{{B}}}}}_{T T} &{} \widetilde{{\mathbf {\mathsf{{B}}}}}_{T \partial T} \\ \end{bmatrix}, \end{aligned}$$

where $\overline{\textsf {P}}_T\in {\mathbb {R}}$ is the mean value of the pressure inside T, $\widetilde{\textsf {P}}_T$ is the vector corresponding to high-order pressure modes, and the matrix ${\mathbf {\mathsf{{B}}}}_T$ has been partitioned row-wise according to this decomposition. Enforcing that the residuals are zero in (14) and rearranging the unknowns and equations, we infer that the discrete solution satisfies

$$\begin{aligned} \left[ \begin{array}{cc|cc} {\mathbf {\mathsf{{A}}}}_{T T} &{} \widetilde{{\mathbf {\mathsf{{B}}}}}_{TT}^\intercal &{} {\mathbf {\mathsf{{A}}}}_{T\partial T} &{} \overline{{\mathbf {\mathsf{{B}}}}}_{T T}^\intercal \\ \widetilde{{\mathbf {\mathsf{{B}}}}}_{T T} &{} {\mathbf {\mathsf{{0}}}} &{} \widetilde{{\mathbf {\mathsf{{B}}}}}_{T \partial T} &{} {\mathbf {\mathsf{{0}}}} \\ \hline {\mathbf {\mathsf{{A}}}}_{\partial T T} &{} \widetilde{{\mathbf {\mathsf{{B}}}}}_{T\partial T}^\intercal &{} {\mathbf {\mathsf{{A}}}}_{\partial T \partial T} &{} \overline{{\mathbf {\mathsf{{B}}}}}_{T\partial T}^\intercal \\ \overline{{\mathbf {\mathsf{{B}}}}}_{TT} &{} {\mathbf {\mathsf{{0}}}} &{} \overline{{\mathbf {\mathsf{{B}}}}}_{T\partial T} &{} {\mathbf {\mathsf{{0}}}} \end{array} \right] \left[ \begin{array}{c} \textsf {U}_T \\ \widetilde{\textsf {P}}_T \\ \hline \textsf {U}_{\partial T} \\ \overline{\textsf {P}}_T \end{array}\right] = \left[ \begin{array}{c} \textsf {F}_T \\ \textsf {0} \\ \hline \textsf {G}_{\partial T} \\ \widehat{\textsf {G}}_{\partial T} \end{array}\right] . \end{aligned}$$

(16)

The only unknowns that are globally coupled are those collected in the subvector $\begin{bmatrix} \textsf {U}_{\partial T} \\ \overline{\textsf {P}}_T \end{bmatrix}$, while the remaining unknowns collected in $\begin{bmatrix} \textsf {U}_T \\ \widetilde{\textsf {P}}_T \end{bmatrix}$ can be eliminated by expressing them in terms of the former. After performing this local elimination, the condition (16) that the residuals associated with T are zero becomes

$$\begin{aligned} {\mathbf {\mathsf{{S}}}}_T^{\texttt {v \& p}}\begin{bmatrix} \textsf {U}_{\partial T} \\ \overline{\textsf {P}}_T \end{bmatrix} = \begin{bmatrix} \textsf {G}_{\partial T} \\ \widehat{\textsf {G}}_{\partial T} \end{bmatrix} - \begin{bmatrix} {\mathbf {\mathsf{{A}}}}_{\partial T T} &{} \widetilde{{\mathbf {\mathsf{{B}}}}}_{\partial TT}^\intercal \\ \overline{{\mathbf {\mathsf{{B}}}}}_{TT} &{} {\mathbf {\mathsf{{0}}}} \end{bmatrix} \begin{bmatrix} {\mathbf {\mathsf{{A}}}}_{T T} &{} \widetilde{{\mathbf {\mathsf{{B}}}}}_{TT}^\intercal \\ \widetilde{{\mathbf {\mathsf{{B}}}}}_{T T} &{} {\mathbf {\mathsf{{0}}}} \end{bmatrix}^{-1} \begin{bmatrix} \textsf {F}_T \\ \textsf {0} \end{bmatrix}, \end{aligned}$$

(17)

where ${\mathbf {\mathsf{{S}}}}_T^{\texttt {v \& p}}$ denotes the Schur complement of the top left block of the matrix in (16), that is,

$$\begin{aligned} {\mathbf {\mathsf{{S}}}}_T^{\texttt {v \& p}} = \begin{bmatrix} {\mathbf {\mathsf{{S}}}}_{\partial T\partial T}^{\texttt {v \& p}} &{} {\mathbf {\mathsf{{S}}}}_{\partial T T}^{\texttt {v \& p}} \\ {\mathbf {\mathsf{{S}}}}_{T\partial T}^{\texttt {v \& p}} &{} {\mathbf {\mathsf{{S}}}}_{T T}^{\texttt {v \& p}} \\ \end{bmatrix} {:}=\begin{bmatrix} {\mathbf {\mathsf{{A}}}}_{\partial T \partial T} &{} \overline{{\mathbf {\mathsf{{B}}}}}_{T\partial T}^\intercal \\ \overline{{\mathbf {\mathsf{{B}}}}}_{T\partial T} &{} {\mathbf {\mathsf{{0}}}} \end{bmatrix} - \begin{bmatrix} {\mathbf {\mathsf{{A}}}}_{\partial T T} &{} \widetilde{{\mathbf {\mathsf{{B}}}}}_{T\partial T}^\intercal \\ \overline{{\mathbf {\mathsf{{B}}}}}_{TT} &{} {\mathbf {\mathsf{{0}}}} \end{bmatrix}\begin{bmatrix} {\mathbf {\mathsf{{A}}}}_{T T} &{} \widetilde{{\mathbf {\mathsf{{B}}}}}_{TT}^\intercal \\ \widetilde{{\mathbf {\mathsf{{B}}}}}_{T T} &{} {\mathbf {\mathsf{{0}}}} \end{bmatrix}^{-1}\begin{bmatrix} {\mathbf {\mathsf{{A}}}}_{T\partial T} &{} \overline{{\mathbf {\mathsf{{B}}}}}_{T T}^\intercal \\ \widetilde{{\mathbf {\mathsf{{B}}}}}_{T \partial T} &{} {\mathbf {\mathsf{{0}}}} \end{bmatrix}. \end{aligned}$$

Remark 2

(Differences between the static condensation strategies) The two static condensation strategies outlined above coincide for $k=0$. For $k\geqslant 1$, the first, obvious difference is that the second results in a smaller global system, since high-order pressure unknowns are eliminated in addition to element-based velocity unknowns. There is, however, a second, more subtle difference. As a matter of fact, while the block ${\mathbf {\mathsf{{S}}}}_{\partial T \partial T}^{\texttt {v \& p}}$ in (17) is full, the block ${\mathbf {\mathsf{{S}}}}_{\partial T \partial T}^{\texttt {v}}$ in (15) preserves the pattern of ${\varvec{A}}_{\partial T \partial T}$ (which is composed of block-diagonal blocks, see Remark 1). As a result, the first static condensation strategy results in a sparser, albeit larger, matrix. The numerical tests in the next section show that the sparsity prevails over size resulting in cheaper matrix-vector products, so that the first static condensation strategy is in fact more efficient.

Notice that this difference would disappear if we replaced the Laplace operator in the momentum equation (1a) by ${{\,\mathrm{div}\,}}(\nu \varvec{\nabla }_\mathrm{s}\cdot )$, with $\varvec{\nabla }_\mathrm{s}$ denoting the symmetric part of the gradient operator applied to vector-valued fields, as would be required for a viscosity coefficient $\nu :\varOmega \rightarrow {\mathbb {R}}^+$ variable in space. As demonstrated in the next section by means of numerical experiments the performance of the multilevel iteration is strongly influenced by the static condensation strategy when working with graded meshes: static condensation of high-order pressure modes provides worse convergence rates and degrades the efficiency of the solution strategy.

4.2 Inheritance by Means of Galerkin Projections

We show in this section how the operators can be inherited from level $\ell$ to $\ell +1$. For X mesh element or face, we let $\{\psi _1^{X,\ell },\psi _2^{X,\ell }, \cdots ,\psi _P^{X,\ell }\}$ be a basis of ${\mathcal {P}}^{k_\ell }(X)$ (with P denoting the dimension of this vector space) and $\{\psi _1^{X,\ell +1},\psi _2^{X,\ell +1},\cdots ,\psi _Q^{X,\ell +1}\}$ a basis of ${\mathcal {P}}^{k_{\ell +1}}(X)$ (with Q denoting the dimension of this vector space). The algebraic counterpart ${\mathbf {\mathsf{{I}}}}_{\ell ,X}^{\ell +1}$ of the local restriction operator ${\mathcal {I}}_{\ell ,X}^{\ell +1}$ defined by (9) reads

$$\begin{aligned} {\mathbf {\mathsf{{I}}}}_{\ell ,X}^{\ell +1} =\begin{pmatrix} \int _X \psi _i^{X,\ell +1} \psi _j^{X,\ell } \end{pmatrix}_{i=1,\cdots ,Q,\,j=1,\cdots ,P}, \end{aligned}$$

and the algebraic counterpart ${\mathbf {\mathsf{{I}}}}_{\ell +1}^{\ell ,X}$ of the local prolongation operator ${\mathcal {I}}^{\ell ,X}_{\ell +1}$ is

$$\begin{aligned} {\mathbf {\mathsf{{I}}}}^{\ell ,X}_{\ell +1} = \big ({\mathbf {\mathsf{{I}}}}_{\ell ,X}^{\ell +1}\big )^\intercal . \end{aligned}$$

Interestingly, when using hierarchical orthonormal bases and the basis for ${\mathcal {P}}^{k_{\ell +1}}(X)$ is obtained by restriction of the basis for ${\mathcal {P}}^{k_\ell }(X)$, both the prolongation and restriction operators are represented by unit diagonal rectangular matrices. In particular, for the local restriction operator it holds

$$\begin{aligned} \big ({\mathbf {\mathsf{{I}}}}_{\ell ,X}^{\ell +1}\big )_{i,j}=\delta _{ij}, \quad \text {for all }i=1, \cdots ,Q \text { and all }j=1,\cdots ,P. \end{aligned}$$

As a result, intergrid transfer operators do not need to be computed nor stored in memory.

With a little abuse of notation, we also denote by ${\mathbf {\mathsf{{I}}}}_{\ell ,X}^{\ell +1}$ and ${\mathbf {\mathsf{{I}}}}_{\ell +1}^{\ell ,X}$ the local restriction and prolongation operators applied to vector-valued variables, which are obtained assembling component-wise the corresponding operators acting on scalar-valued variables. The matrix ${\mathbf {\mathsf{{A}}}}_T^{\ell +1}$ discretizing the viscous term at level $\ell +1$ can be inherited from the corresponding matrix ${\mathbf {\mathsf{{A}}}}_T^\ell$ at level $\ell$ applying the restriction operators block-wise (compare with (13)):

$$\begin{aligned} {\mathbf {\mathsf{{A}}}}_T^{\ell +1} = \begin{bmatrix} {\mathbf {\mathsf{{I}}}}_{\ell ,T}^{\ell +1} \,{\mathbf {\mathsf{{A}}}}^\ell _{TT} \, {\mathbf {\mathsf{{I}}}}^{\ell ,T}_{\ell +1} &{} {\mathbf {\mathsf{{I}}}}_{\ell ,T}^{\ell +1} \, {\mathbf {\mathsf{{A}}}}^\ell _{TF_1} \, {\mathbf {\mathsf{{I}}}}^{\ell ,F_1}_{\ell +1} &{} \cdots &{} {\mathbf {\mathsf{{I}}}}_{\ell ,T}^{\ell +1} \, {\mathbf {\mathsf{{A}}}}^\ell _{TF_N} \, {\mathbf {\mathsf{{I}}}}^{\ell ,F_N}_{\ell +1}\\ {\mathbf {\mathsf{{I}}}}_{\ell ,F_1}^{\ell +1} \,{\mathbf {\mathsf{{A}}}}^\ell _{F_1 T} \, {\mathbf {\mathsf{{I}}}}^{\ell ,T}_{\ell +1} &{} {\mathbf {\mathsf{{I}}}}_{\ell ,F_1}^{\ell +1} \, {\mathbf {\mathsf{{A}}}}^\ell _{F_1 F_1} \, {\mathbf {\mathsf{{I}}}}^{\ell ,F_1}_{\ell +1} &{} \cdots &{} {\mathbf {\mathsf{{I}}}}_{\ell ,F_1}^{\ell +1} \, {\mathbf {\mathsf{{A}}}}^\ell _{F_1 F_N} \, {\mathbf {\mathsf{{I}}}}^{\ell ,F_N}_{\ell +1}\\ \vdots &{} \vdots &{} &{} \vdots \\ {\mathbf {\mathsf{{I}}}}_{\ell ,F_N}^{\ell +1} \,{\mathbf {\mathsf{{A}}}}^\ell _{F_N T} \, {\mathbf {\mathsf{{I}}}}^{\ell ,T}_{\ell +1} &{} {\mathbf {\mathsf{{I}}}}_{\ell ,F_N}^{\ell +1} \, {\mathbf {\mathsf{{A}}}}^\ell _{F_N F_1} \, {\mathbf {\mathsf{{I}}}}^{\ell ,F_1}_{\ell +1} &{} \cdots &{} {\mathbf {\mathsf{{I}}}}_{\ell ,F_N}^{\ell +1} \, {\mathbf {\mathsf{{A}}}}^\ell _{F_N F_N} \, {\mathbf {\mathsf{{I}}}}^{\ell ,F_N}_{\ell +1}\\ \end{bmatrix}. \end{aligned}$$

Applying this procedure recursively shows that, for any level $\ell \geqslant 1$, the matrix ${\mathbf {\mathsf{{A}}}}_T^{\ell }$ can be obtained from the fine matrix ${\mathbf {\mathsf{{A}}}}_T^0$. Note that pre- and post-multiplications of the matrix blocks by the restriction and the prolongation operators, respectively, result in a block shrink. When using orthonormal basis functions, these matrix multiplications can be avoided altogether and replaced with inexpensive sub-block extractions.

In order to further reduce the computational costs, Galerkin projections can be performed on the statically condensed fine grid operator, so that static condensation of coarse grid operators is avoided altogether. For example, having computed the fine-level block of the Schur complement ${\mathbf {\mathsf{{S}}}}_{\partial T\partial T}^0$ (given by either formula (15) or (17)), the corresponding block ${\mathbf {\mathsf{{S}}}}_{\partial T\partial T}^{\ell +1}$ at level $\ell +1$ is computed applying recursively the following relation:

$$\begin{aligned} {\mathbf {\mathsf{{S}}}}^{\ell +1}_{\partial T \, \partial T} = \begin{bmatrix} {\mathbf {\mathsf{{I}}}}_{\ell ,F_1}^{\ell +1} \, {\mathbf {\mathsf{{S}}}}^{\ell }_{F_1 F_1} \, {\mathbf {\mathsf{{I}}}}^{\ell ,F_1}_{\ell +1} &{} \cdots &{} {\mathbf {\mathsf{{I}}}}_{\ell ,F_1}^{\ell +1} \, {\mathbf {\mathsf{{S}}}}^{\ell }_{F_1 F_N} \, {\mathbf {\mathsf{{I}}}}^{\ell ,F_N}_{\ell +1}\\ \vdots &{} &{} \vdots \\ {\mathbf {\mathsf{{I}}}}_{\ell ,F_N}^{\ell +1} \, {\mathbf {\mathsf{{S}}}}^{\ell }_{F_N F_1} \, {\mathbf {\mathsf{{I}}}}^{\ell ,F_1}_{\ell +1} &{} ... &{} {\mathbf {\mathsf{{I}}}}_{\ell ,F_N}^{\ell +1} \, {\mathbf {\mathsf{{S}}}}^{\ell }_{F_N F_N} \, {\mathbf {\mathsf{{I}}}}^{\ell ,F_N}_{\ell +1} \end{bmatrix}. \end{aligned}$$

To conclude, the resulting sub-blocks are assembled into the global matrix.

5 Numerical Investigation of h-Dependency

5.1 Mesh Sequences

In order to assess and compare the performance of p-multilevel preconditioners, we consider four h-refined mesh sequences of the two-dimensional domain $(-1,1)^2$, see Fig. 1, and three h-refined mesh sequences of the three-dimensional domain $(0,1)^3$, see Fig. 2. In two space dimensions, we consider both standard and graded meshes composed of triangular and trapezoidal elements. In three space dimensions, we consider standard meshes composed of prismatic and pyramidal elements and graded meshes composed of tetrahedral elements. While standard meshes have homogeneous meshsize, graded meshes feature mesh elements that become narrower and narrower while approaching the domain boundaries, mimicking computational grids commonly employed in CFD to capture boundary layers. In order to build h-refined graded mesh sequences, the mesh nodes are first positioned according to Gauss-Lobatto quadrature rules of increasing order, then randomly displaced by a small fraction of their distance. Accordingly, the reduction of the meshsize is non-linear in case of graded h-refined mesh sequences.

Fig. 1

Two-dimensional meshes (one mesh for each h-refined mesh sequence here considered). From left to right: Delaunay triangular mesh, trapezoidal mesh, graded trapezoidal mesh, graded triangular mesh

Fig. 2

Three-dimensional meshes (one mesh for each h-refined mesh sequence here considered). From left to right: pyramidal mesh, prismatic mesh, graded tetrahedral mesh

5.2 Setting

5.2.1 Manufactured Analytical Solution

We consider the following smooth analytical behaviours of the velocity and pressure fields: if $d=2$, we let $\varOmega {:}=(-1,1)^2$ and set

$$\begin{aligned} \begin{aligned} {\varvec{u}}(x,y)&= - \text{e}^x \, \left[ y \, \cos (y) + \sin (y) \right] \, \varvec{i} + \text{e}^x \, (y \, \sin (y)) \, \varvec{j},&\quad&\forall (x,y)\in \varOmega , \\ p(x,y)&= 2 \, \text{e}^x \, \sin (y),&\quad&\forall (x,y)\in \varOmega , \end{aligned} \end{aligned}$$

where $\{\varvec{i}, \varvec{j}\}$ is the canonical basis of ${\mathbb {R}}^2$ while, for $d=3$, we set $\varOmega {:}=(0,1)^3$ and

$$\begin{aligned} \begin{aligned} {\varvec{u}}(x,y,z)&= 2 \, \sin (\pi x)\varvec{i} - \pi \, y \, \cos (\pi x) \varvec{j} -\pi \, z \, \cos (\pi x) \varvec{k},&\quad&\forall (x,y,z)\in \varOmega , \\ p(x,y,z)&= \sin (\pi x) \; \cos (\pi y) \; \sin (\pi z),&\quad&\forall (x,y,z)\in \varOmega , \end{aligned} \end{aligned}$$

where $\{\varvec{i},\varvec{j},\varvec{k}\}$ is the canonical basis of ${\mathbb {R}}^3$. Dirichlet boundary conditions are enforced on all but one of the surfaces (edges in 2D) composing $\partial \Omega$, where Neumann boundary conditions are enforced instead. The boundary data and forcing term are inferred from the exact solution.

5.2.2 Multilevel Solver Options

We consider high-order and higher-order versions of the HHO and DG schemes corresponding to the polynomial degrees $k = 3$ and $k = 6$, respectively. The theoretical h-convergence rates for DG are $k+1$ for the velocity error in the $L^2$-norm and k for the velocity gradient and the pressure error in the $L^2$-norm. The theoretical h-convergence rates for HHO are $k+2$ for the velocity reconstruction error in the $L^2$-norm and $k+1$ for the gradient of the velocity reconstruction and the pressure error in the $L^2$-norm. For the HHO-hp scheme, both the element velocity and the reconstructed velocity display the same convergence rates, but the former is additionally divergence free on standard meshes. For this reason, the element velocity field is used in the error computations. For all the numerical test cases, we report in the tables the $L^2$-errors on the velocity (“${\varvec{u}}_h$” column), velocity gradients (“$G{\varvec{u}}_h$” column), pressure (“$p_h$” column), and divergence (“$D{\varvec{u}}_h$” column).

The solution of the linear systems is based on an FGMRES iterative solver preconditioned with a p-multilevel V-cycle iteration of three levels ($L=2$): for $k_0=k=3$ (fine level), we set $k_1=2$ on the intermediate level and $k_2=k_L=1$ on the coarse level; for $k_0=k=6$ (fine level), we set $k_1=3$ on the intermediate level and $k_2=k_L=1$ on the coarse level. Numerical tests not reported here for the sake of conciseness show that taking $k_L = 0$ as the coarsest level for HHO discretizations results not only in a reduced memory footprint, but also in a significant increase in the number of iterations. This trade-off results in computational times comparable to $k_L = 1$.

On the fine and intermediate levels, the pre- and post-smoothing strategies consist in two iterations of ILU preconditioned GMRES (notice that, at the global level, velocity-related unknowns come first and pressure-related unknowns next in order to facilitate the computation of the ILU preconditioner). The number of smoothing iterations has been experimentally selected so as to guarantee the best computational efficiency on the meshes considered in the numerical tests. Other choices for the smoothers could be considered such as, e.g., the ones proposed in the recent work [6]; we postpone the investigation of this topic to a future work. On the coarse level, we employ an LU solver when working in two space dimensions and ILU preconditioned GMRES solver when working in three space dimensions. Since enforcing looser tolerances on the coarse level does not alter the number of outer FGMRES iterations, we require three orders of magnitude decrease of the true (unpreconditioned) relative residual in three space dimensions. The relative residual decrease for the outer FGMRES solver is set to $10^{-13}$ when $k=3$ and to $10^{-14}$ when $k=6$. These tight tolerances are considered in order to monitor the numerical convergence rates up to the machine precision. We carefully monitored convergence history to make sure that stagnation of residuals does not occur; hence relative comparison between the solution times and the number of iterations of the different schemes remains valid when real-life stopping criteria are employed. All test cases were performed with FGMRES restarting equal to 5. Larger values negatively affect the performance for DG approximations, while HHO approximations are rather insensitive to this parameter.

5.2.3 Performance Evaluation

For all the numerical test cases we compare the performance and efficiency of solver strategies based on the following.

• Number of FGMRES outer iterations (“ITs” column).

• Number of coarse solver iterations (“$\hbox {ITs}_L$” column). Note that one iteration means that a direct solver is employed.

• Wall clock time required for linear system solution (“CPU time Sol.” column).

• Wall clock time required for matrix assembly (“CPU time Ass.” column). We remark that the computational cost of building the Schur complement is included since static condensation is performed element-by-element during matrix assembly.

• Wall clock time required for matrix assembly plus linear system solution (“CPU time Tot.” column).

• Efficiency with respect to linear scaling of the computational expense with the mesh cardinality (“Eff.” column). 100% efficiency means that for a fourfold increase of the number of elements we get a fourfold increase of the total (matrix assembly plus linear system solution) wall clock time. We remark that efficiency is computed considering two subsequent grids of the mesh sequence (whose data are reported in two successive table rows).

5.3 Comparison Based on Matrix Dimension and Matrix Non-zero Entries

The cost of a Krylov iteration scales linearly with the number of matrix non-zero entries (MNZs) plus the number of Krylov spaces times the matrix dimension (equal to the number of degrees of freedom, DOFs), see, e.g., [50]. Multilevel Krylov solvers utilize only a few smoother iterations on the fine and intermediate levels and iteratively solve on the coarse level, where the number of MNZs and DOFs is favourable, see Sect. 3.3. Accordingly, with respect to solver efficiency, the most relevant discretization-dependent parameters are the MNZs of the fine and coarse matrices and the number of DOFs of the coarse level: fine-level MNZs influence the cost of the most expensive matrix-vectors products, performed once per smoother iteration; coarse level MNZs influence the cost of the least expensive matrix-vector products, performed once per iteration of the coarse solver (that is, many times per multilevel iteration); the number of DOFs of the coarse level influences the cost of the Gram-Schmidt orthogonalization carried out within the GMREs algorithm on the coarse level.

Static condensation of the element-based unknowns is an effective means of improving solver efficiency in the context of hybridized methods. For HHO-dp, we compare the uncondensed (HHO-dp uncond) implementation to the static condensation strategies described in Sect. 4.1. We recall that both static condensation procedures involve the local elimination of velocity unknowns attached to mesh elements, and the difference lies in the treatment of pressure DOFs. According to (17), all pressure modes except the constant value are statically condensed in the HHO-dp v&p-cond strategy while, according to (15), pressure modes are not statically condensed in the HHO-dp v-cond strategy. For HHO-hp, we consider static condensation of the element unknowns for both the velocity and the pressure (HHO-hp v&p-cond), so that only skeletal unknowns appear in the global systems.

DOFs and MNZs of HHO discretizations are associated with element variables and face variables. DG discretizations rely only on element variables. The formulas for computing DOFs and MNZs reported in Table 2 show the following.

• The number of DOFs associated with element variables is proportional to the dimension of the polynomial space ${\mathbb {P}}_{d}^{k}$ and to the number of mesh elements.

• The number of DOFs associated with face variables is proportional to the dimension of ${\mathbb {P}}_{d-1}^{k}$ and to the number of mesh faces.

• The number of MNZs associated with element variables is proportional to the square of the dimension of ${\mathbb {P}}_{d}^{k}$ and to the number of mesh elements.

• The number of MNZs associated with face variables is proportional to the square of the dimension of ${\mathbb {P}}_{d-1}^{k}$ and to the number of mesh faces.

MNZs are also influenced by the stencil of the discretization and the fill-in of the Schur complement, as explained in Remark 2. Since the ratio between the dimensions of ${\mathbb {P}}_{d}^{k}$ and ${\mathbb {P}}_{d-1}^{k}$ is $\frac{k+d}{d}$, we have the following rules of thumb:

$$\begin{aligned} \begin{aligned}&\text {face variables have fewer DOFs than element variables if } \frac{{{\,{\mathrm{card}}\,}}({\mathcal {F}}_h)}{{{\,{\mathrm{card}}\,}}({\mathcal {T}}_h)} {<} \frac{k+d}{d}, \\&\text {face variables have fewer MNZs than element variables if } \frac{{{\,{\mathrm{card}}\,}}({\mathcal {F}}_h)}{{{\,{\mathrm{card}}\,}}({\mathcal {T}}_h)} \frac{2{{\,{\mathrm{card}}\,}}({\mathcal {T}}_F){-}1}{{{\,{\mathrm{card}}\,}}({\mathcal {T}}_F){+}1} {<} \left( \frac{k+d}{d}\right) ^2, \end{aligned} \end{aligned}$$

(18)

where $\frac{2{{\,{\mathrm{card}}\,}}({\mathcal {T}}_F){-}1}{{{\,{\mathrm{card}}\,}}({\mathcal {T}}_F){+}1}$ is the ratio between the stencil of face variables and element variables, respectively. This simple observation allows to interpret the results of Tables 3, 4, 5 and 6, where the DOFs and MNZs counts for the methods and implementations considered in this work are reported. Placeholders correspond to combinations of meshes, polynomial degrees, schemes, and static condensation options that are either not possible or have not been considered in numerical tests. The data are reported only for the finest grids of each mesh sequence for $k\in \{1,3,6\}$ (the case $k=1$ is also included as it is relevant for estimating the efficiency of the coarse solver).

Some comments regarding the DOFs counts reported in Tables 3, 4 and 5 are as follows. As expected, the HHO-dp uncond DOFs count is the largest. In 2D and 3D, HHO-dp v&p-cond and DG, respectively, have the fewest DOFs count on the coarse level ($k=1$). This can easily be interpreted based on (18), as the condition is harder to meet in 3D than in 2D. In 2D, the number of coarse level DOFs for HHO-dp v-cond, HHO-hp, and DG are very similar. In 2D and 3D, higher-order statically condensed HHO shows some advantage over DG in terms of DOFs.

Some comments regarding the MNZs counts reported in Tables 3, 4 and 5 are as follows. In 2D, HHO-dp v&p-cond and v-cond have fewer MNZs than DG, at all polynomial degrees. In 3D, HHO-dp v&p-cond and v-cond have fewer MNZs than DG for both $k=3$ and $k=6$, with HHO-dp v-cond being the most efficient. HHO-dp v-cond is very close to DG for $k=1$. The fact that HHO-dp v-cond outperforms HHO-dp v&p-cond is due to increased fill-in of the Schur complement matrix arising from (17), see Remark 2. HHO-hp v&p-cond improves DG only for $k=6$, while DG is significantly better for both $k=1$ and $k=3$. Similar to strategy (17) for HHO-dp, the aforementioned static condensation procedure increases the fill-in of the blocks pertaining to skeletal velocity unknowns with respect to the uncondensed operator.

Table 2 Formulas for computing the matrix dimension (equal to the number of DOFs) and number of matrix non-zero entries (MNZs) of nonconforming discretization. Several static condensation options are considered for HHO-dp, see text for details

Table 3 Matrix dimension (equal to the number of DOFs) on 2D meshes. Note that graded quadrilateral meshes are not included because they coincide with trapezoidal meshes in terms of DOFs

Table 4 Number of matrix non-zero entries (MNz) on 2D meshes. Note that graded quadrilateral meshes are not included because they coincide with trapezoidal meshes in terms of MNZs

Table 5 Matrix dimension (equal to the number of DOFs) on 3D meshes

Table 6 Number of matrix non-zero (MNZs) entries on 3D meshes

5.4 Comparison of Static Condensation Strategies

In this section we evaluate the performance of the multilevel solution strategy for Scheme I (HHO-dp) comparing the two approaches for static condensation described in Sect. 4.1; see in particular (17) (HHO-dp v&p-cond) and (15) (HHO-dp v-cond). We also consider the uncondensed formulation (HHO-dp uncond) as a reference to evaluate the performance gains.

In case of regular 2D mesh sequences, the results reported in Table 7 confirm that static condensation leads to significant gains (on average, the computation time halves) when compared with the uncondensed implementation. The results reported in Table 8, where graded 2D mesh sequences are considered, show that the HHO-dp v&p-cond strategy (static condensation of both velocity element unknowns and high-order pressure modes) leads to a suboptimal performance of the multigrid preconditioner in case of stretched elements: notice the increase in the number of FGMRES iterations when the mesh is refined. A similar behaviour, even if less pronounced, is observed for the uncondensed implementation. The results reported in Table 9, where 3D mesh sequences are considered, confirm the strategy HHO-dp v-cond (static condensation of element velocity unknowns only) leads to the best performance in terms of execution times, both in the case of standard and graded meshes. We remark that the gains are to be ascribed to fewer FGMRES iterations and a smaller number of matrix non-zero entries, see Table 6.

It is interesting to remark that accuracy and convergence rates are not influenced by the static condensation procedure as soon as the relative residual drop satisfies the prescribed criterion. Solver fails to converge for HHO v&p-cond over fine-graded triangular meshes, see Table 8. Note that the prescribed maximum number of iteration (1 K) of the FMGRES solver is reached and the convergence rates are spoiled.

Table 7 Evaluation of p-multilevel solution strategies for solving high-order $k=3$ HHO-dp over 2D regular mesh sequences. Solvers are applied to uncondensed and statically condensed matrices (identified by different colors) considering two alternative Schur complement implementations, see text for details. See Sect.  5.2.2 for solver options

Table 8 Evaluation of p-multilevel solution strategies for solving high-order $k=3$ HHO-dp over 2D graded mesh sequences. Solvers are applied to uncondensed and statically condensed matrices (identified by different colors) considering two alternative Schur complement implementations, see text for details. See Sect. 5.2.2 for solver options

Table 9 Evaluation of p-multilevel solution strategies for solving high-order $k=3$ HHO-dp over 3D mesh sequences. Solvers are applied to uncondensed and statically condensed matrices (identified by different colors) considering two alternative Schur complement implementations, see text for details. See Sect.  5.2.2 for solver options

5.5 Comparison Based on Accuracy and Efficiency of the Solver Strategy

In this section we compare the three discretizations of the Stokes problem presented in Sect. 2 based on accuracy and performance of the multilevel solver strategy. For the HHO scheme HHO-dp, in accordance with the results of Sect.  5.4, the static condensation strategy v-cond is used for all meshes in both two and three space dimensions. For the HHO scheme HHO-hp, we consider static condensation of the element unknowns for both the velocity and the pressure (HHO-hp v&p-cond), so that only skeletal unknowns appear in the global systems. The results for 2D regular and graded sequences are reported in Tables 10, 11, 12 and 13, respectively. The results for 3D mesh sequences are reported in Tables 14 and 15.

As a first point, we remark that the theoretical convergence rates are confirmed for all the test cases performed on regular 2D and 3D mesh sequences. When higher-order ($k=6$) discretizations are considered and machine precision is reached, the converge rates deteriorate, as expected. Interestingly, all the schemes suffer from a convergence degradation for ${{\,{\mathrm{card}}\,}}({\mathcal {T}}_h)$ between 192 and 1 546 over the graded tetrahedral mesh sequence. This is probably due to mesh elements of extremely bad quality generated as a result of grading plus random node displacement, see Sect. 5.1. Overall, both HHO-dp and HHO-hp outperform DG in terms of accuracy with order of magnitudes gains observed moving towards finer meshes. This is due to better asymptotic convergence rates (one order higher) as well as better accuracy on coarse meshes. One could, alternatively, compare the $(k+1)$-version of DG with the k-version of $\texttt {HHO}{}$: this would result in the same convergence rates for both methods, but would of course further increase the gap in terms of efficiency.

p-Multilevel solvers guarantee uniform convergence with respect to the mesh density when standard 2D and 3D mesh sequences are considered: note that the number of FGMRES iterations is almost uniform all along the mesh sequence. Interestingly, HHO-dp discretizations show uniform convergence with respect to the mesh density on graded quadrilateral meshes, while DG is most affected by mesh grading, especially for $k=6$. For HHO-hp, the number of iterations increases with mesh density on graded quadrilateral meshes. Nevertheless, the number of iterations over coarse meshes is remarkably small and grows up to match the iterations count of HHO-dp over fine meshes. The solver convergence deteriorates with the mesh density in case of graded triangular and tetrahedral mesh sequences: the increase in the number of iterations is clearly visible but not pathological for HHO discretizations.

Interestingly, p-multilevel solvers show improved robustness with respect to the polynomial degree when applied to HHO discretizations: moving from high-order ($k=3)$ to higher-order ($k=6$) entails a mild iterations increase for HHO, while the iteration count doubles for DG. In 2D, this behaviour has a strong impact on computation times: HHO is up to three and eight times faster than DG at high-order and higher-order, respectively. HHO-dp outperforms DG because of the reduced number of matrix non-zero entries and the reduced matrix dimension, see Tables 3 and 4: the former influences the cost of smoothing iterations while the latter strongly influences the cost of the LU factorization on the coarse level.

Let us consider the performance of the multilevel solver in 3D. HHO-dp is two times and four-to-five times faster than DG in terms of solution times for $k=3$ and $k=6$, respectively. HHO-hp is slower than HHO-dp in terms of solution times and faster than DG by a small amount, with the exception of the pyramidal elements mesh sequence for $k=3$. The difference in computational cost between HHO-dp and HHO-hp is essentially due to the number of MNZs, see Table 6, while the number of FGMRES iterations is comparable. Since, in 3D, the coarse level solver is generally more efficient for DG, the HHO advantage results from the efficiency of the smoothers and the reduced number of FGMRES iterations. In particular, we remark that DG has fewer DOFs than HHO for $k=1$, see Table 5. Moreover, DG and HHO-dp v-cond have a comparable MNZ count for $k=1$, significantly smaller than the MNZ count of HHO-hp v&p-cond, see Table 6.

Overall, the gain in terms of total execution times is less significant than in 2D. When working with HHO in three space dimensions, assembly times are a considerable fraction of the total computation time: matrix assembly is twice as expensive as linear system solution for HHO-dp for $k=6$. As opposite, for DG, solution times dominate. Increased assembly costs are essentially due to the solution of the local problems involved in static condensation. An important observation is that, since the assembly procedure is perfectly scalable while ILU preconditioned smoothers are not, HHO discretizations might show better scalability results as compared to DG in massively parallel computations.

We conclude this section commenting about solver efficiency (last column in Tables 10, 11, 12, 13, 14 and 15). It is clear that higher-order discretizations ($k=6$) achieve better efficiency than high-order discretizations ($k=3$), in both 2D and 3D. This outlines the intrinsic limitation of p-multilevel solution strategies: when considering fine meshes, the performance of the coarse solver might limit the efficiency because the number of DOFs and MNZs on the coarse level can not be chosen arbitrarily low. Accordingly, p-multilevel solver are best suited for those situations where arbitrarily coarse meshes with higher-order polynomials can be employed.

Table 10 Evaluation of p-multilevel solution strategies performance while decreasing h ($d=2$ standard meshes, $k=3$). See Sect. 5.2.2 for solver options. DOF and MNZ specs are reported in Tables 3 and 4, respectively

Table 11 Evaluation of p-multilevel solution strategies performance while decreasing h ($d=2$ graded meshes, $k=3$). See Sect. 5.2.2 for solver options. DOF and MNZ specs are reported in Tables 3 and 4, respectively

Table 12 Evaluation of p-multilevel solution strategies performance while decreasing h ($d=2$ standard meshes, $k=6$). See Sect. 5.2.2 for solver options and Figs. 3 and 4 for a graphical representation. DOFs and MNZs specs are reported in Tables 3 and 4, respectively

Table 13 Evaluation of p-multilevel solution strategies’ performance while decreasing h ($d=2$ graded meshes, $k=6$). See Sect. 5.2.2 for solver options and Figs.  3 and 4 for a graphical representation. DOF and MNZ specs are reported in Tables 3 and 4, respectively

Table 14 Evaluation of p-multilevel solution strategies’ performance while decreasing h ($d=3$, $k=3$). See Sect. 5.2.2 for solver options and Figs.  5 and 6 for a graphical representation. DOF and MNZ specs are reported in Tables 5 and 6, respectively

Table 15 Evaluation of p-multilevel solution strategies performance while decreasing h ($d=3, k=6$). See Sect. 5.2.2 for solver options and Figs. 5 and 6 for a graphical representation. DOF and MNZ specs are reported in Tables 5 and 6, respectively

5.6 Comparison Based on CPU Time

Fig. 3

Accuracy versus computation time while decreasing h, trapezoidal elements mesh sequence. Graphical representation of the data reported in Tables 10 (left panel) and 12 (right panel)

Fig. 4

Accuracy versus computation time while decreasing h, distorted and graded triangular elements mesh sequence. Graphical representation of the data reported in Tables 11 (left panel) and 13 (right panel)

Fig. 5

Accuracy versus computation time while decreasing h, prismatic elements mesh sequence. Graphical representation of the data reported in Tables 14 (left panel) and 15 (right panel)

Fig. 6

Accuracy versus computation time while decreasing h, distorted and graded tetrahedral elements mesh sequence. Graphical representation of the data reported in Tables 14 (left panel) and 15 (right panel)

To close this section, we provide a synthetic comparison based on CPU time for various choices of mesh families and polynomial degrees. Specifically, Figs. 3, 4, 5 and 6 display the $L^2$-norms of the errors on both the velocity and pressure for selected mesh families and maximum polynomial degrees $k=3$ and $k=6$. In all the cases, the HHO schemes outperform the DG schemes, with the HHO-dp variant being the most efficient. Only for the prismatic mesh sequence considered in Fig. 5 the performance of the DG scheme comes close to that of the HHO on coarser meshes (on finer meshes, the reduced order of convergence results in worse performance for DG). We remark that the formula given in (18) predicts a different performance gap between HHO and DG for tetrahedral and prismatic meshes since prisms have twice the number of faces.

6 Numerical Investigation of k-Dependency

In this section we investigate the performance of the multilevel solver while increasing the polynomial degree. We consider discretizations of degree $k=3,6,10$ over the coarsest grids of the 2D and 3D mesh sequences described in Sect. 5.1. We omit the graded quadrilateral mesh since the results are comparable with those obtained over the trapezoidal mesh. Dirichlet boundary conditions are enforced on all but one of the surfaces (edges in 2D) composing $\partial \Omega$, where Neumann boundary conditions are enforced instead. The boundary data and forcing term are inferred from the exact solution, see Sect. 5.2.1.

The solution of the linear systems is based on an FGMRES iterative solver preconditioned with a p-multilevel V-cycle iteration: for $k_0=k=3$ (fine level), we consider a two-level ($L=1$) preconditioner with $k_1=k_L=1$ on the coarse level ({3,1} preconditioner in tables); for $k_0=k=6$ (fine level), we consider a three-level ($L=2$) preconditioner with $k_1=3$ on the intermediate level and $k_2=k_L=1$ on the coarse level ({6,3,1} preconditioner in tables); for $k_0=k=10$ (fine level) we consider a four-level ($L=3$) preconditioner with $k_1=6$, $k_2=3$ on the intermediate levels and $k_3=k_L=1$ on the coarse level ({10,6,3,1} preconditioner in tables). We remark that, in order to preserve the efficiency of the multigrid iteration while increasing k, we increase the stride between the degree of subsequent polynomial spaces in the multilevel stack. Notice that the ratio between the dimension of polynomial spaces of degree $k+1$ and k obeys the following rule:

$$\begin{aligned} \frac{\dim ({\mathbb {P}}_d^{k+1})}{\dim ({\mathbb {P}}_d^k)} = 1+\frac{d}{k+1}. \end{aligned}$$

On the fine and intermediate levels, the pre- and post-smoothing strategies consist in two iterations of ILU preconditioned GMRES. On the coarse level, we employ an LU solver when working in two space dimensions and ILU preconditioned GMRES solver when working in three space dimensions. The relative (unpreconditioned) residual decrease for the outer FGMRES solver is set to $10^{-13}$ when $d=2$ and to $10^{-14}$ when $d=3$. The relative (unpreconditioned) residual decrease for the GMRES solver on the coarse level is set to $10^{-3}$ in three space dimensions.

We compare the performance of the three schemes presented in Sect. 2. For all the numerical test cases, accuracy is evaluated computing the $L^2$-errors on the velocity (“${\varvec{u}}_h$” column), velocity gradients (“$G{\varvec{u}}_h$” column), pressure (“$p_h$” column) and divergence (“$D{\varvec{u}}_h$” column). Similarly, performance is evaluated based on number of iterations and wall clock times, see Sect. 5.2.3. The results are reported in Tables 16 and 17 considering 2D and 3D meshes, respectively. p-Multilevel solvers deliver almost uniform convergence with respect to the polynomial degree when applied to HHO discretizations: notable exceptions are HHO-dp over the trapezoidal elements grid and HHO-hp over the pyramidal elements grid. The increase in the iteration number for higher-order DG discretizations is more evident: in 3D, e.g., the iteration count doubles moving from $k=3$ to $k=10$.

As a final comment regarding accuracy at very high-order polynomial degrees, we remark that HHO discretizations seem to be more sensitive than DG to round-off errors related to finite precision. In particular, HHO shows better precision than DG at $k=6$ but, in some cases, the accuracy of DG is slightly better at $k=10$, when the errors approach machine precision.

Table 16 Performance of p-multilevel solution strategies (k-dependency in space dimension $d=2$). See Sect. 6 for further details

Table 17 Performance of p-multilevel solution strategies (k-dependency in space dimension $d=3$). See Sect. 6 for further details

7 Scalability

In this section we include basic scalability results for p-multilevel solvers applied to HHO-dp discretizations. Even if a complete analysis and comparison of the parallel performance of nonconforming discretizations is outside the scope of the paper, we ought to show that additive Schwarz method (ASM) preconditioners are an effective means of achieving satisfactory parallel efficiency. We consider the finest grid of the pyramidal mesh sequence (counting of 24 K elements) and an HHO-dp scheme with $k=5$. Static condensation acts on the sole velocity unknowns (HHO-dp v-cond), as described in (15). The multilevel solver strategy is the same employed in serial computations for $k=6$, but smoother preconditioners are suitably designed, as outlined in what follows.

The parallel implementation is based on the distributed memory paradigm and requires to partition the computational mesh in several subdomains. In case of HHO methods, not only the mesh but also the mesh skeleton needs to be partitioned: as a result, each mesh entity (element or face) belongs to one and only subdomain. Each subdomain is assigned to a different computing unit that performs matrix assembly for the local mesh elements pertaining to the subdomain. Mesh partitioning directly reflects into matrix partitioning in the sense that all entries of the matrix rows (PETSc matrix implementation is row-major) pertaining to local mesh entities are allocated and stored in local memory. Once matrix assembly is completed, the linear system is approximately solved in each subdomain. Depending on the preconditioner strategy, the solver performance might degrade increasing the number of subdomains, see e.g., [55].

A commonly used ASM preconditioner strategy for DG discretizations consists in employing an ILU decomposition in each subdomain matrix suitably extended to include the matrix rows of ghost elements, that is, neighbors of local mesh elements that belong to a different subdomain. This implies that the local matrix is extended to encompass the stencil of the DG discretizations, see [43] for additional details. We consider a similar strategy for HHO discretizations: each subdomain matrix is extended to include the matrix rows of ghost faces, that is, faces of the local mesh elements that belong to a different subdomain. Interestingly, even if the resulting local matrix does not encompass the stencil of the HHO discretization, mass conservation defect takes into account all element’s faces.

As a result of the ASM described above, the amount of overlap between subdomain matrices, i.e., the number of matrix entries that are repeated in more than one subdomain, is smaller for HHO than for DG. Consider, for example, two subdomains sharing a face: if the face is local for subdomain A, it is a ghost face for subdomain B and vice-versa. Accordingly, only one of the two subdomain matrices is extended for HHO discretizations. As opposite, since each of the two mesh elements sharing the face has a ghost neighbour, both subdomain matrices are extended for DG discretizations.

Scalability is measured increasing the number of execution units from 16 to 256: in particular we consider a total of five steps doubling the number of execution units at each step. We ran our tests on a four two-socket nodes cluster with eight 32-cores AMD EPYC 7501 CPUs. Each CPU has a non-uniform memory access (NUMA) topology of four 8-core dies and two memory channels per die. Execution-units are pinned so that each NUMA is either empty (no process running) or full (8 processes running), thereby ensuring that the memory bandwidth is independent from the number of MPI processes. Notice that, when running on 256 subdomains, each subdomain counts of approximately 96 local elements.

The results reported in Table 18 confirm that the ASM preconditioner strategy provides satisfactory parallel performance: the number of outer FGMRES iterations is uniform while increasing the number of execution units, and only a mild increase in the iteration count is observed for the ASM preconditioned GMRES solvers on the coarse level. The efficiency parameter (last column in Table 18) measures strong scalability: 100% efficiency with N execution units would imply coarsened operators and an N/16 fold reduction of total computation time with respect to the baseline computation performed with 16 execution units.

Table 18 Parallel performance of p-multilevel solution strategies applied to HHO-dp discretizations with $k=5$

8 Conclusions and Perspectives

The multilevel V-cycle iteration based on p-coarsened operators and ILU preconditioned Krylov smoothers is an effective solution strategy for high-order HHO discretizations of the Stokes equations. The corresponding global linear systems can be solved up to machine precision in a reasonable amount of V-cycle preconditioned FGMRES iterations (less than 20). This is remarkable, considering that severely graded mesh sequences have been tackled in both 2D and 3D.

Comparing p-multilevel solvers for HHO and DG discretizations based on FGMRES iteration count, it appears that, at least in the test cases considered in this work, the former are more robust than the latter with respect to both the meshsize and the polynomial degree. When standard h-refined mesh sequences are considered, HHO formulations show uniform convergence with respect to the meshsize, irrespective of the considered polynomial degree. On graded h-refined mesh sequences, the iteration count increases over finer meshes, more severely so for DG discretizations. Similarly, when doubling the polynomial degree (passing from $k=3$ to $k=6$) for a fixed meshsize, we observe that the iteration count is more stable for HHO schemes.

Since code ruse and code optimization are still possible (the HHO implementation in our code is more recent and probably less optimized), we avoid drawing conclusions regarding computation times. The synthetic results reported in Sect. 5.6, however, seem to point out an advantage for HHO in terms of precision versus CPU time. It has to be noticed, however, matrix-free implementations of DG methods (not considered here) can lead to significant gains on element shapes like hexahedra [46]. As a general remark, the following observations suggest that p-multilevel solution strategies are a compelling choice in case of HHO formulations.

• HHO displays an advantage over DG both in terms of matrix dimension and number of non-zero entries when the polynomial degree is sufficiently high;

• p-multilevel solvers for HHO show better solver robustness with respect to the polynomial degree.

The results in the present work are extremely encouraging and open up new perspectives concerning the efficient solution of linear systems resulting from the HHO and DG discretization of incompressible flow problems. The next obvious step will be to include the convective term and study the robustness for high Reynolds numbers. Another interesting research path consists in exploring alternative approaches for HHO that consider Schur complement solvers, where one only needs to invert the velocity block with multigrid, whereas a pressure mass matrix can be used as a spectrally equivalent approximation of the Schur complement (see, e.g., [40]). The comparison with DG discretization will be all the more interesting, as numerical evidence in [17] seems to suggest that Schur complement solvers are more affected than monolithic solvers by mesh regularity.