The relationship between shape parameters and kurtosis in some relevant models

Abstract

When a distributional model is chosen, the analytic relation between its shape parameters and the values taken by some kurtosis indexes, especially if they are unconventional, is rarely known. In addition, different indexes may provide contrasting evidence about the level of global kurtosis, when the parameters of the model are varied. That happens because just few parameters act “plainly” on kurtosis, namely so as to produce consistent modifications of the shape of the graph on both its sides. Many parameters, instead, affect kurtosis along with a change of the skewness of the distribution, that is by “inflating” a single side of the graph (usually a tail) at the expense of the other. Thanks to some relevant examples, this paper tries to provide general indications to recognize the two kinds of parameters above and to interpret their effect on the classical Pearson’s standardized fourth moment and on some lesser known kurtosis indexes. Specifically, it is shown that only a decomposed analysis of indexes can help to understand their apparent contradictions, especially when some of them are too sensitive to changes in the tails. Finally, some applications are provided.

1 Introduction

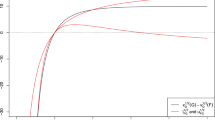
A close look at the literature reveals that it is hard to share a unified vision of kurtosis. That is not just a theoretical debate, because it was largely proved that the uncritical identification with Pearson’s standardized fourth moment $\beta _2$ can lead to some controversial interpretation when measuring departure from normality. As an example, Kaplansky (1945), Darlington (1970) and Hildebrand (1971) showed that $\beta _2$ is sensitive to aspects that are only partially related to kurtosis, such as bimodality. The problems arising in the empirical analysis of kurtosis based on samples, in addition, were recently highlighted in Borroni and De Capitani (2022), where some guidelines to choose from classical and unconventional indexes are also provided. In any case, even when the distribution is known, it seems that the most effective way to look at kurtosis is to follow Balanda and MacGillivray (1988), who identify it as a “location and scale-free movement of probability mass from the shoulders of a distribution into its center and tails” (see also Zenga, 2006). Despite the obvious vagueness of such a definition, its founding element is that the movement causing kurtosis should not alter location and scale or, equivalently, that to compare kurtosis of two distributions, one need to assure that they share the same location and scale, however they are measured (see also Johnson et al., 1994). That issue is particularly relevant to analyze the effect of the variation of the parameters of a given model on the level of kurtosis. For instance, it is unanimously accepted that kurtosis is inversely proportional to the degrees of freedom of a T-Student, so that one is often asked to work coherently with such a rule. However, when we jointly plot two T-Student curves, say with 3 and 15 degrees of freedom respectively (Fig. 1), we soon realize that their main visual difference rests in the tails, as if a decrease in the degrees of freedom can only cause a movement of probability mass from the center to the tails.

Fig. 1

Plot of two T-Student densities with 3 (solid) and 15 (dashed) degrees of freedom

Obviously, that wrong conclusion overlooks the different scales of the two distributions: when they are properly standardized, indeed, it is clear that the movement occurs from the shoulders towards the tails and the center (see the first panel of Fig. 2). Interestingly, a clearer picture of the joint role of tails and center is obtained when, to sterilize for the scale, the standard deviation is substituted by the mean deviation around the median or the mean (as depicted by the second panel of Fig. 2).

Fig. 2

Plots of two T-Student densities with 3 (solid) and 15 (dashed) degrees of freedom, sterilized for the scale by means of the standard deviation (left) and the mean deviation around the mean (right)

Beyond such well-accepted examples, the aim of this paper is to get further into the relationship between the shape parameters of some known models and the level of kurtosis of the underlying distribution. Naturally, our analysis will be conducted by looking first at the visual effects of parameters on the graph, in the above-discussed sense, and then by checking for the coherence of these effects with the values taken by some kurtosis indexes. We will see that, even though it is obvious to expect a difference in the sensitivity of every index, sometimes there are contrasting effects on their values, despite the variation of parameters shifts the graph in a clear direction. Very often, that is due to the presence of a second, thoroughly connected aspect of a distribution: its asymmetry (see also Blest, 2003 and Jones et al., 2011). Notice that, by definition, skewness is a characteristic which affects differently the two “sides” of a distribution, that is the ones obtained by dividing it according to a location measure (usually the mean or the median). Following Zenga (1996), then, a careful analysis of kurtosis in the presence of skewness can be possibly conducted by looking at the shoulders and the tails of the two sides of the distribution separately (their “centers" being the parts of the graph lying on the left and on the right of the chosen location measure).

Now suppose to concentrate on, say, the left side and to analyze the effect of a shape parameter $\theta$ characterizing the distribution of a random variable $X_{\theta }.$ One can set different values of $\theta$ and compare their corresponding left curves, i.e. the parts of the density obtained when $X_{\theta } \le l(X_{\theta })$, if $l(X_{\theta })$ denotes the chosen location measure. However, to get an unbiased comparison, a certain level of uniformity is to be guaranteed. The most obvious problem is that the compared curves are just “portions” of the original densities, i.e. they do not necessarily integrate equally, unless $l(X_{\theta })$ is the median of $X_{\theta }.$ Thus, for every compared $\theta ,$ a possible solution is to work conditionally to the event $X_{\theta } \le l(X_{\theta }),$ so that, consistently, the right curve should be conditioned to $X_{\theta } > l(X_{\theta }).$ This approach is used, for instance, in the “kurtosis diagram” of Zenga (1996), where the properties of the conditional distributions of the two variables

$$\begin{aligned} S_l(X_{\theta }):= (l(X_{\theta }) - X_{\theta }) \, \vert \, X_{\theta } \le l(X_{\theta }) \quad \text{ and } \quad D_l (X_{\theta }):= (X_{\theta } - l(X_{\theta })) \, \vert \, X_{\theta } > l(X_{\theta }) \end{aligned}$$

(1)

are considered to get a picture of kurtosis on the left side and on the right side of $X_{\theta }.$ Being that our aim is just to get a decomposed graph of the density of $X_{\theta }$, the deviations from l considered in (1) are not relevant. Indeed, in Zenga’s approach, they are actually motivated by the need to get non-negative variables, as detailed in the following. In any case, even when just the conditional densities of $X_{\theta }$ are used, to build a faithful graph, they must also share the same support. Obviously, this fact cannot be assured if $l(X_{\theta })$ varies with $\theta .$ However, one may take advantage of the invariance of kurtosis to translations or, more generally, to linear transformations. In what follows, we will use the conclusions drawn in De Capitani and Polisicchio (2016): consider two values $\theta _1$ and $\theta _2$ of $\theta$ and denote $X_{\theta _1}$ and $X_{\theta _2}$ simply as $X_1$ and $X_2.$ Suppose further to compare the left and the right parts of the densities of $X_{1}$ and of $X_{2},$ denoted as $f_1$ and $f_2$ respectively. One can simply split the graph of $f_{1}$ according to the value of $l(X_1)$ and draw, on the same plot, the density of the fictitious variable $X^*_{2},$ which is obtained by the following mixture:

$$\begin{aligned} f^*(x):= f_S(x) \, P \left[ X_{1} \le l(X_{1}) \right] + f_D(x) \, P \left[ X_{1} > l(X_{1}) \right] . \end{aligned}$$

(2)

In the formula above, $f_S$ and $f_D$ depend on the distribution of the random variable ${\tilde{X}}_{2},$ which is obtained by linear transformation of $X_{2}$ as

$$\begin{aligned} \tilde{X}_{2}:= \left\{ \begin{array}{ll} b_S \, \left( X_{2} - l(X_{2}) \right) + l(X_{1}) &{} \text{ if } X_{2} \le l(X_{2}) \\ b_D \, \left( X_{2} - l(X_{2}) \right) + l(X_{1}) &{} \text{ if } X_{2} > l(X_{2}) \end{array} \right. \end{aligned}$$

(3)

where $b_S = \text{ E } \left[ S_l (X_{1}) \right] \, /\, \text{ E } \left[ S_l (X_{2}) \right]$ and $b_D = \text{ E } \left[ D_l (X_{1}) \right] \, /\, \text{ E } \left[ D_l (X_{2}) \right] .$ Specifically, $f_S$ is the conditional density of $\tilde{X}_{2}$ given that $\tilde{X}_{2} \le l(X_{1}),$

$$\begin{aligned} f_S (x):= \frac{1}{P \left[ X_{2} \le l(X_{2}) \right] } \, \frac{1}{b_S} \, \, f_2 \left( \frac{1}{b_S}\, (x - l(X_{1})) + l(X_{2}) \right) \quad x \le l(X_{1}), \end{aligned}$$

(4)

while $f_D$ is the conditional density of $\tilde{X}_{2}$ given that $\tilde{X}_{2} > l(X_{1}),$

$$\begin{aligned} f_D (x):= \frac{1}{P \left[ X_{2}> l(X_{2}) \right] } \, \frac{1}{b_D} \, \, f_2 \left( \frac{1}{b_D}\, (x - l(X_{1})) + l(X_{2}) \right) \quad x > l(X_{1}). \end{aligned}$$

(5)

Notice that the transformation in (3) is built to retain the relevant characteristics and the degree of kurtosis of $X_2$ (for instance, $X_2$ and $X^*_2$ have the same kurtosis diagram), while making it directly comparable with $X_1.$ First, when transforming $X_2$ in ${\tilde{X}}_2$, the location $l(X_2)$ is translated to $l(X_1)$ so that $P\left[ X_{2} \le l(X_2) \right] = P \left[ {\tilde{X}}_{2} \le l(X_1) \right] .$ That makes it sensible to split even the graph of the fictitious variable $X^*_{2}$ according to $l(X_1).$ Indeed, as obtained by the definition of the conditional densities (4) and (5) and by the the weights chosen in the mixture (2), one can notice that

$$\begin{aligned} P\left[ X^*_{2} \le l(X_1) \right] = P \left[ X_{1} \le l(X_1) \right] . \end{aligned}$$

(6)

The statement above guarantees that, if $f_1$ and $f^*$ are plotted in the same graph and split according to $l(X_1),$ both the side-graphs and the whole graphs of the two compared distributions integrate equally. Actually, when l is the mean, the median or any quantile of the distribution, splitting the graph of $X^*_2$ according to $l(X_1)$ means to use its own location, because it is easily shown that $l(X_1)=l(X^*_2)$. Whatever location measure is chosen to split the graph, anyway, $X^*_2$ and $X_1$ have always the same expectation. Indeed, the slopes in the linear transformation (3) are set to guarantee that

$$\begin{aligned} \text{ E } \left[ X^*_2 \, \vert \, X^*_2 \le l(X_1) \right]&= \text{ E } \left[ {\tilde{X}}_2 \, \vert \, {\tilde{X}}_2 \le l(X_1) \right] \\&= - \text{ E } \left[ S_l (X_{1}) \right] + l(X_1) \\&= \text{ E } \left[ X_1 \, \vert \, X_1 \le l(X_1) \right] \end{aligned}$$

and that, consistently,

$$\begin{aligned} \text{ E } \left[ X^*_2 \, \vert \, X^*_2> l(X_1) \right]&= \text{ E } \left[ {\tilde{X}}_2 \, \vert \, {\tilde{X}}_2> l(X_1) \right] \\&= \text{ E } \left[ D_l (X_{1}) \right] + l(X_1) \\&= \text{ E } \left[ X_1 \, \vert \, X_1 > l(X_1) \right] . \end{aligned}$$

Thus, by (6), one gets

$$\begin{aligned} \text{ E } \left[ X^*_2 \right]&= \text{ E } \left[ X^*_2 \, \vert \, X^*_2 \le l(X_1) \right] \, P\left[ X^*_{2} \le l(X_1) \right] + \text{ E } \left[ X^*_2 \, \vert \, X^*_2> l(X_1) \right] \, P\left[ X^*_{2}> l(X_1) \right] \\&= \text{ E } \left[ X_1 \, \vert \, X_1 \le l(X_1) \right] \, P\left[ X_1 \le l(X_1) \right] + \text{ E } \left[ X_1 \, \vert \, X_1> l(X_1) \right] \, P\left[ X_1 > l(X_1) \right] \\&= \text{ E } \left[ X_1 \right] . \end{aligned}$$

Another look at $X^*_2$ not only shows that it shares the location of $X_1,$ but that it has also the same scale. By the equalities above, indeed,

$$\begin{aligned} \text{ E } \left[ \left( l(X_1) - X^*_2 \right) \, \vert \, X^*_2 \le l(X_1) \right]&= \text{ E } \left[ \left( l(X_1) - X_1 \right) \, \vert \, X_1 \le l(X_1) \right] \\ \text{ E } \left[ \left( X^*_2 - l(X_1) \right) \, \vert \, X^*_2> l(X_1) \right]&= \text{ E } \left[ \left( X_1 - l(X_1) \right) \, \vert \, X_1 > l(X_1) \right] , \end{aligned}$$

which, again by (6), gives

$$\begin{aligned} \text{ E } \left[ \, \left| X^*_2 - l(X_1) \right| \, \right] = \text{ E } \left[ \, \left| X_1 - l(X_1) \right| \, \right] . \end{aligned}$$

(7)

After noticing that $l(X_1) = l(X^*_2),$ eq. (7) shows that that $X^*_2$ and $X_1$ has the same mean deviation around l. Thus, the comparison is made under a sterilization of both location and scale, as required above for symmetric distributions. Actually, the fact that $X^*_2$ and $X_1$ are forced to have the same expectation, the same location l and, by eq. (6), even the same cumulative probability at l guarantees, in a sense, a sterilization of skewness as well, at least if one is willing to measure such a phenomenon by the difference between the mean and the median of a distribution. More specifically, when l is the median, the equality $\text{ E } \left[ X^*_2 \right] = \text{ E } \left[ X_1 \right]$ guarantees that $X^*_2$ and $X_1$ share the same difference between the mean and the median. Similarly, when l is the mean, (6) guarantees that the same difference between the cumulative probability at the mean and at the median is obtained for both distributions.

To appreciate the coherence of the proposed method of comparison with the discussion above about symmetric distributions, consider the example in Fig. 3. The first panel of that figure reports the result obtained when comparing two T-student distributions (with 3 and 15 df), whose graphs are split according to the mean. Clearly, no problems arise here for location, because both distributions are symmetric around zero. However, the comparison made through the fictitious density (2) introduces the needed sterilization for the different scale. Being that such a task is accomplished by the mean deviation around the mean, the same comparison reported in Fig. 2 (second panel) is thus obtained, even if the two densities are split here around the mean zero. The second panel of Fig. 3, instead, reports a similar comparison when the skew-T model is considered (details in the following). Notice that the plot of (2) does not always produce a continuous density. Nonetheless, one needs to look at the two sides of the graph separately. Moreover, any conclusion drawn on a single side of the graph must be referred to that side of kurtosis, without being sure that the same holds true for the other side or for the whole distribution.

Fig. 3

Plots of the left/right parts of two symmetric and two skewed distributions. Left panel: two T-Student densities with 3 (solid) and 15 (dashed) degrees of freedom. Right panel: two skew-T densities, both with skew-parameter 0.5,  with 3 (solid) and 15 (dashed) degrees of freedom

Even a first look at the second panel of Fig. 3 makes it clear that, when kurtosis is entangled with skewness, providing an overall judgment about its level is an hard task, because the two sides of the plot are often likely to produce contrasting evidence. That problem, of course, reflects on the evaluation given by an overall index, unless it can be decomposed as well. Basically, that is the idea under the measurement of kurtosis provided by Zenga (1996): by noticing that a movement of probability mass from, say, the left shoulder increases the concentration of that mass out of the center of $S(X_{\theta })$ towards its extremes, the left contribution to kurtosis can be measured by the Gini’s concentration ratio. After dropping dependence on the parameter $\theta ,$ one gets, for every random variable X, 

$$\begin{aligned} K^-_2(l):= \frac{\text{ E } \left[ \left| S_l(X) - S_l(X^{\prime }) \right| \right] }{2 \, \text{ E } \left[ S_l(X) \right] } \end{aligned}$$

(8)

where $X^{\prime }$ is an independent copy of X. Notice that the definition in (8) depends on the chosen location measure l: the usual choices are the mean and the median, which will be denoted as $\mu$ and $\gamma$ respectively in the following (see De Capitani and Polisicchio, 2016). Obviously a similar reasoning can be applied to the right side of the distribution, to get

$$\begin{aligned} K^+_2(l):= \frac{\text{ E } \left[ \left| D_l(X) - D_l(X^{\prime }) \right| \right] }{2 \, \text{ E } \left[ D_l(X) \right] }, \end{aligned}$$

(9)

so that an overall index is obtained as

$$\begin{aligned} K_2(l):= K^-_2(l) \, P \left[ X \le l(X) \right] + K^+_2(l) \, P \left[ X > l(X) \right] . \end{aligned}$$

(10)

Of course, one of the advantages of $K_2(l)$ rests in its natural decomposability, even if, to agree with the judgment provided by the overall index, one must also agree with the weights chosen for the two parts of the distribution, as detailed in the following.

In this paper, we will test the relationship between some shape parameters and $K_2(\mu )$ or $K_2(\gamma ).$ Beyond considering their differences, we will compare them with other known indexes. Firstly, we will evaluate other measures based on Zenga’s logic, i.e. those obtained by assimilating concentration with relative variability:

$$\begin{aligned} K_1(l)&:= \left[ 1- \frac{\text{ E}^2 \left[ S_l(X)\right] }{\text{ E } \left[ S^2_l(X)\right] } \right] \, P \left[ X \le l(X) \right] + \left[ 1- \frac{\text{ E}^2 \left[ D_l(X)\right] }{\text{ E } \left[ D^2_l(X)\right] } \right] \, P \left[ X> l(X) \right] \nonumber \\&:= K^-_1(l) \, P \left[ X \le l(X) \right] + K^+_1(l) \, P \left[ X > l(X) \right] , \end{aligned}$$

(11)

where, again, $l=\mu$ or $l=\gamma$ (see Zenga, 1996). Secondly, we will consider Pearson’s standardized fourth moment $\beta _2$ and, to be compliant with the discussion above, we will decompose it as

$$\begin{aligned} \beta _2&:= \frac{1}{\sigma ^4} \, \text{ E } \left[ (\mu -X)^4 \, \vert \, X \le \mu \right] \, P \left[ X \le \mu \right] + \frac{1}{\sigma ^4} \, \text{ E } \left[ (X-\mu )^4 \, \vert \, X> \mu \right] \, P \left[ X> \mu \right] = \nonumber \\&:= \beta _2^- \, P \left[ X \le \mu \right] + \beta _2^+ \, P \left[ X > \mu \right] . \end{aligned}$$

(12)

Notice that the decomposition provided by (12) is far from being natural. In addition, it forces to split the two sides of a distribution according to the mean. These facts depict, in a sense, the drawbacks of $\beta _2,$ which will be outlined in the following. Nonetheless, we will also see that there are actually many points of touch between $\beta _2$ and the other considered indexes. For other possible decompositions of $\beta _2,$ and for the possible substitution of the mean with the median, the interested reader can refer to Fiori (2007).

Each of the following sections from 2 to 5 is focused on a specific model which, in our opinion, is relevant both for the applicability to many empirical situations and for the general indications that it can provide. Sect. 6 summarizes these indications. Finally, Sect. 7 describes some applications and it sketches possible lines of future research.

2 Gamma distribution

In models possessing a single shape parameter, its variation is likely to result not only in a change of kurtosis, but also in simultaneous modifications of other characteristics, markedly of skewness. More interestingly, that variation may induce different changes in the left and in the right part of a distribution, as discussed above. A relevant example is provided by the Gamma model in its standard form:

$$\begin{aligned} f(x) = \frac{1}{\Gamma (\alpha )} \, x^{\alpha -1} \, \text{ e}^{- x} \qquad x \ge 0, \end{aligned}$$

(13)

where $\Gamma (\alpha )= \int _0^{\infty } u^{\alpha -1} \, \text{ e}^{- u} \, \text{ d}u$ denotes the Gamma function. As known, when the parameter $\alpha >0$ increases, the shape of the distribution becomes more and more similar to the Normal density. Graphically, that fact can be appreciated, first, by the occurrence of a mode when $\alpha$ is as high as 1 (while, when $0< \alpha <1,$ the density tends to infinity as x tends to zero) and by the appearance of a peak when $\alpha >1.$ Moreover, as $\alpha$ increases, the fatness of the right tail tends to even out and the left tail shows up (see Fig. 4).

Fig. 4

Plots of the density (13) when $\alpha =0.5$ (solid), $\alpha =2$ (dashed) and $\alpha =3.5$ (dotted)

Movements of the parameter $\alpha$, then, lead to the variation of many characteristics of the distribution but, while the effect of location and scale can be easily sterilized by looking at its standardization (see Johnson et al., 1994), the entanglement of skewness and kurtosis creates a somewhat confounding effect: without a proper sterilization for skewness, when $\alpha$ increases, kurtosis is simultaneously decreased due to a movement of the probability mass away from the right tail and increased by a similar movement of probability towards the center. As a consequence, even if all kurtosis indexes reasonably tend to their values in the case of the Normal distribution if $\alpha$ gets large, the characteristics of the paths leading to those value may markedly differ.

Fig. 5

Plots of $K_2(\mu ) /0.4142$ and $\beta _2 /3$ in the Gamma model as $\alpha$ ranges from 0.5 to 5.

Figure 5 illustrates such a fact: to improve readability of the graphs, $\alpha$ is left to vary just from 0.5 to 5 and the two indexes $K_2(\mu )$ and $\beta _2$ are plotted against the shape parameter, after dividing them by the values taken in the case of the Normal distribution (0.4142 and 3 respectively). One can notice first that the initial evaluation of kurtosis (i.e. the one for $\alpha = 0.5$) is quite different for the two indexes: $K_2(\mu )$ (first panel) depicts a distribution with less kurtosis than the Normal, being around 76% of the Normal value; on the contrary, $\beta _2$ (second panel) is five times higher than its reference value, which results in a strong level of kurtosis. If we think about the shape of the Gamma model when $\alpha =0.5,$ we can clearly identify two aspects: the unboundedness of the density on the left side, which shifts probability around zero, and the fatness of the right tail. In the rough effort of explaining the different attitude of the two indexes, then, one can simply think that $K_2(\mu )$ is more sensitive to the first phenomenon, which is undoubtedly a symptom of low kurtosis, while $\beta _2$ mostly concentrates on the fatness of the right tail, which acts conversely. Such an explanation, in effect, would also fit the different paths to the limiting value which characterize the two indexes: while the mass moves away from zero and the density gets bounded, $K_2(\mu )$ increases; on the contrary, $\beta _2$ has a simultaneous decrease due to the movement of the mass away from the right tail.

Fig. 6

Comparison of two Gamma densities when $\alpha = 2$ (solid) and $\alpha = 3.5$ (dashed), separated into their left and right parts

If we look at the problem not just from the point of view of the final value of an index, the conclusions above are only partially correct. A way to reconcile the results provided by $K_2(\mu )$ and $\beta _2,$ indeed, is to examine the decomposition of the distribution and of the indexes, as discussed in the Introduction. Figure 6 shows the graphs obtained by setting the two values $\alpha =2$ (solid curves), $\alpha = 3.5$ (dashed curves) and by “splitting" the two corresponding Gamma densities as described above. When the parameter increases, the probability mass moves from the shoulder to the center and to the tail in the left side, while an opposite movement is observed in the right part. Consequently, the overall judgment on how $\alpha$ affects kurtosis must depend on two factors: the sensitivity used for the tail and the center when evaluating the shape modification of the left/right part and the weight applied to each part when the whole distribution is considered.

Clearly, a choice in the weighting system above is made when a specific index is applied. As known, $K_2(\mu )$ measures the concentration of $S_{\mu }(X)$ and of $D_{\mu }(X)$ first and then it weights results by $P \left[ X \le \mu \right]$ and $P \left[ X > \mu \right]$ respectively. Notice that the chosen concentration measure, Gini’s ratio, is invariant under scale functions, which means that transformations like (3), made to get comparable graphs in the two sides of the distribution, cannot affect the value of the index. Similar conclusions hold for $\beta _2$ as decomposed in (12), but while it is clear that $K_2(\mu )$ and $\beta _2$ apply the same weight to the left and to the right part, a difference may be appreciated in the evaluation provided for the tail and for the center in each part. Being built on the fourth power of the difference from the mean, for instance, $\beta _2^-$ is likely to mostly weight the left tail. This means that, when the left part gives room mainly for the center (like when $\alpha =2$), the extent of left kurtosis is under-evaluated; nonetheless, if a movement of probability towards the left tail occurs (like when $\alpha$ is shifted from 2 to 3.5), $\beta _2^-$ should show an increasing pattern.

Fig. 7

Plots of $K_2(\mu )$ and $\beta _2$ in the Gamma model, when $\alpha$ ranges from 0 to 5. Both overall indexes (solid) are decomposed into their left (dashed) and right (dotted) contributions

The intuition above is confirmed by Fig. 7: the unweighted left/right parts of $K_2(\mu )$ and $\beta _2$ are plotted against increasing values of the shape parameter of the Gamma distribution. Looking at the left parts of both indexes (dashed curves), one can notice that, coherently with the conclusions for Fig. 6, left kurtosis increases with $\alpha .$ However, it is clear that such a phenomenon mostly affects $K_2^-(\mu ),$ while $\beta _2^-$ takes (comparatively) low values with just a mildly increasing pattern. Conversely, on the right side (dotted curves), $K_2^+(\mu )$ and $\beta _2^+$ share a similar decreasing pattern. However, notice that, while the former shows a curve somewhat symmetric to the left part, the latter starts from very high values, due to its strong sensitivity to the right tail. As for the weight given in each index to the left/right part, one may notice that, when $\alpha$ is small, $P \left[ X \le \mu \right]$ takes values close to one (being, for instance, 0.6827 when $\alpha =0.5$) and that it decreases quite slowly with $\alpha$ (being still over the half when $\alpha =5$). As a result, both $K_2(\mu )$ and $\beta _2$ (solid curves in Fig. 7) weight more left kurtosis than the right. However, the values taken by $\beta _2$ in the left part of the distribution, whose support is bounded below by zero, are comparatively markedly smaller than the ones in the right part, so that the overall $\beta _2$ is mostly sensitive to the effect of the right tail. Due to the symmetry of the left and the right part, conjugated with an unbalanced weighting system, $K_2(\mu )$ is, instead, mostly influenced by the thickening of the center of the distribution.

The analysis of decomposed indexes above does not aim at establishing the superiority of one of them, unless the researcher wants deliberately to favor some aspects of kurtosis. By contrast, it can provide a useful tool to interpret indexes correctly and possibly to reconcile opposite pieces of evidence. That logic can be applied, of course, in the comparison of other kurtosis measures. In this sense, Fig. 7 can be juxtaposed to Fig. 8 where, in the same settings, the decomposition of Zenga’s $K_2(\gamma )$ is reported.

Fig. 8

Plot of $K_2(\gamma )$ in the Gamma model, when $\alpha$ ranges from 0 to 5. The overall index (solid) is decomposed into its left (dashed) and right (dotted) contributions

Notice that the paths of the left and right kurtosis are very similar to the ones reported in the first panel of Fig. 7 for $K_2(\mu ),$ despite one would expect that the strong skewness can induce distinct results whether the mean or the median is chosen as a cutting point for the two parts of the distribution. The real distinction between $K_2(\mu )$ and $K_2(\gamma ),$ indeed, rests in the weight chosen for the two sides, which is constantly equal to 1/2 when $\gamma$ is used. As a result, left and right kurtosis almost compensate in such a case, so that $K_2(\gamma )$ is nearly constant, with a non-monotonic pattern, slightly decreasing when $\alpha$ is low and slowly increasing as $\alpha$ grows. That is a case where looking just at the overall index can provide misleading information: on the basis of the sole $K_2(\gamma ),$ indeed, one would just conclude that the distribution has a kurtosis similar the Normal model, thus ignoring that its shape is quite different and that the observed level is actually the effect of a compensation.

Fig. 9

Plots of $K_1(\mu )$ and $K_1(\gamma )$ in the Gamma model, when $\alpha$ ranges from 0 to 5. Both overall indexes (solid) are decomposed into their left (dashed) and right (dotted) contributions

Interestingly, the conclusions drawn for $K_2(\mu )$ and $K_2(\gamma )$ can be equally retraced for $K_1(\mu )$ and $K_1(\gamma )$ respectively. In the usual settings, Fig. 9 illustrates that. One is thus tempted to conclude that the $K_1-$ indexes do not provide new information about kurtosis and that computing the complete sets of Zenga’s indexes is substantially useless. However, the same conclusions do not necessarily holds for models other than the Gamma, as shown in the following. Moreover, one cannot forget that, when such kurtosis indexes are estimated from sampled data, their performance may markedly differ (see Borroni and De Capitani, 2022).

3 Johnson’s $S_U-$system of distributions

The example of the Gamma model shed some light into the entanglement of kurtosis to skewness: the main conclusion of our analysis is that, when both phenomena coexist, kurtosis is better evaluated by separating the contributions given by the left and the right part of the distribution. As for the relationship of kurtosis indexes with shape parameters, the same example showed, in addition, that it may be altered by their different abilities to interpret movements of mass affecting the tails. Of course, no index will ever fully separate kurtosis from skewness, but it is also clear that, to compare the ability to accomplish that task, a model possessing a single shape parameter might not be particularly useful. Indeed, variations of a unique parameter not only will induce concomitant changes in both kurtosis and skewness, but those changes are also likely to occur in a fixed proportion.

Fig. 10

$\beta _2$ as a function of $\beta _1^2$ in the Gamma model ($\alpha$ ranges from 0.05 to 5)

This fact arises clearly for the Gamma model, as evidenced by Fig. 10 where the values of $\beta _2$ (corresponding to $\alpha$ ranging from 0.05 to 5) are plotted against those of $\beta _1^2,$ the square of the standardized third central moment. As known (see Johnson et al, 1994), a linear relation exists so that, for every unit increase of $\beta _1^2,$ $\beta _2$ increases by 1.5 times. Of course, different conclusions (including non-linearity) might be obtained, even in the same model, when the kurtosis index is changed and/or paired with a different skewness measure. Nonetheless, it is clear that a deeper comparative analysis among indexes could be carried out only if a family is found where the relationship between kurtosis and skewness can be altered at convenience. A somewhat similar aim led Johnson (1949) to develop the known $S_U-$system of unbounded distributions, with density

$$\begin{aligned} f(x) = \frac{\delta }{\sqrt{2 \pi }} \, \frac{1}{\sqrt{y^2+1}} \, \text{ exp } \left\{ - \frac{1}{2} \left[ \xi + \delta \, \text{ log } \left( y+\sqrt{y^2+1}\right) \right] ^2 \right\} \qquad y \in \Re , \end{aligned}$$

(14)

which actually possesses two shape parameter, $\delta >0$ and $\xi \in \Re .$ When the latter is 0, the distribution is symmetric and the parameter $\delta$ is often regarded an inverse measure of fatness of the tails (see Brys et al., 2006). Conversely, even if $\xi$ cannot be merely regarded as a parameter of skewness, obliquity increases with $\vert \xi \vert \ne 0$ and the distribution is negatively (positively) skewed when $\xi >0$ ($\xi <0$). Thus, the family can be conveniently used to model every combination of the levels of kurtosis and skewness. Specifically, while Johnson (1949) only showed that the two parameters can be fixed to obtain any couple $(\beta _2,\beta _1),$ we will use the model to explore different forms of the relationship between kurtosis and skewness, as one parameter is fixed and the other moves.

Fig. 11

Plots of $K_2(\mu ) /0.4142$ and $\beta _2 /3$ in the $S_U-$system, when $\xi =0$ and $\delta$ ranges from 1 to 3.

If we start from the simple situation $\xi =0,$ all kurtosis indexes are easily shown to agree in detecting a high level of kurtosis, decreasing with $\delta ,$ that is with the lightening of the tails. There are, of course differences among the evaluations provided by indexes: as an example, Fig. 11 reports the plots of $K_2(\mu )$ (first panel) and $\beta _2$ (second panel) when $\xi =0$ and $\delta$ ranges from 1 to 3. Similarly to the settings of Fig. 5, both indexes were divided by their values in the Normal case. Despite no confounding effects by skewness arises here, one can still realize that the tail behavior has a huge impact on $\beta _2$ when $\delta$ is too low.

Of course the effect of the parameter $\delta$ on the shape of the distribution is difficultly interpreted when $\xi \ne 0.$ To understand this issue, Fig. 12 reports the graphs of the density (14) when $\xi =1$ (solid curve) and $\xi =1.5$ (dashed curve), while $\delta$ is set to 1 in both cases.

Fig. 12

Graphs of the density (14), when $\delta =1$ and $\xi =1$ (solid) or $\xi =1.5$ (dashed)

A clear movement of the probability mass towards the left tail stands out when $\xi$ increases. This movement clearly makes the distribution more skewed but this fact is here accompanied by relevant changes in kurtosis as well. In this respect, a careful look shows that, actually, the most effective variation occurs in the right part of the distribution. In other words, the increase of weight of the left tail is comparatively masked by the fact that this tail was already fat, due to a low level of the parameter $\delta .$ As for the Gamma example above, such conclusions can be clarified by building separate graphs for the left and the right parts.

Fig. 13

Comparison of the densities in Fig. 12, separated into their left and right parts

The first panel of Fig. 13 shows that, despite a certain increase of kurtosis when $\xi =1.5,$ the left parts of the two distributions do not markedly differ. Conversely, in the comparison of their right parts (second panel), one can distinctly notice a movement of the probability mass from the tail and the center toward the shoulder of the distribution, i.e. a decreasing effect on kurtosis as $\xi$ increases.

Fig. 14

Same comparison of Fig. 13, when $\delta$ is shifted to 4.

Interestingly, when $\delta$ is set to 4, even if the shift of $\xi$ from 1 to 1.5 still leads to a similar path (increase of left-kurtosis and decrease of right-kurtosis), the two changes are now almost balanced (see Fig. 14). One can thus expect that, in this situation, the overall kurtosis is less affected by variations of the parameter $\xi$ than what happens if $\delta$ is low and the tails are fat. This shows clearly that the value set for $\delta$ can modify the kind of relationship between kurtosis and skewness in the considered model. If an exercise similar to the one depicted in Fig. 10 is repeated for the $S_U-$system, for instance, just a nearly linear relationship between $\beta _2$ and $\beta _1^2$ exists. Moreover, its slope equals approximately 2.05 when $\delta =1$ and lowers to 1.35 when $\delta =4.$

Fig. 15

Plots of $K_2(\mu )$ and $\beta _2$ in the $S_U-$system, when $\delta =4$ and $\xi$ ranges from 0 to 4. Both overall indexes (solid) are decomposed into their left (dashed) and right (dotted) contributions

Turning back to indexes, as above outlined, one should expect that their values is clearly affected by variations of $\xi$ only when $\delta$ is set to a low level. In this regard, Fig. 15 show a nearly constant path of $K_2(\mu )$ (first panel) and $\beta _2$ (second panel), when $\delta =4,$ despite $\xi$ ranges from 0 to 4. Actually $\beta _2$ reports a slightly increasing effect of $\xi ,$ while the opposite is true for $K_2(\mu ).$ That difference is possibly due to the residual sensitivity of $\beta _2$ to the burdening of the left tail, despite the mild effect on kurtosis. Notice that, when the indexes are decomposed, the path of their left and right branches is quite similar, with variations of mild intensity.

Fig. 16

Plots of $K_2(\mu )$ and $\beta _2$ in the $S_U-$system, when $\delta =1$ and $\xi$ ranges from 0 to 4. Both overall indexes (solid) are decomposed into their left (dashed) and right (dotted) contributions

A pretty different thing is observed in Fig. 16, when $\delta$ is set to a value as low as 1. The clear effect of the variation of $\xi$ on the overall kurtosis leads to markedly different behaviors of the indexes. In the first panel, $K_2(\mu )$ is seen to decrease with $\xi ,$ which means that the index is mostly sensitive to the changes occurring in the right part of the distribution (see the second panel of Fig. 13). Such a conclusion is supported by the path of the right (dotted) branch in the decomposition of $K_2(\mu )$: a situation substantially opposite to the one depicted by Fig. 7 for the Gamma model is observed. Coherently, as $\xi$ moves from 0 to 4, $\beta _2$ (second panel of Fig. 14) concentrates on the burdening of the left tail, so that its left (dashed) branch shows a fast increase which predominates in the overall index. Both indexes tend to even out when $\xi$ is high, but their final assessment of kurtosis is quite different.

Fig. 17

Plots of $K_2(\gamma )$ and $K_1(\mu )$ in the $S_U-$system, when $\delta =1$ and $\xi$ ranges from 0 to 4. Both overall indexes (solid) are decomposed into their left (dashed) and right (dotted) contributions

Differently from the Gamma model, the weighting of the left/right part seems to affect just mildly the paths of Zenga’s overall indexes, as observed when the cutting point is changed from the mean to the median. The first panel of Fig. 17 supports such a conclusion: along with its side branches, the overall $K_2(\gamma )$ behave quite similarly to what depicted in the first panel of Fig. 16 for $K_2(\mu ).$ As a further term of comparison, the second panel of Fig. 17 reports the plots related to $K_1(\mu )$: despite the slightly different values shown (recall that $K_1(\mu )=0.3634$ in the Normal model), it is clear that $K_1(\mu )$ leads to the same conclusions of the $K_2-$ indexes for the relationship between kurtosis and the parameter $\xi .$ This fact is true in general, regardless of the value taken by $\delta ,$ and it holds for $K_1(\gamma )$ as well (the related plots are not reported for the sake of brevity).

4 Skew-T distribution

Due to its flexibility, the $S_U-$system of unbounded distributions provided us with a good example to understand the sensitivity of kurtosis measures to the shifts of shape parameters. The presence of the parameter $\xi ,$ mainly controlling skewness, let us understand that this phenomenon can, in a sense, contrast kurtosis, at least when the latter has some initial high levels. Before getting further into that conclusion, however, it has to be emphasized that the second parameter $\delta$ of Johnson’s system regulates mainly the fatness of the tails: especially when there is a certain level of skewness, then, one is not sure that movements of $\delta$ are necessarily connected with modifications of the tails and of the center as well. Thus, some further insight need to be searched in models where a first parameter is supposed to act simultaneously on the tails and the center, while a second parameter introduces different levels of skewness. This section evaluates the skew-T model (see Azzalini and Capitanio, 2014), where the usual role of the degrees of freedom $\nu$ in the T-distribution is conjugated with a skew-parameter $\alpha .$ The resulting density is

$$\begin{aligned} f(x)= \frac{2}{\Gamma (\frac{1}{2} \nu ) \, \sqrt{\pi \nu }} \, \left( 1+\frac{x^2}{\nu } \right) ^{-\frac{\nu +1}{2}} \int _0^{\infty } \text{ e}^{-u} \, u^{-\frac{\nu -1}{2}} \, \Phi \left( \frac{\alpha x \, \sqrt{2u}}{\sqrt{x^2+\nu }} \right) \, \text{ d}u \end{aligned}$$

(15)

(where $\Phi$ denotes the cumulative distribution function of the standard Normal distribution). When $\alpha =0,$ (15) reduces to the T-distribution and it gets more right-skewed as $\alpha$ takes positive increasing values; moreover, when $\nu \rightarrow \infty ,$ (15) gives the skew-Normal model (see Azzalini and Capitanio, 2014).

Fig. 18

Plots of $K_2(\mu ) /0.4142$ and $\beta _2 /3$ in the skew-T distribution, when $\alpha$ ranges from 0 to 10 and $\nu$ is set to 5 (dashed) or 50 (solid)

Despite the suspected difference regarding the center, the skew-T model gives conclusions very similar to the one in the previous section: when the initial kurtosis is high (which means, in these settings, that $\nu$ takes a low value), even a small level of skewness can reduce it. Conversely, when there are many degrees of freedom and $\alpha$ is raised, kurtosis is almost unaffected, at least for ordinary levels of skewness. To get into details, one may look at the first panel of Fig. 18, where the value taken by $K_{2}(\mu )$ (divided by 0.4142) is plotted against $\alpha$ ranging from 0 to 10. Two curves are built, by fixing $\nu$ to 5 (dashed) and to 50 (solid) respectively: for mild shifts of $\alpha$ from 0, the steep pattern of the former clearly juxtaposes to the flatness of the latter. In addition, like in the Johnson’s model above, the cause of the contrasting effect of skewness on kurtosis can be traced back not just in the tail which gets fatter, but in the modification of other part of the distribution, where relevant movements of mass occur from the tail and the center toward the shoulder (recall Fig. 13). That intuition is supported by the decomposition of $K_2(\mu ),$ which is reported in the first panel of Fig. 19 for the case $\nu =5.$

Fig. 19

Plots of $K_2(\mu )$ and $K_1(\mu )$ in the skew-T distribution, when $\nu =5$ and $\alpha$ ranges from 0 to 10. Both overall indexes (solid) are decomposed into their left (dashed) and right (dotted) contributions

Indeed, notice that the increase in the right-kurtosis, as measured by $K_2^+(\mu ),$ tends to even out when $\alpha$ gets over some ordinary levels but that, conversely, the left part of $K_2(\mu )$ has a constantly decreasing pattern. Finally, the second panel of the same Fig. 19 indicates that such conclusions hold for $K_1(\mu )$ as well (and actually also for all Zenga’s indexes, even if the related plots are not reported for the sake of brevity).

Fig. 20

Plots of $K_2(\gamma )$ and $K_1(\gamma )$ in the skew-T distribution, when $\alpha =1.5$ and $\nu$ ranges from 5 to 20. Both overall indexes (solid) are decomposed into their left (dashed) and right (dotted) contributions

When the interest shifts from the parameter $\alpha ,$ which mainly regulates skewness, to a more “pure” parameter of kurtosis like $\nu ,$ the two branches of a decomposed index show compliant patterns, as one would expect. In Fig. 20, a mild level of skewness is fixed by setting $\alpha =1.5$ and the decomposition of two Zenga’s indexes, $K_2(\gamma )$ (first panel) and $K_1(\gamma )$ (second panel), is reported when $\nu$ moves from 5 to 20. Notice that both sides of the indexes show a decreasing pattern, even if the effect of $\nu$ fades out from a certain level on. In addition, the decrease of the right branches seems to be strengthened by the presence of a certain level of skewness.

Turning to $\beta _2,$ one could claim that the conclusions drawn for Zenga’s indexes are not met. The second panel of Fig. 18, indeed, reports an increasing pattern of $\beta _2$ when $\nu =5$ (dashed curve) and $\alpha$ is raised from 0 to 10,  so that a contrasting effect of skewness on kurtosis seems not to be detected here. Even when $\nu$ is raised to 50 (solid curve), skewness still causes increasing values of $\beta _2,$ although around very low levels. The apparent contradiction between the evaluation provided by Zenga’s indexes and $\beta _2,$ however, is just the consequence of a somewhat overwhelming effect of the right tail. Being quite sensitive to it, indeed, $\beta _2$ raises indefinitely when (positive) skewness burdens the right tail, while the modifications occurred in the left part of the distribution are masked in the overall index. This fact is clearly shown in the first panel of Fig. 21: when $\nu$ is fixed to 5 and skewness is raised by moving $\alpha$ from 0 to 10,  the left and the right branches of $\beta _2$ have patterns similar to those observed for $K_2(\mu )$ above (first panel of Fig. 19). Despite that, the comparatively huge value of $\beta _2^+$ and the unbalanced weighting system for the two sides tend to favor the evaluation provided for the right part. A decomposed analysis, then, reveals coherence among all considered indexes. That is also true when the effect of a parameter regulating mainly kurtosis, like $\nu ,$ is considered. Indeed, the second panel of Fig. 21, which is built by setting $\alpha =1.5$ and by moving $\nu$ from 5 to 20,  is consistent with what observed for $K_2(\gamma )$ and $K_1(\gamma )$ in Fig. 20 although, again, the predominant role of the side with a fat tail is observed.

Fig. 21

Decomposed plots of $\beta _2$ in the skew-T distribution. First panel: $\nu =5$ and $\alpha$ ranges from 0 to 10;  second panel: $\alpha =1.5$ and $\nu$ ranges from 5 to 20.

5 Zenga’s income distribution

The discussion in the two previous section highlighted that kurtosis is the sum of many aspects of the shape of a distribution, which may show fat and pronounced tails (so called tailedness), high values of the density around a single point (so called peakedness) or an inflated side at the expense of the other (so called skewness). As a consequence, kurtosis is difficultly measured by such indexes, like $\beta _2,$ which concentrate on a single aspect, without wondering if they possibly balance. To understand that issue, then, one can look at distributions which are quite flexible in terms of the shape, while maintaining almost constant levels of global kurtosis. Mainly as a model for income distributions, Zenga (2010) introduced a family which, under some limitations, has that property.

Under some restrictions on parameters, suitable for our analysis, the density can be defined as

$$\begin{aligned} f(x) = \frac{1}{\text{ B }(\alpha , \theta ) \, x^{3/2}} \left[ \text{ IB } \left( x; \alpha + \frac{1}{2}, \theta -1 \right) \, \text{ I}_{(0,1)} (x) + \text{ IB }\left( \frac{1}{x}; \alpha + \frac{1}{2}, \theta -1 \right) \, \text{ I}_{[1,\infty )} (x) \right] \end{aligned}$$

(16)

where $\text{ B } (a,b) = \int _{0}^{1} u^{a-1} \, (1-u)^{b-1} \, \text{ d}u$ and $\text{ IB } (z;a,b) = \int _{0}^{z} u^{a-1} \, (1-u)^{b-1} \, \text{ d}u$ denote the Beta function and the incomplete Beta function respectively ($a>0;$ $b>0;$ $0<z\le 1$). In the settings of (16), the first moment is constantly equal to unity, while the two shape parameters are such that $\alpha >0$ and $\theta >1$ (see Zenga, 2010) and De Capitani and Zini, 2013) for a general definition of the density). The density has a Paretian right tail, which lightens with $\alpha ;$ as a consequence, it possesses the $r-$th moment just for $\alpha >r-1.$ For our purposes, in order to guarantee a fair comparison of all kurtosis indexes including $\beta _2,$ we will then be limited to the case $\alpha >3.$ Moreover, many application of the model to real income data show that $\theta$ is often as high as $2.5-3,$ which also guarantees that the curve has a “mild” peak.

Fig. 22

Graphs of the density (16), when $\theta =3$ and $\alpha = 3.5$ (solid) or $\alpha = 5$ (dashed)

As a first example, Fig. 22 reports two graphs of the density (16), where $\theta =3$ and $\alpha =3.5$ (solid) or $\alpha =5$ (dashed). One can notice that the increase of $\alpha$ reduces the fatness of both tails, but also that a simultaneous effect of peakedness is observed. Specifically, a movement of mass from the tails of the distribution towards its shoulders seems to coexist with an opposite effect towards the center. Differently from what observed for other models (see, for instance, the Gamma density above), however, this double movement of probability mass affects, almost in the same way, both the right and the left side. As a result, one can expect that the increase of $\alpha$ can shift neither the kurtosis level of any side neither that of the overall distribution.

Fig. 23

Comparison of the densities in Fig. 22, separated into their left and right parts

To test such a conclusion, Fig. 23 reports the usual separate comparison of the right and the left parts of the two densities: when $\alpha$ is raised from 3.5 to 5, just a slight variation of the kurtosis level is seen, both because the solid and dashed curves do not markedly differ and because an opposite, possibly compensating, effect is observed in the left and the right part.

Turning to indexes, then, it is clear that Zenga’s distribution can be useful to test their ability to measure the overall effect of parameters on kurtosis, without being influenced by movements of single aspects of the shape.

Fig. 24

Plots of $K_2(\mu )$ and $K_1(\mu )$ in the Zenga’s distribution, when $\theta =3$ and $\alpha$ ranges from 3.5 to 7. Both overall indexes (solid) are decomposed into their left (dashed) and right (dotted) contributions

Figure 24 confirms that ability for $K_2(\mu )$ (first panel) and $K_1(\mu )$ (second panel): while their side components follow a path which essentially reflects a tendency to symmetry as $\alpha$ increases, the overall indexes recognize a compensation of the two sides and remain substantially constant. Notice that both indexes agree on a level of kurtosis slightly over the Normal model. In addition, despite the graphical effect in Fig. 24, one can notice that even the values of the side components are quite stable with $\alpha$, more clearly for $K_2(\mu )$ where the left and the right kurtosis show levels very close to the overall index. No substantial changes can be appreciated when the cutting point is set to the median instead of the mean: Fig. 25, indeed, reports the results of a similar exercise for $K_2(\gamma )$ and $K_1(\gamma )$ and leads to similar conclusions, especially if $\alpha$ is as high as 4.

Fig. 25

Plots of $K_2(\gamma )$ and $K_1(\gamma )$ in the Zenga’s distribution, when $\theta =3$ and $\alpha$ ranges from 3.5 to 7. Both overall indexes (solid) are decomposed into their left (dashed) and right (dotted) contributions

When the interest is shifted to indexes based on high-order moments, as for $\beta _2,$ despite Zenga’s model suggests a constant level of global kurtosis, one would expect a prevalent influence of the effect of the tails. A confirmation is provided by the first panel of Fig. 26, where $\beta _2$ and its side components are plotted against $\alpha$ with a fixed $\theta =3$: one can notice the excessive level of the right kurtosis, its definite influence on the overall index and, above all, the non-constant path as $\alpha$ increases.

Fig. 26

Left: plot of $\beta _2$ in the Zenga’s distribution, when $\theta =3$ and $\alpha$ ranges from 3.5 to 7;  the overall index (solid) is decomposed into its left (dashed) and right (dotted) contributions. Right: $\beta _2$ as a function of $\beta _1^2$ in the Zenga’s distribution ($\theta =3$ and $\alpha$ ranges from 3.5 to 7)

In a sense, the distorting effect of tailedness on the evaluation provided by $\beta _2$ seems to be more severe here than what happens in other models where a parameter regulates the heaviness of a single tail. Looking at the Gamma and at the Zenga’s models together, indeed, one can notice that, in both cases, decreasing values of the parameter $\alpha$ creates a pronounced right tail which results in skewness and kurtosis, as measured by $\beta _1$ and $\beta _2$ respectively. However, the effect on the latter seems to be prevalent in the Zenga’s model, at least if one compares the relationship between $\beta _2$ and $\beta _1^2$ depicted above in Fig. 10 (Gamma) with a similar plot reported in the right panel of Fig. 26 (Zenga’s): while the increase of $\beta _2$ is just proportional to that of $\beta _1^2$ in the first case, a quadratic pattern is distinctively observed in the second situation. That could be even considered as a distinctive characteristic of Zenga’s distribution over similar models with Paretian tail.

Fig. 27

Plots of $K_2(\mu ) /0.4142$ and $\beta _2 /3$ in the Zenga’s distribution, when $\alpha =5$ and $\theta$ ranges from 3 to 7.

Some interesting features arise also when a varying $\theta$ is considered. In the ranges established for our analysis, Fig. 27 reports the plots of $K_2(\mu ) /0.4142$ (first panel) and $\beta _2 /3$ (second panel) when $\alpha$ is fixed to 5 and $\theta$ moves from 3 to 7. While an almost constant, slightly decreasing pattern is observed for the former index, the classical $\beta _2$ has an unexpected parabolic trend, which appears as the consequence of a weakening balance effect.

Fig. 28

Graphs of the density (16), when $\alpha =5$ and $\theta = 3$ (solid), $\theta = 4$ (dashed) or $\theta = 7$ (dotted)

To help the interpretation of the different paths above, Fig. 28, compares three Zenga’s densities, all with $\alpha = 5$ and with increasing values of $\theta$ (3 = solid; 4 = dashed; 7 = dotted). One can distinguish two kinds of modification of the shape: on the right side, the tail thickens, mildly in the beginning; on the left side, a clear movement of mass from the tail and the center toward the shoulder is observed. Obviously, this fact is likely to produce different patterns in the two side-components of each index, but the final evaluation will depend both on the magnitude of such components and on their weight. Despite it usually concentrates on the fatness of tails, $\beta _2$ turns out to be initially more influenced by the decreasing kurtosis in the left side of the distribution. However, from values of $\theta$ as high as 5, the role of the heavy right tail starts to be relevant. Conversely, it seems that $K_2(\mu )$ can always balance the two contrasting effects on the shape, with a certain propensity for what happens to the left side. As the distribution is quite skewed, one may think that the high weight given to $K_2^-(\mu )$ can be the ultimate reason of that. However, the first panel of Fig. 29, providing the detailed decomposition, shows that even the magnitude of the left component of $K_2(\mu )$ is crucial for the final evaluation. That can be further demonstrated by looking at the decomposition of the related $K_2(\gamma )$ in the second panel of Fig. 29: even if the weight given to the left and the right component is constantly equal to 1/2 here, the pattern of the overall index is quite similar to the one just commented.

Fig. 29

Plots of $K_2(\mu )$ and $K_2(\gamma )$ in the Zenga’s distribution, when $\alpha =5$ and $\theta$ ranges from 3 to 7. Both overall indexes (solid) are decomposed into their left (dashed) and right (dotted) contributions

6 General remarks

Researchers often use data both to estimate suitable models and to understand specific characteristics of the underlying distribution, which range from the obvious side of location and scale to more cumbersome aspects reflecting departure from normality. This paper concentrated on kurtosis. Excepts than in a limited number of models, however, quite rarely kurtosis is purely regulated by a single parameter. More often, to give a realistic description of the phenomenon under study, not only one needs to use multiple shape parameters, but kurtosis is also differently linked to each of them and to other aspects of non-normality, like skewness. When an index of kurtosis is evaluated on data, then, assessing the extent of its sampling error becomes problematic. Even if the efficiency of the estimators used for parameters can be easily evaluated, indeed, getting similar information about the estimator used for kurtosis is made difficult due to the absence of an analytic relation between the two items. As a consequence, when a dataset provides, for instance, a large level of kurtosis, one is not sure whether that estimated value is caused by outliers or if it is just the consequence of the underlying distribution. More dangerously, in other cases, the model may even prevent the existence of some kurtosis measures as functions of parameters and that may be the unknown cause of sample values which are indefinitely large (see Borroni and De Capitani, 2022). Notice that a certain knowledge about the relationship between shape parameters and kurtosis measures is also needed when the interest shifts from estimation to testing. Indeed, researchers are likely to use inferential tests to know if kurtosis exceeds a given level or to compare kurtosis in different distributions and in different sides of a single distribution. But, as a consequence, they also need to assess the power of the test under use, as a function of parameters.

Of course, once a model is chosen and it is paired with some kurtosis measures, one can go further into their specific relationship. However, we think that some general guidelines can be given to be aware about the pitfalls and the remedies which characterize every analysis. To this purpose, this paper concentrated on some examples which are relevant, in our opinion. In the following, we will try to list some general conclusions provided by the considered models.

First of all, the researcher should be aware that the relationship between parameters and kurtosis can not be simply examined by looking at the modifications in the graph of the density. Beyond the (simply identified) confounding role of the scale, indeed, the most tangled situations are observed when kurtosis is accompanied by skewness. More specifically, even if sometimes there are parameters whose variation induces a shift of kurtosis in a clear direction, characterizing both sides of the distribution (like when the probability mass moves towards both tails), more often parameters act differently on kurtosis and skewness in the two sides. But, while skewness measures, in a sense, just the dissimilarity of the left and the right side, kurtosis has to provide an overall judgment about both sides and, in addition, it must account for modifications both of the tails and the center of the distribution. One might then often face situations where a single tail is fat (due to an increase of skewness in that direction), the other tail is light (or even absent) and the center of the distribution is difficultly interpreted (sometimes without a clear peak). Our suggestion is that the graph need to be decomposed into two sides, after making them comparable as detailed in the Introduction. That decomposition is likely to reveal two aspects: what is the side where kurtosis mostly varies upon parameters and what is the direction of such variations in both sides. The examples in this paper showed a somewhat general rule: a variation of skewness in a given direction (left or right) has a contrasting effect on kurtosis in the opposite side of the distribution and a compliant effect in the same side; however, despite what one would expect, the first effect is often more intense than the second one. In addition, relevant effects on global kurtosis due to variations of skewness are only observed when its initial level is low.

Clearly, one cannot simply talk about variations of kurtosis without measuring them. A second conclusion of this study, then, is that decomposed graphs should be accompanied by decomposed indexes. Obviously, selecting a specific index implies to privilege some of the multiple aspects of kurtosis. As a consequence, different indexes are likely to provide different, sometimes contrasting, evidence. However, a decomposed analysis can reveal the mechanism leading to a final measurement and thus it can help to understand that some contradictions among indexes are often only apparent. To get into details, when a researcher decides, for instance, to use the classical Pearson’s $\beta _2,$ she/he is probably aware that it will be mostly sensitive to the tails of the distributions. Nonetheless, she/he must be also aware that, if a parameter causes a movement of skewness in a given direction, $\beta _2$ will usually concentrate on the modification of shape in this single side of the distribution or that, equivalently, the index will neglect the contrasting effect of skewness on kurtosis in the opposite side. The decomposition of $\beta _2,$ however, can explain the matter by revealing that, even if the contrasting effect of skewness is correctly accounted for by the corresponding side-index, the latter takes values too low to compensate for those on the other side, where the tail gets fat. When the interest of the researcher is shifted to Zenga’s indexes, she/he will not probably face any contradictions with $\beta _2,$ provided that a decomposed analysis is conducted. Indeed, Zenga’s side-indexes are likely to be coherent both with the modifications of the two sides of the density and with the decomposed parts of $\beta _2,$ even if their magnitude will be rarely inflated by the burdening of a single tail. Depending on the extent of modification of the two sides of the graph and on the weighting system which bases the index, then, the overall judgment will privilege a certain side of the distribution, possibly with some minor differences among Zenga’s indexes.

As a final remark, we want to underline that, when a specific model is chosen for the statistical analysis, the researcher should make the prior effort of classifying, even roughly, its shape parameters. Our examples showed that, even if they are rare, some parameters regulate “purely” kurtosis, which basically means that they can induce similar modifications of both sides of the distribution and that relevant differences among indexes are not observed. In addition to them, other parameters influence kurtosis and skewness at the same time, which implies that usually a single side (often a single tail) is amplified at the expense of the other. This second class of parameters is likely to provide different patterns of modification of the two sides of the graph and, consequently, different (possibly contrasting) evidence among kurtosis indexes. Finally, notice that sometimes kurtosis is modified by the joint action of the two kinds of parameters above: while a decomposed analysis is still a solution, then, the researcher must be aware that indexes like $\beta _2,$ which are hugely sensitive to the tails can produce unexpected results, possibly masking some compensating effects on the global level of kurtosis.

7 Some applications

Measuring kurtosis in the presence of a distributional model is a common task in several statistical procedures. Thus, we think that the indications provided in Sect. 6 could prove to be useful in many fields of application. Following the suggestions of two anonymous referees, however, we want now to concentrate on two areas which are likely to benefit from our conclusions. Specifically, we will try to emphasize that a careful measurement of kurtosis, based on a decomposed analysis and on the use of alternative indexes, could result in some advantages in projection pursuit and in the treatment of financial data. This fact introduces also new lines of research, as detailed in the following subsections.

7.1 Projection pursuit

Despite kurtosis is often regarded as a univariate characteristic, its relevance in the analysis of multivariate data has been recently recognized as an important tool in the field of projection pursuit (Huber, 1985). Since Gnanadesikan and Kettenring (1972), the need to project a set of multivariate points onto a lower dimensional space (often the real line) to locate outliers or, somewhat equivalently, to find clusters with possibly different sizes has struggled against the computational effort to work with infinitely many directions for such projections. The works by Peña & Prieto (2000, 2001a, b), however, pointed out that some “interesting” directions can be found by minimizing or maximizing the kurtosis of the projected data. Roughly speaking, that is justified by the fact that, when properly projected, a set of points which are well separated from the bulk of data (even though concentrated in a given region) is likely to cause the burdening of a single tail or the occurrence of a second peak in the resulting distribution. Interestingly, these are exactly the kinds of modifications of the shape accounted for by kurtosis, which concentrates on the characteristics of the tails and of the center. To prove the efficacy of that reasoning, many Authors reverted to specific models of contamination, sometimes as simple as just mixtures of univariate distributions (see Peña and Prieto, 2001a and the related discussion). In the following we will do the same to discuss the conclusions drawn in the sections above.

Fig. 30

Plots of the mixtures of a standard Normal with a Normal density with mean $\delta$ and standard deviation 0.5, when a weight 0.05 (solid curves) or 0.4 (dashed curves) is applied. Left panel: $\delta$ is set to 2. Right panel: $\delta$ is set to 5.

Figure 30 reports the shapes of the densities obtained by mixturing a standard Normal with a second Normal whose mean and standard deviation are $\delta$ and 0.5 respectively. A weight $\alpha$ is applied to the second element of the mixture, to accounts for the possible levels of contamination suffered from a set of data and it is set to 0.05 (solid curve) or to 0.4 (dashed curve). It is clear that when $\alpha$ is low and the mean of the contaminating distribution is not too large ($\delta = 2$ in the first panel), a burdening of the right tail is observed. When $\alpha$ is high, however, contamination results in the occurrence of a second mode. In addition, the second panel of Fig. 30 shows that, when $\delta$ is raised to 5, bimodality gets clear still from a mild level of $\alpha ,$ even if the resulting secondary low peak can be somehow confused with the main tail. In any case, both panels seem to point out that a positive contamination can be primarily appreciated by the modification of the right tail of the resulting distribution. However, the decomposed graphical analysis developed in this paper can be usefully applied, to show that even the left part of the final density is to be considered.

Fig. 31

Decomposed plots (left and right parts) of the mixtures of a standard Normal with a Normal density with standard deviation 0.5 and mean 2 (solid curves) or 3 (dashed curves), when the latter is weighted by 0.05.

At this aim, Fig. 31 reports the decomposed graphs of two mixtures obtained with the same level $\alpha =0.05$ and two different means for the contaminating distribution ($\delta =2$ for the solid curve and $\delta =3$ for the dashed curve). The first panel of Fig. 31 compares the left sides of the two mixtures: it can be noticed that, even in the presence of a mild contamination, a positive shift of $\delta$ decreases left-kurtosis, due to a movement of mass from the tail and the center to the left shoulder. Conversely, the second panel of Fig. 31, which is obviously referred to the right parts of the two mixtures, shows that this side of kurtosis increases with the level of $\delta .$

Fig. 32

Decomposed plots (left and right parts) of the mixtures of a standard Normal with a Normal density with standard deviation 0.5 and mean 2 (solid curves) or 3 (dashed curves), when the latter is weighted by 0.4.

Unfortunately, on the same right side, the picture of kurtosis gets rather confused when, in the same settings, the level of contamination is raised to $\alpha =0.4$ (see the second panel of Fig. 32). Despite a clear lightening of the right tails, indeed, the effect on the center is now difficultly interpreted due to the occurrence of an “intermediate” peak. Overall, one may argue that the right-kurtosis decreases with $\delta$ in the figure, but it can be equivalently suspected that this is not a general rule and that it may change with a slightly different tuning of parameters. In effect, that is a first reflection of a mostly serious problem of the relationship between (positive) contamination and the shape of the resulting distribution, specifically of its right part: under some circumstances, a monotone relation between the direction of contamination and the resulting level of kurtosis does not seem to exist. One may be convinced about that by looking at the second panel of Fig. 33 which, in the same settings as above, is built with $\alpha =0.2$: the opposite effects of an increased $\delta$ on the right tail and on the center seem to be nearly compensated here. However, if we look now at the first panels of both Figs. 32 and 33, we realize that the decomposed analysis provides a clear addition: the left parts of the graphs show that the decreasing patterns of left-kurtosis is preserved for all considered levels of contamination and also that such a decay is strengthened by the level of $\alpha .$

Fig. 33

Decomposed plots (left and right parts) of the mixtures of a standard Normal with a Normal density with standard deviation 0.5 and mean 2 (solid curves) or 3 (dashed curves), when the latter is weighted by 0.2.

The existing literature developed many tools to take advantage of the above-discussed link between kurtosis and outliers/clusters identification. However, it mainly concentrated on the use of the standardized fourth moment as a pursuit index and on the possible simplification of the related computations (see Loperfido, 2021 and the references therein). On the side of the measures to be chosen for kurtosis, we think that some further help could be given by indexes which are decomposable, as long as by indexes which have a balanced sensitivity for both the tails and the center of the distribution. That will be an element for a future research. Here, we will be limited to some considerations regarding the contamination model above and two kurtosis indexes, $\beta _2$ and $K_2(\mu ).$

Fig. 34

Plots of $\beta _2$ and $K_2(\mu )$ computed on the the mixture of a standard Normal with a Normal density with standard deviation 0.5 and mean ranging from 1 to 10,  when the latter is weighted by 0.05. Both overall indexes (solid) are decomposed into their left (dashed) and right (dotted) contributions

Figure 34 (first panel) reports the plots obtained for $\alpha = 0.05$, when Pearson’s $\beta _2$ is decomposed into its parts and the mean $\delta$ is raised from 1 to 10. As known (Peña & Prieto, 2001a), the overall index has an increasing pattern in the case of a mild contamination, which justify the search for directions which maximize it. We point out that this piece of evidence depends strongly on the right-index $\beta _2^+,$ which reaches very high values due to the overwhelming effect of the right tail. Conversely, the left part $\beta _2^-$ shows a decreasing pattern, even if with comparatively small levels. Despite the weight given on the left of the mean is high (due to the the kind of contamination considered), the overall $\beta _2$ reflects mainly the attitude of the right part. Notice that such a conclusion is taken at the expense of a non perfectly monotonic patterns of $\beta _2,$ which may result in an unsuccessful search sometimes. Thus, we think that, under similar circumstances, the maximization of the sole right part of Pearson’s $\beta _2$ or, somewhat less effectively, the minimization of $\beta _2^-$ could be advised. If we look at $K_2(\mu )$ in the same settings (second panel of Fig. 34), we get similar conclusions: the right part $K_2^+(\mu )$ provides the best guidance for interesting projections, because of its definite increasing pattern. The minimization of the left-index $K_2^-(\mu )$ can be possibly advised as well, but a search based on the overall index is likely to be ineffective.

Fig. 35

Plots of $\beta _2$ and $K_2(\mu )$ computed on the the mixture of a standard Normal with a Normal density with standard deviation 0.5 and mean ranging from 1 to 10,  when the latter is weighted by 0.4. Both overall indexes (solid) are decomposed into their left (dashed) and right (dotted) contributions

It is also known that, when the level of contamination is raised to $\alpha =0.4,$ Pearson’s $\beta _2$ has a decreasing pattern with $\delta .$ That is highlighted in the first panel of Fig. 35, which shows, however, that the strength of its decay is not comparable to that of the increase shown for mild contamination levels. $\beta _2^-$ is likely to be the most effective indicator here: its decrease is the leading element of the overall index, both because of the weighting of the two parts and of the magnitude of $\beta _2^+.$ With respect to the case $\alpha =0.05,$ indeed, $\beta _2^+$ takes low (though increasing) values, which are fully compensated by those taken by $\beta _2^-$ in the determination of the overall $\beta _2.$ In other words, one could claim that, differently from the case $\alpha =0.05,$ when the level of contamination is as high as $\alpha =0.4$ the decreasing pattern of the left part cannot be masked by the burdening of the right tail. This fact can be better appreciated when the decomposed plot of $K_2(\mu )$ for the case $\alpha =0.4$ is considered in the second panel of Fig. 35: a clear decreasing pattern is observed for both side-components of the index, a symptom that the index can properly temper the effect of the right tail.

Fig. 36

Plots of $\beta _2$ and $K_2(\mu )$ computed on the the mixture of a standard Normal with a Normal density with standard deviation 0.5 and mean ranging from 1 to 10,  when the latter is weighted by 0.2. Both overall indexes (solid) are decomposed into their left (dashed) and right (dotted) contributions

The above-outlined ability of $K_2(\mu )$ can be possibly best appreciated in the most complicated case: a mean level of contamination. Figure 36 (first panel) reports the decomposed analysis for $\beta _2$ in the usual mixture model with $\alpha =0.2$ and it exemplifies what first noticed by Hubert (2001): the overall $\beta _2$ has a non-monotone (almost constant) pattern here, a fact which leaves its maximization/minimization unjustified (see also Alashwali and Kent, 2016 for a related discussion using two-group multivariate Normal mixtures). Looking at the decomposed plot of $\beta _2,$ however, one may notice that its constancy is an inconvenience of averaging, because the left part $\beta _2^-$ has still a clear decreasing pattern, while the right part $\beta _2^+$ reflects the usual confounding effect of the tail. Notice that the same conclusions do not hold for $K_2(\mu ),$ whose right part is ultimately decreasing, like for the left part and for the overall index (second panel of Fig. 36).

To conclude, due to the need to account for both tail burdening and bimodality of the projected distribution, we claim that the use of decompositions of kurtosis indexes could be a good addition for pursuit purposes. Clearly, this conjecture is to be proved by a careful research, which needs to consider a wider set of models, including, for instance, mixtures of multivariate distributions or symmetrically contaminated models. Nonetheless, we hope that our limited analysis can stimulate the interest on this topic. As a matter of fact, the literature did not concentrate on the location of the best direction for projection, but in the search for a whole set of directions which could be as wide as possible to guarantee success in the following task of classification (see, for instance Peña and Prieto, 2007). Clearly, enlarging the set of pursuit indexes means to burden the process of optimization, too. Incidentally, one may notice, then, that kurtosis-based projection methods took advantage over the pursuit effort by looking also at some generalizations of kurtosis itself in a multivariate framework. Peña et al. (2010), for instance, showed that interesting directions can be revealed by the spectral decomposition of the so-called kurtosis matrix, independently introduced by Cardoso (1989) and Mòri et al. (1993). Such a generalization proved to be of a major use in some related fields of multivariate analysis as well, like for invariant coordinate selection (Tyler et al., 2009). As a matter of fact, there is currently an increasing interest in generalized matrices of kurtosis (see also Loperfido, 2017 and Kollo, 2008), which let us wonder if the tools analyzed in this paper can be similarly extended to the multivariate setting. We think that this is an important theme and that it deserves a future research.

7.2 Financial data

Kurtosis-based projection pursuit has many applications in the analysis of financial data, even on the side of portfolio selection and on that of the identification of outliers in time-dependent financial series (see the recent contribution by Loperfido, 2020). In this paper, we will not enter into details of these kinds of applications. Nonetheless, we will try to outline the usefulness of some conclusions drawn in the previous sections when the shape of returns distribution is studied. This application was chosen since, in empirical finance, the occurrence of high kurtosis levels in stock returns distributions is so ubiquitous that it received the status of a stylized fact.

When analyzing the behavior of stock returns, the investor is typically interested in the simultaneous evaluation of profitability and riskiness. These two characteristics are usually measured by simple indicators. For the measurement of the former, expected returns are universally adopted. To the contrary, a plethora of indicators were proposed in order to evaluate riskiness. Starting from the seminal work of Markowitz (1952), variability indexes such as standard deviation and mean absolute deviation were firstly used at this end but, over the years, the adoption of such indicators has been also widely criticized. The main problem is that the cited measures do not evaluate only the “risky” component of variability (i.e. that below the expected return), but also the “profitable” one (i.e. that above). To overcome this drawback, the concept of downside deviation was later introduced (see Sortino and Van der Meer, 1991; Sortino and Price, 1994). After denoting by X the random returns of an asset, in analogy with what reported in (10), (11) and (12), the variance $\sigma ^2$ of X can be decomposed as follows:

$$\begin{aligned} \sigma ^2&=\text{ E } \left[ (X-\mu )^2 \right] \nonumber \\&= \text{ E } \left[ S_\mu ^2(X) \right] \, P \left[ X\le \mu \right] + \text{ E } \left[ D_\mu ^2(X) \right] \, P \left[ X>\mu \right] \nonumber \\&= \text{ E } \left[ (X-\mu )^2 \, \vert \, X\le \mu \right] \, \, P\left[ X\le \mu \right] + \text{ E } \left[ (X-\mu )^2 \, \vert \, X>\mu \right] \, \, P \left[ X>\mu \right] \nonumber \\&=\sigma ^{2-}\, P \left[ X\le \mu \right] +\sigma ^{2+}\, P \left[ X>\mu \right] \; . \end{aligned}$$

(17)

The quantity $\sigma ^{2-}P[X\le \mu ]$ in (17) is usually defined as the downside deviation of X. Of course, $\sigma ^{2-}$ can be used and interpreted similarly. Thus, in agreement with the decompositions of kurtosis indexes above, we will analyze it in place of the classical downside deviation. A similar decomposition can be applied to the mean absolute deviation $\delta _\mu$ of X:

$$\begin{aligned} \delta _\mu&= \text{ E } \left[ \vert X-\mu \vert \right] \\&= \text{ E } \left[ S_{\mu } (X) \right] \, P \left[ X\le \mu \right] + \text{ E } \left[ D_\mu (X) \right] \, P\left[ X>\mu \right] \\&= \text{ E } \left[ \vert X-\mu \vert \ \, \, \vert \, \, X\le \mu \right] \, P \left[ X\le \mu \right] + \text{ E } \left[ \vert X-\mu \vert \, \, \vert \, \, X>\mu \right] \, P \left[ X>\mu \right] \\&=\delta _\mu ^{-}\, P \left[ X\le \mu \right] +\delta _\mu ^{+}\, P \left[ X>\mu \right] \;. \end{aligned}$$

The quantity $\delta _\mu ^{-}$ measures riskiness as well, since it is sensitive only to the “risky” component of variability. Obviously, the residual $\sigma ^{2+}$ and $\delta _\mu ^{+}$ quantify the “profitable” component.

When kurtosis is interpreted from the financial point of view, arguments similar to those for variability can be followed: a fat left tail in the distribution of X is to be regarded as a risky feature, while a fat right tail is not. In this light, the decomposed approach to kurtosis proposed above can be used to perform a separate analysis of risky and non-risky tails. Specifically, the left-kurtosis components $K_2^-(\mu )$, $K_1^-(\mu )$, and $\beta _2^-$ in formulas (10), (11) and (12) represent the “risky” component of kurtosis, while $K_2^+(\mu )$, $K_1^+(\mu )$, and $\beta _2^+$ represent the “profitable” side.

To exemplify the use of a decomposed approach, the daily returns of five assets quoted on NYSE were analyzed: Johnson Controls International (JCI), Banco Santander (SAN), Medifast Inc (MED), Shell plc (SHEL) and Medtronic plc (MDT). The considered time period ranges from 2019 to 2021, but data were analyzed separately for the three years, in order to evaluate the different behavior of returns before (year 2019), during (year 2020), and after (year 2021) the COVID19 pandemic. For the sake of brevity, just the results for two kurtosis indexes are reported here: Table 1 refers to $K_2(\mu ),$ while Table 2 is for $\beta _2$. Both tables show the (decomposed) values of the related measures of variability as well, along with the estimated weights $F(\mu )$ of the left components of all indexes.

Table 1 Analysis of daily returns distribution of JCI, MED, SHEL, SAN, and MDT in the period 2019–2021

Table 2 Analysis of daily returns distribution of JCI, MED, SHEL, SAN, and MDT in the period 2019–2021

Concerning the variability of the considered assets, a huge increase of $\delta _\mu$ and $\sigma ^2$ is observed in 2020 with respect to 2019. The greatest increase regards SHEL ($+285\%$ for $\sigma ^2$ and $+251\%$ for $\delta _\mu$), the lowest is for MED ($+34\%$ for $\sigma ^2$ and $+28\%$ for $\delta _\mu$). In the remaining cases the percentage increase from 2019 to 2020 ranges from $+137\%$ to $+153\%$ for $\sigma ^2$ and from $+124\%$ to $+136\%$ for $\delta _\mu$. In 2021, variability significantly decreases with respect to 2020. For all the considered assets, that decrease does not completely compensate the increase observed in the previous year. This fact is particularly clear for SHEL: the 2021 variability is about twice that for 2019 ($+82\%$ for $\sigma ^2$ and $+95\%$ for $\delta _\mu$). To the contrary, MED is the only asset for which in 2021 the variability substantially comes back to the 2019 level ($+2\%$ for $\sigma ^2$ and $+4\%$ for $\delta _\mu$). Looking at the left and right components of $\sigma ^2$ and $\delta _\mu$, one may notice two main scenarios:

• for JCI and MDT, the left and the right variations are almost balanced;

• for SAN, MED and SHEL, the right component of variability (as measured by $\sigma ^{2+}$ and $\delta _\mu ^+$) increases more than the left ($\sigma ^{2-}$ and $\delta _\mu ^-$) from 2019 to 2020, but it has a slower decrease from 2020 to 2021 with respect to the opposite side. As a result, the greater variability observed in 2021 with respect to 2019 is mainly ascribable to the increase of the right component. This is particularly clear for MED where, on the whole period from 2019 to 2021, a decrease of left variability ($-18\%$ for $\sigma ^{2-}$ and $-3\%$ for $\delta _\mu ^-$) is accompanied by an increase of the right side ($+32\%$ for $\sigma ^{2+}$ and $+11\%$ for $\delta _\mu ^+$).

On the side of kurtosis, each asset follows a peculiar pattern and a disagreement between the evaluations provided by $\beta _2$ and $K_2(\mu )$ arises. For all considered assets, $K_2(\mu )$ outlines a similar temporal dynamic: global kurtosis significantly increases from 2019 to 2020 and decreases from 2020 to 2021. The decrease observed in 2021 is sufficient to bring kurtosis below the 2019 level for JCI, MED and SHEL; for SAN and MDT, it leads to a level which is substantially equal in 2021 and in 2019. The kurtosis pattern depicted by $\beta _2$ is qualitatively similar to the one reported for $K_2(\mu )$ just when JCI and SAN are considered. Differently, for MED, SHELL and MDT, global yearly kurtosis decreases still from 2019 to 2020. By performing a decomposed analysis on left and right kurtosis, the temporal dynamics provided by $K_2(\mu )$ and $\beta _2,$ along with their differences, can be better understood. Specifically:

• for all assets but JCI, the right-kurtosis index $K_2^+(\mu )$ increases more than $K_2^-(\mu )$ from 2019 to 2020. From 2020 to 2021 both $K_2^+(\mu )$ and $K_2^-(\mu )$ decrease but, while the decay of $K_2^-(\mu )$ brings left kurtosis even below its 2019 level, that of $K_2^+(\mu )$ is not sufficient to do the same for the right side. This fact is particularly evident for MED where the global $K_2(\mu )$ has substantially the same level in 2019 and 2021, but the contribution of $K_2^-(\mu )$ and $K_2^+(\mu )$ is interchanged: in 2019 left kurtosis is greater than the right, while in 2021 the opposite relation holds. Concerning JCI, the only difference with the above-described pattern stems from the fact that the right kurtosis steady reduces from 2019 to 2021.

• high values of $\beta _2^-$ in 2019 for assets MED, SHEL, and MDT are observed. These assets are exactly the same exhibiting a difference between the dynamics of global kurtosis as measured by $K_2(\mu )$ and by $\beta _2.$ By looking at their return series in 2019, a single highly-negative return (about –15%) is easily found in all cases (see, for example, Fig. 37, where the series of MED is represented). Those single values have a huge impact, causing high values for $\beta _2^-$ and probably explaining the different dynamic reported for the global $\beta _2.$ In spite of that, the decomposed analysis still suggests that, from 2019 to 2021, the contribution to global kurtosis of the right part has increased for all assets, with the exception of JCI.

Fig. 37

Time series of MED daily returns distribution in 2019

To exemplify further the usefulness of the decomposed analysis of the paper, the distributions of MED returns over the three considered years were also graphically analyzed with the method introduced in Sect. 1. The related densities were obtained via kernel density estimation (KDE) using a Gaussian kernel. A certain amount of over-smoothing was applied in KDE, to obtain sufficiently regular densities and meaningful plots. The adopted bandwidth is reported in each figure caption. MED was chosen among the considered datasets, since it exhibits a peculiar pattern of kurtosis indexes, as above described. Specifically, recall that this asset has the same value of $K_2(\mu )$ in 2019 and 2021, but its composition is reversed on the whole period: even if the pattern is firstly increasing and finally decreasing for both components, indeed, in 2019 $K_2^-(\mu )$ is greater than $K_2^+(\mu ),$ while the opposite holds for 2021.

Fig. 38

Comparison of MED daily returns distribution in 2019 and 2020 (left panel) and in 2020 and 2021 (right panel). All the densities are estimated via KDE with Gaussian kernel and bandwidth equal to 0.0137. The bandwidth is obtained by multiplying the one obtained with the Scott (1992) method by the factor 1.5 in order to produce sufficiently smooth and easy-to-compare densities

In Fig. 38 (first panel), the 2019 and 2020 densities are compared. The plot clearly shows, on both its sides, that the density for 2020 can be obtained from the one for 2019 (after a proper standardization), by moving a certain amount of probability mass from the shoulders to the center and the tails, thus producing a distribution with higher kurtosis. A similar (though oppositely directed) interpretation can be given to the second panel of Fig. 38, where the reported densities depict the passage from 2020 to 2021: kurtosis decreases on both its sides. In Fig. 39 the years 2019 and 2021 are compared: the first panel, reporting the decomposed densities, shows a significant difference around the center. To the contrary, the behavior on the shoulders and on the tails seems quite similar and the densities intersects more than two times on each side (differently to what usually happens when a relevant change in kurtosis is observed). That is not surprising, since the two compared distributions have substantially the same global kurtosis. In order to get to the bottom of the behavior of the single tails, the second panel of Fig. 39 represents the two densities on a logarithmic scale. By matching the two panels of the figure, one can observe a different change in kurtosis at the two sides of the distributions: on the left, the graph for 2019 shows more probability mass near the center and on the tail (that is, the left kurtosis is higher in 2019 than in 2021); on the right, such a phenomenon is true for 2021 (thus, the right kurtosis is higher in 2021 than in 2019). Finally, even if one may appreciate relevant graphical differences in the two estimated densities (especially for their left parts), in our opinion, they are too minor to justify the relative variation of -68% observed for $\beta _2^-$ from 2019 to 2021. The corresponding relative variation of $K_2^-(\mu )$ is $-$8.9%, which appears to be more consistent with the results in Fig. 39.

Fig. 39

Comparison of MED daily returns distribution in 2019 and 2021 on natural scale (left panel) and on logarithmic scale (right panel). All densities are estimated via KDE with Gaussian kernel and bandwidth equal to 0.0137. The bandwidth is obtained by multiplying the one obtained with the Scott (1992) method by the factor 1.5 in order to produce sufficiently smooth and easy-to-compare densities