Comparative modelling results between a separable and a non-separable form of principal stretches–based strain energy functions for a variety of isotropic incompressible soft solids: Ogden model compared with a parent model

Abstract

This paper presents a comparative analysis on the application of two models from the family of principal stretches–based strain energy functions to a wide range of incompressible rubber-like materials, including hydrogels, foams, silicone elastomers, filled rubbers and biomaterials. The two models of concern here are the seminal Ogden model of the separable form, and a more general non-separable form parent model proposed by the author. To this end, the three-term Ogden model, with corresponding six model parameters, and the one-term parent model with four model parameters, are applied to exemplar extant deformation datasets of the aforementioned rubber-like materials, and the ensuing modelling results are then compared. This comparison encompasses the quality of the obtained fits as measured by the resulting relative errors, and the mechanistic validity of the ensuing strain energy function as assessed by the convexity of the iso-energy plots in the principal stretches $\left({\lambda }_{1},{\lambda }_{2}\right)$ plane. The studied modes of deformation involve a wide range of deformation types including uniaxial, biaxial, simple shear and inflation. It is shown that for the considered range of materials and deformations, the optimal fits obtained by the Ogden model either (i) possess higher relative errors; or (ii) offer a marginal improvement but with the loss of convexity. This loss of convexity is further exemplified on considering an additional soft tissue dataset. Finally, an important implication of the separable versus non-separable functional forms of the two models in application to the deformation of elastomers will be demonstrated, where a separable function proves to be an inappropriate choice. In all these applications, the proposed parent model, by contrast, will be shown to provide equally good or better fits, with fewer model parameters, while remaining free of the foregoing undesirable modelling outcomes.

1 Introduction

In a prior study by the author [2], a principal stretch–based strain energy function $W$ of the non-separable form was developed for application to the finite deformation of incompressible soft solids as:

$$W=\sum_{i=1}\frac{3\left({n}_{i}-1\right)}{2{n}_{i}}{\mu }_{i}N\left[\frac{1}{3N\left({n}_{i}-1\right)}\left({\lambda }_{1}^{{\alpha }_{i}}+{\lambda }_{2}^{{\alpha }_{i}}+{\lambda }_{3}^{{\alpha }_{i}}-3\right)-\mathrm{ln}\left(\frac{{\lambda }_{1}^{{\alpha }_{i}}+{\lambda }_{2}^{{\alpha }_{i}}+{\lambda }_{3}^{{\alpha }_{i}}-3N}{3-3N}\right)\right] ,$$

(1)

where ${\mu }_{i}$ [Pa], ${n}_{i}$ [-], $N$ [-], ${\alpha }_{i}$ [-] are model parameters and ${\lambda }_{j}$ ($j=\mathrm{1,2},3)$ are the principal stretches subject to ${\lambda }_{1}{\lambda }_{2}{\lambda }_{3}=1$ to ensure incompressibility. Note that parameter $N$ in the general form of the model in Eq. (1) is not subscripted — it is single-valued. It was shown that this model is parent to many of the currently established models in the literature, ranging from the limiting chain extensibility models such as the Gent model [17] to the constrained tube models [14], and other models including the seminal Ogden [25] model. It can be verified that in the limit $N\to \infty$ we have for the $W$ function in Eq. (1):$\underset{{N}_{i}\to \infty }{\mathrm{lim}}W=\sum_{i}\frac{{\mu }_{i}}{2}\left({\lambda }_{1}^{{\alpha }_{i}}+{\lambda }_{2}^{{\alpha }_{i}}+{\lambda }_{3}^{{\alpha }_{i}}-3\right),$ and by setting ${\mu }_{i}=\frac{2{\mu }_{p}}{{\alpha }_{p}}$ and ${\alpha }_{p}={\alpha }_{i}$ the seminal Ogden model is recovered:

$$W=\sum_{p}\frac{{\mu }_{p}}{{\alpha }_{p}}\left({\lambda }_{1}^{{\alpha }_{p}}+{\lambda }_{2}^{{\alpha }_{p}}+{\lambda }_{3}^{{\alpha }_{p}}-3\right) .$$

(2)

Note therefore that the separable-form Ogden model is a special case of the non-separable form parent model (1).

The Ogden model has proved a powerful and versatile strain energy function for modelling the deformation behaviour of rubber-like materials. Indeed, to the knowledge of the author, the three-term Ogden model was the first closed-form function that enabled achieving favourable simultaneous fits to the canonical Treloar dataset [29] of uniaxial, (equi-)biaxial and pure shear deformations [25]. However, as the recent efforts of the author have documented [6,7,8], in some applications, the Ogden model appears to suffer from the loss of convexity in iso-energy plots. This loss of convexity in a strain energy function implies the breakdown of the one-to-one correspondence in the stress-deformation relationship and the presence of hysteresis effects [26], and may lead to undesirable material and numerical instabilities (see, e.g., [18]). Therefore, to preclude such disagreeable effects, a model must ideally prove to remain convex over all possible domains of deformation of the subject material.

A second drawback associated with the application of the Ogden model, when using three terms and above, is the issue surrounding the finding of the optimal model parameters and the uniqueness of the optimum fit. As analysed by Ogden et al. [27], it is possible to obtain different combinations of ‘optimal’ model parameters when fitting the Ogden model of the third or fourth orders to the experimental data. If the functional form of the model does not axiomatically guarantee convexity, then many, if not all, of these ‘optimal’ parameter value sets would not result in a convex strain energy either.

A third disadvantage discussed in details by Yeoh [33], that may arise from the previous two points, is the issue of the stability of the predicted stress-deformation behaviours using a higher-term Ogden model. While including more terms in a model provides further degrees of freedom to achieve a ‘better’ fit, it does not necessarily guarantee that the constitutive behaviour of the material will be better captured. Indeed, the additional degrees of freedom introduced by considering unwarranted extra terms often only leads to a model that fits better the experimental errors. Therefore, higher orders of the Ogden model are naturally more prone to being unstable; i.e., may lead to unrealistic behaviours outside the range of the experimental data.

The foregoing three points underline that ideally a model must possess minimal number of parameters with structural/mathematical objectivity, and must have a functional form that ensures remaining a priori convex and stable in all domains of deformation. Most of all, however, a ‘good’ model is judged based on how closely it reproduces and predicts the experimental data. As systematically reviewed by Destrade et al. [15], producing minimum relative errors is a robust index in ranking the ability of a ‘good’ model. This minimisation may be better achieved by seeking the fit within alternative spaces to the engineering or Cauchy spaces, such as the Mooney space [15] or the recently proposed generalised Mooney space [4]. Nevertheless, the relative error is a very good indicator of the performance of a chosen model in relation to describing the subject data. With six model parameters, the three-term Ogden model is perhaps expected to provide the least relative errors. However, as will be shown in the sequel, in many applications, the Ogden model results in higher relative errors compared with the four-parameter one-term proposed parent model.

In view of the foregoing points and findings, and in order to facilitate a more informed decision in choosing an appropriate strain energy function for application to the finite deformation of rubber-like materials, it is the aim of this manuscript to provide a direct comparison between the modelling results of the classical (three-term) Ogden model and the one-term parent model of the author. The deformation datasets considered herein pertain to a wide range of incompressible isotropic rubber-like materials including (hydro)gels, foams, silicone elastomers and filled rubbers, complimented by exemplar soft tissue and natural rubber datasets of note. The deformation modes using these datasets have been obtained to encompass uniaxial, biaxial, simple shear and inflation deformations. It will be shown that over this considered range of applications, the six-parameter (three-term) Ogden model either produces higher levels of relative errors compared with the four-parameter (one-term) counterpart parent model, or provides marginal improvements but at the cost of losing convexity.¹ In Sect. 2, we provide a brief overview of the theoretical preliminaries required for the modelling campaign of this work. In Sect. 3, we present the modelling results, comparing the predictions of the two models and examining the convexity of the ensuing strain energy functions. This investigation is carried out via considering the iso-energy plots of the two functions in the plane of principal stretches $\left({\lambda }_{1},{\lambda }_{2}\right)$. In Sect. 4, some discussion points will be conferred, including an important implication of the separable functional form of the Ogden model versus the non-separable functional form of the counterpart parent model on modelling a dataset of natural unfilled rubbers due to Vangerko and Treloar [31]. It will be shown that a separable function of the principal stretches, such as the Ogden model, is inherently inappropriate for modelling such behaviours. In addition, a soft tissue dataset pertaining to the deformation of human brain (cortex) tissue will also be considered, as a further example of applications where the Ogden model may lose convexity. No such issues will arise on using the (one-term) parent counterpart model. Concluding remarks are given in Sect. 5.

2 Theoretical preliminaries

The details of the derivation and development of the model in Eq. (1) has been presented in [2]. For reasons discussed in Sect. 1 and in more details in [2], namely to avoid prescribing unwarranted number of constitutive parameters and to minimise the issues in finding the unique fit, here we restrict our attention to the one-term form of this model:

$$W=\frac{3\left(n-1\right)}{2n}\mu N\left[\frac{1}{3N\left(n-1\right)}\left({\lambda }_{1}^{\alpha }+{\lambda }_{2}^{\alpha }+{\lambda }_{3}^{\alpha }-3\right)-\mathrm{ln}\left(\frac{{\lambda }_{1}^{\alpha }+{\lambda }_{2}^{\alpha }+{\lambda }_{3}^{\alpha }-3N}{3-3N}\right)\right] ,$$

(3)

with four model parameters. Note that parameter $N$ structurally controls the extensibility limit, such that for the $\mathrm{ln}$ (■) function to be well-defined in a general deformation, we must have:

$$\left\{\begin{array}{l}\lambda_{1}^{\alpha} + \lambda_{2}^{\alpha} + \lambda_{3}^{\alpha} < 3N\Rightarrow\frac{\left(\lambda_1\lambda_2\right)^{\alpha}\left(\lambda_{1}^{\alpha} + \lambda_{2}^{\alpha}\right) + 1}{3\left(\lambda_{1}\lambda_{2}\right)^{\alpha}} < N,\quad\mathrm{if}\;N > 1,\\ \lambda_{1}^{\alpha} + \lambda_{2}^{\alpha} + \lambda_{3}^{\alpha} > 3N\Rightarrow\frac{\left(\lambda_{1}\lambda_{2}\right)^{\alpha}\left(\lambda_{1}^{\alpha} + \lambda_{2}^{\alpha}\right) + 1}{3\left(\lambda_{1}\lambda_{2}\right)^{\alpha}}>N,\quad\mathrm{if}\;0 < N < 1,\end{array}\right.$$

(4)

subject to the incompressibility constraint. As pointed out by Murphy [24] and Horgan and Murphy [19], a more global condition ensuring (4) may be of the form:

$$\mathrm{max} \left\{{\lambda }_{1},{\lambda }_{2},{\lambda }_{3}\right\}<{\lambda }^{*} ,$$

(5)

where ${\lambda }^{*}$ is a constant whose value depends on the type of deformation. From Eqs. (4) and (5), it is therefore observed that parameter $N$ effectively controls the maximum allowable principal stretch. Algebraically, we will require that:

$$n , N\in {\mathbb{R}}^{+} ,$$

(6)

i.e., to be positive real-valued parameters. The parameter $\mu$ is related to the infinitesimal shear modulus ${\mu }_{0}$ via:

$$\mu =\frac{4n{\mu }_{0}}{{\alpha }^{2}} \frac{1-N}{1-nN} ,$$

(7)

with $\alpha$ being a real-valued parameter:

$$\alpha \in {\mathbb{R}}.$$

(8)

The model in Eq. (3), subject to the requirements and definitions described by Eqs. (4) to (8), remains well-defined and a priori convex over all defined domains of deformation. It is worth noting that in the special cases where $n=3$, $\alpha =2$ and $\left\{n=3,\alpha =2\right\}$, we recover the models proposed in [6], [1, 8] and [3], respectively.

Remark. While in the original development of model (1), or equivalently (3), we algebraically require for $n$ and $N$ to be positive, it must be pointed out that numerically, $\mu$, $n$ and $N$ may assume both positive or negatives values, so far as the combination of these three parameters in Eq. (7) renders ${\mu }_{0}>0$. It is therefore admissible, from a phenomenological point of view, to allow $N<0$ or $n<0$ too. This possibility has been discussed and analysed at length by Anssari-Benam and Horgan [7]. In view of Eq. (7), for ${\mu }_{0}$ to be positive when $N<0$, a sufficient condition is $\mu ,n>0$, and when $n<0$, we require that $\mu >0$ and $N>1$. Two exemplar datasets for which the obtained best fits by model (3) possess the foregoing range of parameters will be considered in Sect. 3, and as will be seen, the ensuing iso-energy curves of the $W$ function remain convex, and therefore, $W$ remains a mechanistically valid strain energy function.

The components of the principal Cauchy stress ${T}_{j}$ $(j=\mathrm{1,2},3)$ may be computed via:

$${T}_{j}={\lambda }_{j}\frac{\partial W}{\partial {\lambda }_{j}}-p ,$$

(9)

where $p$ is the arbitrary hydrostatic pressure enforcing incompressibility. For the one-term model in Eq. (3), the $T-\lambda$ relationships for uniaxial, equi-biaxial and pure shear deformations may be obtained on using Eq. (9) as:

$$\left\{\begin{array}{l}T_{uni}=\frac{\mu\alpha}{2n}\frac{\lambda^\alpha+2\lambda^{-0.5\alpha}-3nN}{\lambda^\alpha+2\lambda^{-0.5\alpha}-3N}\left(\lambda^\alpha-\frac1{\lambda^{0.5\alpha}}\right),\\\begin{array}{c}\\T_{eq-bi}=\frac{\mu\alpha}{2n}\frac{2\lambda^\alpha+\lambda^{-2\alpha}-3nN}{2\lambda^\alpha+\lambda^{-2\alpha}-3N}\left(\lambda^\alpha-\frac1{\lambda^{2\alpha}}\right),\end{array}\\\begin{array}{c}\\T_{ps}=\frac{\mu\alpha}{2n}\frac{\lambda^\alpha+1+\lambda^{-\alpha}-3nN}{\lambda^\alpha+1+\lambda^{-\alpha}-3N}\left(\lambda^\alpha-\frac1{\lambda^\alpha}\right).\end{array}\end{array}\right.$$

(10)

Note that for a generic biaxial deformation, the $T-\lambda$ relationship using model (3) reads:

$${\left(T_{bi}\right)}_j=\frac{\mu\alpha}{2n}\frac{\lambda_1^\alpha+\lambda_2^\alpha+\left(\lambda_1\lambda_2\right)^{-\alpha}-3nN}{\lambda_1^\alpha+\lambda_2^\alpha+\left(\lambda_1\lambda_2\right)^{-\alpha}-3N}\left[\lambda_j^\alpha-\left(\frac1{\lambda_1\lambda_2}\right)^\alpha\right],\;j=1,2.$$

(11)

For the simple shear deformation, the $T-\gamma$ relationship using model (3) may be obtained by noting that the principal stretches in this deformation are:

$$\lambda_1=\lambda=\frac\gamma2+\sqrt{1+\frac{\gamma^2}4},\;\ \lambda_2=\lambda^{-1}=-\frac\gamma2+\sqrt{1+\frac{\gamma^2}4},\;\lambda_3=1,$$

(12)

with $\gamma$ being the amount of shear. Using Eq. (9), we then find the following $T-\gamma$ relationship:

$${T}_{ss}=\frac{\mu \alpha }{2n} \gamma \frac{{\lambda }^{\alpha }+{\lambda }^{-\alpha }+1-3nN}{{\lambda }^{\alpha }+{\lambda }^{-\alpha }+1-3N} \left(\frac{{\lambda }^{\alpha }-{\lambda }^{-\alpha }}{{\lambda }^{2}-{\lambda }^{-2}}\right) .$$

(13)

Finally, in the case of inflation of a thin spherical shell, the relationship between the inflation pressure $P$ and the stretch $\lambda$ is given by [25]:

$$P=2\frac{{h}_{0}}{{r}_{o}} {\lambda }^{-3} {T}_{eq-bi} ,$$

(14)

where ${h}_{0}$ and ${r}_{o}$ are the undeformed thickness and radius of curvature, respectively. For model (3), using Eq. (10)₂, the following $P-\lambda$ relationship is readily obtained:

$$P=2\frac{{h}_{0}}{{r}_{o}} \frac{\mu \alpha }{2n} \frac{2{\lambda }^{\alpha }+{\lambda }^{-2\alpha }-3nN}{2{\lambda }^{\alpha }+{\lambda }^{-2\alpha }-3N} \left({\lambda }^{\alpha -3}-\frac{1}{{\lambda }^{2\alpha +3}}\right) .$$

(15)

Similarly, for the (three-term) Ogden model, we find that:

$$\left\{\begin{array}{l}{\left(T_{uni}\right)}_{Ogden}=\sum\limits_{p=1}^3\mu_p\left(\lambda^{\alpha_p}-\frac1{\lambda^{0.5\alpha_p}}\right),\\\begin{array}{c}\\{\left(T_{eq-bi}\right)}_{Ogden}=\sum\limits_{p=1}^3\mu_p\left(\lambda^{\alpha_p}-\frac1{\lambda^{2\alpha_p}}\right),\end{array}\\\begin{array}{c}\\{\left(T_{ps}\right)}_{Ogden}=\sum\limits_{p=1}^3\mu_p\left(\lambda^{\alpha_p}-\frac1{\lambda^{\alpha_p}}\right),\end{array}\end{array}\right.$$

(16)

for the uniaxial, equi-biaxial and pure shear deformations, respectively, while for the generic biaxial deformation, we get:

$${ \left[{\left({T}_{bi}\right)}_{j}\right]}_{Ogden}=\sum_{p=1}^{3}{\mu }_{p} \left[{\lambda }_{j}^{{\alpha }_{p}}-{\left(\frac{1}{{\lambda }_{1}{\lambda }_{2}}\right)}^{{\alpha }_{p}}\right] ,\;j=\mathrm{1,2}.$$

(17)

The $T-\gamma$ relationship using the (three-term) Ogden model is also of the form:

$${\left({T}_{ss}\right)}_{Ogden}=\sum_{p=1}^{3}{\mu }_{p}\gamma \left(\frac{{\lambda }^{{\alpha }_{p}}-{\lambda }^{-{\alpha }_{p}}}{{\lambda }^{2}-{\lambda }^{-2}}\right) ,$$

(18)

while the $P-\lambda$ relationship is:

$${\left(P\right)}_{Ogden}=2\frac{{h}_{0}}{{r}_{o}} \sum_{p=1}^{3}{\mu }_{p}\left({\lambda }^{{\alpha }_{p}-3}-\frac{1}{{\lambda }^{2{\alpha }_{p}+3}}\right) .$$

(19)

These relationships will be used in Sect. 3 for the fitting campaign.

3 Comparing the correlations with the experimental data

While the relative errors pursuant to the application of the one-term model in Eq. (3) and the three-term Ogden model for a natural unfilled rubber specimen have been compared in [2], it was not the aim of that study to provide a direct comparison between the modelling results obtained from the application of these two models to a broader range of rubber-like materials. That purpose is pursued in this work. For doing so, here we consider a variety of rubber-like materials ranging from hydrogels to foams, silicone elastomers and filled rubbers. The datasets considered here are due to Lahellec et al. [22] and Fujikawa et al. [16] (for carbon filled rubbers), Yan et al. [32] (for polymeric foams), Yohsuke et al. [34] and Saadedine et al. [28] (for extremely soft polymer gels and hydrogels), Jiang et al. [20] (for silicone elastomers), and the inflation of a typical rubber balloon due to Beatty [10]. These studies have been chosen as exemplars for which the modelling drawbacks recounted in Sect. 1, as a result of the application of the Ogden model, showcase themselves in comparison with the results obtained by using the one-term model counterpart of Eq. (3).

To this end, the relevant stress-deformation relationships for each model; i.e., Eqs. (10), (11), (13) and (15) for model (3) and Eqs. (16)–(19) for the three-term Ogden model, are simultaneously fitted to the related deformation modes from each aforementioned dataset. The best fit is achieved by minimising the residual sum of squares (RSS) function defined as: $\mathrm{RSS}={\sum_{i}\left({T}^{model}-{T}^{experiment}\right)}_{k}^{2}$, where k is the number of data points. The minimisation is performed via an in-house developed code in MATLAB^®, using the genetic algorithm (GA) function. The coefficient of determination R² values are reported as a measure of the goodness of the obtained fits. The presented relative error (%) in the plots is calculated as: $\left|\frac{{T}^{model}-{T}^{experiment}}{{T}^{experiment}}\right|\times 100$.

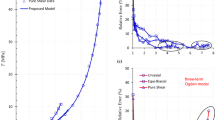
We start by comparing the modelling results for filled rubber specimens. The considered datasets here for this purpose are due to Lahellec et al. [22] pertaining to a commercial rubber material developed by the Michelin group, and Fujikawa et al. [16] for carbon black filled styrene butadiene rubber specimens. Figure 1 compares the fitting plots for the former dataset, and Table 1 contains the model parameter values for both models. The tabulated datapoints of this dataset has been presented in, e.g. [8].

Fig. 1

Modelling results for the filled rubber specimens of Lahellec et al. [22] using (a) the proposed model in Eq. (3); and (b) the three-term Ogden model. Panel (c) presents the ensuing iso-energy plots in the principal stretches plane $\left({\lambda }_{1},{\lambda }_{2}\right)$ for both strain energy functions

Table 1 Obtained model parameters for the Lahellec et al. [22] dataset

While the R² values for the fits using both models are in excess of 0.99, the relative errors are higher on using the Ogden model over the model in Eq. (3). It is evident from the plots in Fig. 1 that the three-term Ogden model does not accurately capture the trend in the experimental data, particularly in simple shear. In addition, the iso-energy plots in the principal stretches plane $\left({\lambda }_{1},{\lambda }_{2}\right)$ demonstrate that the fit obtained by the Ogden model results in the loss of convexity, while model (3) does not suffer from this undesirable effect (see Fig. 1c).

The plots in Fig. 2 compare the modelling results for another filled rubber specimen, namely carbon black filled styrene butadiene rubber, for uniaxial, equi-biaxial and pure shear deformation datasets due to Fujikawa et al. [16]. Note that in keeping with the original source of the data in [16], here the presented plots are the nominal stress $\mathbf{P} (={\mathbf{F}}^{-1}\mathbf{T})$ versus the stretch. The obtained model parameter values are summarised in Table 2. The tabulated datapoints for this dataset is provided in the Appendix, Table 1.

Fig. 2

Modelling results for the filled rubber specimens of Fujikawa et al. [16] using (a) the proposed model in Eq. (3); and (b) the three-term Ogden model. Note that the stress measure in the plots is the nominal stress $P$

Table 2 Obtained model parameters for the Fujikawa et al. [16] dataset

For this dataset, the application of the three-term Ogden model does not result in non-convexity (hence, the iso-energy plots are not shown in Fig. 2). However, as the relative error plots demonstrate, this model with its extra two model parameters over the proposed model (3) fails to provide an improved fit. The relative errors pertaining to the application of the Ogden model to this dataset are typically higher than those obtained by using model (3). The foregoing two exemplar datasets therefore indicate that the Ogden model is not perhaps best suited for application to the finite deformation of filled rubbers. Model (3), on the other hand, appears to provide robust fits to the deformation of these specimens.

The next dataset we consider here is due to Yan et al. [32] for a polymeric foam specimen under uniaxial compression and simple shear. Foams are generally considered to be (slightly) compressible, and thus a compressible form of the strain energy function would ideally be required for modelling their deformation (e.g., see [9]). However, frequent occasions may be encountered in the literature wherein foams have been modelled using incompressible models by way of a first approximation. Since our primary aim in this work is to assess the performance of the considered two models in relation to predicting the experimental data rather than quantifying the constitutive parameters of the material, we too model this dataset using the incompressible three-term Ogden and the proposed models. Table 3 presents the values of the model parameters obtained, and Fig. 3 compares the fitting plots of both models. The tabulated datapoints for this dataset has been presented in, e.g., [9]. Note from Table 3 that the value of $N$ for this dataset is $N<0$; however, as the convexity plots in Fig. 3c indicate, the strain energy remains convex.

Table 3 Model parameters obtained for the Yan et al. [32] dataset

Fig. 3

Modelling results for the polymeric foam specimen of Yan et al. [32] using (a) the proposed model in Eq. (3); and (b) the three-term Ogden model. Panel (c) presents the ensuing iso-energy plots in the principal stretches plane $\left({\lambda }_{1},{\lambda }_{2}\right)$ for both strain energy functions

From the R² values in Table 3 and the relative error plots in Fig. 3, it is evident that the four-parameter model (3) provides more accurate fits to this dataset than the six-parameter Ogden model. In addition, it is again observed that the application of the three-term Ogden model renders loss of convexity, as shown in Fig. 3c. Therefore, based on these primary results, the application of the proposed model in Eq. (3) to the deformation of polymer foams may be merited.

While the compressible form of the Ogden model, the so-called Ogden hyperfoam model, may improve the modelling results further, it is worth noting that the three-term Ogden hyperfoam model incorporates nine model parameters, which further exacerbates the problem of finding a unique ‘optimal’ fit and the ‘optimal’ set of model parameter values. The fitting results here indicate that the extension of the proposed model in Eq. (3) to the compressible form may too prove beneficial.

The next type of rubber-like materials we consider here are soft gels. To this end, we first consider the datasets due to Saadedine et al. [28], containing uniaxial deformation data for hydrogel specimens with various amounts of added cross-linkers, from 1 to 40 mg, denoted by M1, M5, M10 and M40 specimens, respectively. The collated experimental datapoints for these tests have been presented in a tabulated format in the Appendix, Table 2. Figure 4 illustrates the fitting results, and Table 4 summarises the obtained model parameters’ values.

Fig. 4

Modelling results for the cross-linked hydrogel specimens of Saadedine et al. [28] using (a) the proposed model in Eq. (3); and (b) the three-term Ogden model. Panel (c) presents the ensuing iso-energy plots in the principal stretches plane $\left({\lambda }_{1},{\lambda }_{2}\right)$ for the M1 specimen as an example

Table 4 Model parameters for the cross-linked hydrogel specimens due to Saadedine et al. [28]

It may be observed from the relative error plots in Fig. 4 that the three-term Ogden model provides marginally improved fits compared with model (3). However, the iso-energy plots (Fig. 4c) demonstrate that the Ogden model again loses convexity. The presented plots pertain to the M1 specimen, as an example. The same trend is also observed for the other specimens (not reported here). This loss of convexity by the Ogden model comes at the cost of only an average improvement in the relative errors by 1.79%, with two extra model parameters compared with model (3).

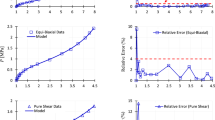
From the family of polymer gels, we consider another dataset from the work of Yohsuke et al. [34], reporting on uniaxial, equi-biaxial and pure shear deformations of cross-linked poly(acrylamide) (PAAm) hydrogels. The tabulated datapoints for this dataset are presented in Table 3 of the Appendix. The model parameter values for the obtained best fits are given in Table 5, and Fig. 5 illustrates the fitting results.

Table 5 Obtained model parameters for the PAAm hydrogel specimens of the Yohsuke et al. [34] dataset

Fig. 5

Modelling results for the hydrogel specimens of Yohsuke et al. [34] using (a) the proposed model in Eq. (3); and (b) the three-term Ogden model

While the application of the three-term Ogden model to this dataset does not result in the loss of convexity; it is observed that the relative errors using the Ogden model exceed those of the model in Eq. (3). Therefore, similar to the case of filled rubbers, the application of the Ogden model to the deformation of hydrogel specimens appears to result in either a less accurate prediction of the data compared with that of model (3), or/and may give rise to the loss of convexity. For modelling the finite deformation of hydrogels, too, it appears that the four-parameter model (3) provides a robust choice.

We now consider a dataset for a silicone-based elastomer due to Jiang et al. [20]. Therein, they report on equi-biaxial and general biaxial deformations of a commercial silicone elastomer membrane. An interesting feature of their work is that it is one of the rare, to the knowledge of the author, studies to perform general biaxial tests on the specimens. Data obtained form equi-biaxial tests, when used for calibrating models, inflict a series of shortcomings pertaining to what is known as collinearity, which hinders obtaining unique model parameter values [11, 13]. To this end, the performance of many of the existing models in the literature, if simultaneously fitted to datasets which also include general biaxial deformation data, remains unclear. Here, we provide the fitting results to this dataset in Fig. 6. Table 6 contains the obtained model parameters’ values. The tabulated datapoints have been presented in the Appendix, Table 4.

Fig. 6

Modelling results for the silicone elastomer specimens of Jiang et al. [20] using (a) the proposed model in Eq. (3); and (b) the three-term Ogden model. Panel (c) presents the ensuing iso-energy plots in the principal stretches plane $\left({\lambda }_{1},{\lambda }_{2}\right)$ for both models

Table 6 Model parameters for the Jiang et al. [20] dataset

The observed modelling results for this silicone elastomer specimen are similar to the preceding results, namely that the application of the three-term Ogden model typically results in higher relative errors compared with the proposed model (3) and the loss of convexity.

The final dataset we consider in the section pertains to the inflation of a typical rubber balloon due to Beatty [10]. This dataset was previously considered in [5]; however, the difficulties associated with modelling this data was later brought to the author’s attention.² In effect, the gradient of the $P-\lambda$ curve for this dataset in reaching the limit-point instability, i.e., the first maximum pressure, appears to be unusually steep (for a detailed definition and analysis of the elastic instabilities in inflation of rubber-like shells see, e.g., Mangan and Destrade [23]). Therefore, some of the existing models in the literature underestimate the maximum pressure for this dataset by a considerable margin. Here, we provide the modelling results for this dataset, using model (3) and the three-term Ogden model. Figure 7 illustrates the fitting results, and Table 7 summarises the obtained model parameters’ values. Note that the tabulated datapoints for this dataset have been provided in [5].

Fig. 7

Modelling results for the typical inflation of a rubber balloon due to Beatty [10]: (a) comparison between the proposed model in Eq. (3) and the three-term Ogden model; (b) the relative errors; and the ensuing iso-energy plots in the principal stretches plane $\left({\lambda }_{1},{\lambda }_{2}\right)$ for (c) model (3) and (d) the Ogden model. Note that the dotted vertical lines in panel (a) represent the stretch at which the maximum pressure is predicted to occur (${\lambda }_{Model}^{max}=1.42$ predicted by model (3), and ${\lambda }_{Ogden}^{max}=1.52$ predicted by the Ogden model)

Table 7. Model parameters for the inflation dataset due to Beatty [10]

While the three-term Ogden model provides a marginally improved fit, as reflected in the relative error plots of Fig. 7b and the R² values in Table 7, we observe again the ensuing loss of convexity for this model in plots of Fig. 7d. Note that for this dataset, the value of parameter $n$ in model (3) is negative; however, the model remains convex as presented in Fig. 7c. It is also of note that the predicted stretch for the maximum pressure by the Ogden model, shown by the dotted red line in Fig. 7a corresponding to ${\lambda }_{Ogden}^{max}=1.52$, is notably displaced compared with that of the experimental data. In comparison, the predicted stretch by model (3), shown by the blue dotted line in Fig. 7a, is much closer to the data (corresponding to ${\lambda }_{Model}^{max}=1.42$).

4 Some discussion points

A frequently encountered occurrence using the (three-term) Ogden model applied to the exemplar datasets considered in this study is the likelihood of loss of convexity (of the iso-energy curves) by this model for the ‘optimal’ provided fits. This finding further reinforces the results of the author’s previous studies [6,7,8] for which the application of the Ogden model to deformation datasets of a soft tissue (brain) was shown to result in non-convex iso-energy plots in the $\left({\lambda }_{1},{\lambda }_{2}\right)$ plane. While this issue surrounding the Ogden model is not known to the author to be present for natural rubber applications, our results here appear to show that for softer rubber-like materials such as gels, foams, and soft tissues, the application of the Ogden model may risk this undesirable effect. More importantly, perhaps, is the fact that a three-term Ogden model with six constitutive parameters does not provide a significant improvement to the accuracy of the obtained fits compared with the proposed four parameter model (3), and when there is an improvement, it appears to be at the expense of the loss of convexity. These trends are also reflected in the results of Fig. 8, which provides a comparison between the modelling results obtained by the application of both models to the uniaxial tension–compression and simple shear of human brain (cortex) tissue, due to Budday et al. [12].

Fig. 8

Modelling results for the human brain (cortex) tissue due to Budday et al. [12] using (a) the proposed model in Eq. (3) with $\mu$ = 0.02 [kPa], $N$ = 7.52 [-], $\alpha$ = − 15.93 [-] and $n$ = 19.99 [-] (R² > 0.99); and (b) the three-term Ogden model with ${\mu }_{1}$ = − 3.12 [kPa], ${\mu }_{2}$ = 1.24 [kPa], ${\mu }_{3}$ = 10 [kPa], ${\alpha }_{1}$ = − 8.06 [-], ${\alpha }_{2}$ = 6.37 [-] and ${\alpha }_{3}$ = − 3.06 [-] (R² > 0.99). Panel (c) presents the ensuing iso-energy plots in the principal stretches plane $\left({\lambda }_{1},{\lambda }_{2}\right)$ for both strain energy functions. Note that with these model parameters, model (3) is not defined beyond the domain of deformation shown in the convexity plot

However, and perhaps more pertinent than the marginal fitting improvement that one model may offer over the other, and the issue of convexity or lack thereof, there is an inherent shortcoming associated with the functional form of all Valanis-Landel [30] type separable strain energy functions, including the Ogden model. This limitation may best be exemplified via the datasets of Jones and Treloar [21] and Vangerko and Treloar [31], as originally discussed by Ogden [26]. Jones and Treloar [21] performed pure shear deformation tests on rubbers specimens at various fixed ${\lambda }_{2}$ values, up to ${\lambda }_{2}=2.62$. Their results show that the shapes of the stress-stretch curves remain invariant to the value of ${\lambda }_{2}$; the curves only undergo a vertical translation by the change in ${\lambda }_{2}$. This feature can, of course, be captured via a separable form of $W$, as it will have the following form: $W\left({\lambda }_{1},{\lambda }_{2},{\lambda }_{3}\right)=w\left({\lambda }_{1}\right)+w\left({\lambda }_{2}\right)+w\left({\lambda }_{3}\right)$. However, later, Vangerko and Treloar [31] extended the work of Jones and Treloar [21] to higher levels of ${\lambda }_{2}$, e.g., up to ${\lambda }_{2}=3.38$, and demonstrated that at those higher levels of ${\lambda }_{2}$, the stress-stretch curves significantly deviate from the previously observed vertical translation trend. For capturing this behaviour, therefore, a separable form of $W$ is insufficient. By contrast, the non-separable function model (1), or equivalent model (3), does not suffer from such problems. Here in Fig. 9, we present the fitting results of both models to the reported dataset in [31], for a rubber specimen containing 5% sulphur. The fits have been obtained by simultaneous fitting of the stress-stretch datasets at all ${\lambda }_{2}$ levels using each model. It is clear that the Ogden model runs into difficulty capturing the deformation behaviour at ${\lambda }_{2}=3.38$, while the favourable results of the application of model (3) is of note. The relative error plots for this fit have not been presented, as the difference in the quality of fits is visibly clear.

Fig. 9

Modelling results for the rubber specimen of Vangerko and Treloar [31] using (a) the proposed model in Eq. (3) with $\mu$ = 0.59 MPa, $N$ = 7.21 [-], $\alpha$ = 1.77 [-] and $n$ = 1.17 [-] and R.² values in excess of 0.99; and (b) the three-term Ogden model with ${\mu }_{1}$ = − 0.27 [MPa], ${\mu }_{2}$ = 0.58 [MPa], ${\mu }_{3}$ = − 0.49 [MPa], ${\alpha }_{1}$ = − 1.01 [-], ${\alpha }_{2}$ = 3.18 [-] and ${\alpha }_{3}$ = 3.17 [-]. The abscissa is ${T}_{1}-{T}_{2}$, as reported in [31]. The symbols for the experimental data are also in coordination with the original plot [31]

5 Concluding remarks

It may not be an exaggeration to stipulate that the seminal Ogden model serves as a gold-standard strain energy function in application to the finite deformation of rubber-like materials. However, this study demonstrates that many applications may be found in which the Ogden model may produce ill-posed effects such as the loss of convexity. Our results indicate that this undesirable outcome may particularly be frequented, but not limited to, when the Ogden model is applied to the deformation of the ‘softer’ rubber-like materials such as gels, foams and soft tissues; see also Fig. 1 in relation to the filled rubber specimens. The proposed parent model, by contrast, remained free of such shortcomings in all applications.

Another comparative result demonstrated by this study is that the ‘quality’ of the fits achieved by the higher order Ogden model may still be improved using models with fewer constitutive parameters. In most of the modelling applications presented here, the one-term four-parameter model (3) provided lower relative errors compared with the three-term six-parameter Ogden model counterpart. The quality of the fits provided by the two-term Ogden model, which has the same number of parameters as model (3), is demonstrably lower than those provided by model (3). For brevity, those results were not included in this study, but may readily be deduced from the presented results here. The proposed four-parameter model (3) proves to be a robust modelling tool for accurate predictions of the deformation of a wide range of rubber-like materials as considered in this study.

The separable functional form of the Ogden model presents another nuanced limitation for application to the deformation of some rubber-like materials. Separable strain energy functions predict a translation of the stress-deformation curves (say in direction 1) when the material is kept stretched at a constant level say in direction 2; i.e. ${\lambda }_{2}$ is constant. However, as with the results in Fig. 9, this assumption may only be deemed valid for the lower ranges of ${\lambda }_{2}$. A separable strain energy function, therefore, cannot model the full deformation behaviour of the subject specimen over the whole domain of deformation. The proposed non-separable function model (3), by contrast, was able to provide a more accurate description of this behaviour, and as such provides the robustness required to model the full-range deformation.

In view of these results, the application of the proposed parent model (1), or its one-term form model (3), to the finite deformation of rubber like materials of various assortments, ranging from hydrogels to natural and filled rubbers, appears to be well justified and merited.

Appendix. The tabulated datasets

Table 8

Table 9

Table 10

Table 11

Table 8 Tabulated dataset due to Fujikawa et al. [16]

Table 9 Tabulated dataset due to Saadedine et al. [28]

Table 10 Tabulated dataset due to Yohsuke et al. [34]

Table 11 Tabulated dataset due to Jiang et al. [20]