Large Isotropic Elastic Deformations: On a Comprehensive Model to Correlate the Theory and Experiments for Incompressible Rubber-Like Materials

Abstract

A comprehensive model, i.e., a model that: (i) suitably captures the mechanical behaviour of various types of rubber-like materials; (ii) describes the constitutive behaviour of a subject rubber-like specimen under different deformation modes via a single set of model parameter values, and (iii) is parent to many of the existing models of distinct types, is presented in this paper for application to the finite deformation of incompressible isotropic rubber-like materials. The model breaks away from Rivlin’s principal invariants $I_{i}$ and Valanis-Landel’s separable function of principal stretches $\lambda _{i}$ representations, and instead adopts a general non-separable functional form $W( \lambda _{1}, \lambda _{2}, \lambda _{3} )$, subject to the incompressibility constraint. By way of example, the application of the model to extant datasets from four types of rubber-like materials that exhibit discernible mechanical behaviours, namely natural unfilled and filled rubbers, hydrogels and (extremely) soft tissue specimens, will be considered. The favourable correlation between the model predictions and the considered experimental datasets, obtained via simultaneous fitting of the model to the data of various deformations, will be demonstrated. It will be shown that most of the landmark models in the literature including the $W( I_{1}, I_{2} )$ form Mooney-Rivlin, the Gent-like limiting chain extensibility, the nonaffine tube and the separable principal stretches-based type Ogden models are all a special sub-set of the presented parent model, and are all recovered from this model. An important implication of the non-separable functional form of the model will be conferred, through a specific dataset, where the predictions of the separable functions prove inherently inadequate. The consequences of these improvements for a more accurate modelling of the finite deformation of incompressible isotropic rubber-like materials will also be discussed.

1 Introduction

Within the framework of nonlinear elasticity, the mechanical behaviour of hyperelastic, rubber-like materials may be conveniently described in mathematical terms via a strain energy function $W$. From this function $W$, subsequently, appropriate stress-strain relationships may be derived for various boundary value problems. The so obtained stress-strain relationships may then be formally taken as a mathematical means of representing the acquired experimental data.

In the case of incompressible rubber-like materials, which is the focus of this work, the current literature suggests that the most frequently adopted representations of the $W$ function, in mathematical terms, have either been on the basis of Rivlin’s principal invariants $I_{i}$ formulation [1] or the separable form of the principal stretches $\lambda _{i}$ adduced by Valanis and Landel [2]. To this end, many landmark models in the literature including the neo-Hookean model proposed by Treloar [3], that of Mooney [4] and its generalised invariant form by Rivlin known as the Mooney-Rivlin model [1], the principal stretches-based model by Ogden [5], the non-Gaussian statistical treatment of the molecular chains with the inverse Langevin function by Kuhn and Grün [6] and the ensuing developments in limiting chain extensibility models proposed by Arruda and Boyce [7], Gent [8] and the modification to the Gent model by Pucci and Saccomandi [9], the cubic function presented by Yeoh [10], the full network model of Beatty [11], and the phenomenological model of Lopez-Pamies [12], may be recounted.

The point of departure in this work, however, is the notion discussed by Destrade et al. [13], that the foregoing variety of models in the literature is perhaps an indication that a universal model is yet to be proposed, or accepted. The term ‘universal’, in this context and henceforth, is interpreted as comprehensive, representing the following three-fold concept: (i) a comprehensive model is one that can suitably be applied to, and capture, the mechanical behaviour of a variety of rubber-like materials, not only limited to a specific sub-set material type; (ii) a comprehensive model is capable of describing various deformation modes of a specimen with a single set of model parameter values, which itself requires containing a necessary and sufficient set of constitutive parameters; and (iii) a comprehensive model is the parent model to most, if not all, of the existing models in the literature; i.e., the existing models are a special sub-set of the comprehensive model. This work attempts to devise and present a strain energy function $W$ which satisfies these three notions.

All foregoing three aspects of comprehensiveness have important mathematical and mechanistic modelling implications. It is now well documented that not all models in the literature admit a single set of model parameter values to describe various deformation modes of the same specimen; i.e., do not suitably capture the experimental datasets via simultaneous fitting (see, e.g., the review of Marckmann and Verron [14] and that of recent by Dal et al. [15]). This implies that such models are perhaps not comprised of the correct set of constitutive parameters for the considered hyperelastic materials.

The performance of most, if not all, models in the literature encounters further problems when the models are applied to datasets from different types of rubber-like specimens which exhibit discernible mechanical behaviours. For example, as recently studied by Anssari-Benam and Horgan [16, 17], even some of the most celebrated models cannot suitably capture the mechanical behaviour of both unfilled and filled rubbers. This shortcoming implies, then, that the application of most of the existing models in the literature is at best limited to only a specific type of rubber-like materials.

As regards their mathematical formulation, while some of the existing strain energy functions under specific combination of parameters, or via their Taylor series expansion, recover the functional form of some of the more basic models, most models in the literature possess independent functional forms and are not known to be recovered from a single parent model. As archetypal examples, take the seminal Mooney-Rivlin, Ogden and Gent models. These models are not known to stem from a single more general parent model. While the Mooney-Rivlin model readily recovers the neo-Hookean strain energy function, this model is not known to be the parent model to other $W( I_{1}, I_{2} )$ functions. The Ogden model, while recovering the neo-Hookean and Mooney-Rivlin models under certain combinations of its model parameters, is not known to be a special case of a more generalised model. The Gent model also reduces to the neo-Hookean model in the limit of $J_{m} \rightarrow \infty$; however, similar to other limiting chain extensibility models approximating the inverse Langevin function, is not known to stem from a (closed-form) parent model. The same sentiment applies to the class of models often known as constrained tube models, which assume distinct functional forms compared with their affine network model counterparts.

Undoubtedly, it would seem more desirable to have a comprehensive model at hand that overcomes the foregoing issues and thereby provides a reliable degree of universality on all three aspects of the notion, as defined earlier. In this work, accordingly, a new strain energy function is presented, by breaking away from Rivlin’s invariant and Valanis-Landel’s separable principal stretches frameworks. Instead, a new non-separable form of representation for $W$ is adopted as $W( \lambda _{1}, \lambda _{2}, \lambda _{3} )$, consistent with algebraic requirements as will be demonstrated in the sequel, as:

$$ W= \frac{3 \left ( n-1 \right )}{2n} \mu N \left [ \frac{1}{3N \left ( n-1 \right )} \left ( \lambda _{1}^{\alpha} + \lambda _{2}^{\alpha} + \lambda _{3}^{\alpha} -3 \right ) - \ln \left ( \frac{\lambda _{1}^{\alpha} + \lambda _{2}^{\alpha} + \lambda _{3}^{\alpha} -3N}{3-3N} \right ) \right ], $$

(1)

where $n$, $N$, $\alpha$ and $\mu$ are model parameters to be defined later (in §2), and $\lambda _{i}$ are the principal stretches subject to: $\lambda _{1} \lambda _{2} \lambda _{3} =1$, in order to ensure the condition of incompressibility. The mode in Eq. (1) is the one-term expansion of a more general form:

$$\begin{aligned} W= \sum _{i=1} \frac{3 ( n_{i} -1 )}{2 n_{i}} \mu _{i} N \biggl[ \frac{1}{3N ( n_{i} -1 )} \bigl( \lambda _{1}^{\alpha _{i}} + \lambda _{2}^{\alpha _{i}} + \lambda _{3}^{\alpha _{i}} -3 \bigr) - \ln \biggl( \frac{\lambda _{1}^{\alpha _{i}} + \lambda _{2}^{\alpha _{i}} + \lambda _{3}^{\alpha _{i}} -3N}{3-3N} \biggr) \biggr]. \end{aligned}$$

(2)

Note that parameter $N$ in the general form of the model in Eq. (2) is not subscripted, as this parameter controls the limit of extensibility and, as will be discussed later, determines the maximum allowable principal stretch – it is therefore single-valued. Here, however, we will not pursue expansions beyond the first term, i.e., Eq. (1), for the following two reasons: (i) as will be shown in §3, the model (1) provides favourable (simultaneous) fits to the variety of datasets and types of specimens considered, which obviates the need to proceed with higher terms; and (ii) there are clear disadvantages in prescribing unwarranted excessive number of constitutive parameters to describe the (macro-level) mechanical behaviour of a specimen (the shortcomings related to having an excessive number of model parameters will be discussed more in §2).

In proceeding towards the stated aim of this work, the theoretical preliminaries for the proposed model will be presented in §2. It will be demonstrated that the models (1) and (2) are indeed the parent models to many of the existing models in the literature including the Mooney-Rivlin, Gent, Ogden and a class of constrained tube models, inter alia. The application of the model (1) to datasets of various types of rubber-like materials including natural (unfilled) and filled rubbers, hydrogels and isotropic soft tissues will be demonstrated in §3. To this end, the canonical dataset due to Treloar [18] for a (vulcanised) natural rubber specimen, the dataset due to Lahellac et al. [19] for a commercialised filled rubber material developed by the Michelin tyre company, a dataset pertaining to poly(acrylamide) (PAAm) hydrogels due to Yohsuke et al. [20], and the Budday et al. [21] dataset on the deformation of human brain (cortex) will be considered. The favourable application of the model via simultaneous fitting to the different deformation modes of each specimen will be demonstrated, with low relative errors, atypical of most of the existing models in the literature that have been thus far applied to the same datasets. While for all the provided fits by the proposed model (1) the iso-energy plots in the principal stretches $\left ( \lambda _{1}, \lambda _{2} \right )$ plane remain convex, a comparison with the Ogden model is presented for the brain tissue dataset, specifically, in which the latter model loses this convexity. Some points of discussion are then offered in §4. An important implication regarding the non-separable functional form of model (1) will be discussed, using an exemplar dataset due to Vangerko and Treloar [22], where the separable $W$ functions prove inherently insufficient. Concluding remarks will then be conferred in §5. Given that the proposed model is parent to most of the celebrated existing models in the literature, contains relatively low number of model parameters (four), and provides favourable (simultaneous) fits to the variety of deformation modes from different types of specimens, it will be convened by way of conclusion that model (1) provides a reliable degree of comprehensiveness for application to the deformation of incompressible isotropic rubber-like materials.

2 The Comprehensive Model

2.1 Theoretical Background

The motivation behind the functional form of $W$ in Eq. (1) stems from the model used by Anssari-Benam and Bucchi [23, 24]. Derived from the non-Gaussian treatment of the statistical mechanics of molecular chains, Anssari-Benam and Bucchi [23] utilised the following strain energy function from the family of limiting chain extensibility models for application to the deformation of the elastin network in heart valves, and subsequently for rubber-like materials [24]:

$$ W \left ( I_{1} \right ) =\mu N \left [ \frac{1}{6N} \left ( I_{1} -3 \right ) - \ln \left ( \frac{I_{1} -3N}{3-3N} \right ) \right ],\quad I_{1} < 3N,\ N>1, $$

(3)

where $I_{1}$ is the first principal invariant of the left Cauchy-Green deformation tensor $\mathbf{B}\ \left ( = \mathbf{F F}^{\mathrm{T}} \right )$, defined in terms of the principal stretches as $I_{1} = \lambda _{1}^{2} + \lambda _{2}^{2} + \lambda _{3}^{2}$, $N$ is the number of Kuhn segments, or links, in a molecular chain, and $\mu$ is a material parameter related to the infinitesimal shear modulus $\mu _{0}$ via $\mu = \mu _{0} \left ( \frac{3-3N}{1-3N} \right )$. See also the review by Puglisi and Saccomandi [25] for an in-depth micromechanical interpretation of the parameters in generalised neo-Hookean strain energy functions based on the kinetic molecular theory. Note that the constraints in (3) ensure that the $\ln \left ( \blacksquare \right )$ function is well defined. It was recently brought to the author’s attention that the model in Eq. (3) is a special case of the nonaffine tube model first introduced by Davidson and Goulbourne [26]; see Eq. (27) therein. The response function ($\partial W/\partial I_{1}$) of the model in Eq. (3) is also related to that of the Gent model, as noted by Horgan [27]. However, in comparison, the more accurate predictions of this model over the Gent model have been demonstrated (see, e.g., [24, 28]). This model was then successively adopted for application to the mechanical behaviour of rubber-like materials for various boundary value problems including the investigation of elastic instabilities [16, 28–32].

As shown by Anssari-Benam [33], the model in Eq. (3) is itself indeed a sub-set of a more general class of strain energy functions whose response functions are constructed as a [1/1] rational Padé approximant in $I_{1}$ of the form:

$$ W= \frac{3(n-1)}{2n} \mu N \left [ \frac{1}{3N(n-1)} \left ( I_{1} -3 \right ) - \ln \left ( \frac{I_{1} -3N}{3-3N} \right ) \right ],\quad I_{1} < 3N, $$

(4)

where the additional model parameter $n$ is related to the rate of strain-hardening at a given $N$ and is positive. In the special case where $n=3$, the model (4) recovers the Anssari-Benam and Bucchi model given in Eq. (3). Note that parameter $\mu$ is now related to the infinitesimal shear modulus $\mu _{0}$ through: $\mu = \mu _{0} \frac{n \left ( 1-N \right )}{1-nN}$. While both $N$ and $n$ in the original derivation of the models (3) and (4) were constrained to be integers, Anssari-Benam and Horgan [16, 17] later showed that phenomenologically there is no reason for such a restriction, and generalised those constraints to: $n, N\in \mathbb{R}^{+}$. Subject to this new constraint, and that in (4), the $\ln \left ( \blacksquare \right )$ function remains well defined. It was demonstrated by Anssari-Benam and Horgan [17] that model (4) is indeed the parent to the celebrated Gent model, reducing to the Gent model in the limit $n\rightarrow \infty$. Moreover, the functional form of the model (4) proved rich enough to provide favourable fits to the deformation of both unfilled and filled rubbers, as demonstrated in [17], making this model one of the very few available models in literature with such a capability, next to the model by Lopez-Pamies [12, 34].

Models (3) and (4) are within Rivlin’s representation form in terms of the principal invariant(s). As alluded to by Treloar [35], the main mathematical reason in adopting the principal invariants representation by Rivlin was to restrict the functional form of $W$ to even powers of the principal stretches (e.g., $\lambda _{i}^{2}$ and $\lambda _{i}^{-2}$ etc), so as to ensure that the strain energy function is always positive. It is interesting to note that in the original development of the theory by Rivlin, the mathematical definition of the principal stretches is such that $\lambda _{i}$ may assume negative values; e.g., in the case of pure rotation of the body – see Sect. 4 of [1]. However, as per Ogden’s representation of the strain energy function [5], the restriction of $\lambda _{i}$ to even powers is not necessary, since the modern definition of the stretch already confines $\lambda _{i}$ to positive values. Therefore, mathematically, it is not required that a strain energy function $W$ to be an even function of the principal stretches, or so to be represented in terms of the principal invariants $I_{i}$.

However, equally, when expressed in terms of the principal stretches $\lambda _{i}$, a strain energy function $W$ is not required to be necessarily a separable functional form in terms of $\lambda _{i}$. Therefore, the Valanis-Landel or Ogden representations are not the most generic form that a strain energy function $W$ can assume. Indeed, as discussed in [35], the Ogden representation, for example, precludes certain possible functional forms such as the $\ln \left ( \blacksquare \right )$ function, which is of particular interest here in view of models (3) and (4). Accordingly, therefore, we further relax the separable functional form assumption and consider the general non-separable form of $W$ as:

$$ W\equiv W \left ( \lambda _{1}, \lambda _{2}, \lambda _{3} \right ), $$

(5)

subject only to the condition that $W$ is symmetric with respect to the principal stretches; i.e., remains invariant with any permutation of $\lambda _{i}$s. In the scope of the current work where only incompressible materials are of concern, we note that the condition of incompressibility also holds such that $\lambda _{1} \lambda _{2} \lambda _{3} =1$.

In this spirit, a generalisation of this kind for model (3) was proposed by Anssari-Benam et al. [36] for application to the deformation of (human) brain tissue of the form:

$$ W=\mu N \left [ \frac{1}{6N} \left ( \lambda _{1}^{\alpha} + \lambda _{2}^{\alpha} + \lambda _{3}^{\alpha} -3 \right ) - \ln \left ( \frac{\lambda _{1}^{\alpha} + \lambda _{2}^{\alpha} + \lambda _{3}^{\alpha} -3N}{3-3N} \right ) \right ], $$

(6)

where $\mu$, $N$ and $\alpha$ are model parameters, with $\lambda _{1} \lambda _{2} \lambda _{3} =1$. Note that parameter $\mu$ is related to the infinitesimal shear modulus $\mu _{0}$ by: $\mu = \mu _{0} \frac{4 \left ( 3-3N \right )}{\alpha ^{2} \left ( 1-3N \right )}$. On fitting this model simultaneously to uniaxial tension, compression and simple shear deformation datasets of the human brain tissue due to Budday et al. [21], improved fits were obtained compared with that of the Ogden model [36]. More importantly, the iso-energy plots in the $\left ( \lambda _{1}, \lambda _{2} \right )$ plane for model (6) were shown to remain convex, while the Ogden model (including one-term and up to higher terms) loses this convexity in various applications to brain tissue deformation datasets (e.g., in Mihai et al. [37] when applied to a single deformation mode, in Budday et al. [21, 38] for various deformations modes, and in Mihai et al. [39] under simultaneous fitting). Therefore, with only three parameters, model (6) showed a promising prelude as an alternative principal-stretches based model for application to incompressible isotropic hyperelastic materials.

2.2 Mathematical Representation

Motivated by foregoing early developments, here we suggest a similar generalisation to model (4), as with model (6), to obtain the following four-parameter functional representation of $W$:

$$ W= \frac{3 \left ( n-1 \right )}{2n} \mu N \left [ \frac{1}{3N \left ( n-1 \right )} \left ( \lambda _{1}^{\alpha} + \lambda _{2}^{\alpha} + \lambda _{3}^{\alpha} -3 \right ) - \ln \left ( \frac{\lambda _{1}^{\alpha} + \lambda _{2}^{\alpha} + \lambda _{3}^{\alpha} -3N}{3-3N} \right ) \right ], $$

i.e., the model in Eq. (1). The structural parameters of the model assume the same role as in the original derivation of models (3) and (4). The parameter $N$, as before, controls the deformation limit(s), such that for the $\ln \left ( \blacksquare \right )$ function to be well-defined we must have:

$$ \left \{ \begin{aligned}[c] &\lambda _{1}^{\alpha} + \lambda _{2}^{\alpha} + \lambda _{3}^{\alpha} < 3N \Rightarrow \frac{\left ( \lambda _{1} \lambda _{2} \right )^{\alpha} \left ( \lambda _{1}^{\alpha} + \lambda _{2}^{\alpha} \right ) +1}{3 \left ( \lambda _{1} \lambda _{2} \right )^{\alpha}} < N,\quad \text{if } N>1, \\ &\lambda _{1}^{\alpha} + \lambda _{2}^{\alpha} + \lambda _{3}^{\alpha} >3N \Rightarrow \frac{\left ( \lambda _{1} \lambda _{2} \right )^{\alpha} \left ( \lambda _{1}^{\alpha} + \lambda _{2}^{\alpha} \right ) +1}{3 \left ( \lambda _{1} \lambda _{2} \right )^{\alpha}} >N,\quad \text{if } 0 < N< 1, \end{aligned} \right . $$

(7)

for a general deformation, and subject to the incompressibility constraint. The condition (7) may be further specialised depending on the deformation being considered; however we will not require deriving explicit relationships here. We note that, as has been discussed by Murphy [40] and Horgan and Murphy [41] in relation to the limiting chain extensibility models, a more global imposition of the constraint (7) may be of the form:

$$ \max \left \{ \lambda _{1}, \lambda _{2}, \lambda _{3} \right \} < \lambda ^{*}, $$

(8)

where $\lambda ^{*}$ is a constant whose value depends on the type of deformation. From (7) and (8) it is therefore observed that parameter $N$ effectively controls the maximum allowable principal stretch. Algebraically, we will require that:

$$ n, N\in \mathbb{R}^{+}, $$

(9)

i.e., to be positive real-valued parameters.

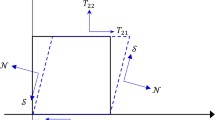
In order to establish the relationship between the parameter $\mu$ of model (1) and the infinitesimal shear modulus $\mu _{0}$, we note that the principal stretches $\lambda _{i}$ in simple shear deformation may be determined from the eigenvalues of the left Cauchy-Green deformation tensor $\mathbf{B}$ as:

$$ \lambda _{1} = \frac{\gamma}{2} + \sqrt{1+ \frac{\gamma ^{2}}{4}},\qquad \lambda _{2} = \lambda _{1}^{-1} =- \frac{\gamma}{2} + \sqrt{1+ \frac{\gamma ^{2}}{4}},\qquad \lambda _{3} =1, $$

(10)

where $\gamma$ is the amount of shear. The Cauchy stress $T_{12} (= T_{21} )$ may then be computed from $W$ as:

$$ T_{12} = \frac{\partial W}{\partial \gamma} = \frac{\mu \alpha}{2n} \frac{1}{\sqrt{\gamma ^{2} +4}} \frac{\lambda _{1}^{\alpha} + \lambda _{1}^{-\alpha} +1-3nN}{\lambda _{1}^{\alpha} + \lambda _{1}^{-\alpha} +1-3N} \left ( \lambda _{1}^{\alpha} - \frac{1}{\lambda _{1}^{\alpha}} \right ), $$

(11)

where upon noting that $\frac{1}{\sqrt{\gamma ^{2} +4}} = \frac{\gamma}{\lambda _{1}^{2} - \lambda _{1}^{-2}}$ may be re-written as:

$$ T_{12} = \frac{\mu \alpha}{2n} \gamma \frac{\lambda _{1}^{\alpha} + \lambda _{1}^{-\alpha} +1-3nN}{\lambda _{1}^{\alpha} + \lambda _{1}^{-\alpha} +1-3N} \left ( \frac{\lambda _{1}^{\alpha} - \lambda _{1}^{-\alpha}}{\lambda _{1}^{2} - \lambda _{1}^{-2}} \right ). $$

(12)

In the infinitesimal limit, where $\lambda _{1} \rightarrow 1$, we note that:

$$ \lim _{\lambda _{1} \rightarrow 1} \frac{\lambda _{1}^{\alpha} - \lambda _{1}^{-\alpha}}{\lambda _{1}^{2} - \lambda _{1}^{-2}} = \frac{\alpha}{2}, $$

(13)

so that Eq. (12) reduces to:

$$ T_{12} = \frac{\mu \alpha ^{2}}{4n} \frac{1-nN}{1-N} \gamma , $$

(14)

which establishes that:

$$ \mu _{0} = \frac{\mu \alpha ^{2}}{4n} \frac{1-nN}{1-N}\quad \text{or}\quad \mu = \frac{4n \mu _{0}}{\alpha ^{2}} \frac{1-N}{1-nN}. $$

(15)

Finally, note that $\alpha$ is a real-valued parameter:

$$ \alpha \in \mathbb{R}. $$

(16)

The model (1), subject to the condition (7), with algebraic requirements described by (9) and (16) for parameters $n$, $N$ and $\alpha$, respectively, and parameter $\mu$ defined in terms of the infinitesimal shear modulus $\mu _{0}$ given by Eq. (15), remains well-defined over the domain of deformation.

The four-parameter model (1) may be considered the one-term expansion of the more general from (2); i.e.:

$$ W= \sum _{i=1} \frac{3 ( n_{i} -1 )}{2 n_{i}} \mu _{i} N \biggl[ \frac{1}{3N ( n_{i} -1 )} \bigl( \lambda _{1}^{\alpha _{i}} + \lambda _{2}^{\alpha _{i}} + \lambda _{3}^{\alpha _{i}} -3 \bigr) - \ln \biggl( \frac{\lambda _{1}^{\alpha _{i}} + \lambda _{2}^{\alpha _{i}} + \lambda _{3}^{\alpha _{i}} -3N}{3-3N} \biggr) \biggr], $$

where the algebraic requirements on $n_{i}$, $N$ and $\alpha _{i}$ are similar to those given by (9) and (16). The infinitesimal shear modulus $\mu _{0}$, then, will also be the sum of the right-hand side terms in Eq. (15)₁. As highlighted in §1, note that $N$ is not subscripted. The reason for this may now be more evident from (7) and (8). It may be observed that parameter $N$ is related to, and controls, the maximum allowable principal stretch $\lambda ^{*}$, and as such possesses a single value. The expansion of this model beyond the first term, however, will not be advocated or pursued here, as apart from the favourable results obtained by the four-parameter model (1), to be shown in §3, the multi-term form may give rise to the following mechanistic and mathematical challenges.

First, as discussed in detail by Yeoh [42], while including more terms in a model provides further degrees of freedom to achieve a ‘better’ fit, it does not necessarily guarantee that the constitutive behaviour of the material will be better captured. Indeed, the additional degrees of freedom introduced by considering unwarranted extra terms often only lead to a model that fits better the experimental errors. The questions as to how many material parameters, and which set of combinations of those parameters, must be deemed appropriate may partially be addressed via the structural roots of a model, where the contained model parameters are ought to enjoy structural objectivity and meaning. Given the structural bases of the invariant forms of the model (1); i.e., models (3) and (4), the inclusion of the parameters $n$, $N$ and $\mu$ in (1) is structurally well-justified. Moreover, Destrade et al. [13] proposed that a strain energy function $W$ must at least be compatible with the results of the fourth-order weak nonlinear elasticity theory. It has been shown by Ogden [43] that, up to the fifth order, a strain energy function $W$ must include four independent constants. In this sense, therefore, the inclusion of four parameters in the model appears to be constitutively well-justified, and thus the model (1) satisfies these compatibility requirements with its four parameters (see Appendix A for a preliminary demonstration). Therefore, no extra terms seem to be required.

Second, a detailed analysis surrounding the numerical sensitivities of the fitting process when models with a high number of parameters are employed, and issues related to finding a unique optimum fit to the experimental data, has been presented by Ogden et al. [44]. That study identifies two distinct issues: (i) it is possible to obtain more than one optimal set of model parameters when using such models to fit the experimental data; and (ii) the optimal values of the model parameters, and the fitting process as a whole, become very sensitive to the numerical method being employed. Both these points give rise to issues of uniqueness and the objectivity of the quantified parameters. While the primary focus of that study was on the three- and four-term Ogden model, i.e., six and eight model parameters, its findings may well be extended to other models embodying such high numbers of model parameters. These results, together with the foregoing discussion by Yeoh [42], discourage any expansion of model (2) beyond the first term, i.e., model (1). Nevertheless, the general form (2) has been presented here for occasions where the use of additional terms may be deemed judicious.

Remark 1

It is in order, at this juncture, to bring to the attention of the reader an important point regarding the mathematical representations of the strain energy function $W$. Rivlin [45, 46] has demonstrated that invariant-based and principal stretches-based representations are essentially of the same kind, and subject to the necessary and sufficient conditions presented by Rivlin and Sawyers [47], the Valanis-Landel separable representation form is a special case of Rivlin’s invariant-based representation of the $W$ function. Indeed, given that [47]:

$$ \lambda _{i} = \frac{1}{\sqrt{3}} \left \{ I_{1} +2 \sqrt{\left ( I_{1}^{2} -3 I_{2} \right )} \cos \left [ \frac{1}{3} \left ( \varphi +2\pi i \right ) \right ] \right \}^{0.5},\quad i=1,2,3, $$

(17)

where:

$$ \varphi = \cos ^{-1} \frac{2 I_{1}^{3} -9 I_{1} I_{2} +27}{2 \left ( I_{1}^{2} -3 I_{2} \right )^{\frac{3}{2}}}, $$

the model (1) may also be re-written as an explicit function of the principal invariants. However, appreciably, such an undertaking will only result in a lengthy and complex mathematical representation, which in view of the simple principal stretch-based functional form that model (1) is represented by, is unnecessary. A true departure from these mathematical forms is achieved via the implicit elasticity framework devised by Rajagopal and co-workers [48–50]; however, this premise falls beyond the scope of the current work.

2.3 Parenthood

A key feature of the notion of comprehensiveness employed in this work, as discussed in §1, is that a comprehensive model is one that is an umbrella, or the parent, to the existing models, i.e., the existing models fall under the remit of the comprehensive model as a special sub-class. It can be verified that model (1), or equivalently the general from (2), is the parent model to many of the landmark strain energy functions in the current literature. Here we consider the following archetypal examples.

2.3.1 The Classical Neo-Hookean and Mooney-Rivlin Models

It may be observed from Eq. (1) that in limits when $N\rightarrow \infty$ or $n\rightarrow 1$, we will have:

$$ \lim _{N\rightarrow \infty} W = \lim _{n\rightarrow 1} W = \frac{1}{2} \mu \left ( \lambda _{1}^{\alpha} + \lambda _{2}^{\alpha} + \lambda _{3}^{\alpha} -3 \right ), $$

(18)

which, in the special case where $\alpha =2$ readily reduces to the neo-Hookean strain energy function. Similarly, if we take the two-term form of the model we will get:

$$ \lim _{N \rightarrow \infty} W = \lim _{n\rightarrow 1} W = \frac{1}{2} \mu _{1} \left ( \lambda _{1}^{\alpha _{1}} + \lambda _{2}^{\alpha _{1}} + \lambda _{3}^{\alpha _{1}} -3 \right ) + \frac{1}{2} \mu _{2} \left ( \lambda _{1}^{\alpha _{2}} + \lambda _{2}^{\alpha _{2}} + \lambda _{3}^{\alpha _{2}} -3 \right ), $$

(19)

where by setting $\alpha _{1} =2$ and $\alpha _{2} =-2$ the Mooney-Rivlin model is recovered.

2.3.2 The Gent Model

From the model in Eq. (1) we obtain in the limit $n\rightarrow \infty$ that:

$$ \lim _{n\rightarrow \infty} W =- \frac{1}{2} 3N\mu \ln \left ( - \frac{\lambda _{1}^{\alpha} + \lambda _{2}^{\alpha} + \lambda _{3}^{\alpha} -3N}{3N-3} \right ). $$

(20)

The $W$ function in Eq. (20) is of the type considered by Horgan and Murphy [41]. By noting from Eq. (15)₂ that in the limit $n\rightarrow \infty$:

(21)

and substituting (21) into (20) we get:

$$ \lim _{n\rightarrow \infty} W =-6 \frac{\left ( N-1 \right )}{\alpha ^{2}} \mu _{0} \ln \left ( - \frac{\lambda _{1}^{\alpha} + \lambda _{2}^{\alpha} + \lambda _{3}^{\alpha} -3N}{3N-3} \right ). $$

(22)

By setting the limiting chain extensibility parameter $J_{m}$ in the Gent model as: $J_{m} =3N-3$, Eq. (22) is re-written as:

$$ \lim _{n\rightarrow \infty} W =-2 \frac{J_{m}}{\alpha ^{2}} \mu _{0} \ln \left ( 1- \frac{\lambda _{1}^{\alpha} + \lambda _{2}^{\alpha} + \lambda _{3}^{\alpha} -3}{J_{m}} \right ), $$

(23)

which readily recovers the Gent model when $\alpha =2$.

2.3.3 The Ogden Model

On using the multi-term model (2) in the limit $N \rightarrow \infty$ we find:

$$ \lim _{N\rightarrow \infty} W = \sum _{i} \frac{\mu _{i}}{2} \left ( \lambda _{1}^{\alpha _{i}} + \lambda _{2}^{\alpha _{i}} + \lambda _{3}^{\alpha _{i}} -3 \right ). $$

(24)

The functional form of the Ogden model is represented by: $W= \sum _{p} \frac{\mu _{p}}{\alpha _{p}} ( \lambda _{1}^{\alpha _{p}} + \lambda _{2}^{\alpha _{p}} + \lambda _{3}^{\alpha _{p}} -3 )$, and thus by setting $\mu _{i} = \frac{2 \mu _{p}}{\alpha _{p}}$, model (2) reduces to the Ogden model in the limit $N\rightarrow \infty$.

2.3.4 The Nonaffine Tube Model

A class of models in the literature consider the entanglements, of an otherwise affine network of molecular chains, as a topological tube constraint; see, e.g., [26] and [51] for an overview. On considering a non-Gaussian statistical treatment of the network and the entanglements, and using the Padé approximation to the inverse Langevin function, Davidson and Goulbourne [26] provide a closed-form solution for the nonaffine tube model. That model, however, is recovered as a limit case of model (2). On using the three-term expansion of the model, and letting $n_{1} =3$, $n_{2}, n_{3} \rightarrow 1$, we find:

$$\begin{aligned} \lim _{n_{1} =3,~n_{2}, n_{3} \rightarrow 1} W &= \mu _{1} N \left [ \frac{1}{6N} \left ( \lambda _{1}^{\alpha _{1}} + \lambda _{2}^{\alpha _{1}} + \lambda _{3}^{\alpha _{1}} -3 \right ) - \ln \left ( \frac{\lambda _{1}^{\alpha _{1}} + \lambda _{2}^{\alpha _{1}} + \lambda _{3}^{\alpha _{1}} -3N}{3-3N} \right ) \right ] \\ &\quad {}+ \frac{1}{2} \mu _{2} \left ( \lambda _{1}^{\alpha _{2}} + \lambda _{2}^{\alpha _{2}} + \lambda _{3}^{\alpha _{2}} -3 \right ) + \frac{1}{2} \mu _{3} \left ( \lambda _{1}^{\alpha _{3}} + \lambda _{2}^{\alpha _{3}} + \lambda _{3}^{\alpha _{3}} -3 \right ). \end{aligned}$$

(25)

By setting $\alpha _{1} =2$, $\alpha _{2} =1$, $\alpha _{3} =-1$, $\mu _{2} = \mu _{3} = G_{e}$, and $\mu _{1} = G_{c}$, where $G_{e}$ and $G_{c}$ are model parameters designated by Davidson and Goulbourne [26], the nonaffine tube model is readily recovered; see Eq. (27) in [26]. By extending the forgoing analyses, it can be demonstrated that the proposed model recovers many other existing models in the literature; however we refrain from reproducing further analyses here.

2.4 Stress-Deformation Relationships

To conclude §2, here we derive the Cauchy stress-deformation relationships on using model (1) for the classical boundary value problems of uniaxial, equi-biaxial, pure and simple shear deformations, which we will employ in the next Section to demonstrate the fitting capability of the model to the considered extant experimental datasets. Using the principal stretches $\lambda _{i}$, we note that the principal Cauchy stresses $T_{j}$, $j=1,2,3$, for isotropic incompressible materials under large elastic deformations is computed via:

$$ T_{j} = \lambda _{j} \frac{\partial W}{\partial \lambda _{j}} -p, $$

(26)

where $p$ is the arbitrary hydrostatic pressure enforcing the condition of incompressibility.

2.4.1 Uniaxial Deformation

Under uniaxial deformation, the principal stretches may be given by:

$$ \lambda _{1} =\lambda ,\qquad \lambda _{2} = \lambda _{3} = \lambda ^{-0.5}, $$

(27)

which, on using model (1) and Eq. (26) yields the following $T-\lambda$ relationship:

$$ T_{\mathit{uni}} = \frac{\mu \alpha}{2n} \frac{\lambda ^{\alpha} +2 \lambda ^{-0.5\alpha} -3nN}{\lambda ^{\alpha} +2 \lambda ^{-0.5\alpha} -3N} \left ( \lambda ^{\alpha} - \frac{1}{\lambda ^{0.5\alpha}} \right ). $$

(28)

2.4.2 Equi-Biaxial Deformation

For the equi-biaxial deformation the principal stretches are:

$$ \lambda _{1} = \lambda _{2} =\lambda ,\qquad \lambda _{3} = \lambda ^{-2}, $$

(29)

which result in the following $T-\lambda$ relationship for model (1):

$$ T_{eq-bi} = \frac{\mu \alpha}{2n} \frac{2 \lambda ^{\alpha} + \lambda ^{-2\alpha} -3nN}{2 \lambda ^{\alpha} + \lambda ^{-2\alpha} -3N} \left ( \lambda ^{\alpha} - \frac{1}{\lambda ^{2\alpha}} \right ). $$

(30)

2.4.3 Pure Shear Deformation

In the case of pure shear deformation, the principal stretches are given by:

$$ \lambda _{1} =\lambda ,\qquad \lambda _{2} =1,\qquad \lambda _{3} = \lambda ^{-1}. $$

(31)

Accordingly, the $T-\lambda$ relationship using model (1) becomes as follows:

$$ T_{ps} = \frac{\mu \alpha}{2n} \frac{\lambda ^{\alpha} +1+ \lambda ^{-\alpha} -3nN}{\lambda ^{\alpha} +1+ \lambda ^{-\alpha} -3N} \left ( \lambda ^{\alpha} - \frac{1}{\lambda ^{\alpha}} \right ). $$

(32)

2.4.4 Simple Shear Deformation

The $T-\gamma$ relationship for the simple shear deformation using model (1) was presented in §2.2, Eqs. (10) to (12), and are summarised here for the convenience of the reader. The principal stretches in this deformation are:

$$ \lambda _{1} =\lambda = \frac{\gamma}{2} + \sqrt{1+ \frac{\gamma ^{2}}{4}},\qquad \lambda _{2} = \lambda ^{-1} =- \frac{\gamma}{2} + \sqrt{1+ \frac{\gamma ^{2}}{4}}, \qquad \lambda _{3} =1, $$

(33)

with $\gamma$ being the amount of shear, which yield the following $T-\gamma$ relationship:

$$ T_{ss} = \frac{\mu \alpha}{2n} \gamma \frac{\lambda ^{\alpha} + \lambda ^{-\alpha} +1-3nN}{\lambda ^{\alpha} + \lambda ^{-\alpha} +1-3N} \left ( \frac{\lambda ^{\alpha} - \lambda ^{-\alpha}}{\lambda ^{2} - \lambda ^{-2}} \right ). $$

(34)

These relationships will be used in the next section for fitting with the experimental data.

3 Correlation with the Experimental Data

Of the three aspects of the notion of comprehensiveness discussed in §1, the third, namely the parenthood aspect, was demonstrated in the previous Section for our proposed model. The other two aspects; i.e., the ability of the model to capture multiple deformations of the subject specimen via simultaneous fitting with a single set of model parameter values, and the capability for suitable application to various types of rubber-like materials, will be put to test in this section.

To this end, we consider extant experimental datasets pertaining to four distinct types of rubber-like materials including (vulcanised) natural rubber, filled rubber, cross-linked (PAAm) hydrogels and (extremely) soft tissue specimens. The natural rubber dataset is due to the canonical study of Treloar [18], the filled rubber dataset is from a commercial specimen developed by the tyre manufacturing company Michelin due to Lahellec et al. [19], the hydrogel dataset is due to Yohsuke et al. [20] and the soft tissue dataset is from human brain (cortex) samples reported by Budday et al. [21].

The reason for considering these four datasets here, as archetypical examples, is as follows. The Treloar [18] dataset has become the barometer for gauging the basic performance of a model in relation to rubber elasticity applications. In addition, since many studies, including the reviews by Marckmann and Verron [14] and Dal et al. [15], have used this dataset in relation to the assessment of various models, comparisons between the results of this study and those from other models are straightforward to draw. However, natural unfilled rubbers have a distinctly different behaviour to their filled-rubber counterparts [15, 52], and models that can suitably capture the behaviour of both types of rubbers are rare in the literature. Therefore, the dataset due to Lahellec et al. [19] is additionally considered in order to provide a platform to showcase the capability of the model for application to both unfilled and filled rubbers. Hydrogels are very soft elastomers that undergo large deformations and exhibit a different mechanical behaviour compared with rubbery materials. Given the extensive application of hydrogels in, e.g., biomaterials science and regenerative medicine, here we consider the dataset by Yohsuke et al. [20] on cross-linked PAAm hydrogel specimens, reporting on the uniaxial, equi-biaxial and pure shear deformations. Finally, the brain tissue has proved to be challenging for the existing models to provide a suitable prediction of its mechanical behaviour; see, e.g., [37] and [53] for a discussion on the shortcomings of the existing models in this regard. The consensus appears to be on the application of the Ogden model to the brain tissue biomechanics. However, as shown at length in [16] and [36], the one-term and higher-term Ogden models produce ill-posed results in such applications including the loss of convexity of the iso-energy plots in the $\left ( \lambda _{1}, \lambda _{2} \right )$ plane, and mis-prediction of the direction of concavity in stress-strain curves. Therefore, the brain tissue dataset appears to be a well-motivated choice for challenging the capability of the proposed model. These four datasets together provide a solid basis for demonstrating the comprehensive applicability of model (1) to a wide range of rubber-like materials.

Accordingly, the stress-deformation relationships in Eqs. (28), (30), (32) and (34) are simultaneously fitted to the relevant deformation modes from each aforementioned datasets. The fitting procedure employed is similar to our previous undertakings. To characterise the model parameters, optimisation is sought by fitting the $T-\lambda$ (and/or $T-\gamma$) relationships simultaneously to the associated deformation datasets. The best fit is achieved by minimising the residual sum of squares (RSS) function defined as: $\mathrm{RSS} = \sum _{k} \left ( T^{\mathit{model}} - T^{\mathit{experiment}} \right )_{k}^{2}$, where $k$ is the number of data points. The minimisation is performed via an in-house developed code in MATLAB^®, using the genetic algorithm (GA) function. The coefficient of determination R² values are reported as a measure of the goodness of the obtained fits. The presented relative error (%) in the plots is calculated as: $\left \vert \frac{T^{\mathit{model}} - T^{\mathit{experiment}}}{T^{\mathit{experiment}}} \right \vert \times 100$. In the interest of brevity, we present all the obtained values of the model parameters from the foregoing curve-fitting campaign in a single table, namely Table 1.

Table 1 The values of the model parameters obtained via simultaneous fitting of model (1) to the considered datasets

The plots in Fig. 1 demonstrate the modelling results for the Treloar [18] dataset.¹ The proposed model (1) captures the deformations favourably, with typically low relative errors (Fig. 1b). In order to give the reader a quantitative feel of the model performance, the relative errors arising from the application of the three-term Ogden model (with six model parameters) have also been provided (Fig. 1c). It is of interest to note that except for the equi-biaxial data, the relative errors resulting from the application of the (three-term) Ogden model are typically higher than those of model (1), particularly towards the larger levels of deformation (indicated in Figs. 1b and 1c). Therefore, it is observed that with fewer model parameters, the proposed model provides more favourable fits to the data (e.g., uniaxial and pure shear). The tabulated numerical data points for this dataset have been provided in a previous study (see, e.g., [24]).

Fig. 1

Modelling results for the Treloar [18] data using model (1): (a) the fits provided by the model via simultaneous fitting to uniaxial, equi-biaxial and pure shear datasets; (b) the ensuing relative errors. (c) The relative errors arising from the application of the three-term Ogden model as reported in [5] with $\mu _{1} =0.62\text{ MPa}$, $\mu _{2} =0.001\text{ MPa}$, $\mu _{3} =-0.01\text{ MPa}$, $\alpha _{1} =1.3$ [-], $\alpha _{2} =5$ [-] and $\alpha _{3} =-2$ [-]

Next, we present the results obtained via simultaneous fitting of model (1) to the uniaxial and simple shear dataset of Lahellec et al. [19]. This dataset pertains to a commercial filled rubber specimen developed by the Michelin tyre manufacturing company. It illustrates the typical apparent ‘shear-softening’ behaviour pertinent to the filled rubbers. Many, if not most, of the existing models in the literature do not exhibit the capability to fit to this dataset (see, e.g., [12, 19]), and datasets from other elastomers (e.g., silicone polymers [34]) that display the same stress-deformation characteristics. Indeed, the only two models that have been successfully applied to this dataset in the literature are that of Lopez-Pamies [12] and the invariant form of the proposed model, Eq. (4), employed by Anssari-Benam and Horgan [17]. Figure 2 illustrates the favourable application of the proposed model (1) to this dataset. For comparison, the relative errors arising as a result of the application of the (two-term) Lopez-Pamies model (with four parameters) to this dataset, as given in [12], has also been presented (Fig. 2c). While the Lopez-Pamies model provides relatively lower levels of error for the uniaxial dataset, the relative errors for simple shear deformation are considerably higher than those provided by model (1). The tabulated numerical data points for this dataset have been provided in a previous study (see, e.g., [17]).

Fig. 2

Modelling results for the Lahellec et al. [19] dataset using model (1): (a) the fits provided by the model via simultaneous fitting to uniaxial and simple shear datasets; (b) the ensuing relative errors. (c) The relative errors arising from the application of the two-term Lopez-Pamies as reported in [12] with $\mu _{1} =2.23\text{ MPa}$, $\mu _{2} =1.92\text{ MPa}$, $\alpha _{1} =0.6$ [-] and $\alpha _{2} =-68.73$ [-]

In Fig. 3 we present the fitting results of the model (1) to the dataset due to Yohsuke et al. [20] for cross-linked PAAm hydrogels under uniaxial, equi-biaxial and pure shear deformations. The results illustrate that the model successfully captures the deformation behaviour of the specimens, with relative errors typically below 6%. The tabulated numerical data points for this dataset is provided in Appendix B, Table 2.

Fig. 3

Modelling results for the Yohsuke et al. [20] data using model (1): (a) the fits provided by the model via simultaneous fitting to uniaxial, equi-biaxial and pure shear datasets; (b) the ensuing relative errors

Finally, we present the application of model (1) to the deformation dataset of the brain (cortex) tissue due to Budday et al. [21]. A particular challenge in modelling the deformation of the human brain tissue, also reflected in this dataset, is the asymmetry observed in the experimental compression-tension data, as well as the highly nonlinear simple shear behaviour of the tissue [21, 37–39, 53]. Figure 4 demonstrates the favourable application of model (1) to this dataset – see the plots in panel (a). The tabulated numerical data points have been provided in a previous study (see, e.g., [36]). Currently, the literature suggests that the Ogden model is one of the few strain energy functions capable of capturing these behaviours (see, e.g., [21, 37–39, 53]). For comparison, the modelling results obtained on using one-, two- and three-term Ogden models, $W= \sum _{p} \frac{\mu _{p}}{\alpha _{p}} \left ( \lambda _{1}^{\alpha _{p}} + \lambda _{2}^{\alpha _{p}} + \lambda _{3}^{\alpha _{p}} -3 \right )$, are also shown (plots in panels (b) to (d), respectively).

Fig. 4

Modelling results for the human brain tissue dataset due to Budday et al. [21] using: (a) model (1); (b) one-term ($\mu = -0.15\text{ kPa}$ and $\alpha = -19.12$ [-]); (c) two-term ($\mu _{1} = -0.10\text{ kPa}$, $\alpha _{1} = -22.56$ [-], $\mu _{2} = 0.08\text{ kPa}$ and $\alpha _{2} = 7.51$ [-]); and (d) three-term ($\mu _{1} = -3.12$ [kPa], $\mu _{2} = 1.24$ [kPa], $\mu _{3} = 10$ [kPa], $\alpha _{1} = -8.06$ [-], $\alpha _{2} = 6.37$ [-] and $\alpha _{3} = -3.06$ [-]) Ogden models

While higher-term Ogden models appear to improve the relative errors of the fits, the improvement offered by say the three-term (six parameters) Ogden model over model (1) is marginal. However, and perhaps more fundamental, the plots in Fig. 5 show that all ensuing modelling results obtained via using the Ogden model for this dataset suffer from the ill-posed effect of the loss of convexity of iso-energy plots in the principal stretches $\left ( \lambda _{1}, \lambda _{2} \right )$ plane. By contrast, these plots for model (1) remain convex over the domain of deformation. This dataset therefore exemplifies that the implication of choosing a model for application to the deformation of various soft solids is beyond simply the apparent improved fit or the number of model parameters.

Fig. 5

The iso-energy plots of: (a) the proposed model (1); (b) one-term; (c) two-term; and (d) three-term Ogden models, for the brain deformation dataset [21]. Note that model (1) is not defined beyond the domain of deformation shown in the plot

The foregoing exemplar datasets considered in this section therefore indicate that model (1) provides a reliable degree of universality for application to various rubber-like materials, including natural filled and unfilled rubbers, polymer gels and (extremely) soft tissues such as the brain.

4 Some Points of Discussion

The capability of model (1) in describing the various modes of deformation of the specimens considered in §3 with a single set of material parameter values, together with the ability of the model to capture the deformation of a variety of rubber-like materials with distinct mechanical behaviours (including natural unfilled and filled rubbers and soft tissues), speaks to the degree of universality of the proposed model. The fact that the functional form of the model is also the parent to many of the existing models in the literature with different mathematical types including the Mooney-Rivlin $W \left ( I_{1}, I_{2} \right )$ form, the Gent-like limiting chain extensibility models, and the separable form of the principal stretches such as the Ogden model, provides further reassurance. A different notion of universality, however, manifests itself through the universal relationships, which hold true for the deformations undergone by the considered class of materials irrespective of the choice of $W$. Local universal relationships can be derived from the coaxiality of Cauchy stress $\mathbf{T}$ and the left Cauchy-Green deformation $\mathbf{B}$ tensors; i.e., $\mathbf{TB} = \mathbf{BT}$, as shown, for example, by the seminal work of Saccomandi [54]. For a $W$ function to satisfy those universal relationships, many studies have shown, via experimental observations [55, 56] or theoretical derivations [54, 57, 58], that it must embody an $I_{2}$ term in its functional form. See also [51] for a review of the role of $I_{2}$ in modelling nonlinear elasticity. Note that the said dependence on $I_{2}$ is a necessary condition, but is not sufficient alone; i.e., not all functional forms of dependence on $I_{2}$ will necessarily satisfy the universal relationships. As Eq. (17) indicates, model (1) is a general function of the invariants $I_{1}$ and $I_{2}$, and as such checks the necessary condition to satisfy the universal relationships.

While satisfying the foregoing necessary condition does not automatically guarantee that model (1) will in general satisfy the universal relationships, it is worth noting that not many models in the literature that have successfully been applied to the deformation of both unfilled and filled rubbers indeed satisfy this necessary condition. Some examples in this regard include the seminal model of Lopez-Pamies [12], also used in [34], and that in Eq. (4) used in [17], which both are $I_{1}$-based models and therefore all the usual shortcomings associated with the generalised neo-Hookean strain energy functions may also be extended to those two models. The former is also a purely phenomenological model, whereas the parameters in model (1), except for $\alpha$, all ($\mu$, $N$ and $n$) enjoy a direct structural and mathematical underpinning – see §2.1. These advantages therefore favour the application of the proposed model herein to the mechanics of unfilled and filled rubbers. The favourable application of the invariant-based sub-set form of model (1); i.e., the model in Eq. (4), to the deformation of various other elastomers has been recently shown by Anssari-Benam and Horgan [17]. The proposed model (1) provides even more improved results; however, for concision those results are not reproduced here as they only serve to reaffirm the trend already demonstrated in §3 with the considered datasets.

There is an important implication associated with the generic non-separable functional form of model (1). As discussed in detail by Ogden [59], pp. 492-494, the data by Jones and Treloar [60] provide some experimental justification for considering a separable form of $W$. Jones and Treloar [60] performed pure shear deformation tests at various fixed $\lambda _{2}$ values, up to $\lambda _{2} =2.62$. Their results, as analysed by Ogden [59], show that the shapes of the stress-stretch curves remain invariant to the value of $\lambda _{2}$; the curves only undergo a vertical translation by the change in $\lambda _{2}$. This feature can, of course, be captured via a separable form of $W$, as it will have the following form: $W \left ( \lambda _{1}, \lambda _{2}, \lambda _{3} \right ) =w \left ( \lambda _{1} \right ) +w \left ( \lambda _{2} \right ) +w \left ( \lambda _{3} \right )$. However, it is interesting to note the results of Vangerko and Treloar [22], where they extended the work of Jones and Treloar [60] to higher levels of $\lambda _{2}$, e.g., up to $\lambda _{2} =3.38$. Vangerko and Treloar’s results [22] clearly demonstrate deviations from the vertical translation trend observed in the shape of the stress-stretch curves in [60], at higher levels of $\lambda _{2}$. For capturing this behaviour, therefore, a separable form of $W$ is insufficient. By contrast, the non-separable function of model (1) circumvents such a limitation. The plots in Fig. 6a show the simultaneous fitting of model (1) to the reported dataset in [22] for a rubber specimen with 5% sulphur. The experimental data in Fig. 6 illustrate that at higher levels of $\lambda _{2}$, the stress-stretch curves are not vertically translated. The favourable application of model (1) to the data is of note. For comparison with a separable model, the modelling results using a three-term Ogden model are also presented in Fig. 6b. The shortcoming of this separable $W$ to model the behaviour at $\lambda _{2} =3.38$ is evident. The tabulated numerical data points are provided in Appendix B, Table 3.

Fig. 6

Modelling results using the dataset due to Vangerko and Treloar [22] for a rubber specimen with 5% of sulphur, at various fixed $\lambda _{2}$ values via: (a) model (1) with $\mu = 0.59\text{ MPa}$, $N = 7.21$ [-], $\alpha = 1.77$ [-] and $n = 1.17$ [-]; and (b) the three-term Ogden model with $\mu _{1} = -0.27$ [MPa], $\mu _{2} = 0.58$ [MPa], $\mu _{3} = -0.49$ [MPa], $\alpha _{1} = -1.01$ [-], $\alpha _{2} = 3.18$ [-] and $\alpha _{3} = 3.17$ [-]. The data has been presented as reported in [22], i.e., $T_{1} - T_{2}$ versus $\lambda _{1}$. The symbols for the experimental data are also in coordination with the original plot [22]. R² values for all fits in excess of 0.98 except for the Ogden model at $\lambda _{2} =3.38$ for which R$^{2} = 0.93$

It is also important to highlight that the loss of convexity in the iso-energy plots for a strain energy function implies the breakdown of the one-to-one correspondence in the stress-deformation relationship and the presence of hysteresis effects [59], and may lead to undesirable material and numerical instabilities (see, e.g., [61, 62]). As the brain tissue dataset in §3 demonstrated, not all models in the literature are capable of providing a good fit while maintaining the iso-energy plots convex in the $\left ( \lambda _{1}, \lambda _{2} \right )$ plane. Judging by the considered datasets, model (1) shows no vulnerability to these deficiencies.²

5 Concluding Remarks

On considering a general non-separable form of the strain energy function $W$ in terms of the principal starches $\lambda _{i}$, a structurally motivated $W$ function was devised in this study for application to the finite deformation of incompressible isotropic rubber-like materials. The model, presented in Eq. (1), contains four constitutive parameters, namely $\mu$, $N$, $n$ and $\alpha$, which enjoy structural or mathematical underpinnings. The former three parameters are directly related to the non-Gaussian statistical treatment of the molecular chains, while the latter one enforces the algebraic requirement that the powers of the principal starches $\lambda _{i}$ needn’t be restricted to even values. Model (1), or its general multi-term form (2), is the parent model to many of the existing landmark models in the literature from distinct types of mathematical families, including the Mooney-Rivlin $W \left ( I_{1}, I_{2} \right )$, Gent-like limiting chain extensibility, and the Ogden separable form of the principal stretches model types. No other model in the literature has thus far been shown to be the umbrella to all these different types of existing models. The proposed model favourably captures the mechanical behaviour of various types of rubber-like materials with distinctly discernible deformation characteristics, including natural unfilled and filled rubbers, hydrogels and (extremely) soft biological tissues. The model predicts the constitutive mechanical behaviour of each specimen under various modes of deformation with a single set of model parameter values. All these features point to one conclusion: the proposed model (1) in this work portends a comprehensive mathematical representation of the observed mechanical behaviour of isotropic incompressible rubber-like materials, and provides a more accurate prediction of their deformations. Based on these results, the extension of the model to incorporate compressibility, anisotropy and rate-effects may be merited.

Appendices

Appendix A: Compatibility with Fifth Order Elasticity

The contents of this appendix emerged from stimulating discussions with Professor Michel Destrade who subsequently encouraged me to derive the relationships presented in the sequel. For simplicity, and without loss of generality, let us consider the simple tension deformation where $\lambda _{1} =\lambda$ and $\lambda _{2} = \lambda _{3} = \lambda ^{-0.5}$. The strain energy function $W$ in Eq. (1) therefore takes the following form:

$$ W= \frac{3 \left ( n-1 \right )}{2n} \mu N \left [ \frac{1}{3N \left ( n-1 \right )} \left ( \lambda ^{\alpha} +2 \lambda ^{-0.5\alpha} -3 \right ) - \ln \left ( \frac{\lambda ^{\alpha} +2 \lambda ^{-0.5\alpha} -3N}{3-3N} \right ) \right ]. $$

(35)

By noting that $\lambda =1+e$, the function $W$ in Eq. (35) may be expanded to the fifth order in $e$ using the Taylor series expansion around zero as:

$$ W= \frac{3}{2} \mu _{0} e^{2} +\mathcal{A} e^{3} +\mathcal{D} e^{4} +\mathcal{G} e^{5}, $$

(36)

where $\mu _{0}$ is the infinitesimal shear modulus, and:

$$\begin{aligned} \begin{aligned}[c] &\mathcal{A} = \frac{1}{4} \mu _{0} \left ( \alpha -6 \right ),\\ &\begin{aligned}[c] \mathcal{D}= \frac{\mu _{0}}{32 \left ( N-1 \right ) \left ( nN-1 \right )} &\left [ \left ( 3 \alpha ^{2} -12 \alpha +44 \right ) \left ( N^{2} n+1 \right ) + \left ( 3 \alpha ^{2} +12 \alpha -44 \right ) \left ( Nn+N \right ) \right . \\ &\left . -12 \alpha ^{2} N \right ], \end{aligned} \\ &\begin{aligned}[c] \mathcal{G} = \frac{\mu _{0}}{64 \left ( N-1 \right ) \left ( nN-1 \right )} &\left [ \left ( \alpha ^{3} -12 \alpha ^{2} +28\alpha -80 \right ) \left ( N^{2} n+1 \right ) \right . \\ &\left . + \left ( 3 \alpha ^{3} -12 \alpha ^{2} -28\alpha +80 \right ) \left ( Nn+N \right ) -8 \left ( \alpha ^{3} -6 \alpha ^{2} \right ) N \right ]. \end{aligned} \end{aligned} \end{aligned}$$

(37)

Note that $\mathcal{A}$, $\mathcal{D}$ and $\mathcal{G}$ in Eq. (37) are distinct from the parameters traditionally used in fourth-order incompressible elasticity as in, e.g., [13, 63, 64]. Similarly, by expanding $T_{\mathit{uni}}$ in Eq. (28) in $e$ to the fourth order we find:

$$ T = 3 \mu _{0} e+3 \left ( \mu _{0} + \mathcal{A} \right ) e^{2} + \left ( 3 \mathcal{A} +4 \mathcal{D} \right ) e^{3} + \left ( 4 \mathcal{D} +5 \mathcal{G} \right ) e^{4} +\mathcal{O} \left ( e^{5} \right ). $$

(38)

This example illustrates that there is a one-to-one correspondence between the model parameters $\mu$, $n$, $N$, $\alpha$ and $\mu _{0}$, $\mathcal{A}$, $\mathcal{D}$ and $\mathcal{G}$, which in principle proves the compatibility of model (1) with fifth order elasticity.

Appendix B: The Tabulated Experimental Datapoints

Table 2 The tabulated dataset of Yohsuke et al. [20] for cross-linked poly(acrylamide) (PAAm) hydrogel specimens.

Table 3 The tabulated dataset of Vangerko and Treloar [22] for a rubber specimen with 5% of sulphur.