Trajectory Optimization and Multiple-Sliding-Surface Terminal Guidance in the Lifting Atmospheric Reentry

Abstract

In this paper, the problem of guiding a vehicle from the entry interface to the ground is addressed. The Space Shuttle Orbiter is assumed as the reference vehicle and its aerodynamics data are interpolated to properly simulate its dynamics. The transatmospheric guidance is based on an open-loop optimal strategy which minimizes the total heat input absorbed by the vehicle while satisfying all the constraints. Instead, the terminal phase guidance is achieved through a multiple-sliding-surface technique, which is able to drive the vehicle toward a specified landing point with desired heading angle and vertical velocity at touchdown, even in the presence of nonnominal initial conditions. The terminal guidance strategy is successfully tested through a Monte Carlo campaign, in the presence of stochastic winds and wide dispersions on the initial conditions at the terminal area energy management, in more critical scenarios with respect to the orbiter safety criteria.

1 Introduction

The design of reusable vehicles, able to successfully achieve safe planetary reentry, requires a reliable and effective guidance architecture. Unsurprisingly, the interest in guidance and control technologies for atmospheric reentry and landing of winged vehicles has increased, as the flexibility and controllability of the reentry trajectory can be enhanced through the use of lifting bodies, resulting in a greater accuracy in the landing point. However, this introduces a further sensitivity to the environmental conditions, such as atmospheric perturbations, as well as non-critical failures in the aerodynamic control surfaces.

Several space programs are foreseeing the use of lifting vehicles, like the European Space Rider [1] and the Reusability Flight Experiment (ReFEx) by DLR [2], as well as the Dream Chaser by Sierra Nevada Corporation, which is based on a philosophy similar to that of the Space Shuttle Orbiter and will be tested as a transport vehicle toward the International Space Station [3]. Furthermore, the reentry trajectory of blunt bodies with modest aerodynamic efficiency (if compared with the typical values obtained in commercial aviation) can be aerodynamically controlled, as for NASA Orion vehicle [4]. During the atmospheric arc, however, different sources of dispersions may deviate the vehicle from its nominal trajectory. Therefore, real-time generation of trajectory represents an asset for a terminal descent guidance algorithm, for the purpose of guaranteeing safe landing even in the presence of nonnominal conditions and dispersions due to the preceding transatmospheric phase.

The early studies about the reentry trajectories of lifting vehicles emerge through the works by Frostic and Vinh [5, 6], Broglio [7] and Chapman [8], who reduced the reentry problem to a single second-order nonlinear ordinary differential equation. The guidance and control strategy of the Space Shuttle relied on the modulation of the bank angle to follow a pre-computed reference drag profile, which can be related to the downrange flown by the vehicle; thus, it could only account for small deviations from the nominal conditions [9]. Mease and Kremer [10] revisited the Shuttle reentry guidance, using nonlinear geometric methods. Later on, Benito and Mease [11] developed and applied a new controller based on model prediction, where the bank angle is modulated to minimize an effective cost function that accounts for the error in drag acceleration and downrange. Nonlinear predictive control was employed by Minwen and Dayi to generate skip entry trajectories for low lift-to-drag vehicles [12], though assuming constant lift and drag coefficients. Most recently, Lu [13] considered a unified guidance methodology based on a predictor-corrector algorithm, for vehicles with different aerodynamic efficiency, while satisfying the boundaries on the thermal flux and load factor. All these works focus on the development of a suitable controller capable of addressing control saturation and inequality entry constraints, given the limited control authority during the early atmospheric phase; however, the problem of interfacing the reentry guidance with a suitable terminal guidance algorithm is not fully investigated. As a consequence, the development of an integrated entry and landing guidance algorithm for a realistic vehicle is still of interest.

Instead, a more limited number of papers addressed the terminal descent and landing, which is traveled after the terminal area energy management (TAEM) interface. Kluever [14] developed a guidance scheme for an unpowered vehicle with limited normal acceleration capabilities, in a simplified bidimensional model. Bollino et al. [15] employed a pseudospectral-based algorithm for optimal feedback guidance of spacecraft from the entry interface until the final approach, although the aerodynamic modeling is approximated through analytical expressions. A pseudospectral method was also investigated by Fahroo and Doman [16] in mission scenarios with actuation failures, but still in a bidimensional framework. Finally, reinforcement learning was used for autonomous guidance algorithms for precise landing [17]. Recently, sliding mode control was proposed as an effective nonlinear approach to yield real-time feedback control laws able to drive an unpowered space vehicle toward a specified landing site [9, 18].

In this work, an open-loop optimal guidance is developed for the transatmospheric arc, capable of minimizing the total heat input while driving the vehicle toward the TAEM. The Space Shuttle Orbiter is taken as the reference vehicle and an analytical method is proposed to keep the maximum thermic flux below the safety limit, while accounting for the saturation on the control variables. Finally, the multiple-sliding-surface guidance is employed to drive the vehicle from the TAEM to the landing point, with accurate aerodynamic modeling, including stochastic winds and large dispersions on the initial values of the state and control variables. In a previous work, sliding-mode control was already employed as a nonlinear approach to yield real-time feedback guidance laws in an accurate dynamic framework, including winds and large deviations from the initial trajectory variables [19]. In this study, significant improvements are developed with respect to the previous research:

• sliding-mode guidance is tested for a longer time period (i.e., from the TAEM to ground);

• the aerodynamic modeling is based on real data rather than approximate analytical expressions;

• the saturation of the control variables is accounted inside the expression of the control input, so that only feasible trajectories are generated;

• the guidance gains are updated through an adaptive strategy, allowing further extension of the capability of the algorithm.

Moreover, previous studies on multiple-sliding-surface guidance relied on largely simplified dynamics, with no apparent forces nor wind modeling, as well as approximate aerodynamic coefficients [9, 18]. In short, this research has the following objectives: (i) develop and apply an open-loop optimal guidance law to drive the Space Shuttle Orbiter from the entry interface to the TAEM, while satisfying all the constraints and minimizing the total heat; (ii) develop and apply a multiple-sliding-surface terminal guidance law to a vehicle with a realistic aerodynamic modeling; (iii) test the effectiveness of the terminal descent guidance to achieve safe landing despite the initial dispersions and winds.

2 Reentry Dynamics

The reentry vehicle is modeled as a 3-degrees-of-freedom (3-DOF) lifting body and the position of the centre of mass is identified by a set of three spherical coordinates $(\textit{r},\lambda _g,\varphi )$, where $\textit{r}$ is the instantaneous radius, $\lambda _g$ the geographical longitude and $\varphi$ the latitude. The additional variables are given by the relative velocity with respect to the Earth surface $\textit{v}_r$, the heading angle $\zeta _r$ and the flight path angle $\gamma _r$. The Space Shuttle Orbiter is taken as the reference vehicle for numerical simulations, as there is plenty of available data in literature about its aerodynamic characteristics and mission profile. Therefore, it represents a suitable benchmark for novel guidance algorithms. Table 1 collects the reference data for the Space Shuttle Orbiter, which will be later employed for the reentry simulations.

Table 1 Space Shuttle Orbiter: reference values [20, 21]

2.1 Reference Frames

Several reference frames must be defined to describe the reentry dynamics. In the following, the notation ${{\textbf {R}}}_j (\vartheta)\;(j=1,2,3)$ denotes an elementary rotation about axis j by angle $\vartheta$:

• The Earth-Centered-Inertial frame (ECI) $(\hat{{\varvec{c}}}_1,\hat{{\varvec{c}}}_2,\hat{{\varvec{c}}}_3)$ has unit vector $\hat{{\varvec{c}}}_3$ aligned with the Earth rotational axis, while $\hat{{\varvec{c}}}_1$ points toward the vernal axis.

• The Earth-Centered Earth-Fixed frame (ECEF) $(\hat{{\varvec{i}}},\hat{{\varvec{j}}},\hat{{\varvec{k}}})$ is rigidly attached to the Earth. The unit vector $\hat{{\varvec{i}}}$ intersects the Greenwich reference meridian at all times, while $\hat{{\varvec{k}}}$ is aligned with the Earth rotational axis. The angle between the unit vector $\hat{{\varvec{i}}}$ and the vernal axis at time t is given by

  $$\begin{aligned} \theta _G(t) = \theta _G(t^*) + \omega _e(t-t^*), \end{aligned}$$

  (1)

  where $t^*$ is a generic time instant (for simplicity, $\theta _G(t^*)=0$ is assumed), while $\underrightarrow{\varvec{\omega }_e}=\omega _e \hat{{{\varvec{k}}}}$ is the Earth rotational velocity, assumed as constant. The ECEF-frame is obtained from the ECI-frame through a single rotation,

  $$\begin{aligned} \left[ \begin{array}{c} \hat{{{\varvec{i}}}} \\ \hat{{{\varvec{j}}}} \\ \hat{{{\varvec{k}}}} \end{array} \right] = {{\textbf {R}}}_3(\theta _G) \left[ \begin{array}{c} \hat{{{\varvec{c}}}}_1 \\ \hat{{{\varvec{c}}}}_2 \\ \hat{{{\varvec{c}}}}_3 \end{array} \right] . \end{aligned}$$

  (2)

• The Auxiliary Landing frame (AL) $(\hat{{{\varvec{r}}}}_L, \hat{{{\varvec{E}}}}_L, \hat{{{\varvec{N}}}}_L$) has origin at the landing point. The unit vector $\hat{{{\varvec{r}}}}_L$ is directed upward along the vertical direction, while $\hat{{{\varvec{E}}}}_L$ and $\hat{{{\varvec{N}}}}_L$ point toward the local East and North direction, respectively. If $\varphi _{rwy}$ and $\lambda _{rwy}$ denote the geographical latitude and longitude at the landing point, then

  $$\begin{aligned} \left[ \begin{array}{c} \hat{{{\varvec{r}}}}_L \\ \hat{{{\varvec{E}}}}_L \\ \hat{{{\varvec{N}}}}_L \end{array} \right] = {{\textbf {R}}}_2(-\varphi _{rwy}) {{\textbf {R}}}_3(\lambda _{rwy}) \left[ \begin{array}{c} \hat{{{\varvec{i}}}} \\ \hat{{{\varvec{j}}}} \\ \hat{{{\varvec{k}}}} \end{array} \right] . \end{aligned}$$

  (3)

  In this study, the origin of the AL-frame is placed at the threshold of the NASA Shuttle Landing Facility, identified by the following coordinates:

  $$\begin{aligned} \varphi _{rwy}= 28.6328^{\circ } \ \text {N}, \ \ \ \ \ \ \ \lambda _{rwy}= 80.7060^{\circ } \ \text {W}. \end{aligned}$$

  (4)

• The Local Horizontal frame (LH) $(\hat{{{\varvec{r}}}}, \hat{{{\varvec{E}}}}, \hat{{{\varvec{N}}}})$ is attached to the reentry vehicle. The unit vector $\hat{{{\varvec{r}}}}$ is aligned with the instantaneous position vector$\underrightarrow{{{\varvec{r}}}}$, while $\hat{{{\varvec{E}}}}$ and $\hat{{{\varvec{N}}}}$ are directed, respectively, along the East and North direction. The LH-frame can be obtained from the ECEF-frame through the sequence of two elementary rotations,

  $$\begin{aligned} \left[ \begin{array}{c} \hat{{{\varvec{r}}}} \\ \hat{{{\varvec{E}}}} \\ \hat{{{\varvec{N}}}} \end{array} \right] = {{\textbf {R}}}_2(-\varphi ) {{\textbf {R}}}_3(\lambda _g) \left[ \begin{array}{c} \hat{{{\varvec{i}}}} \\ \hat{{{\varvec{j}}}} \\ \hat{{{\varvec{k}}}} \end{array} \right] . \end{aligned}$$

  (5)

• The Auxiliary Orbital frame (AO) $(\hat{{{\varvec{r}}}}, \hat{\varvec{\theta }}_r, \hat{{{\varvec{h}}}}_r)$ is defined with reference to the vehicle relative velocity,

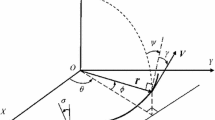
  $$\begin{aligned} \underrightarrow{{{\varvec{v}}}_r} = \underrightarrow{{{\varvec{v}}}_I} - \underrightarrow{\varvec{\omega }_e} \times \underrightarrow{{{\varvec{r}}}}, \end{aligned}$$

  (6)

  where $\underrightarrow{{{\varvec{v}}}_{I}}$ and $\underrightarrow{{{\varvec{v}}}_{r}}$ are, respectively, the inertial and relative velocity. The unit vector $\hat{\varvec{\theta }}_r$ is aligned with the projection of the relative velocity vector $\underrightarrow{{{\varvec{v}}}_{r}}$ on the horizontal plane, defined by the set of vectors $(\hat{{{\varvec{E}}}}, \hat{{{\varvec{N}}}})$. The AO-frame and the LH-frame are linked through an elementary rotation by the heading angle $\zeta _r$ (see Fig. 1),

  $$\begin{aligned} \left[ \begin{array}{c} \hat{{{\varvec{r}}}} \\ \hat{\varvec{\theta }}_r \\ \hat{{{\varvec{h}}}}_r \end{array} \right] = {{\textbf {R}}}_1(\zeta _r) \left[ \begin{array}{c} \hat{{{\varvec{r}}}} \\ \hat{{{\varvec{E}}}} \\ \hat{{{\varvec{N}}}} \end{array} \right] . \end{aligned}$$

  (7)

• The Relative Velocity frame (RV) $(\hat{{{\varvec{n}}}}_r, \hat{{{\varvec{v}}}}_r, \hat{{{\varvec{h}}}}_r)$ is obtained from the AO-frame through a clockwise rotation along axis 3 by the flight path angle $\gamma _r$ (see Fig. 1),

  $$\begin{aligned} \left[ \begin{array}{c} \hat{{{\varvec{n}}}}_r \\ \hat{{{\varvec{v}}}}_r \\ \hat{{{\varvec{h}}}}_r \end{array} \right] = {{\textbf {R}}}_3(-\gamma _r) \left[ \begin{array}{c} \hat{{{\varvec{r}}}} \\ \hat{\varvec{\theta }}_r \\ \hat{{{\varvec{h}}}}_r \end{array} \right] . \end{aligned}$$

  (8)

  Figure 1 shows the LH- and RV-frames, together with the ECI-frame.

• The Wind Axes frame frame (WA) $(\hat{{{\varvec{n}}}}_W, \hat{{{\varvec{v}}}}_W, \hat{{{\varvec{h}}}}_W)$ is defined with reference to the vehicle velocity with respect to the local velocity of the atmosphere $\mathbf {{{\varvec{v}}}_a}$,

  $$\begin{aligned} \underrightarrow{{{\varvec{v}}}_a} = \underrightarrow{\varvec{\omega }_e} \times \underrightarrow{{{\varvec{r}}}} + \underrightarrow{{{\varvec{v}}}_\textrm{wind}}, \end{aligned}$$

  (9)

  where $\underrightarrow{{{\varvec{v}}}_\textrm{wind}}$ is the velocity perturbation induced by the local winds. Therefore, the vehicle velocity relative to the atmosphere is

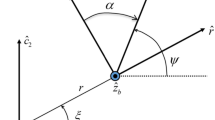
  $$\begin{aligned} \underrightarrow{{{\varvec{v}}}_W} = \underrightarrow{{{\varvec{v}}}_I}-\underrightarrow{{{\varvec{v}}}_a}= \underrightarrow{{{\varvec{v}}}_I}-(\underrightarrow{\varvec{\omega }_e} \times \underrightarrow{{{\varvec{r}}}} + \underrightarrow{{{\varvec{v}}}_\textrm{wind}}) = \underrightarrow{{{\varvec{v}}}_r}-\underrightarrow{{{\varvec{v}}}_\textrm{wind}}, \end{aligned}$$

  (10)

  where the unit vector $\hat{{{\varvec{v}}}}_{W}$ is aligned with the velocity vector $\underrightarrow{{{\varvec{v}}}_{W}}$. This vector is defined in the RV-frame through a counterclockwise rotation along axis 1 by angle $\alpha _W$ and a following clockwise rotation along axis 3 by angle $\beta _W$. Then, the unit vector $\hat{{{\varvec{n}}}}_{W}$ is contained in the plane of symmetry of the vehicle and is directed upward in horizontal flight conditions. It is worth remarking that, in aeronautical flight, usually this axis corresponds to the z-axis and has opposite direction. The following relation relate the WA-frame and the RV-frame:

  $$\begin{aligned} \left[ \begin{array}{c} \hat{{{\varvec{n}}}}_W\\ \hat{{{\varvec{v}}}}_W \\ \hat{{{\varvec{h}}}}_W \end{array} \right] = {{\textbf {R}}}_2(\sigma ) {{\textbf {R}}}_3(-\beta _W) {{\textbf {R}}}_1(\alpha _W) \left[ \begin{array}{c} \hat{{{\varvec{n}}}}_r \\ \hat{{{\varvec{v}}}}_r \\ \hat{{{\varvec{h}}}}_r \end{array} \right] , \end{aligned}$$

  (11)

  where $\sigma$ is the bank angle.

• The Auxiliary Body Axes frame (ABA) $(\hat{{{\varvec{i}}}}_B, \hat{{{\varvec{j}}}}_B, \hat{{{\varvec{k}}}}_B)$ is aligned with the body axes of inertia. The unit vector $\hat{{{\varvec{k}}}}_B$ is orthogonal to the vehicle plane of symmetry, while the two remaining unit vectors lie on it. If $\beta$ is the sideslip angle and $\alpha$ the angle of attack, then

  $$\begin{aligned} \left[ \begin{array}{c} \hat{{{\varvec{i}}}}_B \\ \hat{{{\varvec{j}}}}_B \\ \hat{{{\varvec{k}}}}_B \end{array} \right] = {{\textbf {R}}}_3(-\alpha ) {{\textbf {R}}}_1(\beta ) \left[ \begin{array}{c} \hat{{{\varvec{n}}}}_W \\ \hat{{{\varvec{v}}}}_W \\ \hat{{{\varvec{h}}}}_W \end{array} \right] . \end{aligned}$$

  (12)

  Figure 2 shows the set of unit vectors $(\hat{{{\varvec{i}}}}_B, \hat{{{\varvec{j}}}}_B, \hat{{{\varvec{k}}}}_B)$ and the relation with the WA-frame through the aerodynamic angles, under the hypothesis of no winds.

• The Body Axes frame (BA) $(\hat{{{\varvec{x}}}}_B, \hat{{{\varvec{y}}}}_B, \hat{{{\varvec{z}}}}_B)$ has axis $\hat{{{\varvec{x}}}}_B$ aligned with the longitudinal axis, while $\hat{{{\varvec{z}}}}_B$ is directed downward in horizontal flight conditions. Then,

  $$\begin{aligned} \left[ \begin{array}{c} \hat{{{\varvec{x}}}}_B \\ \hat{{{\varvec{y}}}}_B \\ \hat{{{\varvec{z}}}}_B \end{array} \right] = \left[ \begin{array}{ccc} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} -1 \\ -1 &{} 0 &{} 0 \end{array} \right] \left[ \begin{array}{c} \hat{{{\varvec{i}}}}_B \\ \hat{{{\varvec{j}}}}_B \\ \hat{{{\varvec{k}}}}_B \end{array} \right] = {{\textbf {R}}}_A \left[ \begin{array}{c} \hat{{{\varvec{i}}}}_B \\ \hat{{{\varvec{j}}}}_B \\ \hat{{{\varvec{k}}}}_B \end{array} \right] . \end{aligned}$$

  (13)

• The Frozen Inertial frame (FI) $(\underrightarrow{\hat{{{\varvec{i}}}}_0}, \underrightarrow{\hat{{{\varvec{j}}}}_0}, \underrightarrow{\hat{{{\varvec{k}}}}_0})$ is introduced to describe the attitude of the vehicle. Its inertial axes are defined as follows:

  • during the transatmospheric phase, they coincide with the local East, South and Nadir directions at the initial position of the vehicle;

  • during the terminal phase, they coincide with the local East, South and Nadir directions at the landing point at the initial time (of the terminal phase).

  If subscript $_0$ denotes a generic coordinate at initial time, then the following relation holds:

  $$\begin{aligned} \left[ \begin{array}{c} \hat{{{\varvec{i}}}}_0 \\ \hat{{{\varvec{j}}}}_0 \\ \hat{{{\varvec{k}}}}_0 \end{array} \right]= & {} \left[ \begin{array}{ccc} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} -1 \\ -1 &{} 0 &{} 0 \end{array} \right] \left[ \begin{array}{c} \hat{{{\varvec{r}}}}_{L0} \\ \hat{{{\varvec{E}}}}_{L0} \\ \hat{{{\varvec{N}}}}_{L0} \end{array} \right] = {{\textbf {R}}}_A \left[ \begin{array}{c} \hat{{{\varvec{r}}}}_{L0} \\ \hat{{{\varvec{E}}}}_{L0} \\ \hat{{{\varvec{N}}}}_{L0} \end{array} \right] \nonumber \\= & {} {{\textbf {R}}}_A {{\textbf {R}}}_2(-\varphi _0) {{\textbf {R}}}_3(\lambda _{a0}) \left[ \begin{array}{c} \hat{{{\varvec{c}}}}_{1} \\ \hat{{{\varvec{c}}}}_{2} \\ \hat{{{\varvec{c}}}}_{3} \end{array} \right] , \end{aligned}$$

  (14)

  where $(\varphi _{0}, \lambda _{a0})$ are the latitude and absolute longitude of the origin of the reference frame. Then, the attitude of the vehicle can be specified by linking the BA-frame and the FI-frame through a sequence of three elementary rotations:

  • a counterclockwise rotation along axis 3 by angle $\psi$ (yaw angle):

    $$\begin{aligned} -\pi \le \psi \le \pi ; \end{aligned}$$

    (15)

  • a counterclockwise rotation along axis 2 by angle $\theta$ (pitch angle):

    $$\begin{aligned} -\dfrac{\pi }{2} \le \theta \le \dfrac{\pi }{2}; \end{aligned}$$

    (16)

  • a counterclockwise rotation along axis 1 by angle $\phi$ (roll angle):

    $$\begin{aligned} -\pi \le \phi \le \pi . \end{aligned}$$

    (17)

  Therefore,

  $$\begin{aligned} \left[ \begin{array}{c} \hat{{{\varvec{x}}}}_B \\ \hat{{{\varvec{y}}}}_B \\ \hat{{{\varvec{z}}}}_B \end{array} \right] = {{\textbf {R}}}_1(\phi ) {{\textbf {R}}}_2(\theta ) {{\textbf {R}}}_3(\psi ) \left[ \begin{array}{c} \hat{{{\varvec{i}}}}_0 \\ \hat{{{\varvec{j}}}}_0 \\ \hat{{{\varvec{k}}}}_0 \end{array} \right] = {{\textbf {R}}}_{FI \rightarrow B} \left[ \begin{array}{c} \hat{{{\varvec{i}}}}_0 \\ \hat{{{\varvec{j}}}}_0 \\ \hat{{{\varvec{k}}}}_0 \end{array} \right] . \end{aligned}$$

  (18)

Figure 3 shows the different reference frames and their relations.

Fig. 1

Representation of the LH- and RV- frames: $\lambda _a = \theta _G+\lambda _g$ identifies the absolute longitude

Fig. 2

Visualization of the ABA frame under no winds

Fig. 3

Reference frames and elementary rotation matrices

2.2 Atmospheric Modeling

The atmosphere is modeled as a fluid, with all the species homogeneously mixed and behaving as a perfect gas. Then, under the hypotheses of hydrostatic equilibrium and adiabatic interactions, the density $\rho$ can be written as function of the altitude z,

$$\begin{aligned} \rho (z) = \rho (z_0) e^{-\dfrac{z-z_0}{H}}, \end{aligned}$$

(19)

where H is the scale height and $z_0$ a reference altitude. The values of the scale height and density corresponding to different altitude intervals are collected in [22]. An accurate distribution of the density can be obtained through a piecewise exponential function,

$$\begin{aligned} \rho (z) = \rho (z_k) e^{-\dfrac{z-z_k}{H_k}}, \ \ \ z_k \le z \le z_{k+1} \end{aligned}$$

(20)

where $H_k$ is the scale height corresponding to the interval $\left[ z_k, z_{k+1}\right]$.

Another necessary parameter is the speed of sound $v_s$, which depends on the local atmospheric temperature,

$$\begin{aligned} v_s=\sqrt{\dfrac{\gamma p}{\rho }} = \sqrt{\gamma \dfrac{R^*}{M}T}, \end{aligned}$$

(21)

where p is the pressure, T the temperature, $\gamma$ the heat capacity ratio, $R^*$ the molar gas constant and M the molar mass. In this case, a fourth-degree polynomial is employed to interpolate the sound speed, from the data collected in [23].

2.3 Aerodynamics Modeling

The simulation of the reentry dynamics of the Shuttle Orbiter requires the computation of the aerodynamic coefficients $C_L$, $C_D$ and $C_Q$, which in general depend on several parameters:

$$\begin{aligned} C_{L,D,Q} = C_{L,D,Q}(\alpha ,\beta , M, Re) \end{aligned}$$

(22)

where M is the Mach number and Re the Reynolds number. In this study, the following hypotheses are assumed: (i) the dependence of the aerodynamic coefficients with the Reynolds number is neglected [21]; (ii) the effects of the angle of attack and sideslip angle on the aerodynamic coefficients are decoupled [21], i.e., the lift and drag coefficients are assumed to depend on $\alpha$ and M, while the side force coefficient depends on $\beta$ and M,

$$\begin{aligned} C_L = C_L (\alpha , M), \end{aligned}$$

(23)

$$\begin{aligned} C_D = C_D (\alpha , M), \end{aligned}$$

(24)

$$\begin{aligned} C_Q = C_Q (\beta , M). \end{aligned}$$

(25)

The aerodynamic coefficients of the Space Shuttle Orbiter as a function of the Mach number and the aerodynamic angles can be obtained through wind tunnel tests and are collected in [21]. Let us assume that a given curve at Mach number $M_1$ is sampled with n points,

$$\begin{aligned} (\alpha _{k}^{M_1}, C{_{L_{k}}}^{M_{1}}) \ \ \ \ k=1,\ldots ,n. \end{aligned}$$

(26)

The coordinates of the sampled points can be rearranged in a matricial form,

$$\begin{aligned} \alpha ^{M_1} = \left[ \begin{array}{c} \alpha _1^{M_1} \\ ... \\ \alpha _k^{M_1} \\ ... \\ \alpha _{n}^{M_1} \end{array} \right] , \ \ \ \ \ \ \ \ C_L^{M_1} = \left[ \begin{array}{c} {C}{_{{L}_{1}}}^{M_1} \\ ... \\ C{_{L_{k}}}^{M_1} \\ ... \\ C{_{L_{n}}}^{M_1} \end{array} \right] . \end{aligned}$$

(27)

Then, the sampled points are interpolated to yield the value of the lift coefficient $C_L^1$ for a generic angle of attack $\alpha$ and Mach number $M_1$. Let us suppose that the value of the lift coefficient $C_L$ at a given Mach number M is required. Then, an adjacent curve at Mach $M_2$ can be identified, so that

$$\begin{aligned} M_1 \le M \le M_2. \end{aligned}$$

(28)

Similarly, the curve corresponding to $M_2$ is sampled with m points,

$$\begin{aligned} (\alpha _k^{M_2}, C{_{L_k}}^{M_2}) \ \ \ \ k=1,\ldots m, \end{aligned}$$

(29)

to yield the value $C_L^2$ for the same angle of attack $\alpha$. Finally, the lift coefficient $C_L$ is retrieved through a linear interpolation,

$$\begin{aligned} C_L = C_L^{1}+ \dfrac{C_L^2-C_L^1}{M_2-M_1}(M-M_1). \end{aligned}$$

(30)

The same procedure can be applied to compute the drag and side force coefficients for a generic $\alpha$, $\beta$ and M.

2.4 Trajectory Equations

The reentry vehicle is modeled as a 3-degrees-of-freedom (3-DOF) rigid body. The trajectory equations describe the motion of the center of mass due to the effect of the active forces. Even though this research addresses only the trajectory dynamics, the aerodynamic angles will be eventually employed to retrieve the attitude of the vehicle in the inertial reference frame.

2.4.1 Kinematics Equations

The kinematics equations relate the instantaneous position vector $\underrightarrow{{{\varvec{r}}}}$ with the velocity vector $\underrightarrow{{{\varvec{v}}}_r}$ and are expressed in the AO-frame. The kinematics equations are [24]

$$\begin{aligned} {\dot{r}}= & {} \textit{v}_r \sin {\gamma _r}, \end{aligned}$$

(31)

$$\begin{aligned} {\dot{\lambda }}_g= & {} \dfrac{\textit{v}_r \cos {\gamma _r}\cos {\zeta _r}}{r \cos {\varphi }}, \end{aligned}$$

(32)

$$\begin{aligned} {\dot{\varphi }}= & {} \dfrac{\textit{v}_r \cos {\gamma _r}\sin {\zeta _r}}{r}. \end{aligned}$$

(33)

2.4.2 Dynamics Equations

The dynamical equations are directly obtained from Newton’s law,

$$\begin{aligned} m \underrightarrow{{{\varvec{a}}}} = \underrightarrow{{{\varvec{A}}}} + \underrightarrow{{{\varvec{G}}}} + \underrightarrow{{{\varvec{T}}}}, \end{aligned}$$

(34)

where $\underrightarrow{{{\varvec{a}}}}$ is the inertial acceleration of the center of mass of the vehicle, $\underrightarrow{{{\varvec{G}}}}$ is the gravitational force, $\underrightarrow{{{\varvec{T}}}}$ is the thrust, while $\underrightarrow{{{\varvec{A}}}}$ is the aerodynamics force, which is the sum of lift $\underrightarrow{{{\varvec{L}}}}$, drag $\underrightarrow{{{\varvec{D}}}}$ and sideforce $\underrightarrow{{{\varvec{Q}}}}$,

$$\begin{aligned} \underrightarrow{{{\varvec{A}}}}= \underrightarrow{{{\varvec{L}}}}+\underrightarrow{{{\varvec{D}}}}+\underrightarrow{{{\varvec{Q}}}}. \end{aligned}$$

(35)

The aerodynamic forces can be conveniently expressed in the wind axes,

$$\begin{aligned} \underrightarrow{{{\varvec{L}}}}= & {} \tilde{\textit{L}} \hat{{{\varvec{n}}}}_W = \dfrac{1}{2} C_L S_\textrm{ref} \rho \textit{v}_W^2 \hat{{{\varvec{n}}}}_W, \end{aligned}$$

(36)

$$\begin{aligned} \underrightarrow{{{\varvec{D}}}}= & {} - \tilde{\textit{D}} \hat{{{\varvec{v}}}}_W = -\dfrac{1}{2} C_D S_\textrm{ref} \rho \textit{v}_W^2 \hat{{{\varvec{v}}}}_W, \end{aligned}$$

(37)

$$\begin{aligned} \underrightarrow{{{\varvec{Q}}}}= & {} \tilde{\textit{Q}} \hat{{{\varvec{h}}}}_W = \dfrac{1}{2} C_Q S_\textrm{ref} \rho \textit{v}_W^2 \hat{{{\varvec{h}}}}_W, \end{aligned}$$

(38)

where $S_\textrm{ref}$ is the reference area of the vehicle. Then, the aerodynamic force must be projected onto the RV-frame $(\hat{{{\varvec{n}}}}_r, \hat{{{\varvec{v}}}}_r, \hat{{{\varvec{h}}}}_r)$ through the angles $\alpha _W$, $\beta _W$ and $\sigma$. The acceleration components are denoted with $(A_n, A_v, A_h)$ and are given by

$$\begin{aligned} \underrightarrow{{{\varvec{A}}}}= & {} \left[ \begin{array}{cc} \textit{A}_n&\textit{A}_v \ \textit{A}_h \end{array} \right] \left[ \begin{array}{c} \hat{{{\varvec{n}}}}_r \\ \hat{{{\varvec{v}}}}_r \\ \hat{{{\varvec{h}}}}_r \end{array} \right] \nonumber \\= & {} \left[ \begin{array}{ccc} \dfrac{\tilde{L}}{m}&-\dfrac{\tilde{D}}{m}&\dfrac{\tilde{L}}{Q} \end{array} \right] {{\textbf {R}}}_2(\sigma ) {{\textbf {R}}}_3(-\beta _W) {{\textbf {R}}}_1(\alpha _W) \left[ \begin{array}{c} \hat{{{\varvec{n}}}}_r \\ \hat{{{\varvec{v}}}}_r \\ \hat{{{\varvec{h}}}}_r \end{array} \right] . \end{aligned}$$

(39)

Under the hypothesis of no thrust, the dynamics equations are [24]

$$\begin{aligned} \dot{v_r}= & {} -\dfrac{\mu }{r^2}\sin {\gamma _r}+A_{\textit{v}}+\omega _e^2 r \cos {\varphi }(\cos {\varphi }\sin {\gamma _r}-\sin {\varphi }\cos {\gamma _r}\sin {\zeta _r}), \end{aligned}$$

(40)

$$\begin{aligned} \dot{\zeta _r}= & {} -\dfrac{\textit{v}_r}{r}\tan {\varphi }\cos {\gamma _r}\cos {\zeta _r}+\dfrac{A_h}{\textit{v}_r\cos {\gamma _r}}+2\omega _e\cos {\varphi }\tan {\gamma _r}\sin {\zeta _r} \end{aligned}$$

(41)

$$\begin{aligned}{} & {} -\dfrac{\omega _e^2 r}{\textit{v}_r\cos {\gamma _r}} \sin {\varphi }\cos {\varphi }\cos {\zeta _r}-2\omega _e \sin {\varphi }, \nonumber \\ \dot{\gamma _r}= & {} \Big [-\dfrac{\mu }{r^2\textit{v}_r}+\dfrac{\textit{v}_r}{r}\Big ]\cos {\gamma _r}+\dfrac{A_n}{\textit{v}_r}+2\omega _e \cos {\varphi }\cos {\zeta _r} \nonumber \\{} & {} +\dfrac{\omega _e^2 r}{\textit{v}_r}\cos {\varphi }(\cos {\varphi }\cos {\gamma _r}+\sin {\varphi }\sin {\gamma _r}\sin {\zeta _r}), \end{aligned}$$

(42)

where $\mu$ is the Earth’s gravitational parameter.

2.5 Attitude Kinematics

This research does not address the attitude dynamics and control, i.e., the instantaneous and commanded are implicitly assumed to be coincident throughout the simulation time. However, the analysis of the Bryant angles can provide meaningful information as well. The attitude of the vehicle with respect to the inertial frame is described by matrix ${{\textbf {R}}}_{FI \rightarrow B}$; from inspection of Fig. 3, matrix ${{\textbf {R}}}_{FI \rightarrow B}$ can be linked to the other rotation matrices,

$$\begin{aligned} {{\textbf {R}}}_{FI \rightarrow B} = {{\textbf {R}}}_A {{\textbf {R}}}_3 (-\alpha ) {{\textbf {R}}}_1(\beta ) {{\textbf {R}}}_2(\sigma ) {{\textbf {R}}}_3(-\beta _W) {{\textbf {R}}}_1(\alpha _W) {{\textbf {R}}}_3 (-\gamma _r) \ \cdot \nonumber \\ \cdot \ {{\textbf {R}}}_1(\zeta _r) {{\textbf {R}}}_2(-\varphi ) {{\textbf {R}}}_3(\lambda _g) {{\textbf {R}}}_3(\theta _G) {{\textbf {R}}}_3(\lambda _{a0})^T {{\textbf {R}}}_2(-\varphi _0)^T {{\textbf {R}}}_A^T. \end{aligned}$$

(43)

If ${{\textbf {R}}}_{FI \rightarrow B}(i,j)$ denotes the entry of the matrix in the ith row and jth column, then the Bryant angles can be easily retrieved as

$$\begin{aligned}{} & {} \theta = -\arcsin {({{\textbf {R}}}_{FI \rightarrow B}(1,3))}, \end{aligned}$$

(44)

$$\begin{aligned}{} & {} {\left\{ \begin{array}{ll} \sin {\psi } = \dfrac{{{\textbf {R}}}_{FI \rightarrow B}(1,2)}{\cos {\theta }} \\ \cos {\psi }=\dfrac{{{\textbf {R}}}_{FI \rightarrow B}(1,1))}{\cos {\theta }} \end{array}\right. } \end{aligned}$$

(45)

$$\begin{aligned}{} & {} {\left\{ \begin{array}{ll} \sin {\phi } = \dfrac{{{\textbf {R}}}_{FI \rightarrow B}(2,3)}{\cos {\theta }} \\ \cos {\phi }=\dfrac{{{\textbf {R}}}_{FI \rightarrow B}(3,3)}{\cos {\theta }}. \end{array}\right. } \end{aligned}$$

(46)

3 Transatmospheric Phase

The beginning of the transatmospheric arc is conventionally located at the entry interface (EI), at about 122 km. The Orbiter is traveling at 7300 m/s with a 40$^{\circ }$ angle-of-attack [24, 25]. During the period of high heating rate, the Orbiter flies the maximum angle of attack consistent with the crossrange requirement [26]. The reentry phase ends as the Orbiter reaches the TAEM interface, at approximately 25 km of altitude, 762 m/s of speed and 110 km from the landing runway [25].

3.1 Formulation of the Problem

The goal of the transatmospheric guidance is to drive the vehicle from the EI toward the TAEM, while keeping the thermic flux per unit area at the stagnation point $\textit{q}_s$ below the maximum value and minimizing the total heat per unit area absorbed by the vehicle:

$$\begin{aligned} Q = \int _0^{t_f} q_s \, dt. \end{aligned}$$

(47)

Table 2 collects the boundary conditions for the atmospheric arc, which reflects the typical descent profile of the Space Shuttle [25, 27].

Table 2 Boundary conditions for the transatmospheric arc

The algorithm must keep the thermic flux below the maximum allowable value, equal to 681.39 kW/m$^2$, even lower than the typical value reported in the literature, i.e., 794.43 kW/m$^2$ [28]. The dynamic pressure must be less than 16.375 kPa [27]. The thermic flux at the leading edge can be computed as $q_s=q_a q_r$, where

$$\begin{aligned} q_r= & {} \; a \sqrt{\rho }(b v_r)^n, \end{aligned}$$

(48)

$$\begin{aligned} q_a= & {} \; c_0 + c_1 \alpha +c_2 \alpha ^2 + c_3\alpha ^3, \end{aligned}$$

(49)

with $a = 779.6685$ W $\cdot$ (kg m)$^{-2}$, $b = 3.2808 \cdot 10^{-4}$ m$^{-1}$, $n = 3.07$, $c_0=1.0672181$, $c_1 = 0.19213774 \ \cdot \ 10^{-1}$ deg$^{-1}$, $c_2 = 0.21286289 \ \cdot \ 10^{-3}$ deg$^{-2}$ and $c_3 = 0.10117249 \ \cdot \ 10^{-5}$ deg$^{-3}$ [28]. The derivative of the thermic flux can be easily computed as

$$\begin{aligned} {\dot{q}}_s = F q_a+q_rG {\dot{\alpha }}, \end{aligned}$$

(50)

where F and G are auxiliary functions that do not depend on the input variable (${\dot{\alpha }}$),

$$\begin{aligned} {\left\{ \begin{array}{ll} F = \dfrac{a}{2 \sqrt{\rho }} {\dot{\rho }} (b v_r)^n+na\sqrt{\rho } (bv_r)^{n-1} b {\dot{v}}_r \\ G = c_1 + 2c_2 \alpha + 3 c_3 \alpha ^2. \end{array}\right. } \end{aligned}$$

(51)

The descent of the vehicle through the atmosphere is controlled through modulation of the angle of attack and bank angle. In particular, the angle of attack varies according to four distinct flight profiles:

• constant-angle-of-attack flight from the entry interface until $M=M^*$, where $M^*$ is the optimized Mach number at the end of the first reentry phase (cfr. Sect. 3.2);

• variable-angle-of-attack flight to avoid exceeding the maximum value of the thermal flux. The time derivative of the angle off attack is selected to yield ${\dot{q}}_s=0$ (cfr. Eq. (50)),

  $$\begin{aligned} {\dot{\alpha }} = -\dfrac{F}{G} \dfrac{q_a}{q_r}; \end{aligned}$$

  (52)

• variable-angle-of attack flight following a sinusoidal profile from $M=M^*$ to $\tilde{M}=6,$

  $$\begin{aligned} \alpha (M)=A \sin {\left( \pi \dfrac{M-\dfrac{M^*+\tilde{M}}{2}}{M^*-\tilde{M}} \right) } + B, \end{aligned}$$

  (53)

  with

  $$\begin{aligned} A = \dfrac{38^{\circ }-20^{\circ }}{2}, \end{aligned}$$

  (54)
  $$\begin{aligned} B = \dfrac{38^{\circ }+20^{\circ }}{2}. \end{aligned}$$

  (55)

  This phase allows to reduce the angle of attack during the hypersonic regime (i.e., 38$^{\circ }$) to the maximum angle of attack compatible with a supersonic speed (i.e., 20$^{\circ }$) [21];

• variable-angle-of-attack flight optimized by the guidance algorithm. The optimized parameters are interpolated with a procedure similar to that of Sect. 2.3.

3.2 Open-Loop Guidance

The guidance strategy is based on a parametric minimization of the following cost function:

$$\begin{aligned} J = k_r \Delta _r + k_y \Delta _y + k_z \Delta _z + k_v \Delta _v + k_{\zeta } \Delta _z + k_{\gamma }\Delta _{\gamma } + k_q \int _0^{t_f} q_s \, dt, \end{aligned}$$

(56)

where the coefficients $k_r,k_y,k_z,k_v,k_{\zeta },k_{\gamma },k_q$ are chosen to balance the different contributions in the cost function,

$$\begin{aligned} k_r= & {} \; 10^3 \ \hbox { m}\ ^{-1}, \ \ \ k_y =k_z= 10^2 \ \hbox {m} ^{-1}, \ \ \ k_v = 10^4 \ \text {s} \,\hbox {m}^{-1}, \end{aligned}$$

(57)

$$\begin{aligned} k_{\zeta }= & {} \; k_{\gamma } = 5 \cdot 10^7 \ \hbox { rad}\ ^{-1}, \ \ \ k_q = 10^{-1} \ \hbox {m} ^{2} \,\hbox {J}^{-1}. \end{aligned}$$

(58)

The gains are selected after extensive trial-and-error and are iteratively tuned until the dispersions at the end of the transatmospheric arc are compliant with the performance of the terminal guidance algorithm. Instead, the terms $\Delta$ in Eq. (56) are the deviations of the final state variables (reported in subscripts) from the desired values. Then, the reentry trajectory is sampled at equally-spaced time instants $t_k$ from the entry interface to the TAEM and the open-loop guidance law is determined through parametric optimization of the following parameters:

• 16 values of the bank angle $\sigma _k$. The guess parameters are set to ± 50$^{\circ }$; the algorithm also constrains the bank angle between $\pm 70^{\circ }$;

• 15 values of the angle of attack $\alpha _k$ from $M=6$ to the TAEM. The guess parameters are linearly decreasing from 20$^{\circ }$ to 14$^{\circ }$;

• the total time of flight $t_f$ from the entry interface to the TAEM; the guess value is set to 25 min;

• the Mach number $M^*$ at the end of the constant-angle-of-attack flight profile; the guess value is set to $M=10$;

• the argument of latitude $u_0$ at the initial time; the guess value is set to 80$^{\circ }$.

The total time of flight is also normalized with respect to its guess value. Numerical optimization utilizes a heuristic approach, i.e., an implementation of the particle swarm algorithm [29]. The algorithm employs 300 particles, with 500 maximum iterations, 200 maximum stall iterations and function tolerance set to 10$^{-5}$.

3.3 Numerical Results

Table 3 collects the results of the optimization. The sideslip angle is nominally set to zero because it yields an increase in the thermic load. Therefore, the side force is not taken into account for the simulation of the reentry guidance. In Table 3, the variable $d_f$ denotes the final distance along the Earth surface between the final point in the atmospheric arc and the landing site:

$$\begin{aligned} d_f = R_\textrm{eq} \arccos {(\sin {L_f}\sin {L_{rwy}}+\cos {L_f}\cos {L_{rwy}}\cos {(\lambda _f-\lambda _{rwy})})} \end{aligned}$$

(59)

where $R_\textrm{eq}=6378$ km is the mean equatorial radius [27].

Table 3 Displacements of the state variables at the TAEM

From inspection of Table 3, the guidance algorithm is able to drive the vehicle through the transatmospheric arc, with limited dispersions on the final state at the TAEM, along a descent path close to the actual trajectory of the Orbiter (cfr. Table 2).

Fig. 4

Time histories of the altitude along the transatmospheric arc

Fig. 5

Time histories of the relative velocity along the transatmospheric arc

Figure 4 points out that the vehicle is performing a skip entry, as the lift force rotates the velocity vector up to a positive flight path angle. This results also in a typical profile for the relative velocity $v_r$ (Fig. 5). Indeed, when the altitude approaches a minimum (pull-up altitude), a significant reduction in the relative velocity follows due to the greater aerodynamic drag decelerating the vehicle. However, even though the vehicle is braking, the velocity increases in the first time interval ([0,200] s). Also, each bounce on the atmosphere yields a transition between negative and positive flight path angles, as highlighted in Fig. 6.

Fig. 6

Time histories of the flight path angle along the transatmospheric arc

Fig. 7

Time histories of the dynamical pressure along the transatmospheric arc

Figure 7 shows the time histories of the dynamical pressure: the maximum value is reached toward the TAEM, where the density is significantly greater; however, it is lower than the limit of the vehicle (cfr. Sect. 3.1).

Fig. 8

Time histories of the thermal flux along the transatmospheric arc

Fig. 9

Time histories of the angle of attack along the transatmospheric arc

Fig. 10

Time histories of the bank angle along the transatmospheric arc

Figures 8 and 9, respectively, depict the time histories of the thermal flux and of the angle of attack. In particular, the modulation of the angle of attack after 200 s yields the saturation of the thermic flux as described in Eq. (52). Even though the angle of attack is significantly high, the results show the effectiveness of the proposed strategy. Also, the curve in Fig. 9 follows the designed sinusoidal profile between 900 and 1100 s, while the vehicle is transitioning from a hypersonic flight regime ($\alpha _{\max }=38^{\circ }$) to a supersonic flight regime ($\alpha _{\max }=20^{\circ }$). The saturation of the angle of attack is highlighted in the last flight phase, where the algorithm constrains the variable among feasible values in order not to approach the stall condition. Finally, Fig. 10 shows the evolution of the bank angle along the descent, which is saturated by the algorithm between $\pm 70^{\circ }$ to compute a feasible trajectory. The oscillations between the maximum values allow to control the crossrange component while reducing the projection of the lift force along the vertical plane as well. This technique is referred to as bank reversal [26].

4 Terminal Guidance

Along the transatmospheric arc, different factors may deviate the reentry trajectory from the reference profile. Therefore, the terminal guidance must be able to guarantee safe landing despite a wide range of initial conditions.

4.1 Formulation of the Problem

The terminal descent and landing problem consists in driving the landing vehicle from the TAEM to the specified landing point while guaranteeing:

• a desired vertical velocity at touchdown, compliant with the structural limit of the landing gear;

• the correct alignment of the vehicle with the landing runway.

4.2 Simplified Dynamics Equations

Trajectory generation is addressed in a simplified dynamical framework, where the following hypotheses are assumed:

• the gravitational field is uniform and equal to $g_0=9.7975$ m/s$^2$;

• the apparent forces are neglected;

• the term $v_r/r$ in Eq. (42) is negligible with respect to the term depending on $A_h$.

Under these hypotheses, the kinematics and dynamics equations are simplified into

$$\begin{aligned} {\dot{x}}= & {} \; v_r^{(G)} \sin {\gamma _r^{(G)}} \end{aligned}$$

(60)

$$\begin{aligned} {\dot{y}}= & {} \; v_r^{(G)} \cos {\gamma _r^{(G)}} \cos {\zeta _r^{(G)}} \end{aligned}$$

(61)

$$\begin{aligned} {\dot{z}}= & {} \; v_r^{(G)} \cos {\gamma _r^{(G)}} \sin {\zeta _r^{(G)}} \end{aligned}$$

(62)

$$\begin{aligned} {\dot{v}}_r^{(G)}= & {} \; -g \sin {\gamma _r^{(G)}} + A_v \end{aligned}$$

(63)

$$\begin{aligned} {\dot{\zeta }}_r^{(G)}= & {} \; \dfrac{A_h}{v_r^{(G)}\cos {\gamma _r^{(G)}}} \end{aligned}$$

(64)

$$\begin{aligned} {\dot{\gamma }}_r^{(G)}= & {} \; \dfrac{g_0 \cos {\gamma _r^{(G)}}}{v_r^{(G)}}+\dfrac{A_n}{v_r^{(G)}} \end{aligned}$$

(65)

where $\gamma _r^{(G)}$ and $\zeta _r^{(G)}$ are the flight path angle and heading angle with respect to the AL-frame, while (x, y, z) are the Cartesian coordinates in the same reference frame,

$$\begin{aligned} \left[ \begin{array}{c} x \\ y \\ z \end{array} \right] ^T= & {} \left[ \begin{array}{c} r \cos {\varphi _{rwy}}\cos {\lambda _{rwy}} \\ r \cos {\varphi _{rwy}} \sin {\lambda _{rwy}} \\ r \sin {\varphi _{rwy}} \end{array} \right] ^T {{\textbf {R}}}_3(\theta _G) {{\textbf {R}}}_3^T (\lambda _{rwy}) {{\textbf {R}}}_2^T (-\varphi _{rwy}) \nonumber \\{} & {} - \left[ \begin{array}{c} R_{eq} \\ 0 \\ 0 \end{array} \right] ^T. \end{aligned}$$

(66)

4.3 Boundary Conditions

The initial conditions are given by the state variables at the TAEM. In nominal conditions, the vehicle crosses the TAEM interface a distance of 111 km from the landing point, with a velocity of 762 m/s [25]. Also, the angle of attack is 14 degrees. The landing point is positioned 762 m beyond the runway threshold and is identified by the set of geographical coordinates $(\varphi _{rwy},\lambda _{rwy})$. Then, these coordinates can be expressed in the AL-frame as

$$\begin{aligned}{} & {} \left[ \begin{array}{c} x_r \\ y_r \\ z_r \end{array} \right] ^T = (R_{eq} + CM) \left[ \begin{array}{c} \cos {\varphi _{rwy}}\cos {\lambda _{rwy}} \\ \cos {\varphi _{rwy}} \sin {\lambda _{rwy}} \\ \sin {\varphi _{rwy}} \end{array} \right] ^T \nonumber \\{} & {} \quad {{\textbf {R}}}_3(\theta _G) {{\textbf {R}}}_3^T (\lambda _{rwy}) {{\textbf {R}}}_2^T (-\varphi _{rwy}) - \left[ \begin{array}{c} R_{eq} \\ 0 \\ 0 \end{array} \right] ^T, \end{aligned}$$

(67)

where $CM = 5.98$ m denotes the height of the center of mass of the vehicle with respect to the runway (cfr. Table 1). The following final constraints are established:

$$\begin{aligned} {\dot{x}}(t_r) = {\dot{h}}_{des}, \end{aligned}$$

(68)

$$\begin{aligned} \zeta _r (t_r) = \zeta _{rwy}, \end{aligned}$$

(69)

where ${\dot{h}}_{des}$ is set to $-1$ m/s to remain well inside the safety specifications for the landing gear, which prescribe a limiting vertical velocity of about $-3$ m/s (10 ft/s [25]), while $\zeta _{rwy}$ is the heading angle of runway 15 of the NASA Space Shuttle Landing Facility with respect to the local East direction, equal to $-$ 60.24$^{\circ }$.

4.4 Constraints

During the terminal descent, the control inputs must be saturated in order to generate feasible trajectories,

$$\begin{aligned} 0 \ \text {deg} \le \alpha _c \le 20 \ \text {deg}, \ \ \ -50 \ \text {deg} \le \sigma _c \le 50 \ \text {deg}. \end{aligned}$$

(70)

In particular, the angle of attack is kept below 20$^{\circ }$ in order not to approach the aerodynamic stall.

4.5 Wind Modeling

The wind velocity is assigned in the LH-frame,

$$\begin{aligned} {\left\{ \begin{array}{ll} u_R = 0 \\ u_E = u_W \cos {\theta _W} \\ u_N = u_W \sin {\theta _W}, \, \end{array}\right. } \end{aligned}$$

(71)

where $u_W$ denotes the wind magnitude and $\theta _W$ its direction in the horizontal plane, both assumed as constant. The wind magnitude and direction are compliant with the landing criteria for the Space Shuttle Orbiter landing [30]:

• the peak crosswind cannot exceed 7.7 m/s, reduced to 6.2 m/s at night. If the mission duration is greater than 20 days, the limit is 6.2 m/s, either during day and night;

• the headwind cannot exceed 12.9 m/s;

• the tailwind cannot exceed 5.1 m/s average, 7.7 m/s peak.

However, a more challenging scenario is taken into account for the numerical simulations, with a peak crosswind and tailwind components set to 7.7 m/s and a peak headwind component equal to 12.9 m/s. The wind components along the runway direction ($u_{Wax}$) and transversal direction ($u_{Wtr}$) are randomly assigned according to a normal distribution between the minimum and maximum wind intensity. If $\theta _W^{rwy}$ denotes the wind direction with respect to the runway direction, then

$$\begin{aligned} \sin {\theta _W^{rwy}} = \dfrac{u_{Wtr}}{\sqrt{u_{Wtr}^2+u_{Wax}^2}}, \quad \cos {\theta _W^{rwy}} = \dfrac{u_{Wax}}{\sqrt{u_{Wtr}^2+u_{Wax}^2}}. \end{aligned}$$

(72)

Then, the wind intensity and direction in the horizontal plane are retrieved as

$$\begin{aligned} \theta _W= & {} \theta _W^{rwy} + \zeta _f, \end{aligned}$$

(73)

$$\begin{aligned} u_W= & {} \sqrt{u_{Wtr}^2+u_{Wax}^2}. \end{aligned}$$

(74)

The wind components must be projected along the RV-frame,

$$\begin{aligned} {\varvec{{v}}}_\textrm{wind} = {{\textbf {R}}}_1^T(\zeta _r) {{\textbf {R}}}_3^T(-\gamma _r) \left[ \begin{array}{ccc} u_R&u_E&u_N \end{array} \right] ^T. \end{aligned}$$

(75)

In the RV-frame the vehicle velocity relative to the atmosphere is given by

$$\begin{aligned} {{\varvec{v}}}_W = \left[ \begin{array}{ccc} -v_\textrm{wind,1}&v_{r}-v_\textrm{wind,2}&-v_\textrm{wind,3} \end{array}\right] ^T. \end{aligned}$$

(76)

Finally, the angles $\alpha _W$ and $\beta _W$ can be retrieved as

$$\begin{aligned}{} & {} \beta _W = \arcsin {\dfrac{-v_{w,3}}{v_W}}, \end{aligned}$$

(77)

$$\begin{aligned}{} & {} {\left\{ \begin{array}{ll} \sin {\alpha _W} = \dfrac{-v_{w,1}}{v_W \cos {\beta _W}} \\ \cos {\alpha _W} = \dfrac{v_r-v_{w,2}}{v_W \cos {\beta _W}} . \end{array}\right. } \end{aligned}$$

(78)

4.6 Guidance Strategy

The control input ${{\varvec{u}}} = \left[ \begin{matrix} {\dot{C}}_L \\ {\dot{\sigma }} \end{matrix} \right]$ is given by the time derivatives of the lift coefficient and bank angle. The derivation of the control variables is reported in [19] and yields an expression for ${{\varvec{u}}}$ as a function of the state variables.

4.6.1 Saturation of the Control Inputs

The control variables must be constrained between reasonable values to generate feasible trajectories. However, to overcome potential numerical issues, the saturation of the control variables is addressed by means of auxiliary variables leveraging the asymptotic behaviour of the arctan function. As a first step, the variables ${{\varvec{w}}}=\left[ \begin{matrix} w_1&w_2 \end{matrix} \right] ^T$ are introduced, so that

$$\begin{aligned} \left[ \begin{matrix}C_L \\ \sigma \end{matrix} \right]= & {} \dfrac{1}{\pi } \left[ \begin{matrix} C_{L\textrm{max}}-C_{L\textrm{min}} &{} 0 \\ 0 &{} \sigma _\textrm{max}-\sigma _\textrm{min}\end{matrix} \right] \left[ \begin{matrix} \arctan {w_1} \\ \arctan {w_2}\end{matrix} \right] \nonumber \\{} & {} + \dfrac{1}{2} \left[ \begin{matrix}C_{L\textrm{max}}+ C_{L\textrm{min}} \\ \sigma _\textrm{max} + \sigma _\textrm{min} \end{matrix} \right] . \end{aligned}$$

(79)

The time derivative of Eq. (79) yields

$$\begin{aligned} {{\varvec{u}}}= & {} \left[ \begin{array}{c}{\dot{C}}_L \\ {\dot{\sigma }} \end{array} \right] = \dfrac{1}{\pi } \left[ \begin{array}{ccc} \dfrac{C_{L\textrm{max}}-C_{L\textrm{min}}}{1+w_1^2} &{} 0 \\ 0 &{} \dfrac{\sigma _\textrm{max}-\sigma _\textrm{min}}{1+w_2^2}\end{array} \right] \left[ \begin{array}{c} {\dot{w}}_1 \\ {\dot{w}}_2 \end{array} \right] \nonumber \\= & {} {{\textbf {K}}} \left[ \begin{array}{c}{\dot{w}}_1 \\ {\dot{w}}_2 \end{array} \right] = {{\textbf {K}}} {{\varvec{w}}}, \end{aligned}$$

(80)

where matrix ${{\textbf {K}}}$ is nonsingular. Therefore the new control variables are given by

$$\begin{aligned} {{\varvec{w}}} = [{{\textbf {K}}}]^{-1}{{\varvec{u}}}. \end{aligned}$$

(81)

4.6.2 Gain Selection

The guidance algorithm requires extensive tuning for the control gains $n_1$ and $n_2$ [19]. The choice of the control gains $n_1$ and $n_2$ strongly affects the outcome of the numerical simulations. In this study, the gain $n_2$ is set to 5 after extensive trial and error. With regard to gain $n_1$, an adaptive strategy is employed: its value is updated at the beginning of each sampling intervals $[t_k,t_{k+1}]$. In particular, the value increases from a minimum value ($n_1=1$) at TAEM to a maximum value ($n_1=4$) when the altitude is zero,

$$\begin{aligned} n_1 = 1+(4-1) \cdot \Bigg ( 1- \dfrac{x_0^k}{x_0} \Bigg )^{10}, \end{aligned}$$

(82)

where $x_0^k$ is the altitude at time $t_k$. This strategy allows employing a higher value of the control gain only during the final flare, where the guidance algorithm must handle quick maneuvers with short response time.

4.6.3 Guidance Algorithm

In this subsection, a description of the guidance algorithm is provided. The integration time is divided in time intervals with the same duration (1 s). In each sampling intervals $[t_k, t_{k+1}]$, the following operations are iteratively computed:

• given the instantaneous state at $t_k$, the simplified dynamics Eqs. (63) through (65) are integrated;

• the control variables $(C_L, \sigma )$ are interpolated;

• the complete dynamics Eqs. (40) through (42) are integrated;

• the initial state at $t_{k+1}$ is updated.

4.7 Numerical Results

A total number of 500 simulations are run and the initial conditions are randomly generated with upper/lower bounds set to $\pm 2 \sigma _s$ (where $\sigma _s$ denotes the standard deviation of the variable of interest). Table 4 collects the initial conditions, which reflect the actual reference flight profile of the Space Shuttle [25]. From inspection of Table 4, it is also clear that the guidance algorithm is tested over a 100 km$^{2}$ area and a wide range of velocities. Instead, the standard deviations on the angle of attack and on the bank angle are stricter as these parameters significantly affect the results of the simulations. Also, the final conditions along the transatmospheric arc (cfr. Table 3) lie inside the admissible deviations for the terminal guidance.

Table 4 Terminal guidance: initial conditions and standard deviations

Instead, Table 5 collects the results of the Monte Carlo campaign.

Table 5 Results of the Monte Carlo campaign

All simulations are successful, meaning that the final vertical velocity at touchdown is below $-$ 3 m/s, complying with the safety limit of the landing gear [25]. The Cartesian coordinates are reported as downrange ($r_\textrm{down}$) and crossrange ($r_\textrm{cross}$) components to better visualize the position of the vehicle along the runway. These can be easily retrieved from the ALI-frame through a rotation along axis 1,

$$\begin{aligned} r_\textrm{down} = \left[ \begin{matrix}x&y&z \end{matrix} \right] {{\textbf {R}}}_1^T (\zeta _{rwy}) \left[ \begin{matrix} 0&1&0 \end{matrix} \right] ^T, \end{aligned}$$

(83)

$$\begin{aligned} r_\textrm{cross} = \left[ \begin{matrix}x&y&z \end{matrix} \right] {{\textbf {R}}}_1^T (\zeta _{rwy}) \left[ \begin{matrix} 0&0&1 \end{matrix} \right] ^T. \end{aligned}$$

(84)

From inspection of Table 5, it is evident that the algorithm is able to drive the vehicle to the prescribed landing point, located 762 m beyond the runway threshold (cfr. Sect. 4.3), with limited crossrange component and vertical velocity at touchdown, and the proper alignment with the runway. This is confirmed by inspection of Fig. 11, that shows the stream of trajectories from the TAEM to the landing runway.

Fig. 11

Stream of trajectories

Fig. 12

Time histories of the vertical velocity

The vertical velocity at touchdown is close to the desired value (Fig. 12) and the standard deviation guarantees in all cases a safe touchdown. Also, inspection of Fig. 13 highlights that the vehicle is aligned with the landing runway despite the initial dispersions on the heading angle.

Fig. 13

Time histories of the heading angle

Finally, Figs. 14 and 15 show the time histories of the angle of attack and bank angle.

Fig. 14

Time histories of the angle of attack

Fig. 15

Time histories of the bank angle

The angle of attack is saturated in order not to overcome the maximum value. Also, the standard deviation on the final angle of attack is far from the aerodynamic stall, which is expected to occur at angles $\alpha$ exceeding 25$^{\circ }$ [21]. The commanded maneuvers do not require any saturation for the bank angle; however, Fig. 15 exhibits some oscillations just before touchdown, though the fluctuations do not yield any impact of the wing tips with the ground.

Fig. 16

Time histories of the yaw angle

Fig. 17

Time histories of the pitch angle

Fig. 18

Time histories of the roll angle

Figures 16, 17, 18 show the time histories of the Bryant angles, which allow to visualize the attitude of the vehicle in the inertial frame. Remarkably, these variables exhibit similar behaviour as other ones: for instance, the roll angle is indistinguishable from the bank angle, because during the terminal descent the longitudinal axis and the relative velocity are almost coincident.

Fig. 19

Time histories of the load factor $n_z$

Figure 19 shows the time histories of the vertical load factor, computed as

$$\begin{aligned} n_z = \dfrac{\tilde{L}}{mg_0}. \end{aligned}$$

(85)

It is evident that the flare maneuvers do not yield any excessive load factors on the vehicle, which are below the maximum values (cfr. Table 1).

Fig. 20

Distribution of the landing spots

Finally, Fig. 20 depicts the distribution of the landing spots. Most of the points are located at the specified landing site (762 m beyond the threshold), with a few trajectories impacting the ground before the specified landing point. These simulations correspond to environmental conditions with a strong tailwind component, which is the most critical scenario for a lifting vehicle with no propulsion. However, in the worst simulation the landing spot is located 699 m beyond the threshold, thus within an acceptable safety margin.

5 Concluding Remarks

This paper addresses the problem of driving a winged vehicle (as, for example, the Space Shuttle Orbiter) from the entry interface to landing, while satisfying all the constraints. The transatmospheric guidance is based on an open-loop algorithm that minimizes the total heat input and saturates the maximum thermic flux. The terminal guidance is based on a multiple-sliding-surface strategy, which yield a real-time feedback law for the time derivatives of the lift coefficient and bank angle. The simulation setup includes a complete dynamic framework with an accurate aerodynamics modeling based on wind tunnel tests. The numerical results show the ability of the proposed guidance to modulate the angle of attack to avoid exceeding the maximum thermal flux, while compensating for winds and dispersions of position and velocity from the nominal trajectory during the terminal phase. The vehicle reaches the assigned landing point with the proper alignment with the runway and prescribed vertical velocity.