1 Introduction

In recent years, human and robotic missions to the Moon are attracting a renewed interest by the scientific community, and some lunar missions are planned in this decade. The development of a safe and reliable guidance and control architecture for autonomous lunar descent and soft touchdown represents a challenging and crucial issue for enabling in situ operations, with the prospect of establishing a permanent lunar settlement.

The problem of guiding a spacecraft to safely land on the Moon, reaching the lunar surface with desired (small) velocity and adequate attitude, dates to the space-race years. Luna 9, the first spacecraft to succeed in surviving a lunar landing, relied on a simple guidance scheme, consisting in a single attitude maneuver at 8300 km of altitude and a powered descent phase, initiated at 75 km of altitude and terminated at 5 m of altitude [1]. This ensured touchdown with a velocity ranging between 4 and 7 m/s along the local vertical direction [2]. More sophisticated solutions were rapidly developed during the Apollo program, with the Apollo 11 and the following missions relying on an explicit descent guidance, developed by Klumpp [3]. He designed the landing trajectory as a sequence of two phases: (i) breaking and approach phase (near-optimal in the breaking arc), and (ii) terminal-descent phase, which was a hybrid automatic-manual solution. Since then, Apollo-like algorithms were proposed, and found a great benefit from the rapid development of computational capabilities in the last 50 years. Recent contributions on the study of guidance and control techniques tailored to lunar descent and touchdown are due to Chomel and Bishop [4], who proposed a targeting algorithm based on generating a two-dimensional trajectory, used as a reference for three-dimensional guidance. Lee [5] assumed a continuous time-varying thrust profile and referred to a nominal trajectory similar to that used in the Apollo 11 mission, capable of guaranteeing safe touchdown conditions, together with acceptable fuel consumption, which was a free parameter in Klumpp’s guidance. The effects of external torques and limited thrust magnitude on the powered descent arcs was recently examined by Reynolds and Mesbahi [6], who designed a maneuver evolving onto an inertially fixed plane, similarly to what occurred in the Luna 9 mission. Hull [7] investigated optimal guidance for quasi-planar lunar descent with thrust throttling over a flat Moon. Several mission-oriented publications dealt with effective terrain-relative navigation techniques [8, 9], able to provide the measurements needed for a successful touchdown, or investigated solutions that include hazard detection and avoidance [10, 11]. With regard to the terminal descent and touchdown phase, Rijesh et al. [12] proposed a purely geometrical solution, which ensures soft touchdown and is an adaptation of the circular guidance formulated by Vincent [13].

This research considers the descent path of a space vehicle, from periselenium of its operational orbit to the lunar surface, under the assumption that the descent path is planar. Although this can be regarded as a restrictive assumption, the terminal-descent path is nearly planar in real mission scenarios. The parking orbit about the Moon is properly selected in the preceding phases of the mission, and lies in an orbital plane that contains the expected landing site. It is worth remarking that along a two-dimensional trajectory, attitude motion is identified by a single angle. The descent trajectory is split in two arcs: (a) approach path, up to a specified altitude, and (b) terminal descent and soft touchdown. For phase (a), a new local-flat near-optimal guidance is used, which is based on iterative projection of the spacecraft position and velocity. A minimum-time problem is defined using the locally flat coordinates, and consists in finding the optimal thrust direction that minimizes the time of flight for achieving the desired conditions at the end of phase (a). Attitude control is aimed at pursuing the desired spacecraft orientation. This study employs an adaptive tracking scheme that compensates for the inertia uncertainties. Arc (b) is aimed at gaining the correct vertical alignment and low velocity and angular rate at touchdown. For phase (b) a predictive bang-off-bang guidance algorithm is proposed aimed at guaranteeing the desired final conditions, while providing the proper allocation of side jet ignitions. While the main motor is employed for decelerating the landing vehicle, side jets are used to gain the correct attitude and simultaneously reduce the horizontal velocity. Actuation of side jets is implemented using pulse width modulation, in both phase (a) and phase (b). Monte Carlo simulations are run, with the intent of demonstrating the effectiveness of the guidance, control, and actuation architecture at hand for lunar descent and safe touchdown, in the presence of nonnominal flight conditions related to initial displacements on position, velocity, attitude, and angular rate.

2 Spacecraft Dynamics

The descent vehicle is subject to the only gravitational attraction of the Moon and is assumed to be equipped with a main thruster, aligned with the longitudinal axis, and four side jets (arranged in pairs). The main gravitational term and the \(J_{2}\) term of the selenopotential are included in the dynamical model. Let T and \(F_{{{\text{tot}}}}\) represent respectively the thrust magnitudes supplied by the main engine and by a pair of side jets. The mass ratio, denoted with \(\varsigma = {m \mathord{\left/ {\vphantom {m {m_{0} }}} \right. \kern-\nulldelimiterspace} {m_{0} }}\) (where \(m_{0}\) is the initial mass) obeys \(\dot{\varsigma } = - {{n_{T} } \mathord{\left/ {\vphantom {{n_{T} } {c_{M} }}} \right. \kern-\nulldelimiterspace} {c_{M} }} - {{n_{SJ} } \mathord{\left/ {\vphantom {{n_{SJ} } {c_{SJ} }}} \right. \kern-\nulldelimiterspace} {c_{SJ} }}\), where \(n_{T} : = {T \mathord{\left/ {\vphantom {T {m_{0} }}} \right. \kern-\nulldelimiterspace} {m_{0} }}\) and \(n_{SJ} : = {{F_{tot} } \mathord{\left/ {\vphantom {{F_{tot} } {m_{0} }}} \right. \kern-\nulldelimiterspace} {m_{0} }}\). In this study T is constant and \(F_{{{\text{tot}}}}\) decreases exponentially with time due to propellant depletion. Symbols \(c_{M}\) and \(c_{SJ}\) denote the effective exhaust velocities of the main thruster and the side jets, respectively. Trajectory and attitude equations, reported in the next subsections, govern the spacecraft dynamics.

2.1 Trajectory

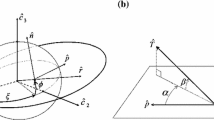
The descent trajectory is described in the Moon-centered inertial reference frame, associated with the right-hand sequence of unit vectors \(\left( {\hat{c}_{1} ,\hat{c}_{2} ,\hat{c}_{3} } \right)\). Its origin is located at the center of the Moon and axes \(\left( {\hat{c}_{1} ,\hat{c}_{2} } \right)\) identify the lunar equatorial plane. The initial elliptic orbit is assumed to be equatorial, with periselenium aligned with \(\hat{c}_{1}\). Since the descent path is assumed to be planar, the position can be identified by the following two variables: radius r and right ascension \(\xi\), taken counterclockwise from \(\hat{c}_{1}\) (cf. Fig. 1). The spacecraft velocity \({\mathop{\varvec{v}}\limits_{\rightarrow} }\) can be projected into the rotating frame \(\left( {\hat{r},\hat{t}} \right)\), where \(\hat{r}\) is aligned with the position vector \({\mathop{\varvec{r}}\limits_{\rightarrow} }\) and \(\hat{t}\) points toward the local horizontal (and is in the direction of the spacecraft motion). The components of \({\mathop{\varvec{v}}\limits_{\rightarrow} }\) are denoted with \(\left( {v_{r} ,v_{t} } \right)\) and termed respectively radial and transverse (or horizontal) component. The descent vehicle is controlled through the thrust direction, identified by the angle \(\alpha\), taken clockwise from \(\hat{t}\), as illustrated in Fig. 1. The governing equations for \(\left( {r,\xi ,v_{r} ,v_{t} } \right)\) are

$$\dot{r} = v_{r} \quad \dot{\xi } = \frac{{v_{t} }}{r}\quad \dot{v}_{r} = - \frac{\mu }{{r^{2} }} + \frac{{v_{t}^{2} }}{r} + a_{T} \sin \alpha - \frac{3\mu }{{2r^{4} }}R_{M}^{2} J_{2} \quad \dot{v}_{t} = - \frac{{v_{r} v_{t} }}{r} + a_{T} \cos \alpha$$
(1)

where \(a_{T}\) is the instantaneous thrust acceleration, given by \(a_{T} = \left( {{{n_{T} } \mathord{\left/ {\vphantom {{n_{T} } \varsigma }} \right. \kern-\nulldelimiterspace} \varsigma }} \right)\), whereas \(\mu\), \(R_{M}\), and \(J_{2}\) are the lunar gravitational parameter, equatorial radius, and oblateness coefficient, respectively. Descent is assumed to start from periselenium of the lunar orbit, and this allows identifying the initial conditions for the four variables \(\left( {r,\xi ,v_{r} ,v_{t} } \right)\).

Fig. 1
figure 1

Reference frames for trajectory and attitude

Full size image

2.2 Attitude

This study considers only planar motion in the \(\left( {\hat{c}_{1} ,\hat{c}_{2} } \right)\)-plane. The spacecraft instantaneous orientation is associated with the body frame \(\left( {\hat{x}_{b} ,\hat{y}_{b} ,\hat{z}_{b} } \right)\), whose origin is in the instantaneous center of mass of the vehicle, its axes coincide with the principal axes of inertia, \(\hat{x}_{b}\) is aligned with the longitudinal axis, and \(\hat{z}_{b}\) coincides with the axis of rotation (orthogonal to \(\left( {\hat{c}_{1} ,\hat{c}_{2} } \right)\)). Therefore, the spacecraft attitude is identified through only angle \(\psi\) (cf. Fig. 1) which identifies the direction of \(\hat{x}_{b}\) and is taken counterclockwise from \(\hat{c}_{1}\). The attitude equation is given by

$$\dot{J}_{z} \dot{\psi } + J_{z} \ddot{\psi } = M_{z}$$
(2)

where \(J_{z}\) is the moment of inertia of the spacecraft about \(\hat{z}_{b}\) and \(M_{z}\) is the torque component along the same axis; \(M_{z}\) is generated by the torque actuators.

3 Guidance Algorithms

The descent path is split into two arcs: (a) approach phase, starting from periselenium of the lunar orbit and ending with zero velocity at a specified altitude Hint, and (b) final descent and touchdown, from altitude Hint to the lunar surface. The junction condition corresponds to hovering at modest altitude. This allows checking the spacecraft instrumentation and instantaneous flight conditions, and facilitates the design of an abort maneuver, in the presence of unfavorable contingencies. Phase (a) is much longer than arc (b); nevertheless, phase (b) is crucial for the purpose of attaining the desired conditions at touchdown, i.e. vertical velocity magnitude not exceeding 1 m/s, zero horizontal velocity, longitudinal axis aligned with the vertical direction, and zero angular velocity. Two distinct algorithms are proposed in this work, for the two trajectory arcs.

3.1 Phase (a): Locally-flat near-optimal guidance

For the approach phase (a), this research proposes a near-optimal guidance scheme based on local projection of the spacecraft position and velocity. The guidance algorithm is run repeatedly and starts at equally-spaced discrete times \(\left\{ {t_{k} } \right\}_{k = 0, \ldots ,N - 1}\). The symbol \(\Delta t_{S}\) denotes the sampling time interval, i.e. \(\Delta t_{S} = t_{k + 1} - t_{k} \, \left( {k = 1, \ldots ,N - 2} \right)\); the last interval is shorter, because the guidance and control algorithm stops when the desired conditions are reached with satisfactory accuracy. At time \(t_{k}\), the spacecraft position and velocity \({\mathop{\varvec{r}}\limits_{\rightarrow} }\) and \({\mathop{\varvec{v}}\limits_{\rightarrow} }\) are denoted with \({\mathop{\varvec{r}}\limits_{\rightarrow} }_{k}\) and \({\mathop{\varvec{v}}\limits_{\rightarrow} }_{k}\), and are associated with \(\left( {r_{k} ,\xi_{k} ,v_{r,k} ,v_{t,k} } \right)\). Let \(\left( {\hat{x}_{k} ,\hat{y}_{k} } \right)\) denote two unit vectors obtained from \(\left( {\hat{c}_{1} ,\hat{c}_{2} } \right)\) through a counterclockwise rotation about \(\hat{c}_{3}\) axis by angle \(\xi_{k}\). The locally flat variables \(\left( {x,y,v_{x} ,v_{y} } \right)\) are introduced, with values at \(t_{k}\) corresponding to the components of \({\mathop{\varvec{r}}\limits_{\rightarrow} }_{k}\) and \({\mathop{\varvec{v}}\limits_{\rightarrow} }_{k}\) along \(\left( {\hat{x}_{k} ,\hat{y}_{k} } \right)\), i.e.

$$x_{k} = r_{k} \quad y_{k} = 0\quad v_{x,k} = v_{r,k} \quad v_{y,k} = v_{t,k}$$
(3)

The locally flat variables are governed by the following equations of motion [9]

$$\dot{x} = v_{x} \quad \dot{y} = v_{y} \quad \dot{v}_{x} = \tilde{a}_{T} \sin \theta - g\quad \dot{v}_{y} = \tilde{a}_{T} \cos \theta$$
(4)

where angle \(\theta\) identifies the thrust direction in \(\left( {\hat{x}_{k} ,\hat{y}_{k} } \right)\), g denotes the (local) gravitational acceleration, and \(\tilde{a}_{T}\) is the thrust acceleration. In the context of locally flat coordinates, a different symbol is used for the latter variable, because a fundamental assumption on \(\tilde{a}_{T}\) will be proven to lead to further remarkable analytical developments. Using \(\left( {x,y,v_{x} ,v_{y} } \right)\), the desired conditions at the end of phase (a) are

$$x_{f} = R_{M} + H_{{\text{int}}} \quad v_{x,f} = 0\quad v_{y,f} = \omega_{M} R_{M}$$
(5)

where \(\omega_{M}\) and \(R_{M}\) denote respectively the lunar rotation rate and radius. The final condition on \(v_{y,f}\) considers the modest inertial velocity of a point on the lunar surface (at equator).

The optimal thrust angle \(\theta\) is sought that minimizes the time of flight needed to fulfill the boundary conditions, while holding the state Eq. (4), i.e.

$$\theta_{{}}^{*} = \arg \mathop {\min }\limits_{\theta } t_{f} \quad {\text{subject to}}\,{\text{Eqs}}{.}\,\left( 4 \right) - \left( 5 \right)$$
(6)

where “*” denotes the optimal value of the related variable.

The problem at hand admits an analytical solution that depends on the initial values of the adjoint vector conjugate to the state Eq. (4), if \(\tilde{a}_{T}\) and g are assumed constant in Eq. (4). To prove this, a Hamiltonian H and the auxiliary function \(\Phi\) are introduced,

$$H = \lambda_{1} v_{x} + \lambda_{2} v_{y} + \lambda_{3} \left( {\tilde{a}_{T} \sin \theta - g} \right) + \lambda_{4} \tilde{a}_{T} \cos \theta$$
(7)
$$\Phi = t_{f} + \upsilon_{1} \left[ {x_{f} - \left( {R_{M} + H_{{\text{int}}} } \right)} \right] + \upsilon_{2} v_{x,f} + \upsilon_{3} \left( {v_{y,f} - \omega_{M} R_{M} } \right)$$
(8)

where \(\left\{ {\lambda_{j} } \right\}_{j = 1, \ldots ,6}\) and \(\left\{ {\upsilon_{j} } \right\}_{j = 1, \ldots ,5}\) are respectvely the adjoint variables conjugate to the state Eq. (4) and to the boundary conditions (5). The necessary conditions for optimality include the boundary conditions for the adjoint variables [14],

$$\lambda_{1,f} = \upsilon_{1} \quad \lambda_{2,f} = 0\quad \lambda_{3,f} = \upsilon_{2} \quad \lambda_{4,f} = \upsilon_{3}$$
(9)

accompanied by the adjoint equations

$$\dot{\lambda }_{1} = - \frac{\partial H}{{\partial x}} = 0\quad \Rightarrow \quad \lambda_{1} = \lambda_{1,0}$$
(10)
$$\dot{\lambda }_{2} = - \frac{\partial H}{{\partial y}} = 0\quad \Rightarrow \quad \lambda_{2} = \lambda_{2,0} = \lambda_{2,f} = 0$$
(11)
$$\dot{\lambda }_{3} = - \frac{\partial H}{{\partial v_{x} }} = - \lambda_{1} \quad \Rightarrow \quad \lambda_{3} = \lambda_{3,0} - \lambda_{1,0} t$$
(12)
$$\dot{\lambda }_{4} = - \frac{\partial H}{{\partial v_{y} }} = - \lambda_{2} \quad \Rightarrow \quad \lambda_{4} = \lambda_{4,0} - \lambda_{2,0} t = \lambda_{4,0}$$
(13)

The Pontryagin minimum principle leads to expressing the control angles in terms of the adjoint variables,

$$\theta_{{}}^{*} = \arg \mathop {\min }\limits_{\theta } H\quad \Rightarrow \quad \sin \theta = - \frac{{\lambda_{3} }}{{\sqrt {\lambda_{3}^{2} + \lambda_{4}^{2} } }}\quad \cos \theta = - \frac{{\lambda_{4} }}{{\sqrt {\lambda_{3}^{2} + \lambda_{4}^{2} } }}$$
(14)

The condition \(\lambda_{4,0} = 0\) leads to \(\theta = \pm {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}\), which implies violation of the final conditions, therefore \(\lambda_{4,0} \ne 0\). Hence, the closed-form expressions of \(\left\{ {\lambda_{1} ,\lambda_{3} ,\lambda_{4} } \right\}\) can be scaled by \(\lambda_{4,0}\), to yield

$$\sin \theta = - \frac{{\tilde{\lambda }_{3,0} - \tilde{\lambda }_{1,0} t}}{{\sqrt {\left( {\tilde{\lambda }_{3,0} - \tilde{\lambda }_{1,0} t} \right)^{2} + 1} }}\quad \cos \theta = - \frac{1}{{\sqrt {\left( {\tilde{\lambda }_{3,0} - \tilde{\lambda }_{1,0} t} \right)^{2} + 1} }}$$
(15)

where \(\tilde{\lambda }_{j,0} = {{\lambda_{j,0} } \mathord{\left/ {\vphantom {{\lambda_{j,0} } {\lambda_{4,0} }}} \right. \kern-\nulldelimiterspace} {\lambda_{4,0} }} \, \left( {j = 1,3} \right)\). The analytical expressions (15) are used in Eq. (4) and lead to obtaining closed-form solutions for all of the state variables [14],

$$\begin{aligned} x & = x_{0} + \left( {v_{x,0} - \frac{{\tilde{a}_{T} }}{{\tilde{\lambda }_{1,0} }}\sqrt {1 + \tilde{\lambda }_{3,0}^{2} } } \right)t - g\frac{{t^{2} }}{2} - \frac{{\tilde{a}_{T} }}{{\tilde{\lambda }_{1,0}^{2} }}\left[ {\frac{{\tilde{\lambda }_{3,0} - \tilde{\lambda }_{1,0} t}}{2}\sqrt {1 + \left( {\tilde{\lambda }_{3,0} - \tilde{\lambda }_{1,0} t} \right)^{2} } } \right] \\ & \quad - \frac{{\tilde{a}_{T} }}{{2\tilde{\lambda }_{1,0}^{2} }}\sinh^{-1} \left( {\tilde{\lambda }_{3,0} - \tilde{\lambda }_{1,0} t} \right) + \frac{{\tilde{a}_{T} }}{{\tilde{\lambda }_{1,0}^{2} }}\left[ {\frac{{\tilde{\lambda }_{3,0} }}{2}\sqrt {1 + \tilde{\lambda }_{3,0}^{2} } + \frac{1}{2}\sinh^{-1} \left( {\tilde{\lambda }_{3,0} } \right)} \right] \\ \end{aligned}$$
(16)
$$v_{x} = v_{x,0} - gt + \frac{{\tilde{a}_{T} }}{{\tilde{\lambda }_{1,0} }}\left[ {\sqrt {1 + \left( {\tilde{\lambda }_{3,0} - \tilde{\lambda }_{1,0} t} \right)^{2} } - \sqrt {1 + \tilde{\lambda }_{3,0}^{2} } } \right]$$
(17)
$$v_{y} = v_{y,0} + \frac{{\tilde{a}_{T} }}{{\tilde{\lambda }_{1,0} }}\left[ {\sinh^{-1} \left( {\tilde{\lambda }_{3,0} - \tilde{\lambda }_{1,0} t} \right) - \sinh^{-1} \left( {\tilde{\lambda }_{3,0} } \right)} \right]$$
(18)

The closed-form expression for y is not reported because it is useless in the subsequent steps. The preceding solutions for \(\left\{ {x,v_{x} ,v_{y} } \right\}\) are evaluated at \(t_{f}\) and inserted in the boundary conditions, to yield a system of 3 nonlinear equations in 3 unknowns, i.e. \(\left\{ {\tilde{\lambda }_{1,0} ,\tilde{\lambda }_{3,0} ,t_{f} } \right\}\). Numerical solvers (such as the embedded routine fsolve in Matlab) can be used to find the numerical solution of this system in extremely short times (on the order of 0.01 s), provided that a proper initial guess is supplied. To do this, the analysis described in [14] can be used. A suitable first-attempt solution is proven to be [14]

$$t_{f}^{\left( G \right)} = \frac{{v_{y,f} - v_{y,0} }}{{\tilde{a}_{T} }}\frac{{\tan \theta_{0}^{\left( G \right)} - \tan \theta_{f}^{\left( G \right)} }}{{\sinh^{-1} \left( {\tan \theta_{f}^{\left( G \right)} } \right) - \sinh^{-1} \left( {\tan \theta_{0}^{\left( G \right)} } \right)}}\quad \tilde{\lambda }_{1,0}^{\left( G \right)} = \frac{{\tan \theta_{0}^{\left( G \right)} - \tan \theta_{f}^{\left( G \right)} }}{{t_{f}^{\left( G \right)} }}\quad \tilde{\lambda }_{3,0}^{\left( G \right)} = \tan \theta_{0}^{\left( G \right)}$$
(19)

where \(\theta_{0}^{\left( G \right)}\) and \(\theta_{f}^{\left( G \right)}\) are two guess values for the thrust angle \(\theta\) at \(t_{0}\) and \(t_{f}\), respectively; in this work, \(\theta_{0}^{\left( G \right)} = 180{\text{ deg}}\) and \(\theta_{f}^{\left( G \right)} = 120{\text{ deg}}\). The first value corresponds to a thrust direction pointing against the instantaneous velocity (at \(t_{0}\)).

The guidance algorithm repeats the preceding solution process at each sampling time \(t_{k}\), which becomes the initial time \(t_{0}\) of the optimal control problem. The final time \(t_{f}\) can be regarded as the time-to-go, and will be denoted with \(t_{go}\) hence forward. However, constant values of g and \(\tilde{a}_{T}\) are needed in each guidance interval \(\left[ {t_{k} ,t_{k + 1} } \right]\), which has duration \(\Delta t_{S}\). For the gravitational acceleration, the initial value is chosen, i.e. \(g = {\mu \mathord{\left/ {\vphantom {\mu {r_{k}^{2} }}} \right. \kern-\nulldelimiterspace} {r_{k}^{2} }}\). Instead, for the thrust acceleration, the average value of \(a_{T}\) in \(\left[ {t_{k} ,t_{k + 1} } \right]\) is employed. Let \(n_{k}\) denote the thrust acceleration at \(t_{k}\), given by \(n_{k} = {{n_{T} } \mathord{\left/ {\vphantom {{n_{T} } {\varsigma_{k} }}} \right. \kern-\nulldelimiterspace} {\varsigma_{k} }} \, \left( {\varsigma_{k} : = \varsigma \left( {t_{k} } \right)} \right)\). In \(\left[ {t_{k} ,t_{k + 1} } \right]\) the thrust acceleration \(a_{T}\) equals \({{n_{k} c_{M} } \mathord{\left/ {\vphantom {{n_{k} c_{M} } {\left[ {c_{M} - n_{k} \left( {t - t_{k} } \right)} \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {c_{M} - n_{k} \left( {t - t_{k} } \right)} \right]}}\). Hence, in \(\left[ {t_{k} ,t_{k + 1} } \right]\) the constant value \(\tilde{a}_{T}\) is set to

$$\tilde{a}_{T} = \frac{1}{{\Delta t_{S} }}\int\limits_{{t_{k} }}^{{t_{k + 1} }} {\frac{{n_{k} c_{M} }}{{c_{M} - n_{k} \left( {t - t_{k} } \right)}}{\text{d}}t} = - \frac{{c_{M} }}{{\Delta t_{S} }}\ln \left( {1 - \frac{{n_{k} }}{{c_{M} }}\Delta t_{S} } \right)$$
(20)

3.2 Phase (b): Predictive bang-off-bang guidance

Phase (b) starts at the end of arc (a), and is aimed at reaching the lunar surface with low vertical velocity, and zero horizontal velocity and angular rate. The threshold value for \(v_{r}\), is denoted with \(v_{r,th}\). This means that the desired velocity at touchdown is constrained to \([v_{r,th} ,0[\).

The main thruster is responsible for decelerating the spacecraft. However, especially at the very beginning of phase (b), the spacecraft has incorrect alignment, therefore it is convenient to use the main thruster for reducing the horizontal velocity, provided that \(\hat{x}_{b} \cdot {\mathop{\varvec{v}}\limits_{\rightarrow} }_{k} < 0\). Instead, the side jets are used mainly for attitude maneuvering. Yet, when the correct alignment is attained, they can be ignited in pair (on the same side of the descent vehicle), to reduce the horizontal velocity. The following steps, repeated iteratively at each sampling time \(t_{k}\), form the predictive bang-off-bang guidance scheme, aimed at identifying the ignition times for both the main thruster and the side jets:

  1. 1.

    evaluate the expected radial velocity at \(t_{k + 1}\), \(v_{r,k + 1}^{\left( E \right)}\), assuming vertical descent and no propulsion in \(\left[ {t_{k} ,t_{k + 1} } \right]\);

  2. 2.

    evaluate the expected radial velocity at touchdown, \(v_{r,f}^{\left( E \right)}\), assuming vertical descent from time \(t_{k + 1}\) and thrust always on and directed vertically; if touchdown does not occur and the altitude starts increasing, set \(v_{r,f}^{\left( E \right)}\) to infinity;

  3. 3.

    evaluate the direction cosine \(R_{11}\) defined by \(R_{11} : = \hat{x}_{b} \cdot \hat{r}_{k}\), with \(\hat{r}_{k}\) denoting the unit vector aligned with the radial direction (from the center of the Moon) at \(t_{k}\);

  4. 4.

    evaluate \(\eta_{M} : = \hat{x}_{b} \cdot {\mathop{\varvec{v}}\limits_{\rightarrow} }_{k}\);

  5. 5.

    allocate the side jets (for either attitude maneuvering or horizontal velocity correction):

    1. a.

      if \(\left( {R_{11} < 0.9} \right){\text{ or }}\left( {\left| {v_{t,k} - \omega_{M} r_{k} } \right| < 0.1\,{\text{m}}/{\text{s}} } \right)\), then ignite the side jets for attitude maneuvering;

    2. b.

      if \(\left( {R_{11} > 0.999} \right){\text{ and }}\left( {\left| {v_{t,k} - \omega_{M} r_{k} } \right| > 0.1\,{\text{m/s}} } \right)\), then ignite the side jets for horizontal velocity correction;

    3. c.

      if \(\left( {0.9 \le R_{11} \le 0.999} \right){\text{ and }}\left( {\left| {v_{t,k} - \omega_{M} r_{k} } \right| > 0.1\,{\text{m}}/{\text{s}} } \right)\), then allocate a fraction of the sampling time interval to attitude maneuvering, and the rest to horizontal velocity correction; the lengths of the two partitions of the sampling time interval depend on \(R_{11}\);

    4. d.

      if \(\left( {R_{11} > 0.999} \right){\text{ and }}\left( {\left| {v_{t,k} - \omega_{M} r_{k} } \right| \le 0.1\,{\text{m}}/{\text{s}} } \right)\), then switch off the side jets;

  6. 6.

    define the ignition of the main engine in \(\left[ {t_{k} ,t_{k + 1} } \right]\), on the basis of an hysteretic scheme:

    1. a.

      either if (thrust was off in \(\left[ {t_{k - 1} ,t_{k} } \right]\) and \(v_{r,th} \le v_{r,f}^{\left( E \right)} \le 0\)) or \(\left( {\left( {R_{11} < 0.9} \right){\text{ and }}\left( {\eta_{M} \ge 0} \right)} \right)\), then the main engine is off in \(\left[ {t_{k} ,t_{k + 1} } \right]\);

    2. b.

      either if (thrust was on in \(\left[ {t_{k - 1} ,t_{k} } \right]\) and \(v_{r,th} \le v_{r,f}^{\left( E \right)} \le 0\)) or \(\left( {\left( {R_{11} < 0.9} \right){\text{ and }}\left( {\eta_{M} < 0} \right)} \right)\), then the main engine is on in \(\left[ {t_{k} ,t_{k + 1} } \right]\);

    3. c.

      either if (\(v_{r,f}^{\left( E \right)} < v_{r,th}\)) and \(\left( {R_{11} \ge 0.9} \right)\), then the main engine is on in \(\left[ {t_{k} ,t_{k + 1} } \right]\);

    4. d.

      either if (\(v_{r,f}^{\left( E \right)} > 0\)) and \(\left( {R_{11} \ge 0.9} \right)\), then the main engine is off in \(\left[ {t_{k} ,t_{k + 1} } \right]\).

The previous conditions in steps (5) and (6) are checked sequentially, e.g. if condition (6)b is fulfilled, then the main engine is ignited in \(\left[ {t_{k} ,t_{k + 1} } \right]\), and conditions (6)c and (6)d need not to be checked. The preceding scheme yields a bang-off-bang sequence of ignitions for the main thruster and the side jets. When the latter are used for attitude maneuvering, the attitude control algorithm, in conjunction with pulse modulation, identifies the actual ignition times in the time interval \(\left[ {t_{k} ,t_{k + 1} } \right]\).

4 Attitude Control Algorithm

In this study, \(J_{z}\) and \(\dot{J}_{z}\) are not measured, thus the following adaptive attitude control algorithm is employed [15]:

$$M_{z}^{c} = \hat{J}_{z} z + \hat{\dot{J}}_{z} \dot{\psi }\quad {\text{where}}\quad z = \ddot{\psi }_{c} - \beta_{1} \dot{e} - \beta_{0} e\quad {\text{and}}\quad e = \psi - \psi_{c}$$
(21)

in which \(M_{z}^{c}\) is the commanded torque for the torque actuators, \(\beta_{0} > 0\) and \(\beta_{1} > 0\) are constant design gains, \(\psi_{c}\) is the commanded attitude angle determined by the guidance algorithm, whereas \(\hat{J}_{z}\) and \(\hat{\dot{J}}_{z}\) are adaptive parameters, subject to the following adaptation law:

$$\left[ {\begin{array}{*{20}c} {\dot{\hat{J}}_{z} } \\ {\dot{\hat{\dot{J}}}_{z} } \\ \end{array} } \right] = - \gamma \left[ {\begin{array}{*{20}c} 0 & z \\ 0 & {\dot{\psi }} \\ \end{array} } \right]{\varvec{P}}\left[ {\begin{array}{*{20}c} e \\ {\dot{e}} \\ \end{array} } \right]$$
(22)

where \(\gamma > 0\) is a design gain, and P is the symmetric positive definite matrix that satisfies the Lyapunov equation \({\mathbf{PA}} + {\mathbf{A}}^{T} {\mathbf{P}} = - {\mathbf{I}}_{2 \times 2}\), with

$${\mathbf{A}} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - \beta_{0} } & { - \beta_{1} } \\ \end{array} } \right]$$
(23)

The following steps lead to selecting the gains \(\beta_{0} > 0\) and \(\beta_{1} > 0\). When \(J_{z} = \hat{J}_{z} , \, \dot{J}_{z} = \dot{\hat{J}}_{z}\), and \(M_{z} = M_{z}^{c}\), the attitude closed-loop Eqs. (21)–(22) reduce to

$$\ddot{e} + \beta_{1} \dot{e} + \beta_{0} e = 0$$
(24)

which is a differential equation of the form \(\ddot{e} + 2\omega_{n} \zeta \dot{e} + \omega_{n}^{2} e = 0\), in which \(\zeta\) is the damping ratio, and \(\omega_{n}\) is the natural angular frequency. Clearly, \(\zeta\) and \(\omega_{n}\) are related to \(\beta_{1}\) and \(\beta_{0}\) as follows: \(\beta_{1} = 2\zeta \omega_{n}\), \(\beta_{0} = \omega_{n}^{2}\). Thus, proceeding by trial-and-error the following values are selected: \(\zeta = 0.7{\text{ and }}\omega_{n} = 4\,{\text{s}}^{ - 1}\), which lead to \(\beta_{0} = 16\) \(\beta_{1} = 5.6\). The gain for the adaptation law is set to \(\gamma = 100\) on a trial-and error basis.

5 Pulse-Modulated Actuation

The control torque (\(M_{z}\)) is provided by a set of 4 monopropellant thrusters, located in pairs at a distance \(D/2\) from the longitudinal axis of the spacecraft and producing a thrust onto the \(\left( {\hat{c}_{1} ,\hat{c}_{2} } \right)\)-plane. A pair of thrusters is ignited using the pulse width modulation (PWM) technique. PWM converts the commanded torque \(M_{z}^{c}\) into the ignition time \(t_{{{\text{ON}}}}\) of the pulsed thrusters,

$$t_{{{\text{ON}}}} = \left\{ {\begin{array}{*{20}l} {DC} \hfill & {{\text{if}}\,\left| {M_{z}^{c} } \right| \ge M_{\max } } \hfill \\ {\frac{{\left| {M_{z}^{c} } \right|}}{{M_{\max } }}DC} \hfill & {{\text{if}}\,M_{\min } < \left| {M_{z}^{c} } \right| < M_{\max } } \hfill \\ 0 \hfill & {{\text{if}}\,\left| {M_{z}^{c} } \right| \le M_{\min } } \hfill \\ \end{array} } \right.$$
(25)

where DC denotes the duty cycle and represents a design parameter for the modulator [16], whereas \(M_{\max } = DF_{SJ}\), with \(F_{SJ}\) denoting the thrust magnitude provided by each side jet. The sign of \(M_{z}^{c}\) determines which pair of side jets is ignited. Instead, \(t_{{{\text{ON}}}}^{{\left( {\min } \right)}}\) is the minimum duration of the duty cycle, which is a technological specification that depends on the maximum operational frequency of the pulsed thrusters [17]. Finally, \(M_{\min } : = DF_{SJ} \left( {{{t_{{{\text{ON}}}}^{{\left( {\min } \right)}} } \mathord{\left/ {\vphantom {{t_{{{\text{ON}}}}^{{\left( {\min } \right)}} } {DC}}} \right. \kern-\nulldelimiterspace} {DC}}} \right)\) is the minimum torque provided by the actuators.

6 Numerical Simulations

The Peregrine lander [18] is selected as the prototypical vehicle. Although its geometry is more complex, it can be modeled as a cylinder, with diameter D of 2 m and height of 2 m. Its initial mass and principal moments of inertia [19] equal \(m_{0} = 1283\,{\text{kg}}\), \(I_{xx,0} = 1827\,{\text{kg}}\,{\text{m}}^{2}\), and \(I_{yy,0} = I_{zz,0} = 819\,{\text{kg}}\,{\text{m}}^{2}\). At the initial time, the main engine provides a thrust of 4730 N, whereas each side jet supplies 200 N [20]. The respective effective exhaust velocities are \(c_{M} = 3\,{\text{km}}/{\text{s}}\) and \(c_{SJ} = 2.158\,{\text{km}}/{\text{s}}\). For the main thruster, the preceding value corresponds to an average thrust acceleration (approximately) equal to 0.5 \({\text{g}}_{0} \, \left( {{\text{g}}_{0} = 9.8\,{\text{m}}/{\text{s}}^{2} } \right)\). For the side jets, decrease of the thrust magnitude due to reduction of the pressurant gas is modeled, and obeys an exponential law with time constant equal to 7027 s [21]. The latter is a characteristic parameter that depends on the tank volume and the fluid properties [22].

At the initial time, the spacecraft travels an elliptic, equatorial lunar orbit, with periselenium and aposelenium altitudes equal to 15 km and 100 km, respectively. The nominal initial attitude corresponds to zero angular velocity and \(\psi_{0} = - 90{\text{ deg}}\). Moreover, actuation devices are characterized by the following paramteters: \(t_{{{\text{ON}}}}^{{\left( {\min } \right)}} = 0.01\,{\text{s}}\) and \(DC = 0.1\,{\text{s}}\).

The guidance, control, and actuation architecture proposed in this study is tested in the presence of non-nominal flight conditions, namely errors in (i) the initial components of position and velocity and (ii) initial attitude and angular rate. The sampling time interval is set to 5 s for phase (a) and 0.2 s for phase (b). The intermediate altitude Hint is set to 50 m, whereas the threshold velocity is \(v_{r,th} : = - 1\,{\text{m}}/{\text{s}}\). The \(J_{2}\) harmonic of the selenopotential is responsible of further deviations from the nominal flight conditions, because the guidance algorithm considers only a piecewise constant gravitational acceleration. A Monte Carlo campaign, composed of 100 simulations, is run, with the intent of testing the G&C methodology at hand. Initial stochastic displacements on the position and velocity variables are assumed, with zero mean and the following standard deviations: \(r_{0}^{\left( \sigma \right)} = 2\,{\text{km}}\) and \(v_{0}^{\left( \sigma \right)} = 50\,{\text{m}}/{\text{s}}\), where \(\chi_{0}^{\left( \sigma \right)}\) denotes the initial standard deviation of the generic variable \(\chi\) and \(v_{0}^{\left( \sigma \right)}\) represents the standard deviation on the initial velocity magnitude; the random direction of the displacement on the initial velocity has uniform distribution in the interval \(\left[ {0,2\pi } \right]\). Similarly, the initial attitude is perturbed by introducing stochastic displacements to \(\psi\) and \(\dot{\psi }\), with zero mean and standard deviations \(\psi_{0}^{\left( \sigma \right)} = 30{\text{ deg}}\) and \(\dot{\psi }_{0}^{\left( \sigma \right)} = 10\,{\text{deg/s}}\).

Figure 2 portrays the time histories (obtained in the MC campaign) of altitude and velocity components in phase (a), as well as the commanded and actual attitude angles \(\psi_{c}\) and \(\psi\) (in a single MC simulation), which are nearly indistinguishable for the entire time of flight. The relative transverse velocity, illustrated in Figs. 2 and 3, is defined as \(v_{t,R} = v_{t} - \omega_{M} r\) and takes into account the (modest) rotation rate of the Moon. Figure 2 depicts the time histories of altitude velocity components, and angular rate \(\omega_{z} \, \left( { = \dot{\psi }} \right)\) (from the MC campaign) in phase (b), whereas Fig. 4 portrays the time history of the modulated torque (in a single MC run), in phase (b). Finally, Fig. 5 illustrates the zoom on the time histories of altitude, velocity components, and angular rate, in the last seconds before touchdown.

Fig. 2
figure 2

Time histories of altitude, velocity components, and attitude angle (phase (a))

Full size image
Fig. 3
figure 3

Time histories of altitude, velocity components, and angular rate (phase (b))

Full size image
Fig. 4
figure 4

Time history of the torque component, in a single MC simulation (phase (b))

Full size image
Fig. 5
figure 5

Zoom on time histories of altitude, velocity components, and angular rate (phase (b))

Full size image

The final altitude of the center of mass equals 0.95 m, and takes into account its actual position inside the descent vehicle. The statistics on the final values at touchdown regard the velocity components for both the center of mass and the four pads that touch the lunar surface. Tables 1 and 2 report these statistics, which unequivocally testify to the excellent performance of the guidance, control, and actuation architecture at hand.

Table 1 Lunar descent and touchdown: statistics obtained from the MC campaign (\(\overline{{\Delta \chi_{f} }}\) = mean value of the error on the desired final value of \(\chi\); \(\chi_{f}^{\left( \sigma \right)}\) = standard deviation of the final value of \(\chi\); \(\overline{t}_{f}\) = mean value of the time of flight; \(t_{f}^{(\sigma )}\) = standard deviation of the time of flight)
Full size table
Table 2 Lunar descent and touchdown: statistics obtained from the MC campaign for the four pads (\(\overline{{\Delta \chi_{f} }}\) = mean value of the error on the desired final value of \(\chi\); \(\chi_{f}^{\left( \sigma \right)}\) = standard deviation of the final value of \(\chi\))
Full size table

7 Concluding Remarks

This work proposes and applies a new guidance, control, and actuation architecture for autonomous lunar descent and landing. The descent path is split in two phases: (a) approach and (b) terminal descent and touchdown. In phase (a), an explicit near-optimal guidance, based on the local projection of the spacecraft velocity and position, is proposed and applied. A minimum-time problem is defined using the locally flat coordinates, and consists in finding the optimal thrust direction that minimizes the time of flight for achieving the desired hovering conditions at the end of phase (a). The optimal control problem is amenable to a closed-form solution, which is a fundamental prerequisite for the guidance implementation as a real-time iterative process. Availability of closed-form expressions allows translating the minimum-time (differential) problem of interest into three nonlinear equations in three unknowns. Their numerical values can be obtained as a real-time process, because a suitable guess, related to intuitive dynamical variables, is available. The method at hand iteratively yields a closed-form function of time for the thrust angle, which identifies the near-optimal (commanded) thrust direction. The latter represents the desired alignment condition for the spacecraft longitudinal axis. This is pursued by the attitude control system, which includes an adaptive tracking scheme (capable of compensating for the inertia uncertainties) and side jets as actuation devices. Arc (b) is aimed at gaining simultaneously (i) correct vertical alignment, (ii) low velocity, and (iii) reduced angular rate at touchdown. In phase (b) a predictive bang-off-bang guidance algorithm is proposed and applied to reach the desired final conditions, while providing the proper allocation of side jet ignitions. While the main thruster is employed for decelerating the landing vehicle, side jets are used to gain the correct attitude and simultaneously reduce the horizontal velocity. Actuation of side jets is implemented using pulse width modulation, in both phase (a) and phase (b). Monte Carlo simulations are run, and demonstrate the effectiveness of the guidance, control, and actuation architecture at hand for lunar descent and safe touchdown, in the presence of significant non-nominal flight conditions related to initial displacements on position, velocity, attitude, and angular rate.