Speed up random walk by leveraging community affiliation information

Abstract

Large online networks are most massive and opulent data sources these days. The inherent growing demands of analyses related data fetching conflict greatly with network providers’ efforts to protect their digital assets as well as users’ increasing awareness of privacy. Restrictions on web interfaces of online networks prevent third party researchers from gathering sufficient data and further global images of these networks are also hidden. Under such circumstances, only techniques like random walk approaches that can run under local neighborhood access will be adopted to fulfill large online network sampling tasks. Meanwhile, the presence of highly clustered community like structure in large networks leads to random walk’s poor conductance, causing intolerable and hard-to-foresee long mixing time before useful samples can be collected. With lack of techniques incorporate online network topology features being the context, in this paper we focus on taking use of community affiliation information that possibly comes with metadata when querying objects in online networks, and proposed a speeded version of random walk by raising the probability of inter-community edges being selected. Assuming the community structure is well established as promised, the community speeded random walk expects better conductance and faster convergence. Our method forces the sampler to travel rapidly among different communities that conquers the bottlenecks and thus the samples being collected are of higher quality. We also consider the scenario when community affiliation is not directly available, where we apply feature selection algorithms to select features as community.

1 Introduction

Online networks (ON) have long been serving a vital role in data tasks over a broad range of topics either for research or commercial purposes for the considerably tremendous amount of information being created, exchanged and archived every second. They can be very representative data reproduction of real-world information notably with semi-structured data objects. Comparing to the complicated natural language context in real world, ONs offer a more analysis friendly arena. As their scales’ growing up, more interests rise to dig into these rich data sources, inherently making efficient sampling and analysis techniques over large networks an important topic to explore.

With these being stated, respectable number of researches have already been cast to learn ON data (Wilson et al. 2012), adding impressive and fruitful outcomes to practical applications ranging from demographic studies, locating trends in public affairs to economics or marketing purposed inferences. While challenges also emerges along with the inflating of the network scale and data volume, restricting the feasibility of many known statistical tools to be appropriately applied.

1.1 Problem motivation

Mostly, ONs can be modeled as directed or un-directed graphs with objects (e.g. users, products, etc.) or object groups as nodes, and the interaction relationships (e.g. follower/followee, co-purchase,co-author, etc.) as identical or weighted edges. In order to efficiently analyze ON buried information, very commonly we’ll have to deal frequently with graphs with ON characteristics, answering global or conditional aggregates and statistics such as sum, average, and count (e.g. the average age of all users, total users of a community or entire network).

One major barrier for these tasks is the absence of global information from most ONs (De Choudhury et al. 2010; Zhou et al. 2016). With data now being valuable digital assets and a rising awareness of privacy and security after many famous disclosures like the Cambridge Analytica scandal (Wikipedia Contributors 2019a), there are plenty of reasons for ON providers to keep details of their networks away from the public. Unless the providers are willing to release public data, it is not possible to observe the network graphs in a global scope.

Hence in the very majority of practical problems involving ON, third party researchers only have topical vision of the graphs from where they landed through provided web/API interfaces. Query to a node in the networks barely reveals little information on its immediate neighborhood. Also for similar concerns and to prevent any malicious users from sending harmfully many requests causing performance issues, large ON providers make great efforts to enhance their web crawlers defencing features, limiting the number of queries/transactions can be committed in a certain time window from a single source (Efstathiades et al. 2016).

Under such circumstances approaches based on the retrieval of entire graph, considering the huge size of ON nowadays, are wiped out due to the prohibitively expensive third party query cost. More practical data interfaces are calling for effective localized alternatives to tackle the challenges.

1.2 Existing techniques

As a result, ON involved studies resort to sampling methods that collect samples from networks following a pre-determined distribution. Then estimations of desired data aggregation can then be calculated via sampled data used in place of ground truths. Few existing statistical approaches but the random walk family techniques (Grimmett 2010), being capable of sampling under designed stationary distribution after a period of ”burn-in” and running locally without knowing global topology, can fulfill the requirements and fit into practical interface limitations. More specifically, simple random walk (SRW), with its adaptability to different scenarios as well as ease of implementation, has been widely adopted and considered a golden baseline of the sampling techniques, on which I focused to compare and evaluate our proposed method in the paper.

However, these techniques used by majority of current works (Gjoka et al. 2010; Katzir and Hardiman 2015; Pons and Latapy 2005) involving ON sampling are mostly topology oblivious techniques that do not intentionally leverage any special property of real-world networks. Instead, they are for general-purpose graphs that, roughly speaking, work well so long as the underlying graph features a large conductance (which is in graph theory known to be a key factor affecting convergence speed for random walks Avin et al. 2018). Unfortunately, the conductance of real world social networks is often substantially lower than expected (Leskovec et al. 2009). This creates the dilemma for all random walk techniques of possibly intolerable long waiting time known as the “burn-in” periods (or mixing time), when large numbers of queries or transactions are required before the random walks’ sampling distributions can converge to desired stationaries and start to draw samples. The prolonged burn-ins are a result of real-world networks’ tendency to exhibit highly clustered topology (Traud et al. 2012) which generates bottle-necks hard for random walks to cross through (Pons and Latapy 2005; Ravasz and Barabási 2003). Without sufficient knowledge of entire networks, it’s also difficult to foresee the mixing costs or monitor actual convergence.

1.3 Speed up random walk by leveraging community affiliation

Assuming the existing random walk approaches’ getting trapped in one or several communities is due to the low inter-community travel probabilities, we then consider a novel problem of how to significantly increase the conductance of large ONs with highly clustered topology by leveraging community information (Papagelis et al. 2013).

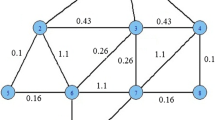
Here first we shall state the concept of ”community” in our paper and its relation to graph conductance before propose our idea. Though universal definition of community is pretty ambiguous, from intuition (see example in Fig. 1) communities are well knitted clusters of node collections in a graph with a few ties to the rest of the system, inside which more edges are often observed than crossing among them. Social communities in the context of social networks can be any subgroups of people are all friends to each other or have very few degree of separation (Luce and Perry 1949), and online communities can then be extended to any meaningful collection of objects. According to the definition, graph conductance of a certain set of nodes S is given by $\frac{P(S,\overline{S})}{\min (\pi (S),\pi (\overline{S}))}$ (Bollobás 1998) with P being the probability to leave S and $\pi$ being the sampling probability. This could be relatively low for the nature of community to be less likely connected to other part of graph.

Fig. 1

A highly clustered large network

Intuitively, increasing the weight of crossing community edges will significantly increase the conductance and conquer these bottlenecks. Our proposed community affiliation incorporated random walk (CRW) shows a way to address the task by choosing next step uniformly among communities instead of neighbors. CRW forces the sampler to jump through communities and leads to rapid exploration of the entire graph. On the other hand, we are still able to re-balance the random walk to a reversible Markov chain by introducing Metroplis Hastings (MH) algorithm (Wikipedia Contributors 2019b) so that an identical stationary distribution as current random walk approaches (e.g. SRW) can be guaranteed.

In the process we take use of the community affiliation information (i.e. the community value a node has a membership with: C(x)), that is any meaningful community definition per information available on hand (e.g. organizations could be a reasonable choice). And we could encounter different interfaces with ideal ones sometimes where a ”perfect community affiliation information” is given based on knowledge (explicit and well-defined C(x)). Then a direct application of CRW will be applied. While in cases C(x) is not immediately available, workarounds are required to give inference on these values. In this paper we focus on selecting candidate metadata attributes to make affiliation inferences. Though there have been a wide selection of more precise community detection algorithms adopted in current literature, they either conflict with our lacking of topology knowledge or come with unacceptable query costs ($O(n^2)$ or so) (Bedi and Sharma 2016), which have been dumped here.

1.4 Contribution outline

In this paper, we show our design of a topology oriented, or more specifically, community affiliation based approach CRW to speed up random walk based sampling techniques used over ONs, and discuss the application of them being used facing different data interface.

Our contributions also include comprehensive sets of experiments over both synthetic data and real-world online data sets (Leskovec and Krevl 2014), using the original SRW as a baseline comparison, to verify the correctness, effectiveness and efficiency of CRW.

After clarifying the terminologies and notations that we will be using as well as briefly reviewing related concepts in preliminaries. We’ll detailed expand original CRW design in Sect. 3 with assumption of perfect community affiliation. Theoretical analysis is given to prove the mathematical fundamental behind CRW, attached with the experiment results. In Sect. 4 we discuss the scenario of implicit community information when inferences are required. Among several solutions we choose to adopt feature selection algorithm to locate attributes as ground truth communities. We also place experiments of real-world data sets for this workaround to evaluate. Then we summarize our outcomes and think about possible future improvements in conclusion.

2 Preliminaries

2.1 Graph model of online networks

In this paper, we consider all networks of interest to be un-directed graphs $G = (N,E)$, with |N| nodes and |E| edges. Any $x \in N$ represents a node interface that contains the objects’ meta information (e.g., user name, profile, product info), and an edge $e(x,y) \in E, x,y \in N$ means there’s an interaction between the two nodes (e.g. two users are ’friends’, co-occurence of 2 authors). We use $\mathrm {d}(x)$ to denote the degree (i.e. number of edges incident to the node) of node x, and likewise $\mathrm {n}(x)$ as the set of nodes in x’s neighborhood (i.e. $\mathrm {n}(x)=\{y|e(x,y) \in E, y \in N\}$).

The model is capable of summarizing major ONs in arbitrary categories. For directed interaction like Twitter’s followee/follower-ship (followee as in edges and follower as out edges), the transformation to un-directed graph is simply taking unions of node’s in and out neighborhood $( e(x,y)\vee e_(y,x) \rightleftharpoons e(x,y))$.

Mostly web interface of ONs in real world only allows local neighborhood queries. Namely we only have knowledge of queried nodes set $X_0$ and the neighborhood $n(x_0)$ of node $x_0$ for all nodes in $X_0$ (Zhou et al. 2016). We also assume the knowledge of known nodes include other metadata that can be used for community affiliation decision, either explicitly or indirectly (Papagelis et al. 2013).

2.2 Sampling via random walk

Then we take a brief look at majorly used random walk techniques that is naturally fitting to these restrictive web interfaces due to their capability of running locally yet gaining unbiased samples to certain distribution from the entire network.

Random walk Given a graph G and a starting node $x_0$, we select the next node $x_1$ from its neighborhood $n(x_0)$ according to a transition matrix $P(x,y), x,y\in N$ and then query the selected node to gain its neighborhood. The process would be repeated for a number of iterations until desired samples are drawn. This is a Markov Chain Monte Carlo (MCMC) approach with N as the state space. We will then review some important properties of random walks (Grimmett 2010).

Stationary distribution The sequence of nodes selected is a random walk on G with finite state space N and P(x, y) being its irreducible and aperiodic transition matrix. Because these random walks are finite Markov chains that are time-reversible, as long as a random walk can reach all nodes in N in finite time space (depending on how P is chosen), the probability distribution for the walk to land on each node will converge to a stationary distribution$\pi$ after a number of ’burn-in’ steps (or mixing time) (Geyer 2011), which is then used as the sampling distribution in many analysis works. By the condition of Markov chain convergence (Levin et al. 2006), the edge measure Q(x,y) which is the probability of moving from node x to y at stationary distribution, should be identical among all node pairs. Namely:

$$\begin{aligned} Q(x,y)=\,& {} \pi (x)\cdot P(x,y)\nonumber \\ Q(x,y)= \,&{} Q(y,x), e(x,y) \in E \end{aligned}$$

(1)

The theory of stationary distribution provides foundation for most existing analysis tools for ON sampling.

Simple random walk Among the popular random walk techniques, simple random walk (SRW) is still the one considered as a golden baseline (Gjoka et al. 2010). It selects the next-hop node y uniformly at random among the neighbors n(x) of the current node x. More specifically, for SRW whose transition matrix P is simply:

$$\begin{aligned} P(x,y)= {\left\{ \begin{array}{ll} \frac{1}{\mathrm {d}(x)}, &{}e(x,y) \in E\\ 0, &{}else \end{array}\right. } x,y \in N \end{aligned}$$

(2)

Its stationary distribution is proportional to the node degrees: $\pi (x) \propto \mathrm {d}(x)$, and would be given by:

$$\begin{aligned} \pi _{\mathrm {SRW}}(x)= \frac{\mathrm {d}(x)}{2|E|} \end{aligned}$$

(3)

Metropolis Hastings Based Random Walk Metropolis Hasting based random walks are applications of the Metropolis Hasting (MH) algorithm,wiki:MH that is capable of correcting transition probabilities and achieve convergence to some specifically designed stationary distributions. In MH, a proposal distribution (an initial transition matrix without correction) g(x, y) is chosen, and it come with an acceptance probability matrix $\alpha (x,y)$ calculated by the condition mentioned in Eq. 1. Starting from node $x_0$, a candidate move is generated from the proposal g(x, y) in $n(x_0)$. Let the candidate be node y, the move is then censored with the probability $1 - \alpha (x_0,y)$. That is, with probability $\alpha (x_0,y)$, y is ”accepted” as the next state $x_1$, and otherwise $x_0$, with the remaining probability $1- \alpha (x_0,y)$, is adopted as $x_1$ and y is dumped. The detailed calculation of MH’s transition matrix $P_{\mathrm {MH}}(x,y)$ would be given:

$$\begin{aligned} \alpha (x,y)= & {} {\left\{ \begin{array}{ll} \min [\frac{\pi (y)g(y,x)}{\pi (x)g(x,y)},1], &{} \text { if } \pi (x)g(x,y)>0\\ 0 &{} \text { otherwise } \end{array}\right. } \end{aligned}$$

(4)

$$\begin{aligned} P_{\mathrm {MH}}(x,y)=\, & {} \alpha (x,y)\cdot g(x,y) \end{aligned}$$

(5)

In this manner we’d be able to design both proposal and stationary distributions as desired that fits to our motivation. In fact, one notable application of MH in random walk techniques is to curve SRW’s stationary to a uniform distribution on N. In this paper, our proposed CRW will caused a different stationary distribution than SRW, where we will illustrate how we can use MH to curve it back thus a strict comparison can be conducted.

Mixing time As stated, random walk requires a ”burn-in” period before its convergence, also know as the mixing time, which is regarded as a crucial measurement of performance. It is the time required by a random walk for the distance to stationary to be sufficiently small (a pre-determined threshold $\varepsilon$). The mixing time is defined by:

$$\begin{aligned} t_{mix} (\varepsilon ) =\min \left\{ t: \max _{x,y\in V,y\in n(x)}|P^t(x,y)-\pi (y)| < \varepsilon \right\} , \end{aligned}$$

(6)

where the threshold $\varepsilon$ is usually set to $\frac{1}{4}$ (Levin et al. 2006). Mixing time captures the number of steps a random walk needs to converge to a satisfying state from starting state. Less mixing time is an indication of faster sampling and less auto-correlation (i.e. higher quality samples).

2.3 Conductance

Graph conductance is also called bottleneck ratio, which is known to hard bound the mixing time. Definition of commonly used term conductance can be summarized as following (Bollobás 1998). For a graph G, a cut $(S,\overline{S})$ is a partition of N into two disjoint subsets. We denote the conductance of cut $(S,\overline{S})$ in a graph G as:

$$\begin{aligned} \varphi (S)=\frac{Q(S, \overline{S})}{\pi (S)} \end{aligned}$$

(7)

The conductance of the whole graph is the minimum conductance over all the possible cuts:

$$\begin{aligned} \phi (G)=\min _{S \subset N,\pi (S)\le \frac{1}{2}}\varphi (S) \end{aligned}$$

(8)

The lower bound $\phi (G$) places on mixing time $t_{mix}$ satisfies the inequality (Levin et al. 2006) of:

$$\begin{aligned} t_{mix}=t_{mix}(1/4)\ge \frac{1}{4\phi (G)} \end{aligned}$$

(9)

Thus conductance can be a direct indicator for random walk performance. And it should be noted that conductance of different stochastic processes with regard to the same target graph G might be different, and we’ll be using notations with subscripts (e.g. $\phi _{\mathrm {SRW}}(G)$) to differentiate among those conductance measures.

2.4 ”Community-Structured” graph and community affiliation information

According to current literature (Leskovec et al. 2009; Traud et al. 2012; Girvan and Newman 2002), large real-world networks tend to exhibit a highly-clustered topology, or so called ”community-structured” topology. While in graph theory the definition of ”community” is ambiguous, there exists greatly many popular definitions and a very rich context of techniques have been proposed to detect, measure and define the term. Intuitively, communities are groups of well knitted nodes in the graph, whose real-world reflections could probably involve interactive relationships (e.g. friends, family), shared properties (e.g. interests) or similar roles (e.g. key opinion leaders) within the graph (Jebabli et al. 2018; Hric et al. 2014). For instance, if we consider students from same institution on Facebook, the possibility of connections within would be much higher than those to outside of the institution, which makes institutions as naturally ground truth communities. On the other hand, because of the absence of universal adopted definition, different divisions of a same graph can all be appropriate community selections and there might be overlapping in the communities (Yang and Leskovec 2015; Li et al. 2018).

In this paper, we first combine the definition of conductance and give our definition for ”community-structured” graph:

Definition 1

We define a graph $G=(N,E)$ as a community-structured graph if the conductance of SRW on this graph satisfies Eq. 10:

$$\begin{aligned} \phi _{\mathrm {SRW}}(G)=\min _{{\mathcal {C}}'\in {\mathcal {C}},\pi ({\mathcal {C}}')\le \frac{1}{2}} \left( \frac{Q({\mathcal {C}}', \overline{{\mathcal {C}}'})}{\pi ({\mathcal {C}}')}\right) = \varphi _{\mathrm {SRW}}({\mathcal {C}}') \end{aligned}$$

(10)

Where ${\mathcal {C}}$ is a partition of graph G ${\mathcal {C}} = \{C_1,C_2,C_3, \ldots ,C_n\}$, with its union $\cup _{C\in {\mathcal {C}}}C=N$. Also, we define ${\mathcal {C}}'\subset {\mathcal {C}}$ where ${\mathcal {C}}' \cup \overline{{\mathcal {C}}'} = {\mathcal {C}}$. ${\mathcal {C}}'$ might consists of one or more communities in set ${\mathcal {C}}$, i.e., ${\mathcal {C}}'=\{C_a, a\subseteq \{1,2, \ldots ,n\}\}$.

We assume a community-structured graph’s conductance at ${\mathcal {C}}'$ takes the minimal value over the whole graph, i.e., $\varphi _{\mathrm {SRW}}({\mathcal {C}}')=\phi _{\mathrm {SRW}}(G)$. Thus, the reason random walk get stuck in place and encounter slow convergence is due to low conductance inter-communities. On the other hand SRW, as most popular random walk algorithm, is an ideal choice to place our comparison over. We further define ”Community affiliation information” as node $x \in N$’s membership of communities:

$$\begin{aligned} C(x)=C_i, \iff x\in C_i, i>0 \end{aligned}$$

(11)

2.5 Measurements of performance

For sampling algorithms, it’s always the case we compare sample quality versus the cost. Costs could be in a manner of the most precious resource involved in sampling, and with regard to ONs will be the query times. Sample qualities are ideally compared by the distance of sampled distribution to ground truth, while in real-world works it’s usually intractable as unacceptably large number of samples are required especially when sampling space is massive. Considering the interface restriction before, we’ll have to choose alternative measures.

Effective sample size (ESS) as an measure of information quantity a sampler carries, can be considered as the sample’s independent and identically distributed (i.i.d.) sample equivalence. It tells the auto-correlation of sample and thus is a good indicator of sample quality. We use Stan’s method (Carpenter et al. 2017) to estimate ESS in experiments. The next measure involved is the empirical total variance or alternatively the L1 norm distance,wiki:norm of samples and target distribution. Although the analytical sampling distribution of random walks can hardly be calculated, we can still use frequencies of data points to approximately estimate the values. And We also compare CRW’s community coverage speed over SRW by defining a measurement, hitting time (query cost versus number of communities reached), to verify our claim that CRW travels much faster inter communities. Random walks are know to have ”fake convergence” on highly clustered graphs when the walks are trapped in several communities and the diagnostics are stable (Brooks and Gelman 1998). In such cases the samples collected might not be a good representation of entire graph. Hitting time could reveal the proportion of graph being explored.

2.6 Graph generative models

For latter use of theoretical analysis and easier experiments, simulation of ONs from graph generating models are required before step into larger real world data sets. We reviewed popular graph generative models and choose to use the Lancichinetti–Fortunato–Radicchi benchmark graph (LFR) (Lancichinetti et al. 2008).

LFR model captures both the power law degree distribution of large networks and the community structure. It first generate an |N| node graph having the degree sequence with power law exponential $\tau _1$ at a mean degree of $\overline{\mathrm {d}(x)}$. A mixing parameter $\mu$ is chosen to decide the fraction of edges for each node that is inner-community. Community sizes are then generated by power law exponential $\tau _2$, sum of which is equal to the node count |N|. The minimal and maximal sizes should satisfy: $min(|C_i|)>min(\mathrm {d}(x))$and$max(|C_i|)>max(\mathrm {d}(x))$. Nodes of the graph are randomly assigned to some community if community size is not violated. The leftover nodes are then iteratively been assigned to random communities and kick random nodes out as new leftovers if target community is full until no nodes are alone without a community assignment. Final step of LFR is a rewiring of each nodes to meet the mixing factor $\mu$ of inner-community edge ratio without change the degrees. As the model has complimentary community affiliation information and capture major features of large ONs, we consider it an ideal fit for our experiment.

3 Community affiliation based random walk

In this section, we proposed a twisted random walk (CRW) giving priority to edges crossing communities to be selected. We firstly discuss the main design of the algorithm, followed by a theoretical analysis showing a conductance surpassing using CRW over SRW on same community-structured graph. We assume a perfect knowledge on community information in this section and extend our discussion to tackle less informative scenarios later in Sect. 4.

3.1 Basic design

At the ease of implementation and flexibility of being adapted to arbitrary interface, SRW is considered as a ”golden standard” for random walk like sampling techniques, and is adopted by very majority data tasks involving ON sampling (Gjoka et al. 2010; Katzir and Hardiman 2015). However, SRW’s performance on community-structured graphs could be significantly slowed due to the low probability of exiting communities. The transition matrix of SRW that uniformly picks a neighbor gives all the edges identical margin probability of being chosen. While community-structured graphs are much densely connected intra-communities than inter-communities, preventing SRW from travelling smoothly through the entire graph. For instance, if we consider a barbell graph with corresponding two communities, the only one edge connecting two different communities in the graph carries an incredibly low probability of being selected (i.e. $\frac{1}{2|E|}$). Even if SRW is able to reach one of the two connected nodes, the chance of pick the cross-community edge is still relatively low as the nodes have much stronger connectivity to their own communities.

Intuitively one will want to raise the weight of crossing community edge to encourage random walk sampler to travel through it Zhou et al. (2016). We came up with a rough idea of CRW that take use of community affiliation information of nodes (see Fig. 2).

Fig. 2

CRW’s choice of next hop (When random walk reaches node x, CRW choose a community first, thus probability of exit current community at the node is raised to $\frac{2}{3}$ while SRW will give $\frac{1}{2}$ with treating edges identically)

After CRW reaches at node x that is connected to at least one other community, it step into the decision of which neighbor to be the next hop. Instead of picking uniformly at random among $\mathrm {n}(x)$ as SRW, CRW picks a community c uniformly at random firstly from all different communities in x’s neighborhood, then pick one among all x’s neighbors that is a member of c at random to be the candidate. And the sampling probability, although intractable at this point, can be later curved by MH algorithm to desired.

3.2 Theoretical analysis

In this section, we’re going to discuss the theoretical fundamental behind CRW.

3.2.1 Transition matrix and stationary distribution

By definition of conductance $\varphi (C)$ at cut $(C,\overline{C})$ in Eq. 7, the weight of cross-community edges can be assigned arbitrarily large to achieve better value. CRW choose communities uniformly at random each step in order to place identical transition probability to each of them. Hence a naive transition function of any node pair x and y would be given by:

$$\begin{aligned} \begin{aligned} g(x,y)=\frac{1}{|I(x)|}\frac{1}{|O(x,y)|.} \end{aligned} \end{aligned}$$

(12)

In Eq. 12, I(x) denotes the set of different communities in neighborhood of x, i.e. $I(x) = \{C(y)|e(x,y) \in E\}$. We also denote O(x, y) as set of the neighbors of x that belongs to same community as node y, i.e., $O(x,y)=\{z|e(x,z) \in E, z\in C(y)\}$.

Obviously the transition function result in CRW’s different stationary distribution from SRW. For the purpose of fair and strict comparison, we use MH algorithm described in Sect. 2 to curve the stationary distribution to the same as that of SRW, namely our desired $\pi (x)=\frac{\mathrm {d}(x)}{2|E|}$. With g(x, y) as the proposal and acceptance matrix $\alpha (x,y)$ calculated using Eq. 4, the transition matrix of CRW is given by:

$$\begin{aligned} P_{\mathrm {CRW}}(x,y)=\frac{1}{|I(x)|}\frac{1}{|O(x,y)|}\cdot \alpha (x,y), \end{aligned}$$

(13)

which ensures CRW keeps a same stationary distribution as SRW.

3.2.2 Conductance analysis

Next we prove the conductance on ”community-structured” graph using CRW is greater than or equal to the conductance of same graph using SRW, and so CRW will expect a quicker convergence according to Eq. 9.

As defined in Sect. 2, node set N of graph G is partitioned into disjoint subset of nodes, namely communities, ${\mathcal {C}}=\{C_1,C_2,C_3 \ldots ,C_n\}$. And we define ${\mathcal {C}}'\subset {\mathcal {C}}$ as a set consisting of one or more communities in ${\mathcal {C}}$: ${\mathcal {C}}'=\{C_a, a\subseteq \{1,2, \ldots n\}\}$. And we also claim that community-structured graph satisfy: $\phi _{\mathrm {SRW}}(G)=\varphi _{\mathrm {SRW}}({\mathcal {C}}')$. Here introduced Theorem 1:

Theorem 1

For a given graph$G=(N,E)$, if it satisfies the community-structured given in Definition 1, the conductance of CRW$\phi _{\mathrm {CRW}}(G)$overGis greater than or equal to the conductance of SRW overG$\phi _{\mathrm {SRW}}(G)$.

Proof

As stated earlier in this section, we set CRW’s stationary same as SRW for a straightforward comparison versus baseline, hence we only need to compare $Q({\mathcal {C}}',\overline{{\mathcal {C}}'})$ using different approaches. (Recap that Q(x, y) is the probability of moving from x to y at stationary distribution, and $Q({\mathcal {C}}',\overline{{\mathcal {C}}'})=\sum _{x\in {\mathcal {C}}',y\in \overline{{\mathcal {C}}'}}Q(x,y)$, see Sect. 2). Given SRW’s transition matrix $P_{\mathrm {SRW}}(x,y)=\frac{1}{d(x)}$ and that of CRW derived in Eq. 13, we’ll have:

$$\begin{aligned} Q_{\mathrm {SRW}}({\mathcal {C}}',\overline{{\mathcal {C}}'})= & {} \sum _{x\in {\mathcal {C}}',y\in \overline{{\mathcal {C}}'}}\frac{\mathrm {d}(x)}{2|E| \text { and } e(x,y)\in E}\frac{1}{\mathrm {d}(x)}\nonumber \\= & {} \sum _{x\in {\mathcal {C}}',y\in \overline{{\mathcal {C}}'}}\frac{1}{2|E|} \end{aligned}$$

(14)

and:

$$\begin{aligned} \begin{aligned}&Q_{\mathrm {CRW}}({\mathcal {C}}',\overline{{\mathcal {C}}'}) \\&\quad = \sum _{x\in {\mathcal {C}}'} \sum _{y\in \overline{{\mathcal {C}}'}, e(x,y)\in E \text { and } \alpha (x,y)<1}\frac{\mathrm {d}(y)}{2|E|}\frac{1}{|I(y)|}\frac{1}{|O(y,x)|} \\&\qquad + \sum _{x\in {\mathcal {C}}'} \sum _{y\in \overline{{\mathcal {C}}'}, e(x,y)\in E \text { and } \alpha (x,y)>=1}\frac{\mathrm {d}(x)}{2|E|}\frac{1}{|I(x)|}\frac{1}{|O(x,y)|}\\ \end{aligned} \end{aligned}$$

(15)

To further expand Eq. 15, we define f(x, y): $f(x,y)=|I(x)|\cdot |O(x,y)|$, where

$$\begin{aligned} E[f(x,y)|x]=\sum _{y \in n(x)}\frac{|I(x)||O(x,y)|}{|I(x)||O(x,y)|}=\mathrm {d}(x). \end{aligned}$$

(16)

Since $\frac{1}{f(x,y)}$ is convex with regard to f(x,y), from Jenson’s inequality (Jensen 1906) we have:

$$\begin{aligned} \begin{aligned} E\left[ \frac{\mathrm {d}(x)}{f(x,y)}\right]&=E\left[ \mathrm {d}(x)\cdot E\left( \frac{1}{f(x,y)}|x\right) \right] \\&\ge E\left[ \mathrm {d}(x)\cdot \frac{1}{E(f(x,y|x)}\right] = 1 \end{aligned} { ,} \end{aligned}$$

(17)

and thus our estimation of $Q_{\mathrm {CRW}}({\mathcal {C}}',\overline{{\mathcal {C}}'})$ is:

$$\begin{aligned} \begin{aligned}&E[Q_{\mathrm {CRW}}({\mathcal {C}}',\overline{{\mathcal {C}}'})]\\&\quad =\frac{1}{2|E|}\cdot \left( \sum _{x\in {\mathcal {C}}'} \sum _{y\in \overline{{\mathcal {C}}'}, e(x,y)\in E \text { and } \alpha (x,y)<1}E\left[ \frac{\mathrm {d}(y)}{f(y,x)}\right] \right. \\&\left. \qquad + \sum _{x\in {\mathcal {C}}'} \sum _{y\in \overline{{\mathcal {C}}'}, e(x,y)\in E \text { and } \alpha (x,y)>=1}E\left[ \frac{\mathrm {d}(x)}{f(x,y)}\right] \right) \\&\quad \ge \sum _{x\in {\mathcal {C}}',y\in \overline{{\mathcal {C}}'} \text { and } e(x,y)\in E}\frac{1}{2|E|} \end{aligned} \end{aligned}$$

(18)

Finally, combining Eqs. 7, 14, 15, 18 we’ll have the conductance over G using CRW:

$$\begin{aligned} E[\varphi ({\mathcal {C}}')_{CRW}]=\, & {} \frac{E[Q_{\mathrm {CRW}}({\mathcal {C}}',\overline{{\mathcal {C}}'})]}{\pi ({\mathcal {C}}')}\nonumber \\\ge \,& {} \frac{\sum _{x\in {\mathcal {C}}',y\in \overline{{\mathcal {C}}'} \text { and } e(x,y)\in E}\frac{1}{2|E|}}{\pi ({\mathcal {C}}')}\nonumber \\= \,& {} \varphi ({\mathcal {C}}')_{SRW} \end{aligned}$$

(19)

$\square$

3.3 Algorithm

Summing up the discussion above, here’s a brief look of CRW:

3.4 Experimental evaluation

3.4.1 Synthetic data using the LFR benchmark model

As mentioned in Sect. 2, we choose the LFR Benchmark Model that captures both degree distribution features as well as the community structure of large ONs to verify our theoretical claim. Starting from small graph at $|N|=500$ for the purpose of convenient visualizing, we tested and draw the walk paths of CRW over SRW (see Fig. 3). The graph is generated at a mixing factor $\mu =0.1$, which gives $P(e(x,y) \in E\, \& \,C(x) \ne C(y))=\mu$. (i.e. the approximate conductance at cuts of communities would be around 0.1). Due to the low cross community probability, SRW spend quite a long period wandering in a small neighborhood before it’s able to leave while CRW has already reached most of the communities.

Fig. 3

SRW and ORW’s paths in LFR benchmark graph

With the promising performance on small graph, we set up parameter to gain graph of a larger size, and summarized the parameter settings and basic statistics for both graphs we tested in Table 1.

Table 1 The LFR benchmark graphs tested

3.4.2 Real world data sets

Besides tests on synthetic graphs, we also set up experiments on real world large data sets from SNAP (Leskovec and Krevl 2014) repositories‘ section of networks with ground truth communities. Yang and Leskovec (Yang and Leskovec 2015) provided a series of networks with community affiliation being set to comprehensive real-world concepts, among which we select three covering different ON topics.

Youtube data set (Mislove et al. 2007) contains user created groups where other users can join. Edges represents user’s mutual subscription-ships, and users in a group are considered a community. DBLP data set (Yang and Leskovec 2015) is researcher’s co-authorship network that edges are given to those pairs who at least co-publish 1 article. The ground truth community of the data is chosen to be the journals and conferences, where authors who published at least once are considered a member. Finally, EU email network,EUcore is constructed from members of an European research institution that department affiliation information are used directly as communities. The edges are those who have email interaction for at least once.

Cleaning of data As mentioned in Sect. 2, we consider all graph in the context un-directed so the data sets are transformed accordingly, and isolated nodes are removed. In fact all random walk related experiments on graphs are tested on the largest connected component on graphs. The used data sets are collected in a manner of measuring best real-world communities on original graphs, thus over-lapping is allowed for different community definitions and not all nodes are assigned a community value. In our experiment we remove all overlapping by assign nodes to the first community we read, and take the induced graph of those who have a community value. The statistics of these data sets are summarized in Table 2, and we also noticed that real world network tends to form more communities than synthetic data.

Table 2 The real world data sets tested

We then discuss our experiment measurements followed by our test results.

3.4.3 Performance measures

Effective sample size Random walks are MCMC processes known to be collecting samples with high auto-correlations, for which we want to know the i.i.d. equivalence of the chains. Effective sample size(ESS) is widely used to measure the number of individual draws required to achieve the same expected precision from samples of interest over the same distribution. It’s a direct indicator of the sample quality and how well Markov chains have mixed. We run Stan’s (2017) ESS estimation on our collected samples to compare 2 methods, and a detailed ESS estimation strategy was illustrated by Geyer (2011).

Hitting time And yet we’ll need to verify our claiming that CRW explore entire graph much faster, the regular diagnostics used to monitor convergence (and thus conclude the chain’s exploration of sample space) might be less powerful in community structured graphs as it’s known that diagnostics could be inconsistent if the chains don’t hold over-dispersion (Brooks and Gelman 1998). On large ONs with massive sample space (|N|), being trapped in small communities is a cause for these false positive, and hence we define the hitting time as the community coverage (number of communities sample S reached) at query cost t.

$$\begin{aligned}&H(S,t)=|{\mathcal {C}}_h(S[:t])|, where\nonumber \\&{\mathcal {C}}_h(S)=\{{\mathcal {C}}_i| \exists s \in S, C(s)={\mathcal {C}}_i\} \end{aligned}$$

(20)

Hitting time is very explicit sign of whether the random walks are able to explore graph thoroughly.

Total Variance As described in Sect. 2, random walks are monitored by their distance to the stationary distribution from its sampling distribution. We might use any measurement that detects the distance, and we choose to implement the total variance (or interchangeably L1 norm) (Wikipedia Contributors 2019c). In practice the sampling distribution calculation are often intractable, where we applied the empirical distribution over our observed samples. We use both the community irrelevant degree distribution together with community distribution to compare two algorithms.

3.4.4 Experimental results

In each single trial of the experiments, starting point of both algorithms are randomly picked at uniform with samples being collected along the paths and the algorithms walk for same length. The random walk length depends on the graph size |N| until we observe approximate convergence. Each data set has been tested for 30 replications through the above process and the mean measurements are thus calculated and plotted.

Fig. 4

Test results of LFR benchmark graphs

Fig. 5

Test results of real world data sets

Plotted result of the experiments are showed in Figs. 4 and 5. Firstly we see a very promising result that CRW overcomes SRW in the manner of ESS on tests over all data sets, which indicates a lower correlation of samples collected by our method. With these being observed, the expected precision of estimators driven by the samples will naturally be higher by definition of ESS. As ESS grows linearly with cost, CRW is in fact collecting usable samples at a higher rate.

Not surprisingly, CRW’s dominance in hitting time is also significant. The algorithm travels very fast inter communities at the beginning state that ensure the sample will spread the entire graph. For graphs with large amount of smaller communities, CRW will need a longer time to explore but maintains its advantage over SRW. It then can avoid the false positive in convergence due to an under exploration of the graph.

We compare both methods on total distribution variance with regard to both degree and community distribution. For community irrelevant parameters like degree, the two methods are indifferent in performance since samples from a small portion of graph is representative if degree distribution isn’t correlated with position in graph. But if we check for community distribution, we observed CRW’s outperforming in general. The result also proved our claiming that SRW might report convergence due to some diagnostics when it’s still inconsistent at other dimension. As a result, for community-structured graphs SRW’s estimators might be less precise than expected and CRW can be considered instead.

We noted that our algorithm isn’t beating SRW on the EU graph despite its perfectly structured community affiliation (each node belongs to exactly one department with no nodes left). We were confident that department fits the community definition well and shall expect a good performance, so we tested for the conductance of the cuts for all department cuts. The average conductance is as high as around 0.9 while other graphs are much lower. Considering its high average degree for a |N| of 1005, it’s not hard to understand that the community structure of the graph is very weak in this data set. This is a sign that well-defined ground truth communities might not agree with a topology wise good community, of which the topic is also explored by some recent literature (Newman and Clauset 2016; Hric et al. 2014). However, though indifferent in total variance, CRW is still capable of higher ESS rate and faster community reaching.

To conclude, CRW explores graphs with community-structured topology rapidly by crossing through different communities, leading to less correlation of the samples collected than SRW and shall expect a better performance on topology sensitive graph data. As long as a graph’s community structure is well established and captured by the chosen affiliation information, CRW is better in all three dimension of measurements we choose, while we’ll have to pay attention to the possible disagreement between ground truth community and topology communities.

4 Dealing with community inference

4.1 Community detection algorithms

In this section we discuss the very realistic scenario when no perfect community affiliation information is explicitly reachable. We firstly think of using established community detection algorithms which is already very well studied in many works (Bedi and Sharma 2016; Newman and Girvan 2004).

We first dump the global wise detection algorithms calls for a thorough knowledge of the graph, and found that major methods to infer unknown community affiliation information running locally lies on an exploration starting from the seed node/nodes (Tang et al. 2017) and try to minimize modularity or maximize node similarity (Newman and Clauset 2016). Either way encounters an local exploration that leads to multiplication of queries we need to know each node. Hence we think of developing our cost-effective algorithms to infer C(x) leveraging the node features as queries to web applications usually comes with metadata other than the graph topology.

4.2 Naive community affiliation inference

One intuitive idea is to directly choose community affiliation using extra knowledge on feature similarities among nodes in different communities. For instance a similar taste in music genre for music forums, close check-in geo-locations for those applications involving GPS or products with similar key words (Girvan and Newman 2002). These non-rigorous criteria, although not explicitly show strong affiliation, give us an in-expensive alternative to bet on C(x) without any extra cost. We simply pick an (or several if necessary) attribute A, and assign $C(x)=A(x)$.

Pros of the method not only come from the easy implementation and flexibility over all networks, but taking use of researchers’ prior knowledge as well. The con is obviously strong assumption on relevance between community structure and arbitrary attribute we pick, which lies heavily on individual knowledge and preferences. The result might not be consistent per the choice of different community definition.

4.3 Community affiliation inference with attribute selection

Then we come up with the attribute (or feature) selection techniques that are widely used in statistical learning to select a subset of features best fit to the model of calculating a classification variable (James 2013). Feature selection detects attributes with the strongest correlation with the output variable through training sufficient inputs and outputs, and then forms a classifier by calculating empirical probabilities over the whole result space given a set of input attributes it selected. We choose to use popular ”Minimum-redundancy–maximum-relevance” (mRMR) (Peng et al. 2005) algorithm in later experiment.

As we mention above, random walks tend to get stuck in densely connected parts corresponding to communities (Pons and Latapy 2005). Therefore it’s reasonable to suppose that most samples we gain from very short random walks belong to a same community. I.e., we assume $C(s_0)=C(s_t)$ when t is relatively small. In real world networks, its pretty convenient for us to gain a set of starting nodes who are nearly impossible to be in the same community (e.g. products in totally different languages, topics and categories, people from extremely different geological places and have no explicit common friends). If we are able to perform many short runs starting from the set of seeds, we can get the input and output data points for attribute selection. If we write all short random walks as S, the attributes of node x being A(x) with coefficient $\chi$, we’ll optimize: $\mathbf A(S) \cdot \chi =C(S)$.

It should be pointed out that the sample space by the process above is incomplete, and further our scenario call for a complete partition of the graph, thus we’ll be only using mRMR for selection and use the subset being selected directly as an classifier. Calculating for probability is inappropriate for the above reason, and hence we need to limit the number of attributes in subset to avoid over partition. We summarize our idea as follows:

• 1. Collect Samples using multiple short random walks We pick M starting nodes and assume C(x) is known by simply assign numerical identifier as the value. Then short SRW with T steps are performed from these seeds. We could repeat the process for R times as well for each starting point and have $T * R * M$ samples (with possible duplicates).

• 2. Discard irrelevant attributes manually (optional) The step is optional. Although attribute selections algorithms themselves will detect irrelevant attributes while sometimes large cost from the requirement on sample size are assigned to ensure the accuracy of the result. We would take any effort to avoid query cost, so if some attributes are explicitly irrelevant we would dump it before start running mRMR. It should be noted that this step is not the same as naive inference in last subsection, as we only ignore those that are almost absolutely irrelevant (e.g. communities are very not likely to be based on time of registration especially on those content based networks).

• 3. Adapt attribute selection algorithms For all the samples s we collected from the same starting node $s_0$ we assign $C(s)=C(s_0)$, and load the attributes from metadata of corresponding nodes to mRMR. We limit the number of attributes in our selected subsets to relatively small if the mutual information isn’t significantly improved with later variables. Finally we use the selected attributes $\mathbf A '$ as a direct classifier, namely $C(x)=C(y) \iff \mathbf A '(x)=\mathbf A '(y)$.

4.4 Experiments

We also tested CRW with inference on real world data set. On SNAP we are able to find the amazon product metadata which collected earlier (Leskovec et al. 2007). The data comes with a number of raw attributes including but not limiting to identifier, category hierarchy, sales, etc, in which we extract similar products as edges. After an initial cleaning we found the majority of products, at that moment, is under the large ”Books” category, so we take the induced graph of all books nodes as our data source to make the community structure more ambiguous. We also eliminate the identifier as it seem to be randomly distributed and is irrelevant, and remove all nodes appear in similar products but have no meta information. The cleared data set’s basic statistics are: $|N|=270347, |E|=741124, {d(x)}=5.48$.

4.4.1 CRW with naive selection

It seems to be not hard to decide a naive choice of community affiliation as categories are pretty plausible candidates, while the data set come with a category of up to 7 layers of category hierarchy which makes our choice pretty arbitrary. We decide to be very conservatively using the subcategory of book subjects, and run the same experiment as shown in Sect. 3 (see Fig. 6).

Fig. 6

The Amazon product data of books under naive attribute selection

The assumption has been strong when the result isn’t disappointing though. At no cost CRW is still able to maintain its leading position over SRW, which means the naive assumption did help the diffusion of CRW’s exploring the network. At the same time, the shrinkage of our dominance is also the indicator of weaker community structure of our current partition at subcategory.

4.4.2 CRW with mRMR

Finally we implement our idea of mRMR powered community inference by selecting the starting seed books from 10 different subjects with widely spread sales ranking and ensure there’s no immediate common neighbor. In real world network this can be feasible at acceptable cost, by randomly browsing users/products on different tags/categories and make one query to each of then to get their neighborhood.

We then collect 5 replications of a 5 step short run on each seed, labeling each group numerically as the collecting order. These values are regarded as the output C(x) for mRMR, and all raw metadata from original data are extracted as attributes being inputs. We again labeled categorical data by numbers according to different values, with all missing inputs be filled as -1 (a common strategy for mRMR). We show our analysis results of choosing a size 5 subset in Table 3, while other size choices are not giving significant difference.

Table 3 mRMR scores of 5 attributes selection

By our design to avoid over partition of graph, we shall neglect any variables that wont help the model too much, which in this case is dumping all but the 3rd level category as it contributes to the majority of mutual information (mRMR score is 3.201) in the model. We then use the result as a classifier and rerun the experiment.

The result in Fig. 7 shows a slightly better performance especially in ESS, and yet maintain performance in all other dimensions. In addition, it should be noted that the exploration of communities and the total variations can be very different when community number grows so direct comparison of 2 set of experiment is not perfectly fair, and meantime the subcategory itself is also a fairly good candidate in mRMR. The experiments prove that either method could be effective and chosen accordingly, while mRMR inference backed by stronger statistical fundamental might be considered first as the extra cost is negligible.

Fig. 7

The Amazon product data of books under mRMR

5 Conclusion and future discussion

In this paper we propose a community information leveraging random walk, CRW, to overcome poor graph conductance caused by the very commonly presence of communities like structure in large online networks. We showed theoretically that the proposed method has improved conductance and thus will converge faster. For graphs without explicit community affiliations we showed how feature selection algorithms can incorporate metadata available and help to select features as ground truth community. Our experiments on both synthetic and real world large networks demonstrate that CRW promisingly explores the network better and gains higher quality samples using same number of queries with SRW being a baseline.

We’ve thought of some extension discussion options. Firstly the choice of our feature selection algorithm is by our knowledge being mRMR, where there might be newer and more powerful analytical tools (Dai et al. 2017) as our task involves plenty of categorical data. And our transformation of categorical data right now would simply be mapping them to arbitrarily numerical data, and it might be a source of false correlation. We might discuss the possibly better processing (Bateni et al. 2019) of these variables in future works.