Rapid training of quantum recurrent neural networks

Abstract

Time series prediction is essential for human activities in diverse areas. A common approach to this task is to harness recurrent neural networks (RNNs). However, while their predictions are quite accurate, their learning process is complex and, thus, time and energy consuming. Here, we propose to extend the concept of RRNs by including continuous-variable quantum resources in it and to use a quantum-enhanced RNN to overcome these obstacles. The design of the continuous-variable quantum RNN (CV-QRNN) is rooted in the continuous-variable quantum computing paradigm. By performing extensive numerical simulations, we demonstrate that the quantum network is capable of learning-time dependence of several types of temporal data and that it converges to the optimal weights in fewer epochs than a classical network. Furthermore, for a small number of trainable parameters, it can achieve lower losses than its classical counterpart. CV-QRNN can be implemented using commercially available quantum-photonic hardware.

1 Introduction

Fast and accurate time series analysis and prediction lie at the heart of digital signal processing, and machine learning algorithms help implement them (Gamboa 2017; Lim and Zohren 2021). They feature a wide palette of use cases ranging from audio and video signal processing and compression (Ma et al. 2020), temporal signal classification (Hüsken and Stagge 2003), speech processing and recognition (Amodei et al. 2016; Dahl et al. 2012; Sak et al. 2014), economic (Saad et al. 1998), and earth system observation (Bonavita et al. 2021; Holmstrom et al. 2016), to applications in seismology (Kong et al. 2018) and biomedicine (Goecks et al. 2020). A method that is particularly well suited for the analysis of temporal correlations in data sequences is recurrent neural networks (RNNs) (Sherstinsky 2020). This is because they accumulate information about subsequent input data, which amounts to a cumulative memory effect seen in their computations. However, training large RNNs, such as highly parametrized long short-term memory (LSTM) architecture (Hochreiter and Schmidhuber 1997), can be computationally intensive, requiring significant memory and processing power (Salehinejad et al. 2018). Hence, neural networks such as gated recurrent unit (GRU) (Cho et al. 2014), minimal gated unit (MGU) (Zhou et al. 2016, and their variations (Dey and Salem 2017; Heck and Salem 2017) were developed with the aim of attaining comparable performance to more complex models while utilizing fewer parameters, thereby reducing the computational expenses associated with training.

Quantum machine learning (QML) (Schuld et al. 2014; Biamonte et al. 2017) holds promise of augmenting the machine learning process by employing quantum resources and speeding up computations. To this end, both qubit (discrete-variable, DV) and continuous-variable (CV) data encodings are extensively studied (Garg and Ramakrishnan 2020; García et al. 2022). CV systems can be implemented with quantum-photonic platforms and trapped ions. Improvements in machine learning models using quantum computation can be achieved either by speeding up the algorithm (Rebentrost et al. 2014; Schuld et al. 2016; Liu et al. 2021) or by reducing the number of epochs required for training. The latter approach is at the focus of this work. It is usually pursued by means of parameterized quantum circuits (Schuld et al. 2021; Farhi and Neven 2018; Schuld et al. 2020; Benedetti et al. 2019) where the values of quantum gates’ parameters come as a result of circuit training. This recursive process is similar in spirit to the feed-forward neural network algorithm (Svozil et al. 1997). This method has recently been proven to be useful for satellite image classification (Sebastianelli et al. 2022), joint probability distribution modeling (Zhu et al. 2022), and time series analysis (Bausch 2020; Takaki et al. 2021; Chen et al. 2022; Emmanoulopoulos and Dimoska 2022).

Until now, quantum-enhanced implementations of RNNs that have been used for time series analysis were designed for multiple-qubit data input. One such quantum modification of RNNs is the recurrent quantum neural network (RQNN) (Bausch 2020). In this network, each cell is built from a parametrized neuron, and amplitude amplification serves as a nonlinear function applied after each cell call. To date, it was the first fully quantum recurrent neural network, specifically designed to address the challenges of the vanishing and exploding gradient problem, while also demonstrating strong performance on complex tasks. On the contrary, the quantum recurrent neural network (QRNN) (Takaki et al. 2021) consists of cells made of parametrized quantum circuits, which are capable of performing unitary transformations on all input qubits. This network effectively leverages parametrized quantum circuits for temporal learning tasks. An alternative approach to temporal data prediction is based on quantum long short-term memory (QLSTM) (Chen et al. 2022). It employs a classical architecture, in which LSTM cells are replaced with parametrized quantum circuits optimized during the training process. This study aimed to develop a hybrid network capable of learning sequential data. The resulting architecture demonstrated faster convergence compared to its classical counterparts for specific tasks. The idea of constructing the quantum gated recurrent unit (QGRU) was proposed and analyzed in Chen et al. 2020. The successful integration of QGRU and attention mechanism resulted in a neural network with improved nonlinear approximation and enhanced generalization ability. In the last two cases, the implementation was based on internal measurements of the quantum state to realize necessary additional operations and rule sets, which rendered these approaches semi-classical. A different variant of the quantum recurrent neural network was proposed in Hibat-Allah et al. (2020), where a variational wave-functions were used to learn the approximate ground state of a quantum Hamiltonian. The authors shows that the network is capable of representing several many-body wave functions and allows for the efficient calculation of physical estimators. Finally, the Hopfield network, which is a form of an RNN, has awaited several implementations on a quantum computer (Rebentrost et al. 2018; Rotondo et al. 2018; Tang et al. 2019). This approach offers the potential for faster and resource-efficient training compared to its classical counterparts.

Here, we propose a RNN-based quantum algorithm for rapid and rigorous analysis and prediction of temporal data in the CV regime (CV-QRNN). CV-QRNN capitalizes on the parameterized quantum circuit proposed in Killoran et al. (2019). Its operation cycle consists of three phases: entering data, processing them, and performing a measurement. The measurement result, together with the next data point, constitutes the input for the next cycle. To the best of our knowledge, we are the first to construct and study a QRNN in the CV regime for time series processing. We train CV-QRNN for sequence data prediction, forecasting, and image classification and compare the results with the state-of-the-art LSTM implementation. By means of extensive numerical simulations, we demonstrate significant reduction of the number of epochs required for CV-QRNN training to achieve similar results compared to a fully classical implementation with a comparable number of tunable parameters.

This paper is organized as follows. Section 2 describes CV-QRNN’s theoretical model and its architecture. In Sect. 3, we demonstrate results of our numerical simulations, with the methods described in Sect. 4. The conclusions and discussion are provided in Sect. 5.

2 Theoretical model

2.1 Continuous-variable quantum information processing

There are two main quantum information frameworks explored. In one of them, information is encoded in discrete variables that are represented by qubits, and in the other one in continuous variables, embodied by qumodes. Both schemes facilitate universal quantum computation, i.e., they can implement an arbitrary unitary evolution with arbitrarily small error (Weedbrook et al. 2012; Lloyd and Braunstein 1999). While qubits are a counterpart of classical digital computation with bits, CVs resemble analog computing. Here, we focus on the CV quantum framework.

Fig. 1

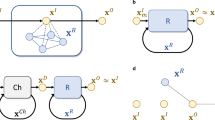
Schema of a recurrent neural network. At every time step t, an input vector $\varvec{x}_t$ is injected to the network cell (brown square) that is parametrized by a hidden state $\varvec{h}_t$. After all the input data have been processed, output sequences $\widetilde{\varvec{y}}_\tau$ are produced, and they serve as the next input to the RNN (dashed arrows). Parameters of the network (not shown on the figure) are described in the text. Additional sets of rules $\mathcal {R}$ included in the network cells upgrade RNN to LSTM or GRU architectures

Quantum CV systems hold promise of performing computations more effectively than their DV counterparts (Lloyd and Braunstein 1999). In particular, thanks to the ability of CV systems to deterministically prepare large resource states and to measure results with high efficiency using homodyne detection, they scale up easily (Gu et al. 2009), leading e.g., to instantaneous quantum computing (IQP) (Douce et al. 2017). These hypothesis is also reinforced by the fact that classical analog computation has been shown to be effective in solving differential equations, some optimization problems, and simulations of nonlinear physical systems (Vergis et al. 1986), where it is able to achieve accurate results in a very short time (Chua and Lin 1984). Analog accelerators have been proposed as an efficient implementation of deep neural networks (Xiao et al. 2020).

Universal CV quantum computation requires a set of single-qumode gates and one controlled two-qumode gate that will generate all possible Gaussian operations, as well as one single-qumode nonlinear transformation of polynomial degree 3 or higher (Lloyd and Braunstein 1999; Weedbrook et al. 2012). In the case of quantum photonic circuits, qumodes are realized by photonic modes that carry information encoded in the quadratures of the electromagnetic field. These quadratures possess a continuous spectrum and constitute the CVs with which we compute. All Gaussian gates can be built from simple linear devices such as beam splitters, phase shifters, and squeezers (Knill et al. 2001). Nonlinearity is usually achieved by cross-Kerr interaction (Stobińska et al. 2008), but it can also be induced by the measurement process, either photon-number-resolving (Scheel et al. 2003) or homodyne (Filip et al. 2005).

Fig. 2

CV-QRNN architecture. a Single layer L acts on $n = n_1 + n_2$ qumodes (horizontal lines) and consists of displacement gates D, squeezing gates S, and multiport interferometers I. A vector $\varvec{x} \in \mathbb {R}^{n_2}$ encodes the input data, while $\varvec{\zeta } = \{\varvec{\theta _1}, \varvec{\varphi _1}, \varvec{r_1}, \varvec{r_2},\varvec{\theta _2}, \varvec{\varphi _2}, \varvec{\alpha _1},\varvec{\alpha _2}, \gamma \}$ denotes all trainable parameters of the network. Red dashed lines split the layer into three parts, responsible for (from left to right) encoding, interaction, and measurement. b Data sequence is processed recurrently by iterating layer L over all inputs $\varvec{x_1},\ldots ,\varvec{x}_{T_x}$. All the qumodes are initialized with the vacuum state $\vert 0 \rangle ^{\otimes n_{1,2}}$. After each iteration, the output $\widetilde{\varvec{x}}'_t$ is measured, mulitplied by parameter $\gamma$, and all bottom wires are reset to the vacuum state. The first prediction of the network $\widetilde{\varvec{y}}_0$ is taken only after all data points have been processed. The subsequent prediction $\widetilde{\varvec{y}}_\tau$ is the output of the layer $L\left( \widetilde{\varvec{y}}_{\tau -1}, \varvec{\zeta } \right)$

The implementation of CV-QRNN will involve the displacement gate

$$\begin{aligned} D(\alpha ) := \textrm{exp}\left\{ \alpha \hat{a}^\dagger - \alpha ^{*}\hat{a} \right\} , \end{aligned}$$

(1)

where $\alpha$ is a complex displacement parameter, $\hat{a}$ ($\hat{a}^\dagger$) is a qumode annihilation (creation) operator, respectively. We will also use the squeezing gate

$$\begin{aligned} S(r) := \textrm{exp}\left\{ \frac{r}{2}(\hat{a}^2 + \hat{a}^{\dagger 2})\right\} , \end{aligned}$$

(2)

where r is a complex squeezing parameter, as well as the phase gate

$$\begin{aligned} R(\varphi ) := \textrm{exp}\left\{ -i\varphi \hat{a}^\dagger \hat{a} \right\} , \end{aligned}$$

(3)

with phase $\varphi \in (0,2\pi )$. We will also harness the beam splitter gate, which is the simplest two-input and two-output interferometer,

$$\begin{aligned} B(\theta ) := \textrm{exp}\left\{ \theta (\hat{a}^\dagger \hat{b} - \hat{a}\hat{b}^\dagger ) \right\} , \end{aligned}$$

(4)

where $\theta \in (0,\frac{\pi }{2})$, $\hat{a}$ and $\hat{b}$ ($\hat{a}^\dagger$ and $\hat{b}^\dagger$) are annihilation (creation) operators of two interfering qumodes, respectively. Any arbitrary multiport interferometer, denoted here by $I(\varvec{\theta }, \varvec{\varphi })$, can be implemented with a network of phase and beam splitter gates (Reck et al. 1994). In our work, we will use the Clemets decomposition (Clements et al. 2016) to achieve this goal. All described gates are implementable with the commercially available quantum-photonic hardware. To realize nonlinear operations, CV-QRNN will harness the tensor product structure of a quantum system (Zanardi et al. 2004), which is capable of providing nonlinearity by means of measurement, in the spirit of Refs. Killoran et al. 2019; Takaki et al. 2021. This will free us from the necessity of utilizing strong Kerr-type interactions that are difficult to implement.

2.2 Recurrent neural networks

Our quantum-enhanced RNN architecture (CV-QRNN) is inspired by the vanilla RNN depicted in Fig. 1 (Sherstinsky 2020). This is a standard network layout which is trained by iterating over the elements of an input data sequence. Then, during the prediction phase, the output values are looped back to the input to obtain subsequent results.

In the RNN, $T_x$ n-bit input sequences $\{\varvec{x}_i\}_{i=0}^{T_x}$ ($\varvec{x}_i \in \mathbb {R}^n$, indicated as green squares in Fig. 1) are sequentially processed by a cell (brown square) to produce $T_y$ m-bit output sequences $\{\widetilde{\varvec{y}}_i\}_{i=0}^{T_y}$ ($\widetilde{\varvec{y}}_i \in \mathbb {R}^m$, pink squares). At each time step t, the RNN cell is characterized by a hidden state vector $\varvec{h}_t \in \mathbb {R}^d$, which serves as a memory that keeps the internal state of the network. It is updated as soon as a new data point is injected into the network in step $t+1$

$$\begin{aligned} \varvec{h}_{t+1} = \left\{ \begin{array}{ll} g_h(W_x \varvec{x}_{t} + W_h \varvec{h}_{t} + \varvec{b}_h), &{} 0 \le t \le T_x\\ g_h(W_x \widetilde{\varvec{y}}_{t-T_x-1} + W_h \varvec{h}_{t} + \varvec{b}_h), &{} t > T_x \end{array}\right. \end{aligned}$$

(5)

where $W_x, W_h$ are weight matrices of dimensions $d\times n$ and $d \times d$, respectively, $\varvec{b}_h \in \mathbb {R}^d$ is a bias vector, $g_h$ is an element-wise nonlinear activation function. $\varvec{h}_0$ is an initial hidden state which is a parameter of the network.

The output sequences are computed only after all input data points were processed by the RNN

$$\begin{aligned} \widetilde{\varvec{y}}_\tau = g_o\left( W_y \varvec{h}_{T_x+\tau } + \varvec{b}_y \right) , \end{aligned}$$

(6)

where $W_y$ is a weight matrix of dimension $m \times d$, $\varvec{b}_y \in \mathbb {R}^m$ is a bias vector and $g_o$ is an element-wise nonlinear activation function, which can be different from $g_h$.

Next, we validate the accuracy of the results produced by the network. To this end, we compute a cost function C that allows us to compare $\{\widetilde{\varvec{y}}_t\}_{t=0}^{T_y}$ with the desired result $\{\varvec{y}_t\}_{t=0}^{T_y}$. In the case of the sequence prediction and forecasting task, the mean square error was adopted:

$$\begin{aligned} C_{MSE}\left( \{\widetilde{\varvec{y}}_t\}_{t=0}^{T_y}, \{\varvec{y}_t\}_{t=0}^{T_y}\right) = \frac{1}{m} \sum \limits _{t=0}^{T_y} \Vert \widetilde{\varvec{y}}_t - \varvec{y}_t\Vert ^2, \end{aligned}$$

(7)

while for the classification task—the binary cross entropy, in which only a single output $\widetilde{\varvec{y}}_0 \equiv \widetilde{\varvec{y}}$ is compared to the expected label $\varvec{y}_0 \equiv \varvec{y}$

$$\begin{aligned} C_{BCE}\left( \widetilde{\varvec{y}}, \varvec{y}\right) \!=\! \frac{1}{m} \sum \limits _{i=1}^m \!-\! \left( y_i \log (\widetilde{y}_i) \!+\! (1-y_i) \log (1 \!-\! \widetilde{y}_i) \right) . \end{aligned}$$

(8)

Minimization of the cost function by means of backpropagation helps us to optimize parameters of the network. The state-of-the-art LSTM and GRU architectures introduce a modification to RNNs by complementing the hidden layer with additional sets of rules $\mathcal {R}$ that determine how long the information about previous data points should be kept (Hochreiter and Schmidhuber 1997). It is implemented by functions acting on copies of input and hidden layer data, which amplify or vanish selected values from previous iterations. We use LSTM as a classical reference system to which we compare the performance of CV-QRNN. We find this comparison fair because LSTM is one of the most widely used schemes in industrial applications (Van Houdt et al. 2020) that is similar in its architecture and mode of operation to CV-QRNN. In this paper, we use its implementation, which follows the original proposal found in Ref. (Hochreiter and Schmidhuber 1997).

2.3 CV-QRNN architecture

The detailed CV-QRNN layout, shown in Fig. 2, is based on a vanilla RNN. This is because GRU and LSTM architectures cannot be directly implemented on a quantum computer as a result of the no-cloning theorem (the no-cloning theorem forbids to copy quantum information). In addition, quantum memories, which are required to implement internal rules in the latter networks, are unfeasible.

The wires represent the n-dimensional tensor product of the qumodes, and the rectangles represent the quantum gates. Each qumode is initially prepared in the vacuum state $|0\rangle$, which is collectively denoted as $|0\rangle ^{\otimes n}$. To highlight the fact that every gate acts on n qumodes simultaneously, but each qumode sees different gate parameters, we use the following notation: $D(\varvec{v}) \equiv \bigotimes _i D(v_i)$ and $S(\varvec{v}) \equiv \bigotimes _i S(v_i)$, where $\varvec{v} = \left( v_1,\ldots ,v_n \right) ^{\text {T}}$, $\bigotimes$ is the tensor product, D and S are a single-qumode displacement and squeezing gates, respectively.

A single quantum layer L, shown in Fig. 2a, acts in the following way: first, it encodes classical data $\varvec{x}$ into the quantum network by means of a displacement gate $D(\varvec{x})$ that acts on $n_2$ qumodes prepared in the vacuum state $\vert 0 \rangle ^{\otimes n_{2}}$ (bottom wire). Next, all $n=n_1+n_2$ qumodes (top and bottom wires) are processed in a multiport interferometer $I(\varvec{\theta _1}, \varvec{\varphi _1})$ followed by squeezing gates $S(\varvec{r_{1,2}})$, another interferometer $I(\varvec{\theta _2}, \varvec{\varphi _2})$, and displacement gates $D(\varvec{\alpha _{1,2}})$. As a result of this, the layer L outputs a highly entangled state that involves all n qumodes. Eventually, $n_2$ qumodes are subjected to a homodyne measurement and reset to the vacuum state, while $n_1$ qumodes are passed to the next iteration.

The qumodes that are measured are dubbed the input modes, while these left untouched—the register modes. The output of the former, $\widetilde{\varvec{x}}$, equals to the mean value of the measurement results $\widetilde{\varvec{x}}'$ multiplied by the trainable parameter $\gamma$. For convenience of notation, we denote all the gates’ parameters in the network as $\varvec{\zeta } = \{ \varvec{\theta _1}, \varvec{\varphi _1}, \varvec{r_1}, \varvec{r_2},\varvec{\theta _2}, \varvec{\varphi _2}, \varvec{\alpha _1},\varvec{\alpha _2}, \gamma \}$. Thus, the layer L is characterized by $2\left( n^2 \!+\! \max (1,n - 1) \right)$ $+ n + 1$ parameters in total, which are randomly initialized before the first run.

Sequential processing of data points $\{\varvec{x}_i\}_{i=0}^{T_x}$ is shown in Fig. 2b. As soon as the quantum layer $L(\varvec{x}_t, \varvec{\zeta })$ is executed in the time step t, the bottom $n_2$ qumodes are reset to the vacuum state $\vert 0 \rangle ^{\otimes n_2}$ and fed to the next layer $L(\varvec{x}_{t+1},\varvec{\zeta })$ along with $n_1$ qumodes that were never measured. This process is iterated T times. The data point that follows $\varvec{x}_{T_x}$ is $\widetilde{\varvec{x}}_{T_x} \equiv \widetilde{\varvec{y}}_0$ and the process continues, i.e., the layer $L(\widetilde{\varvec{y}}_{\tau }, \varvec{\zeta })$ outputs $\widetilde{\varvec{y}}_{\tau +1}$, for the next $T_y$ steps. Only the output $\varvec{y}_0,\ldots ,\varvec{y}_{T_y}$ is then analyzed.

3 Numerical simulations

To assess the quantum-enhanced performance of the CV-QRNN architecture depicted in Fig. 2, we compared its performance with a classical LSTM (Fig. 1). Our figure of merit was the reduction in the number of epochs required to obtain a clear plateau in subsequent values of the cost function C, which achieve the same order of magnitude as for the reference classical network. The comparison involved running the quantum algorithm under a software simulator of a CV quantum computer, which was used to calculate the measurement outputs of the layer L and optimize the trainable parameters $\varvec{\zeta }$. Reference data were obtained by processing the same input with a state-of-the-art LSTM implementation. For our experiments, we chose two tasks to be realized by both networks: time series prediction and forecasting, as well as data classification. The former demonstrated the ability of CV-QRNN architecture to compute subsequent data values from initial samples of periodic or quasi-periodic functions. The latter was a textbook classification problem of recognizing MNIST handwritten digits based on the initial learning of the network. It allowed us to show that even a small number of parameters was suitable for correct discrimination between data sets.

Task 1 – sequence prediction and forecasting. We define prediction as computing only a single value of the function f(x) based on the previous T data points in a sequence and forecasting as computing several consecutive values to achieve a longer output. For this task, we chose quasi-periodic Bessel function of degree 0, $f(x)\equiv J_0(x)$. It has wide applications in physics and engineering, as it describes various natural processes (Korenev 2002). Since the oscillation amplitude vanishes for large x, forecasting of this function is non-trivial. The Bessel function was used to generate 200 equidistant points $\left( x_i,J_0(x_i)\right)$, where $x_0=0$ and $x_{200} \approx 4\Omega$ and $\Omega$ designates the function period. Next, taking $\overline{x}_i = J_0(x_i)$, we computed the sequence $\{\overline{x}_i\}_{i=0}^{200}$. It was split equally between the training and test data sets, so that each set contained 2 periods of the function. The network was trained to predict $\overline{x}_{i+T}$ based on the input that consisted of $T-1$ previous data points. For each input $\{\overline{x}_i, \ldots , \overline{x}_{i+T-1}\}$, where $i=0,\ldots ,200-T$, the network returned the output y, which was trained to be as close to $x_{i+T}$ as possible. We used $T=4$ (the rationale for this choice is presented below). The standard baseline model for this task was to repeat the last input point as the output value, $\overline{x}_{i+T} = \overline{x}_{i+T-1}$. The results achieved for other functions, such as sine, triangle wave, and damped cosine, are shown in the Appendix 2.

Fig. 3

Cost function C (Eq. (7)) computed for CV-QRNN (blue line, training data; light gray, testing) and LSTM (orange line, training; dark gray, testing), as a function of the number of epochs in the task of predicting the values of the Bessel function $J_0(x)$ (Task 1). Shaded regions represent the standard deviation, and solid lines are the average for 5 runs of the simulation. The CV-QRNN achieves values of C below $10^{-4}$ already after 10 epochs and reaches $10^{-5}$ below 100 epochs. Such values are accessible for the corresponding LSTM after 200 epochs. The dashed line indicates the cost function for the simplest baseline strategy in which the last input value is repeated as the predicted value

The results of the first task are depicted in Fig. 3, which shows the cost function C (Eq. 7) as a function of the number of training epochs, plotted separately for the training and test data sets. The outputs are compared for CV-QRNN and LSTM networks, for which we used the same hyperparameters, such as batch size, learning rate, and a similar number of trainable parameters. The cost function C for the quantum network reaches the same value after 100 epochs as for the classical network after 200 epochs. We noticed that in the former case, the cost function drops rapidly in the first few epochs, and for the same number of epochs, it achieves lower values compared to the classical network.

Prediction and forecasting capabilities of both networks are visualized in Fig. 4, where output values are compared directly with the previously generated test sequence. This plot depicts how the Bessel function is gradually approximated after some number of computation epochs. It shows that while CV-QRNN copes well with the task and the prediction is especially well realized, LSTM is much worse in prediction and fails in forecasting even after 100 epochs of training.

Fig. 4

Progress of training on the data generated with Bessel function $J_0(x)$, for CV-QRNN (top row) and LSTM networks (bottom row). Blue points represent the reference data, orange points are predictions based on $T=4$ previous points, and the gray ones are the forecasted values. Vertical dashed line marks the point where the data was split for training (left) and testing (right) sequences

We also investigated the dependence of CV-QRNN prediction on the input sequence length T (Fig. 5). For this, we have trained the network with 3 qumodes for $T=2n$, with $n=1,...,10$, for 50 epochs and computed the cost function C. We observe that the worst prediction is achieved for $T=2$, which is expected since the recurrent feature of the network is barely used in this case. However, for T values ranging from 4 to 16, the cost function stabilized at approximately $\sim 10^{5}$. For $T=18$ and $T=20$, we observe large fluctuations in the value of the cost function, with the best value found being less than for $T=10$ and the worst— about the same as for $T=2$. We believe that these fluctuations are caused by the limited memory of our network, which has a fixed number of parameters, in conjunction with the cut-off dimension described in Sect. 4. In our experiments, we used $T=4$ which was a compromise between the computation time and final cost function value.

Task 2 – MNIST image classification. The second task, which was tested on the CV-QRNN architecture, was the classification of handwritten digits from the MNIST data set (Deng 2012). Due to the fact that simulating qumodes and their interactions is resource-heavy, we have narrowed down the test to the binary classification problem of digits “3” and “6.” Additionally, we downsampled the original images from $28 \times 28$ pixels to $7 \times 7$. We used 1000 images, which were divided between training (80%) and test (20%) sets. The image pixels were sequentially injected into the network from left to right and from top to bottom, giving the sequence $\{x_{i}\}_{i=0}^{48}$. The labels were $y \in \{0,1\}$, where 0 corresponded to digit “3” and 1 to digit “6.” For the simulations, we used the quantum network with 3 qumodes, with one qumode being an input qumode and the rest two acting as register modes. A comparable classical LSTM network was implemented with the standard machine learning library. For both quantum and classical networks, we have used the binary cross entropy loss for the calculation of the cost function C (Eq. (8)). Additionally, the results were assessed with an accuracy function, which is defined as the percentage of properly classified images.

Figure 6 illustrates the accuracy progression during the training for the MNIST data set. The classical network achieves a prediction accuracy of 90% in approximately 5 epochs, and the final accuracy stabilizes at around 93%. On the other hand, the quantum network attains a final accuracy of approximately 85%. This experiment demonstrates that the quantum network is capable of learning the MNIST number recognition task successfully. However, the classical architecture, with a comparable number of parameters, achieves better results and requires fewer epochs compared to the quantum network.

4 Methods

The quantum network was implemented using the Strawberry Fields package (Killoran et al. 2019) that allows the user to easily simulate CV circuits.¹ It also provides a backend written in TensorFlow (Abadi et al. 2015), which makes it possible to use its already implemented functions to optimize the network parameters. For this purpose, we use the ADAM algorithm, which is commonly applied to find the optimal parameters of the network (Zhang 2018). ADAM merges two techniques: adaptive learning rates and momentum-based optimization. The initial learning rate was 0.01 (quantum) and 0.001 (classical) for the time series prediction (Task 1) and 0.01 (quantum and classial) for the classification of MNIST handwritten digits (Task 2). The data was processed in batches of 16 for Task 1, which allowed us to speed up the calculation without losing much precision. For Task 2, batch size was 1. The hyperparameters were chosen empirically.

Fig. 5

The cost function C (Eq. (7)) after 50 epochs of training CV-QRNN for different lengths of input sequence T. The median values for 5 separate runs are depicted by an orange line, while the boxes represent the data between the first and third quartile. The whiskers indicate the range between minimum and maximum values of the data points. For $T=18$ and $T=20$, 10 separate runs were analyzed. Training sequences were generated with Bessel function, as described in the text. The choice of $T=4$ in our numerical simulations results from the observation that for larger lengths, the gain is not so large while the computing resources and time grows exponentially

Fig. 6

Accuracy (the percentage of properly classified outputs) computed for CV-QRNN (blue line, training data; light gray, testing) and LSTM (orange line, training; dark gray, testing), as a function of the number of epochs in the task of the classification of the MNIST data set (Task 2). Shaded regions represent the standard deviation while solid lines are the average for 5 runs of the simulation. The classical network achieves the accuracy above $90\%$ in about 5 epochs, and final accuracy stabilizes around $93\%$. The quantum network final accuracy is around $85\%$

Since the quantum CV computations are done in an infinite-dimensional Hilbert space, the dimensionality of the system needs to be truncated to be able to be modeled on a classical computer. The highest accessible Fock state is called a cutoff dimension. In our simulations, we have used the cutoff dimension of 6. Furthermore, we added the regularization term of the form $L_T = \eta \left( 1 - \text {Tr} \rho \right) ^2$ to the cost function, where $\text {Tr} \rho$ is the trace of the state after the last layer has been processed, and $\eta$ is a weight empirically chosen to be 10 (Killoran et al. 2019).

The implementation of classical LSTM has been realized using the TensorFlow package (Abadi et al. 2015). We use the layer tf.keras.layers.LSTM, which takes as a parameter the dimensionality of the hidden state. We set this parameter to match the number of trainable parameters in CV-QRNN, to make both implementations comparable. The remaining arguments of the LSTM implementation were left at default values.

The calculations were performed with two hardware platforms. The time series prediction task (Task 1) was realized on a laptop with CPU Intel Core i5-10210U (8 cores) running at 4.2GHz, and 16 GB of RAM. The calculations took between 1 and 24 h for CV-QRNN training over 50 epochs, depending on the data input length. The training for the MNIST data classification (Task 2) was realized with a cluster with CPU Intel Xeon E5-2640 v4 processors, 120 GB of RAM, and Titan V GPUs equipped with 128 GB of memory. It took approximately 2 days for 25 epochs and 1000 images of 49 pixels each.

5 Discussion

We performed extensive numerical simulations of CV-QRNN with a CV quantum simulator software and compared its performance to the state-of-the-art implementation of classical LSTM. Our simulations showed that CV-QRNN possesses features that make it highly advantageous in time series processing compared to the classical network. The quantum network arrived at its optimal parameter values (cost function below $10^{-5}$) within 100 epochs, while a comparable classical network achieved the same goal after 200 epochs, and therefore, the speed gain achieved 200%. Similar results were obtained for other sets, presented in Appendix 2.

Faster RNN training is a hot topic currently investigated by AI researchers (García-Martín et al. 2019), who notice that it becomes a more important goal than achieving high accuracy. High requirements for computing power and energy consumption in large machine learning models constitute serious roadblocks for their deployment. They directly translate into large operational costs, but also into an environmental footprint, and therefore, they must be resolved. Therefore, the computation speedup merged with lower environmental influence is an unbeatable advantage of quantum platforms which directly address the limitations faced by classical solutions.

Our work opens possible prospects for future research in the development of quantum RNNs. It also underlines the importance of the CV quantum computation model. The quantum platform we chose makes our solution highly compelling, because the CV architecture we propose can be implemented with existing off-the-shelf quantum photonic hardware, which operates at room temperature. To develop such a platform, one needs lasers, which produce coherent sources of light, and basic elements (squeezers, phase shifters, beam splitters), which are already routinely implemented in photonic chips and are characterized by very low losses. Homodyne detection achieves very high efficiency and is implemented with photodiodes and electronics. To obtain suitable nonlinearity, required for the activation function, we used the tensor product structure of the quantum circuit together with the measurement, which freed us from using additional nonlinear elements. One of the unbeatable advantages of this platform is true quantum operation, without the need of performing measurements of the reference qubits or qumodes inside each algorithm iteration to implement internal rules of the hidden layer. However, measurement of selected qumodes and use of this output for a subsequent iteration are perfectly doable. A similar approach was already demonstrated in the coherent Ising machine and is planned for its quantum successor (Inagaki et al. 2016; Yamamura et al. 2017; Honjo et al. 2021). There, a very long optical fiber loop acted as a delay line to synchronize electronic and photonic paths of the circuit.

A natural next step for our project would be to repeat the computations with real quantum hardware instead of a simulator. This is the problem faced by many scientific papers in the domain of quantum machine learning, as they usually do not rely on one of a few available hardware configurations. For example, previously studied quantum RNN architectures such as QLSTM or QGRU relied on unphysical operations such as copying of a quantum state, which could not be achieved with real quantum hardware.

There are also several open questions that would be worth answering in future work. One of them is the framework in which a comparison between classical and quantum networks would be possible in a fair way. In our work, we used the criterion of the same number of parameters; however, there are approaches that focus on provable advantages of a quantum network (Gyurik and Dunjko 2022; Huang et al. 2022). Moreover, our simulations, due to the availability of limited computational resources and exponential scaling of requirements, were performed only for a small number of qumodes. Therefore, in future research, we would like to verify if a similar quantum advantage is still present for a larger network. The faster training of the quantum network compared to its classical counterpart can also be investigated by applying the concept of effective dimension introduced in Abbas et al. (2021). By utilizing the quantum Fisher information matrix, which provide an insight into the curvature of the network’s parameter landscape, the effective dimension offers a means to understand this phenomenon. This approach has the potential to facilitate a qualitative and equitable assessment of the trainability of various models in future research. Lastly, it would be particularly interesting to study CV-QRNN performance with real-world data such as hurricane intensity (Giffard-Roisin et al. 2018), where a clear data pattern is not obvious.

Appendices

Appendix 1. Noise influence

We analyzed the influence of noise on the predictions returned by CV-QRNN in Task 1. Two types of noise were investigated. The first was caused by losses in the channels and was estimated in the following way: let $\hat{a}$ be a bosonic mode and $\beta \in [0,1]$ be the loss parameter; then the lossy channel is described by

$$\begin{aligned} \hat{a}' = \text {Tr}_{\hat{b}} \left( \sqrt{1-\beta }~\hat{a} + \sqrt{\beta }~\hat{b} \right) , \end{aligned}$$

(9)

where $1-\beta$ is energy transitivity. For $\beta =0$, we obtain the original mode $\hat{a}$, and for $\beta =1$, we lose all the information. The dependence of final cost function on parameter $\beta$ is shown in Fig. 7a.

The other type of noise is located in the data itself. To model it, we added uniformly distributed random values to the time series, $\text {Uniform}(-\varepsilon , \varepsilon )$, where $\varepsilon$ is a parameter. The dependence of final cost function on the parameter $\varepsilon$ is presented in Fig. 7b.

Importantly, we did not observe significant change in the prediction for a network with a channel loss up to 0.2. The cost function for $\beta = 0.4$ is twice as big as for no noise at all. The network still performs well, even the forecasting of multiple data points (cf. Fig. 7a). In the case of the noisy data, we observed no influence up to $\varepsilon = 0.01$. With $\varepsilon = 0.03$, we obtained the value of the loss function, which is almost an order of magnitude larger than with no loss at all. Figure 7b also shows that for $\varepsilon > 0.03$ the network loses its ability to forecast.

Fig. 7

The influence of the noise on the cost function C (Eq. (7)): a for noise in the channel parametrized by $\beta$ and b for noise in the data, parametrized by $\varepsilon$. Both parameters are described in Appendix 1. Shaded region shows the standard deviation, while solid lines depicts a mean of 5 runs of the simulation. In the small boxes, the prediction of the network for the parameter shown by dashed arrow are presented. For clarity, we have omitted legends, but the colors are the same as in Fig. 4

Fig. 8

Cost functions C (Eq. (7)) during the training of the network for different data sets: a sine wave, b composition of 2 sine waves with different periods, c triangle wave, d exponentially damped cosine wave

Appendix 2. Additional data sets

Here, we present results for other data sets: sine wave (Figs. 8a and 9), sum of two sine waves with period $2\pi$ and $\pi$ (Figs. 8b and 10), triangle wave (Figs. 8c and 11),  and exponentially damped cosine wave (Figs. 8d and 12). We depict the cost function during the training of the network in Fig. 8. The prediction and forecasting ability is presented in Figs. 9, 10, 11, and 12 for data sets described previously. For these data sets, we found similar results as for the Bessel function, which was described in the main text.

Fig. 9

Progress of training on the data generated with sine function $\sin (x)$, for CV-QRNN (top row) and LSTM networks (bottom row). Blue points represent the reference data, orange points are predictions based on $T=4$ previous points, and the gray ones are the forecasted values. Vertical dashed line marks the point where the data was split for training (left) and testing (right) sequences

   

Fig. 10

Progress of training on the data generated with function ${\frac{1}{2} \sin (x) + \frac{1}{2} \sin (2x)}$, for CV-QRNN (top row) and LSTM networks (bottom row). Blue points represent the reference data, orange points are predictions based on $T=4$ previous points, and the gray ones are the forecasted values. Vertical dashed line marks the point where the data was split for training (left) and testing (right) sequences

   

Fig. 11

Progress of training on the data generated with triangle wave function, for CV-QRNN (top row) and LSTM networks (bottom row). Blue points represent the reference data, orange points are predictions based on $T=4$ previous points, and the gray ones are the forecasted values. Vertical dashed line marks the point where the data was split for training (left) and testing (right) sequences

   

Fig. 12

Progress of training on the data generated with function ${\textrm{exp}(-\frac{x}{10}) \cdot \cos (x)}$ (so called damped oscillation), for CV-QRNN (top row) and LSTM networks (bottom row). Blue points represent the reference data, orange points are predictions based on $T=4$ previous points, and the gray ones are the forecasted values. Vertical dashed line marks the point where the data was split for training (left) and testing (right) sequences