Abstract
At the High Luminosity Large Hadron Collider (HL-LHC), traditional track reconstruction techniques that are critical for physics analysis will need to be upgraded to scale with track density. Quantum annealing has shown promise in its ability to solve combinatorial optimization problems amidst an ongoing effort to establish evidence of a quantum speedup. As a step towards exploiting such potential speedup, we investigate a track reconstruction approach by adapting the existing geometric Denby-Peterson (Hopfield) network method to the quantum annealing framework for HL-LHC conditions. We develop additional techniques to embed the problem onto existing and near-term quantum annealing hardware. Results using simulated annealing and quantum annealing with the D-Wave 2X system on the TrackML open dataset are presented, demonstrating the successful application of a quantum annealing algorithm to the track reconstruction challenge. We find that combinatorial optimization problems can effectively reconstruct tracks, suggesting possible applications for fast hardware-specific implementations at the HL-LHC while leaving open the possibility of a quantum speedup for tracking.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Track reconstruction is a critical and computationally intensive step for data analysis at high energy particle accelerator experiments (The HEP Software Foundation 2019). The track of a charged particle within a magnetic field is locally approximated by a helix; measurement of the curvature of this helix enables the determination of the components of the particle’s momentum that are transverse to the magnetic field. Furthermore, in collider physics, tracks are crucial for a variety of measurements such as reconstruction of decay vertices (Collaboration 2014), identification of jet flavor (Chatrchyan et al 2013; Sirunyan et al 2018; Aad et al 2016; Aaboud et al 2018), pileup mitigation (Tech. Rep. CMS-PAS-JME-14-001 2014; Khachatryan et al 2015; Sirunyan et al 2019) and are particularly important in complementing calorimeter measurements at low energy.
The High-Luminosity LHC (HL-LHC) upgrade, which is expected to be completed in 2026, will increase the number of simultaneous collisions (pileup) per proton bunch crossing from approxim40 to up to 200 (Apollinari et al. 2017). Under these conditions, conventional algorithms, such as a Kalman filter, scale worse than quadratically with respect to the number of hits and are expected to require excessive computing resources (The HEP Software Foundation 2019). A variety of alternatives to current particle tracking methods are being pursued (Cerati et al. 2018; Funke et al. 2014; Farrell et al. 2018) to tackle the enhanced combinatorics of tracking at the HL-LHC.
It is an open question as to whether quantum annealing (QA) implementable in current hardware offers any scaling speedup over classical methods. Nonetheless, for specific optimization problems, quantum annealing (Kadowaki and Nishimori 1998) outperforms classical heuristics like simulated annealing (SA) (Farhi and Goldstone 2002; Albash and Lidar 2018), and competitive performance has already been demonstrated for certain machine learning tasks (Mott et al. 2017; Li et al. 2018). It can present a promising avenue for particle tracking if we represent it as an appropriate optimization problem. In this work we describe a prototype for a charged particle track reconstruction method using a programmable quantum annealer.
2 Track reconstruction as a QUBO
2.1 Problem construction
The problem of track reconstruction can be formally stated as follows: given a set of hits (data from detector-particle interactions) with different spatial positions, the goal is to cluster them into collections of hits that come from the same particle. The current methods used for tracking can be broadly classified into sequential and global methods. Sequential methods construct tracks one by one: for example, the road method (Strandlie and Fruhwirth 2010) and the Kalman filter (Billoir 1984). Global methods construct all tracks at once and are, at the core, clustering algorithms in some feature space such as for example the Hough transform (Hough 1959; Cheshkov 2006) and Hopfield network (also called the Denby-Peterson network (Denby 1988; Peterson 1989; Stimpfl-Abele and Garrido 1991)). Most of these methods scale worse than quadratically with the number of tracks per event. In particular, the scaling of the combinatorial track finder algorithm as a function of the number of concurrent proton-proton interaction per bunch crossing in the LHC (referred to as “pileup”) would no longer be feasible at higher track density (Cms tracking pog performance plots for 2017 with phasei pixel detector 2017).
Using quantum annealing (QA), we can solve certain combinatorial optimization problems (Farhi et al. 2000). Any quadratic unconstrained binary optimization (QUBO) problem can be naturally mapped to an Ising spin problem and can be encoded into the machine Hamiltonian (Lucas 2014). QUBO problems can be formally expressed as:
where Xi ∈{0,1} are the components of X, \(h_{i} \in \mathbb {R}\) represents an external interaction, and \(J_{ij}\in \mathbb {R}\) represents a two-body interaction. The objective is to find the assignment of X that minimizes E. This becomes the Hamiltonian of an Ising model after replacing each Xi by \(\frac {1}{2}(s_{i}+1)\), where si ∈{− 1,1}, and dropping the resulting constant term \(\frac {1}{2}{\sum }_{i} h_{i} + \frac {1}{4}{\sum }_{i<j} J_{ij}\).
We map the track reconstruction problem to a QUBO problem through a procedure motivated by the Denby-Peterson method (Denby 1988; Peterson 1989). However, we make modifications to improve its performance for the HL-LHC, adding specific terms to the QUBO that correspond to LHC-type detector geometry and conditions. Finally, we present classical pre-processing heuristics that are computationally efficient, allowing us to evaluate the track reconstruction problem on a programmable quantum annealer and using simulated annealing (SA).
We use data from the TrackML Particle Tracking Challenge on Kaggle (Calafiura et al 2018), simulating the HL-LHC. The open dataset consists of 8850 events each consisting of approximately 105 hits which cluster to about 104 tracks. Around 15% of the data is noise, with hits corresponding to no tracks. We use the spatial data along with the ground truth tracks to assess the performance and accuracy of the algorithm.
2.2 Denby-Peterson method
The Denby-Peterson (DP) track reconstruction method (Denby 1988; Peterson 1989) interprets the track reconstruction problem as an track segment classification problem. It has been earlier proposed and validated for the ALEPH (Stimpfl-Abele and Garrido 1991), ARES (Baginyan et al. 1994), and ALICE (Pulvirenti et al. 2004) experiments with promising results. More recently, the method has been deployed in the LHCb experiment muon system (Passaleva 2008).
The DP method optimizes an energy function that resembles a QUBO. Before briefly describing the original algorithm, we schematically show its intended results in Fig. 1. We begin with edges between pre-selected pairs of hits (top of Fig. 1). After optimizing the DP energy function, we expect a value of 1 to be assigned to all correct edges (bottom of Fig. 1) and a value of 0 to be assigned to all incorrect edges.
Let the set S contain N binary variables sab representing all unique edges between a hit a and a hit b, subject to the constraint that hit a is closer to the center than hit b (for uniqueness). If sab = 1 then the two hits are assumed to have been generated by the same particle.
Each term of the energy function is designed for geometric rewards and penalties weighted by parameters α and β, biasing the tracks to be composed of short track segments that lie on a smooth curves with no bifurcations. Given the Cartesian angle 𝜃abc between the two line segments when they are transformed into cylindrical coordinates (i.e., helical tracks appear as straight lines as in the rz-plane), line segment lengths rab,rbc,
and a λ to distinguish similar angles, the total energy of any given set S is given by:
Although the DP method offers a good starting point for tracking, several modifications can be made to the QUBO to provide it with additional information describing the HL-LHC configuration. In particular, we can encode expectations of the particles’ trajectories and the detector geometry to simplify the optimization problem, enabling larger events to be successfully annealed.
2.3 Modified QUBO for HL-LHC
We begin with the same QUBO formulation:
We define the geometric reward to match the helical tracks observed in the LHC. If segments sab and sbc share a point b, the reward is given by (see Fig. 2):
where ϕabc is the azimuthal angle between the line segments in rectangular coordinates (i.e., helical tracks appear helical as in Fig. 1). Since we wish to track charged particles moving in a uniform magnetic field, we expect them to trace helical paths. The 𝜃abc term models this expectation, while the ϕabc term biases tracking towards high-momentum particles with weight ρ. By dividing by track length, we bias the tracking algorithm to favor a chain of short track segments. Note that we standardize the space in r,ϕ,z by dividing by characteristic lengths 1000,π and 1000 respectively so the tracking is not biased in any particular coordinate direction. Furthermore, we threshold the edge affinity term to encourage a sparse graph for annealing, setting the reward weight to 0 if \(\cos \limits ^{\lambda }(\theta _{abc}) < \tau \) for a free parameter threshold τ = 0.996.
As in the original DP method, we add a penalty for bifurcation:
The two sums over b≠c and a≠c correspond to an inhibition of sharing hits at the beginning and the end of the segment respectively.
Furthermore, as particles are created in a small region (5.5 mm in the TrackML open dataset; Calafiurs et al. 2018) along the z axis close to the origin, segments are expected to point towards the origin in the rz-plane. We model these expectations of the z-intercept by extrapolating pairs of line segments and applying a penalty if they do not intercept near the origin. To extrapolate the connected pair of track segments (for a more precise estimate of the z-intercept than extrapolating a single pair of hits), we consider the cross-term between sab and sac rather than a single track segment.
We propose a prior probability bias P(sab) of an edge being true based on its orientation in the rz-plane, adjusted by a constant inhibition term. Hence, we add a final term to our QUBO:
where the prior probability P(sab) is calculated using a Gaussian kernel density estimation (KDE) of training data, described in more detail in Supplementary Information.
The final QUBO incorporating all terms is given by:
The parameters are optimized by Bayesian optimization, sampling regions of the parameter space that are expected to provide the largest improvement in the objective function according to Bayesian inference. The optimization was run with 10 random starts to establish the initial prior probabilities, and then a total of 100 parameter sets were sampled on TrackML events with 500 particles/event to maximize the F1 score (the harmonic mean between purity and efficiency) using SA. The optimal values are summarized in Table 1.
2.4 Heuristic pre-processing and problem decomposition methods
Single sensors are assembled with enough overlap to offer an hermetic coverage within each layer. The high energy produced particles might therefore generate multiple hits per layer. Duplicate hits can be removed empirically with geometrical considerations and minimal assumptions on the track parameters; we do use the ground truth information stored in the Monte Carlo event simulation to assist the processing. The additional hits can be added at limited extra cost during post-processing, so we consider this simplification justified. Removing such closely spaced hits effectively normalizes the distance between adjacent hits, allowing a single set of parameters to be chosen in the QUBO formulation.
Note that pattern recognition is performed in both the barrel (central or low pseudorapidity region) and endcap (edge or high pseudorapidity regions) detectors despite the higher density of tracks. The detector geometry is more complex in the barrel–endcap transition regions, in that tracks no longer travel through layers sequentially, which requires more complex heuristic methods.
To anneal an entire event at the HL-LHC, we would require a fully connected quantum annealer with a qubit for each candidate edge. Given 105 hits, this corresponds to a total of 1010 qubits (edges). This is well beyond the size of current and near-term quantum annealers, currently limited to a few thousand qubits. Similar issues are frequently encountered in other domains, and problem decomposition methods are therefore an important and active area of study in QA, based, e.g., on the belief propagation or divide-and-conquer algorithms (Bian et al. 2016). Here, to address the same need, we develop alternative heuristic methods with time complexity O(h2) where h is the number of hits, to reduce the number of edges and hence the number of qubits required. This ultimately allows events with 103 to 104 hits to be annealed on a quantum annealer with only 33 fully connected logical qubits. Since iterating over the data to construct a QUBO problem already runs in O(h4) time (we must iterate over all pairs of edges), these additional pre-processing heuristics do not significantly add computational time as the event size increases. Importantly, the complexity analysis is done without considering any possible speedup from parallel computation.
To limit the possible number of edges, we divide the event up into 32 overlapping sectors in the xy-plane, where each sector is 1/16th of the full azimuthal angle and half-overlaps with its neighboring sectors. In the TrackML dataset, we find that > 99% of edges are within a single sector, and thus accurately solving individual sectors would guarantee correct reconstruction of over 99% of the event in post-processing. We then apply the procedure consisting of selecting candidate edges with Gaussian kernel density estimation followed by subdividing the QUBO into smaller optimization problems (see Fig. 3).
To provide a general method for detector geometries beyond that of the TrackML dataset, we use Gaussian kernel density estimation (KDE) to determine the prior probability that a given edge between two hits is true using data samples outside the test set. Since tracks typically originate from the interaction point near the origin, we train the Gaussian KDE on the z-intercept and the angle in the rz-plane of line segments based on ground truth in the TrackML data.
We apply a cut on the Gaussian KDE to reduce the size of the QUBO, yielding 93% of all the true edges with approximately 1% purity. Given h hits, this has time complexity \(O\left (h^{2}\right )\) as we traverse over all edges. We may then construct the QUBO outlined earlier, again traversing all pairs of edges with complexity \(O\left (h^{4}\right )\).
Since we wish to anneal our problem using a small number of qubits, we further subdivide the problem into disjoint sub-graphs, separating individual communities of hits connected by edges. To do so, we perform a flood-fill search (Torbert 2016) to label each edge and prune the candidate edges from each node to only include the 5 edges with the highest single-edge biases in the QUBO. Thus, this sub-division procedure also runs in time \(O\left (h^{2}\right )\). We proceed to anneal the multiple QUBO problems with the number of problems scaling like the number of sub-graphs, i.e., as O(h2) since the sub-graphs divide the event into disjoint edge communities. The sub-graphing process is further detailed in the Supplementary Information.
2.5 Annealing procedure
Due to the QUBO construction of assigning each possible edge to a variable in the QUBO problem, we expect SA with no pre-processing to solve the tracking problem in exponential time with respect to the number of edges h2, i.e., \(O\left (\exp \left (ch^{2}\right )\right )\) for a constant c > 0. After our sub-graphing procedure, we divide the event into K = O(h2) sub-graphs, and we expect total annealing time to grow as \({\sum }_{i=1}^{K} \exp \left (cm_{i}\right )\) where mi is the number of edges in sub-graph i. Hence, the overall scaling would depend on the distribution of mi, as analyzed in the Supplementary Information.
Since the sub-graphing procedure only reduces the complexity of the annealing (by dividing the larger QUBO into smaller sub-QUBOs), the procedure’s complexity is bounded from above by \(O\left (\exp \left (ch^{2}\right )\right )\). To verify this, we use SA and measure the convergence time as a function of the distribution of sub-graph sizes, as shown in Supplementary Information.
Although QA is not thought to generally yield a ground state solution to a QUBO problem in polynomial time, it may reduce the size of the constant c in the time complexity \({\sum }_{i=1}^{K} \exp \left (cm_{i}\right )\), potentially offering a significant speedup over classical methods (Boixo S. et al. 2014; Rønnow et al. 2014). To assess the possibility of a quantum speedup, we implement our procedure on a programmable quantum annealer built by D-Wave Systems Inc. Bunyk et al. (2014) and housed at the University of Southern California’s Information Sciences Institute. The D-Wave 2X architecture has 1,098 superconducting flux qubits arranged in a Chimera graph, in which each qubit is coupled to at most 6 others. To increase connectivity we perform a minor-embedding operation by mapping each QUBO problem onto ferromagnetic chains of qubits (Choi 2008, 2011; Klymko et al. 2014; Cai et al. 2014); the result is a fully connected graph of 33 logical qubits, each of which is used to represent an edge.
We optimize the ratio between coupling within each chain to the largest coupling in the Hamiltonian to equal a factor of 3. We find that this prevents chains from breaking (via noise from thermal excitations and domain walls) while still allowing qubits to flip to ensure that the transverse field Hamiltonian drives the dynamics (Venturelli et al. 2015). For each annealing run, we re-embed the problem 10 times with randomized cross-term signs (gauges) to average out noise on local fields and couplers (Job and Lidar 2018). For each gauge, we perform 10,000 annealing runs before selecting the lowest-energy solution from all the outputs. We note that as the inherent noise in the annealing hardware improves in the future, fewer runs and gauges would be required. To test the effect of the annealing time (which in principle must be optimized in order to extract the true time to solution (Albash and Lidar 2018; Rønnow et al. 2014)), we compare runs from 5 to 800 μs.
3 Results
To evaluate the performance of the annealing algorithm, we benchmark against random edge selection after pre-processing. Random edge selection simply randomly selects edges as true according to the expected fraction of true edge segments in the pre-processed data. Comparison to random edge selection demonstrates that the patterns of hits are not found during pre-processing, but rather by solving the QUBO.
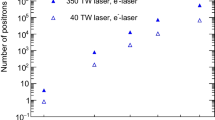
After measuring the overall tracking performance of our methodology, we present results on the scalability of our algorithm for both SA and QA to evaluate the possibility of a quantum speedup. We report error bars representing the 1 standard deviation (σ) spread of sector-by-sector purity and efficiency for TrackML events, indicating the robustness of the methodology. Particle multiplicity and pileup are linearly dependent, where 2,000 particles per event corresponds to an average of 40 pileup.
3.1 Tracking efficiency and purity
To compare the QA and SA performance in terms of particle multiplicity (see Fig. 4) and particle momentum (see Fig. 5), we use two metrics:
QA and SA benchmarked against random annealing after pre-processing heuristics. All values are reported with 1σ error bars for tracks with at least 3 hits indicating the spread of event sectors. Additionally, the pre-processing places an upper bound of around 93% efficiency (indicated by the dashed line)
Due to the limited size of the D-Wave machine (33 fully connected logical qubits), we can only fit up to 500 tracks on the quantum annealer. However, to show that the performance of the algorithm does not significantly deteriorate at higher multiplicity, we include further results from SA.
As particle multiplicity increases, the random edge selection track efficiency and purity approach zero, while the SA and QA reconstructions maintain their performance. This suggests that the majority of tracking is completed in solving the QUBO rather than in our heuristic pre-processing methods. While quantum annealing on D-Wave hardware does not outperform SA, it consistently obtains a solution of similar quality. The SA algorithm’s slightly better performance may be attributable to a lack of noise in embedding the Hamiltonian as well as the ability to fully encode the problem without chains of qubits that cause additional error in the readout process.
We present the performance in terms of track efficiency and purity across several physical variables (see Figs. 6 and 5). For reference, 96% of true edge segments in the TrackML dataset belong to tracks that are 8 to 18 hits in length. Metrics are calculated for tracks at least 3 hits in length. Only SA was used in the figures to improve the statistical uncertainty with a larger number of events.
The tracking algorithm shows consistent performance across the full range of pseudorapidity \(\eta = -\log \tan \frac {\theta }{2}\), where 𝜃 is the polar angle between particle momentum and the beam axis (see Fig. 6). Similarly, tracking performance remains constant with azimuthal angle ϕ in the xy-plane, indicating the consistency of the tracking algorithm since events are typically homogeneous in ϕ. Track reconstruction performance increases with transverse momentum pT, recording higher-momentum particles with both higher efficiency and purity since tracks are straighter and thus better-suited to the QUBO formulation. The drop in efficiency at high pT is observed in many solutions of the TrackML challenge (Calafiura et al 2018) and might be an artifact of the dataset simulation.
3.2 Feasibility of quantum speedup
In general, it is unlikely that QA can achieve polynomial time on this problem, but there is room for a potential quantum speedup if QA can reduce the exponential scaling. To fully test a quantum speedup (Rønnow et al. 2014), a complete analysis of the problem scaling would require identifying the optimal anneal time for each problem size (Albash and Lidar 2018), which we did not attempt other than a crude sampling of several annealing times (see Fig. 7). Quantum annealing yields very similar results with no clear trend using various annealing times (5, 20, 50, 100, 200 and 800 μs), suggesting that we lack data at sufficiently small timescales to fully determine the time scaling while using D-Wave since the QUBO problems are satisfactorily solved by the shortest possible anneal time allowed by the hardware (5 μs) even for the largest events. Indeed, contrary to SA, the performance on D-Wave deteriorates slightly with additional annealing time, most probably due to the effects of 1/f noise, in which low frequency components impact performance at long anneal times (D-Wave White Paper: Improved coherence leads to gains in quantum annealing performance 2019).
Comparison of the purity and efficiency for different annealing times (5 to 800 μs) on the D-Wave 2X with respect to the purity and efficiency for a 5 μs anneal time. The dashed lines show 1σ error bars calculated from the sector-by-sector distribution of differences between the purity or efficiency for a given anneal time and the 5 μs anneal time
To fully assess the quantum speedup question would require a larger programmable quantum annealer such that a larger QUBO can be encoded, resulting in a minimum as a function of problem size in the time to solution when annealing. Moreover, the minimum annealing time allowable by hardware may need to be reduced in order to obtain an estimate of the necessary wall-clock annealing time; Fig. 7 suggests that shorter annealing times can reduce the time required by D-Wave without sacrificing performance. Given the scaling of the QUBO size as O(h2) and our limit of 500 tracks on the 33 fully connected logical qubits of the D-Wave 2X, an event with 10,000 tracks (corresponding to HL-LHC conditions) would have a factor of 400 more edges and thus we expect that a programmable quantum annealer with a similar architecture to D-Wave must have approximately 10,000 fully connected qubits to fully process a sub-graphed event at the HL-LHC. This is twice as many qubits as in the next generation D-Wave processor based on the (increased connectivity but not fully connected) Pegasus architecture (Boothby et al. 2019).
4 Related work
There is limited research on performing track reconstruction using quantum annealing. Track reconstruction using quantum annealing has been explored in Ref. Bapst et al. (2019), using triplets of hits (as opposed to doublets in our approach) which increases pre-processing time to O(h6) as we iterate through all pairs of triplets for constructing the QUBO. However, the solution proposed by the authors is limited to tracking in a simpler detector sub-region of simulated LHC data. It uses extensive classical pre-processing using the ATLAS track-seeding code and internal QUBO-solving methods in the D-Wave API that use further classical pre-processing and have higher overhead. In contrast, we require no track seeding and demonstrate tracking in both the barrel and endcap regions, explicitly controlling the annealing methodology in solving the QUBO. This allows us to show that the annealing procedure is computationally responsible for the majority of particle tracking, not the pre-processing methods.
The application of quantum associative memory for track pattern recognition and its circuit-based implementation on current hardware has previously been theoretically explored by members of the same team (Shapoval and Calafiura 2019). Unlike our approach, the quantum associative memory framework is completely supervised: track candidates are tested by comparing them to simulated track patterns, which must be stored in quantum memory. Because we use a parameterized QUBO formulation of the tracking problem, we do not need to store simulated track data. On the contrary, our approach is based on physical models where the weights of the QUBO are guided by both physical expectations and simulated data.
Finally, quantum annealing has been proposed for a different but closely related problem of vertex reconstruction (Das et al. 2019). This application is limited to events with up to 15 particle tracks, and it does not aim at reconstructing tracks, but rather aggregates them in a fixed number of vertices.
5 Conclusion
We demonstrate one of the first big data applications of quantum annealing, reducing a large-scale problem to be successfully solved experimentally on D-Wave hardware with high purity and efficiency in tracking performance. Ultimately, we find that charged particle tracking can be successfully interpreted as a segment classification problem in a quadratic unconstrained binary optimization (QUBO) framework, using efficient classical pre-processing followed by quantum or simulated annealing. Although current annealing hardware limitations impose stringent constraints on the size of the optimization problem, we propose a methodology to systematically reduce the size of the QUBO sufficiently to achieve experimental implementation on current quantum hardware. Our work indicates that tracking problems at the High-Luminosity LHC may be studied with competitive efficiency and purity results on programmable quantum annealers in the future, while the question of a quantum speedup in this context remains open.
Although currently available quantum hardware does not allow shorter anneal times to be probed, the favorable scaling observed thus far leaves open the possibility for advantageous real-world applications of quantum annealers in a scientific context. One of the key elements of data acquisition at a hadron collider experiment is the trigger system (Khachatryan et al. 2017) that selects, in almost real time, the most interesting collision events from the rudimentary high rate events, which number many orders of magnitude more. The trigger system reduces the rate of collisions under consideration from 40 MHz to 1–2 kHz with fast algorithms, dedicated on-board on-chip hardware and subsequent processing in software farms. In this context, the reconstruction of the charged particles must be done rapidly (on the order of μs at the hardware level) and efficiently. The approach proposed in this work could eventually provide a solution for fast tracking at the trigger level.
Besides providing potential applications for quantum annealing, our methodology establishes the utility of classical simulated annealing for modern tracking problems, and may thus be run on high-performance Field Programmable Gate Array (FPGA) simulated annealing hardware (Tsukamoto et al. 2017) with up to 8192 bits, as well as the Coherent Ising Machine (Inagaki et al. 2016) with 2000 fully connected spins. As these are classical annealing approaches, they are expected to require exponential time to solve the track reconstruction problem. However, they are fully connected, overcoming embedding challenges associated with the D-Wave annealer and enabling larger problems to be encoded with fewer bits. By exploiting the performance advantages of FPGAs and classical annealers, one could perform preliminary tracking at the trigger level. Furthermore, instead of tuning the QUBO parameters to maximize the harmonic mean of track efficiency and purity, the QUBO parameters may be tuned for either high track efficiency (to reduce overall data size) or high track purity (to eliminate entire tracks from the dataset) before applying traditional tracking methods (such as Kalman filters). The approach presented in this paper could be used as a first step of an iterative tracking procedure, otherwise already in use in experiments like the Compact Muon Solenoid. As quantum annealing technology continues to improve, future work may evaluate wall-clock benchmarks against classical specialized hardware, assessing the viability of using quantum hardware at high energy physics experiments.
We note that the spin states found by the D-Wave annealer suggest that sufficiently good solutions to the tracking problem QUBO may be found by programmable quantum annealers without fully solving the QUBO for its ground state. Thus, despite not directly identifying a quantum speedup in this work, we conclude that there remains practical potential of quantum annealing for charged particle tracking. Moreover, as of the time of writing, quantum annealing is the only quantum hardware approach that can accommodate tracking problems large enough to be of any practical interest.
References
The HEP Software Foundation (2019) . Comput Softw Big Sci 3:7. ISSN 2510-2044, https://doi.org/10.1007/s41781-018-0018-8
Collaboration T. C. (2014) J Instrum 9:P10009. https://doi.org/10.1088%2F1748-0221%2F9%2F10%2Fp10009
Chatrchyan S. et al (2013) (CMS). JINST 8:P04013. 1211.4462
Sirunyan A. M. et al (2018) (CMS). JINST 13:P05011. 1712.07158
Aad G. et al (2016) (ATLAS). JINST 11:P04008. 1512.01094
Aaboud M. et al (2018) (ATLAS). JHEP 08:089. 1805.01845
Tech. Rep. CMS-PAS-JME-14-001 (2014) . CERN, Geneva. http://cds.cern.ch/record/1751454
Khachatryan V. et al (2015) (CMS). JINST 10:P02006. 1411.0511
Sirunyan A. M. et al (2019) (CMS), vol 14. 1903.06078
Apollinari G., Béjar Alonso I, Brüning O, Fessia P., Lamont M., Rossi L., Tavian L. (2017) CERN Yellow rep. Monogr. 4:1
Cerati G., Elmer P., Krutelyov S., Lantz S., Lefebvre M., Masciovecchio M., McDermott K., Riley D., Tadel M., Wittich P. et al (2018) J Phys Conf Ser 1085:042016. https://doi.org/10.1088%2F1742-6596%2F1085%2F4%2F042016
Funke D., Hauth T., Innocente V., Quast G., Sanders P., Schieferdecker D. (2014) . J. Phys. Conf. Ser. 513:052010
Farrell S., et al. (2018) In: 4th International Workshop Connecting The Dots 2018 (CTD2018) Seattle, Washington. 1810.06111, http://lss.fnal.gov/archive/2018/conf/fermilab-conf-18-598-cd.pdf
Kadowaki T., Nishimori H. (1998) . Phys. Rev. E 58:5355. https://link.aps.org/doi/10.1103/PhysRevE.58.5355
Farhi E., Goldstone J. (2002) S Gutmann arXiv preprint quant-ph/0201031
Albash T., Lidar D. A. (2018) . Phys. Rev. X 8:031016. https://link.aps.org/doi/10.1103/PhysRevX.8.031016
Mott A., Job J., Vlimant J.-R., Lidar D., Spiropulu M. (2017) . Nature 550:375 EP. https://doi.org/10.1038/nature24047
Li R. Y., Di Felice R., Rohs R., Lidar DA (2018) . npj Quantum Inf 4:14. https://doi.org/10.1038/s41534-018-0060-8
Strandlie A., Fruhwirth R (2010) . Rev. Mod. Phys. 82:1419
Billoir P. (1984) . Nuclear Instrum Methods Phys Res 225:352. ISSN 0167-5087, http://www.sciencedirect.com/science/article/pii/0167508784902746
Hough P. V. C. (1959) . Conf Proc C590914:554
Cheshkov C. (2006) Nuclear Instrum Methods Phys Res Sect Acceler Spectrometers, Detect Assoc Equip 566:35, ISSN 0168-9002, tIME 2005, http://www.sciencedirect.com/science/article/pii/S0168900206008059
Denby B. (1988) Comput Phys Commun 49:429, ISSN 0010-4655, http://www.sciencedirect.com/science/article/pii/0010465588900045http://www.sciencedirect.com/science/article/pii/0010465588900045
Peterson C. (1989) Nuclear Instrum Methods Phys Res Sect A: Acceler Spectrom Detect Assoc Equip 279:537, ISSN 0168-9002, http://www.sciencedirect.com/science/article/pii/0168900289913004
Stimpfl-Abele G., Garrido L. (1991) Comput Phys Commun 64:46, ISSN 0010-4655, http://www.sciencedirect.com/science/article/pii/001046559190048P
Cms tracking pog performance plots for 2017 with phasei pixel detector (2017), https://twiki.cern.ch/twiki/bin/view/CMSPublic/TrackingPOGPerformance2017MC#Timing
Farhi E., Goldstone J., Gutmann S., Sipser M. (2000) arXiv:quant-ph/0001106
Lucas A. (2014) . Front Phys 2:5
Calafiura P. et al (2018) In: Proceedings, 14th International Conference on e-Science: Amsterdam, pp 344
Baginyan S., Glazov A., Kisel I., Konotopskaya E., Neskoromnyi V., Ososkov G. (1994) Comput Phys Commun 79:165, ISSN 0010-4655, http://www.sciencedirect.com/science/article/pii/0010465594900655
Pulvirenti A., Badal A A, Barbera R., Re G. L., Palmeri A., Pappalardo G., Riggi F. (2004) Nuclear Instrum Methods Phys Res Sect Acceler Spectrom Detect Assoc Equip 533:543, ISSN 0168-9002, http://www.sciencedirect.com/science/article/pii/S0168900204016754
Passaleva G. (2008) In: 2008 IEEE Nuclear Science Symposium Conference Record, pp. 867–872, ISSN 1082-3654
Bian Z., Chudak F., Israel R. B., Lackey B., Macready W. G., Roy A. (2016) Frontiers in ICT 3:14, ISSN 2297-198X, https://www.frontiersin.org/article/10.3389/fict.2016.00014
Torbert S (2016) Applied computer science. Springer
Boixo S., Rønnow TF, Isakov S. V., Wang Z., Wecker D., Lidar D. A., Martinis J. M., Troyer and M. (2014) Nat Phys 10:218, 1304.4595
Rønnow TF, Wang Z., Job J., Boixo S., Isakov S. V., Wecker D., Martinis J. M., Lidar D. A., Troyer M. (2014) Science 345:420, ISSN 0036-8075, https://science.sciencemag.org/content/345/6195/420
Bunyk P. I., Hoskinson E. M., Johnson M. W., Tolkacheva E., Altomare F., Berkley A. J., Harris R., Hilton J. P., Lanting T., Przybysz A. J. et al (2014) IEEE Transactions on Applied Superconductivity 24:1, ISSN 1051-8223
Choi V. (2008) Quantum Inf Process 7:193, ISSN 1573-1332. https://doi.org/10.1007/s11128-008-0082-9
Choi V. (2011) Quantum Inf Process 10:343, ISSN 1573-1332. https://doi.org/10.1007/s11128-010-0200-3
Klymko C., Sullivan B. D., Humble T. S. (2014) Quant Inf Proc 13:709. https://doi.org/10.1007/s11128-013-0683-9
Cai J., Macready W. G., Roy A. (2014) arXiv:http://arXiv.org/abs/1406.2741
Venturelli D., Knysh SMS, O’Gorman B., Biswas R., Smelyanskiy V. (2015) . Phys. Rev. X 5:031040. https://doi.org/10.1103/PhysRevX.5.031040
Job J, Lidar D. (2018) Quantum Sci Technol 3:030501. 10.1088%2F2058-9565%2Faabd9b
D-Wave White Paper: Improved coherence leads to gains in quantum annealing performance (2019). https://www.dwavesys.com/sites/default/files/14-1037A-A_Improved_coherence_leads_to_gains_QA_performance.pdf
Boothby K., Bunyk P., Raymond J., Roy A. (2019) Tech. Rep., D- Wave Systems Inc., https://www.dwavesys.com/sites/default/files/14-1026A-C_Next-Generation-Topology-of-DW-Quantum-Processors.pdf
Bapst F., Bhimji W., Calafiura P., Gray H., Lavrijsen W., Linder L. (2019) arXiv:https://arxiv.org/abs/1902.08324
Shapoval I., Calafiura P (2019) arXiv:https://arxiv.org/abs/1902.00498
Das S., Wildridge A. J., Vaidya S. B., Jung A. (2019) arXiv:https://arxiv.org/abs/1903.08879
Khachatryan V., Anderson D., Apresyan A., Bornheim A., Bunn J., Chen Y., Duarte J., Mott A., Newman H., Pena C. et al (2017) J Instrum 12, art
Tsukamoto S., Takatsu M., Matsubara S., Tamura H. (2017) . Fujitsu Sci Techn J 53:8
Inagaki T., Haribara Y., Igarashi K., Sonobe T., Tamate S., Honjo T., Marandi A., McMahon P. L., Umeki T., Enbutsu K. et al (2016) Science 354:603, ISSN 0036-8075. https://science.sciencemag.org/content/354/6312/603
Kirkpatrick S., Gelatt C. D., Vecchi M. P. (1983) Science 220:671, ISSN 0036-8075. https://science.sciencemag.org/content/220/4598/671
Zlokapa A., Mott A., Job J., Vlimant J-R, Lidar D., Spiropulu M. (2020) Phys Rev A 102:062405. https://doi.org/10.1103/PhysRevA.102.062405
Acknowledgements
Part of this work was conducted at “iBanks,” the AI GPU cluster at Caltech. We acknowledge NVIDIA, SuperMicro and the Kavli Foundation for their support of “iBanks.”
Funding
This work is partially supported by DOE/HEP QuantISED program grant, QCCFP/Quantum Machine Learning and Quantum Computation Frameworks (QCCFP-QMLQCF) for HEP, Grant No. DE-SC0019219. JMD is supported by Fermi Research Alliance, LLC under Contract No. DE-AC02-07CH11359 with the U.S. Department of Energy, Office of Science, Office of High Energy Physics. The work of DL and JJ was partially supported by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), via the U.S. Army Research Office contract W911NF-17-C-0050.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zlokapa, A., Anand, A., Vlimant, JR. et al. Charged particle tracking with quantum annealing optimization. Quantum Mach. Intell. 3, 27 (2021). https://doi.org/10.1007/s42484-021-00054-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42484-021-00054-w