1 Introduction

In recent years, reinforcement learning (RL) experienced a renaissance based on the breakthrough in neural networks (NN) and growing computational power. RL’s basic idea is learning by trial and error, motivated by the human learning process. One of the greatest successes was AlphaGO, and AlpahGO ZERO (Silver et al. 2016, 2017) beating the GO world champion multiple times. The program started from tabula rasa and mastered playing the game of GO by learning from self-play. Recent research shows that RL algorithms can even learn to solve complex tasks when relying purely on computational power and time (Baker et al. 2019).

With the promise of fully operational quantum computers in the last decade, researchers started to develop RL algorithms that can be applied in the quantum domain. The first algorithm was provided by Dong et al. (2005). Even though it relies on the principle of quantum computing, it still is a classical algorithm. Briegel and De Las Cuevas (2012) developed the first quantum-based RL algorithm as part of a quantum hybrid framework for RL. This algorithm was successfully applied to a real five-qubit quantum computer. Similar to NNs on classical computers, variational quantum circuits (VQCs) started to generate interest as a quantum hybrid approximation architecture. Chen et al. introduced VQCs as a function approximator in RL (Chen et al. 2019). They modified the well-established DQN (Mnih et al. 2015) algorithm by utilizing a VQC embedded in a NN as an approximator. Due to its similarity to DQN, this approach was termed VQ-DQN. Within their work, they show that VQ-DQN is able to solve the frozen lake and the radiofrequency problem, both discrete problems.

Based on the VQ-DQN approach, this paper shows that the same results can be achieved with a VQC without classical methods. We further compare the classical tabular (Q-learning) and NN-based (DQN) methods to the purely quantum VQ-DQN in terms of iterations until convergence to the optimal behavior, memory usage, and runtime on the frozen lake problem. Thus, our main contributions to RL in the quantum domain are to (1) show that VQ-DQN can solve the frozen lake problem with a pure VQC approximator and (2) provide a rigorous comparison of the standard methods with the novel quantum hybrid approximation utilizing the abovementioned performance measures.

The frozen lake problem consists of a 4 × 4 grid, where the starting state is in the top left corner, and the goal is in the bottom right corner. The player can choose between going up, left, down, or right in every cell; walking against a side of the grid will keep it in the current state. At some points, there are “holes in the ice,” to add some difficulty. If the agent steps into a hole, it loses the current episode. The frozen lake map layout can be found in Fig. 1.

Fig. 1
figure 1

Layout of the frozen lake problem. “S” and “G” mark the start and goal, respectively. Holes are marked in black

Full size image

The paper is organized as follows. Section 2 introduces the concept of RL. Section 2.1 provides the tabular Q-learning algorithm, and Section 2.2 generalizes the idea to Q-learning with NNs to approximate the action-value function. Section 3 provides a brief background on quantum computing (QC) by defining qubits in Section 3.1 and quantum gates in Section 3.2 as the atoms of QC. Section 3.3 connects the previous concepts to quantum algorithms. Section 4 introduces QVC, which will be used in Section 4.1 to define the quantum approximation structure for the action-value function in VQ-DQN. The computational results from comparing the three algorithms are provided in Section 5, followed by an analysis of the results in Section 5.1. The paper concludes in Section 6.

2 Reinforcement learning

RL can be traced back to two ancestors. On the one side, behavioral research in psychology has been pioneered by Pavlov. The English translation of his work is also the first reference of RL (Pavlov 2010). On the other side, it stems from a more data-driven approach to optimal control theory. We give here only a short introduction. However, the interested reader is referred to Sutton and Barto (2018) for more details.

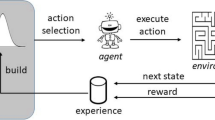
Similarly to optimal control, RL deals with optimization over time. Contrary to the classical approach, however, RL assumes no knowledge of the dynamics of the system to be controlled. We instead assume that the RL agent is completely separated from the environment, which encapsulates the task to be learned. In the frozen lake problem introduced above, the environment contains the game layout and the agent’s current position. At each time step, the environment communicates to the agent its current state st, based on which the agent chooses an action at and returns it. This is usually modeled by a policy π: S → A, i.e., a function that maps from the state to the action space.

In our example, the state would be the agent’s current position, and the action would be in which of the four directions the agent moves next. The environment updates its state based on the action and sends a short-term performance measure rt, the reward, to the agent, before restarting the loop. The agents’ goal is to maximize the sum of rewards, called the return G. In our example, the reward could be 0 unless we reach the final state, in which case the reward is 1. The issue is, however, that the agent can learn arbitrarily long paths to the final state. By shaping the reward to be − 1 for not leaving and 0 for leaving, the agent will learn the shortest path. Some care needs to be taken, though, to treat holes correctly. If the reward for stepping into a hole is − 1 as well, the agent might figure out that it is better to run into the nearest hole since it takes fewer steps than reaching the exit. To avoid these issues, we provide a reward of − 0.01 on a standard step, a reward of − 0.2 for hitting a hole, and a reward of 1 for reaching the exit.

In this paper, we focus on model-free RL methods, which try to find optimal behavior without generating an explicit model of the environment’s dynamics. These split quite naturally into direct methods, which parametrize the function π and try to improve behavior by adjusting its parameters, and indirect methods, which seek to evaluate behavior and base their policies on these evaluations. Here, we focus on the latter. A commonly utilized quantity in such methods is the estimated future return for a given state-action pair, which is usually expressed through the action-value function:

$$ Q^{\pi}(s,a) = {\mathbb{E}}_{\pi}\left[\left.\sum\limits_{t=0}^{T}\gamma^{t} r_{t}(s_{t},a_{t}) \right| s_{0} = s, a_{0} = a\right]. $$
(1)

\({\mathbb {E}}_{\pi }\) indicates that we choose all actions based on a given policy π. Once Qπ is found, π can be improved by checking whether we already selected the action with the highest future return in each state. However, it has been shown that it is not necessary to fully determine Qπ before improving π. More commonly, they are updated alternately.

2.1 Q-Learning

The most direct way to learn optimal behavior would be the Monte Carlo approach, which simulates randomly through the task. Upon finishing the episode, it calculates the Q-values for all visited state-action pairs. To save memory, the average can be updated instead of being recalculated as follows: Let Q(n)(s, a) denote the average after n-th visit and G(s, a) the (n + 1)st observation. We then have

$$ \begin{array}{@{}rcl@{}} Q(s,a)^{(n+1)} &=& \frac{1}{n+1}(nQ^{(n)}(s,a) +G(s,a) ) \end{array} $$
(2)
$$ \begin{array}{@{}rcl@{}} &=& Q^{(n)}(s,a) + \frac{1}{n+1}\\ &&\times(G(s,a) - Q^{(n)}(s,a)). \end{array} $$
(3)

Watkins and Dayan (1992) developed from this the, now famous, Q-learning algorithm, by approximating the future return by the sum of the current reward and the estimation for the future return given by the Q function itself. The idea of splitting future costs into immediate and follow-on costs is well known from dynamic programming. The algorithm for Q-learning can be found in Algorithm 1 in Appendix. To ensure exploration, we choose an action at random with some probability 𝜖, instead of the best action according to the current action-value function.

2.2 DQN

While the above approach works very well, it can only be applied to problems with a reasonably small, discrete action and state space. One solution in problems with a small, discrete action space and continuous state space is to replace the tabular representation of the action-value function with a parameterized approximation. The two most studied choices are linear functions and NNs. The former can be a good choice since, quite often, optimal parameters can be determined analytically. However, they typically lack expressiveness.

For neural networks, the exact opposite is true. It has been shown by Cybenko (1989) and Hornik et al. (1989) that they can approximate measurable functions to arbitrary accuracy. However, finding a suitable set of parameters requires gradient descent-based methods and significant computation time and power. This introduces additional difficulties to the learning regime in RL.

Nevertheless, the best-known success of such an approach, learned to play different Atari games (Mnih et al. 2015). To achieve this, the authors introduced further adjustments to stabilize learning, which have by now been established as standard. Exploiting the fact that Q-learning is an off-policy training algorithm, i.e., that it does not require the use of a policy to be trained for exploration, they introduced a replay memory. Instead of running the updates directly on the observed state, action, reward, next-state quadruple, all these quadruples are saved in a memory. For training, they then sample a batch of training points from that memory. This approach adds stability and makes use of obtained data much more efficiently, which is of particular importance with NNs since they require many training samples. This technique is now established as a standard procedure in such approaches.

Additionally, they used a second, target network, to bootstrap the future reward, instead of the action-value network they are training. From time to time, the action-value network is copied to the target network, which is thus more constant than the training network. Mnih et al. called their approach DQN with experience replay, which can be found in Algorithm 2 in Appendix A.

3 Quantum computing

The following will give a short introduction to the principles of QC by deriving the idea of quantum bits in Section 3.1. This concept is extended to the essential computational elements called quantum circuits in Section 3.2 and concludes with an introduction of quantum algorithms in Section 3.3. Based on this introduction, QVCs, as a quantum hybrid approximation method, are derived in Section 4.

3.1 Qubits

The computational concepts differ significantly in classical computer science and QC since QC is based on quantum theory. Compared to classical bits that can either take the values 0 (false) or 1 (true), a quantum bit (qubit) can be in any superposition of the computational basis states 0 and 1. Using Dirac’s notation, any single-qubit state can be expressed by a linear combination of basis states |ψ〉 = α|0〉 + β|0〉, with \(\alpha , \beta \in \mathbb {C}\) satisfying the normalization condition |α|2 + |β|2 = 1. Thus, α and β define a probability distribution over the basis states and, therefore, are also known as probability amplitudes.

Although a qubit can be in a superposition of computational basis states, it must always be measured to retrieve its information. The measurement will collapse the qubit to one of its basis states. For example, measuring the qubit |ψ〉 will result in measuring the state |0〉 with probability |α|2 and |1〉 with probability |β|2. Thus, even though a single qubit can be in an arbitrary superposition state, a single measurement will only provide the same information as a classical bit. Hence, the same algorithm is repeated multiple times, and the measurement results are averaged to approximate the state distribution.

A geometrical interpretation of a qubit can be derived from explicitly writing α and β as complex numbers |ψ〉 = (α1 + iα2)|0〉 + (β1 + iβ2)|1〉. Thus, a single qubit has four degrees of freedom. The normalization condition traces out one degree of freedom, and without loss of generality, α can be represented as a real number. Applying Eulers’ formula, we can derive the convenient representation

$$ |\psi\rangle = \cos{\frac{\theta}{2}}|0\rangle + e^{i\phi} \sin{\frac{\theta}{2}}|1\rangle, $$
(4)

with 0 ≤ 𝜃 ≤ π and 0 ≤ ϕ ≤ 2π. Equation 4 maps a quantum state to the Bloch sphere shown in Fig. 2. The Bloch sphere provides a representation of a qubit in the 3D space.

Fig. 2
figure 2

Bloch sphere representation of a qubit |ψ〉

Full size image

A complex two-dimensional Hilbert space mathematically describes the state space of a single-qubit system. This definition can be generalized for an n-qubit system to a Hilbert space on \(\mathbb {C}^{m}\) with m = 2n. In quantum systems with more than two qubits, another property arises that is unknown in classical computation; two or more qubits can be in an entangled state, meaning that they can not be written as the product of single-qubit states. This further implies that measuring one qubit will automatically reveal information about the others as well. The simplest example is the state \(\frac {1}{\sqrt {2}}(|00\rangle+|11\rangle)\). For example, if the first qubit is measured in the state |0〉, the second qubit must be in the |0〉 state.

3.2 Quantum gates

Computations on a quantum system are performed by applying quantum gates to the system. A quantum gate is mathematically described by a Unitary matrix U (a complex square matrix holding the identity UU⋆ = U⋆U = I, with U⋆ denoting the complex conjugate of U). One example is th

$$X= \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} $$

gate, which is the quantum equivalent to the classical NOT gate, since it flips the state |0〉 to |1〉 and vice versa. If we look at the X gate as an operation on the Bloch sphere, it is a 180° degree rotation around the x axis. The gates that perform the same operation just at a different axis are the following

$$Y= \begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix} Z = \begin{bmatrix} 1 & 0 \\ 0 & -i \end{bmatrix} $$

these gates are called the Pauli gates.

The rotations can be generalized to arbitrary rotations around a specific axis by the rotation gate RP(𝜃), where P ∈{X, Y, Z} specifies the rotation axis and 0 ≤ 𝜃 ≤ π the angle. The rotation gate is given by

$$ R_{P}(\theta) = e^{i\frac{ \theta}{2}P} = \cos{\frac{\theta}{2}} I + i \sin{\frac{\theta}{2}} P, $$

where I denotes the identity matrix.

The single-qubit gates can be extended to gates that act on multiple qubits. The controlled NOT (CNOT) or CX gate

$$CX = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix} $$

is one example for such a gate, which acts on two qubits by applying the X gate to the second qubit only if the first qubit is in the |1〉 state.

3.3 Quantum circuits

To perform computations on a QC, one has to specify the order of gates and on which qubit they should be applied. Such a quantum algorithm is called a quantum circuit. A quantum circuit to create a fully entangled two-qubit state \(\frac {1}{\sqrt {2}}(|00\rangle+|11\rangle)\) is shown in Fig. 3. Each qubit is represented by a horizontal line, starting with the first qubit at the top. A quantum gate is depicted by a square with its name written in the center. The CNOT gate, as a multi-qubit gate, connects the qubits it acts on by a vertical line. The control qubit is shown as a small, filled circle, while the controlled qubit is marked with a larger open circle. The graphical illustration of a measurement is a small meter symbol.

Fig. 3
figure 3

Example quantum circuit that creates the fully entangled state \(\frac {1}{\sqrt {2}}(|00\rangle+|11\rangle)\) with a measurement at the end

Full size image

4 Variational quantum circuits

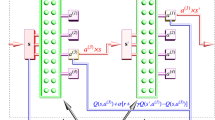
VQCs can be seen as a quantum hybrid approximation architecture. A VQC is a quantum circuit that combines parameterized gates, like rotation gates (see Section 3.1), and controlled gates, to map an input state to a specific output. The expectation value of the system is measured to obtain the result \(\hat {y}\). In some cases, similar to classical NN, a bias term is added to the measurement result. If no bias term is added at the end, we will call it a pure VQC. Like in NN training, a suitable procedure, e.g., stochastic gradient descent, or ADAM, adjusts the circuit parameters 𝜃 to optimize an objective function. This parameter optimization is performed on a classical computer. Therefore, VQC is a hybrid technique. The procedure is shown in Fig. 4.

Fig. 4
figure 4

In VQC approximation, the input parameter is encoded to unitary rotations. Multiple layers of parameterized circuits with trainable parameters are repeated and measured to obtain the output. This is used to computer the loss between the target value and the measured output, to update the circuit parameters

Full size image

The VQC can be separated into two parts. The first part is a state preparation routine U0 initializing the qubits to the desired state, for which multiple encoding techniques exist, like basis state or amplitude encoding (Schuld and Petruccione 2018). The second part is the parameterized circuit U(𝜃), with 𝜃 denoting the parameter vector. There are multiple structures for U(𝜃), where the specific gate types and their order define the structure. Sim et al. (2019) provide an overview of the commonly used circuits.

Figure 5 shows the VQC that was used for the frozen lake study. The circuit starts by encoding the state with the circuit U0. The state is encoded by RX(ϕi) gates with i ∈{1,2,3,4}. The parameters ϕi are determined by converting the state, an integer number between 0 and 15, into a four-digit binary number b4b3b2b1, where the bi ∈{0,1}. The rotation angle is given by the formula ϕi = πbi. Thus, qubit i is initialized in the state |1〉 if bi = 1 and in state |0〉 otherwise.

Fig. 5
figure 5

Example of an VQC on three qubits with RY rotation gates. The U0 block denotes the state preparation routine and the dashed box around the variational part indicates that this block can be repeated multiple times

Full size image

The variational part starts with entangling the qubits using CNOT gates and is followed by parameterized RY(𝜃i) gates. The dashed box surrounding the variational circuit denotes that this part can be repeated several times. The last step is to measure the qubits to obtain the final result.

4.1 Variational quantum deep Q-learning

The idea from Section 2.2 was extended to VQCs as the approximator for the action-value function in Chen et al. (2019), which is called variational quantum deep Q-learning (VQ-DQN). The architecture from Fig. 5 can be used to realize Q(s, a, 𝜃) in Algorithm 2 in Appendix where 𝜃 is the parameter vector of the parameterized gates. The gradient of the VQC with respect to 𝜃 can be computed using the Parameter-Shift Rule (Schuld et al. 2018). Thus, the DQN algorithm can be generalized to a hybrid quantum reinforcement learning method by replacing the NN approximator with a VQC.

Within their publication, Chen et al. used a non-pure VQC to approximate the action-value function. We propose a similar approach to Chen et al. (2019) but using a pure VQC; thus, we do not add a bias term at the end of the VQC. Therefore, our approach approximates the action-value function purely in the quantum domain. Based on this novelty, we call our approach pure VQ-DQN. Furthermore, our approach only uses RY rotations in the trainable U(𝜃) and RX rotations in the encoding U0 block, while Chen et al. (2019) utilize the gate combinations RX,RY,RZ in U(𝜃) and RY,RZ in U0.

5 Results

The three algorithms introduced above are compared in terms of iterations until convergence to the optimal behavior (sample efficiency), memory usage, and runtime, on the frozen lake problem. Before analyzing the results, the optimal parameters will be presented. For the sake of completeness, we include the results reported by Chen et al. (2019) and indicate where the values are missing.

The optimal learning rate, discounting factor, and exploration parameter for the algorithms, as well as the memory size and the target action-value function update frequency for the DQN and (pure) VQ-DQN algorithm, are listed in Table 1.

Table 1 Parameters for optimal performance of the RL algorithms
Full size table

The NN for the DQN approach is a three-layer network with 16 input units, a fully connected 8-unit hidden layer with tanh activation function, and a fully connected output layer with a linear activation function and one output unit for each action. The 16 states are encoded by one-hot encoding. This architecture results in a total of 172 parameters that need to be optimized.

The Q-learning algorithm stores the action-value approximations in a table with 16 × 4 entries. Thus, it has 64 parameters.

The VQC is realized by the architecture shown in Fig. 5. The state-preparation routine U0 is used, and the variation part U(𝜃) is repeated 10 times to approximate the action-values successfully. Therefore, the circuit has a total of 40 parameters that need to be fitted. The pure VQ-DQN algorithm is implemented using the Penny Lane (Bergholm et al. 2018) quantum machine learning framework and PyTorch. Footnote 1

Chen et al. report that they successfully solved the problem with a variational part with three parameters for each qubit, which is repeated twice, plus one bias parameter for each qubit resulting in a total of 28 parameters.

Comparing the algorithms in terms of memory usage shows that the VQ-DQN algorithm needs the least number of parameters, followed by the pure VQ-DQN approach. Q-Learning needs more than 1.5 times as many parameters as the pure VQ-DQN algorithm, and DQN needs the most parameters with more than 4 times the number of parameters of the pure VQ-DQN. Table 2 summarizes the memory usage of the three algorithms, as well as their runtime on a system with an Intel Xeon E5-2630 CPU and a GeForce GTX 1080 Ti GPU. Q-Learning performs best with a runtime of about one-third of a second. DQN finishes 750 training iterations after 190 s, and pure VQ-DQN runs for over 21 h. Pure VQ-DQN was run on a quantum simulator, which is slower than a real quantum computer. Therefore, this should be seen as a worst-case runtime, and it is expected that a real quantum device with dedicated access should perform better. The runtimes for the results of VQ-DQN are not given in Chen et al. (2019).

Table 2 Comparing the memory usage and runtime of the three algorithms for 750 episodes of training
Full size table

The number of training steps (episodes) until the algorithm converged to the optimal solution is depicted in Fig. 6. The algorithms are evaluated after each training step, and the obtained return is averaged over the last 10 episodes. The figure shows that Q-learning converged after 80 iterations to the optimal solution. Pure VQ-DQN needs to observe 190 episodes of training until the optimal behavior is achieved, and the DQN algorithm acts optimally after 290 episodes. Thus, the quantum hybrid approximator needs about 100 episodes fewer for optimal behavior than NNs. Still, both can not compete with standard Q-learning on a problem with small state and action spaces. Chen et al. reported that their approach solves the problem on the 198th training step for the first time and the average of the last 100 episodes converges to the optimal value after the 301st episode.

Fig. 6
figure 6

The graphic shows the return obtained after each episode of training averaged over 10 episodes with the standard deviation in shaded color. The Q-learning algorithm converged after 80 iterations to the optimal solution. The VQC approximator is fully trained after 190 episodes of training and the DQN algorithm acts optimal after 290 episodes. Both DQN and VQ-DQN show an instability around episode 350

Full size image

5.1 Discussion

The results from evaluating the three approaches show that on a small problem, like the frozen lake, Q-learning performs best in terms of runtime and sample efficiency. Only pure VQ-DQN needs less memory for optimal behavior, but it cannot compete with Q-learning due to its long runtime. When including the results from Chen et al., the VQ-DQN approach needs about two-thirds of the pure VQ-DQN algorithm’s memory, which seems to be even more memory efficient.

The (pure) quantum and classical approximation show similar behavior. (Pure) VQ-DQN has a better sample efficiency since it converges around 100 episodes earlier to optimally policy. It further needs far less memory than DQN, but over 21 h of run time is too long to be a near-term alternative for DQN that trains in about 3 min. Unfortunately, Chen et al. do not indicate the runtime of their algorithm.

Overall, Q-learning is the preferred choice for simple problems. When it comes to more complex situations like Atari games, the state space becomes intractable for tabular methods, and an approximator for the action-value function is needed. Nowadays, DQN (or similar algorithms that rely on NNs) established as best practice to solve such problems. However, as we can see from our results, a quantum hybrid approximator like (pure) VQ-DQN performs better than NNs, since it requires less memory and training samples. However, the drawback of quantum hybrid approaches is their runtime. NNs experienced their renaissance once they were computed in parallel by using GPUs. If quantum computing will experience a similar speedup that GPUs provided in classical computing, (pure) VQ-DQN is likely to outperform NN approaches. Furthermore, the quantum computations have been done on a quantum simulator, which lacks computational speed compared to a real quantum device.

6 Conclusion

Within this paper, we showed how the theory of RL (Section 2) could be extended to the quantum domain (Section 4). We then extended the VQ-DQN algorithm to use a novel pure quantum approximator (Section 4.1) and compared the classical tabular RL approach with two approximation methods. DQN approximates the action-value function using a NN, and pure VQ-DQN utilizes a VQC on a quantum computer for the approximation. The results showed that tabular methods are the best choice for small problems like the frozen lake, as was anticipated.

Comparing the classical and quantum approaches revealed that with today’s hardware, DQN shows a better performance, even though it needs more memory and has a lower sample efficiency. At the moment, VQ-DQN with a pure quantum approximator lacks runtime to be competitive. This problem might change in the future when real quantum devices are available for exclusive usage.

The results indicated that the quantum and the classical approximators should be compared on more complex problems, like the Atari games. It would further be interesting to compare the two approaches with linear methods in RL or analyze how different structures of the VQC impact the training.