Thermal and viscous slip effects on electroosmotic Casson nanofluid flow with microorganisms in peristaltic porous media

Abstract

Current work focuses on increasing heat transmission in thermal systems with the incorporation of gyrotactic motile microbes, promoting the creation of structured fluids useful for bio-cooling and nanotechnology. This study explores the effects of electroosmosis and slip boundary conditions in a non-Newtonian Casson nanofluid with mass transfer. Specifically, it looks at bio-convection peristaltic events and conducts a thermodynamic analysis. The Arrhenius activation energy in an asymmetric channel is considered in this study. In addition, the authors evaluate viscous resistance, thermophoresis diffusion, porous surface properties, coupled convection, Brownian diffusion, and thermal viscosity behavior. The results obtained from mathematical expressions together with surface conditions are handled by means of a numerical algorithm implemented by means of the shooting technique through traditional program Mathematica, with the aid of its built-in tool, NDSolve. Many physical parameters, such as entropy generation, the Bejan number, velocity profiles, the density of gyrotactic motile microbes, and the accumulation profile of nanoparticles, are depicted graphically. The graphical study shows that entropy generation increases with a greater Helmholtz-Smoluchowski factor by 10%, but declines as the heat generation/absorption factor increases with same percentage. The Bejan number tends to increase with stronger heat sources by 5%. Application possibilities include improved control and effectiveness in mechanisms that include microfluidic equipment, systems for delivering medications, and biotechnological operations.

1 Introduction

Peristalsis is referred to as a gradual phenomenon that unfolds as a wave traverses through a tube, conduit, or inside the boundaries of a channel. It may also be stated as the streaming motion generated by the sinusoidal waves traveling along a channel in an oscillating manner. Although peristalsis has applications in many disciplines, including medical science, it has attracted a lot of attention in the current study. Researchers have been fascinated by the peristaltic phenomenon because of its numerous applications in a variety of fields, including nuclear reactors, combustion, physiology, turbo-machinery, and fluid pumping through the transmission of sinusoidal waves. When it comes to nanofluids, peristalsis has gained significant importance in both the biological and engineering domains. Latham was the first to investigate peristaltic motion using theoretical and experimental techniques [1]. It is useful in many situations, such as when food is being transported from the mouth to the esophagus, when bile is being propelled through bile ducts, when blood is being circulated in capillaries, when urine is being transferred from the kidney to the bladder, and in many other physiological processes [2]. Shapiro et al. [3] extended their investigation into peristaltic motion in 1969 by introducing the long wavelength estimation and the low Reynolds number assumption. They started a thorough examination into the flow of incompressible, viscous fluids in both axisymmetric and flat geometries. Their analysis was predicated on the existence of extended wavelengths and a small Reynolds number. Interestingly, they observed a decreasing relationship with time between the average flow rate and the pressure rise per wavelength, which closely matched their experimental findings. Furthermore, their research revealed intriguing topological phenomena called "trapping," in which particular sets of flow parameters produced a circulating fluid mass. Eytan [4] investigated the transmission of embryos within the uterus and the movement of ova through the fallopian tubes in 2001. The research of peristaltic motion in a curved enclosure containing a concentration of nanoparticles in a dusty fluid was conducted by Rashed and Ahmed [5]. Their study examined an increase in the Eckert number, which in turn produced higher fluid and dusty components’ velocities. Khan et al. [6] recently presented entropy and electroosmotic analysis for pumping transport of Williamson fluid through a bended conduit. It was observed in that work that the thermal rate is enhanced by the Brinkman number.

A liquid is referred to as a nanofluid if it contains nanoscale particles. Tiny fragments of material with sizes ranging from 1 to 100 nm are known as nanoparticles. To improve traditional fluids' thermal conductivity and heat transmission capacities, these metal particles are scattered throughout them. Nanoparticles are incorporated or blended into operational fluids such as water, lubricants, propylene glycol, and biological fluids to increase heat transfer and thermal conductivity of base fluids. The food industry, energy storage systems, advanced cooling technologies, solar energy collectors, and related sectors are the main industries that use nanofluids. Through experimental research, Choi [7] confirmed that adding nanoparticles to a fluid can improve its heat transfer rate, viscosity, thermal conductivity, and thermal diffusivity [8, 9]. A new technique for increasing heat generation in magnetohydrodynamics (MHD) nanofluids in an asymmetrical channel with peristaltic motion was presented by Khan et al. [10]. Peristalsis was demonstrated by Bhatti and Abdelsalam [11] in hybrid nanofluids that included tantalum and gold particles and took the effect of a magnetic field into consideration. In their study of hybrid nanofluid peristalsis, Hussain et al. [12] concentrated on employing electro-osmosis to increase heat conductivity during peristaltic flow. An extensive investigation of electro-osmotic peristalsis in hybrid nano-fluids was given by Abbasi et al. [13]. Furthermore, Nisar et al. [14] carried out a numerical study of peristalsis using pair stress nanoparticles.

Large-scale fluid flow is represented by the term "bio convection". Gyrotactic motile microbes are those that swim against gravity. The Arrhenius activation energy is the least amount of energy needed to start a reaction. Pedley et al. [15] used bio convection models in a homogeneous fluid to study gyrotactic microorganisms. The effect of gyrotactic microorganisms on bio convection in a conventional nanofluid was investigated by Rao et al. [16]. A study on the peristaltic movement of motile bacteria in the Eyring Powel fluid was carried out by Akbar et al. [17]. Khan et al.'s study [18] examined the effect of bio-convection on a micropolar nanofluid that contained gyrotactic motile bacteria while taking into account a moving needle. The continuous motion of a mixed convection layer around a solid ball with uniformly maintained surface temperature was studied numerically, for both heating and cooling conditions. Peristaltic flow of a non-Newtonian base fluid with nanoparticles concentration has been studied by Saeed et al. [19] to establish effects of slippery surface on the system. It is seen that the temperature gradient climbs due to the growing impact of the heat slip, whilst concentration mitigates due to the increasing concentration slip characteristic. Zeeshan et al. [20] evaluated the contribution of hybrid-nanofluid flow in extending and compressing passageway while accounting for both MHD and thermal impact. The similarity transformation translates the fundamental motion and thermal systems into nonlinear ODEs. The resultant ODEs are subsequently resolved mathematically employing the Homotopy Analysis Method (HAM) and the specified boundary constraints. Nanoparticles (Cu and Ag) are blended into the base liquid solution.

A key idea in thermodynamics, entropy emphasizes the irreversibility of a variety of thermal processes, such as heat transport and chemical reactions. Entropy is used in many different scientific domains, such as heat exchangers and medicine, where it helps with microfluidic processes and optimal drug delivery to promote biotechnology and healthcare. Bejan's research [21] emphasized the importance of randomness in heat transfer energy loss and concentrated on the primary component influencing entropy production. Irreversibility rates are decreased via improved heat transport characteristics. Using numerical simulations, Abu-Qudais et al. [22] predicted the creation of entropy resulting from natural convection in a horizontally oriented cylinder by analyzing various Rayleigh numbers and radii. They discovered that under constant Rayleigh numbers, cylinder size increases decreased overall entropy production. Akbar et al. [23] examined the heat transfer and entropy generation for bio-convective peristalsis of nanofluid with the transfer of mass through an asymmetric channel. The scientists noted that large activation values suppress the temperature distribution. When viscosity properties rise, heat transfer rates at the wall decrease. To lower the entropy production of the system, it is important to increase the porosity parameter. Furthermore, there is a correlation between a decrease in the density of motile bacteria and an increase in the number of bioconvection Peclet. Fluid motion is greatly enhanced by improvements in the buoyancy ratio parameter and bioconvection Rayleigh number.

Electric double layers (EDL) along channel walls are the main cause of electroosmotic flow (EOF), a phenomenon where an electromagnetic field applied across a channel produces fluid circulation. Electroosmotic technologies, such as Lab-on-a-Chip (LOC) goods and microfluidic gadgets, have garnered more attention in recent years. These devices find applications in diverse domains, including pathogen detection, healthcare, and life sciences. The requirement for precise and effective microfluidic technologies has led to a considerable demand for these small, affordable, and easy-to-use devices in the fields of medication delivery and DNA analysis. In many biological, manufacturing, medical, and fluid control procedures, such as fluid dialysis, biological fluid circulation, and pipe isolation, electroosmosis is employed. In their investigation of a Phan-Thien-Tanner fluid in an asymmetric peristaltic container, Prakash and Tripathy [24] included the electrical double layer (EDL) mechanism, emphasizing the important impact of EDL thickness and electric field strength on fluid flow. Yasmeen and Iqbal [25] examined the effects of the electro-osmosis factor (EDL) on mass convection and heat convection in a viscous fluid in a porous medium with peristaltic pumping in a different study. They found that the EDL may decrease medium permeability. A situation involving an electrically conductive fluid in a non-uniform two-dimensional channel exposed to a uniform magnetic field was studied by Zeeshan et al. [26]. According to their findings, the point halfway down the channel receives the biggest pressure surge, and this impact gets stronger at higher fluid parameter values. Wide-ranging uses of electroosmosis can be found in the medical and environmental fields, in industrial processes like fluid dialysis and porous membranes, in natural phenomena like fluid circulation in mammalian skin, and in techniques for tube and conduit division.

Slip effects at the interface between a solid and a fluid are a well-known boundary condition with a variety of real-world applications in research, engineering, and business. Very little effort has been put into studying the flows of non-Newtonian fluids with boundary conditions; most studies of Newtonian and non-Newtonian fluid flows have taken the no-slip condition into consideration. The study mentioned in [27] analyzed velocity slip boundary circumstances for both isoflux and isothermal thermal circumstances as well as convective energy transfer and entropy formation in Newtonian and non-Newtonian fluid circulation between parallel plates. The governing equations of fully developed laminar flows were solved analytically, taking into account both the thermal and hydrodynamic aspects. These solutions took viscous dissipation into consideration and incorporated wall slip constraints. The results reveal that enhancing the slip coefficient boosts the Nusselt and Bejan numbers while reducing the rate at which global entropy is generated. After that in 2020, thermodynamics and heat transmission in a microchannel containing a non-Newtonian nanofluid are examined in [28]. Using the finite volume approach (SIMPLE algorithm), it investigates the impacts of changing wall temperatures; the presence of porous blocks, and slip velocity. When the porosity increases but decreases with a higher thermal conductivity ratio, the Nusselt number locally increases when the Darcy number lowers. An important finding is that frictional entropy production increases by about 800% as the porosity and Darcy number drop.

The absence of studies on the Arrhenius activation energy and bio-convection effects in the context of peristaltic movement incorporating non-Newtonian Casson fluids is disclosed in this review of the literature. It also highlights the disregard for characteristics such as mass transfer, entropy generation in asymmetrical channels including gyrotactic motile microorganisms, electroosmosis, and slip constraints (in terms of heat and velocity). The authors took into account a variety of variables, including thermophoresis diffusion, viscous dissipation, porous media, mixed convection, and Brownian diffusion. The problem has been described in detail and the mathematical model is based on some physical laws which are derived mathematically by wave frame transformations and dimensionless strategy. The solution has been obtained through numerical technique through Mathematica’s numerical equation solver tool NDSolve, with an emphasis on low Reynolds numbers and the long wavelength approximation. Furthermore, the study presents a comprehensive examination of graphical variations and contrasts its findings with earlier studies. The current study is a groundbreaking endeavor with potential implications in categories like microfluidics, nanotechnology, and biomedical research because its primary objective is to close the gap in the literature.

2 Formulation of problem

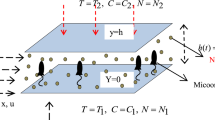
Consider an asymmetrical channel with a combined width of $d_{1} + d_{2}$ that is being passed through by an incompressible nanofluid that has been infused with gyrotactic motile microorganisms. Sinusoidal waves move at a speed of c (m/s) along the walls of this channel. Nanoparticles moving through a porous material, propelled by gyrotactic microbes moving in a Casson fluid of variable viscosities are considered. It is assumed that the porous medium is homogeneous and unidirectional. It is also hypothesized that these microbes are not susceptible to adsorption by the porous material and can move freely through its pores. The vertical $\overline{Y}$-axis in rectangular coordinates runs perpendicular to the horizontal $\overline{X}$-axis, which is aligned parallel to the central line. As shown in Fig. 1, the wall layout places $\overline{Y}$ at $\overline{H}_{2}$ and $\overline{H}_{1}$ designating the locations of the left and right channel walls [10, 19, 24].

$$\begin{aligned} \overline{H}_{1} \left( {\overline{X}, \overline{t}} \right) & = d_{1} + a_{1} {\text{cos}}\left( {\frac{2\pi }{\lambda }\left( {\overline{X} - c \overline{t}} \right)} \right), \\ \overline{H}_{2} \left( {\overline{X}, \overline{t}} \right) & = - d_{2} - a_{2} {\text{cos}}\left( {\frac{2\pi }{\lambda }\left( {\overline{X} - c \overline{t}} \right) + \varphi } \right). \\ \end{aligned}$$

(1)

where $d_{1} , d_{2} ,t, a_{1} , a_{2} , \lambda$ denote channel width, time, amplitude, time and wavelength respectively, and satisfy the following inequality:

$$d_{1}^{2} + d_{2}^{2} + 2a_{1} a_{2} cos\varphi \le \left( {d_{1} + d_{2} } \right)^{2} .$$

(2)

Fig. 1

Geometry of problem

Furthermore, we take notice of how the momentum and energy equations are influenced by porous medium, Arrhenius stimulation energy, thermophoresis diffusion, mixed convection, non-uniform absorption of heat, viscous dissipation, slip boundary conditions, and electro-osmosis. These flow equations, which incorporate the previously indicated parameters, are given below for the laboratory framework [20, 25, 28, 29].

Continuity equation

$$\frac{{\partial \overline{U}}}{{\partial \overline{X}}} + \frac{{\partial \overline{V}}}{{\partial \overline{Y}}} = 0,$$

(3)

Momentum equation

$$\begin{aligned} \rho_{f} \left( {\frac{{\partial \overline{U}}}{{\partial \overline{t}}} + \overline{U}\frac{{\partial \overline{U}}}{{\partial \overline{X}}} + \overline{V}\frac{{\partial \overline{U}}}{{\partial \overline{Y}}}} \right) & = - \frac{{\partial \overline{P}}}{{\partial \overline{X}}} + \frac{{\partial \tau_{{\overline{X}\overline{Y}}} }}{{\partial \overline{Y}}} + \frac{{\partial \tau_{{\overline{X}\overline{X}}} }}{{\partial \overline{X}}} - \left( {1 + \frac{1}{\xi }} \right)\frac{{\mu_{0} }}{{\tilde{k}_{1} }}\overline{U} \\ & \quad + \rho_{f} \beta_{T} g\left( {1 - F_{0} } \right)\left( {T - T_{0} } \right) - \left( {\rho_{p} - \rho_{f} } \right)\beta_{c} g\left( {C - C_{0} } \right) \\ & \quad - \left( {\rho_{m} - \rho_{f} } \right)gF_{\gamma } \left( {F - F_{0} } \right) + \rho_{e} E_{x} , \\ \end{aligned}$$

(4)

$$\rho_{f} \left( {\frac{{\partial \overline{V}}}{{\partial \overline{t}}} + \overline{U}\frac{{\partial \overline{V}}}{{\partial \overline{X}}} + \overline{V}\frac{{\partial \overline{V}}}{{\partial \overline{Y}}}} \right) = - \frac{{\partial \overline{P}}}{{\partial \overline{Y}}} + \frac{{\partial \tau_{{\overline{Y}\overline{Y}}} }}{{\partial \overline{Y}}} + \frac{{\partial \tau_{{\overline{Y}\overline{X}}} }}{{\partial \overline{X}}} - \left( {1 + \frac{1}{\xi }} \right)\frac{{\mu_{0} }}{{\tilde{k}_{1} }}\overline{V} + \rho_{e} E_{y} ,$$

(5)

Temperature distribution

$$\begin{aligned} \left( {\rho C} \right)_{f} \left( {\frac{\partial T}{{\partial \overline{t}}} + \overline{U}\frac{\partial T}{{\partial \overline{X}}} + \overline{V}\frac{\partial T}{{\partial \overline{Y}}}} \right) & = K_{f} \left( {\frac{{\partial^{2} T}}{{\partial \overline{X}^{2} }} + \frac{{\partial^{2} T}}{{\partial \overline{Y}^{2} }}} \right) + \tau_{{\overline{X}\overline{X}}} \frac{{\partial \overline{U}}}{{\partial \overline{X}}} + \tau_{{\overline{X}\overline{Y}}} \left( {\frac{{\partial \overline{V}}}{{\partial \overline{X}}} + \frac{{\partial \overline{U}}}{{\partial \overline{Y}}}} \right) \\ & \quad + \tau_{{\overline{Y}\overline{Y}}} \frac{{\partial \overline{V}}}{{\partial \overline{Y}}} + \left( {1 + \frac{1}{\xi }} \right)\frac{{\mu_{0} }}{{\tilde{k}_{1} }}\left( {\overline{U}^{2} + \overline{V}^{2} } \right) + \phi \left( {T - T_{0} } \right) \\ & \quad + \tau \left( {\rho C} \right)_{f} \left( {\frac{{D_{T} }}{{T_{m} }}\left( {\frac{\partial T}{{\partial \overline{X}}} + \frac{\partial T}{{\partial \overline{Y}}}} \right)^{2} + D_{B} \left( {\frac{\partial T}{{\partial \overline{X}}}\frac{\partial C}{{\partial \overline{X}}} + \frac{\partial T}{{\partial \overline{Y}}}\frac{\partial C}{{\partial \overline{Y}}}} \right)} \right) + \sigma_{f} E_{x}^{2} , \\ \end{aligned}$$

(6)

Nanoparticles concentration

$$\left( {\frac{\partial C}{{\partial \overline{t}}} + \overline{U}\frac{\partial C}{{\partial \overline{X}}} + \overline{V}\frac{\partial C}{{\partial \overline{Y}}}} \right) = D_{B} \left( {\frac{{\partial^{2} C}}{{\partial \overline{X}^{2} }} + \frac{{\partial^{2} C}}{{\partial \overline{Y}^{2} }}} \right) + \frac{{D_{T} }}{{T_{m} }}\left( {\frac{{\partial^{2} T}}{{\partial \overline{X}^{2} }} + \frac{{\partial^{2} T}}{{\partial \overline{Y}^{2} }}} \right) - k_{r}^{2} \left( {C - C_{0} } \right)\left( {\frac{T}{{T_{0} }}} \right)^{n} exp\left( { - \frac{{E_{a} }}{{K_{1} T}}} \right),$$

(7)

Microorganisms equation

$$\frac{\partial F}{{\partial \overline{t}}} + \overline{U}\frac{\partial F}{{\partial \overline{X}}} + \overline{V}\frac{\partial F}{{\partial \overline{Y}}} = D_{N} \left( {\frac{{\partial^{2} F}}{{\partial \overline{X}^{2} }} + \frac{{\partial^{2} F}}{{\partial \overline{Y}^{2} }}} \right) - \frac{bWc}{{\left( {C - C_{0} } \right)}} \left( {\frac{\partial }{{\partial \overline{X}}}\left( {F\frac{\partial C}{{\partial \overline{X}}}} \right) + \frac{\partial }{{\partial \overline{Y}}}\left( {F\frac{\partial C}{{\partial \overline{Y}}}} \right)} \right).$$

(8)

The study includes the Casson stress tensor as [30].

$${{\varvec{\uptau}}}_{i,j} = 2E_{i,j} \left( {\mu_{0} + \frac{{P_{y} }}{{\sqrt {2\pi } }}} \right).$$

(9)

In Eq. (9), we have assumed $P_{y} = 0$ (yield stress) for $\pi = E_{i,j}$ where $E_{i,j}$ is the fluid deformation matrix ($E_{i,j} = \frac{1}{2}\left( {\nabla \overline{\user2{V}} + \left( {\nabla \overline{\user2{V}}} \right)^{t} } \right)$). Stresses in the form of components are given here:

$$\tau_{{\overline{X}\overline{X}}} ,\tau_{{\overline{X}\overline{Y}}} ,\tau_{{\overline{Y}\overline{Y}}} = 2\left( {\mu_{0} + \frac{{P_{y} }}{{\sqrt {2\pi } }}} \right)\left( {\left( {\frac{{\partial \overline{U}}}{{\partial \overline{X}}}} \right),\frac{1}{2}\left( {\frac{{\partial \overline{U}}}{{\partial \overline{Y}}} + \frac{{\partial \overline{V}}}{{\partial \overline{X}}}} \right),\left( {\frac{{\partial \overline{V}}}{{\partial \overline{Y}}}} \right)} \right).$$

(10)

Between the stationary frame and moving frame, the transformations are indicated as [6].

$$\overline{x} = \overline{X} - c\overline{t}, \overline{y} = \overline{Y}, \overline{u}\left( {\overline{x, } \overline{y}} \right) = \overline{U}\left( {\overline{X}, \overline{Y}, \overline{t}} \right) - c, \overline{v}\left( {\overline{x, } \overline{y}} \right) = \overline{V}\left( {\overline{X}, \overline{Y}, \overline{t}} \right).$$

(11)

After implementing the aforementioned modifications to Eqs. (3–8), we acquire

$$\frac{{\partial \overline{u}}}{{\partial \overline{x}}} + \frac{{\partial \overline{v}}}{{\partial \overline{y}}} = 0,$$

(12)

$$\begin{aligned} \rho_{f} \left( {\overline{u}\frac{{\partial \overline{u}}}{{\partial \overline{x}}} + \overline{v}\frac{{\partial \overline{u}}}{{\partial \overline{y}}}} \right) & = - \frac{{\partial \overline{p}}}{{\partial \overline{x}}} + \left( {\frac{{\partial \tau_{{\overline{x}\overline{y}}} }}{{\partial \overline{y}}} + \frac{{\partial \tau_{{\overline{x}\overline{x}}} }}{{\partial \overline{x}}}} \right) - \left( {1 + \frac{1}{\xi }} \right)\frac{{\mu_{0} }}{{\tilde{k}_{1} }}\left( {\overline{u} + c} \right) \\ & \quad + \rho_{f} \beta_{T} g\left( {1 - F_{0} } \right)\left( {T - T_{0} } \right) - \left( {\rho_{p} - \rho_{f} } \right)\beta_{c} g\left( {C - C_{0} } \right) \\ & \quad - \left( {\rho_{m} - \rho_{f} } \right)gF_{\gamma } \left( {F - F_{0} } \right) + \rho_{e} E_{x} , \\ \end{aligned}$$

(13)

$$\rho_{f} \left( {\overline{u}\frac{{\partial \overline{v}}}{{\partial \overline{x}}} + \overline{v}\frac{{\partial \overline{v}}}{{\partial \overline{y}}}} \right) = - \frac{{\partial \overline{p}}}{{\partial \overline{y}}} + \left( {\frac{{\partial \tau_{{\overline{y}\overline{y}}} }}{{\partial \overline{y}}} + \frac{{\partial \tau_{{\overline{y}\overline{x}}} }}{{\partial \overline{x}}}} \right) - \left( {1 + \frac{1}{\xi }} \right)\frac{{\mu_{0} }}{{\tilde{k}_{1} }}\overline{v} + \rho_{e} E_{y} ,$$

(14)

$$\begin{aligned} \left( {\rho C} \right)_{f} \left( {\overline{u}\frac{\partial T}{{\partial \overline{x}}} + \overline{v}\frac{\partial T}{{\partial \overline{y}}}} \right) & = \tau_{{\overline{x}\overline{x}}} \frac{{\partial \overline{u}}}{{\partial \overline{x}}} + \tau_{{\overline{x}\overline{y}}} \left( {\frac{{\partial \overline{v}}}{{\partial \overline{x}}} + \frac{{\partial \overline{u}}}{{\partial \overline{y}}}} \right) + \tau_{{\overline{y}\overline{y}}} \frac{{\partial \overline{v}}}{{\partial \overline{y}}} \\ & \quad + \left( {1 + \frac{1}{\xi }} \right)\frac{{\mu_{0} }}{{\tilde{k}_{1} }}\left( {\left( {\overline{u} + c} \right)^{2} + \overline{v}^{2} } \right) + \phi \left( {T - T_{0} } \right) + \sigma_{f} E^{2}_{x} + K_{f} \left( {\frac{{\partial^{2} T}}{{\partial \overline{x}^{2} }} + \frac{{\partial^{2} T}}{{\partial \overline{y}^{2} }}} \right) \\ & \quad + \tau \left( {\rho C} \right)_{f} \left( {\frac{{D_{T} }}{{T_{m} }}\left( {\frac{\partial T}{{\partial \overline{x}}} + \frac{\partial T}{{\partial \overline{y}}}} \right)^{2} + D_{B} \left( {\frac{\partial T}{{\partial \overline{x}}}\frac{\partial C}{{\partial \overline{x}}} + \frac{\partial T}{{\partial \overline{y}}}\frac{\partial C}{{\partial \overline{y}}}} \right)} \right). \\ \end{aligned}$$

(15)

$$\begin{aligned} \left( {\overline{u}\frac{\partial C}{{\partial \overline{x}}} + \overline{v}\frac{\partial C}{{\partial \overline{y}}}} \right) & = D_{B} \left( {\frac{{\partial^{2} C}}{{\partial \overline{x}^{2} }} + \frac{{\partial^{2} C}}{{\partial \overline{y}^{2} }}} \right) + \frac{{D_{T} }}{{T_{m} }}\left( {\frac{{\partial^{2} T}}{{\partial \overline{x}^{2} }} + \frac{{\partial^{2} T}}{{\partial \overline{y}^{2} }}} \right) \\ & \quad - k_{r}^{2} \left( {C - C_{0} } \right)\left( {\frac{T}{{T_{0} }}} \right)^{n} exp\left( { - \frac{{E_{a} }}{{K_{1} T}}} \right), \\ \end{aligned}$$

(16)

$$\left( {\overline{u}\frac{\partial F}{{\partial \overline{x}}} + \overline{v}\frac{\partial F}{{\partial \overline{y}}}} \right) = D_{N} \left( {\frac{{\partial^{2} F}}{{\partial \overline{x}^{2} }} + \frac{{\partial^{2} F}}{{\partial \overline{y}^{2} }}} \right) - \frac{bWc}{{\left( {C - C_{0} } \right)}} \left( {\frac{\partial }{{\partial \overline{x}}}\left( {F\frac{\partial C}{{\partial \overline{x}}}} \right) + \frac{\partial }{{\partial \overline{y}}}\left( {F\frac{\partial C}{{\partial \overline{y}}}} \right)} \right).$$

(17)

Viscous and thermal slip boundary conditions can be expressed as [31]:

$$\begin{aligned} & \overline{U} + \beta \tau_{{\overline{X}\overline{Y}}} = 0,T = T_{0} + K_{2} \left( {\frac{\partial T}{{\partial \overline{Y}}}} \right),C = C_{0} ,F = F_{0} \;{\text{at}}\;y = h_{1} \\ & \overline{U} - \beta \tau_{{\overline{X}\overline{Y}}} = 0,T = T_{1} - K_{2} \left( {\frac{\partial T}{{\partial \overline{Y}}}} \right),C = C_{1} ,F = F_{1} \;{\text{at}}\;y = h_{2} \\ \end{aligned}$$

(18)

An electric potential is created in the channel because of the presence of EDL on the walls. This layer's mathematical modeling yields the Poisson equation for the distribution of electric potential, as in [12, 13]:

$$\nabla^{2} \overline{\Phi } = - \frac{{\rho_{e} }}{\varepsilon },\,$$

(19)

where $\overline{\Phi } = \frac{ze\Phi }{{k_{B} T}}$ represents the dimensional electric potential.

If there is no overlap, using the Boltzmann distribution, we have

$$n^{ \pm } = n_{0} {\text{exp}}\left[ { \pm \frac{{\overline{\Phi }ez}}{{k_{B} T}}} \right],\,$$

(20)

Here, $n_{0}$ denotes the ion bulk concentration, z denotes the charge balance, $k_{B}$ denotes the Boltzmann constant, and $T$ is the average temperature of the ion-containing fluid. where $n^{ + }$ and $n^{ - }$ are the number of positive and negative ions,$\epsilon$ is the permittivity, and e is the charge on a single electron. The average charge density of charges is $\rho_{e} = e\left( {n^{ + } - n^{ - } } \right)z$. Boundary constraints for electric potential are:

$$\left. \Phi \right|_{{h_{1} }} = b_{1} {\text{ and }}\left. \Phi \right|_{{h_{2} }} = b_{2} .$$

(21)

These number, concentrations of cation and anion are connected to the electric potential by the Nernst–Planck (NP) equation given by

$$\frac{{\partial \overline{n}_{ + } }}{{\partial \overline{t}}} + \overline{u}_{f} \frac{{\partial \overline{n}_{ + } }}{{\partial \overline{t}}} + \overline{v}_{f} \frac{{\partial \overline{n}_{ + } }}{{\partial \overline{t}}} = D\left( {\frac{{\partial^{2} \overline{n}_{ \pm } }}{{\partial \tilde{x}^{2} }} + \frac{{\partial^{2} \overline{n}_{ \pm } }}{{\partial \tilde{y}^{2} }}} \right) \pm \frac{{DZ_{e} }}{{k_{B} T}}\left( {\frac{\partial }{{\partial \tilde{x}}}\left( {\overline{n}_{ \pm } \frac{{\partial {\overline{\Phi }}}}{{\partial \tilde{x}}}} \right) + \frac{\partial }{{\partial \tilde{y}}}\left( {\overline{n}_{ \pm } \frac{{\partial {\overline{\Phi }}}}{{\partial \tilde{y}}}} \right)} \right),$$

(22)

where the diffusion factor, temperature, and Boltzmann value are represented by the characters D, T, and $k_{B}$, respectively. The mobility of the two species is also determined using the Einstein formula, assuming that their ionic diffusion coefficients are equal. Now that the Debye–Huckel approximation has been used to determine the electro-osmotic potential with zeta potential, we get ${\text{ sinh}}\left[ {\frac{{\overline{\Phi }ez}}{{k_{B} T_{av} }}} \right] \sim \frac{{\overline{\Phi }ez}}{{k_{B} T_{sol} }}$.

The normalized electro-osmotic potential is defined as $= \overline{\Phi }/\upzeta$, where $\varsigma$ represents the zeta potential. Final form of potential equation becomes

$$\frac{{d^{2} \Phi }}{{dy^{2} }} = k^{2} \Phi .\,$$

(23)

The potential function achieved is

$$\Phi = {\text{ Csch}}\left( {\left( {h_{1} - h_{2} } \right){\text{k}}} \right)(b_{2} {\text{Sinh}}\left( {{\text{k}}\left( {h_{1} - {\text{y}}} \right)} \right) - b_{1} {\text{Sinh}}\left( {{\text{k}}\left( {h_{2} - {\text{y}}} \right)} \right)),\,$$

(24)

$k = \sqrt {\frac{{2n_{0} }}{{\epsilon k_{B} T}}} \tilde{a}ez = \frac{{d_{1} }}{{\lambda_{d} }}$ (say) is connected to it,${ }\lambda_{d}$ is the Debye length in this case.

The dimensionless phenomenon has been given in below set of equations [32,33,34,35,36,37,38]

$$\begin{aligned} & x = \frac{{\overline{x}}}{\lambda }, y = \frac{{\overline{y}}}{{d_{1} }},u = \frac{{\overline{u}}}{c},v = \frac{{\overline{v}}}{c\delta }, h_{1} = \frac{{\overline{H}_{1} }}{{d_{1} }}, a = \frac{{a_{1} }}{{d_{1} }},b = \frac{{a_{2} }}{{d_{2} }}, p = \frac{{d_{1}^{2} \overline{p}}}{{c\lambda \mu_{0} }}, \theta = \frac{{\left( {T - T_{0} } \right)}}{{(T_{1} - T_{0} )}}, \\ & Re = \frac{{\rho_{f} cd_{1} }}{{\mu_{0} }}, \Pr = \frac{{\mu_{0} C_{f} }}{{K_{f} }}, E_{c} = \frac{{c^{2} }}{{K_{f} \left( {T_{1} - T_{0} } \right)}},Br = PrE_{c} , \varepsilon = \frac{{d_{1}^{2} \phi }}{{K_{f} }},U_{H} = \frac{{\varepsilon \xi E_{x} }}{{\mu_{0} c}}, \\ & Gr = \frac{{g\rho_{f} \left( {T_{1} - T_{0} } \right)d_{1}^{2} }}{{\left( {1 - F_{0} } \right)^{ - 1} c\mu_{0} }}, E = \frac{{E_{a} }}{{K_{f} \left( {T_{1} - T_{0} } \right)}}, \zeta = \frac{{d_{1}^{2} k^{2}_{r} }}{\nu }, u = \frac{\partial \psi }{{\partial y}}, v = - \frac{\partial \psi }{{\partial x}}, \\ & Nr = \frac{{\left( {\rho_{p} - \rho_{f} } \right)g\beta_{c} \left( {C_{1} - C_{0} } \right)d_{1}^{2} }}{{c\mu_{0} }}, k_{1} = \frac{{\tilde{k}_{1} }}{{d_{1}^{2} }},Sc = \frac{\nu }{{D_{B} }}, \\ & Nt = \frac{{\tau D_{T} (T_{1} - T_{0} )}}{{\nu T_{m} }}, Nb = \frac{{\tau D_{B} \left( {C_{1} - C_{0} } \right)}}{\nu }, \gamma = \frac{{F - F_{0} }}{{F_{1} - F_{0} }}, Pe = \frac{bWc}{{D_{N} }}, \phi = \frac{{C - C_{0} }}{{C_{1} - C_{0} }}, \\ & Rb = \frac{{\left( {\rho_{m} - \rho_{f} } \right)F_{\gamma } g\gamma \left( {F_{1} - F_{0} } \right)d_{1}^{2} }}{{c\mu_{0} }}, h_{1} = \frac{{\overline{H}_{2} }}{{d_{2} }}, \sigma = \frac{{F_{0} }}{{F_{1} - F_{0} }}, {\Omega } = \frac{{T_{0} }}{{T_{1} - T_{0} }}, \delta = \frac{{d_{1} }}{\lambda }, \\ & S_{p} = \frac{{\sigma_{f} E_{x}^{2} d_{1}^{2} }}{{\Delta TK_{f} }}, \tau_{XY} = \frac{{\mu_{0} c}}{{d_{1} }}\tau_{{\overline{X}\overline{Y}}} ,\xi = \frac{{\mu_{0} \sqrt {2\pi } }}{{P_{y} }}, Le = \frac{\nu }{{D_{N} }}. \\ \end{aligned}$$

(25)

The shear stress factor in dimensionless form is given as $\tau_{xy} = \left( {1 + \frac{1}{\xi }} \right)\partial u/\partial y$ and the normal components like $\tau_{xx} ,\tau_{yy}$ vanish.

After incorporating above defined dimensionless relation in Eqs. (11–16), and applying the restriction of lubrication approach (small Reynolds number and long wavelength), we finally get the governing equations as below:

$$\left( {1 + \frac{1}{\xi }} \right)\left( {\frac{\partial }{\partial y}\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right) - \frac{1}{{k_{1} }}\left( {1 + \frac{\partial \psi }{{\partial y}}} \right)} \right) + Gr\theta - Rb\gamma - Nr\phi - U_{H} { }\nabla^{2} \Phi = \frac{\partial p}{{\partial x}},$$

(26)

$$\left( {1 + \frac{1}{\xi }} \right)\left( {\frac{\partial }{\partial y}\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right) - \frac{1}{{k_{1} }}\left( {1 + \frac{\partial \psi }{{\partial y}}} \right)} \right) + Gr\theta - Rb\gamma - Nr\phi - U_{H} { }\nabla^{2} \Phi = \frac{\partial p}{{\partial x}},$$

(27)

$$\frac{\partial p}{{\partial y}} = 0,$$

(28)

$$\frac{{\partial^{2} \theta }}{{\partial y^{2} }} + PrNb\frac{\partial \theta }{{\partial y}}\frac{\partial \phi }{{\partial y}} + PrNt\left( {\frac{\partial \theta }{{\partial y}}} \right)^{2} + \frac{Br}{{k_{1} }}\left( {1 + \frac{1}{\xi }} \right)\left( {1 + \frac{\partial \psi }{{\partial y}}} \right)^{2} + Br\left( {1 + \frac{1}{\xi }} \right)\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{2} + \varepsilon \theta + S_{p} = 0,$$

(29)

$$\frac{{\partial^{2} \phi }}{{\partial y^{2} }} + \frac{Nt}{{Nb}}\left( {\frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right) - Sc\phi \left( {1 + {\Omega }\theta } \right)^{{n_{1} }} \zeta exp\left( { - \frac{E}{{\left( {1 + {\Omega }\theta } \right)}}} \right) = 0,$$

(30)

$$\frac{{\partial^{2} \gamma }}{{\partial y^{2} }} - Pe\left( {\frac{\partial \gamma }{{\partial y}}\frac{\partial \phi }{{\partial y}}} \right) - \gamma \frac{{\partial^{2} \phi }}{{\partial y^{2} }}Pe - Pe\sigma \frac{{\partial^{2} \phi }}{{\partial y^{2} }} = 0.$$

(31)

The subsequent results from cross-differentiating Eqs. (25) and (26):

$$Gr\frac{\partial \theta }{{\partial y}} - Rb\frac{\partial \gamma }{{\partial y}} - Nr\frac{\partial \phi }{{\partial y}} + \left( {1 + \frac{1}{\xi }} \right)\frac{{\partial^{2} }}{{\partial y^{2} }}\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right) - \left( {1 + \frac{1}{\xi }} \right)\frac{1}{{k_{1} }}\frac{\partial }{\partial y}\left( {1 + \frac{\partial \psi }{{\partial y}}} \right) - U_{H} { }\frac{\partial }{\partial y}\left( {\nabla^{2} \Phi } \right) = 0.$$

(32)

The parameters appeared in above relations have been defined in nomenclature. Flow rate in wave frames (F) and the laboratory's frame ($\eta )$ are related as:

$$\eta = F + 1 + d,$$

(33)

where F is described in stream function as

$$F = \mathop \smallint \limits_{{h_{2} }}^{{h_{1} }} \frac{\partial \psi }{{\partial y}}dy.$$

(34)

The boundary conditions given in Eq. (17) can be written in dimensionless form are:

For $y = h_{1} ,$

$$\psi = \frac{F}{2}, \frac{\partial \psi }{{\partial y}} = - 1 + \beta_{1} \left( {1 + \frac{1}{\xi }} \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }}, \theta = \beta_{2} \frac{\partial \theta }{{\partial y}}, \phi = 0, \gamma = 0$$

For $y = h_{2}$

$$\psi = - \frac{F}{2}, \frac{\partial \psi }{{\partial y}} = - 1 + \beta_{1} \left( {1 + \frac{1}{\xi }} \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }}, \theta = 1 - \beta_{2} \frac{\partial \theta }{{\partial y}}, \phi = 1, \gamma = 1.$$

(35)

where $\beta_{1} = \frac{{\beta \mu_{0} }}{{d_{1} }}$ and $\beta_{2} = \frac{{k_{2} }}{{d_{1} }}$. The requirements of the dimensional peristaltic wall are:

$$h_{1} = 1 + a{\text{Cos}}\left( {2\pi x} \right), h_{2} = - 1 - b{\text{Cos}}\left( {2\pi x + \varphi } \right).$$

(36)

The final set of Eqs. (27–30) and the boundary conditions (33) are nonlinear coupled differential equations which are difficult to handle by exact method. Here are many techniques to deal with such problem including analytical and numerical method. Authors decided to utilize the most convergent and reliable numerical method which is based on shooting technique for boundary value problem using Mathematica's built-in NDSolve tool. The reason for using this method is that in this technique we do not need to take an initial approximate guess and that is why we get the most accurate readings without much mathematical effort.

3 Investigation of entropy generation

In dimensional form, rate of volumetric entropy creation is represented as [6, 22, 27, 39, 40]:

$$\begin{aligned} S_{G} & = \frac{{K_{f} }}{{(T_{1} - T_{0} )^{2} }}\left( {\left( {\frac{\partial T}{{\partial \overline{X}}}} \right)^{2} + \left( {\frac{\partial T}{{\partial \overline{Y}}}} \right)^{2} } \right) \\ & \quad + \frac{1}{{(T_{1} - T_{0} )}}\left( {\tau_{{\overline{X}\overline{X}}} \frac{{\partial \overline{U}}}{{\partial \overline{X}}} + \tau_{{\overline{X}\overline{Y}}} \left( {\frac{{\partial \overline{V}}}{{\partial \overline{X}}} + \frac{{\partial \overline{U}}}{{\partial \overline{Y}}}} \right) + \tau_{{\overline{Y}\overline{Y}}} \frac{{\partial \overline{V}}}{{\partial \overline{Y}}}} \right) + \left( {1 + \frac{1}{\xi }} \right)\frac{{\mu_{0} }}{{\tilde{k}_{1} (T_{1} - T_{0} )}}\left( {\overline{U}^{2} + \overline{V}^{2} } \right) \\ & \quad + \frac{{\phi \left( {T - T_{0} } \right)}}{{\left( {T_{1} - T_{0} } \right)}} + \frac{{\tau \left( {\rho C} \right)_{f} }}{{(T_{1} - T_{0} )}}\left( {\frac{{D_{T} }}{{T_{m} }}\left( {\frac{\partial T}{{\partial \overline{X}}} + \frac{\partial T}{{\partial \overline{Y}}}} \right)^{2} + D_{B} \left( {\frac{\partial T}{{\partial \overline{X}}}\frac{\partial C}{{\partial \overline{X}}} + \frac{\partial T}{{\partial \overline{Y}}}\frac{\partial C}{{\partial \overline{Y}}}} \right)} \right) + \frac{{\sigma_{f} E^{2}_{x} }}{{(T_{1} - T_{0} )}} \\ \end{aligned}$$

(37)

Utilizing the wave frame and dimensionless transformations, we obtain

$$\begin{aligned} N_{S} = \left( {\frac{\partial \theta }{{\partial y}}} \right)^{2} + \delta^{2} \left( {\frac{\partial \theta }{{\partial x}}} \right)^{2} & + PrNb\left( {\frac{\partial \theta }{{\partial y}}\frac{\partial \phi }{{\partial y}} + \delta^{2} \frac{\partial \theta }{{\partial x}}\frac{\partial \phi }{{\partial x}}} \right) + PrNt\left( {\frac{\partial \theta }{{\partial y}} + \delta \frac{\partial \theta }{{\partial x}}} \right)^{2} \\ & \quad + \varepsilon \theta + \left( {1 + \frac{1}{\xi }} \right)\frac{Br}{{k_{1} }}\left( {\left( {1 + \frac{\partial \psi }{{\partial y}}} \right)^{2} + v^{2} \delta^{2} } \right) + Br\left( {\delta \tau_{{\overline{x}\overline{x}}} \frac{{\partial \overline{u}}}{{\partial \overline{x}}} + \delta^{2} \tau_{{\overline{x}\overline{y}}} \frac{{\partial \overline{v}}}{{\partial \overline{x}}} + \tau_{{\overline{y}\overline{x}}} \frac{{\partial \overline{u}}}{{\partial \overline{y}}} + \delta \tau_{{\overline{y}\overline{y}}} \frac{{\partial \overline{v}}}{{\partial \overline{y}}}} \right) + S_{p} . \\ \end{aligned}$$

(38)

The equation includes five physical characteristics that contribute to the formation of entropy: heat transmission effects, viscous dissipation, porous media effects, non-uniform heat generation effects, mass diffusion and electroosmosis. In dimensionless form $N_{S}$, the Entropy generation rate is represented as $N_{s} = S_{G} /Sc$ and the final expression for $N_{S}$ is found as

$$N_{S} = \left( {\frac{\partial \theta }{{\partial y}}} \right)^{2} + PrNb\left( {\frac{\partial \theta }{{\partial y}}\frac{\partial \phi }{{\partial y}}} \right) + PrNt\left( {\frac{\partial \theta }{{\partial y}}} \right)^{2} + \varepsilon \theta + \left( {1 + \frac{1}{\xi }} \right)\frac{Br}{{k_{1} }}\left( {1 + \frac{\partial \psi }{{\partial y}}} \right)^{2} + Br\left( {1 + \frac{1}{\xi }} \right)\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{2} + S_{p} .$$

(39)

The rate of characteristic entropy generation is identified as $Sc = K_{f} /d_{1}^{2} .$ The ratio of entropy generation resulting from the irreversibility of heat transfer to the overall production of entropy and fluid friction is known as the Bejan number $B_{e}$. Algebraically, it is written as

$$B_{e} = { }\frac{{\left( {\frac{\partial \theta }{{\partial y}}} \right)^{2} }}{{\left( {\frac{\partial \theta }{{\partial y}}} \right)^{2} + PrNb\left( {\frac{\partial \theta }{{\partial y}}\frac{\partial \phi }{{\partial y}}} \right) + PrNt\left( {\frac{\partial \theta }{{\partial y}}} \right)^{2} + \varepsilon \theta + \left( {1 + \frac{1}{\xi }} \right)\frac{Br}{{k_{1} }}\left( {1 + \frac{\partial \psi }{{\partial y}}} \right)^{2} + Br\left( {1 + \frac{1}{\xi }} \right)\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{2} + S_{p} }}.$$

(40)

The Bejan number has a range of 0 to 1.

4 Results and discussions

Graphical and tabular depictions of fluid ingredients and the accompanying variations across multiple key parameters are presented in this section. The numerical results achieved with the widely-used program Mathematica can be observed in these graphs. The parametric ranges used in the study are taken as per published literature and some physical constraints given as $0 \le \alpha \le 1, - 1 \le \varepsilon < 0, 0 < \varepsilon \le 1, 0 \le S_{P} \le 10, 0 \le Sc \le 5, 0 \le \zeta \le 10, 0 < k_{1} \le 2, - 1 \le U_{H} \le 10, 0 \le \xi \le 1, 0 \le Pr \le 10.$ The default parameters are also given as $Gr = 0.5, n_{1} = 2, Nr = 0.1, Rb = 2, Nt = 0.2, Nb = 0.1, {\Omega } = 0.2, \zeta = 0.4, Br = 0.5, k = 0.5, \sigma = 0.1, F = 1, Pe = 0.4, \beta_{1} = 0.2, \beta_{2} = 0.3, a = 0.2, b = 0.1,\varphi = 0.6,x = 0.2.$

Tables 1 and 2 are showing the effects of certain physical factors on the profiles of temperature and velocity, respectively. The varying behavior will be latterly discussed through subsequent figures because similar parameters have been used in graphs of the relevant quantities. In Table 3, we can discuss the comparison of current work with the existing literature. It can be seen that the present readings are in line with the results of Akbar et al. [23] up to three decimal places. An error estimates is also provided to establish the validity of the current work. The temperature distribution function ($\theta$) in relation to changes in the porosity factor ($k_{1}$) and Prandtl number ($Pr$), two important fluid dynamics factors, as depicted in Fig. 2a. Interestingly, it is shown that the temperature ($\theta$) consistently decreases $k_{1}$ increase, while temperature enhances with the rise in $Pr$ values. This relationship is important for real-world applications, such as heat exchangers, where developing efficient heat exchange systems require an understanding of how fluctuations in Prandtl number and permeability affect temperature. The graphical illustration of the thermal generation/absorption parameter in relation to the ambient temperature profile is identically depicted in Fig. 2b. When $\varepsilon$ takes positive values, we see a widening of the curves; for negative values of $\varepsilon$, the curves clearly show a decline. The core region is where the temperature increases, and the corners are the temperature lowers. Finally, we can see how the electroosmotic parameter ($U_{H}$) and the indicator for Joule heating in the base fluid ($S_{P}$) affect each other in Fig. 2c. Temperature reduces with the implementation of electro-osmosis, however grows with higher values of the Joule heating coefficient ($S_{P}$). Understanding temperature variations is critical in disciplines like microfluidics, where precise temperature control is required for applications such as lab-on-a-chip devices, where electroosmosis and Joule heating effects have a significant impact on the effectiveness and precision of chemical and biological studies. At last, Fig. 2d is plotted to show the graphical impact of casson fluid factor $\xi$ and chemical reaction parameter $\zeta$. It implies that temperature declines with the rise of both factors and maximum in the left upper corner

Table 1 Quantitative effects of numerous pertinent parameters on thermal profile

Table 2 Quantitative effects of numerous pertinent parameters on velocity profile

Table 3 The validity of present findings through literature [23]

Fig. 2

Temperature profile for variation in various parameters

The effects of multiple variables on the particle concentration profile are displayed in Fig. 3a, in which the casson fluid factor $\xi$ and chemical reaction parameter $\zeta$ are emphasized. The graphs exhibit downward trend as the amounts of these factors improve, and maximum in the left upper corner. One can easily observe from Fig. 3b that the curves are rising for negative values of $\varepsilon$, while decreases for positive values of $\varepsilon .$ It implies that concentration ($\phi$) is greatest at both ends while smallest in the center. It is noteworthy that these insights have applications in chemical engineering, where it can be critical to optimize processes and reactions to comprehend how viscosity, porosity, and heat generation impact concentration profiles. The striking effects of electroosmosis ($U_{H}$) and the joule heating factor ($S_{P}$)) are shown in Fig. 3c. At each extreme, the concentration ($\phi$) increases until it reaches its maximum and then decreases as these two variables vary more. In microfluidic devices and electro thermal systems, for example, this phenomenon finds practical application in optimizing electro kinetic processes and heat generation. At last, Fig. 3d is plotted to illustrate the pictorial view of velocity slip $\beta_{1}$ and thermal slip $\beta_{2}$ factors on concentration profile respectively. One can observe easily that by increasing the velocity slip parameter values, the fluid becomes more concentrated while by the enhancement of thermal slip factor, a decline in concentration profile is observed.

Fig. 3

Concentration profile for variation in various parameters

We have created Fig. 4a, b to graphically depict the density profile of mobile microorganisms ($\gamma$) with respect to different parameters. The influence of the heat generation/absorption parameter ($\varepsilon$) on ($\gamma$) is well-illustrated in Fig. 4a, where the curves show expansion for negative ε values and a reduction in density for positive $\varepsilon$ values. These results have practical implications for understanding how temperature changes affect microbe density and designing bioreactor systems. In order to notice the graphical influences of slip parameters on motile microorganism’s density, Fig. 4b is sketched. This plot illustrates that with the rise of velocity slip factor the density decreases while an increasing trend in density is noticed for the rising variations of thermal slip parameter. On the other hand, Fig. 4c clearly illustrates the both increasing trend and decline in response to variations in the porosity factor ($k_{1}$) and Prandtl number ($pr$) respectively, with density peaking at the uppermost corner. This study is significant for instances where regulating Prandtl values and porosity may affect the spread of microbes, such as environmental studies and filtering.

Fig. 4

Motile micro-organisms density profile for variation in various parameters

We have shown in Fig. 5a how changes in the porosity factor ($k_{1}$) and Prandtl number ($pr$) affect the velocity function (u). The figure shows that the velocity curves rise noticeably as the Prandtl parameter ($pr$) grows, but these curves decrease when the porosity factor ($k_{1}$) increases. It is noteworthy that the velocity exhibits a typical parabolic trend and peaks within the core area. This knowledge can be used to comprehend how various parameters affect fluid flow in a variety of domains, including fluid dynamics and porous media investigations. Depending on their particular requirements, researchers and engineers can use these insights to optimize systems for effective filtration or transport operations. In Fig. 5b, the curves show an expansion when the heat generation/absorption parameter ($\varepsilon$) is positive, and a fall in velocity when $\varepsilon$ takes on negative values. These results are useful in fluid dynamics and engineering. In thermal systems, heat creation is represented by a positive $\varepsilon$, which raises velocity, whereas heat absorption is represented by a negative $\varepsilon$, which decreases velocity. Understanding this is key for optimizing systems that involve fluid flow dynamics and critical heat transfer.

Fig. 5

Velocity profile for variation in various parameters

One may quantify the degree of disorder in a system using entropy, and it is possible to evaluate it. We explore the idea of entropy generation, which is represented by the entropy production number ($N_{S}$), and investigate the impacts of different parameters in Fig. 6a–c. Figure 6a shows that entropy creation increases for $\varepsilon > 0$, showing that the production of heat is caused by increased disorder. On the other hand, when $\varepsilon < 0$, entropy production decreases and this is consistent with a decrease in system disorder. This behavior illustrates the effects of heat and the creation of entropy. This phenomenon provides insight into how distinct heat processes might impact entropy formation in diverse systems, which is useful in practical applications. It is applicable, for instance, to the design and analysis of thermodynamic systems, materials processing, and combustion engines, where maximizing efficiency and reducing waste requires an understanding of the interaction between heat transmission and entropy formation. The palpable impacts of the dimensionless Casson fluid parameter ($\xi$) and chemical reaction factor ($\zeta$) on the entropy generation number ($N_{S}$) are graphically shown in Fig. 6b. It is easy to see that as both of these factors gradually alter, the curves rise. The upper right corner is where the entropy generation number ($N_{S}$) is highest. Figure 6c shows the graphical effects of the joule heating factor ($S_{P}$) and electroosmosis ($U_{H}$) on entropy production. This graph shows that an increase in $U_{H}$ and $S_{P}$ corresponds to a rise in entropy generation. This observation has implications for understanding how different electrochemical systems, such as fuel cells, microfluidic devices, and electrokinetic processes in analytical chemistry, work and perform better when electroosmosis and joule heating are managed. It provides valuable insights on how to optimally optimize these systems to reduce entropy output and increase overall efficacy. For the sake of observing the graphical impacts of velocity and thermal slip parameters $\beta_{1}$ and $\beta_{2}$ respectively, Fig. 6d is sketched. Entropy creation rises for the rise in the values of both slip factors.

Fig. 6

Entropy profile for variation in various parameters

Bejan number curves are shown in Fig. 7a–c, which provides important context for understanding how different variables interact. The Bejan number, or $B_{e}$, is a crucial metric for determining the relative importance of fluid flow and heat transfer, which yields important insights into system performance. In this analysis, we investigate the effects of the velocity slip parameter ($\beta_{1}$) and thermal slip factor ($\beta_{2}$) on the Bejan number ($B_{e}$), as shown in Fig. 7a. It is easily observed that the Bejan number tends toward greater values on both ends as velocity slip parameter grows, while declines with the rising variations of thermal slip factor, peaking in the rightmost region. For engineering and scientific purposes, it is essential to comprehend how the Bejan number reacts to variations in the slip factors in terms of velocity and temperature. The empirical impacts of the Schmidt number (Sc) and Prandtl number (Pr) are shown in Fig. 7b. A positive association is indicated by the expansion of the Bejan number curves on the right side with rising Schmidt number (Sc). On the other hand, a negative link is shown by the Bejan number curves' fall on the right side when the Prandtl number (Pr) rises. Lastly, it's important to note that Fig. 7c clearly illustrates the impact of the joule heating factor ($S_{P}$) and electro-osmotic factor ($U_{H}$). The graph shows a growing pattern for $S_{P}$ in the right region and a rising trend for $U_{H}$ in the left. Interestingly, the upper-right quadrant is where $B_{e}$ achieves its maximum value. This discovery has useful implications for [name the particular sector or application where these parameters are relevant, such as electrochemical devices, microfluidics, or electro kinetics], where comprehension of these phenomena is essential to maximizing effectiveness and performance.

Fig. 7

Bejan number profile for variation in various parameters

The flow patterns within the channel are influenced by the electroosmotic factor S_p and the heat absorption/generation parameter $\varepsilon$, as seen in the streamline discussion in Figs. 8a–c and 9a–c. But integrating physical thinking into the analysis is crucial to improving our comprehension of these occurrences. First, looking at Fig. 8a–c and the Joule heating factor S_p, the graph shows that the streamlines change noticeably as S_p rises, which causes the stream boluses to diminish. The fluid flow within the channel is influenced by electroosmotic effects, which are responsible for their increasing dominance in this behavior. The physical interpretation of this discovery, which highlights the contribution of electroosmotic forces to the modification of the stream boluses' diameters, must be emphasized. This can entail talking about how larger S_p values intensify the electrokinetic effects and, as a result, affect the fluid distribution inside the channel. Upon examining Fig. 9a–c and the heat absorption/generation parameter $\varepsilon$, the study reveals that greater values of $\varepsilon$ result in fewer circulating contours and larger interior boluses. Examining the underlying physical mechanisms is critical in this case. Elevated $\varepsilon$ values may imply significant heat generation or absorption in the channel, affecting fluid behaviour. This could be explained by considering how heat generation and absorption affect internal bolus size and circulation patterns in fluid dynamics. When the asymmetric construction of the channel is described, it adds another layer of complexity. Investigating the physical origins of this asymmetry, such as boundary conditions or channel shape, can provide valuable information. The system's overall understanding is improved by discussing how asymmetry influences the observed differences in bolus locations on the left and right sides of the domain.

Fig. 8

Flow pattern for a $S_{P} = 0.5$, b $S_{P} = 0.7$, c $S_{P} = 0.9$

Fig. 9

Flow pattern for a $\varepsilon = 0.2$, b $\varepsilon = 0.4$, c $\varepsilon = 0.6$

5 Conclusions

This work provides a thermodynamic evaluation of Casson nanofluid in the context of bioconvection peristalsis driven by electroosmosis, lubricant qualities, gyrotactic microbes, and Arrhenius activation energy. The following list summarizes the main conclusions of this study:

• A temperature increase is correlated with an increase in the activation parameter values.

• Increasing the heat generation factor and changing the thermophoresis constant at the same time can change the rate of heat transfer at surfaces.

• There is a tendency for the Bejan number to grow with stronger heat sources.

There are the answers to the proposed research question from the current study observations

• The creation of entropy increases with a rising Helmholtz-Smoluchowski factor but reduces as the heat generation/absorption factor increases ($\varepsilon < 0$).

• Enhancing porosity can lessen the system's internal entropy creation.

• It is observed that entropy generation can be minimized by large values of Casson fluid parameter.

5.1 Future directions

In future, effects of compliant walls and the different models of nanofluid along with various shapes of nanoparticles can be done.