1 Introduction

The nonlinear flow involving the Peristalsis phenomenon is a shape of fluid movement caused by waves of contraction or expansion propagating along the axial line of a fluid-containing inflatable tube. It is also exploited for tremendous applications in life science and engineering. Living systems include food movement through the digestive tract, eggs within the fallopian tubes, and blood flow within the arteries and the male reproductive tract. Transporting hygienic liquids, caustic liquids, and medicine delivery systems are all typical industrial applications. Due to its significance, many writers have researched peristaltic flow in Newtonian and non-Newtonian fluids. For instance, reflux and net backward flow were associated with Fung and Yih [1], who published the first model on peristaltic pumping using a perturbation technique. Applying the extended frequency estimate for gut movement, Barton and Raynor [2] tackled the complete analysis of the wave-like motion in a cylindrical pipe. Shapiro et al.’s [3] investigation was expanded to account for sinusoidal wall propagation, reflux, entrapment phenomena, and Newtonian fluids flowing steadily along the channel. Irregular channels with extended wavelengths and low Reynolds number estimates were involved in Nadeem et al.’s [4] examination of the wave-like flow of a few strain fluids. Wang et al.’s [5] analysis of the Johnson-Segalman fluid’s peristaltic motion in a tube with a sinusoidal wave was based on physiological fluid flow. Reddy et al. [6] have described the stream of a power-law liquid in an asymmetric channel with the same speed but distinct amplitudes. Srinivas and Kothandapani talked about the problem of how heat moves when a viscous liquid is being carried through a channel using wavy movements [7]. The heat transfer and magnetic field effects on the liquid peristaltic stream in a vertical channel were studied by Mekheimer et al. [8]. Tripathi and Bég [9] analyzed the peristaltic stream in nanofluids through a 2D channel. They demonstrated that there was an inverse relationship between the pressure gradient and the thermophoresis parameter. By reducing the pressure gradient, the thermophoresis parameter is increased. In their research on the influence of nanoparticles on peristaltic flow, Seiyed E. Ghasemi et al. [10] demonstrated that a rise in the thermal Grashof number lowers the axial velocity profile, and an increase in the species Grashof number has the opposite effect. Their research was expanded by Shehzad et al. [11] by incorporating the impacts of numerous parameters on the velocity, temperature, nanoparticle concentration, and heat and mass transfer at the wall. Nowadays, the study of molecular [12] and nanoscale [13] materials in the health and medical industries is facing increasing attention. Hayat et al. explored a viscous nanofluid [14] for magneto-convection peristaltic transport in a porous medium channel. Their study talked about the impact of Joule heating and Soret and Dufour. The nonlinear model is also troubleshooted by employing long wavelengths and low Reynolds numbers. Despite its significant applicability in medical engineering systems, there have been limited investigations into the peristaltic movement of nanofluids. Akbar et al. [15] developed the nanofluid peristaltic stream in a diverging channel in their initial study on connecting the temperature and nanoparticle equations using a homotopy perturbation approach. According to the results, the rise in the number of thermophoresis and pressure have an inverse relationship, whereas increasing the Brownian motion and the thermophoresis parameters causes temperatures to rise. Due to the intrinsic nonlinearity of most engineering problems involving fluid motion and heat transfer equations, a different approach should be used to solve them. In recent decades, some alternative approaches have been devised to generate an analytic solution to the problem, such as the Adomian’s decomposition method [16], homotopy perturbation method (HPM) [17], homotopy asymptotic method (HAM) [18], variational iteration method (VIM) [19], variation of parameters method [20], differential transformation method [21], Least squares method (LSM) [22], Collocation method (CM) [23] and Akbari-Ganji’s method (AGM) [24]. Among the analytical methods that were mentioned, CM is very easy to use, despite its appropriate accuracy. AGM, which is inspired by it, has been presented in recent years and is considered a new and efficient method. Although the use of these methods for complex functions and boundary conditions is not a good choice, they have been successful both in terms of simplicity of application and accuracy of the answer to the problem investigated in this research. In addition to the RK4 numerical method, which is used as a completely accurate solution method and a criterion for measuring the correctness of the answer of other methods, we have used the FlexPDE software, which is based on the finite element method and has the ability to simulate different geometries. Its main advantage is its simplicity and ease of use. In order to approximate the peristaltic flow of nanofluid through a channel that has been used in medication transportation systems, the current paper aims to solve this problem using the methods mentioned. Low Reynolds numbers and long wavelength approximation assumptions simplify the issue. Additionally, with the aid of computational illustrations, the effects of some parameters, including Brownian motion and thermophoresis parameters, thermal, and the basic-density Grashof number, on velocity and nanoparticle fraction profiles are discussed. In fact, after choosing a practical and important problem in the medical industry, the main parameters and dimensionless numbers governing it have been tried to be well-known and introduced. Then, by reviewing different methods and taking help from previous experiences, two analytical methods and two numerical methods with sufficient accuracy and simplicity were used to analyze the fluid behavior in this problem fully, which can ultimately lead to better decision-making in sensitive situations. An example of this application is controlling the bleeding during surgery by creating a magnetic field around the area. In the next section, we will deal with the mathematical modeling of the problem and introduce the effective parameters. In Sect. 3, we describe the solution methods, and in Sect. 4, we show how to apply them. Then, in the next section, we explain the results completely. In the last two sections, we will discuss the innovations and mission of this article and finally summarize the contents.

2 Model development and mathematical analysis

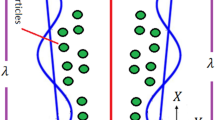
Let us emphasize the peristaltic pumping of a fluid in a nonuniform channel. Progressive sinusoidal waves occur on the top and lower channel walls. We’ve presumed that the channel’s half-width, as depicted in Fig. 1, is the source of our issue. [25] gives the definition of the basic equation for the wall geometry.

Fig. 1
figure 1

Geometry of peristaltic pumping in medicate conveyance system

Full size image
$$\widetilde{h}\left(\widetilde{\xi },\widetilde{t}\right)=a+b \, \sin\frac{2\pi }{\lambda }\left(\widetilde{\xi }-c\widetilde{t}\right)$$
(1)

The variables t, h, and \(\xi\) denote time, the wall’s transverse vibration, and the axial coordinate in the equation. The equations for the conservation of total mass, momentum, thermal energy, and nanoparticle fraction, as well as the Oberbeck-Boussinesq approximation, are [26]:

$$\nabla .{\varvec{V}}=0,$$
(2)
$${\rho }_{f}\left(\frac{\partial {\varvec{V}}}{\partial t}+{\varvec{V}}.\nabla {\varvec{V}}\right)=-\nabla p+\mu {\nabla }^{2}{\varvec{V}}+\left[F{\rho }_{p}+\left(1-F\right)\left\{{\rho }_{f}\left(1-\beta \left(T-{T}_{0}\right)\right)\right\}\right]\mathsf{g},$$
(3)
$${\left(\rho c\right)}_{f}\left(\frac{\partial T}{\partial t}+{\varvec{V}}.\nabla {\varvec{V}}\right)=k{\nabla }^{2}T+{\left(\rho c\right)}_{p}\left[{D}_{B}\nabla \phi .\nabla T+\left(\frac{{D}_{T}}{{T}_{0}}\right)\nabla T.\nabla T\right],$$
(4)
$$\frac{\partial F}{\partial t}+{\varvec{V}}.\nabla F={D}_{B}{\nabla }^{2}\phi +\left(\frac{{D}_{T}}{{T}_{0}}\right){\nabla }^{2}T.$$
(5)

The above equations are correlated with the following boundary conditions:

$$\begin{gathered} T = {T_0}, \, F = {F_0} \, at \, \eta = 0, \hfill \\ T = {T_1}, \, F = {F_1} \, at \, \eta = h. \hfill \\ \end{gathered}$$
(6)

The governing equation for momentum may be formulated as follows using a reasonable option for the reference pressure, whereas nanoparticle concentration is to be diluted:

$${\rho }_{f}\left(\frac{\partial {\varvec{V}}}{\partial t}+{\varvec{V}}.\nabla {\varvec{V}}\right)=-\nabla p+\mu {\nabla }^{2}{\varvec{V}}+\left[\left({\rho }_{p}-{\rho }_{f0}\right)\left(F-{F}_{0}\right)+\left(1-{F}_{0}\right){\rho }_{f0}\beta \left(T-{T}_{0}\right)\right]\mathsf{g}.$$
(7)

The governing Eqs. (2)–(5), given the usual boundary-layer approximation, are [27]:

$$\frac{\partial \widetilde{u}}{\partial \widetilde{\xi }}+\frac{\partial \widetilde{v}}{\partial \widetilde{\eta }}=0,$$
(8)
$${\rho }_{f}\left(\frac{\partial }{\partial \widetilde{t}}+\widetilde{u}\frac{\partial }{\partial \widetilde{\xi }}+\widetilde{v}\frac{\partial }{\partial \widetilde{\eta }}\right)\widetilde{u}=-\frac{\partial \widetilde{p}}{\partial \widetilde{\xi }}+\mu \left(\frac{{\partial }^{2}\widetilde{u}}{{\partial \widetilde{\xi }}^{2}}+\frac{{\partial }^{2}\widetilde{u}}{{\partial \widetilde{\eta }}^{2}}\right)+\left[\left(1-{F}_{0}\right){\rho }_{f0}\beta \left(T-{T}_{0}\right)-\left(\rho -{\rho }_{f0}\right)\left(F-{F}_{0}\right)\right]\mathsf{g},$$
(9)
$${\rho }_{f}\left(\frac{\partial }{\partial \widetilde{t}}+\widetilde{u}\frac{\partial }{\partial \widetilde{\xi }}+\widetilde{v}\frac{\partial }{\partial \widetilde{\eta }}\right)\widetilde{v}=-\frac{\partial \widetilde{p}}{\partial \widetilde{\xi }}+\mu \left(\frac{{\partial }^{2}\widetilde{v}}{{\partial \widetilde{\xi }}^{2}}+\frac{{\partial }^{2}\widetilde{v}}{{\partial \widetilde{\eta }}^{2}}\right)+\left[\left(1-{F}_{0}\right){\rho }_{f0}\beta \left(T-{T}_{0}\right)-\left(\rho -{\rho }_{f0}\right)\left(F-{F}_{0}\right)\right]\mathsf{g},$$
(10)
$${\left(\rho c\right)}_{f}\left(\frac{\partial }{\partial \widetilde{t}}+\widetilde{u}\frac{\partial }{\partial \widetilde{\xi }}+\widetilde{v}\frac{\partial }{\partial \widetilde{\eta }}\right)T=k\left(\frac{{\partial }^{2}T}{{\partial \widetilde{\xi }}^{2}}+\frac{{\partial }^{2}T}{{\partial \widetilde{\eta }}^{2}}\right)+{\left(\rho c\right)}_{p}\left\{{D}_{B}\left(\frac{\partial F}{\partial \widetilde{\xi }}\frac{\partial T}{\partial \widetilde{\xi }}+\frac{\partial F}{\partial \widetilde{\eta }}\frac{\partial T}{\partial \widetilde{\eta }}\right)+\frac{{D}_{T}}{{T}_{0}}\left({\left(\frac{\partial T}{\partial \widetilde{\xi }}\right)}^{2}+{\left(\frac{\partial T}{\partial \widetilde{\eta }}\right)}^{2}\right)\right\},$$
(11)
$$\left(\frac{\partial }{\partial \widetilde{t}}+\widetilde{u}\frac{\partial }{\partial \widetilde{\xi }}+\widetilde{v}\frac{\partial }{\partial \widetilde{\eta }}\right)F={D}_{B}\left(\frac{{\partial }^{2}F}{{\partial \widetilde{\xi }}^{2}}+\frac{{\partial }^{2}F}{{\partial \widetilde{\eta }}^{2}}\right)+\frac{{D}_{T}}{{T}_{0}}\left(\frac{{\partial }^{2}T}{{\partial \widetilde{\xi }}^{2}}+\frac{{\partial }^{2}T}{{\partial \widetilde{\eta }}^{2}}\right).$$
(12)

The following non-dimensional quantities are prescribed:

$$\begin{gathered} \xi = \frac{{\widetilde \xi }}{\lambda },\eta = \frac{{\widetilde \eta }}{a},t = \frac{{c\widetilde t}}{\lambda }u = \frac{{\widetilde u}}{c},v = \frac{{\widetilde v}}{{c\delta }}, \hfill \\ p = \frac{{\widetilde p{a^2}}}{{\mu c\lambda }},h = \frac{{\widetilde h}}{a} = 1 + \omega \, {\sin} \, \left( {2\pi \xi } \right),\delta = \frac{a}{\lambda }, \hfill \\ \omega = \frac{b}{a},\upsilon = \frac{\mu }{{{\rho _{f0}}}},\theta = \frac{{T - {T_0}}}{{{T_1} - {T_0}}},\phi = \frac{{F - {F_0}}}{{{F_1} - {F_0}}},Re = \frac{{{\rho _f}ca}}{\mu }, \hfill \\ G{r_T} = \frac{{\beta g{a^3}(1 - {F_0})({T_1} - {T_0})}}{{{\upsilon ^2}}},G{r_f} = \frac{{\beta g{a^3}(1 - {F_0})({T_1} - {T_0})}}{{\rho {f_0}{\upsilon ^2}}}, \hfill \\ Pr = \frac{{\upsilon {{(\rho c)}_f}}}{k},{N_b} = \frac{{{{\left( {\rho c} \right)}_p}{D_B}({F_1} - F0)}}{k},{N_t} = \frac{{{{\left( {\rho c} \right)}_p}{D_T}\left( {{T_1} - {T_0}} \right)}}{{k{T_0}}}. \hfill \\ \end{gathered}$$
(13)

which \(\xi\) and \(\eta\) represent axial and transverse coordinates, and the terms \(t, u\) and \(v\) show non-dimensional time, axial and transverse velocity. Parameters \(p, h, \delta , \omega , \upsilon , \theta\) and \(\phi\) indicate dimensionless pressure, transverse vibration of the wall, wave number, wave amplitude, kinematic viscosity, temperature, and nanoparticle volume fraction, respectively. \(Re\) and \(Pr\) are the famous Reynolds and Prandtl numbers and \({Gr}_{T}\) and \({Gr}_{f}\) represent thermal and basic-density Grashof numbers. Finally, \({N}_{b}\) and \({N}_{t}\) are Brownian and thermophoresis parameters.

Under the low Reynolds number and big wavelength approximations, the controlling Eqs. (8)–(12) reduce to:

$$\frac{\partial u}{\partial \widetilde{\xi }}+\frac{\partial v}{\partial \widetilde{\eta }}=0,$$
(14)
$$\frac{\partial p}{\partial \widetilde{\xi }}=\frac{{\partial }^{2}u}{\partial {\eta }^{2}}+{Gr}_{T}\theta -{Gr}_{F}\phi ,$$
(15)
$$\frac{\partial p}{\partial \eta }=0,$$
(16)
$$\frac{{\partial }^{2}\theta }{{\partial \eta }^{2}}+{N}_{b}\frac{\partial \theta }{\partial \eta }\frac{\partial \phi }{\partial \eta }+{N}_{t}{\left(\frac{\partial \theta }{\partial \eta }\right)}^{2}=0,$$
(17)
$$\frac{{\partial }^{2}\phi }{{\partial \eta }^{2}}+\frac{{N}_{t}}{{N}_{b}}\frac{{\partial }^{2}\theta }{\partial {\eta }^{2}}=0.$$
(18)

The following boundary conditions are prescribed:

$$\begin{gathered} \theta = 0,\phi = 0,\frac{{\partial u}}{{\partial \eta }} = 0\,at\,\eta = 0, \hfill \\ \theta = 1,\phi = 1,u = 0\,at\,\eta = h. \hfill \\ \end{gathered}$$
(19)

Following the boundary conditions \({\phi |}_{\upeta =0}=0\) and \({\phi |}_{\upeta ={\text{h}}}=1\) and the double integration of Eq. (18) across a confined region, the nanoparticle fraction field can be expressed as follows:

$$\phi =-\frac{{N}_{t}}{{N}_{b}}{e}^{\frac{{N}_{b}+{N}_{t}}{h}\left(h-\eta \right)}\left(\frac{{e}^{\frac{{N}_{b}+{N}_{t}}{h} \eta }-1}{{e}^{{N}_{b}+{N}_{t}}-1}\right)+\frac{n}{{N}_{b}}\eta .$$
(20)

The temperature field is obtained by replacing Eq. (20) in Eq. (17), calculating the double integration of Eq. (17), and applying the boundary conditions, \({\theta |}_{\upeta =0}=0\) and \({\theta |}_{\upeta ={\text{h}}}=1\).

$$\theta ={e}^{\frac{{N}_{b}+{N}_{t}}{h}\left(h-\eta \right)}\left(\frac{{e}^{\frac{{N}_{b}+{N}_{t}}{h} \eta }-1}{{e}^{{N}_{b}+{N}_{t}}-1}\right).$$
(21)

The axial velocity is calculated by replacing Eqs. (20) and (21) in Eq. (15), further integrating Eq. (15) twice and considering the conditions \({\frac{\partial u}{\partial\upeta }|}_{\upeta =0}=0\) and \({u|}_{\upeta ={\text{h}}}=0\).

$$u=\frac{1}{2}\frac{\partial p}{\partial \xi }\left({\eta }^{2}-{h}^{2}\right)+m\left\{{\left(\frac{h}{{N}_{b}+{N}_{t}}\right)}^{2}\left({e}^{-\frac{{N}_{b}+{N}_{t}}{h} \eta }-{e}^{-\left({N}_{b}+{N}_{t}\right)}\right)-\frac{1}{2}\left({\eta }^{2}-{h}^{2}\right)\right\}+\frac{{N}_{b}+{N}_{t}}{6h{N}_{b}}\left({\eta }^{3}-{h}^{3}\right)+\frac{m}{\frac{{N}_{b}+{N}_{t}}{h}}\left(\eta -h\right).$$
(22)

where,

$$m={(Gr}_{T}+\frac{{N}_{t}}{{N}_{b}}{Gr}_{F})\frac{{e}^{{N}_{b}+{N}_{t}}}{{e}^{{N}_{b}+{N}_{t}}-1}.$$
(23)

The volumetric flow rate is given as follows [3]:

$$Q={\int }_{0}^{h}ud\eta.$$
(24)

We may have:

$$Q=-\frac{{h}^{3}}{3}\frac{\partial p}{\partial \xi }+ m\left\{{\left(\frac{h}{{N}_{b}+{N}_{t}}\right)}^{2}\left(\frac{h}{{N}_{b}+{N}_{t}}-\frac{\frac{h}{{N}_{b}+{N}_{t}}-1}{{e}^{\frac{1}{{N}_{b}+{N}_{t}}}}\right)-\frac{{h}^{3}}{{2(N}_{b}+{N}_{t})}+\frac{{h}^{3}}{3}\right\}+\frac{{(N}_{b}+{N}_{t}){Gr}_{F}}{8{N}_{b}}{h}^{3}.$$
(25)

The following is the transformation between the wave frame and the fixed frame:

$$\widetilde{X}=\widetilde{\xi }-c\widetilde{t} , \widetilde{Y}=\widetilde{\eta } , \widetilde{U}=\widetilde{u}-c , \widetilde{V}=\widetilde{v}.$$
(26)

The volumetric flow rate in the wave frame may be computed by:

$$Q={\int }_{0}^{h}(1+U)dY.$$
(27)

The following is the average flow rate over a range of time:

$$\overline{Q }={\int }_{0}^{1}Qdt={\int }_{0}^{1}\left({\int }_{0}^{h}UdY+h\right)dt=Q+1-h=q+1.$$
(28)

Equations (25) and (26) produce the pressure gradient as:

$$\frac{\partial p}{\partial \xi }=-\frac{3}{{h}^{3}}\left(\overline{Q }-1+h\right)++ m\left\{\frac{3}{{\left({N}_{b}+{N}_{t}\right)}^{3}}\left(\frac{h}{{N}_{b}+{N}_{t}}-\frac{\frac{h}{{N}_{b}+{N}_{t}}+h}{{e}^{{N}_{b}+{N}_{t}}}\right)-\frac{3}{{2(N}_{b}+{N}_{t})}+1\right\}+\frac{{3(N}_{b}+{N}_{t}){Gr}_{F}}{8{N}_{b}}.$$
(29)

The pressure difference across a wavelength is given as:

$$\Delta p={\int }_{0}^{1}\frac{\partial p}{\partial \xi }d\xi .$$
(30)

Equations (22) and (26) yield the stream function in the wave frame (complying with the Cauchy–Riemann equations,\(U=\frac{\partial \psi }{\partial \eta }\) and \(V=-\frac{\partial \psi }{\partial \xi }\)) as follows:

$$\psi \left(\xi ,\eta \right)=\frac{1}{2}\frac{\partial p}{\partial \xi }\left(\frac{{\eta }^{3}}{3}-{h}^{2}\eta \right)+m\left\{\frac{1}{{n}^{2}}\left(-\frac{{e}^{-n\eta }}{n}-{e}^{-nh}+\frac{1}{n}\right)-\frac{1}{2}\left(\frac{{\eta }^{3}}{3}-{h}^{2}\eta \right)+\frac{1}{n}(\frac{{\eta }^{2}}{2}-h\eta )\right\}+\frac{n{Gr}_{F}}{6{N}_{b}}\left(\frac{{\eta }^{4}}{4}-{h}^{3}\eta \right)-\eta .$$
(31)

The dimensionless Nusselt number Nu is acquired as:

$$Nu=-\frac{\partial \theta }{\partial \eta }.$$
(32)

3 Applied methods

The methods applied besides numerical ones to solve the problem are as follows:

3.1 Finite elements methods

An approximate solution to boundary value issues for partial differential equations can be found using the finite element method (FEM). FEM divides a complex problem into smaller, more manageable pieces known as finite elements. In particular, the finite elements method models the entire problem by combining straightforward equations into a more extensive system of equations. Additionally, FEM uses variation techniques from the calculus of variations to minimize an associated error function and estimate a solution. FlexPDE Professional software is used to carry out these procedures.

3.2 Collocation method

Assume a differential operator D produces a function p from a function u [16]:

$$D\left(u\left(x\right)\right)=p\left(x\right).$$
(33)

We will use the function \(\widetilde{{\text{u}}}\), which is a series of independent functions, to estimate the value of u. Which is:

$$u\cong \widetilde{u}=\sum_{i=1}^{n}{C}_{i}{\mathrm{\varnothing }}_{i}.$$
(34)

By substituting \(\widetilde{u}\) into D, the operations are not concluded to be totally equal to \(p(x)\). Therefore, an error or residual will appear:

$$E\left(x\right)=R\left(x\right)=D\left(\widetilde{u}\left(x\right)\right)-p(x)\ne 0.$$
(35)

The fundamental idea behind the collocation is to force the residual to. Which is

$${\int }_{x}^{ }R\left(x\right){W}_{i}\left(x\right)=0 , i=\mathrm{1,2},\dots ,n.$$
(36)

where \({W}_{i}\), the total number of weight functions, is precisely equal to \({C}_{i}\), the total number of unidentified constants in u. The solution yields n equations for the undetermined constants \({C}_{i}\). The family of Dirac functions in the domain is where the weighting functions are derived. Consequently, \({W}_{i}\left(x\right)=\delta (x-{x}_{i})\). The Dirac function’s characteristic is

$$\delta \left( {x - x_{i} } \right) = \left\{ {\begin{array}{*{20}l} 1 & {if\, x = x_{i} } \\ 0 & {Otherwise} \\ \end{array} } \right.$$
(37)

And the function Eq. (31) must be equal to zero at particular points.

3.3 Akbari–Ganji’s method

Since nonlinear equations often do not have exact analytical answers, powerful and simple semi-analytical methods can be used to solve them. The Akbari-Ganji method (AGM) is a relatively new technique in this field, which requires only an elementary hypothetical answer that satisfies the initial and boundary conditions of the equations, the governing equations and their derivatives, and the boundary conditions of the problem to solve complex equations.

The first step assumes a function that includes unknown constant coefficients as the final answer. Then, a system of equations will be obtained by applying boundary conditions to the governing equations and their derivatives, and solving them will lead to finding the unknowns. In general, the original idea of this method can be mathematically shown as follows [28]:

$$P:f\left(u,{u}^{\mathrm{^{\prime}}},{u}^{\mathrm{^{\prime}}\mathrm{^{\prime}}},\dots ,{u}^{\left({\text{m}}\right)}\right)=0; \,\, u=u\left(x\right).$$
(38)

The boundary conditions will be used as follows:

$$\left\{\begin{array}{c}u\left(x\right)={u}_{0 }, {u}^{\mathrm{^{\prime}}}\left(x\right)={u}_{1} , . . ., {u}^{\left(m-1\right)}\left(x\right)={u}_{m-1 } at x=0,\\ u\left(x\right)={u}_{{L}_{0} }, {u}^{\mathrm{^{\prime}}}\left(x\right)={u}_{{L}_{1}} , . . . , {u}^{\left(m-1\right)}\left(x\right)={u}_{{L}_{m-1}} at x=L.\end{array}\right.$$
(39)

The solution to the problem is considered as a polynomial of degree n with unknown constant coefficients:

$${\text{u}}\left({\text{x}}\right)={a}_{0}+{a}_{1}{x}^{1}+{a}_{2}{x}^{2}+ \cdots +{a}_{n}{x}^{n}={\sum }_{i=0}^{n}{a}_{i}{x}^{i}.$$
(40)

This equation determined that the final solution was more accurate the more sentences in the above series there were.

In a polynomial of degree n, the coefficients are found using n + 1 unknown coefficients, which requires the same number of equations. The following boundary conditions lead to these equations at the beginning of the interval:

$$\left\{\begin{array}{l}u\left(0\right)= {a}_{0}={u}_{0}\\ u^{\prime}\left(0\right)= {a}_{1}={u}_{1}\\ u^{{\prime}{\prime}}\left(0\right)= {a}_{2}={u}_{2}\\ \\ \ldots \\ \ldots \end{array}\right.$$
(41)

And these at the end:

$$\left\{\begin{array}{l}u\left(L\right)= {a}_{0}+ {a}_{1}L+ {a}_{2}{L}^{2}+ \cdots +{a}_{n}{L}^{n}={u}_{{L}_{0}} \\ {u}^{\mathrm{^{\prime}}}(L)= {a}_{1}+ {2a}_{2}L+ {3a}_{3}{L}^{2}+ \cdots +n{a}_{n}{L}^{n-1}={u}_{{L}_{1}} \\ u^{{\prime}{\prime}}\left(L\right)= {2a}_{2}+ {6a}_{3}L+ {12a}_{4}{L}^{2}+\cdots+{n(n-1)a}_{n}{L}^{n-2}={u}_{{L}_{2}}\\ \ldots \\ \ldots \\ \ldots \end{array}\right.$$
(42)

To obtain the final coefficients and create a system of n + 1 equations and the same number of unknowns, we will first replace the series (40) in Eq. (38). The equation and its derivatives will then be placed at the boundary points to create new equations.

$$\begin{gathered} P:\left\{ {\begin{array}{*{20}{l}} {f\left( {u\left( 0 \right),u^\prime \left( 0 \right),...,{u^{\left( {m - 1} \right)}}\left( 0 \right)} \right)} \\ {f\left( {u\left( L \right),u^\prime \left( L \right),...,{u^{\left( {m - 1} \right)}}(L)} \right)} \end{array}} \right. \hfill \\ P^\prime :\left\{ {\begin{array}{*{20}{l}} {f\left( {u^\prime \left( 0 \right),u^{\prime \prime} \left( 0 \right),...,{u^{\left( {m - 1} \right)}}\left( 0 \right)} \right)} \\ {f\left( {u\prime (L),u^{\prime \prime} (L),...,{u^{\left( {m - 1} \right)}}(L)} \right)} \end{array}} \right. \hfill \\ P^{\prime \prime} :\left\{ {\begin{array}{*{20}{l}} {f\left( {u^{\prime \prime} \left( 0 \right),u^{\prime \prime \prime} \left( 0 \right),...,{u^{\left( {m - 1} \right)}}\left( 0 \right)} \right)} \\ {f\left( {u^{\prime \prime} (L),u^{\prime \prime \prime} (L),...,{u^{\left( {m - 1} \right)}}(L)} \right)} \end{array}} \right. \hfill \\ \ldots \hfill \\ \end{gathered}$$
(43)

Finally, the solution problems are accomplished by series constant coefficients.

4 Implementation of methods

The solution of analytical methods to the problem is as follows:

4.1 Collocation method

Consider the trial functions as:

$$\widetilde{\theta }\left(\upeta \right)={C}_{0}+{C}_{1}\upeta +{C}_{2}{\upeta }^{2}+\dots +{C}_{10}{\upeta }^{10},$$
(44)
$$\widetilde{\phi }\left(\upeta \right)={D}_{0}+{D}_{1}\upeta +{D}_{2}{\upeta }^{2}+\dots +{D}_{10}{\upeta }^{10}.$$
(45)

Residual functions are found as

$${R}_{1}\left({C}_{0},{C}_{1},{C}_{2},\dots ,{C}_{10},\upeta \right)=\frac{{\partial }^{2}\theta }{{\partial \eta }^{2}}+{N}_{b}\frac{\partial \theta }{\partial \eta }\frac{\partial \phi }{\partial \eta }+{N}_{t}{\left(\frac{\partial \theta }{\partial \eta }\right)}^{2},$$
(46)
$${R}_{2}\left({D}_{0},{D}_{1},{D}_{2},\dots ,{D}_{10},\upeta \right)=\frac{{\partial }^{2}\phi }{{\partial \eta }^{2}}+\frac{{N}_{t}}{{N}_{b}}\frac{{\partial }^{2}\theta }{\partial {\eta }^{2}}.$$
(47)

Furthermore, the residual must be approximated to zero. So, 9 different points in the range of \(r\in [\mathrm{0,1}]\) should be selected, as follow:

$${\upeta }_{1}=0, {\upeta }_{2}=1/8, {\upeta }_{3}=2/8, {\upeta }_{4}=3/8, {\upeta }_{5}=4/8, {\upeta }_{6}=5/8, {\upeta }_{7}=6/8, {\upeta }_{8}=7/8, {\upeta }_{9}=1.$$
(48)

These points are substituted in the residual functions, and a set of 9 equations and 11 unknown coefficients are achieved for each function (\(\widetilde{\theta }\) and \(\widetilde{\phi }\)). The boundary conditions are used in these equations, and all unknown coefficients determine the problem’s solution.

For a specific case, when \({N}_{t}=1, {N}_{b}=1, {Gr}_{t}=1, {Gr}_{F}=1, \frac{\partial p}{\partial \xi }=1\) and \(h=1,\) the approximate solutions are as follows:

$$\theta \left(\upeta \right){ \, =\,-0.0001220760687\upeta }^{10}+{0.001220760687\upeta }^{9}{-0.006821000336\upeta }^{8}{+0.02893202827\upeta }^{7}{{+0.02893202827\upeta }^{7}-0.1025494521\upeta }^{6}{+0.3083059192\eta }^{5}{-0.7709856579\eta }^{4}{+1.542019035\eta }^{3}{-2.313034819\eta }^{2}+2.313035262\upeta .$$
(49)

and:

$${{\mathrm{\varnothing }\left(\upeta \right)=0.0001220760687\upeta }^{10}{-0.001220760687\upeta }^{9}{+0.006821000336\upeta }^{8}{-0.02893202827\upeta }^{7}+0.1025494521\upeta }^{6}{-0.3083059192\eta }^{5}{+0.7709856579\eta }^{4}{-1.542019035\eta }^{3}{+2.313034819\eta }^{2}-0.313035262\upeta .$$
(50)

Using Eq. (15), the normalized velocity profile will be obtained:

$$u(\upeta ){=0.000001849637404\upeta }^{12}{-0.00002219564885\upeta }^{11}+{{0.0001515777852\upeta }^{10}{-0.000803667452\upeta }^{9}{+0.003662480432\upeta }^{8}{-0.01468123424\upeta }^{7}+0.05139904387\upeta }^{6}{-0.1542019035\eta }^{5}{+0.3855058032\eta }^{4}{-0.4376784207\eta }^{3}{+0.5\eta }^{2}-0.3333333334.$$
(51)

4.2 Akbari–Ganji’s method

The final solution to the problem is supposed to be polynomials with constant coefficients.

$$\widetilde{\theta }\left(\upeta \right)={C}_{0}+{C}_{1}\upeta +{C}_{2}{\upeta }^{2}+\dots +{C}_{10}{\upeta }^{10},$$
(52)
$$\widetilde{\phi }\left(\upeta \right)={D}_{0}+{D}_{1}\upeta +{D}_{2}{\upeta }^{2}+\dots +{D}_{10}{\upeta }^{10}.$$
(53)

Two equations (\(\widetilde{\theta }\) and \(\widetilde{\phi }\)) are produced for each function when the problem's boundary conditions are applied to the abovementioned series. Nine new equations are needed to determine all the unknown coefficients.

The extra equations and the margin conditions applied to the leading equations and their upper-order derivatives will be secured. By solving these equations, one may determine all of the constant coefficients of the series, which are the solutions to the issue.

For a specific case, when \({N}_{t}=1, {N}_{b}=1, {Gr}_{t}=1, {Gr}_{F}=1, \frac{\partial p}{\partial \xi }=1\) and \(h=1,\) the approximate solutions are as follows:

$$\theta \left(\upeta \right){-0.0003263707572\eta }^{10}{+0.001631853786\eta }^{9}{-0.007343342037\eta }^{8}{+0.02937336815\eta }^{7}-{0.1028067885\eta }^{6}+{0.3084203655\eta }^{5}-{0.7710509138\eta }^{4}+{1.542101828\eta }^{3}-{2.313152742\eta }^{2}+2.313152742\eta .$$
(54)

and:

$${\phi \left(\upeta \right)\,=\,0.0003263707572\upeta }^{10}{-0.001631853789\eta }^{9}{+0.007343342037\eta }^{8}-{0.02937336815\eta }^{7}+{0.1028067885\eta }^{6}-{0.3084203655\eta }^{5}+{0.7710509138\eta }^{4}-{1.542101828\eta }^{3}+{2.313152742\eta }^{2}-2.313152742\eta .$$
(55)

Using Eq. (15), the normalized velocity profile will be obtained:

$$u\left(\upeta \right){ \, =\,\,0.000004945011472\upeta }^{12}{-0.00002967006884\upeta }^{11}+{{0.0001631853786\upeta }^{10}{-0.0008159268931\upeta }^{9}{+0.003671671018\upeta }^{8}-{0.01468668407\upeta }^{7}+0.05140339427\upeta }^{6}-{0.1542101828\eta }^{5}+{0.3855254570\eta }^{4}-{0.4377175807\eta }^{3}+{0.5\eta }^{2}-0.3333086081.$$
(56)

5 Results

The peristaltic flow and nanofluids in medication transportation systems with heat exchange are examined in this study. The combined efforts of CM, AGM, and FEM solve the problem. The results and numerical solutions have been compared to validate the solutions and guarantee the precision of the results. The numerical solution used is the 4th-order Runge–Kutta, which uses the Maple package.

The temperature, nanoparticle fraction, and velocity profiles obtained from each method are plotted in Tables 1, 2, 3 and Fig. 2, which show a satisfactory closeness between the methods used in this research and the numerical one. The tables also show that the CM is more accurate than the AGM and FEM.

Table 1 Comparing the FEM, CM, and AGM solutions versus numerical results for \(\theta (\eta ),\) assuming \({N}_{t}={N}_{b}=1\)
Full size table
Table 2 Comparing the FEM, CM, and AGM solutions versus numerical results for \(\phi (\eta ),\) assuming \({N}_{t}={N}_{b}=1\)
Full size table
Table 3 Comparing the FEM, CM, and AGM solutions versus numerical results for \(u(\eta ),\) assuming \({Gr}_{T}={Gr}_{F}=1\)
Full size table
Fig. 2
figure 2

a Comparing FEM, CM, and AGM arrangements versus numerical results of θ(η) assuming \({N}_{t}={N}_{b}=1\). b Comparing FEM, CM, and AGM arrangements versus numerical results of ϕ(η) assuming \({N}_{t}={N}_{b}=1\). c Comparing FEM, CM, and AGM arrangements versus numerical results of u(η) assuming \({N}_{t}={N}_{b}=1\)

Full size image

Equations (17) and (18), showing the conservation of energy and species, introduce the Brownian movement parameter,\({N}_{b}\), via the mixed derivative term,\({N}_{b}\).∂θ/∂η.∂ϕ/∂η in the former and the second-order temperature derivative (\({N}_{t}\)/\({N}_{b}\))(∂2θ/∂η2) in the latter. \({N}_{b}\), is a crucial variable that affects species diffusion. The regime is heated, as shown in Fig. 3a and b, with an increase in the thermophoresis (\({N}_{t}\)) and Brownian movement parameter (\({N}_{b}\)) on the temperature profile. The increase of these two parameters causes the temperature to increase in the area closer to the channel axis in a similar way. However, the slope of the graphs at the end shows that for η > 1, the fluid response is different. By approaching the wall of the channel at the bulge, Brownian motion and thermophoresis tend to decrease the fluid temperature and cool the regime. In fact, thermophoresis is the migration of nanoparticles in the direction of reducing the temperature gradient, and its role in the temperature field across the channel cannot be ignored.

Fig. 3
figure 3

a Temperature distribution (θ(η)) for different values of Brownian movement parameter (\({N}_{b}\)) assuming \({N}_{t}=1\). b Temperature distribution (θ(η)) for different values of thermophoresis parameter (\({N}_{t}\)) assuming \({N}_{b}=1\)

Full size image

The nanoparticle fraction profile \(\phi \left(\eta \right)\) is shown to decrease as the Brownian movement parameter (\({N}_{b}\)) is increased in Fig. 4a. Nanofluids behave more like fluids than traditional solid–liquid mixtures, which suspend larger particles with millimeter or micrometer scales. A nanofluid is inherently a two-phase fluid, and the random motion of suspended particles accelerates the rate of energy exchange while reducing the concentration in the flow regime. The impact of the thermophoretic parameter (\({N}_{t}\)) on \(\phi \left(\eta \right)\) is depicted in Fig. 4b. The graph shows that the nanoparticle fraction profile decreases as the thermophoresis parameter increases. The large drop observed in the concentration profile, with the increase of the thermophoresis parameter, leads to an increase in the range after \(\eta\) > 1, when the profiles experience strong divergence while maintaining the slope trend of the graphs.

Fig. 4
figure 4

a Nanoparticle fraction profiles (ϕ(η)) for different values of Brownian movement parameter (\({N}_{b}\)) assuming \({N}_{t}=1\). b Nanoparticle fraction profiles (ϕ(η)) for distinctive values of thermophoresis parameter (\({N}_{t}\)) assuming \({N}_{b}=1\)

Full size image

Brownian motion parameters impact the axial velocity (\(u\)), as shown in Fig. 5. These data demonstrate that the maximum value of velocities occurs at the channel center without exception and slowly decreases to zero, reaching the wall’s periphery. An increase in \({N}_{b}\) and \({N}_{t}\) decreases the velocity, which opposes the velocity of the return flow and becomes more positive, as shown in Fig. 5a and b. As a result, the flow is slowed down by thermophoresis and Brownian motion.

Fig. 5
figure 5

a Velocity distribution (u(η)) for different values of Brownian movement parameter \(({N}_{b})\) assuming \({N}_{t}={Gr}_{F}={Gr}_{T}=1\). b Velocity distribution (u(η)) for different values of thermophoresis parameter \(({N}_{t})\) assuming \({N}_{b}={Gr}_{F}={Gr}_{T}=1\). c Velocity distribution (u(η)) for different values of \({Gr}_{T}\) assuming \({N}_{t}={N}_{b}={Gr}_{F}=1\). d Velocity distribution (u(η)) for different values of \({Gr}_{F} \mathrm{assuming }{N}_{t}={N}_{b}={Gr}_{T}=1\). e Velocity distribution (u(η)) for Newtonian fluid and nano-fluid assuming \({N}_{b}={N}_{t}=1\)

Full size image

Figure 5c and d have shown effects on the velocity profile of the species Grashof number (\({Gr}_{F}\)) and the thermal Grashof number (\({Gr}_{T}\)), respectively. The thermal Grashof parameter displays the balance between viscous hydrodynamic force and thermal buoyancy force. For \({Gr}_{T}\)<1, the peristaltic regime is dominated by viscous and for \({Gr}_{T}\)>1 is dominated by buoyancy forces. When \({Gr}_{T}\) =1, both thermal buoyancy and viscous forces are equal in magnitude. As shown in Fig. 5c, the velocity measures decline as the thermal Grashof number increases, and the profiles follow uniform patterns.

The species Grashof number, \({Gr}_{F}\), acts opposite to the thermal Grashof number, as shown in Fig. 5d. An increase in \({Gr}_{F}\) with an increase in the magnitude of the axial velocity, intensifies the return flow. \({Gr}_{F}\) represents the ratio of species buoyancy force to viscous hydrodynamic force.

In Fig. 5e, the results for a Newtonian fluid (\({Gr}_{F}\)=\({Gr}_{T}\)=0) and a nanofluid fluid for the case of buoyancy forces equal to viscous force (\({Gr}_{F}\)=\({Gr}_{T}\)=1) are compared. It demonstrates that, when compared to a Newtonian fluid, nanofluids exhibit less backflow.

For different values of Brownian movement parameters, thermophoresis parameters, and Grashof numbers, changes in pressure difference along one wavelength (\(\Delta P\)) considering the mean flow rate (\(\overline{Q }\)) is shown in Fig. 6a–e. Linear distributions are observed. It is shown that as the Brownian motion parameter is increased, the pressure difference decreases throughout the region (\(\Delta P\)<0), the free pumping region (\(\Delta P\)=0), and the co-pumping region (\(\Delta P\)>0). An essential characteristic of nanofluid drug delivery systems is this effect. According to Fig. 6b, the pressure difference increases as the thermophoresis parameter increases. In both situations, this pattern holds true regardless of the averaged volume flow rate (\(\overline{Q }\)). On the other hand, at all operating flow rates, a pressure difference in nano-peristaltic pumps can be sustained by increasing the Brownian diffusion or thermophoretic effect. Increased pressure difference increases both Grashof numbers, as shown in Fig. 6c and d. According to Fig. 6e, nanofluids exhibit a noticeably greater difference in pressure than Newtonian fluids. This property thus supports nanofluids’ superiority over Newtonian fluids in real-world medical pumps for medical transportation systems. It shows that when a magnetic field is applied to the flow field, a higher pressure gradient is required for the current to flow through the channel. This result indicates that the fluid pressure can be controlled by applying the appropriate magnetic field strength. This phenomenon is useful for controlling excessive bleeding during surgery and critical operations.

Fig. 6
figure 6

The pressure changes due to mean volume flow rate \((\overline{Q })\) changes for a different values of Brownian motion parameter \(({N}_{t})\) when \({N}_{b}={Gr}_{F}={Gr}_{T}=1\); b different values of thermophoresis parameter \(({N}_{b})\) when \({N}_{t}={Gr}_{F}={Gr}_{T}=1\); c different values of \({Gr}_{F}\) when \({N}_{t}={N}_{b}={Gr}_{T}=1\); d different values of \({Gr}_{T}\) when \({N}_{t}={N}_{b}={Gr}_{F}=1\); e Newtonian fluid and nano-fluid when \({N}_{t}={N}_{b}=1\)

Full size image

The effects of the Brownian movement (\({N}_{b}\)), thermophoresis (\({N}_{t}\)), thermal Grashof number (\({Gr}_{T}\)), and basic-density Grashof number (\({Gr}_{F}\)) on trapping are shown in Fig. 7a–f. There are six illustrated streamlined distributions. A different variation of a single parameter has been used for each set. In every situation, the average volume flow rate (\(\overline{Q }\)) is constrained at 0.6, and the amplitude ratio (ω) is stabilized at 0.5. Under certain circumstances, the streamlines along the wave frame’s center line are divided to contain a bolus of fluid particles moving along closed streamlines. Fung and Yih further described this phenomenon as trapping, a feature of peristaltic motion [1]. These physical phenomena may be responsible for blood thrombus formation and food bolus movement in the gastrointestinal tract. The concept of trapping on peristaltic pumping of fluid was introduced by Shapiro et al. [3]. This bolus moves at the same velocity as the wave because it is being held in place by the wave (celerity). According to Fig. 7a and b, the Grashof numbers (\({Gr}_{T} {\text{and}} {Gr}_{F}\)) went up from zero (vanishing buoyancy effects, which corresponds to the Newtonian case of Shapiro et al. [3]) to 0.1 and 0.01, respectively. The magnitude of trapped decreases as Grashof numbers increase.

Fig. 7
figure 7

Streamlines in the wave frame at a \(\omega =0.5, \overline{Q }=0.6, {N}_{b}=1,{N}_{t}=1, {Gr}_{T}=0,{Gr}_{F}=0\) b \(\omega =0.5, \overline{Q }=0.6, {N}_{b}=1,{N}_{t}=1, {Gr}_{T}=0.1,{Gr}_{F}=0.01\) c \(\omega =0.5, \overline{Q }=0.6, {N}_{b}=0.1,{N}_{t}=1, {Gr}_{T}=0,{Gr}_{F}=0\) d \(\omega =0.5, \overline{Q }=0.6, {N}_{b}=1,{N}_{t}=0.1, {Gr}_{T}=0.1,{Gr}_{F}=0.01\) e \(\omega =0.5, \overline{Q }=0.6, {N}_{b}=1,{N}_{t}=0.1, {Gr}_{T}=0.01,{Gr}_{F}=0.01\) f \(\omega =0.5, \overline{Q }=0.6, {N}_{b}=1,{N}_{t}=1, {Gr}_{T}=0.1,{Gr}_{F}=0.05\)

Full size image

It is shown in Fig. 7b and c that the Brownian motion parameter is reduced from 1 to 0.1. The dual boluses trapped in Fig. 7b are reduced to just one bolus in Fig. 7c, which is a significant change. Figure 7b and d showed that the magnitude of boluses slightly increased as the thermophoretic parameter, \({N}_{t}\), decreased from 1 to 0.1. The bolus size is amplified as the thermal Grashof number decreases from 1 to 0.01, as shown in Fig. 7b and e. Finally, Fig. 7b and f illustrated that with an increase in species Grashof number from 0.01 to 0.05, the dual blouse structure is greatly reduced compared with a single bolus. Therefore, nanofluid properties undoubtedly apply a major influence on peristaltic flow patterns.

The Nusselt number is presented in Fig. 8, together with the effects of the Brownian motion parameter (\({N}_{b}\)) and the thermophoresis parameter (\({N}_{t}\)). The Nusselt number decreases with the rise of both values. In addition, the Nusselt number decreases in the channel protrusions and has its highest value in the depressions.

Fig. 8
figure 8

Nusselt number Vs channel length for different a \({N}_{b}\) and b \({N}_{t}\)

Full size image

6 Discussion

The problem chosen for investigation in this study examines a phenomenon observed in many parts of the body, such as the digestive system, male reproductive system, fallopian tubes, bile duct, ureter, and esophagus. Its industrial applications include sanitary liquid transportation, corrosive liquid transportation, blood pumping in heart–lung equipment, novel drug delivery systems, and more. Therefore, to develop related industries and treat diseases, the importance of improving knowledge on this subject is undeniable. Other studies have been carried out in this area, some of which have been mentioned in the introduction. In the present study, we have tried to interpret the graphs and results from a physical point of view. After observing the influence of various parameters, the representation of streamlines is used to better show the shape of the flow in the channel and trapping phenomena, which is omitted in works such as [10, 11]. Two analytical methods are used to approximate the solution of the problem in addition to the numerical method, allowing the equation to be solved quickly and simply. Studies [9, 14] used only numerical methods, and [10] implemented analytical methods (ignoring the role of certain governing parameters). Finally, the changes of Nusselt number along the channel and by varying various parameters were investigated, which has not been addressed in previous studies.

7 Conclusion

The purpose of this paper is to approach the influence of nanofluid properties on flow shape and heat transfer in an axisymmetric sinusoidal channel. In addition to numerical methods (FEM and RK4) to solve the problem, the present study also includes effective analytical methods (CM and AGM) with the ability to approximate the solutions of the equations parametrically. Besides studying the role of various parameters on the velocity, temperature, pressure drop, and nanoparticle concentration functions, streamlines and the Nusselt number behavior along the channel were used to better understand the physics of the problem. Results show that an increase in thermophoresis or Brownian motion parameter leads to an increase in temperature and a decrease in fluid velocity. The role of these two in the changes in nanofluid concentration is different. The first has a direct effect, and the second has an inverse effect on it. The growth of the species Grashof number increases the velocity profile and pressure difference. The thermal Grashof number has the same behavior for the pressure difference and the opposite effect on the fluid velocity. Compared to Newtonian fluids, nanofluids tend to reduce backflow. Nanofluids exhibit a significant rise in pressure differential compared to Newtonian fluids, indicating that they are a more practical fluid for use in medical pumps for drug delivery systems. The Nusselt number fell as Brownian motion and thermophoretic parameters were increased. Additionally, along the channel, changes in the Nusselt number have an inverse relationship with the cross-sectional size of the tube. In this paper, the flow of nanofluid in a two-dimensional horizontal channel was investigated by neglecting the effects of gravity. Three-dimensional investigation of the channel and the effect of angling it in the presence of gravity can be ideas for future research.