1 Introduction

The term "Cross fluid" is normally used as generalized Newtonian fluid whose viscosity depends on shear rate. These fluids are very effective in numerous technological processes, chemical assessment, and industrial systems. Therefore, they have recently grown to be of excellent significance to researchers across the world. Hauswirth et al. [1] studied the impact of porosity in a fluid flow by using the cross model and detected the flow behavior in a new way. Megahed et al. [2] investigated stratified Cross fluid flow behavior by using porosity material with the influence of chemical reaction effect. Vali et al. [3] discussed mass and heat transfer by numerical modeling of cross flow, moreover, examined the energy exchange phenomena in liquid between a parallel plate. Sadaf et al. [4] used Cross mathematical formulation for studied Cilia flow analysis in a horizontal channel. Darvesh et al. [5] examined some important rheology aspects of cross flow in presence of inclined magnetized and variable thermal conductivity consequences. Awais et al. [6] studied thermophysical characteristics of MHD flow, with together effect of chemical reaction and energy dissipation by using cross mathematical model. Furthermore, to for deep investigation of these properties in research [7] radiative magnetohydrodynamic flow was considered over a parabolic surface in presence of activation energy. Ayub et al. [8] discussed the three-dimensional radiative cross fluid flow by focusing nonuniform heat sink/source and buoyancy effect for the Interpretation of high and low infinite shear rate viscosity. Akbar et al. [9] studied MHD Three-dimensional viscous flow together with dissipation and heat radiation. Khan et al. [10] studied MHD micropolar boundary layer flow and examined microstructural slip behavioral response. Hina et al. [11] made a numerical simulation of heat transfer phenomena in a circular cylinder by implementing the Cross mathematical model within fullest extent. Kostić and Oka [12] studied the flow measurement by using Cross mathematical model and put forwarded the idea of heat transfer in a flow. Mangrulkar et al., [13]. made a study of cross fluid flow as a heat exchanger and analyzed some notable features and made recent developments in heat transfer. Imran et al. [14] discussed Ellis’s fluid through in flexible channel in presence of slip effects and entropy generation and exposed the multiple facts. Furthermore, Li et al. [15] made an examination of dual effect of viscous dissipation and buoyancy force three dimensional MHD viscous flow. In particular, the role of heat transfer is a major area of study in the engineering disciplines including civil engineering, mechanical and chemical because of reaction kinetics, material selection, and machinery efficiency. Therefore, the necessary fundamental notions about the characteristics and uses of thermal energy transmission cannot be disregarded because they facilitate comprehension and boost energy transfer's efficiency. Several interesting facts are explored by many researchers worldwide [16,17,18,19,20,21,22,23,24,25,26,27].

The spectral relaxation method is a novel iterative technique that has proven to be especially useful and efficient for solving nonlinear boundary value problems with semi-infinite interval. Its enables user to explore the key facts and prominent characteristics of exponentially decaying flows. The process is founded on the Gauss–Seidel principle, which simplifies equation systems by merely altering their order of statement and solving them. The Gauss–Seidel methodology was utilized in an iteration process to partition and linearize the set of equations before applying the spectral relaxation technique. The controlling subsystems of the algorithm generate a sequence of discretized and solved linear differential equations with variable coefficients. Many researchers used the Spectral relaxation approach for the computational analysis of fluid flow behavior associated with the many engineering and industrial processes. Mosta [28] studied the boundary layer flow with similarity variable by using a novel iterative spectral relaxation scheme. A bivariate spectral relaxation technique for magnetohydrodynamic flow in porous media was discussed by Magagula et al. [29]. Haroon et al. [30] made a spectral relaxation computational analysis for unsteady Magnetohydrodynamics nanofluid flow over a stretching/shrinking surface in the presence of mixed convection. Darvesh et al. [31] examined the flow behavior of inclined magneto Carreau nanofluid by employing a spectral relaxation scheme along with Quadratic multiple regression model. For the numerical investigation of unsteady boundary layer flow Mosta et al. [32] used spectral Quasi linearization and Spectral relaxation jointly. Later Eldin et al. [33] discussed the Static point geometry of a Carreau nanofluid inclined magnetized dipole using a quadratic multiple regression scheme accompanied with spectral relaxation computational method. Ayub et al. [34] utilized the spectral iterative method and made the computational measurement of cross-nanofluid under the influence of inclined magnetic and velocity slip stagnation effects. Moreover, the Unsteady flow subjected with free convective boundary layer over a stretching surface through spectral relaxation approach was determined by Gangadhar et al. [35]. Furthermore, many ongoing theories in this realm aims to optimize the captivating flow computations and address practical issues to make this technology more widespread [36,37,38,39].

In the domain of fluid dynamics, the term "double diffusive" refers to a type of convection that is fueled by two separate density gradients that have divergent diffusion rates. Fluid convection is caused by fluctuations in internal density brought on by gravity. In medicine, it can also mean the haphazard mixing of molecules in the case of distinguished substances because of thermal type motion having randomness; its change in terms of rate is linked with substances concentration and it its amplification because of a magnification in temperature. Antigens and antibodies can be examined with it. Antibodies and antigens like immunoglobulins and extractable nuclear antigens are detected, recognized, and quantified using this technique. Shoaib et al. [40] used the Levenberg Marquardt ANN scheme and made a comprehensive analysis of double-diffusive flow of nanofluid double-diffusive flow. Islam et al. [41] discussed the impacts of Thermophoresis, Brownian motion, and Chemical Reactivity in a fluid flow across an Infinite Vertical Plate. Asogwa et al. [42] pondered double diffusive and convection cross diffusion and their impact in the case of Casson model type liquid across a Riga plate embedded with heat releasing phenomenon. Shoaib et al. [43] studied the double-diffusive phenomenon for nanofluid flow over an inclined plane and explored some key features by using neural network with AI-based Levenberg–Marquardt scheme. The impact of porosity and stratification having nonlinear type behavior on mixed convective on fluid was interrogated by Ram et al. [44]. To study the three-dimensional nanofluid flow Sohail et al. [45] made a significant contribution in the theory of double diffusion by employing a novel optimal Homotopy analysis technique. Yadav et al. [46] looked the impacts of chemical processes with dual role of Soret and Dufour type diffusion phenomena on fluid having viscoelastic type nature soaked in porous medium. Moreover, Ramchandraiah et al. [47] scrutinized Soret as well as Dufour type diffusion for a in a bi dispersive porous medium with Coriolis influence. Patel [48] considered Casson fluid flow model-based for the investigation of the influence of magnetic on stagnated Carreau fluid immersed in a porous media, which was subjected with non-linear thermal radiation and mixed convection. Parker et al. [49] investigated the possibility of quickly determining capacity of heat, thermal conductivity as well as heat diffusivity, in a fluid flow. Concurrent assessment of liquids' thermal conductivity and thermal diffusivity using the transient hot-wire technique was conducted by Nagasaka and Nagashima [50]. Karimi-Fard et al. [51] discussed the double-diffusive convection through a non-Darcian flow in a porous media. Patel and Harshad [52] investigated the effects of cross diffusion accompanied with heat generation on mixed convective MHD Casson fluid flow through porous media with non-linear heat radiation. Wang et al. [53], made an analysis of heat transport mechanisms and thermal conductivity and diffusivity measurements of nanofluids using the 3ω method. Subsequently, the effects of cross diffusion via different permeable material with several aspects and consequences such as thermal transport, mixed convection, magneto hydrodynamic phenomena, double diffusion, viscous dissipation etc. were examined in the following research [54,55,56,57]. After a thorough analysis and comprehension of multiple studies, it was determined that no research has yet been done to investigate the thermal diffusivity of an inclined magnetized Cross fluid with temperature-dependent thermal conductivity. In this current research the author took the advantage of a novel spectral relaxation scheme and studied the numerical investigation of thermal diffusivity of an inclined magnetized Cross fluid with temperature-dependent thermal conductivity, and many other dimensionless parameters that’s effects the heat transferring and have an impact on velocity and temperature profile of the flow behavior in presence of inclined magnetic consequences.

1.1 Novelty

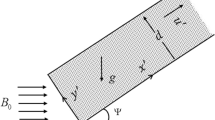
The deep analysis of thermal diffusivity is very essential because it governs rate of heat within a fluid and thus very vital for optimizing and predicting the heat transport processes in many fields, ranging from biomedical engineering to environmental studies and various industrial applications. Therefore, the current study focuses on thermal diffusivity for a fluid flow under the influence of temperature-dependent thermal conductivity and inclined magnetic consequences. Cross mathematical model is used to formulate the governing flow equations of fluid and a computationally efficient spectral relaxation technique is employed for the numerical outcomes. The results of this investigation shed light on how non-Newtonian fluids behave when exposed to temperature changes and magnetic fields and useful and provides insights into the analysis and design of various systems involving thermal transport phenomena (Fig. 1).

Fig. 1
figure 1

Flow behavior

Full size image

1.1.1 Problem formulation

Two-dimensional fluid is moving subjected to an expandable surface having extending rate uw = ax, where a > 0 in this case represents the rate at which sheet is expanding. Porous media is considered to investigate the effect of fluid moving through the pores in the light of Darcy law and permeability of the medium. Magnetic field phenomenon is considered and applied normal direction to the flow direction. The symbols like T, Tw, and \(T_{\infty }\) indicates temperature, wall as well as free stream temperature and moreover C, Cw, and \(C_{\infty }\) reflect concentration, wall as well as free stream respectively. Important aspects like thermophoresis and Brownian diffusion effects are extensively captured in the case of Buongiorno nanofluid model. The vector form of governing system along with there are modified form are setup by consideration of [5, 8, 46] and [49].

$$\nabla .V = 0$$
(1)
$$\rho \frac{dV}{{dt}} = div\left( \tau \right) + b$$
(2)
$$\left( {V.\nabla } \right)T = \alpha_{f} \nabla .\left( {\nabla T} \right)$$
(3)

Equations 4–7 are obtained by applying the second law of thermodynamics, the law of conservation of momentum, and Fick’s law in terms of diffusion. The modeled system of equation under the application of boundary layer theory and above-mentioned assumptions are enumerated below.

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0,$$
(4)
$$\begin{gathered} u\left( {\frac{\partial u}{{\partial x}}} \right) + v\left( {\frac{\partial u}{{\partial y}}} \right) = \left( {\frac{\mu }{\rho }} \right)\frac{{\partial^{2} u}}{{\partial y^{2} }}\left[ {\left( {\left( {\Gamma \frac{\partial u}{{\partial y}}} \right)^{n} + 1} \right)^{ - 1} } \right] - \left( {\frac{\mu }{\rho }} \right)\left( {\frac{\partial u}{{\partial y}}} \right)^{n} \frac{{\partial^{2} u}}{{\partial y^{2} }}\left[ {1 + \left( {\Gamma \frac{\partial u}{{\partial y}}} \right)^{n} } \right]^{ - 2} \Gamma^{n} n + \hfill \\ \gamma g\left( {T_{1} - T_{2} } \right) - u\left( {\frac{v}{{K_{1} }} + \frac{\sigma }{\rho }\left( {\sin^{2} (\omega )B_{0}^{2} } \right)} \right), \hfill \\ \end{gathered}$$
(5)
$$\left( {u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)T = \frac{1}{{\rho c_{p} }}\left( {\frac{\partial }{\partial y}\left( {k\left( T \right)} \right)\frac{\partial T}{{\partial y}}} \right) + D_{TC} \frac{{\partial^{2} C}}{{\partial y^{2} }},$$
(6)
$$\left( {u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)C = D_{SM} \frac{{\partial^{2} C}}{{\partial y^{2} }} + D_{CT} \frac{{\partial^{2} T}}{{\partial y^{2} }},$$
(7)

The boundary constraints for the above set of Eqs. (5–7) are stated in eqtn.8 below.

$$\begin{gathered} \left. \begin{gathered} u = u_{w} = ax, \hfill \\ v = v_{w} , \hfill \\ C = C_{w} \;and\,T = T_{w} \hfill \\ \end{gathered} \right\}\,at\,y = 0\,\,and\,\left. \begin{gathered} u \to 0,\, \hfill \\ T \to T_{\infty } , \hfill \\ C \to C_{\infty } \hfill \\ \end{gathered} \right\}\,as\,y \to \infty . \hfill \\ \;\;\; \hfill \\ \end{gathered}$$
(8)

While the expression regarding temperature-based heat conduction is premeditated by.

$$k\left( T \right) \, = k^{ * } \left( {1 + \beta \left( {\frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }}} \right)} \right)$$
(9)

The following similarity variables are considered for the transformation purpose.

$$\begin{gathered} \eta = \sqrt {\frac{a}{v}y,} \quad \psi = \sqrt {av} xf\left( \eta \right) \hfill \\ T - T_{\infty } = \theta \left( {T_{w} - T_{\infty } } \right)\, = ,\,C - C_{\infty } = \phi \left( {C_{w} - C_{\infty } .} \right) \hfill \\ \end{gathered}$$
(10)

After the utilization transformations displayed above, Eqs. (5–6) together with (7) are enumerated underneath.

$$\begin{gathered} \left( {1 + \left( {wef^{\prime\prime}} \right)^{n} } \right)^{2} = \left[ {\left( {1 - \left( {n - 1} \right)\left( {wef^{\prime\prime}} \right)^{n} } \right)} \right]f^{\prime\prime\prime} \hfill \\ + \lambda^{*} \theta - f^{{\prime}{2}} - ff^{\prime\prime} + \left( {\sin^{2} (\omega )M^{2} + \lambda } \right)f^{\prime}, \hfill \\ \end{gathered}$$
(11)
$$\theta^{\prime\prime} + \beta \left( {\theta \theta^{\prime\prime} + \left( {\theta^{\prime}} \right)^{2} + \Pr \left( {f\theta^{\prime} + N_{d} \phi^{\prime\prime}} \right)} \right) = 0,$$
(12)
$$\phi^{\prime\prime} + Le\left( {f\phi^{\prime}} \right) + L_{d} \theta^{\prime\prime} = 0,$$
(13)
$$\begin{gathered} f{\prime} \left( \eta \right) = 1,\,f\left( \eta \right) = S,\,\,\theta \left( \eta \right) = 1,\,\,at\,\,\eta = 0, \hfill \\ f{\prime} \left( \eta \right) \to 0,\,\,\theta \left( \eta \right) \to 0,\,\,\phi \left( \eta \right) \to 0,\,\,as\,\,\eta \to \infty . \hfill \\ \end{gathered}$$
(14)

Dimensionless sundry parameters in above equations are presented in tabular form mentioned below.

\(M^{2} = \frac{{\sigma B_{0}^{2} }}{\rho a}\)

\(Le = \frac{v}{{D_{SM} }}\)

\(Pr = \frac{{\mu c_{p} }}{{K^{*} }}\)

\(S = \frac{{ - v_{w} }}{{\sqrt {av} }}\)

\(\lambda = \frac{c}{{aK_{1} }}\)

\(\lambda * = \frac{{g\beta_{f} (T_{2} - T_{m} )}}{{u_{w}^{2} }}\)

\(Nd = \frac{{D_{TC} \left( {C_{w} - C_{\infty } } \right)}}{{v(T_{w} - T_{\infty } )}}\)

\(Ld = \frac{{D_{CT} \left( {T_{w} - T_{\infty } } \right)}}{{D_{SM} \left( {C_{w} - C_{\infty } } \right)}}\)

A few Significant physical quantities such as heat, mass delivery rate, and drag phenomenon are provided by.

$$C_{f} = - \frac{{\tau_{w} }}{{\rho \left( {u_{w}} \right)^{2} }},\,Nu_{x} = \frac{{xq_{w} }}{{k\left( {T_{w} - T_{\infty } } \right)}},\,\,Sh_{x} = \frac{{sh_{m} }}{{D_{SM} \left( {C_{w} - C_{\infty } } \right)}}.$$
(15)

Here tw as well as qw are expressed as below.

$$\tau_{w} = \mu \left( {\frac{\partial u}{{\partial y}} + \frac{1}{2}\left( {n - 1} \right)\Gamma^{2} \left( {\frac{\partial u}{{\partial y}}} \right)^{3} } \right),\,q_{w} = - k\frac{\partial T}{{\partial y}},\,h_{m} = - D_{SM} \frac{\partial C}{{\partial y}}.$$
(16)

Dimensionless form of these quantities is.

$$\begin{gathered} \left( {{\text{Re}}_{x} } \right)^{1/2} = \left( {f^{\prime\prime}\left( 0 \right) + \frac{1}{2}\left( {We} \right)^{2} \left( {f^{\prime\prime\prime}\left( 0 \right)} \right)^{3} } \right), \hfill \\ Nu_{x} /\left( {{\text{Re}}_{x} } \right)^{1/2} = - \theta^{\prime}\left( 0 \right), \hfill \\ Sh_{x} /\left( {{\text{Re}}_{x} } \right)^{1/2} = - \phi^{\prime}\left( 0 \right). \hfill \\ \end{gathered}$$
(17)

Symbol \(Re_{x} = \frac{{u_{w}x}}{v_{f}}\) is local Reynolds number.

1.2 Spectral relaxation technique

Different advancement in computational schemes and algorithms continue to drive improvements in numerical simulations for fluid dynamics [54,55,56,57,58,59,60]. In many circumstances a combination of methods is used to explore the different aspects of complex fluid dynamics issues, therefore the choice of a numerical scheme always depends on the specific characteristics of the problem. One of the most effective and popular technique is Spectral relaxation strategy. This method is simply known as (SRT) is an iterative technique, that has shown to be very practical and useful to obtain the solutions of nonlinear boundary value problems with semi-infinite interval definitions and some exponentially decaying flow features. This technique has some prominent properties as well as few notable characteristics that’s why can be more adoptable very smoothly in various situations due to low costly, less complex to use than finite element techniques, high accuracy, and has smooth solutions and are helpful in basic domains. This SRT scheme can be more widely used and has a few notable characteristics.

1.3 High accuracy with good convergence

The SRT is known for their high accuracy in approximating solutions, as well as especially converge exponentially fast, leading to very accurate results.

1.4 Suitability for periodic problems

The method used Chebyshev or Fourier basis functions therefore this Spectral relaxation method is well-suited for problems with periodic boundary conditions.

1.5 Global approximation

This method uses global approximation functions This can be advantageous for problems with smooth or periodic solutions unlike finite difference or finite element methods.

1.6 Simplicity of implementation

This technique is relatively easy and simple to implement, making them accessible for solving a wide range of problems.

1.7 Numerical techniques in MATLAB: fundamental to advanced concepts

There are a few interesting and visually appealing steps in the process. First, the Gauss–Seidel idea of decoupling systems of equations is imported to obtain the technique, which consists of just rewriting the equations in a different order and solving them one after the other. For the current system of equation, the SRT is being used to solve the set equations from (11–13) together with their associated boundary conditions. Then by using in the MATLAB a SRM code is generated. Finally, the SRM algorithm is adopted to sought out the solutions of our model equations of the current problems. The adopted SRM algorithm controlling subsystems produce a collection of linear differential equations.

Step 1: let for iteration we fix.

$$F = F_{r + 1} ,\,\,\,\,\,\,\,\,\theta = \theta_{r + 1} ,\,\,\,\,\phi = \phi_{r + 1} ,and\,\,\,\,\vartheta = \vartheta_{r + 1}$$
(18)

Equations (11–13) take the form.

$$\left( {1 + \left( {wef^{\prime\prime}_{r + 1} } \right)^{n} } \right)^{2} = \left[ {\left( {1 - \left( {n - 1} \right)\left( {wef^{\prime\prime}_{r + 1} } \right)^{n} } \right)} \right]f^{\prime\prime\prime}_{r + 1} + \lambda^{*} \theta_{r + 1} - f^{{\prime}{2}}_{r + 1} - f_{r + 1} f^{\prime\prime}_{r + 1} + \left( {\sin^{2} (\omega )M^{2} + \lambda } \right)f^{\prime}_{r + 1} ,$$
(19)
$$\theta^{\prime\prime}_{r + 1} + \beta \left( {\theta_{r + 1} \theta^{\prime\prime}_{r + 1} + \left( {\theta^{\prime}_{r + 1} } \right)^{2} + \Pr \left( {f_{r + 1} \theta^{\prime}_{r + 1} + N_{d} \phi_{r + 1}^{\prime \prime } } \right)} \right) = 0,$$
(20)
$$\phi^{\prime\prime}_{r + 1} + Le\left( {f_{r + 1} \phi^{\prime}_{r + 1} } \right) + L_{r + 1d} \theta^{\prime\prime}_{r + 1} = 0,$$
(21)
$$\begin{gathered} f^{\prime}_{r + 1} \left( \eta \right) = 1,\,f_{r + 1} \left( \eta \right) = S,\,\,\theta_{r + 1} \left( \eta \right) = 1,\,\,at\,\,\eta = 0, \hfill \\ f^{\prime}_{r + 1} \left( \eta \right) \to 0,\,\,\theta_{r + 1} \left( \eta \right) \to 0,\,\,\phi_{r + 1} \left( \eta \right) \to 0,\,\,as\,\,\eta \to \infty . \hfill \\ \end{gathered}$$
(22)

Step 2: let for iteration we fix.

$$F^{\prime}_{r + 1} = S,\,F_{r + 1} (0) = 0$$
(23)
$$\left( {1 + \left( {wef^{\prime\prime}_{r + 1} } \right)^{n} } \right)^{2} = \left[ {\left( {1 - \left( {n - 1} \right)\left( {wef^{\prime\prime}_{r + 1} } \right)^{n} } \right)} \right]f^{\prime\prime\prime}_{r + 1} + \lambda^{*} \theta_{r + 1} - f^{{\prime}{2}}_{r + 1} - f_{r + 1} f^{\prime\prime}_{r + 1} + \left( {\sin^{2} (\omega )M^{2} + \lambda } \right)f^{\prime}_{r + 1} ,$$
(24)
$$\theta^{\prime\prime}_{r + 1} + \beta \left( {\theta_{r + 1} \theta^{\prime\prime}_{r + 1} + \left( {\theta^{\prime}_{r + 1} } \right)^{2} + \Pr \left( {f_{r + 1} \theta^{\prime}_{r + 1} + N_{d} \phi_{r + 1}^{\prime \prime } } \right)} \right) = 0,$$
(25)
$$\phi^{\prime\prime}_{r + 1} + Le\left( {f_{r + 1} \phi^{\prime}_{r + 1} } \right) + L_{r + 1d} \theta^{\prime\prime}_{r + 1} = 0,$$
(26)
$$\begin{gathered} f^{\prime}_{r + 1} \left( \eta \right) = 1,\,f_{r + 1} \left( \eta \right) = S,\,\,\theta_{r + 1} \left( \eta \right) = 1,\,\,at\,\,\eta = 0, \hfill \\ f^{\prime}_{r + 1} \left( \eta \right) \to 0,\,\,\theta_{r + 1} \left( \eta \right) \to 0,\,\,\phi_{r + 1} \left( \eta \right) \to 0,\,\,as\,\,\eta \to \infty . \hfill \\ \end{gathered}$$
(27)

Step 3: organizing in suitable way.

$$f^{\prime}_{r + 1} = S,\,f_{r + 1} (0) = 0$$
(28)
$$\left( {1 + \left( {weS^{\prime}} \right)^{n} } \right)^{2} = \left[ {\left( {1 - \left( {n - 1} \right)\left( {weS^{\prime}} \right)^{n} } \right)} \right]S^{\prime\prime} + \lambda^{*} \theta_{r + 1} - S^{2} - f_{r + 1} S^{\prime} + \left( {\sin^{2} (\omega )M^{2} + \lambda } \right)S,$$
(29)
$$\theta^{\prime\prime}_{r + 1} + \beta \left( {\theta_{r + 1} \theta^{\prime\prime}_{r + 1} + \left( {\theta^{\prime}_{r + 1} } \right)^{2} + \Pr \left( {f_{r + 1} \theta^{\prime}_{r + 1} + N_{d} \phi_{r + 1}^{\prime \prime } } \right)} \right) = 0,$$
(30)
$$\phi^{\prime\prime}_{r + 1} + Le\left( {f_{r + 1} \phi^{\prime}_{r + 1} } \right) + L_{r + 1d} \theta^{\prime\prime}_{r + 1} = 0,$$
(31)

Step 4: After making the necessary adjustments to change the range from [0, L] to [1, 1], the decoupling equations obtained above are solved using the Chebyshev pseudo-spectral association approach. The parameter L is taken as the scaling parameter.

$$\left. \begin{gathered} A_{1} S_{r + 1} = B_{1} ,\,\,\,A_{2} \theta_{r + 1} = B_{2} ,\,\,A_{3} \phi_{r + 1} = B_{3} ,\,\,\,\,A_{4} \vartheta_{r + 1} = B_{4} \hfill \\ A = D^{1} ,\,\,\,\,\,B = Sr \hfill \\ A_{2} = D^{2} + Diag(\theta_{r + 1} )D \hfill \\ B_{2} = \frac{ - 1}{{\left[ {\left( {1 - \left( {(n - 1)WeS^{\prime^2}_{r + 1} } \right)^{ - 2} } \right)\left( {1 + nWeS^{\prime^2}_{r + 1} } \right)} \right]}}\left[ {\lambda^{*} \theta_{r + 1} - S^{2} - f_{r + 1} S^{\prime} + \left( {\sin^{2} (\omega )M^{2} + \lambda } \right)S} \right] \hfill \\ A_{3} = diag(\left( {1 + \gamma \left( {2 - \eta } \right)\left( {1 + We} \right)} \right)(d + 1))/d(D)^{d} ]D^{2} + diag(\left( {1 + nWe} \right))D + diag(\alpha )I \hfill \\ B_{3} = \frac{1}{{\left( {1 + 2\gamma \eta } \right)\left( {1 + \theta_{r + 1} \varepsilon } \right)}}\left[ {\theta^{\prime\prime}_{r + 1} + \beta \left( {\theta_{r + 1} \theta^{\prime\prime}_{r + 1} + \left( {\theta^{\prime}_{r + 1} } \right)^{2} + \Pr \left( {f_{r + 1} \theta^{\prime}_{r + 1} + N_{d} \phi_{r + 1}^{\prime \prime } } \right)} \right)} \right] \hfill \\ A_{4} = \left( {1 + 2\gamma \eta } \right)\left( {1 + \theta_{r + 1} \varepsilon } \right)D^{2} + diag\left( {\left[ {\theta_{r + 1} + \beta \left( {\theta_{r + 1} \theta^{\prime\prime}_{r + 1} + \left( {\theta^{\prime}_{r + 1} } \right)^{2} + \Pr \left( {f_{r + 1} \theta^{\prime}_{r + 1} + N_{d} \phi_{r + 1}^{\prime } } \right)} \right)} \right]} \right)D \hfill \\ B_{4} = \left( {2\gamma - \frac{1}{2}Al_{b} \eta } \right)\phi^{\prime\prime}_{r + 1} + Le\left( {f_{r + 1} \phi^{\prime}_{r + 1} } \right) + L_{d} \theta^{\prime\prime}_{r + 1} \hfill \\ \end{gathered} \right\}$$
(32)

P denotes grid structure points, and D and I are showing the sloping and identity type matrices, with dimension \((P + 1) \times (P + 1)\) respectively.

The proposed SRM iterative strategy encompasses the following steps and simply interpreted by flow diagram in Fig. 2.

Fig. 2
figure 2

Block diagram of spectral relaxation method [31]

Full size image

2 Graphical results and discussions

2.1 Velocity Profile

The velocity profile due to various emerging parameters are seen by different figures illustrated in Figs. 3, 4, 5, 6 and 7. The purpose of Fig. 3 to investigate how the Weissenberg number (We) affect the velocity field \(f^{\prime}\left( \eta \right)\) in dual situation of an inclined magnetic \(\omega\) consequences. As it is observed that fluid needs relaxation time to unwind because relaxation time is correlated with Weissenberg number. One of the good examples of this phenomenon is paint. Additionally increments in the numeric value of Weissenberg Berg number (We) produces change in inclination which gives the velocity profile magnification which means that velocity amplifies by the virtue of an enrichment in these numbers (We). The decrement in the shear rate viscosity increases the fluid velocity and thus (We) increase also increases. Figure 4 is used to show the effect of a parameter \(\lambda\) on the profile of velocity \(f^{\prime}\left( \eta \right)\). This parameter \(\lambda\) is acting as a which as porosity parameter. Which tells that the phenomenon is associated with the Darcian law, which states a direct relationship between a change in pressure and velocity of fluid. This clearly means that increase in one cause increments in another also and vice versa. One more interesting fact of Darcian theory is that Darcian body force brings a declaration in the motion of fluid because this body force is inversely linked to the permeability of the fluid flow medium in which flow is considered. As seen in the geometry of the flow, the fluid gets difficult to go through the porous medium takes the path in the direction of the vertical wall. Thus, amplification in resistance and fluid viscosity due to change in pressure. A positive variation in an inclined angle from in the range specified as 0 to \(\frac{\pi }{2}\) amplifies viscosity phenomenon and depreciates \(f^{\prime}\left( \eta \right)\). The effect of the parameter M on \({f}{\prime}\left(\eta \right)\) are displayed in Fig. 5. Magnetic effect arises because of magnetohydrodynamic (MHD) phenomenon. The Lorentz force is acknowledged when the electric conducting fluid is flow through a magnetic region. The production of this force is used against the flow motion and causes resistive pattern, and due to this motion of fluid is diminishes. It is notable that the viscosity of fluid decreases because of a magnification in inclined magnetic field M through inclination \(\omega\) and their demonstration are show on \({f}{\prime}\left(\eta \right)\). The performance of the parameter fluid index (n) on the profile of velocity is depicted in Fig. 6. This parameter investigates the effect of n on \(f^{\prime}\left( \eta \right)\) and tells the viscous nature of flow behavior. This term specified the three main looks of the flow which included that amplification occurred for n > 1, diminished occurred for n < 1and gives Newtonian for the value n = 1. When increasing parameter n then the inertial forces are subordinated to the viscous forces which resulting in a decrease in \(f^{\prime}\left( \eta \right)\). Additionally, inclined angle increases from 0 to π/2 causes fluid velocity decreases. Which is a clear evident that magnifying the inclination parameter may cause in Lorentz force strength due to this fact viscosity amplified and producing decrement in the profile of velocity as shown by Fig. 7.

Fig. 3
figure 3

\(f^{\prime}\left( \eta \right)\) through \(\lambda\) effect

Full size image
Fig. 4
figure 4

\(f^{\prime}\left( \eta \right)\) through \(We\) effect

Full size image
Fig. 5
figure 5

\(f^{\prime}\left( \eta \right)\) through \(M\) effect

Full size image
Fig. 6
figure 6

\(f^{\prime}\left( \eta \right)\) through \(n\) effect

Full size image
Fig. 7
figure 7

\(f^{\prime}\left( \eta \right)\) through \(\omega\) effect

Full size image

2.2 Temperature profile

Some important parameters are study for the temperature profile and their effects are on the profile of temperature are their results are plotted in the following Figs. 8, 9, 10, 11, 12, 13 And 14. The performance of the parameters \(\lambda\) and \(\beta\) on the temperature profile \(\theta \left( \eta \right)\) are shown in Figs. 8 and 9. Increasing in inclination will able the fluid to depreciates the viscosity phenomenon and amplifies thermal boundary layer thickness phenomenon. It’s obvious that due to intermolecular colloidal of particles will create the heat transfer which will enhance the thermal conductivity. This colloidal collusion of molecules increases the temperature of the fluid and over all implies the temperature profile for both the parameter. The influence of Dufour number \(Nd\) and Prandtl number \(\Pr\) on \(\theta \left( \eta \right)\) are highlighted in Figs. 10, 11 Darcy forces is inversely linked with permeability phenomenon and these forces provides resistance to fluid which causes a thickness to the fluid flow and escalates the temperature of moving fluid on the expandable sheet. On the other hand, a positive variation in \(\Pr\) number depreciates the temperature profile, and it is seen clear, that an amplification in free convection parameter depreciates fluid velocity and elevates the temperature field. Thus, magnification in the value of \(\Pr\) causes heat to diffuse more quickly, which lowers temperature phenomena inside the liquid as well as heat deliverance. Therefore, its conclude that Thermal boundary thickness escalates in the case of Nd amplifies but lessens in the case of \(\Pr\). The following Figs. 12, 13 are drawn for the purpose of detecting the temperature behavior in context \(M\) and \(n\) parameters. An electrically conducting fluid produces a resistive force. Therefore, this resistive causes the decreasing in velocity due to growing in viscosity of the fluid. Viscosity behavior is quite opposite to temperature which means deliverance of heat thermal is fast and boundary thickness magnify due to upshifting in the value of \(M\). Amplification in viscosity is reported for the case of an upsurge in \(n\). The symbol \(n\) is prominent factor of viscoelastic fluids like tangent hyperbolic, Williamson, Cross, Carreau fluids etc. Shear thickening behavior is seen by increase in n which causes reduction in the fluid motion and amplifies \(\theta \left( \eta \right)\). Figure 14 displays the influence of inclined angle \(\omega\) on thermal profile. \(\omega\) resists fluid motion which implies the viscosity, therefore, enhances fluid temperature also enhances in this case.

Fig. 8
figure 8

\(\theta \left( \eta \right)\) through \(\beta\) effect

Full size image
Fig. 9
figure 9

\(\theta \left( \eta \right)\) through \(\lambda\) effect

Full size image
Fig. 10
figure 10

\(\theta \left( \eta \right)\) through \(Nd\) effect

Full size image
Fig. 11
figure 11

\(\theta \left( \eta \right)\) through \(pr\) effect

Full size image
Fig. 12
figure 12

\(\theta \left( \eta \right)\) through \(M\) effect

Full size image
Fig. 13
figure 13

\(\theta \left( \eta \right)\) through \(n\) effect

Full size image
Fig. 14
figure 14

\(\theta \left( \eta \right)\) through \(\omega\) effect

Full size image

2.3 Concentration profile

In this section a few sundry parameters are analyzed through Figs. 15, 16, 17, 18 And 19 due to which concentration profile is affected. The magnetic parameter \(M\) and \(Ld\) for concentration profile are illustrated in the Figs. 15, 16. The positive variation in the value of magnetic parameter \(M\) and soret parameter \(Ld\) amplifies the concentration of the liquid therefore, the denseness of barrier layer escalates by amplifying \(M\) and \(Ld\). Figures 17, 18 are designed to expose the effect of Lewis number \(Le\) and porosity parameter λ on \(\varphi \left( \eta \right)\). Lewis number is the ratio of momentum diffusivity to mass diffusivity. Mass diffuses abruptly in the case of a magnification in parameter \(Le\). Mass is directly linked with concentration phenomenon and a positive change in \(Le\) depreciates \(\varphi \left( \eta \right)\) The stronger association in concentration and temperature is established which tells that a magnification in \(\lambda\) provides hurdle against the liquid moving path which lessens \(\varphi \left( \eta \right)\) and amplifies temperature of the fluid. That’s why a positive change in λ escalates mass friction field \(\varphi \left( \eta \right)\) and the CBL diminishes by enhancing Le but increases for \(\lambda\). The effect of an inclination \(\omega\) on the concentration field is shown in Fig. 19. The results revealed that concentration boundary layer thickness decreases as \(\omega\) rises, resulting in a decrease in concentration profile.

Fig. 15
figure 15

\(\varphi \left( \eta \right)\) through \(M\) effect

Full size image
Fig. 16
figure 16

\(\varphi \left( \eta \right)\) through \(Ld\) effect

Full size image
Fig. 17
figure 17

\(\varphi \left( \eta \right)\) through \(Le\) effect

Full size image
Fig. 18
figure 18

\(\varphi \left( \eta \right)\) through \(\lambda\) effect

Full size image
Fig. 19
figure 19

\(\varphi \left( \eta \right)\) through \(\omega\) effect

Full size image

2.4 Statistical analysis

Figure 20 illustrated the performance of n on drag coefficient. The viscosity increases and reduces the fluid velocity as well. A decrease in n causes the surface drag friction of the surface the fluid is moving across to increase, amplifying the skin friction phenomenon. The behavior of inclined magnetic field effect \(M\) on drag coefficient is shown in Fig. 21. The fluid flow velocity against the medium velocity is known as surface drag. It is clearly seen that magnification in the value of \(M\) causes the fluid velocity to decrease, diminishing the surface drag phenomenon. Figures 22, 23 displayed the impact of \(\beta\) and \(\Pr\) on heat deliverance rate. Heat deliverance phenomenon is somehow opposite to the temperature phenomenon. Molecules of the fluid collide more randomly and shares more kinetic with each other which amplifies \(\theta \left( \eta \right)\) and diminishes heat deliverance effect. Heat diffuses more quickly and grow up the value of \(\Pr\) depreciates the fluid temperature band increases rate of heat transfer. The influence of \(Ld\) and \(Le\) on Sherwood number are portrayed in Figs. 24, 25. A positive variation in \(Ld\) decreases the Sherwood number but increases because of a magnification in \(Le\).

Fig. 20
figure 20

Influence of n on skin friction

Full size image
Fig. 21
figure 21

Influence of M on skin friction

Full size image
Fig. 22
figure 22

Impact of β on Nusselt number

Full size image
Fig. 23
figure 23

Investigation of Pr on Nusselt number

Full size image
Fig. 24
figure 24

Impact of Ld on Nusselt number

Full size image
Fig. 25
figure 25

Impact of Le on Nusselt number

Full size image

The Tables 1, 2 are designed to display the effect of various prominent parameters including magnetic parameter \(M\), power law index n, thermal conductivity \(\beta\) and \(\Pr\) on drag coefficient and heat deliverance rate. Drag phenomenon in the case of fluid surface escalates by magnifying \(n\) but lessens owing to an amplification in \(M\) as shown in Table 1. Heat transfer rate escalates by magnifying \(\beta\) as well as \(\Pr\). In the light of Table 3, it is noticed that concentration deliverance phenomenon by rising \(Le\) but diminishes in terms of an increase in \(Ld\).

Table 1 \(M\) and \(n\) effects on skin friction coefficient
Full size table
Table 2 Influence of \(\beta\) and \(\Pr\) on Nusselt number
Full size table
Table 3 Effect of \(Ld\) and \(Le\) on Sherwood number
Full size table

2.5 Validity analysis

Table 4 is drawn to show the comparison analysis of the results obtained in the case of drag coefficient due to a positive variation in inclined magnetic field \(M\). When compared to the findings obtained by Patel et al. [50], it is found that the outcomes are extremely genuine and trustworthy.

Table 4 Comparison with existing literature
Full size table

3 Conclusion

The following main outcomes obtained of the current research are given below.

  1. 1)

    Heat delivers more easily due to growth in \(\Pr\) but diminishes owing to an increment in \(\beta\).

  2. 2)

    Increase in the value of M produced resistance therefore, as results decrease in velocity occurs.

  3. 3)

    Viscosity diminishes by increasing the value of cross index which depreciates the velocity of fluid flow.

  4. 4)

    Concentration phenomenon is strongly correlated with \(Ld\) parameter and increase in angle \(\omega\) diminishes the fluid speed.

  5. 5)

    Drag friction increases in the case of n but depreciates in the case of \(M\) because drag friction is acted against fluid flow.

  6. 6)

    The thermal profile \(\theta \left( \eta \right)\) escalates due to grow in \(\beta\) because of molecular collision.

  7. 7)

    The concentration boundary layer thickness decreases as \(\omega\) rises, resulting in a decrease in concentration profile.

3.1 Important prospects and future directions

The prospects of current works greatly lie in the realm of fluid dynamics. Which involve advancements in computational capabilities, multiscale applications, and adaptive approaches. Understanding and simulating variable thermal effects are crucial in various applications, including renewable energy, manufacturing, and climate modeling. The work can be extended for the investigation of fluid flow behavior and heat transfer applications. Involved methods that can efficiently expose the variable thermophysical effects such as combustion processes, environmental heat transfer and thermal management in electronics.