1 Introduction

Nanofluids are suspensions of metallic, non-metallic or polymeric nano-sized powders in a base liquid which are used to increase the heat transfer rate in various applications. In recent years, the concept of nanofluid has been proposed as a route for increasing the performance of heat transfer liquids. Due to the increasing importance of nanofluids, there is a large amount of literature on convective heat transport in nanofluids and problems linked to a stretching surface. An excellent collection of articles on this topic can be found in [1–4]. The majority of the previous studies have been restricted to boundary layer flow and heat transfer in nanofluids. Following the early work by Crane [5], Khan and Pop [6] were among the first researchers to study nanofluid flow due to a stretching sheet. Other researchers studied various aspects of flow and heat transfer in a fluid of infinite extent; see, for instance, Chen [7] and Abo-Eldahab and Abd El-Aziz [8]. A mathematical analysis of momentum and heat transfer characteristics of the boundary layer flow of an incompressible and electrically conducting viscoelastic fluid over a linear stretching sheet was carried out by Abd El-Aziz [9]. In addition, radiation effects on viscous flow of a nanofluid and heat transfer over a nonlinearly stretching sheet were studied by Hady et al. [10]. Theoretical studies include, for example, modeling unsteady boundary layer flow of a nanofluid over a permeable stretching/shrinking sheet by Bachok et al. [11]. Rohni et al. [12] developed a numerical solution for the unsteady flow over a continuously shrinking surface with wall mass suction using the nanofluid model proposed by Buongiorno [13].

The effect of an applied magnetic field on nanofluids has substantial applications in chemistry, physics and engineering. These include cooling of continuous filaments, in the process of drawing, annealing and thinning of copper wire. Drawing such strips through an electrically conducting fluid subject to a magnetic field can control the rate of cooling and stretching, thereby furthering the desired characteristics of the final product. Such an application of a linearly stretching sheet of incompressible viscous flow of MHD was discussed by Pavlov [14]. In other work, Jafar et al. [15] studied the effects of magnetohydrodynamic (MHD) flow and heat transfer due to a stretching/shrinking sheet with an external magnetic field, viscous dissipation and Joule effects.

A model for magnetohydrodynamic flow over a uniformly stretched vertical permeable surface subject to a chemical reaction was suggested by Chamkha [16]. An analysis of the effects of a chemical reaction on heat and mass transfer on a magnetohydrodynamic boundary layer flow over a wedge with ohmic heating and viscous dissipation in a porous medium was done by Kandasamy and Palanimani [17]. Rashidi and Erfani [18] studied the steady MHD convective and slip flow due to a rotating disk with viscous dissipation and ohmic heating. Rashidi et al. [19] found approximate analytic solutions for an MHD boundary-layer viscoelastic fluid flow over a continuously moving stretching surface using the homotopy analysis method. Rashidi and Keimanesh [20] used the differential transform method and Padé approximants to solve the equations that model MHD flow in a laminar liquid film from a horizontal stretching surface. The effect of a transverse magnetic field on the flow and heat transfer over a stretching surface were examined by Anjali-Devi and Thiyagarajan [21]. The influence of a chemical reaction on heat and mass transfer due to natural convection from vertical surfaces in porous media subject to Soret and Dufour effects was also studied by Postelnicu [22].

Despite all this previous work, there is still a lot that is unknown about the flow and heat and mass transfer properties of different nanofluids. For instance, the composition and make of the nanoparticles may have an impact on the performance of the nanofluid as a heat transfer medium. In this paper we investigate unsteady MHD mixed convection boundary layer with suction/injection subject to a number of source terms including Dufour and Soret effects, heat generation, an applied magnetic field and viscous dissipation. Various numerical and or semi-numerical methods can and have been used to solve the equations that model this type of boundary layer flow. These equations are non-similar and coupled. In this paper we use the spectral relaxation method (SRM) that was recently proposed by Motsa [23]. This spectral relaxation method promises fast convergence with good accuracy, has been successfully used in a limited number of boundary layer flow and heat transfer problems (see [24, 25]). In this paper we discuss the fluid flow and heat transfer as well as highlight the strengths of the solution method.

2 Governing equations

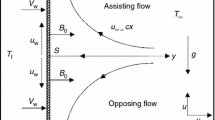
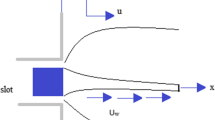
Consider the two-dimensional unsteady laminar MHD mixed convective flow of a nanofluid due to a stretching sheet situated at \(y = 0\) with stretching velocity \(u=ax\), where a is a constant. The temperature and nanoparticle volume fraction at the stretching surface are \(T_{w}\) and \(C_{w}\), respectively, and those of the ambient nanofluid are \(T_{\infty}\) and \(C_{\infty}\), respectively. The x and y directions are in the plane of and perpendicular to the sheet, respectively. The continuity, momentum, energy and concentration equations of unsteady, incompressible nanofluid boundary layer flow are as follows (see Yang [26]):

$$\begin{aligned}& \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} =0, \end{aligned}$$
(2.1)
$$\begin{aligned}& \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} =-\frac{1}{\rho_{nf}} \frac{\partial p}{\partial x}+\frac{\mu_{nf}}{ \rho_{nf}}\frac{\partial^{2} u}{\partial y^{2}} + g\beta_{T}(T-T_{\infty}) + g\beta_{C}(C-C_{\infty})-\frac{\sigma B_{0}^{2}}{\rho_{nf}}u, \end{aligned}$$
(2.2)
$$\begin{aligned}& \frac{\partial T}{\partial t} + u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha_{nf}\frac{\partial^{2} T}{\partial y^{2}} +\frac{Q}{ (\rho c_{p})_{nf}}(T - T_{\infty})+ \frac{\rho_{f}D_{m}K_{T}}{ C_{s}(\rho c_{p})_{nf}}\frac{\partial^{2} C}{\partial^{2} y}, \end{aligned}$$
(2.3)
$$\begin{aligned}& \frac{\partial C}{\partial t} + u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{m}\frac{\partial^{2} C}{\partial y^{2}} + \frac{D_{m}K_{m}}{T_{m}} \frac{\partial^{2} T}{\partial y^{2}} -R(C-C_{\infty}), \end{aligned}$$
(2.4)

where t, u and v are the time, the fluid velocity and the normal velocity components in the x and y orientations, respectively; \(\nu_{nf}\), p, \(\rho_{nf}\), σ, \(B_{0}\), \(\mu_{nf}\), g are the nanofluid kinematic viscosity, the pressure, nanofluid density, electrical conductivity, the uniform magnetic field in the y direction, the effective dynamic viscosity of the nanofluid and gravitational acceleration, respectively; \(\beta_{T}\), \(\beta_{C}\), T, C, \(\alpha _{nf}\), \((\rho cp)_{nf}\), Q are the volumetric thermal expansion coefficient, the solutal expansion coefficient, the temperature of the fluid in the boundary layer, fluid solutal concentration, the thermal diffusivity of the nanofluid, the nanofluid heat capacitance and the volumetric rate of heat generation, respectively; \(\rho_{f}\), \(D_{m}\), \(K_{T}\), \(C_{s}\), \((cp)_{nf}\), \(T_{m}\), R are the density of the base fluid, the mass diffusivity of concentration, thermal diffusion ratio, concentration susceptibility, specific heat of the fluid at constant pressure, mean fluid temperature and the chemical reaction parameter, respectively.

The boundary conditions are as follows:

$$ \begin{aligned} &t\geq0\mbox{:}\quad u=U_{w}(x)=ax, \qquad v=v_{w},\qquad T=T_{w}, \qquad C=C_{w} \quad \mbox{at }y=0, \\ &t\geq0 \mbox{:}\quad u=U_{\infty}(x)=a_{\infty}x,\qquad v=0,\qquad T = T_{\infty},\qquad C= C_{\infty}\quad \mbox{as }y\to \infty, \end{aligned} $$
(2.5)

and the initial conditions are

$$ \begin{aligned} &t< 0\mbox{:}\quad u(x,y,t)=0,\qquad v(x,y,t)=0, \\ &\hphantom{t<0\mbox{:}\quad}T(x,y,t)=T_{w}, \qquad C(x,y,t)=C_{w},\quad \forall{x,y}, \end{aligned} $$
(2.6)

where \(a_{\infty}\) (>0) is the stagnation flow rate parameter, \(a< 0\) for a shrinking surface and \(a > 0\) for a stretching surface. Here \(v_{w}\) is prescribed suction velocity (\(v_{w} < 0\)) or blowing velocity (\(v_{w} >0\)).

In the free stream the momentum equation (2.2) becomes

$$ U_{\infty}\frac{dU_{\infty}}{dx} = - \frac{1}{\rho_{nf}}\frac {\partial p}{\partial x}- \frac{\sigma B_{0}^{2}}{\rho_{nf}}U_{\infty}. $$
(2.7)

Substituting (2.7) in (2.2) the momentum equation is written as

$$\begin{aligned} \begin{aligned}[b] \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} ={}&{ \nu_{nf}}\frac{\partial^{2} u}{\partial y^{2}}+U_{\infty}\frac{dU_{\infty}}{dx}+ (U_{\infty}- u) \frac{\sigma B_{0}^{2}}{\rho_{nf}} \\ &{}+g\beta_{T}(T-T{\infty})+g\beta _{C}(C-C{\infty}). \end{aligned} \end{aligned}$$
(2.8)

The effective dynamic viscosity of the nanofluid was given by Brinkman [27] as

$$ \mu_{nf}=\frac{\mu_{f}}{(1-\phi)^{2.5}}, $$
(2.9)

where ϕ is the solid volume fraction of nanoparticles, \(\mu_{f}\) is the dynamic viscosity of the base fluid. In equations (2.1)-(2.4),

$$\begin{aligned}& (\rho c_{p})_{nf}=(1-\phi) (\rho c_{p})_{f} + \phi(\rho c_{p})_{s}, \\& \rho_{nf}=(1-\phi)\rho_{f} + \phi\rho_{s},\qquad \nu_{nf}=\frac {\mu_{nf}}{\rho_{nf}}, \\& \alpha_{nf}=\frac{k_{nf}}{(\rho c_{p})_{nf}}, \qquad \frac{k_{nf}}{k_{f}}= \frac{(k_{s}+k_{f}) - 2\phi(k_{f} - k_{s})}{(k_{s}+k_{f}) + \phi(k_{f} - k_{s})}, \end{aligned}$$
(2.10)

where \(k_{nf}\) is the thermal conductivity of the nanofluid, \(k_{f}\) and \(k_{s}\) are the thermal conductivities of the fluid and of solid fractions, respectively, and \(\rho_{s}\) is the density of solid fractions, \((\rho c_{p})_{f}\) and \((\rho c_{p})_{s}\) are the heat capacity of the base fluid and the effective heat capacity of a nanoparticle, respectively, \(k_{nf}\) is the thermal conductivity of the nanofluid.

The continuity equation (2.1) is satisfied by introducing a stream function \(\psi(x,y)\) such that

$$ u=\frac{\partial\psi}{\partial y},\qquad v=-\frac{\partial \psi}{\partial x}. $$
(2.11)

We introduce the following non-dimensional variables (see Liao [28]):

$$ \begin{aligned} &\eta= \biggl[\frac{a_{\infty}}{\nu_{f}\xi} \biggr]^{\frac{1}{2}} y, \quad \xi =1-\exp(-\tau), \tau=a_{\infty}t,\qquad \psi= [{a_{\infty} \nu_{f}\xi} ]^{\frac{1}{2}} xf(\xi,\eta ),\\ &\theta(\xi,\eta)=\frac{T-T_{\infty}}{T_{w}-T_{\infty}},\qquad \varPhi (\xi,\eta)=\frac{C-C_{\infty}}{C_{w}-C_{\infty}}, \end{aligned} $$
(2.12)

where \(f(\xi,\eta)\) is a dimensionless stream function, \(\theta(\xi,\eta)\) is the dimensionless temperature and \(\phi(\xi,\eta)\) is the dimensionless solute concentration. By using (2.11) and (2.12), the governing equations (2.3), (2.4) and (2.8) along with the boundary conditions (2.5) are reduced to the following two-point boundary value problem:

$$\begin{aligned}& f'''+\phi_{1} \biggl[ \frac{\eta}{2}(1-\xi)f'' + \xi \bigl(ff''- {f}^{\prime 2}+1+\mathit{Ha}^{2}\bigl(1-f' \bigr)+\mathit{Gr}_{t} \theta+\mathit{Gr}_{c} \varPhi \bigr) \biggr] \\& \quad = \phi_{1} \xi(1-\xi)\frac{\partial f'}{\partial\xi}, \end{aligned}$$
(2.13)
$$\begin{aligned}& \theta'' + \frac{k_{f}}{k_{nf}}\mathit{Pr} \phi_{2} \biggl[\frac{\eta }{2}(1-\xi)\theta' +\xi \bigl(f\theta'+\delta\theta \bigr)+\frac{D_{f}}{\phi_{2}}\varPhi '' \biggr] =\frac{k_{f}}{k_{nf}}\mathit{Pr} \phi_{2}\xi(1-\xi)\frac{\partial \theta}{\partial\xi}, \end{aligned}$$
(2.14)
$$\begin{aligned}& \varPhi '' + \mathit{Sc} \biggl[\frac{\eta}{2}(1-\xi) \varPhi ' + \xi \bigl(f\varPhi '-\gamma \varPhi \bigr)+\mathit{Sr} \theta'' \biggr] = \mathit{Sc} \xi(1-\xi) \frac{\partial \varPhi }{\partial\xi}. \end{aligned}$$
(2.15)

The boundary conditions are as follows:

$$ \begin{aligned} &f(\xi,0)=f_{w}, \qquad f'(\xi,0)= \lambda,\qquad \theta(\xi,0)=1,\qquad \varPhi (\xi,0)=1\quad \mbox{at } \eta=0, \xi \geq0, \\ &f'(\xi,\infty)=1,\qquad \theta(\xi,\infty)=0,\qquad \varPhi (\xi, \infty )=0\quad \mbox{as } \eta\rightarrow\infty, \xi\geq0, \end{aligned} $$
(2.16)

where primes denote differentiation with respect to η, \(\alpha_{f}=k_{f}/(\rho c_{p})_{f}\) and \(\nu_{f}=\mu_{f}/\rho_{f}\) are the thermal diffusivity and kinetic viscosity of the base fluid, respectively. Other non-dimensional parameters appearing in equations (2.13) to (2.15) are Ha, \(\mathit{Gr}_{t}\), \(\mathit{Gr}_{c}\), \(\mathit{Gr}_{c}\), Pr, δ, \(D_{f}\), Sc, γ and Sr, and they denote the Hartmann number, the local temperature Grashof number, the local concentration Grashof number, the Prandtl number, the dimensionless heat generation parameter, the Dufour number, the Schmidt number, the scaled chemical reaction parameter and the Soret number, respectively. These parameters are defined mathematically as

$$ \begin{aligned} &\mathit{Ha}^{2} = \frac{\sigma B_{0}^{2}}{a_{\infty}\rho_{nf}} ,\qquad \mathit{Gr}_{t}=\frac{g\beta_{T}(T_{w}-T_{\infty})}{a_{\infty}^{2}x}, \\ &\mathit{Gr}_{c}= \frac{g\beta_{C}(C_{w}-C_{\infty})}{a_{\infty}^{2}x} ,\qquad \mathit{Pr}=\frac{\nu_{f}}{\alpha_{f}},\qquad \delta= \frac{Q}{a_{\infty}(\rho c_{p})_{nf}}, \\ &D_{f} = \frac{D_{m}K_{T}(C_{w}-C_{\infty})}{C_{s}(C_{p})_{f}\nu_{f}(T_{w}-T_{\infty})}, \qquad \mathit{Sc}= \frac{\nu_{f}}{D_{m}}, \\ &\gamma=\frac{R}{a_{\infty}},\qquad \mathit{Sr}=\frac{D_{m}K_{T}}{T_{m}} \frac{(T_{w}-T_{\infty})}{\nu_{f} (C_{w} - C_{\infty})}. \end{aligned} $$
(2.17)

The boundary conditions are as follows:

$$ \begin{aligned} &f(\xi,0)=f_{w}, \qquad f'(\xi,0)= \lambda,\qquad \theta(\xi,0)=1, \qquad \varPhi (\xi,0)=1\quad \mbox{at } \eta=0, \xi \geq0, \\ &f'(\xi,\infty)=1,\qquad \theta(\xi,\infty)=0, \qquad \varPhi (\xi, \infty)=0\quad \mbox{as } \eta\rightarrow\infty, \xi\geq0. \end{aligned} $$
(2.18)

The nanoparticle volume fractions \(\phi_{1}\) and \(\phi_{2}\) are defined as

$$ \phi_{1}=(1-\phi)^{2.5} \biggl[1-\phi+ \phi \biggl( \frac{\rho_{s}}{\rho_{f}} \biggr) \biggr],\qquad \phi_{2}= \biggl[1-\phi+ \phi \frac{(\rho c)_{s}}{(\rho c)_{f}} \biggr]. $$
(2.19)

In equations (2.18), \(f_{w} =-v_{w}/\sqrt{a_{\infty}\nu_{f} \xi}\) represents suction (\(f_{w}>0\)) or injection (\(f_{w}<0\)) and λ (\(=a/a_{\infty}\)) is the stretching/shrinking parameter.

3 Skin friction, heat and mass transfer coefficients

The skin friction coefficient \(C_{f}\), the local Nusselt number \(\mathit{Nu}_{x}\) and the local Sherwood number \(\mathit{Sh}_{x}\) characterize the surface drag, wall heat and mass transfer rates, respectively.

The shearing stress at the surface of the wall \(\tau_{w}\) is defined as

$$ \tau_{w} = -\mu_{nf} \biggl(\frac{\partial{u}}{\partial{y}} \biggr)_{y=0} =-\frac{U_{\infty}\mu_{f}}{ (1-\phi )^{2.5}x}\sqrt{\frac {U_{\infty}x}{\nu_{f} \xi}} f''(0,\xi), $$
(3.1)

where \(\mu_{nf}\) is the coefficient of viscosity.

The skin friction coefficient is obtained as

$$ C_{fx} = \frac{2\tau_{w}}{\rho_{f} U_{\infty}^{2}}, $$
(3.2)

and using equation (3.1) in (3.2) we obtain

$$ \frac{1}{2} (1-\phi )^{2.5} C_{fx} = - \xi^{-\frac{1}{2}} \mathit{Re}_{x}^{-\frac{1}{2}}f''(0, \xi). $$
(3.3)

The heat transfer rate at the surface flux at the wall is defined as

$$ q_{w} = - k_{nf} \biggl(\frac{\partial{T}}{\partial{y}} \biggr)_{y=0} = - k_{nf}\frac{(T_{w}-T_{\infty})}{x}\sqrt{ \frac{U_{\infty}x}{\nu_{f} \xi}} \theta'(0,\xi), $$
(3.4)

where \(k_{nf}\) is the thermal conductivity of the nanofluid. The local Nusselt number is defined as

$$ \mathit{Nu}_{x} = \frac{xq_{w}}{k_{f} (T_{w} - T_{\infty})}. $$
(3.5)

Using equation (3.4) in equation (3.5), the dimensionless wall heat transfer rate is obtained as

$$ \biggl(\frac{k_{f}}{k_{nf}} \biggr)\mathit{Nu}_{x} = - \xi^{-\frac{1}{2}} \mathit{Re}_{x}^{\frac{1}{2}} \theta'(0, \xi). $$
(3.6)

The mass flux at the wall surface is defined as

$$ q_{m} = - D \biggl(\frac{\partial{C}}{\partial{y}} \biggr)_{y=0} = - D \frac{(C_{w}-C_{\infty})}{x}\sqrt{\frac{U_{\infty}x}{\nu_{f}\xi}} \varPhi '(0, \xi), $$
(3.7)

and the local Sherwood number (mass transfer coefficient) is obtained as

$$ \mathit{Sh}_{x} = \frac{xq_{m}}{D (C_{w} - C_{\infty})}. $$
(3.8)

The dimensionless wall mass transfer rate is obtained as

$$ \mathit{Sh}_{x} = - \xi^{-\frac{1}{2}} \mathit{Re}_{x}^{\frac{1}{2}} \varPhi '(0,\xi), $$
(3.9)

where \(\mathit{Re}_{x}\) represents the local Reynolds number and is defined as

$$ \mathit{Re}_{x} = \frac{xu_{\infty}}{\nu_{f}}. $$
(3.10)

4 Cases of special interest

In this section we highlight two particular cases where equations (2.12) to (2.14) reduce to ordinary differential equations.

4.1 Initial steady flow

For steady flow and a regular fluid, if we assume that \(\xi\to0\), where \(0< \xi\le1\), then \(t \approx0\). Thus \(f(\eta,\xi)\approx f(\eta)\), \(\theta(\eta,\xi) \approx\theta(\eta)\) and \(\varPhi (\eta,\xi)\approx \varPhi (\eta)\). In this case equations (2.12) to (2.14) reduce to

$$\begin{aligned}& f'''+\frac{1}{2} \phi_{1}\eta f'' = 0, \end{aligned}$$
(4.1)
$$\begin{aligned}& \theta'' + \frac{1}{2}\frac{k_{f}}{k_{nf}} \mathit{Pr} \phi_{2} \eta\theta '+\frac{k_{f}}{k_{nf}} \mathit{Pr} D_{f} \varPhi ''= 0, \end{aligned}$$
(4.2)
$$\begin{aligned}& \varPhi '' + \frac{1}{2}\mathit{Sc} \eta \varPhi '+ \mathit{Sc} \mathit{Sr} \theta'' = 0, \end{aligned}$$
(4.3)

subject to the appropriately modified boundary conditions (2.18). The exact solutions of these equations cannot be easily obtained. The numerical solutions were obtained using the spectral relaxation method (SRM).

4.2 Final steady state flow

In this case, we have \(\xi= 1\) when \(t \rightarrow\infty\), corresponding to \(f(\eta,1)= f(\eta)\), \(\theta(\eta,1) = \theta(\eta)\) and \(\varPhi (\eta,1)= \varPhi (\eta)\). Equations (2.12) to (2.14) reduce to the following forms:

$$\begin{aligned}& f'''+f f''- f^{\prime 2}+1+\mathit{Ha}^{2}\bigl(1-f' \bigr)+GR_{t} \theta+\mathit{Gr}_{c} \varPhi = 0, \end{aligned}$$
(4.4)
$$\begin{aligned}& \theta'' + \frac{k_{f}}{k_{nf}}\mathit{Pr} \phi_{2}\bigl(f \theta'+\delta\theta \bigr)+ \frac{k_{f}}{k_{nf}}\mathit{Pr} D_{f} \varPhi ''= 0, \end{aligned}$$
(4.5)
$$\begin{aligned}& \varPhi '' + \mathit{Sc} \bigl(f\varPhi '- \gamma \varPhi + \mathit{Sr} \theta''\bigr) = 0, \end{aligned}$$
(4.6)

subject to the boundary conditions (2.18). Equations (4.1) to (4.6) were solved using the SRM, Motsa [23].

The spectral relaxation method (SRM) is an iterative procedure that employs the Gauss-Seidel type of relaxation approach to linearize and decouple the system of differential equations. Further details of the rules of the SRM can be found in [24, 25]. The linear terms in each equation are evaluated at the current iteration level (denoted by \(r+1\)) and the non-linear terms are assumed to be known from the previous iteration level (denoted by r). The linearized form of (2.13)-(2.15) is

$$\begin{aligned}& f_{r+1}''' + a_{1,r} f_{r+1}'' + a_{2,r} f_{r+1}' - \phi_{1} \xi(1 - \xi) \frac{\partial f'}{\partial\xi} = R_{1,r}, \end{aligned}$$
(4.7)
$$\begin{aligned}& \theta_{r+1}'' + b_{1,r} \theta_{r+1}' + b_{2,r} \theta_{r+1} - \frac{k_{f}}{k_{nf}}\mathit{Pr}\phi_{2} \xi(1- \xi)\frac{\partial\theta }{\partial\xi} = R_{2,r}, \end{aligned}$$
(4.8)
$$\begin{aligned}& \phi_{r+1}'' + c_{r,1} \phi_{r+1}' + c_{2,r} \phi_{r+1} - \mathit{Sc}\xi (1- \xi)\frac{\partial\phi}{\partial\xi} = R_{3,r}, \end{aligned}$$
(4.9)

where

$$\begin{aligned}& a_{1,r} = \phi_{1} \biggl[ \frac{\eta}{2}(1-\xi) + \xi f_{r} \biggr],\qquad a_{2} = -\phi_{1} \xi \mathit{Ha}^{2}, \\& R_{1,r} = - \phi_{1}\bigl[\xi\bigl(1 - f_{r}^{\prime 2} \bigr) + \mathit{Ha}^{2} + \mathit{Gr}_{t} \theta_{r} + \mathit{Gr}_{c} \phi_{r}\bigr], \\& b_{1,r} = \frac{k_{f}}{k_{nf}}\mathit{Pr}\phi_{2} \biggl[ \frac{\eta}{2}(1-\xi ) + \xi f_{r+1} \biggr],\qquad b_{2,r} = \frac{k_{f}}{k_{nf}}\mathit{Pr}\phi_{2} \xi, \\& R_{2,r} = -\frac{k_{f}}{k_{nf}}\mathit{Pr} D_{f} \varPhi _{r}, \\& c_{1,r} = \frac{\eta}{2}(1-\xi)\mathit{Sc} + \xi f_{r+1},\qquad c_{2,r} = -\mathit{Sc}\xi \gamma, \\& R_{3,r} = -\mathit{Sc} \mathit{Sr} \theta_{r+1}''. \end{aligned}$$

Equations (4.7)-(4.9) are now linear and decoupled. The equations can be solved sequentially to obtain approximate solutions for \(f(\eta,\xi)\), \(\theta(\eta,\xi)\) and \(\phi(\eta,\xi)\). In this study, the Chebyshev spectral collocation method was used to discretize in η and finite differences used to discretize in ξ directions. Starting from initial guesses for f, θ and ϕ, equations (4.7)-(4.9) were solved iteratively until the approximate solutions converged within a certain prescribed tolerance level. The accuracy of the results was validated against results from the literature for some special cases of the governing equations.

5 Results and discussion

The system of partial differential equations (2.13) to (2.15) subject to boundary conditions (2.18) were solved numerically using the spectral relaxation method (SRM) for Cu-water and Ag-water nanofluids. The thermophysical properties of the nanofluids used in the numerical simulations are given in Table 1.

Table 1 Thermophysical properties of the base fluid and the nanoparticles [ 29 ] and [ 30 ]
Full size table

To determine the accuracy of our numerical results, the skin friction coefficient is compared with the published results of Jafar et al. [15], Wang [31] and Suali et al. [32] in Tables 2-4. Here we have varied the stretching parameter while keeping other physical parameters fixed. Table 2 gives a comparison of the SRM results with those obtained by Jafar et al. [15] and Wang [31] when \(\mathit{Ha} = \mathit{Gr}_{t} = \mathit{Gr}_{c} = \delta= D_{f} = \mathit{Sc} = \mathit{Sr} = \gamma= \phi= 0\), \(\mathit{Pr} = 1\) and \(\xi=1\) for different values of the stretching/shrinking parameter. It is observed that for increasing λ, the present results are in good agreement with results in the literature.

Table 2 Comparison of the SRM result with Wang [ 31 ] and Jafar et al. [ 15 ] for the skin friction coefficient \(\pmb{f''(0,1)}\) for different stretching rates
Full size table
Table 3 Comparison of the SRM results with Wang [ 31 ] and Jafar et al. [ 15 ] for the skin friction coefficient \(\pmb{f''(0,1)}\) for different stretching rates
Full size table
Table 4 Comparison of the SRM result with Suali et al. [ 32 ] for the skin friction coefficient for different stretching/shrinking sheet rates
Full size table

Table 4 gives the skin friction coefficient for selected stretching λ parameter values. Here we note that as the stretching rate decreases, the skin friction coefficient increases. These results are in good agreement with those obtained by Suali et al. [32].

The effects of the nanoparticle volume fraction on the fluid velocity, temperature, concentration profiles as well as skin friction, local Nusselt and Sherwood numbers are given in Figures 1-4. It is evident that the solute concentration, skin friction and the local Nusselt number decrease with increasing nanoparticle volume fraction while the velocity, temperature, and the local Sherwood number increase. This is because with an increase in nanoparticles volume fraction, the thermal conductivity of the nanofluid increases, which reduces the thermal boundary layer thickness and the temperature gradient at the wall.

Figure 1
figure 1

Effect of nanoparticle value fraction ϕ on velocity for \(\pmb{D_{f} = 0.01}\) , \(\pmb{\lambda= 0.5}\) , \(\pmb{\mathit{Gr}_{t} = 0.01}\) , \(\pmb{\mathit{Gr}_{c} = 0.01}\) , \(\pmb{\mathit{Pr} = 7}\) , \(\pmb{\mathit{Ha} = 2}\) , \(\pmb{\delta= 0.1}\) , \(\pmb{\mathit{Sc} = 1}\) , \(\pmb{\mathit{Sr} = 1}\) , \(\pmb{f_{w} = 1}\) , \(\pmb{\gamma= 0.1}\) and \(\pmb{\xi= 0.5}\) .

Full size image
Figure 2
figure 2

Effect of various nanoparticle value fractions ϕ on (a) temperature profiles and (b) concentration profiles when \(\pmb{D_{f} = 0.01}\) , \(\pmb{\lambda= 0.5}\) , \(\pmb{\mathit{Gr}_{t} = 0.01}\) , \(\pmb{\mathit{Gr}_{c} = 0.01}\) , \(\pmb{\mathit{Pr} = 7}\) , \(\pmb{\mathit{Ha} = 2}\) , \(\pmb{\delta= 0.1}\) , \(\pmb{\mathit{Sc} = 1}\) , \(\pmb{\mathit{Sr} = 1}\) , \(\pmb{f_{w} = 1}\) , \(\pmb{\gamma = 0.1}\) and \(\pmb{\xi= 0.5}\) .

Full size image
Figure 3
figure 3

Effect of various nanoparticle value fractions ϕ on the skin friction coefficient for \(\pmb{D_{f} = 0.01}\) , \(\pmb{\lambda= 0.5}\) , \(\pmb{\mathit{Gr}_{t} = 0.01}\) , \(\pmb{\mathit{Gr}_{c} = 0.01}\) , \(\pmb{\mathit{Pr} = 7}\) , \(\pmb{\mathit{Ha} = 2}\) , \(\pmb{\delta= 0.1}\) , \(\pmb{\mathit{Sc} = 1}\) , \(\pmb{\mathit{Sr} = 1}\) , \(\pmb{f_{w} = 1}\) and \(\pmb{\gamma= 0.1}\) .

Full size image
Figure 4
figure 4

Effect of nanoparticle volume fraction ϕ on (a) the heat transfer coefficient and (b) the mass transfer coefficient when \(\pmb{D_{f} = 0.01}\) , \(\pmb{\lambda= 0.5}\) , \(\pmb{\mathit{Gr}_{t} = 0.01}\) , \(\pmb{\mathit{Gr}_{c} = 0.01}\) , \(\pmb{\mathit{Pr} = 7}\) , \(\pmb{\mathit{Ha} = 2}\) , \(\pmb{\delta= 0.1}\) , \(\pmb{\mathit{Sc} = 1}\) , \(\pmb{\mathit{Sr} = 1}\) , \(\pmb{f_{w} = 1}\) and \(\pmb{\gamma= 0.1}\) .

Full size image

The axial velocity in the case of an Ag-water nanofluid is comparatively higher than that in the case of a Cu-water nanofluid. The temperature distribution in an Ag-water nanofluid is higher than that in a Cu-water nanofluid and this is explained by the observation that the thermal conductivity of silver is higher than that of copper. The concentration boundary layer thickness is higher for the case of a Cu-water than that for the case of an Ag-water nanofluid.

Figure 3 shows that the skin friction coefficient decreases monotonically with increasing ξ. The result is true for both types of fluids. The maximum value of the skin friction in the case of a Cu-water nanofluid is achieved at a smaller value of ξ in comparison with an Ag-water nanofluid. Furthermore, in this paper it is found that the Ag-water nanofluid shows less drag as compared to the Cu-water nanofluid. The dimensionless wall heat transfer rate and the dimensionless wall mass transfer rate are shown as functions of ξ in Figure 4(a) and (b), respectively. We observe that the wall heat transfer rate decreases while the opposite is true in case of the wall mass transfer rate. The Cu-water nanofluid exhibits higher wall heat transfer rate as compared to the Ag-water nanofluid, while the Cu-water nanofluid exhibits less than the Ag-water nanofluid. The presence of nanoparticle tends to increase the wall heat transfer rate and to reduce the wall mass transfer rates with increasing the values of ξ.

Figures 5-7 show the influence of the Hartmann number on the velocity, temperature, skin friction, the local Nusselt number and the local Sherwood number. The effect of the Hartmann number Ha is to increase the nanofluid velocity and the wall heat transfer rate,whereas it reduced the skin friction coefficient and the wall mass transfer rate. A similar observation was made by Jafar et al. [15]. The momentum boundary layer thickness increases with increase in the Hartmann number.

Figure 5
figure 5

Effect of the Hartmann number Ha on velocity profiles for \(\pmb{D_{f} = 0.01}\) , \(\pmb{\phi= 0.2}\) , \(\pmb{\mathit{Gr}_{t} = 0.01}\) , \(\pmb{\mathit{Gr}_{c} = 0.01}\) , \(\pmb{\mathit{Pr} = 7}\) , \(\pmb{f_{w} = 1}\) , \(\pmb{\delta= 0.1}\) , \(\pmb{\mathit{Sc} = 1}\) , \(\pmb{\mathit{Sr} = 1}\) , \(\pmb{\lambda= -1.15}\) , \(\pmb{\gamma= 3}\) and \(\pmb{\xi= 0.5}\) .

Full size image
Figure 6
figure 6

Effect of the Hartmann number Ha on the skin friction coefficient for \(\pmb{D_{f} = 0.01}\) , \(\pmb{\phi= 0.2}\) , \(\pmb{\mathit{Gr}_{t} = 0.01}\) , \(\pmb{\mathit{Gr}_{c} = 0.01}\) , \(\pmb{\mathit{Pr} = 7}\) , \(\pmb{f_{w} = 1}\) , \(\pmb{\delta= 0.1}\) , \(\pmb{\mathit{Sc} = 1}\) , \(\pmb{\mathit{Sr} = 1}\) , \(\pmb{\lambda= -1.15}\) and \(\pmb{\gamma= 3}\) .

Full size image
Figure 7
figure 7

Effect of various values of the Hartmann number Ha on (a) the heat transfer coefficient and (b) the mass transfer coefficient when \(\pmb{D_{f} = 0.01}\) , \(\pmb{\phi= 0.2}\) , \(\pmb{\mathit{Gr}_{t} = 0.01}\) , \(\pmb{\mathit{Gr}_{c} = 0.01}\) , \(\pmb{\mathit{Pr} = 7}\) , \(\pmb{f_{w} = 1}\) , \(\pmb{\delta= 0.1}\) , \(\pmb{\mathit{Sc} = 1}\) , \(\pmb{\mathit{Sr} = 1}\) , \(\pmb{\lambda= -1.15}\) and \(\pmb{\gamma= 3}\) .

Full size image

Figure 6 shows the skin friction coefficient as a function of ξ. It is clear that for Ag-water and Cu-water nanofluids, the skin friction reduces when ξ increases. We note that the Cu-water nanofluid exhibits higher drag to the flow as compared to the Ag-water nanofluid. Figure 7 shows the wall heat and mass transfer rates for a different Hartmann number Ha, it is clear that the value of wall heat transfer rate increases as ξ increases, in the case of an Ag-water nanofluid it is less than in the case of a Cu-water nanofluid. Further, the wall mass transfer rate increases up to the value of ξ before reducing.

Figures 8-11 show the velocity, temperature, concentration of nanofluid with skin friction, the wall heat and mass transfer rates for various values of the suction/injection parameter. We observe that the velocity boundary layer thickness decreases with increasing values of the suction parameter. This is because due to suction, the fluid is removed from the system which reduces the momentum boundary layer thickness. Similarly, the boundary layer thickness increases with increase of the injection parameter as injection allows the fluid to enter the system. The thermal boundary layer thickness decreases due to injection, while it increases with suction. The effect of the suction/injection parameter is to increase the concentration profile at the surface. Beyond this critical value, the concentration profile decreases with increasing suction/injection. The solute concentration boundary layer thickness is larger for the case of a Cu-water nanofluid than that for the case of an Ag-water nanofluid (see Figure 9). The skin friction coefficient decreases with increasing the values of ξ. It is obvious that the skin friction for the case of an Ag-water nanofluid is relatively less than that for the case of a Cu-water nanofluid (see Figure 10).

Figure 8
figure 8

Effect of suction/injection on velocity profiles when \(\pmb{D_{f} = 0.01}\) , \(\pmb{\phi= 0.2}\) , \(\pmb{\mathit{Gr}_{t} = 0.01}\) , \(\pmb{\mathit{Gr}_{c} = 0.01}\) , \(\pmb{\mathit{Pr} = 7}\) , \(\pmb{\mathit{Ha} = 2}\) , \(\pmb{\delta= 0.2}\) , \(\pmb{\mathit{Sc} = 1}\) , \(\pmb{\mathit{Sr} = 1}\) , \(\pmb{\lambda= 0.5}\) , \(\pmb{\gamma= 3}\) and \(\pmb{\xi= 0.5}\) .

Full size image
Figure 9
figure 9

Effect of suction/injection on (a) temperature profiles and (b) concentration profiles for \(\pmb{D_{f} = 0.01}\) , \(\pmb{\phi= 0.2}\) , \(\pmb{\mathit{Gr}_{t} = 0.01}\) , \(\pmb{\mathit{Gr}_{c} = 0.01}\) , \(\pmb{\mathit{Pr} = 7}\) , \(\pmb{\mathit{Ha} = 2}\) , \(\pmb{\delta= 0.2}\) , \(\pmb{\mathit{Sc} = 1}\) , \(\pmb{\mathit{Sr} = 1}\) , \(\pmb{\lambda= 0.5}\) , \(\pmb{\gamma= 3}\) and \(\pmb{\xi= 0.5}\) .

Full size image
Figure 10
figure 10

Effect of the suction/injection parameter on the skin friction coefficient for \(\pmb{D_{f} = 0.01}\) , \(\pmb{\phi= 0.2}\) , \(\pmb{\mathit{Gr}_{t} = 0.01}\) , \(\pmb{\mathit{Gr}_{c} = 0.01}\) , \(\pmb{\mathit{Pr} = 7}\) , \(\pmb{\mathit{Ha} = 2}\) , \(\pmb{\delta= 0.2}\) , \(\pmb{\mathit{Sc} = 1}\) , \(\pmb{\mathit{Sr} = 1}\) , \(\pmb{\lambda= 0.5}\) and \(\pmb{\gamma= 3}\) .

Full size image
Figure 11
figure 11

Effect of the suction/injection parameter on (a) the heat transfer coefficient and (b) the mass transfer coefficient when \(\pmb{D_{f} = 0.01}\) , \(\pmb{\phi= 0.2}\) , \(\pmb{\mathit{Gr}_{t} = 0.01}\) , \(\pmb{\mathit{Gr}_{c} = 0.01}\) , \(\pmb{\mathit{Pr} = 7}\) , \(\pmb{\mathit{Ha} = 2}\) , \(\pmb{\delta= 0.2}\) , \(\pmb{\mathit{Sc} = 1}\) , \(\pmb{\mathit{Sr} = 1}\) , \(\pmb{\lambda= 0.5}\) and \(\pmb{\gamma= 3}\) .

Full size image

The axial distributions of the wall heat and mass transfer rates are shown in Figure 11(a) and (b), respectively. The wall heat transfer rate increased with ξ, and we observe that the heat transfer rate is higher for a Cu-water nanofluid than for an Ag-water nanofluid. It is interesting to note that with suction (\(f_{w}=-1\)), the heat transfer rate is less for an Ag-water nanofluid than for a Cu-water nanofluid up to a certain value of ξ. Beyond this point, the heat transfer rate is higher for an Ag-water nanofluid as compared to a Cu-water nanofluid, while the wall mass transfer rate increases monotonically with ξ to a maximum values before reducing. It is shown that the mass transfer rate is higher for a Cu-water nanofluid than for an Ag-water nanofluid. The opposite behavior is observed in the case of suction when \(f_{w} = -1\). The mass transfer rate for an Ag-water nanofluid is higher than that for a Cu-water nanofluid up to a certain value of ξ, and beyond this critical value, the mass transfer in an Ag-water nanofluid is less than that in a Cu-water nanofluid, Figure 11(b).

The influence of stretching/shrinking on velocity, temperature, solutal concentration profiles, the skin friction coefficient, wall heat and mass transfer rates are shown in Figures 12-15. Figure 12 shows that the momentum boundary layer thickness increases with the stretching/shrinking rate. This may be attributed to the fact than an increase in the stretching parameter enhances the velocity of the nanofluid which in turn enhances the momentum boundary layer thickness.

Figure 12
figure 12

Effect of stretching/shrinking parameter values λ on velocity profiles for \(\pmb{D_{f} = 0.01}\) , \(\pmb{\phi= 0.2}\) , \(\pmb{\mathit{Gr}_{t} = 0.01}\) , \(\pmb{\mathit{Gr}_{c} = 0.01}\) , \(\pmb{\mathit{Pr} = 7}\) , \(\pmb{\mathit{Ha} = 2}\) , \(\pmb{\delta= 0.1}\) , \(\pmb{\mathit{Sc} = 1}\) , \(\pmb{\mathit{Sr} = 1}\) , \(\pmb{f_{w} = 1}\) , \(\pmb{\gamma= 0.1}\) and \(\pmb{\xi= 0.5}\) .

Full size image
Figure 13
figure 13

Effect of various stretching/shrinking parameter values λ on (a) temperature profiles and (b) concentration profiles for \(\pmb{D_{f} = 0.01}\) , \(\pmb{\phi= 0.2}\) , \(\pmb{\mathit{Gr}_{t} = 0.01}\) , \(\pmb{\mathit{Gr}_{c} = 0.01}\) , \(\pmb{\mathit{Pr} = 7}\) , \(\pmb{\mathit{Ha} = 2}\) , \(\pmb{\delta= 0.1}\) , \(\pmb{\mathit{Sc} = 1}\) , \(\pmb{\mathit{Sr} = 1}\) , \(\pmb{f_{w} = 1}\) , \(\pmb{\gamma= 0.1}\) and \(\pmb{\xi= 0.5}\) .

Full size image
Figure 14
figure 14

Effect of stretching/shrinking parameter values λ on the skin friction coefficient for \(\pmb{D_{f} = 0.01}\) , \(\pmb{\phi= 0.2}\) , \(\pmb{\mathit{Gr}_{t} = 0.01}\) , \(\pmb{\mathit{Gr}_{c} = 0.01}\) , \(\pmb{\mathit{Pr} = 7}\) , \(\pmb{\mathit{Ha} = 2}\) , \(\pmb{\delta= 0.1}\) , \(\pmb{\mathit{Sc} = 1}\) , \(\pmb{\mathit{Sr} = 1}\) , \(\pmb{f_{w} = 1}\) and \(\pmb{\gamma = 0.1}\) .

Full size image
Figure 15
figure 15

Effect of various stretching/shrinking parameter values λ on (a) the heat transfer coefficient and (b) the mass transfer coefficient for \(\pmb{D_{f} = 0.01}\) , \(\pmb{\phi= 0.2}\) , \(\pmb{\mathit{Gr}_{t} = 0.01}\) , \(\pmb{\mathit{Gr}_{c} = 0.01}\) , \(\pmb{\mathit{Pr} = 7}\) , \(\pmb{\mathit{Ha} = 2}\) , \(\pmb{\delta= 0.1}\) , \(\pmb{\mathit{Sc} = 1}\) , \(\pmb{\mathit{Sr} = 1}\) , \(\pmb{f_{w} = 1}\) and \(\pmb{\gamma= 0.1}\) .

Full size image

Figure 13 shows that the thermal and concentration boundary layer thicknesses decrease as the stretching rate increases. For the shrinking case, when \(\lambda= -2\), the momentum boundary layer for an Ag-water nanofluid is greater than that for a Cu-water nanofluid, while the opposite is observed for the stretching case when \(\lambda = 2\). The Ag-water nanofluid thermal boundary is higher than that of a Cu-water nanofluid (see Figure 13(a)). The solutal concentration increases up to a critical η, and beyond this critical value the concentration profile decreases (see Figure 13(b)). We observe that solute concentration profiles are larger for the case of a Cu-water than those for the case of an Ag-water nanofluid for the shrinking sheet with \(\lambda= -2\), while the opposite is true for the stretching sheet with \(\lambda= 2\).

Figure 14 shows the effect of stretching/shrinking on the shear stress, while Figure 15 shows the effect of the stretching rate on the wall heat and mass transfer rates. From Figure 14 we note that the shear stress increases with the stretching/shrinking parameter. The shear stress decreases with ξ. Figure 15(a) shows that the heat transfer rate increases with increasing λ. The mass transfer at the wall decreases with the increase in λ. The heat transfer rate is larger for the case of an Ag-water nanofluid compared to that of a Cu-water nanofluid, while the opposite is true for the mass transfer rate (see Figure 15).

6 Conclusions

We have investigated heat and mass transfer in unsteady MHD mixed convection in a nanofluid due to a stretching/shrinking sheet with heat generation and viscous dissipation. Other parameters of interest in this study included the Soret and Dufour effects. In this paper we considered Cu-water and Ag-water nanofluids and assumed that the nanoparticle volume fraction can be actively controlled at the boundary surface. We have solved the model equations using the spectral relaxation method, and to benchmark our solutions, we compared our results with some limiting cases from the literature. These results were found to be in good agreement.

The numerical simulations show, inter alia, that the skin friction factor increases with both an increase in the nanoparticle volume fraction and the stretching rate and that an increase in the nanoparticle volume fraction leads to a reduction in the wall mass transfer rate.