1 Introduction

Many controllers have been developed to control mechatronics and robotic systems. The structures of controllers are mostly considered linear and nonlinear controllers. According to the existing research literature, linear controllers are summarized such as proportional (P), proportional-integral (PI), proportional derivative (PD), proportional integral derivative (PID), linear-quadratic regulator (LQR), linear-quadratic-gaussian (LQG), H-infinity (H∞) and H2-optimal control [1, 2]. Generally, linear controllers are based on the system linearized methods. Linearized models may cause instability and poor performance because they cannot represent the full dynamic of nonlinear systems. Linearization of the system is an approximation and cannot be considered as an appropriate foundation to develop and analyze robust control law designs. Additionally, linear controllers are extremely sensitive to external/internal disturbances that can affect the system output. The performance of linear controllers is completely related to the parameters of the controller to find optimal parameters for a complex nonlinear system [3]. The performance attained is related to the level of the system when it is linear around an operating point. Moreover, the application of linear controllers to any mechatronic system is related to its number of degrees of freedom and nonlinear dynamics complexity. The analysis of nonlinear systems is more complicated due to the high complexity of dynamics. Hence, the development of a sophisticated controller needs a deeper understanding of the system dynamics. During the last decade, different types of non-linear controllers have been developed such as sliding mode control [4], model-free controllers [5], adaptive nonlinear controllers, neural network (NN) control, hybrid PID with NN controllers, adaptive neuro-fuzzy and self-learning controllers [6]. Numerous nonlinear controllers are studied to involve all nonlinear system dynamics. Nonlinear controllers take into consideration all dynamic parameters of the system to achieve high control performance. For the implementation of a nonlinear controller, a linearization model and gains of states are not required. The control of RIPS is a challenge due to the complex nonlinear dynamical model of the system. RIPS always remains a control example of an underactuated mechanical system due to its importance in the field of control engineering. The RIPS has a high degree of nonlinearity and instability. RIPS is a very important system used for the development of balancing control systems such as legged robots, aerial, satellites, robots, two-wheeled transporters, drones and rockets [7].

In the last few years, deep learning (DL) has become a novel artificial intelligence methodology to make nonlinear controllers intelligent by adding self-learning algorithms in the robotic domain [8]. Artificial neural networks (ANNs) could enhance the self-learning of systems to get the required output. Many researchers related to the RIPS have found the effectiveness and robustness of controllers using the NN with fuzzy such as radial basis neuro-fuzzy [9] and fuzzy-based multi-layer feed-forward neural networks [10].

DL has made a vast contribution to solving the complexity of nonlinearity and instability of the systems. Moreover, DL has improved the control performance of systems by setting RL and control in one application. The DL algorithm was developed to control RIPS and industrial robot arms. QL is one of the best RL algorithms and it's usually used to control autonomous robots, car parking problems, quadruped robots, and walking robots [11, 12]. RL uses learning control policies to solve the problem by optimizing reward signals. Nevertheless, QL is used to estimate the value of actions by a maximization step that tends to overvalue rather than undervalue. In this overestimation problem, the agent chooses non-optimal operations for any state due to the large Q values of the agent. The RL algorithm updates the program according to the rewards and observations obtained from the environment to maximize the expected long-term reward [13]. RL is a modelization of how human beings learn by acting on the current state of the environment and obtaining rewards. Furthermore, deep reinforcement learning (DRL) is a combination of RL and DL. RL takes into consideration the errors of agent learning calculation to make decisions. DRL algorithms may take very large inputs and decide the best actions to perform the optimization of the objective. DRL combines DL into the solution which allows agents to make decisions from input data without taking into consideration the state space of the system. DRL has been used for a different application such as video games, language processing, computer vision, transportation, healthcare, finance and robotics. Different algorithms are used in DRL such as QL, DQNL, proximal policy optimization (PPO), deep deterministic policy gradient (DDPG), and soft actor-critic (SAC) [14].

There are different works related to RL for pendulum systems. Dao et al. [15] developed an adaptive reinforcement learning strategy with sliding mode control for unknown and disturbed wheeled inverted pendulum. Zhang et al. [16] proposed a double Q-learning reinforcement learning algorithm based on a neural network for inverted pendulum control. Baek et al. [17] developed reinforcement learning to achieve real-time control of a triple-inverted pendulum. Pal et al. [18] proposed a reinforced learning approach coupled with a proportional-integral-derivative controller for the swing up and balance of an inverted pendulum. Safeea et al. [19] established a Q-learning approach to the continuous control problem of robot inverted pendulum balancing. Lim et al. [20] established a federated reinforcement learning for controlling multiple rotary inverted pendulums in edge computing environments. Chen Ming et al. [21] developed a reinforcement learning-based control of nonlinear systems using the Lyapunov stability concept and fuzzy reward scheme for a cart pole of a pendulum system. Bi et al. [22] proposed a deep reinforcement learning approach towards the pendulum swing-up Problem based on TF agents. Manrique Escobar et al. [23] studied a deep reinforcement learning control system applied to the swing-up problem of the cart pole. Kukker and Sharma [24] proposed a genetic algorithm (GA)-optimized fuzzy Lyapunov RL controller, the controller performance is tested under different types of inverted pendulum systems. In [25] Kukker and Sharma developed stochastic genetic (SA) algorithm-assisted Fuzzy Q-Learning-based robotic manipulator control.

The RL techniques established in this work have important potential for mechatronics and robotic applications compared to the works explored in the literature and their contributions are given below:

  • The developed RL methods permit the development of nonlinear controllers without understanding the physical and dynamic behavior of the system to be controlled. These RL methods are becoming more interdisciplinary, where they combine practices and theories from areas such as modern control, computational intelligence, applied optimization, and operation research to solve complex multi-objective control problems such as RIPS.

  • The developed RL methods are intelligent control solutions that demonstrate computational effectiveness in solving complex control problems. These structures could alleviate the need to build heavy-duty rule-based solution mechanisms. The various intelligent approaches are customized to ensure robust swing-up control of the SLRIP and to dynamically adapt the strategies to dynamic changes in the environment such as external disturbances and unstructured dynamic variations.

  • The developed RL algorithms hold a huge potential to contribute to the design and implementation of real-time controllers for automation and mechatronic systems aiming for optimized performances.

  • The proposed research strategy will advance the state-of-the-art knowledge in RL with a focus on intelligent control applications. Further, this type of research can be employed by a broad range of other robotic systems.

In this paper, the swing-up and stabilization control of a SLRIP is developed by training and testing RL algorithms. The developed RL control methods are compared with the PID and LQR swing-up control. The nonlinear dynamic equations are developed using the Euler–Lagrange method. The environment of the SLRIP is MATLAB/ Simulink. Actions are actuating the horizontal arm. States are the angles and velocities of the pendulum and the horizontal arm. The reward is computed according to the angles of the pendulum and horizontal arm. The reward is zero when the pendulum attends the upright position. An agent trainer system with Q and Q network learning algorithms is proposed for the data training. The QL and DQNL control methods return more accurate results in terms of improvement compared to the PID and LQR control methods.

The rest of this paper is organized as follows. In Sect. 2, the dynamic modeling and nonlinear equations of the system are explained. In Sect. 3, the related principles of RL based on QL and DQNL algorithms for the system control are described. In Sect. 4, the simulation results are described. Finally, Sect. 5, summarizes this paper.

2 Dynamic modeling of the SLRIP

The CAD model of the SLRIP is shown in Fig. 1. The SLRIP consists of a flat horizontal arm with a pivot motion and a metal pendulum installed on its end. The pivot is fixed on the top shaft of a DC servo motor. A counterbalance mass may be fixed to the other end of the flat arm to keep the system inertia in the middle. \(\uptheta_{1}\) and \(\uptheta_{2}\) are angular positions of the 1st and 2nd links, respectively. The system has two degrees of freedom (2 DOF). The SLRIP can be modelized as a serial arm robot chain to find its kinematic model using the Denavit–Hartenberg (DH) convention. The physical parameters of the system and their values are given in Table 1. Table 2 shows the DH parameters of the system.

Fig. 1
figure 1

CAD model of the SLRIP

Full size image
Table 1 List of parameters and their values of the SLRIP
Full size table
Table 2 DH parameters
Full size table

The homogeneous transformation matrix of the system is given in Eqs. (1) and (2). It is calculated using the parameters of DH from Table 2.

$${}_{{\text{i}}}^{{{\text{i}} - 1}} {\text{T}} = \left[ {\begin{array}{*{20}c} {\cos \theta _{{\text{i}}} } & { - \sin \theta _{{\text{i}}} } & 0 & {{\text{a}}_{{{\text{i}} - 1}} } \\ {\sin \theta _{{\text{i}}} {\text{cosa}}_{{{\text{i}} - 1}} } & {\cos \theta _{{\text{i}}} {\text{cosa}}_{{{\text{i}} - 1}} } & { - \sin {\text{a}}_{{{\text{i}} - 1}} } & { - \sin {\text{a}}_{{{\text{i}} - 1}} {\text{d}}_{{\text{i}}} } \\ {\sin \theta _{{\text{i}}} {\text{sina}}_{{{\text{i}} - 1}} } & {\cos \theta _{{\text{i}}} {\text{sina}}_{{{\text{i}} - 1}} } & {\cos {\text{a}}_{{{\text{i}} - 1}} } & {\cos {\text{a}}_{{{\text{i}} - 1{\text{~}}}} {\text{d}}_{{\text{i}}} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(1)
$${}_{3}^{0} {\text{T}} = { }{}_{1}^{0} {\text{T}}{}_{2}^{1} {\text{T}}{}_{3}^{2} {\text{T }}$$
(2)

where

$$\begin{aligned} & {}_{1}^{0} {\text{T}} = { }\left[ {\begin{array}{*{20}c} {\cos \uptheta_{1} } & { - \sin \uptheta_{1} } & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ {\sin \uptheta_{1} } & {\cos \uptheta_{1} } & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]{}_{2}^{1} {\text{T}} = \left[ {\begin{array}{*{20}c} {\sin \uptheta_{2} } & {\cos \uptheta_{2} } & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ 0 & 0 & {\begin{array}{*{20}c} 1 & {{\text{L}}_{1} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\cos \uptheta_{2} } \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} { - \sin \uptheta_{2} } \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] \\ & {}_{3}^{2} {\text{T}} = { }\left[ {\begin{array}{*{20}c} 1 & 0 & {\begin{array}{*{20}c} 0 & {{\text{L}}_{2} } \\ \end{array} } \\ 0 & 1 & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] \\ \end{aligned}$$
(3)
$${}_{3}^{0} {\text{T}} = \left[ {\begin{array}{*{20}c} {\sin \uptheta_{2} \cos \uptheta_{1} } & {\cos \uptheta_{2} \cos \uptheta_{1} } & { - \sin \uptheta_{1} } & {{\text{L}}_{2} \cos \uptheta_{1} \sin \uptheta_{2} - {\text{ L}}_{1} \sin \uptheta_{1} } \\ {\sin \uptheta_{2} \sin \uptheta_{1} } & {\cos \uptheta_{2} \sin \uptheta_{1} } & {\cos \uptheta_{1} } & {{\text{L}}_{1} \cos \uptheta_{1} + {\text{L}}_{2} \sin \uptheta_{1} \sin \uptheta_{2} } \\ {\cos \uptheta_{2} } & { - \sin \uptheta_{2} } & 0 & {{\text{L}}_{2} \cos \uptheta_{2} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(4)

The dynamic equations of the SLRIP are found according to the kinematic model and may be given in matrix form using Eq. (5).

$${\text{D}}\left( \uptheta \right)\ddot{\uptheta } + {\text{C}}\left( {\uptheta ,\dot{\uptheta }} \right) + {\text{G}}\left( \uptheta \right) = \left[ {\begin{array}{*{20}c} { \tau_{1} - {\text{b}}_{1} } \\ { - {\text{b}}_{2} } \\ \end{array} } \right]$$
(5)

where D(θ), \({\text{C}}\left( {\uptheta ,\dot{\uptheta }} \right)\) and G(θ) are mass matrix, Coriolis and Centripetal force vector, and gravity vector, respectively. \(\uptheta\), \({\dot{\uptheta }}\) and \(\ddot{\uptheta }\) are vectors of angular positions, angular velocities, and angular accelerations, respectively. \({\uptau }_{1}\) is the torque input for the system. The mathematical model is found using the “Euler–Lagrange” method. Equation (6) is used to calculate all terms of the mass matrix.

$${\text{D}}\left( {\uptheta } \right) = \mathop \sum \limits_{{{\text{i}} = 1}}^{{\text{n}}} \left[ {\left( {{\text{A}}_{{\text{i}}} } \right)^{{\text{T}}} {\text{m}}_{{\text{i}}} {\text{A}}_{{\text{i}}} + \left( {{\text{B}}_{{\text{i}}} } \right)^{{\text{T}}} {\text{I}}_{{\text{i}}} {\text{B}}_{{\text{i}}} } \right]$$
(6)

\({\text{m}}_{{\text{i}}} { }\) is the mass of the system arms, \({\text{I}}_{{\text{i}}} { } \in {\text{ R }}3 \times 3{ }\) is the inertia tensor of the system arms. \({\text{A}}_{{\text{i}}}\) and \({\text{B}}_{{\text{i}}}\) ∈ R 3 × n are Jacobian matrices. Furthermore, Eq. (7) is used to calculate all terms of Coriolis and Centripetal vector:

$${\text{C}}\left( {\uptheta ,\dot{\uptheta }} \right) = { }\mathop \sum \limits_{{{\text{k}} = 1}}^{{\text{n}}} \mathop \sum \limits_{{{\text{j}} = 1}}^{{\text{n}}} \left[ {{\text{c}}_{{{\text{kj}}}}^{{\text{i}}} \left( \uptheta \right)\dot{\uptheta }_{{\text{k}}} \dot{\uptheta }_{{\text{j}}} } \right]$$
(7)
$${\text{c}}_{{{\text{kj}}}}^{{\text{i}}} \left( \uptheta \right) = \frac{\partial }{{\partial {\uptheta }_{{\text{k}}} }}{\text{ D}}_{{{\text{ij}}}} { }\left( \uptheta \right) - \frac{1}{2}\frac{\partial }{{\partial {\uptheta }_{{\text{i}}} }}{\text{ D}}_{{{\text{kj}}}} { },{ }1 \le {\text{i}},{\text{ j}},{\text{ k}} \le {\text{n }}$$
(8)

Equation (9) is used to calculate the gravity vectors:

$${\text{G}}\left( \uptheta \right) = - { }\mathop \sum \limits_{{{\text{k}} = 1}}^{{\text{n}}} \mathop \sum \limits_{{{\text{j}} = 1}}^{{\text{n}}} \left[ {{\text{g}}_{{\text{k}}} {\text{ m}}_{{\text{j}}} {\text{ A}}_{{{\text{ki}}}}^{{\text{j}}} \left( \uptheta \right){ }} \right]{ }$$
(9)

The methodology to calculate the matrix elements is given as follows: \(\Delta_{{{\text{h}}_{1} }}\) and \(\Delta_{{{\text{h}}_{2} }}\) are gravity center vectors of the 1st and the 2nd links, respectively. The two vectors are determined corresponding to the coordinate systems of arms in Eqs. (10). Moreover, \({\text{I}}_{{{\text{m}}1}}\) and \({\text{I}}_{{{\text{m}}2}}\) are tensors of inertia of the 1st and the 2nd links respectively; given in Eqs. (11).

$$\Delta_{{{\text{h}}_{1} }} = \left[ {\begin{array}{*{20}c} 0 & {\frac{{{\text{L}}_{1} }}{2}} & {\begin{array}{*{20}c} 0 & 1 \\ \end{array} } \\ \end{array} } \right]{ }^{{\text{T}}} ,{ }\,\,{ }\Delta_{{{\text{h}}_{2} }} = \left[ {\begin{array}{*{20}c} {\frac{{{\text{L}}_{2} }}{2}} & 0 & {\begin{array}{*{20}c} 0 & 1 \\ \end{array} } \\ \end{array} } \right]^{{\text{T}}}$$
(10)
$${\text{I}}_{{{\text{m}}1}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & {{\text{I}}_{{{\text{zz}}_{1} }} } \\ \end{array} } \right],{\text{ I}}_{{{\text{m}}2}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & {{\text{I}}_{{{\text{zz}}_{2} }} } \\ \end{array} } \right]{ }$$
(11)

The coordinates of the mass center of arms are computed corresponding to the main coordinate system.

$${\text{h}}_{1} = {}_{1}^{0} {\text{T }}\Delta_{{{\text{h}}_{1} }} = { }\left[ {\begin{array}{*{20}c} {\cos \uptheta_{1} } & { - \sin \uptheta_{1} } & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ {\sin \uptheta_{1} } & {\cos \uptheta_{1} } & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]\,\left[ {\begin{array}{*{20}c} 0 \\ {\frac{{{\text{L}}_{1} }}{2}} \\ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \\ \end{array} } \right]{ } = \left[ {\begin{array}{*{20}c} { - \frac{{{\text{L}}_{1} \sin \uptheta_{1} }}{2}} \\ {\frac{{{\text{L}}_{1} \cos \uptheta_{1} }}{2}} \\ 0 \\ 1 \\ \end{array} } \right]$$
(12)
$${\text{h}}_{2} = {}_{2}^{0} {\text{T }}\Delta_{{{\text{h}}_{2} }} = { }\left[ {\begin{array}{*{20}c} {\frac{{{\text{L}}_{2} \cos \uptheta_{1} \sin \uptheta_{2} { }}}{2}{ } - {\text{L}}_{1} \sin \uptheta_{1} } \\ {\frac{{{\text{L}}_{2} \sin \uptheta_{1} \sin \uptheta_{2} { }}}{2} + {\text{L}}_{1} \cos \uptheta_{1} } \\ {\begin{array}{*{20}c} {\frac{{{\text{L}}_{2} \cos \uptheta_{2} }}{2}} \\ 1 \\ \end{array} } \\ \end{array} } \right]$$
(13)

where

$${}_{2}^{0}\text{T}=\left[ \begin{matrix} \sin {{\theta }_{2}}\cos {{\theta }_{1}} & \cos {{\theta }_{2}}\cos {{\theta }_{1}} & -\sin {{\theta }_{1}} & -\text{ }\!\!~\!\!\text{ }{{\text{L}}_{1}}\sin {{\theta }_{1}}\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ } \\ \sin {{\theta }_{2}}\sin {{\theta }_{1}} & \cos {{\theta }_{2}}\sin {{\theta }_{1}} & \cos {{\theta }_{1}}\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ } & {{\text{L}}_{1}}\cos {{\theta }_{1}} \\ \cos {{\theta }_{2}} & -\sin {{\text{ }\!\!\theta\!\!\text{ }}_{2}} & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]$$
(14)

The Jacobian matrix of the 1st arm is obtained by the calculation of the derivative of the vector \({\text{h}}_{1}\) according to \(\uptheta_{1}\) and \(\uptheta_{2}\). \(\xi_{i}\) denotes the type of joint, in this case \(\xi_{i}\) = 1 because it’s a rotary motion. ‘\({\text{i}}\)’ is a unit vector of the 3rd column of the coordinate system. Furthermore, the variables \({\text{z}}^{1}\) and \(\xi_{1}\) are used. The first arm is a rotational link \(\xi_{1} = 1\) and \({\text{b}}_{1} = \xi_{1} {\text{z}}^{1} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ \end{array} } \right]^{{\text{T}}}\). The Jacobian matrix of the 1st arm is calculated below:

$${\text{z}}^{1} = { }{}_{1}^{0} {\text{R i}}^{2} = \left[ {\begin{array}{*{20}c} {\cos \uptheta_{1} } & { - \sin \uptheta_{1} } & 0 \\ {\sin \uptheta_{1} } & {\cos \uptheta_{1} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\,\left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array} } \right] = { }\left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array} } \right]$$
(15)
$${\text{J}}_{1} = \left[ {\begin{array}{*{20}c} {\frac{\partial }{{\partial \theta _{1} }}\left( { - \frac{{{\text{L}}_{1} \sin \theta _{1} }}{2}} \right)} & {\frac{\partial }{{\partial \theta _{2} }}\left( { - \frac{{{\text{L}}_{1} \sin \theta _{1} }}{2}} \right)} \\ {\frac{\partial }{{\partial \theta _{1} }}\left( {\frac{{{\text{L}}_{1} \cos \theta _{1} }}{2}} \right)} & {\frac{\partial }{{\partial \theta _{2} }}\left( {\frac{{{\text{L}}_{1} \cos \theta _{1} }}{2}} \right)} \\ {\begin{array}{*{20}c} 0 \\ 0 \\ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \frac{{{\text{L}}_{1} \cos \theta _{1} }}{2}} & 0 \\ { - \frac{{{\text{L}}_{1} \sin \theta _{1} }}{2}} & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 1 & 0 \\ \end{array} } \right]$$
(16)

\({\text{J}}_{1}\) of the 1st arm can be divided into two matrices \({\text{A}}_{1}\) and \({\text{B}}_{1}\):

$${\text{A}}_{1} = \left[ {\begin{array}{*{20}c} { - \frac{{{\text{L}}_{1} \cos \uptheta_{1} }}{2}} & 0 \\ {\begin{array}{*{20}c} { - \frac{{{\text{L}}_{1} \sin \uptheta_{1} }}{2}} \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \right],{\text{B}}_{1} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ \end{array} } \right]$$
(17)

The Jacobian matrix of the 2nd arm is calculated using the derivative of the vector \({\text{h}}_{2}\) according to \(\uptheta_{1}\) and \(\uptheta_{2}\). The 2nd arm is rotational which means \(\xi_{2} = 1\) and \({\text{b}}_{2} = \xi_{2} {\text{z}}^{2} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ \end{array} } \right]^{{\text{T}}}\). The Jacobian matrix of the 2nd arm is calculated below:

$${\text{z}}^{2} = { }{}_{2}^{0} {\text{R i}}^{2} = { }\left[ {\begin{array}{*{20}c} {\cos \uptheta_{1} \sin \uptheta_{2} } & {\cos \uptheta_{1} \cos \uptheta_{2} } & { - \sin \uptheta_{1} } \\ {\sin \uptheta_{1} \sin \uptheta_{2} } &a {\cos \uptheta_{2} \sin \uptheta_{1} } & {\cos \uptheta_{1} } \\ {\cos \uptheta_{2} } & { - \sin \uptheta_{2} } & 0 \\ \end{array} } \right]\,\left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array} } \right] = { }\left[ {\begin{array}{*{20}c} { - \sin \uptheta_{1} } \\ {\cos \uptheta_{1} } \\ 0 \\ \end{array} } \right]$$
(18)
$${\text{J}}_{2} = \left[ {\begin{array}{*{20}l} {\frac{\partial }{{\partial \uptheta_{1} }}\left( {\frac{{{\text{L}}_{2} \cos \uptheta_{1} \sin \uptheta_{2} { }}}{2}{ } - {\text{L}}_{1} \sin \uptheta_{1} } \right)} \hfill & {\frac{\partial }{{\partial \uptheta_{2} }}\left( {\frac{{{\text{L}}_{2} \cos \uptheta_{1} \sin \uptheta_{2} { }}}{2}{ } - {\text{L}}_{1} \sin \uptheta_{1} } \right)} \hfill \\ {\frac{\partial }{{\partial \uptheta_{1} }}\left( {\frac{{{\text{L}}_{2} \sin \uptheta_{1} \sin \uptheta_{2} { }}}{2} + {\text{L}}_{1} \cos \uptheta_{1} } \right)} \hfill & {\frac{\partial }{{\partial \uptheta_{2} }}\left( {\frac{{{\text{L}}_{2} \sin \uptheta_{1} \sin \uptheta_{2} { }}}{2} + {\text{L}}_{1} \cos \uptheta_{1} } \right)} \hfill \\ {\frac{\partial }{{\partial \uptheta_{1} }}\left( {\frac{{{\text{L}}_{2} \cos \uptheta_{2} }}{2}} \right)} \hfill & {\frac{\partial }{{\partial \uptheta_{2} }}\left( {\frac{{{\text{L}}_{2} \cos \uptheta_{2} }}{2}} \right)} \hfill \\ 0 \hfill & { - \sin \uptheta_{1} } \hfill \\ 0 \hfill & {{\text{cos }}\uptheta_{1} } \hfill \\ 1 \hfill & 0 \hfill \\ \end{array} } \right]$$
(19)

\({\text{J}}_{2}\) of the 2nd arm is divided into two matrices \({\text{A}}_{2}\) and \({\text{B}}_{2}\):

$${\text{A}}_{2} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - \frac{{{\text{L}}_{2} \sin \uptheta_{1} \sin \uptheta_{2} { }}}{2}{ } - {\text{L}}_{1} \cos \uptheta_{1} } \\ {\frac{{{\text{L}}_{2} \cos \uptheta_{1} \sin \uptheta_{2} { }}}{2}{ } - {\text{L}}_{1} \sin \uptheta_{1} } \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\frac{{{\text{L}}_{2} \cos \uptheta_{1} \cos \uptheta_{2} { }}}{2}{ }} \\ {\frac{{{\text{L}}_{2} \cos \uptheta_{2} \cos \uptheta_{1} { }}}{2}} \\ {\frac{{ - {\text{L}}_{2} \sin \uptheta_{2} }}{2}} \\ \end{array} } \\ \end{array} } \right] \,{\text{B}}_{2} = { }\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array} } & {\begin{array}{*{20}c} { - \sin \uptheta_{1} } \\ {{\text{cos }}\uptheta_{1} } \\ 0 \\ \end{array} } \\ \end{array} } \right]$$
(20)

The mass matrices of the two arms are given in Eqs. (21) and (22), respectively.

$${\text{D}}\left( {\uptheta_{1} } \right) = {\text{ m}}_{1} {\text{ A}}_{1}^{{\text{T}}} {\text{A}}_{1} + {\text{ B}}_{1}^{{\text{T}}} {\text{ I}}_{1} {\text{B}}_{1} = { }\left[ {\begin{array}{*{20}c} {\frac{{{\text{m}}_{1} {\text{L}}_{1}^{2} }}{4} + {\text{I}}_{{{\text{zz}}_{1} }} } & 0 \\ 0 & 0 \\ \end{array} } \right]{ }$$
(21)
$${\text{D}}\left( {\uptheta_{2} } \right) = {\text{ m}}_{2} {\text{ A}}_{2}^{{\text{T}}} {\text{A}}_{2} + {\text{ B}}_{2}^{{\text{T}}} {\text{ I}}_{2} {\text{B}}_{2} = { }\left[ {\begin{array}{*{20}c} {{\text{m}}_{2} \left( {\frac{{{\text{L}}_{2}^{2} {\text{ sin}}^{2} \uptheta_{2} }}{4} + {\text{L}}_{1}^{2} } \right)} & { - \left( {\frac{{{\text{L}}_{1} {\text{ L}}_{{2{ }}} {\text{m}}_{2} {\text{ cos }}\uptheta_{2} }}{2}} \right){ }} \\ { - \left( {\frac{{{\text{L}}_{1} {\text{ L}}_{{2{ }}} {\text{m}}_{2} {\text{ cos }}\uptheta_{2} }}{2}} \right)} & {\left( {\frac{{{\text{ L}}_{{2{ }}}^{2} {\text{m}}_{2} { }}}{4} + {\text{ I}}_{{{\text{zz}}_{2} }} } \right)} \\ \end{array} } \right]{ }$$
(22)

The inertial tensors of arms are calculated based on the main coordinate system:

$${\text{I}}_{1} = {}_{1}^{0} {\text{R I}}_{{{\text{m}}1}} { }{}_{1}^{0} {\text{R}}^{{\text{T}}} { },{\text{ I}}_{2} = {}_{2}^{0} {\text{R I}}_{{{\text{m}}2}} { }{}_{2}^{0} {\text{R}}^{{\text{T}}} { }$$
(23)

\({\text{D}}\left( \uptheta \right)\) matrix of the system is provided in Eq. (24):

$${\text{D}}\left( \uptheta \right) = {\text{ D}}\left( {\uptheta_{1} } \right) + {\text{D}}\left( {\uptheta_{2} } \right) = { }\left[ {\begin{array}{*{20}c} {\frac{{{\text{m}}_{1} {\text{L}}_{1}^{2} }}{4} + {\text{I}}_{{{\text{zz}}_{1} }} + {\text{m}}_{2} \left( {\frac{{{\text{L}}_{2}^{2} {\text{ sin}}^{2} \uptheta_{2} }}{4} + {\text{L}}_{1}^{2} } \right)} & { - \left( {\frac{{{\text{L}}_{1} {\text{ L}}_{{2{ }}} {\text{m}}_{2} {\text{ cos}}\uptheta_{2} }}{2}} \right)} \\ { - \left( {\frac{{{\text{L}}_{1} {\text{ L}}_{{2{ }}} {\text{m}}_{2} {\text{ cos }}\uptheta_{2} }}{2}} \right)} & {\left( {\frac{{{\text{ L}}_{{2{ }}}^{2} {\text{m}}_{2} { }}}{4} + {\text{ I}}_{{{\text{zz}}_{2} }} } \right)} \\ \end{array} } \right]$$
(24)

The elements of the velocity coupling matrix of the two arms are found below:

$$\begin{aligned} {\text{C}}_{1} = & { }\left[ {\begin{array}{*{20}c} {{ }\frac{1}{2}{ }\frac{\partial }{{\partial \uptheta_{1} }}{\text{ D}}_{11} \left( \uptheta \right)} & {{ }\frac{1}{2}{ }\frac{\partial }{{\partial \uptheta_{1} }}{\text{ D}}_{12} \left( \uptheta \right)} \\ {\frac{\partial }{{\partial \uptheta_{2} }}{\text{ D}}_{11} \left( \uptheta \right) - { }\frac{1}{2}{ }\frac{\partial }{{\partial \uptheta_{1} }}{\text{D}}_{21} \left( \uptheta \right)} & {\frac{\partial }{{\partial \uptheta_{2} }}{\text{ D}}_{12} \left( \uptheta \right) - { }\frac{1}{2}{ }\frac{\partial }{{\partial \uptheta_{1} }}{\text{D}}_{22} \left( \uptheta \right)} \\ \end{array} } \right] \\ = & \left[ {\begin{array}{*{20}c} 0 & 0 \\ {\frac{1}{4}\left( {{\text{L}}_{2}^{2} {\text{m}}_{2} \sin \left( {2\uptheta_{2} } \right)} \right)} & {\frac{1}{2}\left( {{\text{L}}_{1} {\text{L}}_{2} {\text{m}}_{2} \sin \left( {\uptheta_{2} } \right)} \right)} \\ \end{array} } \right] \\ \end{aligned}$$
(25)
$$\begin{aligned} {\text{C}}_{2} = & { }\left[ {\begin{array}{*{20}c} {\frac{\partial }{{\partial \uptheta_{1} }}{\text{ D}}_{21} \left( \uptheta \right) - \frac{1}{2}{ }\frac{\partial }{{\partial \uptheta_{2} }}{\text{ D}}_{11} \left( \uptheta \right)} & {\frac{\partial }{{\partial \uptheta_{1} }}{\text{ D}}_{22} \left( \uptheta \right) - \frac{1}{2}{ }\frac{\partial }{{\partial \uptheta_{2} }}{\text{ D}}_{12} \left( \uptheta \right)} \\ {\frac{1}{2}\frac{\partial }{{\partial \uptheta_{2} }}{\text{ D}}_{21} \left( \uptheta \right)} & {\frac{1}{2}{ }\frac{\partial }{{\partial \uptheta_{2} }}{\text{D}}_{22} \left( \uptheta \right)} \\ \end{array} } \right] \\ = & \left[ {\begin{array}{*{20}c} { - \frac{1}{8}\left( {{\text{L}}_{2}^{2} {\text{m}}_{2} \sin \left( {2\uptheta_{2} } \right)} \right)} & { - { }\frac{1}{4}\left( {{\text{L}}_{1} {\text{L}}_{2} {\text{m}}_{2} \sin \left( {\uptheta_{2} } \right)} \right)} \\ {\frac{1}{4}\left( {{\text{L}}_{1} {\text{L}}_{2} {\text{m}}_{2} \sin \left( {\uptheta_{2} } \right)} \right)} & 0 \\ \end{array} } \right]{ } \\ \end{aligned}$$
(26)

The \({\text{C}}\left( {\uptheta ,\dot{\uptheta }} \right)\) vector is found by the verification of the elements' equality of the matrices given below.

$$\left[ {\begin{array}{*{20}c} 0 & 0 \\ {\frac{1}{4}\left( {{\text{L}}_{2}^{2} {\text{m}}_{2} \sin \left( {2\uptheta_{2} } \right)} \right)} & {\frac{1}{2}\left( {{\text{L}}_{1} {\text{L}}_{2} {\text{m}}_{2} \sin \left( {\uptheta_{2} } \right)} \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\dot{\uptheta }_{1}^{2} } & {\dot{\uptheta }_{1} \dot{\uptheta }_{2} } \\ {\dot{\uptheta }_{1} \dot{\uptheta }_{2} } & {\dot{\uptheta }_{2}^{2} } \\ \end{array} } \right]{ }$$
(27)
$$\left[ {\begin{array}{*{20}c} { - \frac{1}{8}\left( {{\text{L}}_{2}^{2} {\text{m}}_{2} \sin \left( {2\uptheta_{2} } \right)} \right)} & { - { }\frac{1}{4}\left( {{\text{L}}_{1} {\text{L}}_{2} {\text{m}}_{2} \sin \left( {\uptheta_{2} } \right)} \right)} \\ {\frac{1}{4}\left( {{\text{L}}_{1} {\text{L}}_{2} {\text{m}}_{2} \sin \left( {\uptheta_{2} } \right)} \right)} & 0 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\dot{\uptheta }_{1}^{2} } & {\dot{\uptheta }_{1} \dot{\uptheta }_{2} } \\ {\dot{\uptheta }_{1} \dot{\uptheta }_{2} } & {\dot{\uptheta }_{2}^{2} } \\ \end{array} } \right]{ }$$
(28)

The \({\text{C}}\left( {\uptheta ,\dot{\uptheta }} \right)\) vector of the system is provided below:

$${\text{C}}\left( {\uptheta ,{ }\dot{\uptheta }} \right) = \left[ {\begin{array}{*{20}c} {\frac{1}{2}\left( {{\text{L}}_{1} {\text{L}}_{2} {\text{m}}_{2} \dot{\uptheta }_{2}^{2} \sin \left( {\uptheta_{2} } \right){ }} \right) + \frac{1}{4}\left( {{\text{L}}_{2}^{2} {\text{m}}_{2} \dot{\uptheta }_{1} \dot{\uptheta }_{2} \sin \left( {2\uptheta_{2} } \right)} \right){ }} \\ { - \frac{1}{8}\left( {{\text{L}}_{2}^{2} { }\dot{\uptheta }_{1}^{2} {\text{ m}}_{2} \sin \left( {2\uptheta_{2} } \right)} \right)} \\ \end{array} } \right]$$
(29)

The gravity vector of the SLRIP is:

$${\text{G}} = \left[ {\begin{array}{*{20}c} 0 \\ { - \frac{1}{2}\left( {{\text{L}}_{2} {\text{g m}}_{2} \sin \left( {\uptheta_{2} } \right){ }} \right)} \\ \end{array} } \right]$$
(30)

The matrix form of the nonlinear equations of the system is given below:

$$\begin{aligned} & \left[ {\begin{array}{*{20}c} {\frac{{{\text{m}}_{1} {\text{L}}_{1}^{2} }}{4} + {\text{I}}_{{{\text{zz}}_{1} }} + {\text{m}}_{2} \left( {\frac{{{\text{L}}_{2}^{2} {\text{ sin}}^{2} \uptheta_{2} }}{4} + {\text{L}}_{1}^{2} } \right)} & { - \left( {\frac{{{\text{L}}_{1} {\text{ L}}_{{2{ }}} {\text{m}}_{2} {\text{ cos}} \uptheta_{2} }}{2}} \right)} \\ { - \left( {\frac{{{\text{L}}_{1} {\text{ L}}_{{2{ }}} {\text{m}}_{2} {\text{ cos }}\uptheta_{2} }}{2}} \right)} & {\left( {\frac{{{\text{ L}}_{{2{ }}}^{2} {\text{m}}_{2} { }}}{4} + {\text{ I}}_{{{\text{zz}}_{2} }} } \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot{\uptheta }_{1} { }} \\ {\ddot{\uptheta }_{2} { }} \\ \end{array} } \right] \\ & + \left[ {\begin{array}{*{20}c} {\frac{1}{2}\left( {{\text{L}}_{1} {\text{L}}_{2} {\text{m}}_{2} \dot{\uptheta }_{2}^{2} \sin \left( {\uptheta_{2} } \right){ }} \right) + \frac{1}{4}\left( {{\text{L}}_{2}^{2} {\text{m}}_{2} \dot{\uptheta }_{1} \dot{\uptheta }_{2} \sin \left( {2\uptheta_{2} } \right)} \right){ }} \\ { - \frac{1}{8}\left( {{\text{L}}_{2}^{2} \dot{\uptheta }_{1}^{2} {\text{ m}}_{2} \sin \left( {2\uptheta_{2} } \right)} \right)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ { - \frac{1}{2}\left( {{\text{L}}_{2} {\text{g m}}_{2} \sin \left( {\uptheta_{2} } \right){ }} \right)} \\ \end{array} } \right] = { }\left[ {\begin{array}{*{20}c} {{ }\tau_{1} - {\text{ b}}_{1} } \\ { - {\text{ b}}_{2} } \\ \end{array} } \right] \left( {31} \right) \\ \end{aligned}$$
(31)

The control input of the system is the torque \(\tau_{1}\) of the servo motor. The applied torque is described by Eq. (32). This torque equation is implemented in the MATLAB/Simscape model.

$${\uptau }_{1} = \frac{{{\upeta }_{{\text{m}}} {\text{k}}_{{\text{t}}} { }}}{{R_{m} }}{\text{V}}_{m} - \frac{{{\upeta }_{{\text{m}}} {\text{k}}_{{\text{t}}} {\text{k}}_{{\text{m}}} }}{{R_{m} }} \dot{\uptheta }$$
(32)

where \({\text{V}}_{m}\) is the motor input voltage, \({\text{k}}_{{\text{t}}}\) is the motor torque constant, \({\text{k}}_{{\text{m}}}\) is the motor speed constant, \({\upeta }_{{\text{m}}}\) is motor efficiency coefficient, \(R_{m}\) is terminal resistance and \(\dot{\uptheta }\) is the angular velocity. A CAD dynamic model of the SLRIP was established via MATLAB/Simscape Toolbox to prove the mathematical model. MATLAB/Simscape and CAD models of the SLRIP are shown in Fig. 2a, b, respectively. To simulate the two models, the initial conditions of the angular positions of arms are chosen as \(\uptheta_{1} = 0 ^\circ\), and \(\uptheta_{2} = 20 ^\circ\). Furthermore, the same results were obtained by two models (Fig. 3).

Fig. 2
figure 2

SLRIP: (a) Simscape model (b) CAD model in Matlab/Simulink

Full size image
Fig. 3
figure 3

Comparison of \(\uptheta_{1}\) and \(\uptheta_{2}\) obtained from mathematical and Simscape models of the SLRIP

Full size image

3 Deep reinforcement learning control for SLRIP

3.1 Q-learning

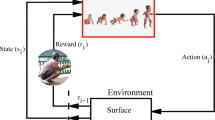
DRL is a combination of DL structure and RL idea, but it focuses more on RL. RL solves decision problems and makes RL technology practically and successfully. Furthermore, RL is a kind of machine learning based on that the system can learn from its environment by training and error minimization. The two main parts of RL are the environment and the agent. The agent is a decision-maker, and the environment defines everything outside the agent. The environment uses the agent input (\(a_{t}\)) to create the state (\(s_{t}\)) and reward \(\left( {r_{t} } \right)\) which are used as inputs for the agent as well. RL algorithm is required for the agent to calculate the optimal actions according to the policy \((\pi\)) in order to attain the maximum value of the reward. RL is a closed-loop system with has a loop connection between the agent and the environment. A loop can be named a step and an episode has N steps. The process of training is accomplished based on the step numbers (\(N_{s}\)) and episode numbers (\(N_{e}\)), where (\(N_{s} \times N_{e}\)) is the loop time. The connection between the state and the action is linked using a table called Q or Q-table as policy [26]. Each value in the table is noted as \(Q \left( {s_{i} ,a_{j} } \right)\) where \(i = \left( {1, 2, \ldots n} \right) , j = \left( {1, 2, \ldots m} \right)\). Table 3 illustrates an example of Q-Table. The block diagram of the Q-learning for SLRIP is shown in Fig. 4. The action is calculated using Eq. (33).

$$a_{t} = \left\{ {\begin{array}{*{20}c} {max Q_{t} \left( {s_{i} ,a_{j} } \right) - with \,probability \left( {1 - {\upvarepsilon }} \right)} \\ {any action \left( {a_{i} ,a_{j} } \right) - with \,probability \underline {{\upvarepsilon }} } \\ \end{array} } \right.$$
(33)

where ε is a value for any random action \(\varepsilon \in \left( {0,1} \right]\). The RL objective is to determine the optimal policy that has a maximum reward. The Q-Table is used to find the best action for each state in the environment. A Bellman equation is used at each state to get the estimated future state and reward that will be compared with other states.

$$Q_{new} \left( {s_{t} ,a_{t} } \right) \leftarrow r_{t + 1} + \gamma \left( {\max Q \left( {s_{t + 1} ,a_{t + 1} } \right)} \right)$$
(34)

where the updater or new Q-value is \(Q_{new} \left( {s_{t} ,a_{t} } \right)\). γ is a discount factor and demonstrates the importance of future rewards to the current state with \(\gamma \in \left( {0,1} \right]\). \(r_{t + 1}\) is the reward received by the agent at time \(t + 1\) while performing an action (a) to move from one state to another. \(\max Q \left( {s_{t + 1} ,a_{t + 1} } \right)\) is the maximum Q-value of the state \(s_{t + 1}\) with action \(a_{t + 1}\) at time \(t + 1\). The agent generates the new action \(a_{t}\) according to the current state \(s_{t}\) using Eq. (33), it will give order to the environment to do the new state and reward \(s_{t + 1}\) and \(r_{t + 1}\) respectively. The state \(s_{t + 1}\) is used to find \(\max Q \left( {s_{t + 1} ,a_{t + 1} } \right)\) in all Q-values related to actions in Table 3. Hence, the \(Q_{new} \left( {s_{t} ,a_{t} } \right)\) is calculated and updated in the Q-Table. Different applications need a high number of states and actions, which makes the Q-table highly large and increases the calculation time of all Q-values. Thus, DQNL is used to avoid Q-Table restrictions. The working of the Q-learning algorithm is given below:

Table 3 Q-Table
Full size table
Fig. 4
figure 4

Block diagram of the Q-Learning control for SLRIP

Full size image
figure a

3.2 Deep Q-network learning

The DQN approximates the Q-value by using a NN model as an alternative to the Q-table of the previous method. The NN creates a prediction model with the input layer which is the environment’ states; the hidden layers, and the output layer is the predicted Q-value. Furthermore, an extra NN model is used as a target model to estimate the \(\max Q \left( {s_{t + 1} ,a_{t + 1} } \right)\) and to calculate the \(Q_{new} \left( {s_{t} ,a_{t} } \right)\)[27].The error between \(Q_{new} \left( {s_{t} ,a_{t} } \right)\) and \(Q_{new\_NN} \left( {s_{t} ,a_{t} } \right)\) will be used to update the weight of the prediction model by applying the gradient descent method.

The loss function is given below:

$$Loss = \left[ {Q_{new} \left( {s_{t} ,a_{t} } \right) - Q_{new\_NN} \left( {s_{t} ,a_{t} } \right) } \right] ^{2}$$
(35)

A set of data is a requirement for the training process. Arbitrary rewards and states are created and need to be sent to the RL agent. The prediction model is applied to predict the \(Q_{new\_NN} \left( {s_{t} ,a_{t} } \right)\) by using the policy of Eq. (33) to choose the optimal action for the environment. Moreover, the environment is in a closed loop with the new reward and state. The set of training data might be given in Eq. (36).

$$E_{t} = \left( {s_{t} , a_{t} , r_{t + 1} ,a_{t + 1} } \right)$$
(36)

where the \(E_{t}\) is saved in an experience reply loop applied in the training step. One random sample \(E_{t}\) is chosen for target and prediction models with \(s_{t}\) and \(s_{t + 1}\) as inputs, respectively. The block diagram of the deep Q-network learning control for SLRIP is shown in Fig. 5. Figure 6 shows the flow chart of the DQNL algorithm.

Fig. 5
figure 5

Block diagram of the Deep Q-network learning control for SLRIP

Full size image
Fig. 6
figure 6

Flow chart of the DQNL algorithm

Full size image

4 Simulation results and discussion

4.1 Proposed methods

In this work, the SLRIP is controlled by training and testing RL algorithms, see Fig. 7. Positions and velocities obtained from 1st and 2nd links are inputs of the RL model. Furthermore, the torque input to the system is the output of the RL model. The control of the SLRIP system is based on two processes: the swing-up of and stabilization of the pendulum. The agents are developed to compute the swing angle of the pendulum until it achieves the upright position. When the pendulum is near the upright position (180° ± 10°) the proximal policy agent switches the stability action. A deep NN agent was implemented for the control of the DQNL. The parameters of the DQNL agent are presented in Table 4. The DQNL agent with 1 input layer, 25 hidden layers, and 1 output layer is proposed for the swing-up control of the SLRIP. The RL environment is the Simscape model of the SLRIP. The observation vector of RL is \(\left[ {\uptheta_{1} , \uptheta_{2} , \dot{\uptheta }_{1} , \dot{\uptheta }_{2} } \right]\). The reward (r) signal of the RL is given in the equation below:

$$r = - \uptheta_{2}^{2} - 0.2\left( {\uptheta_{1} - \uptheta_{2} } \right)^{2} - 0.15 \dot{\uptheta }_{1} + T$$
(37)

where T is the torque input:

$$T = \left\{ {\begin{array}{*{20}l} {35} \hfill & { if \uptheta_{2} \in \left( {180^\circ , \pm 10 ^\circ } \right] and \uptheta_{1} \pm 180 ^\circ } \hfill \\ 0 \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right\}$$
(38)
Fig. 7
figure 7

Simulink model of the DQNL control of the SLRIP

Full size image
Table 4 DQNL agent parameters
Full size table

Figure 7 shows the Simulink model of the DQNL control of the SLRIP. The training performance of the agent is shown in Fig. 8.

Fig. 8
figure 8

Training performance of the agent of the SLRIP

Full size image

The complexity of the DQNL algorithm is related to numerous parameters such as the dimensions of ANN, the number of neurons, episodes, iterations, and even the size of the actions and states of the environment. The parameters of the simulation and RL algorithms are described in Table 5.

Table 5 Parameters of the simulation and RL algorithm
Full size table

As mentioned in Table 5, the agent's inputs are the environment observations vector, reward signal from the environment, and Isdone, a flag to terminate episode simulation. The agent's output is the action (control signal of the system). The parameters of the RL algorithm are the sample rate is 4s, the discount factor is 0.99 and the learning rate is 0.005. The frequency at which the agent receives feedback from the environment is known as the sample rate, while the extent to which the agent updates its internal model based on the newly received information is determined by the learning rate. The MATLAB software is utilized to conduct the simulation experiment. 1000 episodes are chosen for the agent to train the SLRIP model. The mean reward per episode is around 175. The training concluded once all agents reached the stopping criteria for training. The simulation is carried out on a PC with the following configuration: CPU (11th Gen Intel(R) Core(TM) i7-1165G7 @ 2.80GHz 1.69 GHz) and RAM (16 GB). The QL algorithm demonstrates convergence after a 12-h training process, whereas a mere 0.70 h suffice to train the DQNL algorithm, thereby reducing the training time by a significant 94.16%.

The design of QL and DNQL controllers can pose several challenges in simulation, one of the main difficulties is finding a balance between exploration and exploitation. The controller needs to explore the environment to find optimal policies. The determination of an appropriate exploration strategy is an important task, as random exploration can be inefficient, and systematic exploration can lead to sub-optimal performance. The QL and DNQL can struggle with problems that have a large state or action space. As the number of possible states or actions increases, the computation and memory requirements also increase exponentially. The training of QL and DNQL controllers is sensitive to hyperparameter settings and initial conditions, and they struggle to converge to an optimal policy. The learning process can be unstable, with the Q-values oscillating or diverging. Furthermore, ensuring the convergence and stability of the learning algorithm requires careful consideration of learning rates, discount factors, and other parameters. In environments where rewards are sparse or delayed, it can be challenging for Q-learning and DNQL agents to learn effective policies. Without frequent rewards, it may take a considerable amount of time for the agent to learn desired behaviors or to explore the state space adequately. Moreover, in environments where rewards are sparse or delayed, it can be challenging for QL and DNQL agents to learn effective policies. Without frequent rewards, it may take a considerable amount of time for the agent to learn desired behaviors or to explore the state space adequately.

4.2 Results and discussion

The simulation results and discussion are presented in this section. The DQNL algorithm is established for the swing-up control of the SLRIP. The agent should keep the 2nd link in the upright stability position by supplying the system with a suitable torque input. DQNL algorithm should find the optimal input torque value that is needed to balance the pendulum. Moreover, the DQNL algorithm could balance the pendulum and make it stable with high efficiency. Additionally, the swing-up control of SLRIP using the DRL algorithms was tested with the conventional LQR and PID controllers to validate its effectiveness. The simulation results shown in Figs. 9, 10, and 11 indicate that all controllers have succeeded in controlling the SLRIP. The performance of controllers was studied based on the comparison of errors such as integral time absolute error (ITAE), integral time square error (ITSE), integral absolute error (IAE), and integral square error (ISE) and root mean square error (RMSE), which are given in Tables 6, 7, and 8.

Fig. 9
figure 9

Angle position \(\uptheta_{2}\) of the swing-up control of the pendulum link

Full size image
Fig. 10
figure 10

Angle position \(\uptheta_{1}\) of the swing-up control of the horizontal link

Full size image
Fig. 11
figure 11

The input control signal of the swing-up controllers

Full size image
Table 6 Comparison of \(\uptheta_{2}\) for swing-up controllers in terms of IAE, ISE, ITAE, ITSE and RMSE
Full size table
Table 7 Comparison of \(\uptheta_{1}\) for swing-up controllers in terms of IAE, ISE, ITAE, ITSE and RMSE
Full size table
Table 8 Comparison of the input control signal for swing-up controllers in terms of IAE, ISE, ITAE, ITSE, and RMSE
Full size table

According to the results presented in Table 6, it can be inferred that the RMSE serves as a critical parameter for evaluating the effectiveness of the controllers. The QL algorithm yields significantly more precise control outcomes, demonstrating an improvement percentage of 47.74% and 20.71% in terms of RMSE relative to the PID and LQR controllers, respectively. Moreover, the DQNL algorithm yields significantly more precise control outcomes, demonstrating an improvement percentage of 56.30% and 33.70% in terms of RMSE relative to the PID and LQR controllers, respectively. IAE, ISE, ITAE, and ITSE have been computed as popular performance indexes. However, their performance is not the same. Accordingly, an optimization algorithm can be incorporated into QL and DQNL algorithms to adjust the IAE, ISE, ITAE, and ITSE for both RL controllers.

Based on the results presented in Table 7, it can be inferred that the RMSE serves as a critical parameter for evaluating the effectiveness of the controllers. The QL algorithm yields significantly more precise control outcomes, demonstrating an improvement percentage of 41.40% and 2.01% in terms of RMSE relative to the PID and LQR controllers, respectively. Moreover, the DQNL algorithm yields significantly more precise control outcomes, demonstrating an improvement percentage of 48.97% and 14.67% in terms of RMSE relative to the PID and LQR controllers, respectively. IAE, ISE, ITAE, and ITSE have been computed as popular performance indexes. However, their performance is not the same. Accordingly, an optimization algorithm can be incorporated into QL and DQNL algorithms to adjust the IAE, ISE, ITAE, and ITSE for both RL controllers.

According to the results presented in Table 8, it can be inferred that the RMSE serves as a critical parameter for evaluating the effectiveness of the controllers. The QL algorithm yields significantly more precise control outcomes, demonstrating an improvement percentage of 39.72% and 5.77% in terms of RMSE relative to the PID and LQR controllers, respectively. Moreover, the DQNL algorithm yields significantly more precise control outcomes, demonstrating an improvement percentage of 40.29% and 6.66% in terms of RMSE relative to the PID and LQR controllers, respectively. IAE, ISE, ITAE, and ITSE have been computed as popular performance indexes. However, their performance is not the same. Accordingly, an optimization algorithm can be incorporated into QL and DQNL algorithms to adjust the IAE, ISE, ITAE, and ITSE for both RL controllers. Table 9 presents a summary of the improvement percentage in terms of RMSE between RL and classical controllers.

Table 9 Comparison of swing-up controllers in terms of the relative improvements’ percentages of RMSE
Full size table

In summary, The SLRIP is nonlinear and inherently unstable. It requires precise and adaptive control to maintain stability and balance. Traditional control methods developed in this work (PID, LQR) might struggle to handle the complexities and dynamic changes of the system. QL and DQNL are model-free techniques that do not require explicit knowledge of the system dynamics. They can adaptively learn the control policy by interacting with the system and observing its responses, making them suitable for handling nonlinearity and instability. Furthermore, SLRIP requires continuous control actions, such as applying torque to the 1st arm to adjust the pendulum's position. Both QL and DQNL are extended to handle continuous control problems by using function approximation techniques. These techniques enable the agent to learn a continuous control policy that can effectively balance the pendulum on top of the rotating base. In this work, the developed QL and DQNL are relevant for controlling a SLRIP due to their ability to handle nonlinearities, instability, high-dimensional state spaces, and continuous control actions. These algorithms provide an effective framework for training an agent to learn an optimal control policy in such complex and dynamic systems. Based on the findings derived from our analysis and considering the latest scholarly publications in the field, the results indicate great promise. It is essential to establish a double deep Q-network learning algorithm in order to thoroughly compare its performance with other classical controllers, such as the controller proposed by Y Dai et al. in their work [28]. Furthermore, it is crucial to conduct tests with alternative RL agents like the soft actor-critic–proximal policy optimization (SAC–PPO) technique presented in [29]. To ensure the reliability and accuracy of the RL algorithms, it is imperative to utilize real experimental setups, similar to the one employed by D. Brown et al. [30]. Additionally, to further enhance the control outcomes achieved by the RL controllers, it is recommend the development of an adaptive reinforcement learning strategy combined with sliding mode control, as demonstrated in [15].

5 Conclusion

In this paper, the RL algorithms for the swing-up and stabilization control of a SLRIP were developed in MATLAB simulation. The control approach consists of the environment, which is the Simscape model of the SLRIP, and the agent is the controller. QL and DQNL are both model-free control algorithms used without a profound background of understanding of classical control theory. The QL and DQNL agents were developed for the swing-up and stabilization control action of the SLRIP. 1000 episodes were required for the training of the agent. Furthermore, the learning algorithm is sensitive to the selection of parameters such as learning rates or discount factors and these parameters may be effective in the control of SLRIP. According to the obtained results, the QL control method returns more accurate results in terms of improvement percentage from 39.72 to 47.74% and from 2.01 to 20.71% compared to the PID and LQR control methods; respectively. Moreover, the DQNL control method returns more accurate results in terms of improvement percentage from 40.29 to 56.30% and from 6.66 to 33.70% compared to the PID and LQR control methods; respectively. For future works, RL controllers will be validated under a real experimental setup of a SLRIP. Moreover, the developed algorithm will be used to control more complex environments such as double and triple-link rotary inverted pendulum systems to prove the efficiency of the control algorithm.