1 Introduction

The global energy consumption would significantly increase within the following decades. Figure 1 depicts the energy consumption from 2020 to 2050 indicating the surge of the indicator analyzed [1, 2].

Fig. 1
figure 1

World energy demand prediction from 2020 to 2050

Full size image

The first group of main energy sources, that comprises renewable energy, nuclear energy, and fossil energy, all play an important part in providing the need for energy all over the globe. Petroleum, coal, and natural gas (NG) are also the three most significant types of fossil energy. According to various investigations, the primary fuel with the most rapid growth through 2040 will be natural gas [3,4,5]. Figure 2 depicts the overall energy usage by type of fuel. Natural gas is widely recognized as the fossil fuel that has the highest levels of safety, cleanliness, and operational effectiveness [5, 6]. This is because the carbon dioxide (CO2) emission of natural gas is about 41% less than that of other fossil fuels when burned [7].

Fig. 2
figure 2

World energy demand by sources

Full size image

CO2 is one of the resources which has been acknowledged as one of the key contributors to the phenomenon of global warming [8, 9]. Consequently, its removal and reuse from the streams and pollutants produced by industrial processes and the search for reliable and cost-effective absorbents have attracted considerable attention [10]. Absorbance in aqueous amine solutions is the method used substantially in industry for eliminating CO2 from gases. CO2 is absorbed by aqueous amine solutions via both physical and chemical absorption [11,12,13]. Figure 3 represents the process schematic of the amine-based CO2 capture.

Fig. 3
figure 3

The process of amine-based CO2 capture

Full size image

Triethanolamine (TEA), a tertiary amine, was recognized as one of the first amines utilized considering this purpose in industrial gas treatment procedures [14]. While it has been replaced by another type of amine solution such as methyldiethanolamine (MDEA) and monoethanolamine (MEA) [15], it is still prescribed for the elimination of acid gas. Recent developments have expanded the repertoire of solvents beyond amine-based solutions, ushering in new possibilities for carbon capture technologies. Notably, amine blends, as discussed in [16], have gained attention for their potential to enhance CO2 absorption efficiency and reduce energy requirements. Ionic liquids explored comprehensively in literature [17], offer intriguing prospects due to their low volatility and tunable properties, which can be tailored to specific capture scenarios. The utilization of seawater as a solvent, as exemplified by [18], presents an eco-friendly and abundant alternative with unique challenges and advantages. These emerging solvent systems, along with others not mentioned here, constitute a dynamic frontier in CO2 capture research. Hence, a wide variety of laboratory solubility data (H2S and CO2 in aqueous ethanolamine solutions) with a variety range of temperatures, pressures, solvent compositions, and acid gas loadings are now available. This data may be used to better understand the interaction between H2S and CO2 [15, 19,20,21,22]. At higher power dissipation rates, aqueous TEA solutions can absorb CO2 under equilibrium conditions in high shear jet absorbers. Both the absorption height and the required flow rate of the solution are decreased as a result of putting solution in a high shear jet absorber. This absorber will be especially effective for the removal of acid gases with low partial pressures, as well as using this in distant fields and offshore activities [23, 24].

The solubility of CO2 in an aqueous alkanolamine solution and the equilibrium CO2 loading were both calculated using a number of different models [25, 26]. The CO2 solubility in TEA was investigated by Chung [27] using a modified version of the Kent-Eisenberg model, which represents one of the most precise methods that are currently available. In their research, a modified Kent–Eisenberg model successfully matched the experimental equilibrium loading (solubility)/partial pressure pairs at different temperatures and amine concentration levels. The average absolute relative deviation (AARD) for this model was 18.9%, and it included a maximum of 163 data sets. Fouad et al. [26] also compared experimental data of TEA at 50, 75, and 100 °C. Their findings indicated that the average absolute fitting error ranges between 46.1% and 47.8%. For the purpose of offering an alternate solution method for modeling engineering processes and forecasting the variable of interest, a number of intelligent approaches have been used [13, 28,29,30]. Yarveicy et al. [31] designed the extra tree (ET) algorithm in order to anticipate the capacity for CO2 loading. The developed model could predict all the data of TEA (29 data points) with an R2 of 0.993. The AdaBoost classification and regression trees (AdaBoost-CART) was used by Ghiasi et al. [32] to simulate the CO2 loading for MEA, Diethanolamine (DEA), and TEA. Their investigation of CO2 solubility in TEA included 63 data points with an AARD of 1.41%. In addition, the effects of reaction temperature, CO2 partial pressure, and the concentration of amine on the CO2 absorption performance of MEA, DEA, and TEA were investigated by using adaptive neuro-fuzzy inference system (ANFIS) by Ghiasi et al. [28]. Unexpectedly, it was discovered that the predominant experimental condition differed for different amins. In particular, the relative effect of inputs on the CO2 loading was temperature > CO2 partial pressure > concentration of amines for MEA and TEA, but for DEA, the relative effect was adjusted to CO2 partial pressure > reaction temperature > concentration of amines. This was the case because DEA reacts more slowly than MEA and TEA. This study provided useful implications on the variety of amine design, but it has the potential to produce error as a result of insufficient amount of experimental data.

To the best of the authors' knowledge, there are no published white-box correlations for CO2 loading capacity in amine-based solutions. Our present study focuses on TEA-based systems and development of interpretable models using advanced white-box approaches, it is paramount to recognize and appreciate the growing diversity of solvent options, each contributing to the overarching goal of mitigating CO2 emissions. Hence, the purpose of this work is to assess the capacity of robust correlations to predict the equilibrium absorption of CO2 in TEA aqueous solutions. To this aim, experimental data of equilibrium absorption of CO2 in TEA aqueous solutions are gathered from the published literatures [19, 27, 33]. To this end, temperature, CO2 partial pressure, and amine concentration were regarded as input variables and CO2 loading was the output. Three famous robust correlative algorithms, namely genetic programming (GP), gene expression programming (GEP), and group method of data handling (GMDH) are used to estimate CO2 loading in an aqueous system containing TEA. In the following section, we will present the summary of our collected databank and the pre-processing of the dataset used. Furthermore, Sect. 3 provides a detailed explanation of the development of intelligent white-box algorithms. In Sect. 4, we represent various error analyses to evaluate the models’ performance, statistically. Besides, Sect. 5 provides the equations for predicting CO2 loading using GP, GEP, and GMDH techniques, and also gives a comprehensive graphical and statistical assessment of these models.

2 Data gathering and preparation

In order to construct comprehensive correlations, a large database was assembled from literature sources. Experimental values for CO2 absorption in TEA aqueous solutions were gathered from [19, 27, 33]. Table 1 gives specific precise information on the CO2 partial pressure, temperature, amine concentration, and CO2 loading capacity of TEA aqueous systems. The table illustrates the ranges of inputs/output and statistical parameters that were used throughout this investigation.

Table 1 Statistical description of the dataset used in this study
Full size table

Figure 4 presents the distribution of all parameters in the form of box plots. The forecast distribution is symmetrical when it follows a predictable pattern, sometimes represented as a bell curve. The skewness value is positive when the probability function's left side contains the vast majority of the data, and vice versa. In contrast, kurtosis describes the shape of the distribution in relation to the Gaussian distribution. A positive kurtosis, for instance, demonstrates that the statistical model has a larger peak than the usual range does [34]. Table 1 and Fig. 4 declare that the distribution and fluctuation range of the input variables are sufficiently broad to support the development of a general model for the precise prediction of CO2 loading.

Fig. 4
figure 4

Box Plot for all parameters in this study

Full size image

Figure 5 illustrates the input data part plot. Temperature has the greatest influence on the CO2 loading. It must be mentioned that the connection is negative, which suggests that as temperature rises, CO2 loading decreases and vice versa. Another important parameter worth analyzing is pressure. In this case, the relationship is positive.

Fig. 5
figure 5

Correlation matrix of input data in this study

Full size image

3 Model development

For achieving the aim of the study, three robust correlation algorithms were developed for estimation of CO2 loading. The flowchart in Fig. 6 shows the steps of the developed models. Three robust correlations namely genetic programming (GP), gene expression programming (GEP), and group method of data handling (GMDH) were considered in this research. The main goal of this study is to develop a strong correlation considering a white-box algorithm, and the equation developed with this algorithm can be easily used without special software or technical programs, thus, the application of this study is high.

Fig. 6
figure 6

Flowchart of the developed correlations in this study

Full size image

3.1 Genetic programming

Genetic programming (GP) which was proposed by John Koza in 1994 [35], is a famous robust mathematical paradigm for modeling and optimizing tasks [36, 37]. GP has been generated on the basis of genetic algorithm for the aim of generating precise networks and correlations. GP is capable of recognizing and combining beneficial program subexpressions to produce a comprehensive network that maximizes the adaptation between inputs and target values [38]. This white-box technique solves problems in extensive ranges of engineering fields, automatically [39]. Besides, it is a machine learning (ML) methodology developing evolutionary computational programs to accomplish issues for solving problems. Due to GP's flexibility, this algorithm can regenerate a mathematical correlation for estimation of various variables in different industries [40, 41]. The notable benefit of the GP method in comparison to other soft computing approaches, is that the GP paradigm prepares white-box techniques which are interpretable by scientists and engineers, readily [42].

In GP structure, to generate chromosome to be operated on a dataset, an initial population of haphazard functions is created [43]. Next, the network's framework is generated simultaneously with tuning the parameters during computation processes. These chromosomes make the next population which takes over for the following generation. These iterations are repeated until a stopping criterion is satisfied [44]. A schematic flowchart of the GP algorithm is shown in Fig. 7.

Fig. 7
figure 7

Flowchart of the GP technique

Full size image

3.2 Gene expression programming

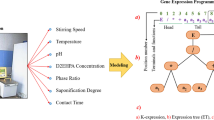
Gene Expression Programming (GEP) which was proposed by Ferreira in 2001 [45], has appeared as an enhanced artificial intelligence based symbolic regression framework [45, 46]. GEP removes some of the Genetic algorithm and GP technique's restrictions in its procedure, mathematically [47]. This paradigm is a well-known evolutionary algorithm for generation of computer programs, automatically. The two principal parameters in GEP are the expression trees (ETs) and chromosomes. On the other hand, GEP involves linear chromosomes with an established length and expressive parse trees with different shapes and sizes [48].

This fact that no specific functional representation should be detected to find out the optimum estimation for the real measurements, is one of the most noteworthy advantages of the GEP method [49]. In each common GEP, each computer program is encoded by fixed-length gene expression string, usually that is developed through nature-inspired operators like crossover and mutation [50]. Due to the simple rules that detect the platform of the ETs and their interactions, it is possible to conclude the phenotypes given the sequence of the genes, immediately [51]. Each GEP framework has various genes that are created of a head that consists of a terminal and a function. A simple flowchart of the GEP model is presented in Fig. 8. As demonstrated in this figure, steps (b) to (g) will be iterated until a stopping requirement is reached.

Fig. 8
figure 8

Flowchart of the GEP algorithm

Full size image

3.3 Group method of data handling

The first version of Group Method of Data Handling or GMDH algorithm was introduced by Ivakhnenko in the 1960s [52]. GMDH tries to solve different problems, mathematically using a set of spectrums of polynomial procedures. This data-driven algorithm can overcome the complexity and non-linearity of the networks as it permits producing precise and explicit correlations between inputs and output variables [53]. GMDH also known as polynomial neural network (PNN) consists of a group of inductive paradigms and can be used in various fields such as optimization, data mining, pattern recognition, modeling, and prediction [54]. By applying this heuristic technique, a system can be presented as a group of neurons in which different neuron couples in every layer are linked through a quadratic polynomial, and thus generate new neurons in the next layer [55]. These layers and relevant neurons provide the linking of input variables to the desired output. Figure 9 depicts a schematic flowchart of the GMDH paradigm, and Fig. 10 shows the scheme of the GMDH applied in this paper. Possessing a self-organizing nature and smooth accessibility for the users are two remarkable benefits of the GMDH method [56]. The output value concluded by the primary GMDH method is calculated as [57]:

$$y = a_{0} + \mathop \sum \limits_{i = 1}^{N} a_{i} x_{i} + \mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} a_{i,j} x_{i} x_{j} + \mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} \mathop \sum \limits_{k = 1}^{N} a_{i,j,k} x_{i} x_{j} x_{k} + \cdots$$
(1)

where, \({x}_{i,j,k,\dots }\) show the input vectors, \({a}_{0,i,j,k,\dots }\) are the polynomial coefficients, and N denotes the number of input variables. Therefore, the quadratic polynomial functions are performed for mixing the neurons in the previous layer in order to generate new variables using the following equation:

$$P_{i}^{GMDH} = a_{0} + a_{1} x_{i} + a_{2} x_{j} + a_{3} x_{i} x_{j} + a_{4} x_{i}^{2} + a_{5} x_{j}^{2}$$
(2)
Fig. 9
figure 9

Flowchart of the GMDH technique

Full size image
Fig. 10
figure 10

Flowchart of the developed GMDH in this study

Full size image

Eventually, the best combination of the two independent variables is recognized according to Eq. 3.

$$\delta_{j}^{2} = \mathop \sum \limits_{{i = N_{t} + 1}}^{N} \left( {y_{i} - P_{i}^{GMDH} } \right)^{2} < \varepsilon ,\quad j = 1 , 2 , \ldots , \left( {\begin{array}{*{20}c} N \\ 2 \\ \end{array} } \right)$$
(3)

In the above formula, \({N}_{t}\) stands for the number of training data. Hence, the subsequent independent variable will be saved if the prementioned stopping condition is reached [58].

4 Evaluation of models

Using multiple statistical indicators, the precision of the suggested models was evaluated. These are the descriptions of the measures listed [59]:

Root mean square error (RMSE):

$$RMSE = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {y_{i} - \hat{y}_{i} } \right)^{2} }$$
(4)

Standard deviation (SD):

$${\text{SD}} = \sqrt {\frac{1}{n - 1}\mathop \sum \limits_{i = 1}^{n} \left( {\frac{{y_{i} - \hat{y}_{i} }}{{y_{i} }}} \right)^{2} }$$
(5)

Mean absolute percentage error (MAPE%):

$$E_{r} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} abs\left( {\left[ {\frac{{y_{i} - \hat{y}_{i} }}{{y_{i} }}} \right]} \right) \times 100$$
(6)

Mean absolute value (MAE):

This prognosis is equivalent to the value that was anticipated for the absolute error loss or the l1-norm loss, both of which serve as measures of risk. If \(\widetilde{yi}\) is the predicted value of the i-th sample, and yi is the actual value, then the following formula may be used to determine the mean absolute error (MAE) over n "samples."

$${\text{MAE}}\left( {y,\hat{y}} \right) = \frac{1}{n}\sum\limits_{i = 0}^{{n_{{{\text{samples}}}} - 1}} {\left| {y_{i} - \hat{y}_{i} } \right|} .$$
(7)

Mean Bias Error (MBE):

$$MBE = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\tilde{y}_{i} - y_{i} } \right)}$$
(8)

The Coefficient of determination (R2):

$$R^{2} = 1 - \frac{{\mathop \sum \nolimits_{t = 1}^{T} \left( {y_{i} - \tilde{y}_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{t = 1}^{T} \left( {y_{i} - \overline{y}_{i} } \right)^{2} }}$$
(9)

where \(\tilde{y}_{i}\) is the predicted value of the i-th sample, yi is the actual value, and \(\overline{y}_{i}\) is the mean of experimental data.

Moreover, graphical analysis was used to validate the models' correctness.

5 Results and discussion

5.1 Development of the correlations

In this study, three robust correlations of GP, GEP, GMDH were developed for prediction of CO2 loading in TEA aqueous solutions. The modeling details, namely hyperparameters for proposed models, are depicted in Table 2. One of the primary advantages of these white-box approaches utilized is that it is rather possible and simple to review and apply their anticipation power employing the comprehensible equations. That is why, this study is dedicated to the presentation of the developed formulas allowing to estimate CO2 loading with three input parameters including CO2 partial pressure (kPa), amine concentration (\(\frac{mol}{L}\)), and temperature (K).

Table 2 Optimal features for implemented models
Full size table

For GP algorithm, the following correlation was developed:

$$\begin{aligned} & {\text{GP}} \\ & \quad CO_{2} \,{\text{loading}} \left( { \frac{{molCO_{2} }}{molamine} } \right) = \left( {\frac{{\left( {a_{0} \times {\text{T}} + \frac{{\left( {a_{1} \times {\text{T}} + a_{2} \times {\text{P}}} \right)}}{{\left( {a_{3} \times {\text{T}} + a_{4} } \right)}}} \right) \times \left( {a_{5} \times {\text{C}} + a_{6} } \right) \times a_{7} }}{{{\text{T}} \times \left( {a_{8} \times {\text{T}} + a_{9} } \right) \cdot \left( {\frac{{a_{10} \times {\text{T}}}}{{a_{11} \times {\text{P}}}} + a_{12} } \right) \times a_{13} }} + a_{14} } \right) \\ & \quad a_{0} = 0.097705 \\ & \quad a_{1} = 1.5222 \\ & \quad a_{2} = 0.65395 \\ & \quad a_{3} = - 0.08609 \\ & \quad a_{4} = 15.551 \\ & \quad a_{5} = 0.14348 \\ & \quad a_{6} = - 1.4122 \\ & \quad a_{7} = - 2224.4 \\ & \quad a_{8} = - 0.082256 \\ & \quad a_{9} = 14.859 \\ & \quad a_{10} = 1.0087 \\ & \quad a_{11} = 1.2999 \\ & \quad a_{12} = 12.532 \\ & \quad a_{13} = 1.4848 \\ & \quad a_{14} = 0.045162 \\ \end{aligned}$$
(10)

For GEP algorithm, the following correlation was developed:

$$\begin{aligned} & {\text{GEP}} \\ & \quad CO_{2} {\text{ loading }}\left( {{ }\frac{{molCO_{2} }}{molamine}{ }} \right) = \left( {\exp \left( {{\text{exp}}\left( {\frac{{{\text{P}} \times {\text{exp}}\left( {a_{0} \times {\text{T}}} \right) \times {\text{T}} \times \left( {a_{1} \times {\text{T}} + a_{2} } \right) \cdot a_{3} \cdot a_{4} }}{{\ln \left( {a_{5} \times {\text{P}}} \right)}}} \right) \cdot a_{6} + a_{7} } \right)} \right. \\ & \quad c_{0} = - 0.051245 \\ & \quad c_{1} = - 1.4244 \\ & \quad c_{2} = 2.2228 \\ & \quad c_{3} = 4.6629 \\ & \quad c_{4} = 0.51884 \\ & \quad c_{5} = 3.2356 \\ & \quad c_{6} = - 0.52106 \\ & \quad c_{7} = 1.4637 \\ \end{aligned}$$
(11)

For GMDH algorithm, the following correlation was developed:

$$\begin{aligned} & {\text{GMDH}}: \\ & \quad CO_{2} loading \left( {\frac{{molCO_{2} }}{molamine}} \right){ } = { } - 1.15938{ } + {\text{ C}} \times 0.95809{ } - {\text{ C}} \times {\text{N}}_{1} \times 0.175229{ } - {\text{ C}}^{2} \times 0.189917{ } + {\text{ N}}_{1} \times 1.36004{ } + {\text{ N}}_{1}^{2} \times 0.143343 \\ & \quad N_{1} = 0.0182987 + N_{2} \times 0.617315 + N_{2} \times N_{3} \times 2.06751 {-} N_{2}^{2} \times 0.542134 + N_{3} \times 0.257519 {-} N_{3}^{2} *1.31129 \\ & \quad {\text{N}}_{2} { } = { }346.54{ } - { }\ln \left( {\text{T }} \right){*}120.329{ } - \ln \left( {\text{T }} \right){\text{*ln}}({\text{P)}} \times 0.851806{ } + { }\left( {\ln \left( {\text{T }} \right)} \right)^{2} \times 10.4474{ } + {\text{ ln}}({\text{P}} \times 4.88665{ } + { }\left( {{\text{ln}}({\text{P}}} \right)^{2} \times 0.0244435 \\ & \quad {\text{N}}_{3} { } = { } - 7.38024{ } - {\text{ ln}}({\text{P}} \times 0.199505{ } + {\text{ln}}({\text{P}} \times {\text{C}} \times 0.0662905{ } + { }(\ln \left( {\text{P}} \right)^{2} \times 0.023719{ } + {\text{C}} \times 6.41163{ } - { }\left( {\text{C)}} \right)^{2} \times 1.32279 \\ \end{aligned}$$
(12)

where C is amine concentration mol/L, P is CO2 partial pressure kPa, and T is temperature (K).

5.2 Statistical evaluation of the models

From Table 3, it is observed that all the models utilized are of high reliability. RMSE values are all between 0.02 and 0.036 which is an extremely low indicators, and SD represents that predictions of all datasets are close to their corresponding experimental values, as all of the SD values are below 0.12. Moreover, R2 is equal to or more than 0.94 in all models, and MAPE% values are not more than 9.1%. In addition, MBE and MAE in all cases are far less than even 0.1. Concerning all said above, GEP, GP, and GMDH are very strong and robust techniques for the forecasting of CO2 loading in TEA aqueous solutions.

Table 3 Statistical assessment of the developed white-box correlations
Full size table

It should be mentioned that despite the effectiveness of all the algorithms applied, GMDH is the most precise and credible one. It has the highest R2 values and lowest RMSE, SD, MAPE, and MAE figures for “Train”, “Test” and “All” groups.

5.3 Graphical evaluation of the models

The most evident representation of all algorithms’ performance is the visual materials. In this paper, five diverse types of graphs were utilized including cross plots, data index graphs, residual error plots, error distribution, and cumulative frequency graphs.

Cross plot is the method to compare both real and anticipated data. As it is seen in Fig. 11, GEP is the most unprecise algorithm among the three developed having the greatest number of substantial outliers. Speaking about GP, errors are quite a few, and data points are generally located within the ± 10% error line, however, observations are slightly remote from 0% error line which reduces the efficiency of the approach. GMDH, on the other hand, has the “thinnest” line of observations located right at 0% line.

Fig. 11
figure 11

Cross plots of the developed models

Full size image

Data Index plot is another great way to visualize how good a correlation is in making predictions. This graph depicts the comparison between what each data point really is and what the robust correlation predicted it to be. From Fig. 12, it is understood that all models utilized cope with the forecast problem really well. The visual imprecision is rather small for GP, GEP, and GMDH.

Fig. 12
figure 12

Comparison of experimental and predicted values by data index

Full size image

Residual error plot depicts the difference between experimental and anticipated estimates as a function of experimental CO2 loading data. As evident from Fig. 13, GMDH has the lowest spread range between − 0.07 and 0.14. Nevertheless, the majority of the points lie within − 0.05 and 0.05 intervals. That makes the GMDH the approach with the smallest number of outliers. GP and GEP are practically similar in this case having the scope of around − 0.07 and 0.16.

Fig. 13
figure 13

Residual error plots for the developed models

Full size image

Figure 14 shows the error distribution for testing and training data. Error distribution is a kind of the visual representation which shows the spread of residual error along x-axis. In Fig. 14, GEP and GP are almost identical having the major data portion lying at the center and the spread range from − 0.2 and 0.6. On the other hand, the GMDH situation is different as it has the interval of roughly − 0.35 and 0.35. The spread is slightly lower compared to the first two algorithms, and the tails are much more centered when GP and GEP have disproportional data allocation which directly influences their accuracy.

Fig. 14
figure 14

Error distribution of predicted value for all developed algorithms

Full size image

Figure 15 is the cumulative frequency which shows absolute relative error versus data frequency. In accordance with it, GMDH is the most accurate one and can predict 80% of the data with less than 0.015 absolute residual error. The corresponding values for GEP and GP robust correlations were 0.03 and 0.06.

Fig. 15
figure 15

Cumulative frequency for all developed models

Full size image

5.4 Trend analysis

As shown, the GMDH algorithm can estimate CO2 loading based on temperature, CO2 partial pressure (kPa), and amine content (mol/L). It needs to be noted that the samples used in this research were acquired from validated experimental findings. As seen in Figs. 16 and 17, the GMDH model well predicts the experimental trend of the different temperatures. Figure 16 shows the expected and experimental outcomes for the samples at 298 K and C = 2.83 mol/L.

Fig. 16
figure 16

Trend analysis of the developed model, relationship between CO2 loading versus partial pressure at T = 298 K and C = 2.83 mol/L

Full size image
Fig. 17
figure 17

Trend analysis of the developed model, relationship between CO2 loading versus partial pressure at T = 353.2 K and C = 2 mol/L

Full size image

The anticipated and experimental outcomes of CO2 loading are also shown in Fig. 17. The created GMDH model could precisely forecast the behavior of samples at 353.2 K and C = 2 mol/L.

5.5 Sensitivity analysis

The relevancy coefficient (r) (also known as the Pearson coefficient) and the output of the GMDH model are considered to estimate the relative importance of the input coefficients for CO2 loading. This formula is also known as the Pearson correlation coefficient. The r value for each input parameter is calculated using the following procedure [60].

$$r\left(inp,x\right)=\frac{\sum_{j=1}^{n}(in{p}_{i,j }-in{p}_{m,i})({x}_{j}-{x}_{m}) }{{\left(\sum_{j=1}^{n}{\left(in{p}_{i,j}-in{p}_{m,i}\right)}^{2}\sum_{j=1}^{n}{\left({x}_{j}-{x}_{m}\right)}^{2}\right)}^{0.5}}$$
(13)

where \(n{p}_{i,j}\), \(in{p}_{m,i}\) represent the jth and average values of the ith input value and \(in{p}_{i,j}\) are T(K), CO2 partial pressure (kPa), and amine concentration. \({x}_{m}\) represents the average of the predicted CO2 loading and \({x}_{j}\) is the jth value of the predicted CO2 loading. The input parameters for the sensitivity analysis are shown in Fig. 18 and are temperature (in Kelvin), CO2 partial pressure (in kPa), and amine concentration (in moles per liter). The data visualization suggests that temperature is the most important factor in determining CO2 loading. Then, CO2 partial pressure and amine concentration are important, respectively.

Fig. 18
figure 18

Sensitivity analysis using the GMDH model

Full size image

The nonparametric equivalent of the Pearson correlation coefficient, the Spearman correlation measures the strength of the relationship between two variables based on their rankings. One of the following formulae may be used to get the Spearman correlation coefficient according to whether there are ties in the sorting (the same rank being given to two or more observations) or not.

In the absence of ties, the following formula will work:

$$\rho =1-\frac{6\sum {d}_{i}^{2}}{n({n}^{2}-1)}$$
(14)

where the difference between two rankings is called di. The total number of observations is n.

The whole Spearman correlation formula, which is a slightly modified version of Pearson's r, must be employed to handle tied ranks.

$$\rho =\frac{\frac{1}{n}\sum_{i=1}^{n}(R\left({x}_{i}\right)-\stackrel{-}{R\left(x\right)}).(R\left({y}_{i}\right)-\stackrel{-}{R\left(y\right)})}{\sqrt{(}\frac{1}{n}{\sum_{i=1}^{n}(R\left({x}_{i}\right)-\stackrel{-}{R\left(x\right)})}^{2}).\frac{1}{n}{\sum_{i=1}^{n}(R\left({y}_{i}\right)-\stackrel{-}{R\left(y\right)})}^{2}}$$
(15)

where, x and y variables' rankings are R(x) and R(y), respectively. The mean rankings are \(\stackrel{-}{R(x)}\) and \(\stackrel{-}{R(y)}\). Figure 19 shows Spearman correlation analysis. As can be seen in this figure, temperature has the highest negative impact, while CO2 partial pressure has the highest positive effect on CO2 loading.

Fig. 19
figure 19

Spearman analysis using the GMDH model

Full size image

The main difference between the Pearson and Spearman coefficients that is the Pearson coefficient works only with a linear relationship between variables, while the Spearman coefficient works with non-linear relationship. It should be also mentioned that Spearman works with rank-ordered variables, while Pearson works with raw data values. The Spearman coefficient is higher than Pearson which means that the data used in this study have correlation which is monotonic but not linear. Pearson coefficient has a lower coefficient for all parameters as pressure and temperature may have a nonlinear relationship with CO2 loading. Overall, it could be concluded that temperature and CO2 partial pressure have almost the same absolute relative effect on CO2 loading.

6 Conclusions

In this study, three advanced white-box algorithms were developed for correlating CO2 loading capacity of triethanolamine (TEA) aqueous solutions using GMDH, GP, and GEP approaches. Temperature of the system, partial pressure of CO2, and amine concentration in the aqueous phase were considered as input parameters. Sensitive analysis (Pearson and Spearman) was used to investigate the impact of input parameters on target value (CO2 loading). The following main conclusions are found in this research:

  • According to statistical and graphical analyses, the GMDH robust correlation showed the highest accuracy compared with GEP and GP. The statistical parameters of R2, RMSE, and MAPE are obtained 0.9813, 0.0222, and 5.76% for GMDH; 0.9713, 0.0275, and 7.54% for GEP and 0.9664, 0.0298, and 8.63% for GP. It can be concluded that the accuracy order of the model for CO2 loading prediction in TEA is GMDH > GEP > GP.

  • The trend analysis of CO2 loading versus CO2 partial pressure at constant temperature was investigated. The trend analysis findings demonstrated that the developed GMDH correlation successfully predicted the variation of CO2 loading with pressure. In order to provide precise predictions, the suggested GMDH model may be used instead of complicated thermodynamic models.

  • In addition, two approaches of sensitivity analysis (Spearman coefficient and Pearson coefficient) were used to examine the effect of input parameters on CO2 loading. The Pearson coefficient showed that temperature is the most important factor in determining the CO2 loading, whereas CO2 partial pressure and amine concentration play smaller roles. The Spearman coefficient has different and higher coefficient than Pearson which shows that the dataset has a nonlinear relationship between variables. This coefficient showed that the pressure and temperature have almost the same impact on CO2 loading. Overall, it could be concluded that temperature and CO2 partial pressure have almost the same absolute relative effect on CO2 loading, while amine concentration has the lowest effect on it.