Numerical conformal mapping for underground unlined tunnels with arbitrary shapes based on Symm’s method

Abstract

Conformal mapping technique is important in theoretical analysis and numerical computation for the fields of stress and displacement. In general, a unlined tunnel with arbitrary shape has no analytical solution for conformal mapping. Therefore, the study of numerical method for conformal mapping has great significance. The basic functions of numerical conformal mapping are given based on Symm’s method in this paper. Furthermore, the inverse mapping functions were deduced according to the relationships between the boundary nodes in physical and mapped plane. Compared to the other numerical methods, the presented method has some advantages such that, it is simple in concept to be understood, and can give the mapping function without iteration process. The method can be used to the forward and inverse numerical conformal mappings for multiple underground unlined tunnels with arbitrary shapes in finite and infinite domains. With the help of method of fundamental solutions (MFS), the interpolation equations were proposed for multiple underground unlined tunnels with arbitrary shapes. Finally, several numerical examples for the groups of U-shaped and rectangle tunnels have been given to verify the effectiveness of this method. The numerical results can convergent to real cases, which show that the proposed method has the properties of good accuracy and strong adaptability.

Article highlights

• Basic numerical forward conformal mapping functions are presented based on Symm’s method.

• Inverse conformal mapping is deduced to compute the original shapes of tunnels.

• MFS is applied to solve the interpolation equations.

1 Introduction

It is important to study the static or dynamic fields of stress and displacement around the underground tunnels [1,2,3,4,5,6,7]. The mechanical problems of tunnel can be solve by finite element method (FEM), finite difference method [1], semi-analytical method [2,3,4] and boundary element method (BEM) [5,6,7]. In some semi-analytical method, the boundaries of underground unlined tunnels or the other holes with arbitrary shapes are usually mapped to unit circle or annulus [8,9,10,11,12]. The complex variable method can then be applied to find the analytical solutions by Cauchy integral around the circles [13, 14]. Therefore, conformal mapping is one of the powerful tools in the pretreatment of stress and displacement analyses for the underground tunnels.

In general, there are few simple closed Jordan curves (e.g. elliptical, airfoil-shaped holes, etc.) have analytical conformal mappings with linear fractional, logarithmic, Joukowsky or Schwarz-Christoffel forms [13, 15]. Most of the conformal mappings for underground unlined tunnels with arbitrary shapes should be found by numerical methods, which are called numerical conformal mapping. The numerical conformal mapping methods include series expansion method, variational method, boundary integral method and Symm’s method, etc. [15]. The series expansion method is widely used to achieve the approximate conformal mapping [8, 9, 16]. This type of method expands the conformal mapping functions into finite series. The conformal mapping function can then be solved by repeatedly iterating the interpolation nodes on physical and mapped boundaries based on the boundary correspondence principle. It is noted that this method can only give solutions for single tunnel in general. Badreddine et al. [17] discussed some other methods, including osculation method and Fourier series method, for computing conformal maps from simply and multiply connected domains. Unfortunately, the above algorithms are relatively complex, and can only give one-direction(forward) conformal mapping. Basing on Symm’s method [18, 19], Amano [20] and Okano et al. [21, 22] applied the charge simulation method to solve the conformal mapping in multiply connected domain. In Symm’s method, the boundary and source nodes should be properly located, or they will give incorrect solutions. Additionally, the curves of boundaries will shift, and the "fence effect" of arguments will occur, if their algorithms are simply used.

In this paper, we give basic equations for numerical conformal mapping for finite or infinite domain including tunnels of arbitrary numbers and shapes based on the method of Okano et al. [21]. It is emphasized that, the basic equations for inverse numerical conformal mapping are deduced firstly in this paper. The method of fundamental solutions (MFS) is employed to solve the interpolation matrices. MFS was firstly proposed by Kupradze and Aleksidze [23, 24]. It is one of the powerful tools in solving Laplace, Helmholtz functions [25], complex analytic functions [26] and other biharmonic functions [27]. Additionally, we have proposed a approximate technique to covert semi-infinite domain to finite one. Several numerical examples have been carried out to verify the effectiveness of presented method for single, double and triple underground tunnels in infinite or semi-infinite domains, respectively. All of the numerical examples have shown that, the numerical conformal mappings can be achieved with high accuracy by our method. The proposed method is clear in concept, simple for algorithm and does not need iteration process.

The rest of paper is organized as follows. In Sect. 2, the basic equations of numerical conformal mapping base on Symm’s method are given and introduced. The interpolation equations of the boundary conditions and additional conditions for the MFS are give in Sect. 3. Several typical numerical examples for various numbers of tunnels included in infinite and semi-infinite domains are given and discussed to verify the effectiveness of the developed method in Sect. 4. Some conclusions are drawn in the last section.

2 Numerical conformal mapping based on Symm’s method

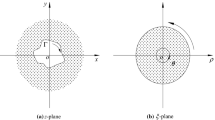
As shown in Fig. 1a, consider that there exists $M + 1$ underground tunnels with closed Jordan curves of arbitrary shapes $L_{0}$, $L_{1}$, $L_{2}$, …, $L_{M}$ in an infinite/finite domain. According to Riemann’s existence theorem, Nehari[28] noted that there exists conformal mapping $\zeta = w(z)$, which maps domains in $z$-plane to two types of bounded canonical slit domains with circular slits in $\zeta$-plane (see Fig. 1b, c). It is noted that the problem degenerates to an infinite domain including $M$ holes with boundaries $L_{m}$ ($m = 1,2,...,M$) if the outer boundary $L_{0}$ does not exist.

Fig. 1

Conformal mapping of arbitrary underground tunnels from $z$-plane to $\zeta$-plane

2.1 Basic equations of forward conformal mapping

According to Symm’s theory [18, 19], the conformal mapping $\zeta = w(z)$ can be given by two conjugate real functions, and be solved by the first kind Fredholm integral function. With the help of Symm’s theory, Okano et al. expressed the forward conformal mapping as follow [21]

$$\zeta = w(z) = (z - z_{0} )\exp [g(z) + {\text{i}}h(z)],\,z \in \overline{D} = D + \sum\limits_{m = 0}^{M} {L_{m} } ,$$

(1)

where $z = x + {\text{i}}y$, $\zeta = \xi + {\text{i}}\eta$, ${\text{i}} = \sqrt { - 1}$, $z_{0}$ is an arbitrary point in domain $D$, $g(z)$ and $h(z)$ are the two real conjugate harmonic functions.

Additionally, the harmonic functions $g(z)$ and $h(z)$ satisfy Laplace equations

$$\Delta g(z) = 0,\,\Delta h(z) = 0,\,z \in D,$$

(2)

where $\Delta = \partial^{2} /\partial x^{2} + \partial^{2} /\partial y^{2}$ is Laplace operator.

It is emphasized that, (a) the harmonic functions $g(z)$ and $h(z)$ are written for convenience, only. In fact, they are functions of real variables $x$ and $y$, i.e. $g(x,y)$ and $h(x,y)$, (b) Eq. (1) satisfies the normalized condition $w(z_{0} ) = 0$ automatically. If $z_{0}$ is included in the boundary $L_{m}$($m \ne 0$), the $m$ th boundary would be mapped to a closed circle (Fig. 1b illustrates the case that $z_{0}$ included in $L_{1}$). If $z_{0}$ is included in the boundary $L_{0}$, and is outside the boundaries $L_{m}$($m \ne 0$), the inner boundaries would be mapped to a series of circular slits inside a unit disk as shown in Fig. 1c.

Thus, the normalized conditions are given as follow

$$w(z_{0} ) = 0,\,w(z^{\prime}_{0} ) = 1,$$

(3)

where $z_{0}$ and $z^{\prime}_{0}$ are normalizing points.

According to Eqs. (1) and (3), we have

$$g(z^{\prime}_{0} ) + {\text{i}}h(z^{\prime}_{0} ) = - \ln (z^{\prime}_{0} - z_{0} )$$

(4)

Additionally, the real part of Eq. (1) is

$$g(z) = - \ln |z - z_{0} | + \ln |\zeta |.$$

(5)

Since $|\zeta | = R_{m}$ on boundary $L_{m}$, the boundary conditions are

$$g(z_{m} ) = - \ln |z_{m} - z_{0} | + \ln R_{m} ,\,m = 0,1,2,...,M,\,R_{0} = 1,$$

(6)

where $z_{m}$ is the point on $L_{m}$.

According to Eq. (6), the outer boundary $L_{0}$ is mapped to unit circle $L^{\prime}_{0}$($R_{0} = 1$) in $\zeta$-plane with normalized point $z^{\prime}_{0}$ on $L_{0}$. The harmonic function $g(z)$ can thus be achieved by solving Eq. (6). Furthermore, the conjugate pair $h(z)$ can be given by Cauchy-Riemann equations [13].

If the boundary $L_{0}$ does not exist (an infinite domain include $M$ tunnels), there are two approaches to solve the conformal mapping function as follows.

• (1) Convert infinite domain to finite one by assuming that there exists a boundary with sufficiently large radius $R_{0}$ ($R_{0} \gg |z_{m} |$). After the conformal mapping being solved, one can re-normalizes the conformal mapping functions by a scaling factor $R_{1}$.

• (2) Set the point $z^{\prime}_{0}$ on an arbitrary tunnel boundary $L_{m}$. Therefore, the boundary $L_{m}$ is mapped to unit circle $L^{\prime}_{m}$ in $\zeta$-plane, and the other holes $L_{j}$ ($j \ne m$) is mapped to circular slits $L^{\prime}_{j}$ with radius $R_{j} > 1$.

2.2 Basic equations of inverse conformal mapping

The inverse conformal mapping is another important topic to be discussed. The inverse conformal mapping is given as follow

$$z = w_{*} (\zeta ) = z_{0} + \zeta \exp [g_{*} (\zeta ) + {\text{i}}h_{*} (\zeta )],\,\zeta \in \overline{D}^{\prime} = D^{\prime} + \sum\limits_{m = 0}^{M} {L^{\prime}_{m} } ,$$

(7)

where $w_{*} (\zeta )$ is inverse conformal mapping, $g_{*} (\zeta )$ and $h_{*} (\zeta )$ are two conjugate harmonic functions in transformed $\zeta$-plane.

The normalized conditions are

$$w_{*} (0) = z_{0} ,\,\ln (z^{\prime}_{0} - z_{0} ) = g_{*} (1) + {\text{i}}h_{*} (1),$$

(8)

Accordingly, the real part of Eq. (7) is

$$g_{*} (\zeta ) = \ln |z^{\prime}_{0} - z_{0} | - \ln |\zeta |.$$

(9)

It is obviously that $|\zeta | = R_{m}$ on the boundary $L^{\prime}_{m}$. The boundary condition can thus be written as

$$g_{*} (\zeta ) = \ln |z^{\prime}_{0} - z_{0} | - R_{m} ,\,m = 0,1,2,...,M,$$

(10)

where $\zeta_{m}$ is the point on $L^{\prime}_{m}$.

With the help of Eqs. (7) and (10), the harmonic function $g_{*} (\zeta )$ and its conjugate pair $h_{*} (\zeta )$ can be solved out, theoretically. In general, the relations between boundary node $\zeta_{m}$ in $\zeta$-plane and boundary node $z_{m}$ are not known when solving the inverse conformal mapping. It is suggested that the forward conformal mapping should be solved firstly. Then, the inverse conformal mapping will be solved out according to the relations determined by forward conformal mapping.

3 Method of fundamental solutions for numerical conformal mapping

The problems for Eq. (2) under boundary conditions (6) or (10) are essentially the potential fields with Dirichlet boundaries, which could be solved by boundary element method (BEM), boundary integral method (BIM) or MFS. Symm solved these Dirichlet problems by Fredholm integral function of the first kind, which is relatively complex in numerical computation. Amano [20] and Okano et al. [21, 22] applied the charge simulation method, which is also called MFS, to solve these problems. The MFS is widely use to solve potential problems with various boundary conditions. It is based on the fundamental solutions of Laplace equation and does not need integral [23, 24, 27].

As shown in Fig. 2a, consider that there exists $M + 1$ tunnels with boundary $L_{m}$ ($m = 0,1,2,...,M$). The approximate solutions $\hat{g}(z)$ and $\hat{g}_{*} (\zeta )$ of the functions ̂ $g(z)$ and $g_{*} (\zeta )$ can be written as follows

$$\hat{g}(z) = \sum\limits_{m = 0}^{M} {\sum\limits_{k = 1}^{{N_{m} }} {\alpha_{mk} G(z,z^{\prime}_{mk} )} } ,\,\hat{g}_{*} (\zeta ) = \sum\limits_{m = 0}^{M} {\sum\limits_{k = 1}^{{N^{\prime}_{m} }} {\beta_{mk} G\left( {\zeta ,\zeta ^{\prime}_{mk} } \right)} } ,$$

(11)

where $\alpha_{mk}$ and $\beta_{mk}$ are real constants to be determined, $z^{\prime}_{mk}$ and $\zeta ^{\prime}_{mk}$ are source nodes inside/outside the boundaries $L_{m}$ and $L^{\prime}_{m}$ of physical and mapped plane as shown in Fig. 2, $N_{m}$ and $N^{\prime}_{m}$ are the numbers of source node, $G(z,z^{\prime}_{mk} )$ and $G(\zeta ,\zeta ^{\prime}_{mk} )$ are the fundamental solutions in $z$-plane and $\zeta$-plane, which can be given by [18,19,20,21,22]

$$G(z,z^{\prime}_{mk} ) = - \frac{1}{2\pi }\ln |z - z^{\prime}_{mk} |,\,G(\zeta ,\zeta ^{\prime}_{mk} ) = - \frac{1}{2\pi }\ln |\zeta - \zeta ^{\prime}_{mk} |,$$

(12)

where operator |.| denotes the distance between two points.

Fig. 2

The boundary and source nodes in the forward and inverse conformal mapping for MFS

According to Chauchy-Riemann eq. [13], the approximate solutions $\hat{h}(z)$ and $\hat{h}_{*} (\zeta )$ can be given as

$$\hat{h}(z) = \sum\limits_{m = 0}^{M} {\sum\limits_{k = 1}^{{N_{m} }} {\alpha_{mk} \arg (z - z^{\prime}_{mk} )} } ,\,\hat{h}_{*} (\zeta ) = \sum\limits_{m = 0}^{M} {\sum\limits_{k = 1}^{{N^{\prime}_{m} }} {\beta_{mk} \arg \left( {\zeta - \zeta ^{\prime}_{mk} } \right)} } ,$$

(13)

where the integral constants are neglected.

The approximate functions $\hat{g}(z) + {\text{i}}\hat{h}(z)$ and $\hat{g}_{*} (\zeta ) + {\text{i}}\hat{h}_{*} (\zeta )$ can then be written as

$$\hat{g}(z) + {\text{i}}\hat{h}(z) = - \frac{1}{2\pi }\sum\limits_{m = 0}^{M} {\sum\limits_{k = 1}^{{N_{m} }} {\alpha_{mk} \ln \left( {z - z^{\prime}_{mk} } \right)} } + \alpha_{0} ,$$

(14)

and

$$\hat{g}_{*} (\zeta ) + {\text{i}}\hat{h}_{*} (\zeta ) = - \frac{1}{2\pi }\sum\limits_{m = 0}^{M} {\sum\limits_{k = 1}^{{N^{\prime}_{m} }} {\beta_{mk} \ln (\zeta - \zeta ^{\prime}_{mk} )} } + \beta_{0} ,$$

(15)

where $\alpha_{0}$ and $\beta_{0}$ are the integral constants in Eq. (13).

The constants $\alpha_{0}$ and $\beta_{0}$ are nonzero in general. The curves of boundaries $L_{m}$ will shift, or the "fence effect" of arguments in complex variable will occur, if the constants $\alpha_{0}$ and $\beta_{0}$ are solved simply by Eqs. (6) and (10). To avoid these effects, a new boundary condition instead of the old one (6) is derived as follows[21]. Substituting $z_{0}$ in Eq. (14), we have

$$\alpha_{0} = - \ln (z^{\prime}_{0} - z_{0} ) - \frac{1}{2\pi }\sum\limits_{m = 0}^{M} {\sum\limits_{k = 1}^{{N_{m} }} {\alpha_{mk} \ln \left( {z^{\prime}_{0} - z^{\prime}_{mk} } \right)} } ,$$

(16)

according to Eq. (4).

We substitute Eq. (16) in Eq. (14), and obtain

$$\hat{g}(z) + {\text{i}}\hat{h}(z) = - \ln (z^{\prime}_{0} - z_{0} ) - \frac{1}{2\pi }\sum\limits_{m = 0}^{M} {\sum\limits_{k = 1}^{{N_{m} }} {\alpha_{mk} \ln \left( {\frac{{z - z^{\prime}_{mk} }}{{z^{\prime}_{0} - z^{\prime}_{mk} }}} \right)} } .$$

(17)

The real part of Eq. (17) is

$$\hat{g}(z) = - \ln |z^{\prime}_{0} - z_{0} | - \frac{1}{2\pi }\sum\limits_{m = 0}^{M} {\sum\limits_{k = 1}^{{N_{m} }} {\alpha_{mk} \ln \left| {\frac{{z - z^{\prime}_{mk} }}{{z^{\prime}_{0} - z^{\prime}_{mk} }}} \right|} } .$$

(18)

With help of Eqs. (6) and (17), the boundary condition on $L_{l}$ is

$$- \frac{1}{2\pi }\sum\limits_{m = 0}^{M} {\sum\limits_{k = 1}^{{N_{m} }} {\alpha_{mk} \ln \left| {\frac{{z - z^{\prime}_{mk} }}{{z^{\prime}_{0} - z^{\prime}_{mk} }}} \right|} } - \ln R_{l} = \ln \left| {\frac{{z^{\prime}_{0} - z_{0} }}{{z_{lj} - z_{0} }}} \right|,$$

(19)

where $z_{lj}$ is the node on boundary $L_{l}$ ($0 \le l \le M$, $0 \le j \le N_{j}$).

After the constant $\alpha_{mk}$ being solved, the numerical conformal mapping can be given as follow

$$\hat{w}(z) = \frac{{z - z_{0} }}{{z^{\prime}_{0} - z_{0} }}\exp \left[ { - \frac{1}{2\pi }\sum\limits_{m = 0}^{M} {\sum\limits_{k = 1}^{{N_{m} }} {\alpha_{mk} \ln \left( {\frac{{z - z^{\prime}_{mk} }}{{z^{\prime}_{0} - z^{\prime}_{mk} }}} \right)} } } \right].$$

(20)

The inverse conformal mapping can be derived as follows. Substituting $\zeta = 1$ into Eq. (15), we have

$$\hat{g}_{*} (1) + {\text{i}}\hat{h}_{*} (1) = - \frac{1}{2\pi }\sum\limits_{m = 0}^{M} {\sum\limits_{k = 1}^{{N^{\prime}_{m} }} {\beta_{mk} \ln (1 - \zeta ^{\prime}_{mk} )} } + \beta_{0} .$$

(21)

By using Eqs. (15) and (21), the integral constant $\beta_{0}$ can be eliminated. Therefore, $\hat{g}_{*} (\zeta ) + {\text{i}}\hat{h}_{*} (\zeta )$ can then be given by

$$\hat{g}_{*} (\zeta ) + {\text{i}}\hat{h}_{*} (\zeta ) = - \frac{1}{2\pi }\sum\limits_{m = 0}^{M} {\sum\limits_{k = 1}^{{N^{\prime}_{m} }} {\beta_{mk} \ln \left( {\frac{{\zeta - \zeta ^{\prime}_{mk} }}{{1 - \zeta ^{\prime}_{mk} }}} \right)} } + \hat{g}_{*} (1) + {\text{i}}\hat{h}_{*} (1).$$

(22)

According to the normalized condition (8), we have

$$\hat{g}_{*} (\zeta ) + {\text{i}}\hat{h}_{*} (\zeta ) = - \frac{1}{2\pi }\sum\limits_{m = 0}^{M} {\sum\limits_{k = 1}^{{N^{\prime}_{m} }} {\beta_{mk} \ln \left( {\frac{{\zeta - \zeta ^{\prime}_{mk} }}{{1 - \zeta ^{\prime}_{mk} }}} \right)} } + \ln \left( {z^{\prime}_{0} - z_{0} } \right).$$

(23)

The real part of Eq. (23) is

$$\hat{g}_{*} (\zeta ) = - \frac{1}{2\pi }\sum\limits_{m = 0}^{M} {\sum\limits_{k = 1}^{{N^{\prime}_{m} }} {\beta_{mk} \ln \left| {\frac{{\zeta - \zeta ^{\prime}_{mk} }}{{1 - \zeta ^{\prime}_{mk} }}} \right|} } + \ln |z^{\prime}_{0} - z_{0} |.$$

(24)

Consequently, the constant $\beta_{mk}$ in Eq. (15) can be solved by Eq. (24) as follow

$$- \frac{1}{2\pi }\sum\limits_{m = 0}^{M} {\sum\limits_{k = 1}^{{N^{\prime}_{m} }} {\beta_{mk} \ln \left| {\frac{{\zeta_{lj} - \zeta ^{\prime}_{mk} }}{{1 - \zeta ^{\prime}_{mk} }}} \right|} } = - \ln |z^{\prime}_{0} - z_{0} | + \ln R_{l} ,$$

(25)

where $\zeta_{lj}$ is the node on boundary $L^{\prime}_{l}$ ($0 \le l \le M$, $0 \le j \le N^{\prime}_{j}$).

After the constant $\beta_{mk}$ being solved, the inverse numerical conformal mapping can be written as

$$\hat{w}_{*} (\zeta ) = z_{0} + (z^{\prime}_{0} - z_{0} )\zeta \exp \left[ { - \frac{1}{2\pi }\sum\limits_{m = 0}^{M} {\sum\limits_{k = 1}^{{N^{\prime}_{m} }} {\beta_{mk} \ln \left( {\frac{{\zeta - \zeta ^{\prime}_{mk} }}{{1 - \zeta ^{\prime}_{mk} }}} \right)} } } \right].$$

(26)

It is emphasized that, the radii $R_{m}$ ($m = 1,2,...,M$) of circular silts on $L^{\prime}_{m}$ are unknown before the constants $\alpha_{mk}$ and $\beta_{mk}$ being determined. Some additional conditions are given as follows. By considering the single-valuedness of mapping function, the integral of $w(z)$ on every cavern boundary $L_{m}$ ($m = 1,2,...,M$) satisfies

$$\int {{\text{d}}w(z)} = - \frac{{\text{i}}}{2\pi }\int_{{L_{m} }} {{\text{d}}\sum\limits_{k = 1}^{M} {\alpha_{mk} \arg (z^{\prime}_{mk} )} } = 0,$$

(27)

i.e.

$$\sum\limits_{k = 1}^{{N_{m} }} {\alpha_{mk} } = 0,\,\,(m = 1,2,...,M),$$

(28)

It is also required that the numerical conformal mapping function ̂ $\hat{w}(z)$ should be invariant of scaling on the coordinate system [21]. And the invariance condition can be given by

$$\sum\limits_{m = 0}^{M} {\sum\limits_{k = 1}^{{N_{m} }} {\alpha_{mk} } } = \sum\limits_{k = 1}^{{N_{0} }} {\alpha_{0k} } = 2\pi ,$$

(29)

where the single-valuedness condition (28) is used.

Based on boundary condition (19), additional conditions (28) and (29), the interpolation matrix of $(M + 1 + \sum\nolimits_{m = 0}^{M} {N_{m} } ) \times (M + 1 + \sum\nolimits_{m = 0}^{M} {N_{m} } )$ (infinite domain) or $(M + \sum\nolimits_{m = 0}^{M} {N_{m} } ) \times (M + \sum\nolimits_{m = 0}^{M} {N_{m} } )$ (finite domain) can be generated to solve $\alpha_{mk}$.

Similar to forward conformal mapping, the additional conditions for inverse conformal mapping are

$$\sum\limits_{k = 1}^{{N_{0} }} {\beta_{0k} } = 2\pi ,\,\sum\limits_{k = 1}^{{N^{\prime}_{m} }} {\beta_{mk} } = 0,$$

(30)

The interpolation matrix can also be generated to solve $\beta_{mk}$ with help of Eqs. (25) and (30). There are some remarks on the inverse conformal mapping as follows.

• (1) The relation of boundary node $\zeta_{lj}$ ($\zeta$-plane) and $z_{lj}$ ($z$-plane) should be considered for the inverse conformal mapping. As mentioned before, the radii $R_{l}$ of boundary $L_{l}$ and the boundary node $\zeta_{lj}$ are unknown prior to forward conformal mapping. A strategy is that, the forward numerical conformal mapping is solved firstly to determine the radius $R_{l}$ and approximate mapping function $\zeta = \hat{w}(z)$. Secondly, the inverse conformal mapping can then be solved according to forward conformal mapping $\zeta_{lj} = \hat{w}(z_{lj} )$, based on Eqs. (25) and (30). It is noted that the radius $R_{l}$ is naturally given after the forward conformal mapping has been solved by the presented method in this paper without iteration.

• (2) Since that there exists additional conditions (30), and the radii $R_{l}$ are known and fixed, the interpolation matrix to solve the constants $\beta_{mk}$ are overdetermined. One of the possible remedies is to set an extra node on every boundary.

• (3) The peripheral conformal mapping[29] should be applied to arrange the source nodes “inside” the circular slits, which is not discussed in this paper.

4 Numerical examples

In this Section, several numerical examples of forward and inverse numerical conformal mappings for unlined U-shaped and unlined rectangle tunnels in an infinite and semi-infinite domain are given to illustrate the effectiveness of proposed method.

In the computations, normalized points $z_{0}$ and $z^{\prime}_{0}$ are located on the origin of U-shaped tunnel and intersection of axis $x$ and U-shaped tunnel boundary, respectively. The numbers of boundary nodes and source nodes for every tunnel are set equally with locations arranged by Sakakibara’s method [29], which we do not discuss in detail. Since that the condition numbers of interpolation matrices are large, the truncated singular value decomposition (TSVD) technique is applied in computation. The flowchats for forward and inverse numerical conformal mapping are given by Fig. 3a, b.

Fig. 3

Flowchart of the numerical conformal mapping

4.1 Tunnel(s) in an infinite domain

Consider that there is(are) 1, 2 or 3 tunnel(s) included in infinite domain as shown in Fig. 4. The sizes are 10 m (width), and 14 m (height) for U-shaped tunnel, and 10 m × 5 m for rectangle tunnel, respectively. For the case of multiple tunnels, the distance between adjoining walls of different tunnel is 5 m. As mentioned in Sec.2.1, there are two approaches to solve the conformal mapping in the infinite domain. The images obtained are similar by these two approaches in numerical tests. We suggest that the approach (1) is preferred for convenience by assuming a sufficiently large radius $R_{0} = 500{\text{m}}$ in these cases.

Fig. 4

Tunnel(s) in an infinite plane (measure: m)

4.1.1 Single tunnel

The numerical examples for a single U-shaped tunnel (as shown in Fig. 4a), are given with the numbers of boundary and source nodes with 16, 32, 64 and 128, respectively.

The images of forward and inverse conformal mappings under different numbers of source nodes $N_{1}$ are shown in Figs.5 and 6. The approximate forward and inverse conformal mapping functions converge to the boundaries of unit circle and U-shaped tunnel when $N_{1}$ and $N^{\prime}_{1}$ increase. It is seen that the numerical solutions with $N_{1} = N^{\prime}_{1} = 64$ can achieve satisfactory results. Figure 7 illustrates the contours of $|\hat{w}(z)|$ for the forward conformal mapping. It is also found that a rather good result can be obtained by $N_{1} = 64$.

Fig. 5

Images of unit circle by forward conformal mapping

Fig. 6

Images of U-shaped tunnel by inverse conformal mapping

Fig. 7

The contours of forward conformal mapping $|\hat{w}(z)|$ for U-shaped tunnel ($N^{\prime}_{1} = 64$)

Tables 1 and 2 demonstrate the relations for $z$ and $\zeta$ on the boundary of U-shaped tunnel and unit circle. Since that the given points are the boundary nodes in MFS, it is seen that the nodes have rather good convergence when $N_{1} \ge 64$.

Table 1 The moduli (m) and arguments ($\times \pi$) of $\zeta$ according to $z$ on U-shaped tunnel boundary for forward conformal mapping

Table 2 The moduli (m) and arguments ($\times \pi$) of $z$ according to $\zeta$ on unit circle for inverse conformal mapping

4.1.2 Double tunnels

The forward numerical conformal mappings for double tunnels of U-shaped and rectangle ones (as shown in Fig. 4b), are given by Fig. 8 with the numbers of boundary and source nodes $N_{1} = N_{2} = 128$. Figure 8a reveals that the outlines convergent to unit circle ($R_{1} = 1$) and circular slit ($R_{2} = 2.0195$) in the forward conformal mapping. Figure 8b gives the contours of forward mapping $|\hat{w}(z)|$ for U-shaped and rectangle tunnels for the forward conformal mapping. Figure 8b also illustrates that the boundaries of unit circle ($R_{1} = 1$) and circular slit ($R_{2} = 2.0195$) fit rather well with the ones of U-shaped and rectangle tunnels.

Fig. 8

The forward numerical conformal mapping for double tunnels with $N_{1} = N_{2} = 128$

4.1.3 Triple tunnels

Figure 9 show the numerical results for the forward numerical conformal mappings of triple tunnels (see Fig. 4c) with the numbers of boundary and source nodes $N_{1} = N_{2} = N_{3} = 128$. Figure 9a reveals that the numerical solution agree well with unit circle ($R_{1} = 1$) and circular slit ($R_{2} = R_{3} = 1.962$). The contours of forward mapping $|\hat{w}(z)|$ in Fig. 9b also confirm that the boundaries of unit circle ($R_{1} = 1$) and circular slit ($R_{2} = R_{3} = 1.962$) are well convergent to the boundaries of U-shaped and rectangle tunnels.

Fig. 9

The forward numerical conformal mapping for triple tunnels with $N_{1} = N_{2} = 128$

4.2 Tunnel(s) in semi-infinite domain

It is necessary to study the semi-infinite problems, if the underground tunnel(s) is(are) located near the ground. Consider that a semi-infinite domain includes 1, 2 or 3 tunnel(s) as shown in Fig. 10. The sizes of the tunnels are the same as those included in the infinite domain. The distances between centers of tunnels and ground are set to be 15 m. In order to apply the presented method, there are two approaches to solve these problems as follows. Approach 1 is to transform the semi-infinite domain to an infinite domain by applying linear fractional mapping, firstly. Then, the proposed method in this paper can be used. Approach 2 is to convert the semi-infinite domain to a sufficiently large finite domain (as mentioned in Sec.2.1). In this paper, we apply Approach 2 to solve this problem by assuming that there exists a outer boundary with sufficiently large radius $R_{0}$, i.e. $R_{0} = 100{\text{m}}$ for single tunnel, and $R_{0} = 150{\text{m}}$ for multiple tunnels, respectively.

Fig. 10

Tunnel(s) in a semi-infinite plane (measure: m)

4.2.1 Single tunnel

The numerical examples for the semi-infinite domain includes a single U-shaped tunnel (as shown in Fig. 10a), are given with the numbers of boundary and source nodes 16, 32, 64 and 128, respectively.

The images of tunnel and assuming outer boundary for the forward and inverse conformal mappings under different numbers of source nodes $N_{0}$ and $N_{1}$ are shown in Figs.11 and 12. The local images for U-shaped tunnel are given by Fig. 13. From these figures, the approximate mapping converges to the corresponding boundaries if $N_{0}$, $N_{1}$, $N^{\prime}_{0}$ and $N^{\prime}_{1}$ increase. Since that the domain is relatively complex, the approximate conformal mapping gradually converge to annulus with $R_{0} = 1$ and $R_{1} = 0.2351$ as $N_{0} = N_{1} = 128$, which can be found in Fig. 11d. It is found in Figs.13d and 14d that the inner and outer boundaries of annulus can also be mapped to the U-shaped tunnel and assuming boundary as $N^{\prime}_{0} = N^{\prime}_{1} = 128$. The contours of $|\hat{w}(z)|$ under $N^{\prime}_{0} = N^{\prime}_{1} = 128$ are shown in Fig. 14. It is seen that the numerical solutions with 128 boundary nodes on each boundary can be obtained with good satisfaction.

Fig. 11

Images of annulus by forward conformal mapping

Fig. 12

Images of U-shaped tunnel and assuming boundary by inverse conformal mapping

Fig. 13

Local images of U-shaped tunnel by inverse conformal mapping

Fig. 14

The contours of forward conformal mapping $|\hat{w}(z)|$ for U-shaped tunnel ($N^{\prime}_{0} = N^{\prime}_{1} = 128$)

Tables 3 and 4 list the consistence of $z$ and $\zeta$ on the boundaries. From these tables, the given nodes on the assuming boundary $L_{0}$ and unit circle $L^{\prime}_{0}$ have good convergence with maximum error 1.86% when $N_{0} = N_{1} \ge 64$. Additionally, it can also be found that the U-shaped tunnel boundary $L_{1}$ is mapped to a circle with radius $R_{1} = 0.2351$ in Table 3.

Table 3 The moduli (m) and arguments ($\times \pi$) of $\zeta$ according to $z$ on U-shaped tunnel boundary for forward conformal mapping

Table 4 The moduli (m) and arguments ($\times \pi$) of $z$ according to $\zeta$ on the annulus for inverse conformal mapping

4.2.2 Double tunnels

For double tunnels of U-shaped and rectangle ones as show in Fig. 10b, the forward numerical conformal mappings are shown by Fig. 15 with the numbers of boundary and source nodes $N_{0} = N_{1} = N_{2} = 128$. Form Fig. 15a, the solution maps double tunnels and assuming boundary to an annulus and a circular slit with radii $R_{0} = 1$, $R_{1} = 0.2506$ and $R_{2} = 0.4734$, respectively. Figure 15b illustrates that the rectangle tunnel is mapped to the circular slit, the U-shaped tunnel and the assuming boundary are mapped to the inner and outer boundaries of annulus, respectively. Since that this case for double tunnels is dissymmetric, there exists a deflection angle for circular slit in transformed plane as shown in Fig. 15a.

Fig. 15

The forward numerical conformal mapping for double tunnels with $N_{0} = N_{1} = N_{2} = 128$

4.2.3 Triple tunnels

The numerical results for triple tunnels of U-shaped and rectangle ones (as show in Fig. 10c) are obtained here. Figure 16 show the mapped images of the boundaries and contours of $|\hat{w}(z)|$ with numbers of boundary nodes $N_{0} = N_{1} = N_{2} = N_{3} = 128$. It is found from Fig. 16a that the triple tunnels and assuming boundary are mapped to an annulus and two circulars slit with radii $R_{0} = 1$, $R_{1} = 0.2656$ and $R_{2} = R_{3} = 0.4867$, respectively. The two circular slits have the same radii of 0.4867, and are symmetry because those tunnels are symmetric about axis $x$. Figure 15b illustrates that the two rectangle tunnels are mapped to the circular slits, U-shaped and rectangle tunnels are mapped to the inner and outer boundaries of annulus, respectively.

Fig. 16

The forward numerical conformal mapping for double tunnels with $N_{0} = N_{1} = N_{2} = N_{3} = 128$

4.3 Discussion for numerical results

In above numerical examples, the interpolation equations constructed by different numbers of boundary nodes and source nodes, are solved by applying TSVD technique. It is emphasized that numerical results depend on the locations of source nodes. To mitigate the singularity problem of fundamental solutions near the source points, a strategy is given as follow. The locations of source nodes are placed at $|z^{\prime}_{mk} | = (3 \sim 5)|z_{mk} |$(outside) $|z^{\prime}_{mk} | = (0.6 \sim 0.8)|z_{mk} |$(inside) corresponding to the locations boundary nodes $z_{mk}$, respectively.

For numerical examples of semi-infinite domain in Sect. 4.2, the semi-infinite domain is converted to a sufficiently large finite domain as mentioned in Sec.2.1. In the further static or dynamic analysis, the stress boundary condition at infinite can be satisfied under the control of conformal mapping. On the the ground surface, the free-stress boundary conditions surface can be satisfied.

To study the performance of the presented method, relative error is defined by $|z - \hat{z}|/|z|$ and $|\zeta - \hat{\zeta }|/|\zeta |$ at the specified points. The relative errors corresponding to the numbers of the source nodes, are shown in Figs.17 and 18. From Fig. 17, it is seen that the relative error converge when the number of nodes increases. If the number of nodes is 128, the maximum error is 0.0157 at $\zeta = - {\text{i}}$ for the inverse conformal mapping as shown in Fig. 17c.

Fig.17

Relative errors corresponding to the numbers of the source nodes in infinite domain

Fig.18

Relative errors corresponding to the numbers of the source nodes in semi-infinite domain

In Fig. 18, it is also found that the relative error converge when the number of nodes increases. The relative errors are lager than those in infinite domain, since that the semi-infinite domain is not symmetric at infinite. The maximum error is 0.0385 at $z = 15 - 80{\text{i}}$ for the forward conformal mapping as shown in Fig. 18b. This maximum error occurs in case of double tunnel since that the distribution of those tunnels is also unsymmetrical.

In summary, the presented method of conformal mapping has effectiveness and good accuracy for single, double and triple tunnels in the infinite and semi-infinite domain, respectively. Unlike the other method, e.g. series expansion, the presented method does not need iteration.

5 Conclusion

A numerical conformal mapping method for finite or infinite domain including unlined tunnels with arbitrary numbers and shapes is proposed based on Symm’s method. A computational technique of MFS to solve the forward and inverse conformal mapping are carried out by considering the boundary and additional conditions.

• (1) The numerical method in this paper has advantages of clear concept, simple algorithm and non-iterative process, and is valid for finite and infinite domain include multiple unlined tunnels.

• (2) According to the forward conformal mapping given by Okano et al. [21], the basic equations of inverse numerical conformal mapping are deduced firstly in this paper. It is noted that some other approaches to conformal mapping, e.g., series expansion method and variational method, are relatively complex, and can not give both forward and inverse conformal mapping. Compared to those method, not only the forward conformal mapping, but also the inverse conformal mapping can be achieved by using the proposed method in this paper.

• (3) The numerical examples show the developed method can obtain the forward and inverse conformal mappings with high effectiveness and good accuracy. When the number of tunnels increases, or the domain is unsymmetrical, the maximum error increases. Consequently, the numbers of boundary nodes and source nodes should be increased to reduce the error. In the numerical examples, the maximum relative errors are 0.0157 for infinite domain and 0.0385 in semi-infinite domain, respectively. It also reveals that the relative errors decrease when the node number increases, which shows that the present method has good convergence for both forward and inverse conformal mapping.

• (4) The proposed numerical method can be a supplementary to the other mapping techniques according to uniqueness of conformal mapping. For example, the inverse conformal mapping $\zeta = w(z)$ for the known $z = w(\zeta )$ given by series expansion method and variational method etc., can be obtained by the numerical method of this paper.