1 Introduction

In order to assess the structural integrity of parts, reliable and accurate defect detection with non-destructive evaluation (NDE), is essential. For fracture mechanics calculations, characteristics like defect size, shape, and position can be used to estimate the defects’ severity [1]. For estimating these defect characteristics, ultrasound is a well-established method [2]. Especially ultrasonic imaging with phased array probes, together with reconstruction techniques, is widely used in the industry. This is due to the increasing available computing power and the higher degree of automation in ultrasound inspection practices [3]. The combination of full matrix capture (FMC), which is a technique where every transmitter and receiver combination is captured, together with the total focusing method (TFM) is suited for the reconstruction of complex flaw patterns [4]. With TFM, originally introduced by [5], the entire probe aperture is used to create a transmitter and receiver image in each pixel of the reconstruction volume. This enables a transmitter- and receiver-side synthetic focusing [5].

Deep learning methods have been researched increasingly in recent years, to automate and improve defect characterization with ultrasound data. In [6], with a phased array ultrasound setup, the grain orientation and defects were estimated for authentic steel welds. Synthetic data were used in this study. With a deep neural network, they estimated the grain orientation and, through this, the velocity model. Afterward, the data were reconstructed with the TFM, with and without the adapted velocity model, to detect the defects. It was found that the defects could be estimated much more accurately when using the predicted grain orientation map in the TFM reconstruction in comparison to isotropic models [6].

Rao et al. [7] presented a fully-convolutional network architecture, which takes as input the FMC dataset and predicts a reconstructed image. In the image, each pixel has its respective velocity attached to it. This architecture, therefore, replaces the TFM completely. The dataset was a simulated specimen representing metal parts bonded with adhesive layers. In the adhesive layer, random defects, so-called kissing bond defects were introduced. It was found that the kissing bond defects and the metal parts were reconstructed accurately by the model [7].

A study directly applying TFM images as input for a neural network can be found in [4]. In this study, defects were localized in TFM images with bounding boxes. The ultrasound waves were simulated in a quadratic domain with circular defects. The neural network was trained only on a single image. Despite this limited training dataset size, the position of the defects was recognized accurately [4].

In order to extract important features, it is possible to preprocess the TFM images. Mwema et al. [8] this for atomic force measurements by utilizing the power spectral density to preprocess images.

Based on the given literature review, the uncertainty within the neural network-based segmentation of TFM images was not investigated. This is the subject of this study. In applications, it is important to make decisions concerning the structural integrity of a part based on defect characteristics. However, the uncertainty estimate within these quantities is conventionally not regarded, which can be quantified with the methods introduced in this study.

article is organized as follows: Sect. 2 introduces the applied methods for generating the dataset and the neural network architectures and evaluation metrics. In Sect. 3, the results are presented and discussed. Finally, Sect. 4 provides the conclusion.

2 Methods

This Section introduces the applied methods of this study. At first, the FMC procedure and TFM are described. Afterward, the simulation setup for generating the data is explained. Further, the neural network architectures for the probabilistic segmentation and the used evaluation metrics are introduced.

2.1 Full matrix capture and the total focusing method

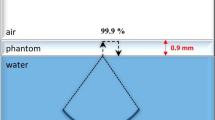
FMC is a data acquisition technique for phased array probes, where every transmitter and receiver combination is captured. The procedure of FMC is displayed in Fig. 1a. In the first firing sequence of the FMC procedure, element one excites an ultrasound wave, which propagates through the whole volume or is reflected at e.g. defects, and all n elements (including the one which transmits ultrasonic wave) record a signal. [9] The captured data constitute the first row of the so-called information matrix A. After the first, the second, the third, and nth elements are fired in the same manner and fill the rest of the information matrix with in total \({\text{n}}^2\) signals [9]. Post-processing can derive all phased array inspection configurations from the matrix, such as plane B-scan or sector B-scan. The TFM outperforms all other configurations since the entire imaging plane is focused as opposed to a single point at a certain depth [5].

This study utilizes synthetic data instead of real ultrasound signals, and as a result, the units used to measure the data are dimensionless, in contrast to the standard unit of volts used for measuring ultrasound signals in real-world applications.

The TFM algorithm starts with transforming every single A-scans using the Hilbert transform \({\widetilde{H}}\). The Hilbert transform only changes the phase information of the signal and not the frequency content. This transform generates an accurate signal envelope for all frequencies, and this smooths reconstructed images without losing any information [10]. The analytical signal Za, derived by applying \({\widetilde{H}}\) to one element of the information matrix \(A_{{\text{i}},{\text{j}}}\), is defined as

$$\begin{aligned} Za_{{\text{i}},{\text {j}}}=A_{{\text {i}},{\text {j}}}+i \cdot {\widetilde{H}}(A_{{\text {i}},{\text {j}}}) \end{aligned}$$
(1)

where i stands for the imaginary unit. After the signals of the information matrix have been converted to the analytical signals \(Za_{i,j}\), the intensity I of each pixel in the imaging plane is calculated by

$$\begin{aligned} I_{x_{\text{f}},y_{\text{f}}}=\vert \sum _{\text {j}=1}^{n} \sum _{\text {i}=1}^{\text {n}} Za_{\text {i},{\text {j}}} (t_{\text {i},\text {j}}) \vert \end{aligned}$$
(2)

where \(x_{\text {f}}\) and \(y_{\text {f}}\) represent the focal spot or pixel in the imaging plane. The time \(t_{i,j}\) is the time at which each receiver j would measure a reflected signal from a transducer i [9]. Figure 1b represents the time t from the first element to the focal point and then to the \(n_{th}\) element, therefore \(t=t_1+t_{\text {n}}\). The signal amplitudes at these respective time points in each signal are summed up for each pixel in the imaging plane. The time point is dependent on the ultrasound velocity of the medium, which needs to be known in advance. The resulting complexed-valued image is normalized in the end in order to get real values. For more information on the TFM, please refer to [5].

Fig. 1
figure 1

In a data acquisition procedure for FMC together with the resulting information matrix and in b illustration of the TFM. The figure was adapted from [9]

Full size image

2.2 Dataset generation by numerical modelling of phased array measurements

In this study, randomly generated synthetic data will be investigated. The data in this study has been produced stochastically, offering the advantage of exploring numerous defect positions and testing scenarios. The simulations, furthermore, did not account for surface roughness. However, in actual structures, surface roughness causes signal attenuation and wave dispersion [11]. Using real specimens to obtain a sufficiently large training dataset would have been challenging. In General, since the data is synthetic, its transferability to real data remains an open question.

For the simulations, the software Salvus from the Mondaic AG [12] was used. Salvus is based on the spectral element method and is capable of conducting waveform simulations on the GPU. A quadratic domain or mesh of the size 60x60 mm was modeled and the acoustic wave equation was solved. Instead of elastic acoustic waves were chosen since they are computationally less expensive. The results, however, are expected to be similar to an elastic simulation since the applied excitation, which was a vector force in the y-direction, mainly introduces longitudinal waves. Further, the p-wave velocity \(v_{\text{p}}\) was used for the TFM reconstruction. The material parameters of aluminum are used (p-wave velocity \(v_{\text{p}}=6380\,\frac{\rm{m}}{\rm{s}}\) and density \(\rho =2700\, \frac{\text{g}}{\text{m}^3}\)). At all edges of the structure except the upper one, absorbing boundaries were applied. The excitation wavelet was the second derivative of a Ricker wavelet with a center frequency of 2.25 MHz, which is a common frequency for ultrasonic testing. The specifications of the simulated phased array probes are given in Table 1.

Table 1 Specifications of the simulated phased array probe
Full size table

In the structured mesh, defects were introduced by removing elements of the mesh where the defects should be present. In order to reduce staircasing, and model the shape of the defect accurately, the mesh was defined with much smaller elements than necessary, for mitigating numerical dispersion. An element size of 1.39 mm (with two elements per wavelength) would be sufficient. However, an element size of 0.27 mm was chosen to reproduce the defect shapes more accurately.

Three different datasets, with different defects, were generated (see Fig. 2). These are:

  • Dataset 1: round defect in a homogeneous medium

  • Dataset 2: complicated defect shapes in a homogeneous medium

  • Dataset 3: round defect in a medium with microstructure noise

For each of these datasets, 1000 simulations were conducted, 700 were used for training, 50 for validation, and 150 for testing. One TFM image of each of the three datasets is displayed in Fig. 2.

Fig. 2
figure 2

TFM images of the three datasets with the boundary of the defect marked in red. Left: round defects. Middle: complicated defect shapes in a homogeneous medium. Right: round defects in a medium with microstructure noise

Full size image

The first dataset (Fig. 2 left) round defects with different random diameters and positions were simulated. The same procedure for the defects was used in the third dataset (Fig. 2 right). However, the connections between 800 neighboring elements were removed randomly. This should mimic the microstructure noise of coarse-grained material, for which the grains can be seen as small scatterers. A similar approach was proposed in [13]. Highly scattering materials are a common problem in ultrasonic testing [14]. The second dataset represents complicated-shaped reflectors. Due to physical constraints, such as the larger shadow zones under elongated defects, and the limitations due to the wavelength, complicated defect shapes are harder to capture accurately [15]. These defects were generated using randomly shaped Bezier curves. A detailed description of this approach is given in [16].

The generation of the three datasets was randomized. For the round defects (datasets 1 and 3), the diameter was randomly selected between 2 and 6 mm. The position of the defects in x- and y- were varied between 2 and 8 mm. When the defect intersected the boundaries of the mesh, with a large defect diameter and a small distance to the edges, a new defect position was selected. The procedure was the same for the complicated defect shapes, although with 2–8 mm, a larger range of defect diameters was chosen.

Figure 3 displays a flow chart outlining the procedure to generate a single sample, which includes a TFM image and its corresponding label.

Fig. 3
figure 3

Flow chart of the simulation procedure for generating one sample

Full size image

2.3 Neural network architectures for probabilistic segmentation

The goal of probabilistic image segmentation is to regard the dataset’s ambiguity in the segmentation process. Probabilistic segmentation was mainly applied in biomedical imaging, as in [17, 18], and [19] since errors in the segmentation could have severe consequences in this field. Similar requirements are also present in NDE, where deep learning is applied more frequently. In NDE, depending on the part, small defects can lead to critical failures of large structures. For this reason, there is a need to assess the performance of the NDE method to evaluate if a defect can be found or not. This is normally done with probability of detection (POD) curves [20]. These, however, give no information on why a single defect may not be found. The uncertainty estimates of segmentation results can bridge that gap and give insight into why certain defects are harder to capture. Furthermore, it makes the neural network more explainable, currently a limiting factor in their application.

For probabilistic image segmentation, different neural network architectures are available in the literature, which takes different aspects of the uncertainty in the segmentation into account [17]. Conventional neural networks for segmentation are deterministic. This means that they will always predict the same segmentation mask for a given input image. This, however, gives a false impression of certainty since, for example, a network trained with a different initialization could predict a different segmentation mask [17]. With an uncertainty estimate, the areas where the model is unsure about its prediction can be estimated. With probabilistic models, it is possible to draw different segmented samples for the same input image. In general, probabilistic models try to find the posterior distribution p over the weights w, given the training dataset X, and its labels Y [21].

$$\begin{aligned} p(w \vert X,Y) \end{aligned}$$
(3)

The labels in this study are binary (defect or no defect). Since the posterior distribution is untraceable, it has to be estimated empirically by sampling from the segmentation models [21]. In this study, three architectures will be used for that purpose and one deterministic U-Net for comparison. The implementation can be found in [22]. The four models are visualized in Fig. 4, and are explained in the following.

Fig. 4
figure 4

Schematic overview of the four evaluated models. In a–d the U-Net with softmax output, the MC dropout U-Net, the ensemble of U-Nets, and the probabilistic U-Net. The feature maps are visualized in blue, the dropout layers in orange. The Figure was adapted from [17] and [18]

Full size image

U-Net with softmax output This is the well-established U-Net architecture on which many variants are built. It is schematically displayed in Fig. 4a. Initially, it was introduced by [23] and has been widely used since then. The vanilla U-Net is purely deterministic and has a softmax output, which gives a probability score for each class [22]. This model is used as a benchmark for the other models.

U-Net with Monte Carlo (MC) dropout MC dropout was introduced by [24] for classification and regression and adapted by [21] for segmentation tasks. The goal is to find the true posterior distribution over several models with different random dropout configurations. Random dropout is used in the training and testing phases. The model used is shown in Fig. 4b and, compared to the vanilla U-Net, has some further dropout layers. The dropout probability was set to 0.5, which is the probability of keeping each weight [17].

Ensemble of U-Nets Combining the prediction of several models is a common approach to improve the performance, and to avoid overfitting. From each individually deterministic model of the ensemble, the segmentation can be sampled [17]. Four models were chosen as an ensemble in this study. The ensemble of models is sketched in Fig. 4c.

Probabilistic U-Net The probabilistic U-Net, as displayed in Fig. 4d, was introduced by [18]. It combines the vanilla U-Net and a conditional variational auto-encoder. The auto-encoder samples in the testing phase from the latent space, and thus makes different predictions for different samples z [17]. For more information concerning the probabilistic U-Net please refer to [18].

The model’s hyperparameter tuning was conducted for the learning rate and batch size. The models were trained with the early stopping criterion based on the validation dataset loss.

2.4 Metrics

To compare the output of the neural networks quantitatively, meaningful metrics need to be used. Most of these metrics work on a thresholded image and are based on the confusion matrix. The confusion matrix is a result of comparing the thresholded prediction with its label. In Fig. 5, a confusion matrix for a binary segmentation problem, which is also the task in this work, is visualized.

Fig. 5
figure 5

Confusion matrix for binary classification

Full size image

From the confusion matrix, the most common segmentation or classification metrics are derived. For a balanced dataset, accuracy is a widely used metric, which is the ratio of the correct classified samples over all samples.

$$\begin{aligned} {\text{accuracy}}=\frac{{\text{TP}}+{\text {TN}}}{{\text {TP}}+{\text {FP}}+{\text {TN}}+{\text {FN}}} \end{aligned}$$
(4)

However, the accuracy gives a false impression about the performance when the dataset is imbalanced. For imbalanced datasets, the F1-score is a suitable metric. It is calculated as the harmonic mean between recall and precision. Recall and precision are defined as

$$\begin{aligned} {\text{recall}}=\frac{{\text{TP}}}{{\text{TP}}+{\text{FN}}}. \end{aligned}$$
(5)

and

$$\begin{aligned} {\text{precision}}=\frac{{\text{TP}}}{{\text{TP}}+{\text{FP}}} \end{aligned}$$
(6)

The F1-score is calculated with

$$\begin{aligned} {\text {F1-score}}=2 \cdot \frac{\text {precison} \cdot \text {recall}}{\text {precison}+\text {recall}}. \end{aligned}$$
(7)

Czolbe et al. [17] proposed, furthermore, an uncertainty metric H based on pixel-wise predictions (not thesholded). It is defined as

$$\begin{aligned} H(p(y \vert x,X,Y))= \sum _{c \in C }p(y=c \vert x,X,Y)\nonumber \\ {\text{log}}_{2}\left(\frac{1}{p(y=c \vert x,X,Y)}\right), \end{aligned}$$
(8)

where \(p(y=c \vert x,X,Y)\) is the probability to predict class \(c \in C\) in one pixel, x is one sample of the training dataset X and y its respective label. Y are the set of labels of the training dataset [17]. The uncertainty H takes low values when the pixel-wise predicted values are close to zero or close to one and higher values in the middle of this range. H gives an impression of how uncertain the model is about its predictions.

3 Results and discussion

This Section introduces, at first, the results of the uncertainty estimation on three datasets. Afterward, the performance of the models based on several segmentation metrics is discussed. In the end, we evaluate model performance on different defect sizes.

3.1 Estimating the uncertainty in the segmentation

In order to estimate the uncertainty within the segmentation, 15 samples were drawn from the respective models. We applied uncertainty estimates (see Eq. 8) on these 15 predicted images, and the results were averaged. Since the U-Net with the softmax output is deterministic, no variation within the 15 samples is present. In Figs. 6, 7, and 8 the mean uncertainty H of the TP, FN, FP, and TN over the whole test dataset and is displayed for the different datasets and models.

Fig. 6
figure 6

Model uncertainty H for dataset 1 with the round defects

Full size image
Fig. 7
figure 7

Model uncertainty H for dataset 2 with the complicated defect shapes

Full size image
Fig. 8
figure 8

Model uncertainty H for dataset 3 with the round defect, and microstructure noise

Full size image

In general, H is high when the model has incorrect (FN, FP) compared to the correct predictions (TP, TN). This was also noticed by [17], who reported a correlation between the uncertainty metric and the segmentation error. The only exception here is the MC dropout model, which shows a higher uncertainty within datasets 2 and 3 for TPs than FNs. The uncertainty of the TNs is much smaller in comparison to the other cases. The reason for the low uncertainty of the TN may be that most of the pixels in one image have no defect, and because of this, the models focus during the training on getting this case correct. Furthermore, most of the pixels with no defect in the image have values close to zero, which simplifies the decision for the model. The probabilistic U-Net shows the lowest uncertainties H for all datasets and the MC dropout model the highest.

To evaluate wether the uncertainties can explain false segmentations, and, therefore, have a relevant meaning for the interpretation, we investigate the uncertainties of three defects from dataset 2. This dataset was chosen since it most clearly shows areas where the models do not work well. Figure 9 shows the uncertainties for three defects. In the top row, the three TFM images are displayed together with the cutout in green, where the uncertainty is investigated. For each model, the uncertainty estimates of 15 predictions were averaged.

Fig. 9
figure 9

Uncertainty of the segmentation of three complicated-shaped defects (dataset 2). For the cutout in the top row, the uncertainties are visualized. The red boundary gives the ground truth, and the blue boundary gives the predicted defects, whereby the average of 15 predictions was taken and thresholded by 0.5

Full size image

It can be seen that, as in the whole test dataset the MC dropout model shows the highest uncertainty and the probabilistic U-Net the lowest one. When the prediction boundaries differ from the ground truth boundaries, high uncertainty values are usually present. In general, the uncertainty values at the boundary of the defects are high. Furthermore, in the shadow zone of the defect the shape of the defect is not captured well and also high uncertainty values are present. For the defect in the first column all models, except the probabilistic U-Net, interpret the multiple reflections as a second defect with high H. In general, the probabilistic U-Net shows the lowest uncertainty within its segmentation and also the qualitatively best segmenting result.

3.2 Performance of the models on each dataset

In this Subsection, the models will be compared based on the segmentation metrics, which have been introduced in Sect. 2.4. The recall, precision, and F1-score are given for the three datasets in Figs. 10, 11, and 12. The accuracy was not used since it is unsuitable for an imbalanced dataset. The metrics were calculated for the whole test dataset, using the average prediction of 15 samples from the models. This was done to find the prediction against which the models converge when sampling from them.

Fig. 10
figure 10

Metric-scores for the dataset 1 with the round defects

Full size image
Fig. 11
figure 11

Metric-scores for the dataset 2 with the complicated defect shapes

Full size image
Fig. 12
figure 12

Metric-scores for the dataset 3 with the round defect, and microstructure noise

Full size image

For all datasets, the model with the highest F1-score, and therefore, the best-performing model, is the probabilistic U-Net. The probabilistic U-Net also shows the lowest uncertainty in its prediction (see Figs. 6, 7, 8, and 9). The MC dropout model has the lowest F1-score and also the highest uncertainty. For dataset 1, the models show the smallest standard deviation, represented by the error bars. This dataset also has the lowest TP, and TN uncertainties (see Fig. 6)

3.3 Performance of the models over the defect size

A common procedure to evaluate the performance of an NDE method is to investigate the system response to defects of different sizes. The maximal amplitude of a defect echo can be used to estimate the size [2]. This is, however, dependent on the wavelength \(\lambda\). When the defect is within a range from \(\lambda /2\) to \(\lambda /4\), resonance effects occur, and with a defect size smaller than \(\lambda /6\), Rayleigh scattering becomes dominant [25].

The defect size was varied from 0.5 to 4.0 mm in 15 steps for all three datasets. The middle point of the defects is located in the middle of the domain at \(x=30\) mm and \(y=30\) mm. Since the F1-score and H are correlated, and the F1-score is a more established metric to evaluate the segmentation performance, it is used in this investigation. For each TFM image representing one defect size, 15 predictions were drawn from the models and averaged. The error bars in Figs. 13, 14, and 15 represent the standard deviations of the F1-score for the 15 predictions. It is assumed that the standard deviation of the F1-score gives an estimate of how the model’s predictions differ and, therefore, how uncertain the model considers its prediction. Since the U-Net with the softmax output is deterministic, no error bar is plotted. The \(\lambda /2\) wavelength for the center frequency of 2.25 MHz is 1.42 mm. The \(\lambda /2\) wavelength is marked in Figs. 13, 14, and 15. For the dataset with the complicated defect shapes, the same defect shape was chosen for all defect sizes and rescaled accordingly. The microstructure noise, introduced by removing the connection between some elements in the mesh, was kept random.

Fig. 13
figure 13

Dependency of the F1-score from the defect size for round defects

Full size image
Fig. 14
figure 14

Dependency of the F1-score from the defect size for complicated defect shapes

Full size image
Fig. 15
figure 15

Dependency of the F1-score from the defect size for round defect and micostructure noise

Full size image

It can be seen that the F1-score increases after the \(\lambda /2\) threshold. A reason for this can be that the linearity between defect size and amplitude of the signals no longer holds [25]. Furthermore, for the probabilistic U-Net, the standard deviation of the F1-score from the drawn samples increases below \(\lambda /2\) for the dataset with the round and complicated defect shapes. As also concluded in the previous investigation, the MC dropout model shows the lowest F1-score. The other models reach similar F1-scores. The standard deviation for the dataset with the microstructure noise is the highest, especially for the probabilistic U-Net.

4 Conclusions

In this study, it was investigated whether the ambiguity within TFM images can be captured by segmenting the data with neural network architectures. Four different architectures were investigated: U-Net with a softmax output, an ensemble of U-Nets, U-Net with Monte Carlo dropout, and the so-called probabilistic U-Net. Concerning the model performance and capturing the uncertainty within the data, the probabilistic U-Net was most suitable for this task. Several physical effects, which lead to uncertainty within the TFM image, were also found to be where the model segmentations had high uncertainty. These physical effects or regions are the shadow zone below the defects, where the ultrasound wave could not propagate, multiple reflections within the TFM image, which are mistaken for a defect, or the ambiguities within the amplitude of the defects when the defects are smaller than \(\lambda /2\). For all of these scenarios, the models show a higher uncertainty in the images. In the future, such uncertainty estimates can be used to identify sources of uncertainty within images of non-destructive measurements. Together with a conventional POD evaluation, this gives a more holistic evaluation of the limitations of an NDT method.