1 Introduction

Functionally graded materials (FGM) consist of discrete volumes of constitutive materials that are changed over different positions in a continuous manner. In this way, the material properties are continuously dispersed and may eliminate common interface problems of laminate composite materials. FG materials, with their improved physical and mechanical properties, are of interest to a wide range of disciplines, including tribology, fracture mechanics, geology, nanotechnology, optoelectronics, and biomechanics. A decade ago, FG materials were introduced to develop micro/nano-devices with better physical properties, including micro/nano electromechanical frameworks, shape memory alloy thin films, and nuclear power microscopes. Numerous scientific and numerical analyses have been published in the literature regarding the dynamic behavior of FG structures under mechanical and thermal loads. In addition, several studies have examined the thermoelastic properties of FGM beams. As a result of their unique mechanical and physical characteristics, FGMs are evolving rapidly and increasingly technologically, with uses in many industries such as engineering, petroleum, medicine, and transportation. Micro and nanomaterials structures have been in high demand for the last decade because of their unique electronic, electrical, and mechanical properties. The properties of nanomaterials make them suitable for use in MEMS/NEMS/piezoelectric devices as elementary structural components. In recent years, laser pulse technology has gained interest as a non-destructive testing method and as a material processing method. By radiating laser light, wave motion can be generated within the material. Hence, laser pulses are important in micro and nano mechanical resonators.

For the study of small-scale structures, Eringen [1,2,3] incorporated the theory of nonlocal continuum mechanics. The stress of a point in a nonlocal continuum depends on the strain state of every other point in the continuum. However, in continuum mechanics, stress at a particular point can be exclusively determined by its strain. Thermoelastic relations in a FG isotropic unbounded media with intermittently variable heat sources were addressed by Mallik and Kanoria [4]. Based on Eringen’s nonlocal mechanics model, Lazar and Agiasofitou [5] derive new results about stress constituents of screw displacements for the anisotropic medium. Yang et al. [6] analyzed the thermal stress in 2D structures composed of FGM with analytical expressions in the RIBEM (radial integration boundary element method) bypassing the time-consuming problem of computing radial integrals with RIBEM. Utilizing a fractional-order model Abouelregal and Mohamed [7] studied the thermoelastic vibrations in FGN due to periodic heat fluxes. Mao et al. [8] researched on the FGM thermoelastic instability (TEI) in presence of frictional heat and resistance of thermal contact. Based on E-B (Euler–Bernoulli) and refined TBT (Timoshenko beam theory), Xu and Meng [9] presented the systematic results for the bending, buckling and free vibration of FG beams. Zhang et al. [10] illustrated the outline of the prevailing literature on free vibration buckling and stability analysis of FGM. Abo-Dahab et al. [11] discussed the FG thin slim strip with one thermal relaxation time in generalized thermoelasticity theory. The effects of vibrations on concrete structures can be reduced by special construction and material conditions [12, 13]. Based on literature available over the past 30 years, Saleh et al. [14] provided the fundamental difficulties and strengths of currently available manufacturing methods for FGMs. Hasona and Adel [15] considered the influence of initial stress on a magneto-thermoelastic FGM with Green Naghdi (GN-II) theory. Sheokand et al. [16] examined the FGM under a dual-phase-lag model with rotation and gravity. Craciun and Soos [17] discussed elliptical hole crack problem in an infinite anisotropic elastic body of a fiber reinforced composite.

Wang and Li [18] introduced memory dependent derivatives based on caputo type definition of fractional derivatives. Ezzat et al. [19, 20], discussed memory dependent derivatives in thermoelectric viscoelastic problem and gave generalized thermal equation for a thermoelastic problem and derived different thermoelastic theories from it. El-Bary [21] studied a 1-D thermal shock problem for a functionally graded magneto thermoelastic half-space with memory dependent derivatives. Abouelregal and Marin [22, 23], small-scale effect in a generalized thermoelastic beam due to rectified sine wave heating and under a harmonic external force. Al-Jamel et al. [24], introduced memory-dependent derivative w.r.t. displacement to define damping in several oscillatory systems of complex dissipation appliances in which memory effects could not be overlooked. Marin et al. [25], studied a Lagrange’s identity to address non-simple elastic materials. Jafari et al. [26] studied a functionally graded plate with a triangular hole subject to uniaxial tensile load. Zhang et al. [27] investigated the applications of nanoparticle-reinforced building materials in civil engineering. Zhang et al. [28] studied the induced magnetic field induced by nanoparticles of tantalum and nickel flows towards an elastic surface. With an internal heat source moving under the influence of rotation, Said [29] studied the propagation of waves in a nonlocal generalized thermoelastic half-space. Lata and Singh [30] studied the non-local magneto-thermoelastic solid with two temperatures subjected to rotation and inclined loads. Using a nonlocal generalized thermoelasticity model, Peng and Chen [31] studied a micro-scale FGM beam with ramping-type heating on the left end for its dynamic thermoelastic response. Abbas et al. [32] used Lord and Shulman's generalized thermoelastic model to study wave propagation in unbounded thermoelastic materials based on nonlocal thermoelasticity.

To investigate the vibrational phenomenon in 2D functionally graded simply supported nanobeams, we have undertaken this research effort with memory-dependent derivatives. The Sect. 2 focuses on the basic equation for an isotropic nonlocal medium and the heat conduction equation with MDD equations. Section 3 describe the mathematical formulation of the study of vibrations in 2D functionally graded nanobeams (FGNs) with memory-dependent derivatives. A sinusoidal variation of temperature is assumed. The dimensionless expressions for axial displacement, thermal moment, lateral deflection, strain, and temperature distribution are found in the transformed domain using Laplace Transforms. Boundary conditions for simply supported nanobeams has been discussed in the Sect. 4. The next two Sects. 5, 6 provide the solution to problem and method for the inversion of Laplace Transform. The Sect. 7 presents the numerical results and shows the effect of different kernel functions, periodic frequency of thermal vibration on all the physical fields graphically with MATLAB software. The Sect. 8 deals with the conclusions of the paper.

2 Basic equations

The constitutive relations for an isotropic nonlocal medium [1] are

$$\sigma_{ij} = \left( {1 - \rho \nabla^{2} } \right)t_{ij} = 2\mu e_{ij} + \lambda e_{ij} - \gamma T\delta_{ij} ,$$
(1)

where, \(\varrho = \left( {\tau l} \right)^{2} ,\tau = \frac{{e_{0} a}}{l},2e_{ij} = \frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}\).

In the absence of heat sources, the equation of heat conduction with MDD following Kaur et al. [33,34,35] is,

$$K\nabla^{2} T = \left( {1 + \chi D_{\chi } } \right)\left( {\rho C_{E} \frac{\partial T}{{\partial t}} + \gamma T_{0} \frac{\partial div u}{{\partial t}}} \right).$$
(2)

Wang and Li [18] presented the first-order MDD with the differentiable function f(t) w. r.t. \(\chi\) > 0 for time \(t\) as:

$$D_{\chi } f\left( t \right) = \frac{1}{\chi }\int_{t - \chi }^{t} {K\left( {t - \xi } \right)f^{\prime}\left( \xi \right)d\xi } .$$
(3)

Depending on the material properties, we choose \(K(t-\xi )\) and \(\chi\). Following Kaur et al. [33,34,35], the K(t − ξ) is considered as

$$K\left( {t - \xi } \right) = 1 - \frac{2\beta }{\chi }\left( {t - \xi } \right) + \frac{{\alpha^{2} }}{{\chi^{2} }}\left( {t - \xi } \right)^{2} = \left\{ {\begin{array}{*{20}l} {1,} \hfill \\ {1 + \left( {\xi - t} \right)/\chi ,} \hfill \\ {\xi - t + 1,} \hfill \\ {\left[ {1 + \left( {\xi - t} \right)/\chi } \right]^{2} ,} \hfill \\ \end{array} } \right.\begin{array}{*{20}l} {\quad \alpha = 0,\beta = 0} \hfill \\ {\quad \alpha = 0,\beta = 1/2} \hfill \\ {\quad \alpha = 0,\beta = \chi /2} \hfill \\ {\quad \alpha = 1,\beta = 1} \hfill \\ \end{array}$$
(4)

where \(\alpha\) and \(\beta\) are constants.

3 Formulation of the problem

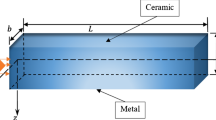
Consider an FG thermoelastic nanobeam (Fig. 1) with Cartesian coordinates of length \((0\le x\le L)\), width \(\left(-\frac{b}{2}\le y\le \frac{b}{2}\right)\) and thickness \(\left(-\frac{h}{2}\le z\le \frac{h}{2}\right)\). Assume that the x-axis is taken along the nano-beam's axis and one of the ends of the nanobeam is the y −z  plane i.e. (x = 0) with the origin located in the centre of this end and with y-axis and z-axis along the width and the thickness direction of the nanobeam. Assume that the nano-beam’s ends are maintained at a uniform temperature T0 and also the cross-section of the nanobeam is uniform along the entire length.

Fig. 1
figure 1

Structural design of the nano-beam

Full size image

The assumed beam has metal-rich (all metal) material properties at the lower surface z = h/2 and ceramic-rich (full-ceramic) at the upper surface z =  − h/2. FGMs are considered to have continuous material properties throughout the thickness direction, such as elasticity modulus, thermal conductivity, mass density, and coupling parameter. Using this model, the gradation of the material's actual property \(P(z)\) in the thickness direction following Abouelregal and Mohamed [7] is described as

$$P\left( z \right) = P_{m} e^{{n_{p} \left( {2z - h} \right)/h}} ,\quad n_{p} = ln\sqrt {P_{m} /P_{c} } .$$
(5)

Following Rao [36], using the theory of E-B beam for a thin beam the displacement components of nanobeams can be taken as

$$u_{1} \left( {x,y,z,t} \right) = - z\frac{\partial w}{{\partial x}}, \quad u_{2} \left( {x,y,z,t} \right) = 0, \quad u_{3} \left( {x,y,z,t} \right) = w\left( {x,t} \right),$$
(6)

Initially, the nanobeam is unstrained and unstressed.

$$w\left( {x,t} \right)_{t = 0} \left| { = \frac{{\partial w\left( {x,t} \right)}}{\partial t}} \right|_{t = 0} = 0,T\left( {x,z,t} \right)\left| {_{t = 0} \frac{{\partial T\left( {x,z,t} \right)}}{\partial t}} \right|_{t = 0} = 0.$$
(7)

Based on Eringen's non-local theory of thermoelasticity, the Eq. (1) using Eqs. (5) and (6) becomes

$$\left( {t_{xx} - \varrho \frac{{\partial^{2} t_{xx} }}{{\partial x^{2} }}} \right) = - E_{m} \left[ {e^{{n_{E} \left( {2z - h} \right)/h}} z\frac{{\partial^{2} w}}{{\partial x^{2} }} + \alpha_{m} e^{{n_{{E_{\alpha } }} \left( {2z - h} \right)/h}} T} \right],$$
(8)

where \(n_{{E_{\alpha } }} = ln\left( {\sqrt {E_{m} \alpha_{m} /E_{c} \alpha_{c} } } \right)\).

Since the nanobeam's upper and lower surfaces are thermally insulated, there is no heat flux across them, therefore \(\frac{\partial T}{\partial z}\) should disappear at \(z = \pm h/2\). Assuming a sinusoidal variation of increment temperature along the thickness direction for a nanobeam i.e.

$$T\left( {x,z,t} \right) = {\Theta }\left( {x,t} \right)\sin \left( {\frac{\pi z}{h}} \right).$$
(9)

The bending moment is defined as

$$M\left( {x, t} \right) = - \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\int_{{\frac{ - b}{2}}}^{\frac{b}{2}} {t_{xx} \left( {x,z,t} \right)zdzdy} } ,$$
(10a)

In Eq. (8) using (10a) we obtain the cross-sectional flexural moment is determined by

$$M\left( {x, t} \right) - \rho \frac{{\partial^{2} M}}{{\partial x^{2} }} = - bh^{2} E_{m} \left[ {h\mu_{E} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \alpha_{m} \mu_{{E_{\alpha } }} {\Theta }} \right],$$
(10b)

where

$$\begin{aligned} & \mu_{E} = \frac{{\left( {n_{E}^{2} + 2} \right)\left( {1 - e^{{ - 2n_{E} }} } \right) - 2n_{E} \left( {1 - e^{{ - 2n_{E} }} } \right)}}{{8n_{E}^{3} }}, \\ & \mu_{{E_{\alpha } }} = \frac{{2n_{{E_{\alpha } }} \left( {\pi^{2} + 4n_{{E_{\alpha } }}^{2} } \right)\left( {1 - e^{{ - 2n_{{E_{\alpha } }} }} } \right) + \left( {\pi^{2} - 4n_{{E_{\alpha } }}^{2} } \right)\left( {1 + e^{{ - 2n_{{E_{\alpha } }} }} } \right)}}{{\left( {\pi^{2} + 4n_{{E_{\alpha } }}^{2} } \right)^{2} }}. \\ \end{aligned}$$

For a FGM nano-beam, the transverse equation of motion is

$$\frac{{\partial^{2} M}}{{\partial x^{2} }} = \frac{{\left( {1 - e^{{ - 2n_{\rho } }} } \right)\rho_{m} }}{{2n_{\rho } }}\frac{{\partial^{2} w}}{{\partial t^{2} }},$$
(11)

Using Eq. (9) in Eq. (8), we get

$$\frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{\rho_{m} \left( {1 - e^{{ - 2n_{\rho } }} } \right)}}{{2E_{m} h^{2} n_{\rho } \mu_{E} }}\frac{{\partial^{2} }}{{\partial t^{2} }}\left( {1 - \varrho \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)w + \frac{{\alpha_{m} \mu_{{E_{\alpha } }} }}{{\mu_{E} }}\frac{{\partial^{2} {\Theta }}}{{\partial x^{2} }} = 0$$
(12)

The Eq. (2) using Eqs. (5) and (6) can be written as

$$K_{m} e^{{n_{K} \left( {2z - h} \right)/h}} \left[ {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial z^{2} }} + 2\frac{{n_{K} }}{h}\frac{\partial T}{{\partial z}}} \right] = \left( {1 + \chi D_{\chi } } \right)\left[ {\rho_{m} C_{{E_{m} }} e^{{n_{{\rho C_{E} }} \left( {2z - h} \right)/h}} \frac{\partial T}{{\partial t}} - z\gamma_{m} e^{{n_{\gamma } \left( {2z - h} \right)/h}} T_{0} \frac{{\partial^{3} w}}{{\partial x^{2} \partial t}}} \right]$$
(13)

here the parameters \({n}_{K}\), \({n}_{\gamma }\) and \({n}_{\rho {C}_{E}}\), are given based on Eq. (3), according to the properties of ceramics and metals, respectively and

$$\gamma_{m} = \frac{{E_{m} \alpha_{m} }}{{1 - 2\nu_{m} }}, \quad \rho_{m} C_{{E_{m} }} = \frac{{K_{m} }}{{\omega_{m} }}.$$

By replacing Eq. (11) into Eq. (13) and integrating the resultant equation w. r.t. z over the beam thickness from − h/2 to h/2, yields

$$\left[ {\frac{{\partial^{2} {\Theta }}}{{\partial x^{2} }}} \right] = \left( {1 + \chi D_{\chi } } \right)\left[ {\overline{\mu }_{{\rho C_{E} }} \eta \frac{{\partial {\Theta }}}{\partial t} - \frac{{\overline{\mu }_{\gamma } \gamma_{m} hT_{0} }}{{K_{m} }}\frac{{\partial^{3} w}}{{\partial x^{2} \partial t}}} \right].$$
(14)

where

$$\begin{aligned} & \overline{\mu }_{{\rho C_{E} }} = \frac{{\mu_{{\rho C_{E} }} }}{{\mu_{K} }},\eta = \frac{{\rho_{m} C_{{E_{m} }} }}{{K_{m} }}, \quad \overline{\mu }_{\gamma } = \frac{{\mu_{\gamma } }}{{\mu_{K} }}, \\ & \mu_{{\rho C_{E} }} = \frac{{2n_{{\rho C_{E} }} \left( {1 + e^{{ - 2n_{{\rho C_{E} }} }} } \right)}}{{\pi^{2} + 4\left( {n_{{\rho C_{E} }} } \right)^{2} }},\quad \mu_{K} = \frac{{2n_{K} \left( {1 + e^{{ - 2n_{K} }} } \right)}}{{\pi^{2} + 4\left( {n_{K} } \right)^{2} }}, \\ & \mu_{\gamma } = \frac{{n_{\gamma } \left( {1 + e^{{ - 2n_{\gamma } }} } \right) + e^{{ - 2n_{\gamma } }} - 1}}{{4\left( {n_{\gamma } } \right)^{2} }}. \\ \end{aligned}$$

The dimensionless quantities are given by

$$\left( {x^{\prime}, z^{\prime},u^{\prime}, w^{\prime},L^{\prime},h^{\prime}} \right) = C_{0} \eta_{0} \left( {x,z,u,w,L,h} \right),\left( {t^{\prime},\xi^{\prime}} \right) = C_{0}^{2} \eta_{0} \left( {t,\xi } \right), \Theta^{\prime} = \frac{\Theta }{{T_{0} }},$$
(15)

If the dimensionless quantities from Eq. (15) are applied to Eqs. (12) and (14), and the primes are suppressed, the equations in the non-dimensional form are as follows:

$$\frac{{\partial^{4} w}}{{\partial x^{4} }} + A_{1} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {1 - \varrho \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)w = - A_{2} \frac{{\partial^{2} {\Theta }}}{{\partial x^{2} }},$$
(16)
$$\left[ {\frac{{\partial^{2} {\Theta }}}{{\partial x^{2} }}} \right] = \left( {1 + \chi D_{\chi } } \right)\left[ {A_{3} \frac{{\partial {\Theta }}}{\partial t} - A_{4} \frac{{\partial^{3} w}}{{\partial x^{2} \partial t}}} \right],$$
(17)
$$M\left( {x, t} \right) = A_{1} \left( {\varrho \frac{{\partial^{2} }}{{\partial t^{2} }} - \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)w - A_{2} {\Theta },$$
(18)

where

$$A_{1} = \frac{{\left( {1 - e^{{ - 2n_{\rho } }} } \right)}}{{2h^{2} n_{\rho } \mu_{E} }}A_{2} = \frac{{T_{0} \alpha_{m} \mu_{{E_{\alpha } }} }}{h},A_{3} = \overline{\mu }_{{\rho C_{E} }} ,A_{4} = \frac{{\overline{\mu }_{\gamma } \gamma_{m} h}}{{\eta_{0} K_{m} }}.$$

The Laplace transform is defined by

$${\mathcal{L}}\left[ {f\left( {x,z,t} \right)} \right] = \int_{0}^{\infty } {e^{ - st} f\left( {x,z,t} \right)dt = \overline{f}\left( {x,z,s} \right)} .$$
(19)

Using Eq. (19) in Eqs. (16) to (18) we get

$$\left( {\frac{{d^{4} }}{{dx^{4} }} - \rho A_{1} s^{2} \frac{{d^{2} }}{{dx^{2} }} + A_{1} s^{2} } \right)\overline{w} = - A_{2} \frac{{d^{2} {\overline{\Theta }}}}{{dx^{2} }},$$
(20)
$$\left[ {\frac{{d^{2} }}{{dx^{2} }} - qA_{3} } \right]{\overline{\Theta }} = - qA_{4} \frac{{d^{2} \overline{w}}}{{dx^{2} }},$$
(21)
$$\overline{M}\left( {x, t} \right) = A_{1} \left( {\rho \,s^{2} - \frac{{d^{2} }}{{dx^{2} }}} \right)\overline{w} - A_{2} \overline{\Theta },$$
(22)

where

$$q = \left( {1 + G} \right)s,\, {\text{G}} = \left[ {\left( {1 - {\text{e}}^{{ - {\text{s}}\upchi }} } \right)\left( {1 - \frac{{2\upbeta }}{{\upchi {\text{s}}}} + \frac{{2\upalpha ^{2} }}{{\upchi ^{2} {\text{s}}^{2} }}} \right) - \left( {\upalpha ^{2} - 2\upbeta + \frac{{2\upalpha ^{2} }}{{\upchi {\text{s}}}}} \right){\text{e}}^{{ - {\text{s}}\upchi }} } \right].$$

Eliminating \(\overline{w}\) or \({\overline{\Theta }}\) in Eqs. (20), (21) we obtain

$$\left[ {D^{6} - AD^{4} + BD^{2} - C} \right]\left( {\overline{w},{\overline{\Theta }}} \right)\left( x \right) = 0,$$
(23)

where \(A = \varrho A_{1} s^{2} + qA_{3} + qA_{2} A_{4} ,B = A_{1} s^{2} + q\varrho A_{1} A_{3} s^{2} ,C = qA_{1} A_{3} s^{2} ,D = \frac{d}{dx}.\)

The differential Eq. (23) takes the form

$$\left( {D^{2} - \lambda_{1}^{2} } \right)\left( {D^{2} - \lambda_{2}^{2} } \right)\left( {D^{2} - \lambda_{3}^{2} } \right)\left( {\overline{w},{\overline{\Theta }}} \right)\left( x \right) = 0,$$
(24)

where \(\pm {\lambda }_{1}, \pm {\lambda }_{2} and\pm {\lambda }_{3}\) are the characteristic roots of the equation \({\lambda }^{6}-A{\lambda }^{4}+B{\lambda }^{2}-C=0\) and hence,

$$\begin{aligned} & \lambda_{1}^{2} + \lambda_{2}^{2} + \lambda_{3}^{2} = A, \\ & \lambda_{1}^{2} \lambda_{2}^{2} + \lambda_{2}^{2} \lambda_{3}^{2} + \lambda_{1}^{2} \lambda_{3}^{2} = B, \\ & \lambda_{1}^{2} \lambda_{2}^{2} \lambda_{3}^{2} = {\text{C}}, \\ \end{aligned}$$

where “\(A,B,C\) are the sum of all the roots, sum of the roots taken two at a time, and the product of all the roots, respectively”.

Assume Lateral Deflection \(\overline{w }\left(x\right)\) and temperature as

$$\left( {\overline{w},{\overline{\Theta }}} \right)\left( x \right) = \sum\nolimits_{i = 1}^{3} { \left\{ {1,B_{i}^{\prime } } \right\}\left[ {B_{i} e^{{\lambda_{i} x}} + B_{i + 3} e^{{ - \lambda_{i} x}} } \right]} ,$$
(25)

where \({B}_{i}, i=1, 2, 3, 4, 5, 6\) are constants where \(B_{i}^{\prime } = - \frac{{\lambda_{i}^{4} + A_{1} s^{2} }}{{A_{2} \lambda_{i}^{2} }} = \beta_{i}\), \(i=1, 2, 3\) are constants.

The Axial Displacement is

$$\overline{u}\left( x \right) = - z\sum\nolimits_{i = 1}^{3} {\lambda_{i} \left[ {B_{i} e^{{\lambda_{i} x}} - B_{i + 3} e^{{ - \lambda_{i} x}} } \right]} .$$
(26)

Thermal Moment is given by

$$\overline{M}_{T} = \mathop \sum \limits_{i = 1}^{3} \left( {\varrho s^{2} - \lambda_{i}^{2} - A_{2} \beta_{i} } \right)\left[ {B_{i} e^{{\lambda_{i} x}} + B_{i + 3} e^{{ - \lambda_{i} x}} } \right].$$
(27)

The strain is given by

$$\overline{e}\left( x \right) = - z\mathop \sum \limits_{i = 1}^{3} \lambda_{i}^{2} \left[ {B_{i} e^{{\lambda_{i} x}} + B_{i + 3} e^{{ - \lambda_{i} x}} } \right] ,$$
(28)

4 Boundary conditions

The boundary conditions for nanobeams with simply supported (SS) ends and maintained at constant temperatures \({T}_{0}\) are as follows:

$$\left. {w\left( {x,t} \right)} \right|_{x = 0} = \left. {w\left( {x,t} \right)} \right|_{x = L} = 0,$$
(29)
$$\left. {\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }}} \right|_{x = 0} = \left. {\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }}} \right|_{x = L} = 0.$$
(30)

In this problem, we consider the first end of a nanobeam x = 0 to be subjected to a dimensionless time-dependent heat flux of constant intensity \({q}_{0}\) as

$$\frac{{\partial {\Theta }}}{\partial x} = q_{0} \cos (\zeta t),\zeta > 0 \,on\, x = 0.$$
(31)

We assume \(\zeta =0\) when a constant heat flux is applied. Furthermore, if the second end of the nanobeam \(x = L\) is thermally insulated, we can express it as

$$\frac{{\partial {\Theta }}}{\partial x} = 0\, on \,x = L.$$
(32)

By applying dimensionless quantities from Eq. (15) and Laplace Transform defined by (19) on Eq. (29)–(32) the dimensionless boundary conditions becomes

$$\left. {\overline{w}\left( {x,s} \right)} \right|_{x = 0} = \left. {\overline{w}\left( {x,s} \right)} \right|_{x = 1} = 0,$$
(33)
$$\left. {\frac{{d^{2} \overline{w}\left( {x,s} \right)}}{{dx^{2} }}} \right|_{x = 0} = \left. {\frac{{d^{2} \overline{w}\left( {x,s} \right)}}{{dx^{2} }}} \right|_{x = 1} = 0.$$
(34)
$$\left. {\frac{{\partial {\overline{\Theta }}}}{\partial x}} \right|_{x = 0} = \frac{{q_{0} s}}{{\zeta^{2} + s^{2} }} = H\left( s \right),\left. {\frac{{\partial {\overline{\Theta }}}}{\partial x}} \right|_{x = 1} = 0.$$
(35)

5 Solution

Replacing the values of \(\overline{w }\) and \(\overline{\Theta }\) from Eqs. (25) in Eqs. (33)–(35), we derive the value of \({B}_{i}\) using cramer,s rule for solving linear equations with i = 6 variables as

$$B_{i} = \frac{{\Delta_{i} }}{\Delta } ,\quad i = 1,2,3,4,5,6.$$
(36)

and

$${\Delta } = \left| \begin{gathered} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\begin{array}{*{20}c} 1 & 1 & 1 \\ {{\uplambda }_{1}^{2} } & {{\uplambda }_{2}^{2} } & {{\uplambda }_{3}^{2} } \\ {{\text{e}}^{{{\uplambda }_{1} }} } & {{\text{e}}^{{{\uplambda }_{2} }} } & {{\text{e}}^{{{\uplambda }_{3} }} } \\ \end{array} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\begin{array}{*{20}c} 1 & 1 & 1 \\ {{\uplambda }_{1}^{2} } & {{\uplambda }_{2}^{2} } & {{\uplambda }_{3}^{2} } \\ {{\text{e}}^{{ - {\uplambda }_{1} }} } & {{\text{e}}^{{ - {\uplambda }_{2} }} } & {{\text{e}}^{{ - {\uplambda }_{3} }} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {{\uplambda }_{1}^{2} {\text{e}}^{{{\uplambda }_{1} }} } & {{\uplambda }_{2}^{2} {\text{e}}^{{{\uplambda }_{2} }} } & {{\uplambda }_{3}^{2} {\text{e}}^{{{\uplambda }_{3} }} } & {{\uplambda }_{1}^{2} {\text{e}}^{{ - {\uplambda }_{1} }} } & {{\uplambda }_{2}^{2} {\text{e}}^{{ - {\uplambda }_{2} }} } & {{\uplambda }_{3}^{2} {\text{e}}^{{ - {\uplambda }_{3} }} } \\ {\lambda_{1} \beta_{1} } & {\lambda_{2} \beta_{2} } & {\lambda_{3} \beta_{3} } & { - \lambda_{1} \beta_{1} } & { - \lambda_{2} \beta_{2} } & { - \lambda_{3} \beta_{3} } \\ {\lambda_{1} \beta_{1} {\text{e}}^{{{\uplambda }_{1} }} } & {\lambda_{2} \beta_{2} {\text{e}}^{{{\uplambda }_{2} }} } & {\lambda_{3} \beta_{3} {\text{e}}^{{{\uplambda }_{3} }} } & { - \lambda_{1} \beta_{1} {\text{e}}^{{ - {\uplambda }_{1} }} } & { - \lambda_{2} \beta_{2} {\text{e}}^{{ - {\uplambda }_{2} }} } & { - \lambda_{3} \beta_{3} {\text{e}}^{{ - {\uplambda }_{3} }} } \\ \end{array} \hfill \\ \end{gathered} \right|$$
(37)

\({\Delta }_{i}\left(i=1, 2, 3,\dots , 6\right)\) are obtained by replacing the columns by \(\left[\begin{array}{cc}\begin{array}{ccc}0,& 0,& 0,\end{array}& \begin{array}{ccc}0,& H\left(s\right),& 0\end{array}\end{array}\right]\) in \({\Delta }_{i}\). Substituting the values from (37) in Eqs. (25)–(28), we get the lateral deflection, thermal moment, axial displacement, temperature distribution, and strain of the FG nanobeam.

6 Inversion of laplace transform

To find the physical domain solution, the transforms in Eqs. (24) to (27), must be inverted using inverse Laplace transform integral defined by

$$f\left( {x,t} \right) = \frac{1}{2\pi i}\int_{{e^{ - i\infty } }}^{{e^{ + i\infty } }} {\overline{f}\left( {x,s} \right)e^{ - st} ds} .$$
(38)

Press et al. [37] described Romberg’s integration method for evaluating integrals with an adaptive step size.

7 Numerical results and discussion

A contemporary alternative to the fractional order derivative (FOD) is the memory-dependent derivative (MDD). The MDD is better suited for temporal remodeling than the FOD. It exhibits the memory effect more clearly. A better MDD model of thermoelasticity was introduced to show the memory effect (the rate of sudden change depends on the past state). “MDD is defined in an integral form of a common derivative with a kernel function on a slip-in interval”. The effect of different kernel functions of MDD and periodic frequency of thermal vibration is illustrated graphically for lateral deflection, axial displacement, strain, temperature, and thermal moment of a 2D functionally graded nanobeams (FGNs). In the case studies, it is assumed that aluminum serves as the lower metal surface and alumina serves as the upper ceramic surface of the metal and ceramic phases of the nanobeam, respectively (see Table 1). Moreover, for the numerical simulations, L/h = 10 and L = 1 and z = h/3 are considered.

Table 1 Thermoelastic and Mechanical properties parameter of the graded nanobeam (T0 = 293 K)
Full size table

Figure 2 displays the deviation in the lateral deflection w w. r.t. beam length with various values of MDD kernel function \(K\left(t-\xi \right)\). It is observed that the w sharply increases as the nano-beam length increases. Lateral deflection w has a maximum value when the \(K\left(t-\xi \right)\) value is 1. Figure 3 depicts the axial displacement w. r.t. beam length with various values of MDD kernel function \(K\left(t-\xi \right)\). It is found that the axial for sharply decreases in the initial range of the length of nano-beam and then shows the small increases for the rest of the range of the nano-beam length.

Fig. 2
figure 2

The lateral deflection w w. r.t. beam length with change in kernel function

Full size image
Fig. 3
figure 3

The axial displacement u w. r.t. beam length with change in kernel function

Full size image

Figure 4 depicts the deviation of temperature for different kernel functions \(K\left(t-\xi \right)\). It is found that the temperature suddenly decreases in the initial range of the nano-beam length and then again depicts the sharp increase for the rest of the range of the nano-beam length with a slight deviation in values for different kernel functions. Figure 5 describes the deviation in the thermal moment \({M}_{T}\) w.r.t. beam length with various values of MDD kernel function \(K\left(t-\xi \right)\). It is found that the \({M}_{T}\) decrease with nano-beam length. \({M}_{T}\) is highest when the \(K\left(t-\xi \right)\) value is \({\left[1+\left(\xi -t\right)/\chi \right]}^{2}\). Figure 6 exhibits the deviation in strain w.r.t. various values of MDD kernel functions \(K\left(t-\xi \right)\). It is detected that the strain decreases along the nano-beam length. The strain is highest when the \(K\left(t-\xi \right)\) is 1. Figure 7 shows the variation in lateral deflection w.r.t. different values of periodic frequency of thermal vibration. It is found higher the value of different values of periodic frequency of thermal vibration lower will be the lateral deviation in the beam. Figure 8 illustrates the axial displacement with the nanobeam length with different periodic frequency of thermal vibration. It is found higher the value of periodic frequency of thermal vibration lower will be the axial displacement in the beam. Figure 9 demonstrates the thermal moment for change in periodic frequency of thermal vibration. It is detected that the higher the value of periodic frequency of thermal vibration lower will be the thermal moment deviation in the beam. Figure 10 illustrates strain with the length of the beam with variable periodic frequency of thermal vibration. It is observed that the greater the value of periodic frequency lower will be the thermal moment deviation in the beam. Figure 11 and Fig. 12 illustrate the axial displacement and strain with the length of the beam for diverse values of z.

Fig. 4
figure 4

The deviation of temperature w. r.t. beam length with change in kernel function

Full size image
Fig. 5
figure 5

The variation of Thermal Moment MT w. r.t. beam length with change in kernel function

Full size image
Fig. 6
figure 6

deviation in strain w. r.t. beam length with change in kernel function

Full size image
Fig. 7
figure 7

The lateral deflection w w. r.t. beam length with change in periodic frequency of thermal vibration

Full size image
Fig. 8
figure 8

The axial displacement w. r.t. beam length with change in periodic frequency of thermal vibration

Full size image
Fig. 9
figure 9

The thermal moment w. r.t. beam length with change in periodic frequency of thermal vibration

Full size image
Fig. 10
figure 10

deviation in strain w. r.t. beam length with change in periodic frequency of thermal vibration

Full size image
Fig. 11
figure 11

The axial displacement w. r.t. beam length with change in z

Full size image
Fig. 12
figure 12

Variation of strain w. r.t. beam length with change in z

Full size image

8 Conclusions

A new mathematical model is developed using Euler–Bernoulli theory to investigate the vibration phenomenon in FG thermoelastic SS nanobeam with heat conduction equation in the context of MDD. The dimensionless expressions for axial displacement, thermal moment, lateral deflection, strain, and temperature distribution are found in the transformed domain using Laplace Transforms, and the expressions in the physical domain are derived by numerical inversion techniques. It is observed that the Kernel function of MDD has a substantial influence on lateral deflection, axial displacement, temperature distribution, thermal moment and strain of the FG thermoelastic beam and yields improved results. A significant effect is shown by the nonlocal parameter in all the fields studied. Periodic frequency of the applied heat flux has a strong effect on thermoelastic displacement, deflection, and temperature. Higher the periodic frequency of the applied heat flux, lower will be the thermoelastic displacement, deflection, strain, and temperature. Adding non-local MDD to thermoelastic models opens up new possibilities for the study of thermal deformations in solid mechanics. This investigation help in the scheme and fabrication of MEMS/NEMS, resonators and sensors. This structure can also be used in semiconductors devices, piezoelectric devices and integrated circuits (IC), and continuum mechanics.