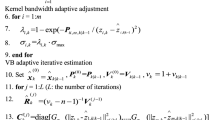1 Introduction

The estimation of states of a physical system using a sequence of noisy measurements has been required in many problems in real life and in science and technology. For example, it may be required in industrial control and automation [1], target tracking [2], navigation [3], financial forecasting [4], video surveillance [5] and weather forecasting [6] etc.

The state equation representing process model and measurement model in discrete time could be given by,

$$x_{k+1}=\phi _k(x_k)+\eta _k, $$
(1)
$$\begin{aligned}&y_k=\gamma _k(x_k)+v_k, \end{aligned}$$
(2)

where \(x_k\in \mathbb {R}^n\) denotes the state vector of a process, and \(y_k \in \mathbb {R}^p\) denotes the measurement at any instant k, where \(k =1,2,3,\cdots ,N\). \(\phi _k\) and \(\gamma _k\) are known nonlinear function. \(\eta _k\) and \(v_k\) are process and measurement noise respectively.

The necessity of robust estimation is required when deviation of the process model from the assumed model is encountered. The model uncertainty may be due to state model error, unmodeled bias or noise modeling error in system. When the physical system is completely and accurately described by an assumed model, the non-robust filter can estimate the states with desired accuracy but when it deviates from the assumed model, the robust filtering approach should be applied to achieve the desired accuracy.

A common approach to robust estimation is based on optimization techniques. Inspired from control theory, \(H_{\infty }\) criterion [7, 8] is applied in estimation problem. In the context of robust control theory, robustness has close connection with \(H_{\infty }\) criterion [9, 10]. To use \(H_{\infty }\) methods, a control designer expresses the control problem as a mathematical optimization problem and then finds the controller that solves this optimization. The resulting controller is only optimal with respect to the prescribed cost function. The risk sensitive estimator is closely linked with \(H_{\infty }\) estimator [11]. In risk sensitive estimation approach the mean value of exponential of the square of the error of estimation scaled by risk sensitive parameter is minimized rather than minimizing only mean of the square of error of estimation. The development of risk sensitive estimator has been motivated for the estimation of the states with more accuracy whenever physical system deviates from assumed model by tuning the risk sensitive parameter, which is its advantage over other filters. In earlier literature several risk sensitive estimator has been found [11,12,13,14] for linear and nonlinear system. It has been based upon Kalman filtering approach for linear system [12, 15] whereas for nonliner system conventionaly it has been based upon extended Kalman filter approach [15]. But the drawback of extended Kalman filter has also found in that due to which it gives poor result for severe nonlinear system. Several other risk sensitive estimators have been found in earlier literature which overcome this disadvantage such as based upon unscented Kalman filter (UKF) [16] as in [17] and many others [18,19,20,21,22,23]. Apart from that, other approaches can also be found in recent literature to hinder the kinematic model error [24] or to tackle dynamic model uncertainty [25] based upon cubature Kalman filter (CKF) [26] .

In this paper, risk sensitive estimator based upon cubature quadrature Kalman filter (CQKF) [27,28,29] named as risk sensitive cubature quadrature Kalman filter (RSCQKF) [22, 23] is applied for tracking of a ballistic target during its re-entry phase. The risk sensitive filter based on cubature quadrature Kalman filter is different from previous risk sensitive nonlinear filters found in earlier literature as it is based upon cubature rule of integration and multiple Gauss-Laguerre quadrature points [28]. Under single Gauss-Laguerre quadrature point, it merge with earlier advanced cubature Kalman filter (CKF). Due to increase in Gauss-Laguerre quadrature points, it is more accurate than earlier advanced risk sensitive cubature Kalman filter and other previous risk sensitive nonlinear filters.

The paper is organized as follows. The next section discuss the recursive solution of risk sensitive estimator. The risk sensitive filter based upon cubature quadrature Kalman filter algorithm is given in Sect. 3. In Sect. 4, simulation results are presented. In Sect. 5, discussion on the results are given and finally conclusion is given in Sect. 6.

2 Risk sensitive estimation

The risk sensitive criteria had been used during estimation to achieve robustness in earlier literature [11,12,13, 15]. The recursive solution of risk sensitive estimator is discussed below.

2.1 Recursive solution of risk sensitive estimator (RSE)

Consider a nonlinear system as in (1) and (2). The process noise is considered with normal distribution with zero mean and known covariance \(Q_{k}\). The measurement noise is also normally distributed with zero mean and known covariance \(R_{k}\). Both the noises are assumed to be mutually uncorrelated.

For risk sensitive estimation, the cost function is defined as

$$\begin{aligned} F(\hat{x}_{1},\hat{x}_{2},\cdots ,\hat{x}_{k})= E \left[ e^{ \left( \mu _{1}\sum _{i=1}^{k-1}g_{1}(x_{i}-\hat{x}_{i})+\mu _{2}g_{2}(x_{k}-\hat{x}_{k})\right) }\right] , \end{aligned}$$
(3)

where E(.) represents the mean. \(g_{1}(.)\) and \(g_{2}(.)\) represents error covariance function as given in Eq. (5). Here the error cost function is scaled by two risk sensitive parameters represented by \(\mu _{1} \ge 0\) and \(\mu _{2}>0\). Considering only \(\hat{x}_{k}\) to be unknown and \(\hat{x}_{i (0\le i\le k-1)}\) for all times \(0,1,\cdots ,k-1\) to be known as \(\hat{x}_{i}^{*}\), (3) can be written as only function of \(\hat{x}_{k}\) as:

$$\begin{aligned} F(\hat{x}_{k}) =E \left[ e^{\left( \mu _{1} \sum _{i=1}^{k-1}g_{1}(x_{i}-\hat{x}_{i}^{*})+\mu _{2}g_{2}(x_{k}-\hat{x}_{k}) \right) } \right] . \end{aligned}$$
(4)

Taking

$$\begin{aligned} g_1(x-\hat{x})=g_2(x-\hat{x})=[x-\hat{x}]^{T}[x-\hat{x}] \end{aligned}$$
(5)

(4) is given as

$$\begin{aligned} F(\hat{x}_{k}) = E \left[ e^{ \left( \mu _{1} \sum _{i=1}^{k-1}[x_{i}-\hat{x_{i}}^{*}]^{T} [x_{i}-\hat{{x}_{i}}^{*}]+ \mu _{2}[x_{k}-\hat{x}_{k}]^{T} [x_{k}-\hat{x}_{k}]\right) } \right] , \end{aligned}$$
(6)

The risk sensitive estimate can be given as

$$\begin{aligned} \hat{x}_{k}^{*}=arg min F(\hat{x}_{k}). \end{aligned}$$
(7)

It should be noted that when \(\mu _{1}=0\), \(\mu _{2}>0\), the cost function has only instantaneous error (It does not include the stored error over past time) and it merges with the minimum mean square error Kalman filter.

The solution to the minimum risk sensitive estimate can be given by the following recursive relation:

The risk sensitive prior probability density function (PDF) for state is given by time update equation as given below.

$$\begin{aligned} z_{k|k-1}=\int _{-\infty }^{+\infty } f(x_{k}|x_{k-1}) e^{(\mu _{1}[x_{k}-\hat{x}_{k|k-1}]^{T} [x_{k}-\hat{x}_{k|k-1}])}z_{k-1|k-1}dx_{k-1} \end{aligned}$$
(8)

Here \(z_{k|k-1}\) represents risk sensitive prior PDF for state variable x and f(.) is likelihood function.

The risk sensitive posterior PDF for state is given by measurement update equation as given below.

$$\begin{aligned} z_{k|k}=f(y_{k}|x_{k})z_{k|k-1} \end{aligned}$$
(9)

Here \(z_{k|k}\) represents risk sensitive posterior PDF for state variable x and f(.) is likelihood function.

The risk sensitive prior estimate is given by

$$\begin{aligned} \hat{z}_{k|k-1}= \underbrace{arg min}_{\delta \in \mathbb {R}^{n}} \int _{-\infty }^{+\infty } e^{(\mu _{2}[x_{k}-\delta ]^{T}[x_{k}-\delta ])}z_{k|k-1}dx_{k}, \end{aligned}$$
(10)

Here \(\hat{z}_{k|k-1}\) represents risk sensitive prior estimate of x.

The risk sensitive posterior estimate is given by

$$\begin{aligned} \hat{z}_{k|k}= \underbrace{arg min}_{\delta \in \mathbb {R}^{n}} \int _{-\infty }^{+\infty } e^{(\mu _{2}[x_{k}-\delta ]^{T}[x_{k}-\delta ])}z_{k|k}dx_{k}. \end{aligned}$$
(11)

Here \(\hat{z}_{k|k}\) represents risk sensitive posterior estimate of x.

Here, it can be seen that the risk sensitive probability density function for state is obtained by exponential of square function of error of x scaled by a risk sensitive parameter \(\mu _1\). Further the risk sensitive estimate of x i.e. \(\hat{z}\) (posterior and prior) is obtained by exponential of square function of error of x scaled by another risk sensitive parameter \(\mu _2\). The risk sensitive parameters can be normalized by replacing \(\mu _2\) by unity and \(\mu _1\) by ratio \(\mu _1/\mu _2\). These risk rensitive parameters can be tuned to obtain the robust estimate and could improve the performance in comparison to original mean square error criterion when process model is deviated from assumed model. Therefore the risk sensitive formulation is better than the original mean square error criterion.

The risk sensitive filter algorithm has been developed with cubature quadrature Kalman filtering framework in this paper. The detail algorithm for cubature quadrature Kalman filter (CQKF) can be found in [27, 28] with advantage of CQKF to CKF and other traditional nonlinear filter. The risk sensitive estimation has been incorporated here to CQKF algorithm by introducing risk sensitive parameter in error covariance update equation. Here the risk sensitive parameter \(\mu _1\) is introduced in prior error covariance update equation (18) in time update step to obtain the risk sensitive estimate.

The risk sensitive filter based upon cubature quadrature Kalman filter algorithm is given in next section named as risk sensitive cubature quadrature Kalman filter algorithm.

3 Risk sensitive cubature quadrature Kalman filter algorithm

The detail of risk sensitive cubature quadrature Kalman filter algorithm is given as follows.

  • Take initial posterior estimate as \(\hat{x}_{0|0}\) and initial posterior covariance as \(\Sigma _{0|0}\).

  • Find cubature quadrature points, \(\kappa _{j}\), and their corresponding weights, \(\mathbb {W}_{j ( j=1, 2,...,n )}\).

Time update step

  • Find the Cholesky decomposition for posterior covariance

    $$\begin{aligned} \Sigma _{k|k}=C_{k|k}C_{k|k}^{T}. \end{aligned}$$
    (12)

  • Calculate cubature quadrature points after Cholesky decomposition of posterior covariance as

    $$\begin{aligned} \zeta _{j,k|k}=C_{k|k}\kappa _{j}+\hat{x}_{k|k}. \end{aligned}$$
    (13)

  • Transform cubature quadrature points as

    $$\begin{aligned} \zeta _{j,k+1|k}=\phi (\zeta _{j,k|k}). \end{aligned}$$
    (14)

  • Calculate prior estimate and prior covariance as

    $$\begin{aligned} \hat{x}_{k+1|k}=\sum _{j=1}^{n}\mathbb {W}_{j}\zeta _{j,k+1|k}, \end{aligned}$$
    (15)
    $$\begin{aligned} \Sigma _{k+1|k}= \sum _{j=1}^{n}\mathbb {W}_{j}[\zeta _{j,k+1|k}-\hat{x}_{k+1|k}][\zeta _{j,k+1|k}-\hat{x}_{k+1|k}]^{T}+Q_{k}. \end{aligned}$$
    (16)

  • The risk sensitive prior estimate remains same

    $$\begin{aligned} \hat{z}_{k+1|k}=\hat{x}_{k+1|k} \end{aligned}$$
    (17)

  • The risk sensitive prior covariance is updated with

    $$\begin{aligned} \Sigma _{k+1|k}^{+}=(\Sigma _{k+1|k}^{-1}-2\mu _{1}I)^{-1}. \end{aligned}$$
    (18)

(Note: The condition \((\Sigma _{k+1|k}^{-1}-2\mu _{1}I)^{-1}>0\) need to be satisfied at each step for risk sensitive covariance to be positive definite. The condition limits upper value of \(\mu _{1}\).)

Measurement update step

  • Find Cholesky decomposition for prior covariance as

    $$\begin{aligned} \Sigma _{k+1|k}^{+}=C_{k+1|k}C_{k+1|k}^{T}. \end{aligned}$$
    (19)

  • Calculate cubature quadrature points after Cholesky decomposition of prior covariance

    $$\begin{aligned} \zeta _{j,k+1|k}=C_{k+1|k}\kappa _{j}+\hat{x}_{k+1|k}. \end{aligned}$$
    (20)

  • Compute predicted measurements for each cubature quadrature points

    $$\begin{aligned} Y_{j,k+1|k}=\gamma (\zeta _{j,k+1|k}). \end{aligned}$$
    (21)

  • Compute the estimate of predicted measurement as weighted sum of predicted measurements for each cubature quadrature points

    $$\begin{aligned} \hat{y}_{k+1|k}=\sum _{j=1}^{n}\mathbb {W}_{j}Y_{j,k+1|k}. \end{aligned}$$
    (22)

  • Find the covariance of predicted measurement

    $$\begin{aligned} \Sigma _{y_{k+1|k}}= \sum _{j=1}^{n}\mathbb {W}_{j}[Y_{j,k+1|k}-\hat{y}_{k+1|k}][Y_{j,k+1|k}-\hat{y}_{k+1|k}]^{T}+R_{k}, \end{aligned}$$
    (23)

  • Find the cross covariance of predicted measurement and prior estimate

    $$\begin{aligned} \Sigma _{x_{k+1}y_{k+1}}=\sum _{j=1}^{n}\mathbb {W}_{j}[\zeta _{j,k+1|k}-\hat{x}_{k+1|k}][Y_{j,k+1|k}-\hat{y}_{k+1|k}]^{T}. \end{aligned}$$
    (24)

  • Compute Kalman gain from covariance of predicted measurement and cross covariance as

    $$\begin{aligned} G_{k+1}=\Sigma _{x_{k+1}y_{k+1}}\Sigma ^{-1}_ {y_{k+1|k}}. \end{aligned}$$
    (25)

  • Calculate posterior estimate as

    $$\begin{aligned} \hat{x}_{k+1|k+1}=\hat{x}_{k+1|k}+G_{k+1}(y_{k+1|k}-\hat{y}_{k+1|k}). \end{aligned}$$
    (26)

  • The risk sensitive posterior estimate remain same as

    $$\begin{aligned} \hat{z}_{k+1|k+1}=\hat{x}_{k+1|k+1}. \end{aligned}$$
    (27)

  • The risk sensitive posterior covariance is given by

    $$\begin{aligned} \Sigma _{k+1|k+1}^{+}=\Sigma _{k+1|k}^{+}-G_{k+1}\Sigma _{y_{k+1}y_{k+1}}G_{k+1}^{T}. \end{aligned}$$
    (28)

4 Simulation result

The above described algorithm is used to track the motion of a ballistic object in its re-entry phase. The ballistic object motion forms a complex dynamic phenomenon in presence of lift force and drag force. Similar problem has also been formulated in earlier literature [30,31,32].

The process model for two dimensional ballistic target motion is described by the following nonlinear discrete time dynamic state equation

$$\begin{aligned} x_{k+1}=\phi (x_{k})+\mathbb {G} \begin{bmatrix} 0 \\ -g \end{bmatrix} + \eta _{k}, \end{aligned}$$

where the state vector is given by

$$\begin{aligned} x_{k}= \begin{bmatrix} \mathbf {x}_{k}&\dot{\mathbf {x}_{k}}&\mathbf {y}_{k}&\dot{\mathbf {y}_{k}} \end{bmatrix}^{T}. \end{aligned}$$

The state vector provides the positions and velocities of target in \(\mathbf {x}\) and \(\mathbf {y}\) Cartesian coordinates at \(k^{th}\) time instant. The nonlinear function \(\phi (x_{k})\) is given by

$$\begin{aligned} \phi (x_{k})=\varphi x_{k}+\mathbb {G}f_{k}(x_{k}), \end{aligned}$$

where

$$\begin{aligned} \varphi = \begin{bmatrix} 1 &{} T &{} 0 &{} 0 \\ 0&{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} T \\ 0 &{} 0 &{} 0 &{} 1 \end{bmatrix}, \mathbb {G}= \begin{bmatrix} T^{2}/2 &{} 0\\ T &{} 0 \\ 0 &{} T^{2}/2 \\ 0 &{} T \end{bmatrix}. \end{aligned}$$

Here, T is the time interval between two consecutive radar measurements. The drag force \(f_{k}(x_{k})\) is directed opposite to the target speed \(\mathbf {u}\) and its magnitude is given by \(0.5\frac{g}{\beta }{\rho }\mathbf { u}^{2}\). The expression for the drag force is given by

$$\begin{aligned} \begin{aligned} f_{k}(x_{k})&=-0.5\frac{g}{\beta }{\rho }(\dot{\mathbf {x}_{k}}^{2}+\dot{\mathbf {y}_{k}}^{2})\times \begin{bmatrix} \text{cos}(\text{tan}^{-1}(\frac{\dot{\mathbf {y}_{k}}}{\dot{\mathbf {x}_{k}}})\\ \text{sin}(\text{tan}^{-1}(\frac{\dot{\mathbf {y}_{k}}}{\dot{\mathbf {x}_{k}}}) \end{bmatrix}\\&=-0.5\frac{g}{\beta }{\rho } \sqrt{\dot{\mathbf {x}_{k}}^{2}+\dot{\mathbf {y}_{k}}^{2}}\begin{bmatrix} \dot{\mathbf {x}_{k}}\\ \dot{\mathbf {y}_{k}} \end{bmatrix}, \end{aligned} \end{aligned}$$

where g is the acceleration due to gravity and \(\beta\) is the ballistic coefficient. The ballistic coefficient \(\beta\) varies with mass, shape and cross sectional area of the target perpendicular to its direction of motion. However, it remains constant if the speed of target becomes supersonic due to formation of shock waves. The shock waves vanish when speed of a target decreases to the speed of sound. Here, we assume \(\beta\) to be a constant as the speed of the target is more than the speed of the sound throughout. The air density \({\rho }\) is given by

$$\begin{aligned} {\rho }=c_{1}e^{-c_{2}\mathbf {y}}, \end{aligned}$$

where

\(c_{1}=1.227\) and \(c_{2}=1.093\times 10^{-4}\) ; for \(\mathbf {y}<9144\) m,

\(c_{1}=1.754\) and \(c_{2}=1.49\times 10^{-4}\) ; for \(\mathbf {y}\ge 9144\) m.

The process noise \(\eta _{k}\) is taken as zero mean white Gaussian with covariance Q given by

$$\begin{aligned} Q=q\begin{bmatrix} \mathbb {\theta } &{} 0 \\ 0 &{} \mathbb {\theta } \end{bmatrix}, \end{aligned}$$

with

$$\begin{aligned} {\theta }=\begin{bmatrix} T^{3}/3 &{} T^{2}/2 \\ T^{2}/2 &{} T \end{bmatrix}. \end{aligned}$$

Here, q is a parameter which accounts for the possible deviation of the process model from the real situation. The truth is simulated for the target trajectory in the MATLAB as shown in Figs. 1, 2, and 3 with \(g=9.8\) ms\(^{-2}\), \(\beta =40000\,\hbox {Kgm}^{-1}\text {s}^{-2}\), \(q=1\,\text {m}^{2}\hbox {s}^{-3}\), and \(T=2\) s with number of path samples \(N=60\). Truth is initialized with \(\mathbf {x}_{0}=232000\) m, \(\mathbf {y}_{0}=88000\) m, \(\mathbf {u}_{0}=2290\) ms\(^{-1}\), \(\gamma _{0}=190^{\circ }\) where \(\gamma\) is the angle between horizontal axis and the direction of motion.

Fig. 1
figure 1

Target trajectory of ballistic target

Full size image
Fig. 2
figure 2

Speed of ballistic target versus time

Full size image
Fig. 3
figure 3

Acceleration of ballistic target versus time

Full size image

The measurement equation is given as

$$\begin{aligned} y_{k}=Hx_{k}+v_{k}, \end{aligned}$$

where \(H=\begin{bmatrix} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0 \end{bmatrix}\), \(y_{k}=\begin{bmatrix} d_{k}&h_{k} \end{bmatrix}^{T}\) is the radar measurement in Cartesian coordinate. Considering radar to be located at the origin and measurements collected are the range r, and elevation \(\varepsilon\); \(d=r\text{cos}\varepsilon\) and \(h=r\text{sin}\varepsilon\) are measurement of the positions along \(\mathbf {x}\) and \(\mathbf {y}\) Cartesian coordinates respectively. \(v_{k}\) is the measurement noise which is white Gaussian with zero mean and covariance \(R_{k}\), given by

$$\begin{aligned} R_{k}=\begin{bmatrix} \sigma ^{2}_{d} &{} \sigma _{dh}\\ \sigma _{dh} &{} \sigma ^{2}_{h} \end{bmatrix}, \end{aligned}$$

where

$$\begin{aligned}&\sigma ^{2}_{d}=\sigma ^{2}_{r}\text{cos}^{2}(\varepsilon _k)+r_k^{2}\sigma _{\varepsilon }^{2}\text{sin}^{2}(\varepsilon _k), \\&\sigma ^{2}_{h}=\sigma ^{2}_{r}\text{sin}^{2}(\varepsilon _k)+r_k^{2}\sigma _{\varepsilon }^{2}\text{cos}^{2}(\varepsilon _k), \\&\sigma _{dh}=(\sigma ^{2}_{r}-r_k^{2}\sigma _{\varepsilon }^{2})\text{sin}(\varepsilon _k)\text{cos}(\varepsilon _k). \end{aligned}$$

Here, \(\sigma _{r}\) and \(\sigma _{\varepsilon }\) are the standard deviations of radar measurement for range and elevetion. The above expression for \(R_{k}\) is derived by measurement conversion from polar to Cartesian coordinate and is good approximation for linear measurement. The detail derivation of measurement noise covariance \(R_{k}\) is shown at the end of this section.

The above described problem of tracking a ballistic object is solved using the risk sensitive cubature quadrature Kalman filter (RSCQKF) with fourth order Gauss-Laguerre approximation and its performance is compared with the cubature quadrature Kalman filter (CQKF) in terms of root mean square error (RMSE). During simulation the radar parameters used are \(\sigma _{r}=100\) m, \(\sigma _{\varepsilon }=0.017\) rad. From the first two measurements, filters are initialized as \(\hat{x}_{0|0}=\begin{bmatrix} d_{1}&\frac{d_{2}-d_{1}}{T}&h_{1}&\frac{ h_{2}-h_{1}}{T} \end{bmatrix}^{T}\). The Initial error covariance matrix is derived as

$$\begin{aligned} P_{0|0}=\begin{bmatrix} \sigma ^{2}_{d} &{} -\frac{\sigma ^{2}_{d}}{T} &{} \sigma _{dh} &{} -\frac{\sigma _{dh}}{T}\\ -\frac{\sigma ^{2}_{d}}{T} &{} 2\frac{\sigma ^{2}_{d}}{T^2} &{} -\frac{\sigma _{dh}}{T} &{} 2\frac{\sigma _{dh}}{T^2}\\ \sigma _{dh} &{} -\frac{\sigma _{dh}}{T} &{} \sigma ^{2}_{h} &{} -\frac{\sigma ^{2}_{h}}{T}\\ -\frac{\sigma _{dh}}{T} &{} 2\frac{\sigma _{dh}}{T^2} &{} -\frac{\sigma ^{2}_{h}}{T} &{} 2\frac{\sigma ^{2}_{h}}{T^2} \end{bmatrix}. \end{aligned}$$

The derivation of \(P_{0|0}\) is given at the end of this section.

The process noise covariance for filter is mismatched with that for truth value. The parameter q of process noise covariance for truth remains unity whereas q for filter is taken as 0.01. The risk sensitive parameter \(\mu _{1}\) is chosen as \(7\times 10^{-9}\). The value of \(\mu _{1}\) is obtained here such that it provide the best achievable performance in terms of RMSE and satisfy the positive definiteness condition of error covariance matrix.

Figures 4 and 5 show the plot of truth and estimated values obtained from RSCQKF for position and velocity respectively.

Fig. 4
figure 4

Truth and estimate of RSCQKF for target position

Full size image
Fig. 5
figure 5

Truth and estimate of RSCQKF for target velocity

Full size image

Figures 6, 7, 8 and 9, show root mean square error plot (out of 100 Monte Carlo runs) of position and velocity estimation obtained from RSCQKF, RSCKF, CQKF and CKF. The RMSE values averaged over time span for position and velocity estimation are tabulated in Table 1. The following points can be concluded from the simulation results:

  • From the Figs. 6, 7, 8 and 9 it can be concluded that CQKF provides results similar with CKF. It is also observed that performance improvement occurs with RSCKF/RSCQKF with respect to risk neutral filters in presence of process model uncertainty.

  • From the Table 1, it can also be claimed that the CQKF is slightly better than CKF. Risk sensitive filters are better than risk neutral filter for wrongly modelled process noise parameter.

Table 1 Average root mean square error of RSCQKF, RSCKF, CQKF and CKF
Full size table
Fig. 6
figure 6

RMSE plot of RSCQKF, RSCKF, CQKF and CKF for \(\mathbf {x}\)-position (in km) of the target

Full size image
Fig. 7
figure 7

RMSE plot of RSCQKF, RSCKF, CQKF and CKF for \(\mathbf {y}\)-position (in km) of the target

Full size image
Fig. 8
figure 8

RMSE plot of RSCQKF, RSCKF, CQKF and CKF for \(\mathbf {x}\)-velocity (in km/s) of the target

Full size image
Fig. 9
figure 9

RMSE plot of RSCQKF, RSCKF, CQKF and CKF for \(\mathbf {y}\)-velocity (in km/s) of the target

Full size image

4.1 Derivation of measurement noise covariance \(R_{k}\) in Cartesian coordinate

As per earlier discussion, the expression for measurement noise covariance, \(R_{k}\), in Cartesian coordinate is derived here. Let us consider

$$\begin{aligned}&d_{k}=\mathbf {x}_{k}+v_{\mathbf {x}k}, \end{aligned}$$
(29)
$$\begin{aligned}&h_{k}=\mathbf {y}_{k}+v_{\mathbf {y}k}, \end{aligned}$$
(30)

where \(\mathbf {x}_{k}\) and \(\mathbf {y}_{k}\) are truth value and \(v_{\mathbf {x}k}\) and \(v_{\mathbf {y}k}\) are measurement noise at \(k^{th}\) time instant associated with \(\mathbf {x}\) and \(\mathbf {y}\) positions in Cartesian coordinates respectively and

$$\begin{aligned}&r_{k}=r'_{k}+v_{rk}, \end{aligned}$$
(31)
$$\begin{aligned}&\epsilon _{k}=\epsilon '_{k}+v_{\epsilon k}, \end{aligned}$$
(32)

where \(r'_{k}\) and \(\epsilon '_{k}\) are truth value and \(v_{rk}\) and \(v_{\epsilon k}\) are measurement noise at \(k^{th}\) time instant associated with radar range and elevation respectively. Now, putting \(d_{k}=r_{k}\text{cos} {\epsilon _k}\) and \(h_{k}=r_{k}\text{sin} {\epsilon _k}\) in Eqs. (29) and (30), we get

$$\begin{aligned}&r_{k}\text{cos} {\epsilon _k}=\mathbf {x}_{k}+v_{\mathbf {x}k}, \end{aligned}$$
(33)
$$\begin{aligned}&r_{k}\text{sin} {\epsilon _k}=\mathbf {y}_{k}+v_{\mathbf {y}k}. \end{aligned}$$
(34)

From Eqs. (31) and (32), putting the value of \(r_{k}\) and \(\epsilon _{k}\) in Eqs. (33) and (34), we get

$$\begin{aligned}&( r'_{k}+v_{rk}) \text{cos} {(\epsilon '_{k}+v_{\epsilon k})}=\mathbf {x}_{k}+v_{\mathbf {x}k}, \end{aligned}$$
(35)
$$\begin{aligned}&( \epsilon '_{k}+v_{\epsilon k}) \text{sin} {(\epsilon '_{k}+v_{\epsilon k})}=\mathbf {y}_{k}+v_{\mathbf {y}k}. \end{aligned}$$
(36)

From Eq. (35)

$$\begin{aligned} r'_{k} \text{cos} {\epsilon '_{k}} \text{cos} v_{\epsilon k} - r'_{k}\text{sin} {\epsilon '_{k}} \text{sin} v_{\epsilon k}+ v_{rk} \text{cos} {\epsilon '_{k}} \text{cos} v_{\epsilon k} - v_{rk}\text{sin} {\epsilon '_{k}} \text{sin} v_{\epsilon k} =\mathbf {x}_{k}+v_{\mathbf {x}k} \end{aligned}$$
(37)

Since \(v_{rk}\sim \aleph (0,\sigma _r^2)\) and \(v_{\epsilon k}\sim \aleph (0,\sigma _\epsilon ^2)\), hence assuming \(v_{\epsilon k}\rightarrow 0\) we have \(\text{cos}v_{\epsilon k}\rightarrow 1\) and \(\text{sin} v_{\epsilon k}\rightarrow v_{\epsilon k}\). Equation (37) can be written as

$$\begin{aligned} r'_{k} \text{cos} {\epsilon '_{k}} - r'_{k}\text{sin} {\epsilon '_{k}} (v_{\epsilon k})+ v_{rk} \text{cos} {\epsilon '_{k}} - v_{rk}\text{sin} {\epsilon '_{k}} (v_{\epsilon k})\nonumber \\ =\mathbf {x}_{k}+v_{\mathbf {x}k} . \end{aligned}$$
(38)

Since, \(\mathbf {x}_{k}=r'_{k} \text{cos} {\epsilon '_{k}}\), we get

$$\begin{aligned} v_{\mathbf {x}k}=v_{rk} \text{cos} {\epsilon '_{k}} -r'_{k}v_{\epsilon k} \text{sin} {\epsilon '_{k}}-v_{rk} v_{\epsilon k} \text{sin} {\epsilon '_{k}}. \end{aligned}$$
(39)

Assuming

$$\begin{aligned} v_{rk} \text{cos} {\epsilon '_{k}} -r'_{k}v_{\epsilon k} \text{sin} {\epsilon '_{k}} \gg v_{rk} v_{\epsilon k} \text{sin} {\epsilon '_{k}}, \end{aligned}$$
(40)

we get

$$\begin{aligned} v_{\mathbf {x}k}=v_{rk} \text{cos} {\epsilon '_{k}} -r'_{k}v_{\epsilon k} \text{sin} {\epsilon '_{k}}. \end{aligned}$$
(41)

Now from Eq. (36)

$$\begin{aligned} r'_{k} \text{sin} {\epsilon '_{k}} \text{cos} v_{\epsilon k} + r'_{k}\text{cos} {\epsilon '_{k}} \text{sin} v_{\epsilon k}+ v_{rk} \text{sin} {\epsilon '_{k}} \text{cos} v_{\epsilon k} + v_{rk}\text{cos} {\epsilon '_{k}} \text{sin} v_{\epsilon k} =\mathbf {y}_{k}+v_{\mathbf {y}k}. \end{aligned}$$
(42)

Since \(v_{rk}\sim \aleph (0,\sigma _r^2)\) and \(v_{\epsilon k}\sim \aleph (0,\sigma _\epsilon ^2)\), hence assuming \(v_{\epsilon k}\rightarrow 0\), we have \(\text{cos}v_{\epsilon k}\rightarrow 1\) and \(\text{sin} v_{\epsilon k}\rightarrow v_{\epsilon k}\). Equation (42) can be given as

$$\begin{aligned} r'_{k} \text{sin} {\epsilon '_{k}} + r'_{k}\text{cos} {\epsilon '_{k}} (v_{\epsilon k})+ v_{rk} \text{sin} {\epsilon '_{k}} + v_{rk}\text{cos} {\epsilon '_{k}} (v_{\epsilon k}) =\mathbf {y}_{k}+v_{\mathbf {y}k}. \end{aligned}$$
(43)

Since, \(\mathbf {y}_{k}=r'_{k} \text{sin} {\epsilon '_{k}}\), we get

$$\begin{aligned} v_{\mathbf {y}k}=v_{rk} \text{sin} {\epsilon '_{k}} + r'_{k}v_{\epsilon k} \text{cos} {\epsilon '_{k}}+ v_{rk} v_{\epsilon k}\text{cos} {\epsilon '_{k}}. \end{aligned}$$
(44)

Assuming

$$\begin{aligned} v_{rk} \text{sin} {\epsilon '_{k}} + r'_{k}v_{\epsilon k} \text{cos} {\epsilon '_{k}} \gg v_{rk} v_{\epsilon k} \text{cos} {\epsilon '_{k}}, \end{aligned}$$
(45)

we get

$$\begin{aligned} v_{\mathbf {y}k}=v_{rk} \text{sin} {\epsilon '_{k}} + r'_{k}v_{\epsilon k} \text{cos} {\epsilon '_{k}}. \end{aligned}$$
(46)

From Eqs. (41) and (46), the measurement noise vector in Cartesian coordinate is given as

$$\begin{aligned} V_{k}=\begin{bmatrix} v_{\mathbf {x}k} \\ v_{\mathbf {y}k} \end{bmatrix}=\begin{bmatrix} v_{rk} \text{cos} {\epsilon '_{k}} -r'_{k}v_{\epsilon k} \text{sin} {\epsilon '_{k}}\\ v_{rk} \text{sin} {\epsilon '_{k}} + r'_{k}v_{\epsilon k} \text{cos} {\epsilon '_{k}} \end{bmatrix}. \end{aligned}$$

The measurement noise covariance \(R_{k}\) in Cartesian coordinate is given by

$$\begin{aligned} \begin{aligned}&R_{k}=E[V_{k}V_{k}^{T}]\\&=E\left( \begin{bmatrix} v_{\mathbf {x}k}\\ v_{\mathbf {y}k} \end{bmatrix}\begin{bmatrix} v_{\mathbf {x}k}&v_{\mathbf {y}k} \end{bmatrix}\right) \\&=E \left( \begin{bmatrix} v_{rk} \text{cos} {\epsilon '_{k}} -r'_{k}v_{\epsilon k} \text{sin} {\epsilon '_{k}}\\ v_{rk} \text{sin} {\epsilon '_{k}} + r'_{k}v_{\epsilon k} \text{cos} {\epsilon '_{k}} \end{bmatrix} \begin{bmatrix} v_{rk} \text{cos} {\epsilon '_{k}} -r'_{k}v_{\epsilon k} \text{sin} {\epsilon '_{k}} \\ v_{rk} \text{sin} {\epsilon '_{k}} + r'_{k}v_{\epsilon k} \text{cos} {\epsilon '_{k}} \end{bmatrix}^T \right) . \end{aligned} \end{aligned}$$

Since, \(v_{rk}\sim \aleph (0,\sigma _r^2)\) and \(v_{\epsilon k}\sim \aleph (0,\sigma _\epsilon ^2)\) are white noise and zero mean Gaussian independent from each other, so putting \(E[v_{rk}v_{rk}]=\sigma _{r}^{2}\) , \(E[v_{\epsilon k}v_{\epsilon k}]=\sigma _{\epsilon }^{2}\) and \(E[v_{rk}v_{\epsilon k}]=0\) we get the expression for \(R_{k}\) as

$$\begin{aligned} R_{k}=\begin{bmatrix} \sigma ^2_{d} &{} \sigma _{dh}\\ \sigma _{dh} &{} \sigma ^2_{h} \end{bmatrix}, \end{aligned}$$
(47)

where

$$\begin{aligned}&\sigma ^2_{d}=\sigma _{r}^{2} \text{cos} ^{2}{\epsilon '_{k}}+ r_{k}^{'2} \sigma _{\epsilon }^{2} \text{sin}^{2}{\epsilon '_{k}}, \end{aligned}$$
(48)
$$\begin{aligned}&\sigma _{dh}=\sigma _{r}^{2} \text{cos} {\epsilon '_{k}} \text{sin} {\epsilon '_{k}}- r_{k}^{'2} \sigma _{\epsilon }^{2} \text{sin}{\epsilon '_{k}}\text{cos}{\epsilon '_{k}}, \end{aligned}$$
(49)
$$\begin{aligned}&\sigma _h^2=\sigma _{r}^{2} \text{sin} ^{2}{\epsilon '_{k}}+ r_{k}^{'2} \sigma _{\epsilon }^{2} \text{cos}^{2}{\epsilon '_{k}}. \end{aligned}$$
(50)

4.2 Derivation of initial error covariance \(P_{0|0}\)

The filter is initialized from first two measurements as

$$\begin{aligned} \hat{x}_{0|0}= \begin{bmatrix} d_{1}&\frac{d_{2}-d_{1}}{T}&h_{1}&\frac{h_{2}-h_{1}}{T} \end{bmatrix}^T. \end{aligned}$$

The initial value of truth is given as

$$\begin{aligned} {x}_{0}= \begin{bmatrix} \mathbf {x}_{1}&\frac{\mathbf {x}_{2}-\mathbf {x}_{1}}{T}&\mathbf {y}_{1}&\frac{\mathbf {y}_{2}-\mathbf {y}_{1}}{T} \end{bmatrix}^T. \end{aligned}$$

The initial error is given as (from Eqs. (29) and (30))

$$\begin{aligned} \begin{aligned} \hat{e}_{0|0}=&\hat{x}_{0|0}-x_{0}\\ =&\begin{bmatrix} v_{\mathbf {x}1}&\frac{v_{\mathbf {x}2}-v_{\mathbf {x}1}}{T}&v_{\mathbf {y}1}&\frac{v_{\mathbf {y}2}-v_{\mathbf {y}1}}{T} \end{bmatrix}^T. \end{aligned} \end{aligned}$$

The initial error covariance \(P_{0|0}\) is given as

$$\begin{aligned} \begin{aligned} P_{0|0}&=E[\hat{e}_{0|0}\hat{e}_{0|0}^T]\\ & = E\left( \begin{bmatrix} v_{\mathbf {x}1}&\frac{v_{\mathbf {x}2}-v_{\mathbf {x}1}}{T}&v_{\mathbf {y}1}&\frac{v_{\mathbf {y}2}-v_{\mathbf {y}1}}{T} \end{bmatrix}^T \begin{bmatrix} v_{\mathbf {x}1}&\frac{v_{\mathbf {x}2}-v_{\mathbf {x}1}}{T}&v_{\mathbf {y}1}&\frac{v_{\mathbf {y}2}-v_{\mathbf {y}1}}{T} \end{bmatrix} \right) . \end{aligned} \end{aligned}$$
(51)

Since, \(v_{\mathbf {x}k}\sim \aleph (0,\sigma _d^2)\) and \(v_{\mathbf {y}k}\sim \aleph (0,\sigma _h^2)\) are white noise and zero mean Gaussian, so putting \(E[v_{\mathbf {x}i}v_{\mathbf {x}j}]=\sigma _{d}^{2}\delta _{ij}\) , \(E[v_{\mathbf {y}i}v_{\mathbf {y} j}]=\sigma _{h}^{2}\delta _{ij}\) and \(E[v_{\mathbf {x}i}v_{\mathbf {y}j}]=\sigma _{dh} \delta _{ij}\) (where \(\delta _{ij}\) is Kronecker delta function), we get the expression for \(P_{0|0}\) as

$$\begin{aligned} P_{0|0}=\begin{bmatrix} \sigma _d^2 &{} \frac{-\sigma _d^2}{T} &{} \sigma _{dh} &{} \frac{-\sigma _{dh}}{T}\\ \frac{-\sigma _d^2}{T} &{} \frac{2\sigma _d^2}{T^2} &{} \frac{-\sigma _{dh}}{T} &{} \frac{2\sigma _{dh}}{T^2}\\ \sigma _{dh} &{} \frac{-\sigma _{dh}}{T} &{} \sigma _h^2 &{} \frac{-\sigma _h^2}{T}\\ \frac{-\sigma _{dh}}{T} &{} \frac{2\sigma _{dh}}{T^2} &{} \frac{-\sigma _h^2}{T} &{} \frac{2\sigma _h^2}{T^2} \end{bmatrix} \end{aligned}$$
(52)

5 Discussion

In this paper, a risk sensitive filter based on cubature quadrature Kalman filter has been applied for tracking of ballistic object during its re-entry phase for wrongly modeled process noise parameter and its improvement in performance over its risk neutral counterpart has been shown. The process model for two dimensional ballistic target motion has been comprehensively described. The expression for measurement noise covariance matrix for measurement model has been derived for Cartesian coordinate from polar coordinate which is a good approximation of linear measurement model. Also the expression for initial error covariance matrix for the filter initialized from the first two measurements has been derived. Moreover, risk sensitive cubature quadrature Kalman filter has been shown to perform better than risk sensitive cubature Kalman filter [21] and hence can be shown to perform better than the risk sensitive filter based on other Gaussian filter found in literature [17,18,19,20], because cubature Kalman filter is more advance than those Gaussian filters.

6 Conclusion

The risk sensitive filter based on cubature quadrature Kalman filter is applied to track the two dimensional ballistic target motion. Since measurement noise covariance matrix for linear measurement model and initial error covariance matrix have been derived, more advanced Gaussian filters with risk sensitive counterpart may also be applied for tracking of two dimensional ballistic target motion. Also application of Gaussian filters with risk sensitive counterpart for three dimensional ballistic target motion will remain under the scope of future research work.