1 Introduction

Reduction of greenhouse gas (GHG) emission, enforced by legislation, is a driving force for minimizing vehicle weight, i.e. lightweighting [1]. Thus, there is a demand for lightweight materials and structures, allowing material replacement without degrading performance of vehicle components. Decisive factors for material selection include raw material cost as well as costs associated with material manufacturing. Lightweighting can be achieved by enhancing material properties of currently used materials, e.g. replacing mild steels with high performance steels at a reduced gauge thickness, or utilizing the benefits of composite- and sandwich materials. Modern development of automotive parts make use of virtual testing to reduce overall costs. Thus, for new materials to be of interest, numerical modeling must be possible, demanding accurate models at reasonable computational cost.

Replacing mild steels with ultra-high strength steels (UHSS) has been one of the most successful material substitutions with regard to lightweighting and reduction of GHG emissions [2]. The development of high-performance steel is an ongoing process, improving properties such as ductility, formability, fracture toughness and crawhworthiness, see e.g. [3, 4]. To expand the use of UHSS, material properties must be further improved and developed for additional weight savings. An alternative may be to utilize the benefits of sandwich structures, as have been demonstrated in [5] and [6], where UHSS sandwich structures were investigated for stiffness and energy absorption, respectively.

For sandwich materials to succeed in the automotive industry, they must be formable and adequately thin to replace sheet metals [7]. This has driven the development of thin sandwich structures, also referred to as micro-sandwich materials. In the late 1980’s Bhart et al. [8] developed a sandwich structure with cell-walls consisting of a micro-sandwich, suitable for stiffness applications. Micro-sandwich materials typically combine metal skins with metal or polymeric cores [7, 9, 10]. Hylite [11] is a micro-sandwich combining aluminum skins with a polypropylene core, exhibiting excellent stiffness properties Kim et al. [12], Burchitz et al. [13], Carradò et al. [14], as well as being formable using drawing, as reported by Hufenbach et al. [15]. Bondal, a micro-sandwich suitable for vibration damping and produced by Thyssenkrupp, was studied experimentally by Kami et al. [16]. The study included T-peel tests for studying bonding strength between core and skins. Additional micro-sandwich materials include LiteCore, studied in part by Tanco et al. [9]. Hybrix™, developed and manufactured by Lamera AB, belongs to a category of micro-sandwich materials with fibrous cores, see e.g. [17, 18]. Pimentel et al. [19] and Pimentel et al. [20] suggested methods for characterizing the Hybrix™ micro-sandwich by in-plane tensile testing. In the works the micro-sandwich material and the skin material were tested separately in tension, after which the properties of the core were obtained by subtracting the response of the skins from the response of the micro-sandwich. The suggested methods does not consider out-of-plane properties of the Hybrix™ core, e.g. transverse tensile/compressive stiffness or out-of-plane shear stiffness. For a sandwich material to maintain its properties, the core must be sufficiently stiff with regard to out-of-plane loading, hindering the core from collapsing. In a previous paper by the authors of the present work, see Hammarberg et al. [21], a novel method for mechanical characterization of the out-of-plane properties of micro-sandwich cores was suggested. The method was successfully used on the micro-sandwich material Hybrix™. A conceptual image of Hybrix™ is presented in Fig. 1.

Fig. 1
figure 1

Conceptual description of the micro-sandwich Hybrix™ [21]

Full size image

Research on modeling of sandwich materials has been carried out by several authors. Typically, layered finite shell elements are suggested for representing layered materials, see e.g. [22,23,24,25]. Layered methods are typically associated with increased computational time, as compared to using an equivalent single layer. In the work by Främby et al. [26], the issue of computational cost is addressed by suggesting an adaptive approach, where the equivalent single layer is locally refined through the thickness during the simulation. Regarding modeling of micro-sandwich materials, out-of-plane properties are typically ignored, assumed to equal in-plane properties, see [19, 20].

The objective of the present work is to investigate how numerical modeling of micro-sandwich materials with cores consisting of randomly distributed fibers, having a preferred alignment in the thickness direction, may be conducted, including elasto-plasticity, damage and fracture, using constitutive routines available in commercial software. The micro-sandwich is modeled as three layers, where the skins are represented by an isotropic, elasto-plastic material model whereas the core is modeled using an anisotropic, elasto-plastic model. To improve accuracy and predictability when modeling the core, an incremental stress state dependent damage model is also included, where onset of damage and fracture are dependent on stress triaxiality. Both models used for the core are calibrated using experimental data from [21]. To validate the numerical models, an experimental T-peel test is performed from which the peeling force, required to separate core and skins, is obtained, see e.g. [16]. The mean peel force of the experiments is compared with the peel force obtained from numerical models, based on the finite element method (FEM). Precise discretization of the core’s micro structure is not feasible. Thus a continuum and discrete approach, used for discretizing the micro-sandwich core, are investigated. The novelty of the work lies in the 3D numerical representation of the micro-sandwich core, using an anisotropic elasto-plastic model, with input data directly obtained from [21] where the core was subjected to the appropriate stress-states, as well as the inclusion of a stress-state dependent damage model, validated experimentally using the T-peel test. This type of modeling approach has not been conducted previously for micro-sandwich materials with randomly distributed fibrous cores.

The outline of the paper is the following: In Sect. 2 the geometries and materials of the paper are presented and in Sect. 3 the finite element modeling of the micro-sandwich material (including constitutive routines and damage models and how these are calibrated) is presented. In Sect. 4 the experimental setup for performing T-peel tests are presented. The final three sections of the paper are dedicated to results (Sect. 5 ) , discussion (Sect. 6) and conclusions (Sect. 7).

2 Geometries and material

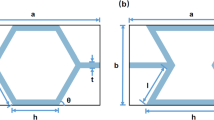
Three load cases were used in the present study. The first two correspond to transverse tension and out-of-plane shear. In Fig. 2, fixtures for loading micro-sandwich specimens of size \(40 \times 15 \times 1.2\) mm\(^{3}\), in accordance with [21], are presented. Figure 2a and b correspond to transverse tension and out-of-plane shear, respectively, from which input data was taken and used for calibrating the numerical models of the present work. The third load case used in the present study corresponds to a T-peel test, used for validation of the numerical models as it provokes core failure and delamination [16], see Fig. 3. All micro-sandwich specimens consisted of Hybrix™ TMK:7609, where 0.3 mm thick carbon steel skins (DC04) were bonded to a 0.6 mm thick core, based on polyamide fibers, see Fig. 4. The skins had a density of 7800 kg/m\(^{3}\), with Young’s modulus and Poisson’s ratio given as 210 GPa and 0.3, respectively.

Fig. 2
figure 2

An illustration of the test fixture used for subjecting the micro-sandwich to a transverse tension and b out-of-plane shear, as presented in [21]. The nuts and washers, used during mounting of the Hybrix™ specimens, were removed before testing

Full size image
Fig. 3
figure 3

T-peel test used for validating numerical models. Side view (a) and front view (b)

Full size image
Fig. 4
figure 4

The skins of the Hybrix™ are based on 0.3 mm thick carbon steel (DC04), enclosing the 0.6 mm core, based on polyamide fibers

Full size image

3 Finite element modeling

The current sections introduce the models used to numerically simulate the micro-sandwich material Hybrix™, using FEM. The constitutive models used in this work are presented in Sect. 3.1. In Sect. 3.2, the method for calibrating the constitutive models are presented, followed by a section presenting the numerical models of the T-peel test, used for validation. All simulations were run using the multi-physics software LS-DYNA and its R12.0 solver [27].

3.1 Constitutive- and damage models

A piecewise linear plasticity model, *MAT_024 [27] within LS-DYNA, was used to numerically represent the skins. Young’s modulus, mass density, Poisson’s ratio and yield stress vs effective plastic strain were given as input data. The input data for the skins is summarized in Table 1 and Fig. 5.

Table 1 Material data for the DC04 steel, used for the skins of the Hybrix™ micro-sandwich
Full size table
Fig. 5
figure 5

Effective stress (von Mises) versus effective plastic strain for the skin material (DC04)

Full size image

Modeling of the core was conducted using an anisotropic, elasto-plastic material model, *MAT_157 [27] within LS-DYNA. In the material model, the anisotropic tensor, \(C_{ijkl}\), relating stresses and strains according to Eq. (1), was given as input.

$$\begin{aligned} \sigma _{ij} = C_{ijkl} \epsilon _{kl}. \end{aligned}$$
(1)

In Eq. (1), \(\sigma _{ij}\) and \(\epsilon _{ij}\) are the stress and strain tensors, respectively, with indices ranging from 1 to 3. The yield surface of MAT_157 is based on Hill’s anisotropic yield criteria [28], where the equivalent stress, \(\bar{\sigma }\), may be expressed as

$$\begin{aligned} \bar{\sigma } = \sqrt{ \sigma _{y0}^2 \sigma _i P_{ij} \sigma _j } \end{aligned}$$
(2)

with

$$\begin{aligned} \sigma _{y0} = \left( \frac{3}{2 (F+G+H)} \right) ^{1/2}. \end{aligned}$$
(3)

In Eq. (2) the stress tensor is expressed using Voigt notation, see Eq. (4), allowing the anisotropic yield tensor, \(P_{ij}\), to be expressed according to Eq. (5).

$$\begin{aligned} \varvec{\sigma }= & {} \left[ \begin{array}{l} \sigma _{11}\\ \sigma _{22}\\ \sigma _{33}\\ \sigma _{23}\\ \sigma _{13}\\ \sigma _{12} \end{array}\right] \end{aligned}$$
(4)
$$\begin{aligned} {\varvec{P}}= & {} \left[ \begin{array}{cccccc} H+G &{}\quad -H &{}\quad -G &{}\quad 0 &{}\quad 0 &{}\quad 0\\ -H &{}\quad H+F &{}\quad -F &{}\quad 0 &{}\quad 0 &{}\quad 0\\ -G &{}\quad -F &{}\quad G+F &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 2L &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 2M &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 2N \end{array}\right] . \end{aligned}$$
(5)

Inserting Eqs. (4) and (5) into Eq. (6), squaring both sides, Hill’s yield criteria is obtained as

$$\begin{aligned} \begin{aligned} f\left( \sigma \right)&\equiv \left[ \right. F \left( \sigma _{22}-\sigma _{33} \right) ^2 + G \left( \sigma _{11}-\sigma _{33} \right) ^2 + H \left( \sigma _{11}-\sigma _{22} \right) ^2 \\&\quad \left. +2L\sigma _{23}^2 + 2M \sigma _{13}^2 + 2N \sigma _{12}^2 \right] ^{1/2} - (\sigma _{y0} + K(\epsilon _{eff,pl})) \end{aligned} \end{aligned}$$
(6)

where F, G, H, L, M and N are material constants, governing the anisotropic yield response, \(\sigma _{y0}\) is the initial yield stress, and K a hardening parameter dependent on the effective plastic strain. From Eq. (6), expressions for F, G, H, L, M and N may be obtained, see Eqs. (7) and (8), where \(\sigma ^{ij}_{y0}\) and \(\tau ^{ij}_{y0}\) are the yield stresses in tension and shear for the corresponding directions, respectively. Furthermore, for the material model, the equivalent stress as a function of effective plastic strain, was prescribed in tabular form.

$$\begin{aligned}&\begin{aligned}&F = \frac{1}{2} \left[ \frac{1}{(\sigma _{y0}^{22})^2} + \frac{1}{(\sigma _{y0}^{33})^2} - \frac{1}{(\sigma _{y0}^{11})^2} \right] \\&G = \frac{1}{2} \left[ \frac{1}{(\sigma _{y0}^{33})^2} + \frac{1}{(\sigma _{y0}^{11})^2} - \frac{1}{(\sigma _{y0}^{22})^2} \right] \\&H = \frac{1}{2} \left[ \frac{1}{(\sigma _{y0}^{11})^2} + \frac{1}{(\sigma _{y0}^{22})^2} - \frac{1}{(\sigma _{y0}^{33})^2} \right] \end{aligned} \end{aligned}$$
(7)
$$\begin{aligned}&\begin{aligned} L&= \frac{1}{2 (\tau ^{23}_{y0})^2} \\ M&= \frac{1}{2 (\tau ^{13}_{y0})^2} \\ N&= \frac{1}{2 (\tau ^{12}_{y0})^2} \end{aligned} \end{aligned}$$
(8)

To account for damage and failure, the Generalized Incremental Stress State Dependent Damage Model (GISSMO), developed and improved by Neukamm et al. [29] and Basaran et al. [30], respectively, was adopted. An incremental formulation of damage accumulation is used:

$$\begin{aligned} \Delta D = \frac{n D^{\left( 1 - 1/n\right) }}{\epsilon _f\left( \eta \right) } \Delta \epsilon _{eff,pl}. \end{aligned}$$
(9)

In Eq. (9), D is the accumulated damage and failure occurs for \(D \ge 1\). n is an exponent governing the nonlinear damage accumulation, \(\Delta \epsilon _{eff, pl}\) is the effective plastic strain, \(\epsilon _f\) is the equivalent plastic failure strain and \(\eta \) is the stress triaxiality

$$\begin{aligned} \eta = \frac{\sigma _{kk}}{\bar{\sigma }}. \end{aligned}$$
(10)

Instability or localization is accounted for by defining an instability measure, \(F_{loc} \le 1\), according to

$$\begin{aligned} \Delta F_{loc} = \frac{n F_{loc}^{\left( 1 - 1/n \right) }}{\epsilon \left( \eta \right) _{p, loc}}\Delta \epsilon _{eff, pl}. \end{aligned}$$
(11)

In Eq. (11), \(\epsilon _{p, loc}\), is the instability strain. When the instability measure reaches unity, the current damage value is stored as \(D_{crit}\), and the current stress, \(\tilde{\sigma }\) is coupled to the damage, reducing load bearing capacity of the corresponding finite element, see Eq. (12), where m is an exponent for damage-related stress fadeout.

$$\begin{aligned} \sigma = \tilde{\sigma } \left[ 1 - \left( \frac{D - D_{crit}}{1 - D_{crit}}\right) ^m \right] \end{aligned}$$
(12)

3.2 Calibration

Calibrations of the constitutive models, presented in Sect. 3.1, were performed using the optimization software LS-OPT [31]. The objective was set to minimize the difference between the experimental force–displacement data of Fig. 6 and the response of the numerical models, in a least square sense. It was assumed that the experimental data of Fig. 6 corresponds to homogeneous states of stress, thus a FEM model consisting of a single layer of solid elements was used during calibration, see Fig. 7. The model consisted of fully integrated solid elements with an edge length of approximately 0.6 mm. Boundary conditions were applied appropriately to recreate the stress-states corresponding to those obtained using the test fixtures of Fig. 3, i.e. transverse tension and out-of-plane shear.

Fig. 6
figure 6

Experimental force–displacement response curves for a tensile testing and b shear testing of the Hybrix™ micro-sandwich, obtained from the work by Hammarberg et al. [21]

Full size image
Fig. 7
figure 7

In a and b the finite element mesh, using fully integrated solid elements, of the Hybrix™ core used for calibrating the constitutive models are presented

Full size image

Figure 6a and b contain the experimental response of the micro-sandwich when subjected to transverse tension and shear loading, respectively, as presented in [21]. In both cases, the force–displacement curves are presented up until the point of failure. Due to the rapid, brittle failure that occurred at the end of the tensile loading, the failure part was not captured with high enough resolution. This part was thus added manually, see Fig. 6a, using a conservative choice of the slope to be compared with the response of the damage model. It was assumed that damage and instabilities of the material were initiated at peak force, see Fig. 6. Thus, the constitutive model, *MAT_157, was used to model the behaviour up until peak load. At peak load the damage model was initiated, reducing the load bearing capacity and eventually eroding the finite elements of the numerical models. This resulted in the use of the two LS-OPT schemes presented in Fig. 8.

3.2.1 Calibration of the anisotropic, elasto-plastic constitutive model

The LS-OPT scheme presented in Fig. 8a was used to calibrate *MAT_157, recreating the response of Fig. 6 up until peak load. The parameters to be tuned were the constituents of the tensors in Eqs. (1) and (5), as well as the hardening curve, defined in the setup state of Fig. 8a. In general, \(C_{ijkl}\), is a fully populated tensor, but in the context of Hybrix™, the fibrous core was assumed to have limited contribution to in-plane stiffness and negligible Poisson’s effect, reducing \(C_{ijkl}\) to

$$\begin{aligned} {\varvec{C}} = \left[ \begin{array}{cccccc} C_{11} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad C_{44} &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad C_{66} \end{array}\right] . \end{aligned}$$
(13)

In Eq. (13), \(C_{11}\) corresponds to the stiffness in the thickness direction (fiber direction) whereas \(C_{44}\) and \(C_{66}\) are the stiffness constants associated with out-of-plane shearing, being equal due to in-plane isotropy. All other components of the anisotropic stiffness tensor were set to zero due to lack of coupling between fibers. In a similar manner, using the in-plane isotropy, i.e., \(G=H\) and \(M=N\), the anisotropic yield tensor, \(P_{ij}\) of Eq. (5), was reduced to

$$\begin{aligned} {\varvec{P}} = \left[ \begin{array}{cccccc} 2G &{}\quad -G &{}\quad -G &{}\quad 0 &{}\quad 0 &{}\quad 0\\ -G &{}\quad G+F &{}\quad -F &{}\quad 0 &{}\quad 0 &{}\quad 0\\ -G &{}\quad -F &{}\quad G+F &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 2L &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 2M &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 2M \end{array}\right] . \end{aligned}$$
(14)

The hardening curve was determined in two steps. The initial part of the curve was obtained by computing effective stress vs. effective plastic strain, based on the data presented in Fig. 6a. The second part of the curve was obtained by curve fitting, using a spline, defined in the stage named “HardeningCurve”, see Fig. 8a. The spline was given six input parameters in terms of three x-y-pairs. The resulting spline was then fitted to a plastic hardening model on the form \(\sigma _y = A+B \epsilon _{eff,pl}^{\beta }\), as suggested by Ludwik [32].

For each iteration of the optimization, the parameters of Eqs. (13) and (14), as well as the obtained hardening curve were used as input data in the “Shear” and “Tensile” stages of Fig. 8a, corresponding to the numerical tensile and shear models, respectively, run until the difference in response between the experimental data and the numerical models had been minimized in a least square sense.

3.2.2 Calibration of the damage- and fracture model

The parameters to be determined for the GISSMO model were the critical strains, \(\epsilon _{p,loc}\), fracture strains, \(\epsilon _f\) and the damage and fading exponents, n and m, respectively. Critical strains and fracture strains were determined directly from experiments. Where the former was taken as the strain corresponding to the maximum load and the latter as the strain at fracture. Thus, for tension, the fracture strain was chosen slightly larger than the critical strain, due to the brittle failure. Since softening did not occur during tensile testing but was significant during shearing, only the shear data was used to determine the remaining parameters, i.e. the damage and fading exponents, using the LS-OPT scheme in Fig. 8b. Thus, the damage and fading exponents were defined as the variable to be determined in the “Setup” stage, used as input for the numerical shear model in the stage named “Shear”. The optimization scheme was run until the difference between the experimental data and the numerical response had been minimized in a least square sense.

Fig. 8
figure 8

In a, the flowchart used for determining the constituents of the anisotropic elastic- and yield tensors (Eq. (13) and (14)), as well as the the hardening curve, is presented. In b, the flowchart used for determining the parameters of the damage model is presented

Full size image

3.3 Validation cases

Validation of the calibrated numerical models, presented in Sects. 3.1 and 3.2, was carried out using a peeling test presented in Fig. 9. In the peeling test, two approaches were used to model the core of the micro-sandwich, namely a continuous and a discrete representation. Using two approaches allowed for investigations regarding how the discretization of the core affected the response of the numerical model. This was of interest since the continuous representation of the core, by definition, introduced coupling between fibers, not present the physical micro-sandwich core. By also introducing a discrete representation of the core, the affect of the discretization approach could be investigated.

In the continuous representation, 20-node solid finite elements were used for both core and skins, sharing nodes in the contact interface, see Fig. 9b. Convergence studies were performed, regarding the number of solid elements required for the skins as well as the core, to obtained converged responses from the numerical models of the T-peel test. In the discrete approach, finite beam elements were used to represent the core, resembling the physical core, whereas fully integrated shell elements, with five integration points through the thickness, were used to represent the skins, see Fig. 9b. A contact condition was used to join skins and core for the discrete approach.

In accordance with Fig. 3, the top nodes of the upper skin were given a prescribed displacement, whereas the corresponding nodes on the bottom skin were fully clamped, to resemble the experimental setup described in Fig. 10. An implicit time integration scheme, with an automatic time step, was used for all simulations.

Fig. 9
figure 9

Two approaches for discretizing the core were used for the T-peel test. In a and b, the core is modeled using a continuum, based on solid finite elements. In c and d, a discrete approach is used where the core is modeled using beam elements

Full size image

4 Experimental T-peel test

The experimental setup of the T-peel test is presented in Fig. 10. Specimens, \(15 \times 150\) mm\(^{2}\), were manufactured by cutting. Grips were prepared by separating the skins, using a knife and pliers. The specimens were then placed in the servo-hydraulic testing machine, Instron 1272, and subjected to a displacement rate of 2 mm/min, i.e. quasi-static conditions. The stroke of the testing machine was limited to 100 mm, corresponding to a peeling distance of 50 mm. Stroke and load was logged by the machine.

Fig. 10
figure 10

Experimental setup for T-peeling test. The specimen is placed in the Instron 1272 testing machine with the upper grip being fixed and the lower displaced, peeling apart the sandwich specimen. During testing, stroke and load is logged

Full size image

5 Results and discussion

In this section, the results of the paper are presented and discussed. Initially, the results related to the calibration of the constitutive models are presented. This is followed by the numerical results from the T-peel test simulations, where two convergence tests were preformed for the continuous representation of the core. Firstly, a convergence study was performed with regard to the number of solid elements required for the skins, after which a convergence study was performed for the core. Lastly, the experimental data is compared with the converged numerical model for the continuum approach as well as the discrete approach used for modeling the core.

5.1 Calibration of constitutive models

Material models *MAT_157 and *MAT_ADD_GISSMO were calibrated, based on the experimental work performed in [21]. Initially, components \(C_{11}\) and \(C_{44}\) of the anisotropic stiffness tensor, \({\varvec{C}}\), as well as the constituents of the anisotropic yield tensor, \({\varvec{P}}\), were determined, see Table 2. The hardening curve, obtained as a spline, was fitted to an equation on the form \(\sigma _y = A + B \epsilon _{eff,pl}^\beta \), presented in Fig. 11a, with parameters according to Table 2. Using the parameters of Table 2, the shear and tensile tests were simulated with results presented in Fig. 11a and b. The shearing response is captured with adequate accuracy. In tension, a brittle failure occurred during the experimental testing. The slope of the loading curve, after peak force, exhibited a great variation, which was added manually with a conservative choice of the slope. In the damage model, the failure strain was chosen slightly larger than the instability strain. This is the reason for the difference in response when comparing the experimental and numerical data, with regard to tension.

Table 2 Parameters determined during calibration of the constitutive model and damage model
Full size table
Fig. 11
figure 11

Obtained data from the calibration of the constitutive- and damage model. In a, the hardening curve of Hybrix™ is presented. In b and c, the response of the numerical model with damage is presented for shear and tension, respectively, and compared with experimental data

Full size image

5.2 T-peeling test

The T-peel test was used to validate the calibrated numerical models by simulating a T-peel test and comparing with experiments. In the present section, the results from the numerical models are presented, initiated with a convergence study with regard to mesh size of skins and core for the continuous modeling approach of the core. The converged numerical models are then compared with the experimental data.

5.2.1 Convergence study for the skins

A convergence study was performed with regard to the required number of solid elements through the thickness of the skins. The number of layers used were 1, 2 and 4, with a single layer of solid elements used for the core. The obtained results, as well as the mesh densities, are presented in Fig. 12. The force–displacement response converges for two layers of solid elements through the thickness, and further increase of the mesh density has insignificant affect on the response. Using a single layer of solid elements for the skins provided a too soft response.

The force–displacement response consists of an initial transient response, after which the numerical models stabilize and a steady state behavior is observed. The initial force peak shown in the figure is caused by the prescribed radius of the skins. A smaller radius is associated with a higher peak force during the transient phase. As the steady state response is reached, the preferred radius is obtained, at an approximately constant peeling force.

Fig. 12
figure 12

a Contains the force–displacement responses obtained for the mesh study regarding the skins for the model presented in b. Three mesh densities were studied for the skins, see c–e, where 1, 2 and 4 layers of solid elements has been used, respectively. At this stage the core was modeled using a single layer of solid elements

Full size image

5.2.2 Convergence study for the core

Using two layers of solid elements for the skins, a convergence study was conducted for the core, using 1, 2 and 4 layers of solid elements through the thickness, respectively. The force–displacement response and mesh densities are presented in Fig. 13. From the force response in Fig. 13a, it is seen that the force drops as the mesh density is increased. Mesh densities are presented in Fig. 13b–d. Furthermore, Fig. 13e and f, show that the bending radius of the skins of the peeling test increase with increasing mesh density. This effect seems to be derived from the number of solid elements remaining on the skins after fracture, contributing to the bending stiffness of the skins, despite the in-plane stiffness and Poisson’s ratio being approximately zero. Thus, as the mesh density is increased a larger part of the core remains attached to the lower skins, stiffening the skins and increasing the radius. As the radius is increased so is the lever arm of the force, reducing the peeling force. The stiffening effect is obviously not present in the Hybrix™ core since there exists no coupling between fibers in the physical core.

To further study the effect of mesh size on the peeling force, a second meshing approach was used to model the core of the T-peel test, using a single layer of solid elements. Three mesh sizes were used, with the mesh being successively halved along the direction of the bond. The force–displacement response and mesh sizes used for modeling the core with a single layer of solid elements are presented in Fig. 14. The force response clearly converges for this approach and does not keep dropping despite the increase in mesh density, as was the case when the mesh density was also increased along the direction of the thickness, see Fig. 13. Thus, it seems probable that the drop in force shown in Fig. 13 is related to the remaining solid elements on the lower skin and not the mesh density. Furthermore, it is clear that using a mesh size of 0.3 mm along the direction of the bond is adequate, and further increase in mesh density is not necessary with regard to the peeling force.

In the following, the numerical model consisting of a single layer of solid elements, with a thickens of 0.15 mm in the direction of the bond, will be used.

Fig. 13
figure 13

a Contains the force–displacement responses obtained for the mesh densities of the core. The three mesh densities are presented in b–d, where 1, 2 and 4 layers of solid elements has been used for the core, respectively. In e and f, the curvature of the skins are compared to illustrate the core’s contribution to stiffening the skins after fracture

Full size image
Fig. 14
figure 14

a Contains the force–displacement responses obtained for models using a single layer of finite elements in the thickness direction of the core. Three mesh densities were studied for the skins, see b–d. From a it is clear that the force–displacement response converges for the mesh density presented in c

Full size image

5.2.3 Comparing experiments and simulations

In Fig. 15a, the force response of the T-peel test is presented for 23 specimens. The mean peel force was computed by excluding the initial 20 % and final 5 % of the experimental force–displacement data, presented in Fig. 15b. Thus, the initial ramp up and the unloading were excluded from the calculation of the mean force. In Fig. 15b, the mean peel force is presented, where the standard deviation is also included together with the maximum and minimum average peel forces. Here, a great dispersion is found for the mean peel force with the lowest and highest peel force differing by a factor of close to two. This dispersion is in agreement with what was reported in the work by Hammarberg et al. [21].

Figure 15b also contains the converged finite element model for the continuum approach as well as the model with a discrete representation of the core, see Fig. 9. Both approaches produced similar response, indicating the necessity of using a single layer of solid elements for the continuum approach for this particular application, due to the otherwise contributed stiffness of the skins discussed previously. The numerical models produce forces approximately equal to the mean of the experimental data. However, since the numerical models undershoots the experimental mean, it may indicate that the experimental data used for calibrating the models is too conservative, e.g. that the effective area used for computing stress is too large, discussed further in [21]. Computational time for the continuum approach was 6.5 h and 5.9 h for the discrete, using 48 Xeon Gold 6248R 3GHz CPUs.

To the best knowledge of the authors, there exists no material model which is able to provide a full description of the Hybrix™. Thus, some simplifications were necessary to introduce into the present study, such as making a distinction between compressive and tensile properties. The numerical models of the paper were able to recreate the experimental data with adequate precision, being within one standard deviation.

Fig. 15
figure 15

a Experimental data of the T-peel test. b Mean and standard deviation of the experimental data is presented and compared with the calibrated numerical models, i.e. the continuum representation of the core and the discrete approach

Full size image

6 Summary of results and discussion

To facilitate the use of micro-sandwich materials, accurate simulation models have to be available for industrial use in, e.g., commercial software. The present paper investigates the possibility of modeling a micro-sandwich material, using commercially available constitutive models. The numerical models indicate the necessity of using a single layer of solid elements through the thickness of the core for the T-peel test. Increasing the number of element layers in the core, results in non-physical stiffening of the skins, after fracture occurs during the peeling process. Adopting higher-order solid elements, reduces the stiffness of the core without having to increase the number of elements and is thus beneficial for the current application. This modeling approach is compared to a numerical model with a discrete representation of the core, using beam elements. Both models produce similar results that agree within one standard deviation with the experimental data of the present work.

It should be mentioned that the input data used for the constitutive models were taken from the work by Hammarberg et al. [21], where several sources of error were discussed. Of particular interest is the discussion regarding the effective area used for computing the stress-strain curves, taken as input data for the present work. Thus, if alignment errors or side effects would cause the effective area to be reduced by 1 mm of the width and length of the specimens, the effective area would be reduced by approximately 10 %. This would be enough to increase the peeling force of the numerical models, to approximately the experimental mean.

Errors introduced in the present work is mostly associated with the experimental T-peel test, such as alignment errors when placing the specimens in the testing machine. Additionally, it would be beneficial to use a testing machine with an increase stroke, allowing each specimen to be tested for a longer period of time.

7 Conclusions

In the present work, methods for modeling micro-sandwich materials were studied, using a constitutive elasto-plastic routine for governing the material response up until instability at which point a damage model was initiated, handling softening and fracture. The numerical models were calibrated for tensile- and shear loading, based on data in a previous work by the authors, see [21]. The constitutive routines used in the present work provides a method for modeling the micro-sandwich material, accounting for both non-linearities as well as damage and fracture. From the numerical T-peel tests it is concluded that care must be taken with regard to the meshing approach and refined methods may be needed in order to handle the contribution of stiffness of the solid elements after fracture. In the present work, for the particular application of a T-peel test, a single layer of 20-node solid elements were adequate to simulate the response. Furthermore, it is concluded that a variation exists with regard to the mechanical properties of the micro-sandwich, due to the dispersion observed for the experimental T-peel test. Thus, it may be concluded that the dispersion observed in the input data, derived from [21], is mainly due to the material itself and not the manner in which it was obtained.

This work has presented a methodology for calibrating constitutive models for numerical simulations of micro-sandwich materials, using commercially available constitutive models, validated by experimental data. This allows for further studies of micro-sandwich materials during manufacturing process, e.g. cold forming.