An analytical approach to design horns and boosters of ultrasonic welding machines

Abstract

This paper presents a new design approach for two main components of an ultrasonic plastic welding machine, booster and horn, based on an analytical model. The design procedure is developed due to the lack of a comprehensive and precise analytical model for rapid design and analysis of these components. The previous analytical models use the one-dimensional wave equation that causes significant errors in designing components with large lateral dimensions. Three-dimensional vibrations are considered for developing an analytical model using the apparent elasticity method. In this way, longitudinal frequency equations are coupled with radial frequency equations by mechanical coupling coefficients. Also, the damping of materials is taken into account. The model can be adapted to calculate the resonant length of the components or calculate the resonant frequency. To verify the model, the results are compared to a numerical simulation. The difference between analytical and numerical resonance frequency is less than 0.02%. Moreover, an experimental modal analysis is performed, which shows 0.9% error with analytical results.

Article highlights

• A new design approach for boosters and horns has been developed based on an analytical model.

• Three-dimensional vibrations are considered in the model using the apparent elasticity method.

• The accuracy of calculating resonant frequencies is more than one-dimensional design method.

1 Introduction

Ultrasonic welding is a standard method for welding particular materials such as plastics. This welding method is based on propagating ultrasound waves along components and heating workpieces due to visco-elastic losses and the friction between surfaces. Ultrasonic horn and booster must be designed to have a longitudinal mode shape in the desired working frequency. The resonant frequency can be altered by dimensional changes [1]. There are two general approaches to design ultrasonic horns and boosters: (i) traditional approach based on one-dimensional wave equation in the longitudinal direction (ii) finite element simulations [2]. Using finite element softwares is very common because of its simplicity, but designing dimensions with this method would be extremely time-consuming. In most cases, the horns are designed conical, exponential, stepped, and cylindrical [3]. Nad et al. [4] examined various shapes of horns and presented the most optimal shape for the design of horns. Dang et al. [5] showed that the horn’s vibrational amplitude with Bezier profile is more significant than other curves. Also, the results showed that this kind of horn is more durable due to less stress concentration and has a uniform amplitude of vibrations in its output surface. On the other hand, the stepped horn has the highest amplitude and suffers more stress concentration in the corners, which reduces its life dramatically. Singh et al. [6] compared stepped and exponential horns with two different materials using ANSYS software. Li et al. [7] modeled a horn according to spring-mass-damper interaction in one direction and two degree-of-freedom (DOF). The results showed a 0.1% difference between experiments and the proposed model for the resonance frequency. Wang and Lin [8] compared six different types of large cylindrical horns to reduce lateral vibrations utilizing COMSOL software. Also, they investigated the vibration uniformity of output surfaces of these horns. They stated that it is challenging to present an analytical solution for large-sized grooved horns because of their complex shapes. Carboni [9] explored the cause of cracking of corners and slots in two kinds of horns by FEM software. Kumar et al. [10] researched the necessity of considering slots on a horn’s body and its effect on displacement uniformity of the output surface and its optimal location. Naseri et al. [11] designed a steel horn using FEM software for equal channel angular pressing (ECAP). Rani et al. [12] designed a horn with different materials and assessed the effect of temperature on the nodal plane experimentally and numerically. Yu et al. [13] modeled a horn using a one-dimensional wave equation. They approximated the length of two elements of the horn with constant cross-section by a 1D analytical model. However, they investigated the effect of temperature on the resonance frequency numerically using FEM software, and they showed that the resonance frequency decreases with the increasing temperature. Kumar and Prakasan [14] designed two different horns for joining metallic parts. They used the sound velocity through the horn for calculating the total length of the horn. Next, they calculated other dimensions using FEM software based on a methodology of trial and error that they had proposed for optimizing essential parameters.

Based on the literature survey, horn and booster were typically designed by FEM software. The presence of an analytical model is necessitated to investigate the effect of each parameter on the resonance frequency by a mathematical model. However, in some of these studies, it is mentioned that the use of a one-dimensional analytical model cannot be reliable and reasonable due to its amount of error caused by the large lateral dimensions of horns.

In this paper, a design procedure is developed due to the lack of a comprehensive and precise analytical model for rapid design and analysis of these components. The previous analytical models use a one-dimensional wave equation that causes significant errors in designing components with large lateral dimensions. Nevertheless, the absence of a unanimous mathematical model for accurate design of these components feels [15]. On the other hand, the traditional approach for designing these parts is not accurate because it considers only one-dimensional vibration. Therefore, a 3D vibrational model should be provided to design these components precisely. The nodal plan location, mode shape, and resonance frequency can be obtained with this model. In this study, a comprehensive mathematical model based on the coupling of longitudinal and radial vibration is developed to calculate horn and booster dimensions, resonance frequency, mode shape, and magnifying factors. To begin with, the analytical model for boosters and horns are presented. Next, the designed horn and booster with the analytical model are analyzed with FEM software to verify the analytical model. Finally, experimental tests have been conducted to verify the result of the model.

2 Analytical modeling

2.1 Theory

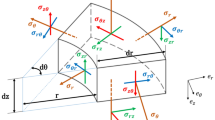
Horns and boosters are usually made up of Ti or Al-7075-T6. These components consist of a solid, hollow cylinder, and exponential sections. When the diameter to length ratio of a component is less than one-quarter of a wavelength, a one-dimensional wave equation can be used to model the components analytically [16]. Nevertheless, in general, there are radial and circumferential displacements in these components that should be considered for a more realistic model, especially in the case of workpieces with large lateral dimensions and short lengths to reduce the amount of error [17]. A cylindrical 3D element is taken, and stresses are exerted on it, shown in Fig. 1.

Fig. 1

The cylindrical element of components

Mechanical coupling coefficient (n), is defined as the ratio of longitudinal stress ($\sigma_{z}$) to lateral stress consist of radial ($\sigma_{r}$) and circumferential stress ($\sigma_{\theta }$).

$$ n = \frac{{\sigma_{z} }}{{\sigma_{r} + \sigma_{\theta } }} $$

(1)

The mechanical coupling coefficient is related to the geometry of the component, and it is usually a negative number. Radial and longitudinal displacement equations are coupled with this parameter.

The longitudinal displacement equation for a cylinder is obtained by solving the differential equation of displacement. ${u}_{z}$ is the displacement and ${k}_{z}$ is the apparent wave number in longitudinal direction.

$$ \frac{{\partial^{2} u_{z} }}{{\partial z^{2} }} + k_{z}^{2} u_{z} = 0 \to u_{z} \left( z \right) = A\cos \left( {k_{z} Z} \right) + B\sin \left( {k_{z} Z} \right) $$

(2)

A and B in Eq. (2) remain unknown constants. The longitudinal displacement equation for an exponential part is:

$$ u_{z} \left( {\text{z}} \right) = e^{ - \beta Z} \left( {A\cos \left( {\left[ {\sqrt {k_{z}^{2} - \beta^{2} } } \right]z_{{}} } \right) + B\sin \left( {\left[ {\sqrt {k_{z}^{2} - \beta^{2} } } \right]z} \right)} \right) $$

(3)

Radial frequency equation for hollow and solid cylinders are obtained by solving the radial differential equation. $u_{r}$ is the displacement and $k_{r}$ is the apparent wave number in radial direction. $J_{0}$ is Bessel functions of the first kind and $Y_{0}$ is Bessel functions of the second kind.

$$ \frac{{\partial^{2} u_{r} }}{{\partial r^{2} }} + \frac{{\partial u_{r} }}{r\partial r} + \left( {k_{r}^{2} - \frac{1}{{r^{2} }}} \right)u_{r} = 0 \to u_{r} \left( r \right) = CJ_{0} \left( {k_{r} r} \right) + DY_{0} \left( {k_{r} r} \right) $$

(4)

By applying boundary conditions for a hollow cylinder (${\sigma }_{r=a}=0, {\sigma }_{r=b}=0$), radial frequency equation is obtained as follows.

$$ \frac{{k_{r} aJ_{0} \left( {k_{r} a} \right) - \frac{{\left( {1 - \nu - 2\nu n} \right)}}{{\left( {1 - \nu n} \right)}}J_{1} \left( {k_{r} a} \right)}}{{k_{r} bJ_{0} \left( {k_{r} b} \right) - \frac{{\left( {1 - \nu - 2\nu n} \right)}}{{\left( {1 - \nu n} \right)}}J_{1} \left( {k_{r} b} \right)}} = \frac{{k_{r} aY_{0} \left( {k_{r} a} \right) - \frac{{\left( {1 - \nu - 2\nu n} \right)}}{{\left( {1 - \nu n} \right)}}Y_{1} \left( {k_{r} a} \right)}}{{k_{r} bY_{0} \left( {k_{r} b} \right) - \frac{{\left( {1 - \nu - 2\nu n} \right)}}{{\left( {1 - \nu n} \right)}}Y_{1} \left( {k_{r} b} \right)}} $$

(5)

a and b are the external and internal radius of the hollow cylinder respectively and $\nu$ is Poisson’s ratio.

By applying boundary conditions ($u_{r = 0} = 0 , \sigma_{r = a} = 0$), radial frequency equation for a solid cylinder (Fig. 2a) is obtained:

$$ ak_{r} J_{0} \left( {k_{r} a} \right) - \left[ {\frac{{\left( {1 - \nu - 2\nu n} \right)}}{{\left( {1 - \nu n} \right)}}} \right]J_{1} \left( {k_{r} a} \right) = 0 $$

(6)

Fig. 2

a Solid and b hollow cylinder

The following assumptions are considered for the analytical model:

• (1) The vibration mode does not change in the wave propagation along the components.

• (2) Shear stresses and strains are ignored.

• (3) The waves inside the components are assumed sinusoidal.

• (4) The diameter change in the components is far from the critical values, so the effect of chamfers and fillets are ignored.

• (5) The acoustic impedance of air is ignored, so the horn or booster that works in the air is called “unloaded,” and its stress is considered zero.

• (6) The machined surfaces for the wrench seat on the booster and horn are ignored.

• (7) The booster and horn’s torsional and bending mode shapes are ignored.

• (8) The effect of the screw that connects the booster and horn is ignored.

• (9) Wave differential equations are considered in the radial and longitudinal directions.

• (10) Differential equations in longitudinal and radial directions are related to each other by the mechanical coupling coefficient.

• (11) To write the radial frequency equation of the exponential segments of the booster and horn, the mean radius of these segments is used.

2.2 Analytical model of booster and horn

Figure 2 presents the booster. The booster is divided into eight segments, including hollow and solid cylinder and exponential part. The geometrical shape of the booster increases the amplitude of oscillations.

According to Eqs. (5) and (6), the radial frequency equations of segments 1 to 8 are as follows [18].

$$ \frac{{k_{ri} a_{i} J_{0} \left( {k_{ri} a_{i} } \right) - \frac{{1 - \upsilon_{i} - 2\upsilon_{i} n_{i} }}{{1 - \upsilon_{i} n_{i} }}J_{1} \left( {k_{ri} a_{i} } \right)}}{{k_{ri} b_{i} J_{0} \left( {k_{ri} b_{i} } \right) - \frac{{1 - \upsilon_{i} - 2\upsilon_{i} n_{i} }}{{1 - \upsilon_{i} n_{i} }}J_{1} \left( {k_{ri} b_{i} } \right)}} - \frac{{k_{ri} a_{i} Y_{0} \left( {k_{ri} a_{i} } \right) - \frac{{1 - \upsilon_{i} - 2\upsilon_{i} n_{i} }}{{1 - \upsilon_{i} n_{i} }}Y_{1} \left( {k_{ri} a_{i} } \right)}}{{k_{ri} b_{i} Y_{0} \left( {k_{ri} b_{i} } \right) - \frac{{1 - \upsilon_{i} - 2\upsilon_{i} n_{i} }}{{1 - \upsilon_{i} n_{i} }}Y_{1} \left( {k_{ri} b_{i} } \right)}} = 0,\quad i = 1,2,8 $$

(7)

$$ k_{ri} a_{i} J_{0} \left( {k_{ri} a_{i} } \right) - \frac{{1 - \upsilon_{i} - 2\upsilon_{i} n_{i} }}{{1 - \upsilon_{i} n_{i} }}J_{1} \left( {k_{ri} a_{i} } \right) = 0\quad , i = 3,4,5,6,7 $$

(8)

To obtain the longitudinal frequency equation, according to Eqs. (2) and (3), the displacement equations for each segment are written, then boundary conditions are applied (Fig. 3). The longitudinal displacement equations of segments 1 to 8 are as follows:

$$ u_{8} \left( {z_{8} } \right) = A\cos \left( {k_{8} z_{8} } \right) + B\sin \left( {k_{8} z_{8} } \right) $$

(9)

$$ u_{7} \left( {z_{7} } \right) = C\cos \left( {k_{7} z_{7} } \right) + D\sin \left( {k_{7} z_{7} } \right) $$

(10)

$$ u_{6} \left( {z_{6} } \right) = e^{{ - \beta_{2} Z_{6} }} \left( {E\cos \left( {\left[ {\sqrt {k_{6}^{2} - \beta_{2}^{2} } } \right]z_{6} } \right) + F\sin \left( {\left[ {\sqrt {k_{6}^{2} - \beta_{2}^{2} } } \right]z_{6} } \right)} \right) $$

(11)

$$ u_{5} \left( {z_{5} } \right) = G\cos \left( {k_{5} z_{5} } \right) + H\sin \left( {k_{5} z_{5} } \right) $$

(12)

$$ u_{4} \left( {z_{4} } \right) = I\cos \left( {k_{4} z_{4} } \right) + J\sin \left( {k_{4} z_{4} } \right) $$

(13)

$$ u_{3} \left( {z_{3} } \right) = K\cos \left( {k_{3} z_{3} } \right) + L\sin \left( {k_{3} z_{3} } \right) $$

(14)

$$ u_{2} \left( {z_{2} } \right) = M\cos \left( {k_{2} z_{2} } \right) + N\sin \left( {k_{2} z_{2} } \right) $$

(15)

$$ u_{1} \left( {z_{1} } \right) = e^{{\beta_{1} Z_{1} }} \left( {O\cos \left( {\left[ {\sqrt {k_{1}^{2} - \beta_{1}^{2} } } \right]z_{1} } \right) + P\sin \left( {\left[ {\sqrt {k_{1}^{2} - \beta_{1}^{2} } } \right]z_{1} } \right)} \right) $$

(16)

Fig. 3

The booster elements and boundary conditions

By considering the assumptions and using boundary conditions in longitudinal equations, Eq. (17) has been obtained. [X] is the unknown coefficient of A, B, C …. The condition for the existence of a solution is that the determinant of the coefficient matrix should be equal to zero. The longitudinal frequency equation is obtained by this condition. Next, with solving radial frequency equations and longitudinal frequency equation, the resonance frequency of the booster and the mechanical coupling coefficient of each segment are calculated.

$$ \left[ {The\, coefficients\,matrix} \right]\left[ X \right] = \left[ {Zreos\, matrix} \right] $$

(17)

Equation 17 for the booster can be expressed as follows.

$$ \left[ {\begin{array}{*{20}l} 0 \hfill & {\alpha 1} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {\alpha 2} \hfill & {\alpha 3} \hfill & {\alpha 4} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {\alpha 5} \hfill & {\alpha 6} \hfill & {\alpha 7} \hfill & {\alpha 8} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\alpha 9} \hfill & {\alpha 10} \hfill & {\alpha 11} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\alpha 12} \hfill & {\alpha 13} \hfill & 0 \hfill & {\alpha 14} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\alpha 15} \hfill & {\alpha 16} \hfill & {\alpha 17} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\alpha 18} \hfill & {\alpha 19} \hfill & 0 \hfill & {\alpha 20} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\alpha 21} \hfill & {\alpha 22} \hfill & {\alpha 23} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\alpha 24} \hfill & {\alpha 25} \hfill & {\alpha 26} \hfill & {\alpha 27} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\alpha 28} \hfill & {\alpha 29} \hfill & {\alpha 30} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\alpha 31} \hfill & {\alpha 32} \hfill & 0 \hfill & {\alpha 33} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\alpha 34} \hfill & {\alpha 35} \hfill & {\alpha 36} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\alpha 37} \hfill & {\alpha 38} \hfill & 0 \hfill & {\alpha 39} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\alpha 40} \hfill & {\alpha 41} \hfill & {\alpha 42} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\alpha 43} \hfill & {\alpha 44} \hfill & 0 \hfill & {\alpha 45} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\alpha 46} \hfill & {\alpha 47} \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} A \hfill \\ B \hfill \\ C \hfill \\ D \hfill \\ E \hfill \\ F \hfill \\ G \hfill \\ H \hfill \\ I \hfill \\ J \hfill \\ K \hfill \\ L \hfill \\ M \hfill \\ N \hfill \\ O \hfill \\ P \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{array} } \right] $$

(18)

The value of each alpha is in the appendix. The non-linear system of equations for the booster is achieved by one longitudinal and eight radial frequency equations. All dimensions and material properties are given in the equations. The resonance frequency and mechanical coupling coefficients of each section remain unknown parameters. Table 1 shows the dimensions of the booster, and Table 2 shows AL 7075-T6 mechanical characteristics.

Table 1 Booster’s dimensions

Table 2 AL 7075-T6 mechanical characteristics

The resonant frequency of the transducer has been measured as 19,943 Hz. The resonant frequency of all components should be matched in order to prevent losss and have a completely longitudinal mode shape. Considering the resonant frequency of the transducer, the results of solving the system of equations using MATLAB are reported in Table 3.

Table 3 Booster’s results

Figure 4 shows the horn. The horn is divided into three segments, including solid cylinder and exponential part.

Fig. 4

The horn elements and boundary conditions

The radial frequency equations of segments 1 to 3 are as follows.

$$ {\text{k}}_{{{\text{ri}}}} {\text{a}}_{{\text{i}}} {\text{J}}_{0} \left( {{\text{k}}_{{{\text{ri}}}} {\text{a}}_{{\text{i}}} } \right) - \frac{{1 - {\upupsilon }_{{\text{i}}} - 2{\upupsilon }_{{\text{i}}} {\text{n}}_{{\text{i}}} }}{{1 - {\upupsilon }_{{\text{i}}} {\text{n}}_{{\text{i}}} }}{\text{J}}_{1} \left( {{\text{k}}_{{{\text{ri}}}} {\text{a}}_{{\text{i}}} } \right) = 0{ },\quad {\text{i}} = 1,2,3 $$

(19)

The displacement equations for each element are as follows.

$$ u_{1} \left( {z_{1} } \right) = A\cos \left( {k_{1} z_{1} } \right) + B\sin \left( {k_{1} z_{1} } \right) $$

(20)

$$ u_{2} \left( {z_{2} } \right) = e^{{ - \beta_{1} Z_{2} }} \left( {C\cos \left( {\left[ {\sqrt {k_{2}^{2} - \beta_{1}^{2} } } \right]z_{2} } \right) + D\sin \left( {\left[ {\sqrt {k_{2}^{2} - \beta_{1}^{2} } } \right]z_{2} } \right)} \right) $$

(21)

$$ u_{3} \left( {z_{3} } \right) = E\cos \left( {k_{3} z_{3} } \right) + F\sin \left( {k_{3} z_{3} } \right) $$

(22)

By placing the boundary conditions into displacement equations, the longitudinal matrix equation of the horn is derived.

$$ \left[ {\begin{array}{*{20}c} 0 & {\alpha 1} & 0 & 0 & 0 & 0 \\ {\alpha 2} & {\alpha 3} & {\alpha 4} & 0 & 0 & 0 \\ {\alpha 5} & {\alpha 6} & {\alpha 7} & {\alpha 8} & 0 & 0 \\ 0 & 0 & {\alpha 9} & {\alpha 10} & {\alpha 11} & 0 \\ 0 & 0 & {\alpha 12} & {\alpha 13} & 0 & {\alpha 14} \\ 0 & 0 & 0 & 0 & {\alpha 15} & {\alpha 16} \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} A \hfill \\ B \hfill \\ C \hfill \\ D \hfill \\ E \hfill \\ F \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{array} } \right] $$

(23)

The non-linear system of equations for horn is achieved by one longitudinal and three radial frequency equations in the same way as the booster. Table 4 shows the dimensions of the horn and Table 5. reports the results of solving the system of equations using MATLAB.

Table 4 Horn’s dimensions

Table 5 The resonant frequency and mechanical coupling coefficients

3 Numerical modeling

ANSYS software is used for numerical analysis. For this purpose, the booster and horn are modeled in the CATIA software (Fig. 5) with the same dimensions in the analytical analysis. Subsequently they are imported into the ANSYS software for modal analysis. In the numerical analysis, the longitudinal resonance frequency, mode shape, and magnification factor of the horn and booster are computed. Also, the results are compared with analytical ones. The mechanical characteristics are demonstrated in Table 2.

Fig. 5

a Horn and b Booster modeled in CATIA

Figure 6 shows generated mesh for the booster. The free mesh type is chosen for this study. The mesh type is triangular, and the number of Nodes is 6481.

Fig. 6

Generated mesh for booster

The booster’s modal analysis results are shown in Fig. 7. The first longitudinal resonance frequency is 19945 Hz, which shows a 0.01% error with the analytical result (19,943 Hz). On the other hand, the magnification factor of the component is 3.6, which shows a 25% error with the analytical result (2.7). Moreover, according to Fig. 7 the nodal plane is placed at a proper distance on the flange. The displacements should be minimum on the flange to cause less effect on the resonance frequency of the booster.

Fig. 7

Booster’s mode shape of the first longitudinal resonance frequency at 19,945.7 Hz

Figure 8 shows the horn’s modal analysis results. The first longitudinal resonance frequency is 19952 Hz, which shows 0.01% error with the analytical result (19,943 Hz) and the magnification factor of the horn is 1.8.

Fig. 8

Horn’s mode shape of the first longitudinal resonance frequency of 19,952.6 Hz

4 Fabrication and experimental tests

The booster and the horn which is designed analytically, are fabricated for the sake of experimental tests. The longitudinal resonance frequency is calculated by modal hammer test for each component. Figure 9. shows fabricated booster and horn. The results of this test show longitudinal resonance frequency of booster and horn is 20110 Hz and 20,137 Hz respectively, which have 0.83% and 0.96% error with analytical results and 0.82% and 0.91% with numerical results.

Fig. 9

Fabricated booster and horn

Figure 10 shows the 3-D mode shape of the booster. Also, frequency response function (FRF) diagrams of these components have been shown in Figs. 11 and 12. The magnification factor of the component is 3, which shows 16.66% and 10% errors with numerical and analytical results respectively.

Fig. 10

Booster’s mode shape

Fig. 11

Booster’s frequency response function (FRF) diagram

Fig. 12

Horn’s frequency response function (FRF) diagram

Table 6 shows a summary of results and comparisons.

Table 6 Measured resonance frequency of the booster and the horn, magnification factor of the booster and comparisons between the results

Table 7 shows the difference between 1 and 3D analytical model results. The calculated resonance frequency of the horn and the booster using a 3D analytical model is more accurate than a 1D model. The reason is that the lateral vibration is taken into account in a 3D analytical model.

Table 7 1D and 3D analytical comparisons

5 Discussion

This study introduced a new approach to designing ultrasonic horns and boosters using a three-dimensional analytical model. The results were compared with numerical simulations and experimental tests. As shown in Table 6 the measured resonance frequency is quite close to its expected amount in the experimental test. According to Table 7 the accuracy of the 3D analytical model is higher than the 1D model due to consideration of lateral vibrations. Also, the magnification factor of the booster was calculated using the 3D analytical model.

Designing ultrasonic boosters and horns is time-consuming and requires trial and error to tune them for a special application, the 3D analytical model eliminates the trial and error process and makes these components easy to modify and optimize.

6 Conclusion

A new analytical design procedure was developed for designing horns and boosters of the ultrasonic plastic welding machine. The design procedure considers the longitudinal and lateral vibration of the component. The error of the conventional 1D vibrational equation is sharply decreased by using the new design procedure. The results of the analytical design were compared with the numerical results and experimental tests. Also, 1D and 3D analytical models were compared and showed that the 3D analytical model is more accurate. The 3D analytical model was more accurate than the 1D model. To sum up, the following results can be drawn from this study:

• 1. The proposed 3D analytical model can eliminate or reduce trial and error steps for designing each component using FEM software which remains a time-consuming process for designers.

• 2. Designed components with this method were more accurate than previous analytical models.

• 3. A reliable mathematical model was proposed to investigate the effect of different length, material properties and radius of elements on the resonant frequency, mode shape, and magnification factor of ultrasonic boosters and horns for the first time.

Moreover, the proposed 3D analytical model can be developed to calculate the frequency response of the complete vibrating set of ultrasonic plastic welding including, transducer, booster, and horn. Also, using the proposed mathematical model, different optimizations can be conducted in order to increase the efficiency of these components.

Appendix

The amount of each alpha in booster’s matrix equation:

${\upalpha }1 = k_{1}$

${\upalpha }2 = {\text{cos}}\left( {k_{1} L_{1} } \right)$

${\upalpha }3 = {\text{sin}}\left( {k_{1} L_{1} } \right)$

${\upalpha }4 = - 1$

${\upalpha }5 = - A_{1} E_{1} k_{1} sin\left( {k_{1} L_{1} } \right)$

${\upalpha }6 = { }A_{1} E_{1} k_{1} {\text{cos}}\left( {k_{1} L_{1} } \right)$

${\upalpha }7 = A_{2s} E_{2} \beta_{1}$

${\upalpha }8 = - A_{2s} E_{2} \sqrt {k_{2}^{2} - \beta_{1}^{2} }$

${\upalpha }9 = e^{{ - \beta_{1} L_{2} }} {\text{cos}}\left( {\sqrt {k_{2}^{2} - \beta_{1}^{2} } L_{2} } \right)$

${\upalpha }10 = e^{{ - \beta_{1} L_{2} }} {\text{sin}}\left( {\sqrt {k_{2}^{2} - \beta_{1}^{2} } L_{2} } \right)$

${\upalpha }11 = - 1$

${\upalpha }12 = A_{2l} E_{2} e^{{ - \beta_{1} L_{2} }} \left( { - \beta_{1} \cos \left( {\sqrt {k_{2}^{2} - \beta_{1}^{2} } L_{2} } \right) - \sqrt {k_{2}^{2} - \beta_{1}^{2} } \sin \left( {\sqrt {k_{2}^{2} - \beta_{1}^{2} } L_{2} } \right)} \right)$

${\upalpha }13 = A_{2l} E_{2} e^{{ - \beta_{1} L_{2} }} \left( { - \beta_{1} \sin \left( {\sqrt {k_{2}^{2} - \beta_{1}^{2} } L_{2} } \right) + \sqrt {k_{2}^{2} - \beta_{1}^{2} } \cos \left( {\sqrt {k_{2}^{2} - \beta_{1}^{2} } L_{2} } \right)} \right)$

${\upalpha }14 = - A_{3} E_{3} k_{3}$

${\upalpha }15 = - A_{3} E_{3} k_{3} {\text{cos}}\left( {k_{3} L_{3} } \right)$

${\upalpha }16 = A_{3} E_{3} k_{3} {\text{sin}}\left( {k_{3} L_{3} } \right)$

${\upalpha }17 = - 1$

${\upalpha }18 = - A_{3} E_{3} k_{3} sin\left( {k_{3} L_{3} } \right)$

${\upalpha }19 = A_{3} E_{3} k_{3} cos\left( {k_{3} L_{3} } \right)$

${\upalpha }20 = - A_{4} E_{4} k_{4}$

${\upalpha }21 = {\text{cos}}\left( {k_{4} L_{4} } \right)$

${\upalpha }22 = {\text{sin}}\left( {k_{4} L_{4} } \right)$

${\upalpha }23 = - 1$

${\upalpha }24 = - A_{4} E_{4} k_{4} sin\left( {k_{4} L_{4} } \right)$

${\upalpha }25 = A_{4} E_{4} k_{4} cos\left( {k_{4} L_{4} } \right)$

${\upalpha }26 = A_{5s} E_{5} \beta_{2}$

${\upalpha }27 = - A_{5s} E_{5} \sqrt {k_{5}^{2} - \beta_{2}^{2} }$

${\upalpha }28 = e^{{ - \beta_{2} L_{5} }} {\text{cos}}\left( {\sqrt {k_{5}^{2} - \beta_{2}^{2} } L_{5} } \right)$

${\upalpha }29 = e^{{ - \beta_{2} L_{5} }} {\text{sin}}\left( {\sqrt {k_{5}^{2} - \beta_{2}^{2} } L_{5} } \right)$

${\upalpha }30 = - 1$

${\upalpha }31 = A_{5l} E_{5} e^{{ - \beta_{2} L_{5} }} \left( { - \beta_{2} \cos \left( {\sqrt {k_{5}^{2} - \beta_{2}^{2} } L_{5} } \right) - \sqrt {k_{5}^{2} - \beta_{2}^{2} } \sin \left( {\sqrt {k_{5}^{2} - \beta_{2}^{2} } L_{5} } \right)} \right)$

${\upalpha }32 = A_{5l} E_{5} e^{{ - \beta_{2} L_{5} }} \left( { - \beta_{2} \sin \left( {\sqrt {k_{5}^{2} - \beta_{2}^{2} } L_{5} } \right) + \sqrt {k_{5}^{2} - \beta_{2}^{2} } \cos \left( {\sqrt {k_{5}^{2} - \beta_{2}^{2} } L_{5} } \right)} \right)$

${\upalpha }33 = - A_{6} E_{6} k_{6}$

${\upalpha }34 = {\text{cos}}\left( {k_{6} L_{6} } \right)$

${\upalpha }35 = {\text{sin}}\left( {k_{6} L_{6} } \right)$

${\upalpha }36 = - 1$

${\upalpha }37 = - A_{6} E_{6} k_{6} sin\left( {k_{6} L_{6} } \right)$

${\upalpha }38 = A_{6} E_{6} k_{6} cos\left( {k_{6} L_{6} } \right)$

${\upalpha }39 = - A_{7} E_{7} k_{7}$

${\upalpha }40 = {\text{cos}}\left( {k_{7} L_{7} } \right)$

${\upalpha }41 = {\text{sin}}\left( {k_{7} L_{7} } \right)$

${\upalpha }42 = - 1$

${\upalpha }43 = - A_{7} E_{7} k_{7} sin\left( {k_{7} L_{7} } \right)$

${\upalpha }44 = A_{7} E_{7} k_{7} cos\left( {k_{7} L_{7} } \right)$

${\upalpha }45 = - A_{8} E_{8} k_{8}$

${\upalpha }46 = {\text{cos}}\left( {k_{8} L_{8} } \right)$

${\upalpha }47 = {\text{sin}}\left( {k_{8} L_{8} } \right)$

The amount of each alpha in horn’s matrix equation:

${\upalpha }1 = k_{1}$

${\upalpha }2 = {\text{cos}}\left( {k_{1} L_{1} } \right)$

${\upalpha }3 = {\text{sin}}\left( {k_{1} L_{1} } \right)$

${\upalpha }4 = - 1$

${\upalpha }5 = - A_{1} E_{1} k_{1} sin\left( {k_{1} L_{1} } \right)$

${\upalpha }6 = { }A_{1} E_{1} k_{1} {\text{cos}}\left( {k_{1} L_{1} } \right)$

${\upalpha }7 = A_{2s} E_{2} \beta_{1}$

${\upalpha }8 = - A_{2s} E_{2} \sqrt {k_{2}^{2} - \beta_{1}^{2} }$

${\upalpha }9 = e^{{ - \beta_{1} L_{2} }} {\text{cos}}\left( {\sqrt {k_{2}^{2} - \beta_{1}^{2} } L_{2} } \right)$

${\upalpha }10 = e^{{ - \beta_{1} L_{2} }} {\text{sin}}\left( {\sqrt {k_{2}^{2} - \beta_{1}^{2} } L_{2} } \right)$

${\upalpha }11 = - 1$

${\upalpha }12 = A_{2l} E_{2} e^{{ - \beta_{1} L_{2} }} \left( { - \beta_{1} \cos \left( {\sqrt {k_{2}^{2} - \beta_{1}^{2} } L_{2} } \right) - \sqrt {k_{2}^{2} - \beta_{1}^{2} } \sin \left( {\sqrt {k_{2}^{2} - \beta_{1}^{2} } L_{2} } \right)} \right)$

${\upalpha }13 = A_{2l} E_{2} e^{{ - \beta_{1} L_{2} }} \left( { - \beta_{1} \sin \left( {\sqrt {k_{2}^{2} - \beta_{1}^{2} } L_{2} } \right) + \sqrt {k_{2}^{2} - \beta_{1}^{2} } \cos \left( {\sqrt {k_{2}^{2} - \beta_{1}^{2} } L_{2} } \right)} \right)$

${\upalpha }14 = - A_{3} E_{3} k_{3}$

${\upalpha }15 = - A_{3} E_{3} k_{3} {\text{cos}}\left( {k_{3} L_{3} } \right)$

${\upalpha }16 = A_{3} E_{3} k_{3} {\text{sin}}\left( {k_{3} L_{3} } \right)$