1 Introduction

With the develop rapidly of electric power electronic technology, modern sensor technology, advanced manufacturing technology, and automatic control technology in recent years, the brushless DC motor (BLDCM) has been widely applied to servo, actuation, positioning, and variable speed applications for its many advantages such as high efficiency, high dynamic response, high reliability and low maintenance [1,2,3]. Moreover, speed regulation is a vital part of BLDCM drive for accurate speed and position control applications, which requires the design of a high-efficiency controller to achieve continuous control performance under diverse working conditions [4,5,6,7,8]. In recent decades, scholars have proposed many speed control methods to improve the operation performance of BLDCM.

Normally, the PID controller is an optimum choice for speed control of the BLDCM due to its simplicity, strong robustness, and widespread applicability [4, 5]. Aiming at the speed control problem of BLDCM, a new variable speed pre-labeled value control strategy of PI controller is proposed in a previous paper [9], and the experiments showed that the speed controller could regulate the rotate speed accurately in a wide application range with prime cost and preferable stability. In [10], a PI-based controller for BLDCM is proposed to improve the sensitivity and reduce the speed overshoot by increasing the proportional gain. However, it can be seen from the simulation results that the overshoot of the speed response under load conditions is still very obvious. Due to various uncertainties and nonlinearity exist in the PID structure, which makes it difficult to determine the PID gain, thus reducing the control system's performance [11]. Therefore, scholars have proposed a large number of intelligent algorithms such as metaheuristic optimization algorithm, fuzzy logic, differential evolution algorithm and deep neural network to improve the robustness of the control system [4,5,6,7,8, 12,13,14,15,16,17,18,19,20]. Moreover, fuzzy logic-based methods provide better results than neural network and sliding mode control algorithms most of the time due to their offline training and chattering phenomenon [16, 21,22,23].

In [22], the speed control of BLDCM is compared and realized by using traditional PI and fuzzy PI controllers, and the fuzzy PI controller improves over the conventional PI in terms of rise time and settling time under no-load and load conditions. In [23], there is a PI regulator for speed regulation of permanent magnet synchronous motor. The PI gain is adaptively adjusted by using the fuzzy logic controller to assure the good effect, and it can be seen from the results that the fuzzy PI regulator outperforms the PI regulator in the presence of mechanical parameter variations and load disturbances, etc. As can be seen from [22, 23] that all parameters are based on the fuzzy logic controller. Although the performance of the fuzzy logic controller depends on the proportional factor of the input and output of the fuzzy logic controller, it also affects the performance of the control system. To overcome these problems, some intelligent algorithms such as genetic algorithms, particle swarm optimization, and other algorithms are used to tune the proportional factor and optimize the constant parameters of PID and fuzzy logic controller [24,25,26,27,28]. In [24], the scale factor of the PID controller based on fuzzy logic is adjusted by a genetic algorithm, and it is applied to speed control of BLDCM. The experimental results show that the speed response is uncertain due to the change of load. In [25], the PI coefficient of the speed controller of BLDCM is also optimized by using a genetic algorithm. However, the velocity response has a big overshoot in the transient phase and a big fluctuation in the steady-state phase. In [26], genetic algorithm is used to optimize the rule base and membership function of fuzzy PID controller, and its superiority is verified under no-load and variable speed conditions, but its steady-state error is slightly larger and needs to be further improved. In [27], the particle swarm algorithm is applied to the PID controller of the direct current drive system. The simulation and experimental results show that the speed response has large over harmonic oscillations in the steady-state. In addition, there are uncertainties due to load changes. In [29], the authors use a new deep perceptron neural network fuzzy adjusted PID controller to control the speed of BLDCM. The experimental results show that the proposed controller does have good robustness and stability to ensure the accurate operation of the motor. However, the iteration of its learning network is indeed a time-consuming project and still needs to be improved. In [30], a class II fuzzy controller based on wavelet neural learning (WNL) is presented to realize the effective control of BLDCM at the set speed. This control mode can well realize speed tracking under no-load, full load, and variable load conditions, but its steady-state error and response speed still need to be enhanced. In [31], a new hybrid control scheme for speed control of Brushless DC motor is proposed, which adopts an improved harmony search (HS) algorithm for parameter tuning of Fractional Order PID controller. The results show that the proposed control scheme can provide better and accurate speed control in a wide speed range, but its robustness is slightly poor.

To solve the problems mentioned above, an adaptive fuzzy proportional integral differential controller called AFPID is proposed in this paper. AFPID consists of a conventional PID controller (C-DIP) and PI + PD architecture with a configurable fuzzy logic controller (C-PID-FLC). C-DIP and C-PID-FLC can realize adaptive switching according to the speed error and give full play to their advantages. The FLC of C-PID-FLC contains two fuzzy reasoning engines, one is the parameter self-tuning of PI control, the other is the scale factor self-tuning of PI control parameters. The PD structure in C-PID-FLC is mainly to reduce oscillation while effectively eliminating static error, overcome overshooting and improve the response speed of the system. When the system reaches a certain stable state of rotation, AFPID adaptively adjusts to the C-PID controller ground on the speed error, which saves the control cost on the premise of ensuring the control performance. Finally, there build a simulation model of the brushless DC motor control system in Matlab/Simulink environment. The performance of AFPID is compared with the traditional PID control method [11], Fuzzy Logic PID control method [22], Genetic algorithm optimized fuzzy PID control method [26], and deep perceptron neural network fuzzy PID control method [29]. The results show that AFPID has a better control effect under the influence of different load disturbances and variable speeds. There are the sensitivity analyses of AFPID under the conditions of changing the resistance, inductance, inertia and flux linkage mechanical parameters of the BLDCM. When the mechanical parameters change, the method responds smoothly and without vibration in the steady-state, indicating that the method has good stability and robustness.

The rest of this article is organized as follows: Sect. 2 introduces the system model applied to BLDCMs. In Sect. 3, the detailed design of AFPID is presented. The experimental simulation results are shown in Sect. 4, and the conclusion is given in Sect. 5.

2 System models

Usually, the mathematical model of BLDCM is written as follows. Voltage state equation of three-phase windings of motor is described as [32]:

$$\left[ \begin{gathered} u_{u} \hfill \\ u_{v} \hfill \\ u_{w} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {R_{u} } & 0 & 0 \\ 0 & {R_{v} } & 0 \\ 0 & 0 & {R_{w} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{u} } \\ {i_{v} } \\ {i_{w} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {L_{u} } & M & M \\ M & {L_{v} } & M \\ M & M & {L_{v} } \\ \end{array} } \right]\frac{{\text{d}}}{{{\text{d}}t}}\left[ {\begin{array}{*{20}c} {i_{u} } \\ {i_{v} } \\ {i_{w} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {e_{u} } \\ {e_{v} } \\ {e_{w} } \\ \end{array} } \right]$$
(1)

where \(u_{u} ,u_{v} ,u_{w}\) is phase voltage of stator winding, \(i_{u} ,i_{v} ,i_{w}\) is phase current of stator winding, \(e_{u} ,e_{v} ,e_{w}\) is counter electromotive force of stator winding, \(R_{u} ,R_{v} ,R_{w}\) is phase impedance of stator winding, \(L_{u} ,L_{v} ,L_{w}\) is self-induction of three-phase winding, and M is two phase winding mutual inductance.

Since the magnetic resistance is independent of the rotor position transformation, the values of self-inductance and mutual inductance of the three-phase winding are fixed. According to the hypothesis that the distribution of the three-phase winding is completely symmetric,

$$L_{u} = L_{v} = L_{w} = L$$
(2)
$$R_{u} = R_{v} = R_{w} = R$$
(3)

Because of the distribution mode of the motor winding, the sum of various currents is 0, i.e.,

$$i_{u} + i_{v} + i_{w} = 0$$
(4)

By substituting Eqs. (3) and (4) into (2), the following equation can be obtained:

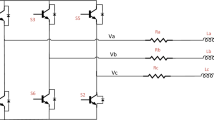
$$\left[ \begin{gathered} u_{u} \hfill \\ u_{v} \hfill \\ u_{w} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} R & 0 & 0 \\ 0 & R & 0 \\ 0 & 0 & R \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{u} } \\ {i_{v} } \\ {i_{w} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {L - M} & 0 & 0 \\ 0 & {L - M} & 0 \\ 0 & 0 & {L - M} \\ \end{array} } \right]\frac{{\text{d}}}{{{\text{d}}t}}\left[ {\begin{array}{*{20}c} {i_{u} } \\ {i_{v} } \\ {i_{w} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {e_{u} } \\ {e_{v} } \\ {e_{w} } \\ \end{array} } \right]$$
(5)

According to Eq. (6), the internal structure of BLDCM can be described as an equivalent circuit diagram [33] given in Fig. 1.

Fig. 1
figure 1

Equivalent circuit of BLDCM

Full size image

In general, the characteristic equation of BLDCM can be expressed as [29, 34]:

$$u(t) = Ri(t) + L\frac{{{\text{d}}i(t)}}{{{\text{d}}t}} + e(t)$$
(6)
$$e(t) = K_{{{\text{emf}}}} \omega_{{{\text{in}}}} (t)$$
(7)
$$T_{e} (t) = K_{{{\text{emf}}}} i(t)$$
(8)
$$T_{e} (t) = J\frac{{{\text{d}}\omega_{{{\text{in}}}} (t)}}{{{\text{d}}t}} + B\omega_{{{\text{in}}}} (t) + T_{m}$$
(9)

where \(u(t)\) is the applied voltage, R is the stator resistance, \(i(t)\) is the circuit current, L is the stator inductance, \(e(t)\) is the electromotive force, \(K_{{{\text{emf}}}}\) is the electromotive force constant, \(\omega_{{{\text{in}}}} (t)\) is the motor speed or angular velocity, \(T_{e} (t)\) is the motor torque, J is the moment of inertia, B is the viscosity coefficient, \(T_{m}\) is the load torque.

3 Design of AFPID

Fuzzy logic control is formed of three main parts, namely membership functions, control rules and control tuning parameters [35]. The prospective target can be achieved by adjusting parts. Especially, the adjustment method of the scaling factor has a great influence on the change of parameters [36]. AFPID is a simple method to adjust the scaling factors, as shown in Fig. 2. AFPID is composed of C-PID with C-PID-FLC. C-PID-FLC locks the proportional gain (\(K_{{{\text{P}}1}}\)) and integral gain (\(K_{{{\text{I}}1}}\)) of PI control in a large range through Fuzzy Logic Controller 1 and then obtains the scaling factors of \(K_{{{\text{P}}1}}\) and \(K_{{{\text{I}}1}}\) through Fuzzy Logic Controller 2. Fuzzy Logic Controller 2 adaptively and dynamically adjusts the output result of Fuzzy Logic Controller 1 according to the scaling factor obtained from the system speed error and the change of error, so that the PI control parameters can be adaptively adjusted twice to ensure the optimality of the control parameters. The PD structure in C-PID-FLC is mainly to reduce oscillation, overcome overshoot and speed up system response while effectively eliminating static errors. When the system reaches a certain stable state of rotation, AFPID can be adjusted to C-PID controller according to the speed error, which saves control costs under the premise of ensuring control performance. The main advantage of this method is to reduce the response overshoot/undershoot phenomenon, shorten the response settling time, and improve the anti-interference ability.

Fig. 2
figure 2

Structure of AFPID

Full size image

According to the structure in Fig. 2, the control signal \(U_{{{\text{PID}}}}\) can be expressed as:

$$U_{{{\text{PID}}}} = \left\{ {\begin{array}{*{20}l} {U_{{{\text{PI}} - {\text{Fz}}^{\prime \prime } }} + U_{{{\text{PD}}}} ,} \hfill & {E \ge \omega \;{\text{r}}/{\text{min}}} \hfill \\ {U_{{{\text{PID}}^{\prime } }} ,} \hfill & {E \le \omega \;{\text{r}}/{\text{min}}} \hfill \\ \end{array} } \right.$$
(10)

where E is the error between the system speed output and input, i.e., \(E = \omega_{m} - \omega_{{{\text{ref}}}}\). When the speed error is less than the critical value \(\omega\) r/min, the C-PID controller is in the active state; When the speed error is greater than the critical value \(\omega\) r/min, the C-PID-FLC is in the active state. The control switch realizes reasonable speed control by selecting an appropriate controller ground on speed error.

The control signal of C-PID-FLC consists of \(U_{{PI - Fz^{\prime \prime } }}\) and \(U_{{{\text{PD}}}}\),

$$U_{{{\text{PI}} - {\text{Fz}}^{\prime \prime } }} = K_{{{\text{P}} - {\text{Fz}}^{\prime \prime } }} E + K_{{{\text{I}} - {\text{Fz}}^{\prime \prime } }} \int {E\;{\text{d}}t}$$
(11)

where \(K_{P - FZ^{\prime\prime}}\) and \(K_{I - FZ^{\prime\prime}}\), respectively, represent the proportional gain and integral gain in the dual fuzzy PI control structure.

$$U_{{{\text{PD}}}} = K_{{\text{P}}} E + K_{{\text{D}}} \frac{{{\text{d}}E}}{{{\text{d}}t}}$$
(12)

where \(K_{{\text{P}}}\) and \(K_{{\text{D}}}\), respectively, represent the proportional gain and differential gain in PD control structure.

The control signal (\(U_{{{\text{PID}}^{\prime } }}\)) of C-PID is

$$U_{{{\text{PID}}^{\prime } }} = K_{{{\text{P}}^{\prime } }} E + K_{{{\text{I}}^{\prime } }} \int {E\;{\text{d}}t} + K_{{{\text{D}}^{\prime } }} \frac{{{\text{d}}E}}{{{\text{d}}t}}$$
(13)

where \(K_{{{\text{P}}^{\prime } }}\), \(K_{{{\text{I}}^{\prime } }}\) and \(K_{{{\text{D}}^{\prime } }}\), respectively, represent the proportional gain, integral gain and differential gain in C-PID control.

3.1 Membership functions (MFs)

The input and output membership function values of Fuzzy Logic Controller 1 are shown in Fig. 3. Suppose the basic domain of input variable error (E) and change of error (CE) is \([ - x_{1} , + x_{1} ]\), the fuzzy domain of E and CE is \([ - \Omega_{F1} , + \Omega_{F1} ]\), \(\Omega_{F1} = 6\). Suppose the basic domain of output variable proportional gain (\(K_{{{\text{P}}1}}\)) and integral gain (\(K_{{{\text{I}}1}}\)) is \([0, + \Omega_{uF1} ]\), \(\Omega_{uF1} = 6\). The fuzzy language variables in the fuzzy subset of input variables are {NB, NS, ZE, PS, PB}, which represent {negative big, negative small, zero, positive small, positive big}; fuzzy language variables in the fuzzy subset of output variables are {VS, MS, S, M, B, MB, VB}, respectively, represent {very small, medium small, small, medium, large, medium large, very large}. The fuzzification operation is equivalent to the transformation between actual variables and fuzzy variables. In this paper, the isosceles triangle is selected as the membership function of the fuzzy variables, due to its convenient representation, easy calculation, and fast response speed. The rule base of the Fuzzy Logic Controller 1 is shown in Table 1. The rule base is mainly obtained by expert experience and practical inspection. When the actual accurate variables and fuzzy variables are converted to each other, there is the quantitative factor, i.e.,

$$\left\{ {\begin{array}{*{20}l} {K_{e1} = \frac{{\Omega_{F1} }}{{x_{e1} }}} \hfill \\ {K_{ce1} = \frac{{\Omega_{F1} }}{{x_{ce1} }}} \hfill \\ \end{array} } \right.$$
(14)
$$\left\{ {\begin{array}{*{20}l} {K_{uF1 - KP1} = \frac{{y_{KP1} }}{{\Omega_{uF1} }}} \hfill \\ {K_{uF1 - KI1} = \frac{{y_{KI1} }}{{\Omega_{uF1} }}} \hfill \\ \end{array} } \right.$$
(15)

where \(K_{e1}\), \(K_{ce1}\), \(K_{uF1 - KP1}\) and \(K_{uF1 - KI1}\), respectively, represent the quantization factors of the input and output variables of Fuzzy Logic Controller 1. \(x_{e1}\), \(x_{ce1}\), \(y_{KP1}\) and \(y_{KI1}\), respectively, represent the actual range of the input and output variables of Fuzzy Logic Controller 1.

Fig. 3
figure 3

Membership functions for a E/CE, b KP1/KI1

Full size image
Table 1 Rule base of KP1/KI1 for fuzzy logic controller 1
Full size table

The input and output membership function values of Fuzzy Logic Controller 2 are shown in Fig. 4. Suppose the basic domain of input variable error (E) and change of error (CE) is \([ - x_{2} , + x_{2} ]\), the fuzzy domain of E and CE is \([ - \Omega_{F2} , + \Omega_{F2} ]\), \(\Omega_{F2} = 3\). Suppose the basic domain of output variable scaling factor (\(u_{1}\)) and scaling factor (\(u_{2}\)) is \([0, + y_{2} ]\). The domain of fuzzy subset taken by scaling factors \(u_{1}\) and \(u_{2}\) is \([0, + \Omega_{uF2} ]\), \(\Omega_{uF2} = 3\). The fuzzy language variables in the fuzzy subset of input variables are {NB, NM, NS, ZE, PS, PM, PB}, which represent {negative big, negative medium, negative small, zero, positive small, positive medium, positive big}; fuzzy language variables in the fuzzy subset of output variables are {VS, MS, S, M, B, MB, VB}, respectively, represent {very small, medium small, small, medium, large, medium large, very large}. Since the adjustment method of the scaling factor has a great influence on the change of the parameters, the fuzzy subset selection of the Fuzzy Logic Controller 2 is more detailed. The quantization factors of the input and output variables of the Fuzzy Logic Controller 2 is:

$$\left\{ {\begin{array}{*{20}l} {K_{e2} = \frac{{\Omega_{F2} }}{{x_{e2} }}} \hfill \\ {K_{ce2} = \frac{{\Omega_{F2} }}{{x_{ce2} }}} \hfill \\ \end{array} } \right.$$
(16)
$$\left\{ {\begin{array}{*{20}l} {K_{uF2 - u1} = \frac{{y_{u1} }}{{\Omega_{uF2} }}} \hfill \\ {K_{uF2 - u2} = \frac{{y_{u2} }}{{\Omega_{uF2} }}} \hfill \\ \end{array} } \right.$$
(17)

where \(K_{e2}\), \(K_{ce2}\), \(K_{uF2 - u1}\) and \(K_{uF2 - u2}\), respectively, represent the quantization factors of the input and output variables of Fuzzy Logic Controller 1. \(x_{e2}\), \(x_{ce2}\), \(y_{u1}\) and \(y_{u2}\), respectively, represent the actual range of the input and output variables of Fuzzy Logic Controller 1.

Fig. 4
figure 4

Membership functions for a E/CE, b \(u_{1} /u_{2}\)

Full size image

3.2 Scaling factors (SFs)

To adjust SFs adaptively, this paper proposes an online adjustment method of independent model fuzzy rule base (Table 2) to update \(u_{s} (s = 1,2)\) in real-time. The computational connections between SFs and the input and output variables of C-PID-FLC are as below:

$$\left\{ {\begin{array}{*{20}l} {U_{{{\text{PI}} - {\text{FZ}}^{\prime \prime } }} = u_{1} K_{{{\text{P}}1}} E + u_{2} K_{{{\text{I}}1}} \int {E\;{\text{d}}t} } \hfill \\ {K_{{{\text{P}} - {\text{FZ}}^{\prime \prime } }} = u_{1} K_{{{\text{P}}1}} } \hfill \\ {K_{{{\text{I}} - {\text{FZ}}^{\prime \prime } }} = u_{2} K_{{{\text{I}}1}} } \hfill \\ \end{array} } \right.$$
(18)

where \(K_{{{\text{P}}1}}\) and \(K_{{{\text{I}}1}}\) are the output variables of Fuzzy Logic Controller 1, \(u_{1}\) and \(u_{2}\) are the output variables of Fuzzy Logic Controller 2.

Table 2 Rule base of \(u_{1} /u_{2}\) for fuzzy logic controller 2
Full size table

3.3 Fuzzy rule base

The rule base of Fuzzy Logic Controller 2 in Table 2 is mainly used to calculate \(u_{s}\). In designing the fuzzy rule base, the following important aspects are considered. To reduce the overshoot/undershoot and decrease the settling time of speed response, the controller output will be adjusted to a smaller value when the error E is small, while E and CE give opposite symbols. For instance, if E is NS and CE is PM, then \(u_{1}\) is S.

The fuzzy rules can also be written in the following form:

$${\text{If}}\;E = E_{i} \;{\text{and}}\;{\text{CE}} = {\text{CE}}_{j} \;{\text{then}}\;u_{s} = u_{ij} (i = 1,2, \ldots ,m,\;j = 1,2, \ldots ,n)$$

where \(E_{i}\), \({\text{CE}}_{j}\) and \(u_{ij}\) are the fuzzy sets defined on E, CE and \(u_{s}\), respectively. These fuzzy sets conditional statements can be reduced to a fuzzy relationship R, namely

$$R = \bigcup\limits_{ij} {(E_{i} \times {\text{CE}}_{j} ) \times u_{ij} }$$
(19)

Each fuzzy rule has a corresponding fuzzy relation, that is \(R1,R2, \ldots R_{mn}\). Therefore, the fuzzy relation R corresponding to the total control rule is:

$$R_{T} = R_{1} \vee R_{2} \vee \cdots \vee R_{mn} = \mathop \vee \limits_{t = 1}^{mn} R_{t}$$
(20)

After obtaining \(R_{T}\), the corresponding control variable change fuzzy set U is obtained according to the quantitative values of E and CE in the theory of domain range and the operation of fuzzy reasoning synthesis rules,

$$U = (E \times EC) \circ R$$
(21)

Then the membership function of the control variable is:

$$\mu_{U} (u_{ij} ) = \vee \mu_{R} (E_{i} ,{\text{CE}}_{j} ,u_{ij} ) \wedge [\mu_{E} (E_{i} ) \wedge \mu_{{{\text{CE}}}} ({\text{CE}}_{j} )]$$
(22)

where \(\mu_{R}\), \(\mu_{E}\) and \(\mu_{{{\text{CE}}}}\), respectively, represent the membership function of fuzzy rules, error signal and change of error.

The output U of fuzzy control is a fuzzy subset, which is a combination of different values of response control language, but the actual controlled object can only accept one control quantity, so it is necessary to transform the fuzzy set into an accurate control quantity. In this paper, the weighted average method is used to calculate the corresponding accurate control quantity.

$$u^{*} = \frac{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {\mu U(uij) * uij} } }}{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {\mu U(uij)} } }}$$
(23)

Then, the conversion from the fuzzy domain of output variables to the basic domain also requires the following conversion of quantization factors:

$$u_{a} = K_{u} * u^{ * }$$
(24)

where \(u^{*}\) is the accurate control quantity determined by the fuzzy set of the control quantity, \(u_{a}\) is the actual control quantity, and \(K_{u}\) is the quantization factor of the output variable.

4 Simulation results

To test the performance of AFPID, a speed control system of BLDCM is given in Fig. 5, which consists of double loops. The inner ring synchronizes the inverter gate signal with the electromotive force. The outer ring realizes the motor speed control through the change of DC bus voltage. Several tests have been carried out to compare the performance of AFPID with PID [11], Fuzzy PID [22], GA + Fuzzy PID [26] and DPNN + Fuzzy PID [29]. The selection of conventional parameters in each controller is mainly determined by expert experience and simulation tests. The specifications of BLDCM and inverter are shown in Table 3 [29, 34].

Fig. 5
figure 5

The structure of a BLDCM speed current control system

Full size image
Table 3 Specifications for BLDCM
Full size table

Before the performance test of AFPID, we simulated and trained the critical value \(\omega\) of the control switch in AFPID under no-load condition, and the training results are shown in Fig. 6. From the training results, it can be seen that AFPID has the best control effect when \(\omega\) = 10 r/min. When \(\omega\) is greater than 10 r/min, the system relies on C-PID too early and causes the overshoot phenomenon; when \(\omega\) is less than 10 r/min, the system relies on C-PID-FLC too long and causes the delay phenomenon. When \(\omega\) = 10 r/min, the response curves of relevant control signals of the system are shown in Fig. 7.

Fig. 6
figure 6

The training results of \(\omega\)

Full size image
Fig. 7
figure 7

The control signals of the system: a \(U_{{{\text{PID}}}}\), b \(U_{{{\text{PI}} - {\text{Fz}}^{\prime \prime } }}\), c \(U_{{{\text{PD}}}}\), d \(U_{{{\text{PID}}^{\prime } }}\)

Full size image

4.1 Speed control of BLDCM with different load disturbance

First of all, the tests are carried out under the condition of fixed load disturbance. In addition, the rated power voltage and rated power of the motor are set by 500 Vdc and 1Kw, respectively. The target rotation speed of 3000 r/min is input to the system, then C-PID-FLC and C-PID are chosen to control the rotation speed by the switch according to the critical value of the rotation speed error E, and a lot of simulation experiments are implemented to obtain the critical value \(\omega\) = 10 r/min. Moreover, a 3 N∙m load disturbance is added at the time of 0.3 s. The performance indexes under the condition of fix load disturbance are given in Table 4, and the comparison of speed variation is shown in Fig. 8.

Table 4 The performance indexes under the condition of fix load disturbance
Full size table
Fig. 8
figure 8

The comparison of speed variation with fix load disturbance: a speed response curve of 0–0.5 s, b speed response curve of 0–0.12 s, c speed response curve of 0.29–0.35 s

Full size image

It can be seen from Fig. 8a, b that the traditional PID control algorithm has the longest convergence time and overshoot, with a maximum overshoot rate of about 2.8%. The traditional fuzzy PID control algorithm has a long convergence time, however, there is no overshoot occurring. The convergence time of the DPNN + FuzzyPID control algorithm is obviously better than traditional PID and Fuzzy PID, and no overshoot phenomenon occurs. The convergence time of GA + FuzzyPID is second only to AFPID with no overshoot. AFPID has the shortest convergence time of 0.040 s, which is 69.47%, 68.25%, 20.00% and 58.76% higher than traditional PID, Fuzzy PID, GA + FuzzyPID and DPNN + FuzzyPID, respectively. In addition, from Fig. 8a, c, it can be seen that after the load disturbance is applied at 0.3 s, the traditional PID control algorithm is most affected by the load, the undershoot rate reaches 5.28%. Besides, it is not restored to a steady state until 0.067 s, accompanied by continuous fluctuation. The error peak value of the traditional fuzzy PID control algorithm by the load disturbance is less than 0.33%, and the algorithm returns to the steady-state after 0.038 s. The error peak value of the GA + FuzzyPID control algorithm by the load disturbance is less than 0.29%, and the algorithm returns to the steady-state after 0.022 s. The error peak value of the DPNN + FuzzyPID control algorithm by the load disturbance is less than 0.22%, and the algorithm returns to the steady-state after 0.029 s. However, AFPID returns to the steady-state very quickly only after 0.017 s while its error peak value by the load disturbance is 3.8 r/min, which shows its excellent anti-interference as well as strong robustness performance.

Next, the tests are carried out under the condition of continuously varying load disturbance. The rated power voltage, rated power and the target rotation speed are the same as above. And the sinusoidal load disturbance is introduced during the speed control process, which is described as \(T_{m} = 3\sin t,\;0 \le t \le 0.5\;{\text{s}}\). The performance indexes under the condition of continuously varying load disturbance are given in Table 5, and the comparison of speed variation is shown in Fig. 9.

Table 5 The performance indexes under the condition of sinusoidal load disturbance
Full size table
Fig. 9
figure 9

The comparison of speed variation with sinusoidal load disturbance: a speed response curve of 0–0.5 s, b transient speed response curve of 0–0.2 s, c transient speed response curve of 0.3–0.35 s

Full size image

As can be seen from Table 5 and Fig. 9, under the change of sine wave load, the convergence time of the traditional PID control algorithm is still the longest, which is 0.133 s, and overshoot occurs. Moreover, it fluctuates greatly in the stable state, but the steady-state error is slightly less than FuzzyPID, GA + FuzzyPID and DPNN + FuzzyPID. The convergence time of FuzzyPID, GA + FuzzyPID and DPNN + FuzzyPID are 0.129 s, 0.056 s and 0.099 s respectively, and the stable states are accompanied by slight fluctuation. Meanwhile, FuzzyPID and DPNN + FuzzyPID still have the tendency to reduce the error at this stage. In addition, AFPID not only has no overshoot phenomenon, but also has a fast convergence rate of 0.041 s, and the stable state also has a slight fluctuation. Compared with the other four algorithms, AFPID has a shorter stability time, faster response speed and minimum steady-state error.

4.2 Speed tracking of BLDCM with no load

The motor is in the no-load state with a speed of 3000 r/min, which is lowered to 1500 r/min at 0.2 s, to 500 r/min at 0.4 s. Figure 10 shows the performance of the speed tracking, and the performance indexes under the condition of continuously varying speeds are given in Table 6.

Fig. 10
figure 10

The comparison of speed tracking with no load: a speed response curve of 0–0.6 s, b transient speed response curve of 0.2–0.3 s c transient speed response curve of 0.4–0.5 s

Full size image
Table 6 The performance indexes under the condition of continuously varying speeds
Full size table

It can be seen from Fig. 10 and Table 6 that the five control methods can well achieve the speed tracking performance under the condition of no-load and variable speeds. The overshoot phenomenon of traditional PID decreases with the decrease of speeds. FuzzyPID, GA + FuzzyPID, DPNN + FuzzyPID, and AFPID maintain the previous control characteristics very well. However, compared to the other four algorithms, AFPID is still optimal in terms of response speed, recovery time and steady-state error, etc.

4.3 Speed tracking of BLDCM with varying mechanical parameters

In this section, the speed tracking and sensitivity analysis of AFPID are carried out according to the changes of mechanical parameters of BLDCM. Given the rotation speed of the motor at 3000 r/min, the mechanical parameter variation conditions are: (1) given the resistance ratio of 1:5:10:15, (2) given the inductance ratio of 1:5:10:15, (3) given the inertia ratio of 1:5:10:15, (4) given the flux linkage ratio of 0.5:1:1.5:2. The AFPID speed tracking curves under these conditions are shown in Figs. 11, 12, 13 and 14. It can be seen from these figures that when the mechanical parameters change, AFPID still maintains good speed tracking performance; When resistance, inductance and inertia change, AFPID only changes in terms of setting time, response speed, overshoot, and undershoot, which will not affect the final output of the system; When the flux linkage changes, AFPID only changes significantly in terms of steady-state error, but still ensures the speed tracking and the change of error does not exceed 0.3%. Through the sensitivity analysis, it can be seen that AFPID is a controller suitable for wide operating conditions, and when the mechanical parameters change of BLDCM, the AFPID responds smoothly and without vibration in the steady-state, which shows that AFPID has good stability and robustness.

Fig. 11
figure 11

The comparison of speed tracking with varying resistance: a speed response curve of 0–0.1 s, b transient speed response curve of 0–0.05 s

Full size image
Fig. 12
figure 12

The comparison of speed tracking with varying inductance: a speed response curve of 0–0.1 s, b transient speed response curve of 0–0.05 s

Full size image
Fig. 13
figure 13

The comparison of speed tracking with varying inertia: a speed response curve of 0–0.1 s, b transient speed response curve of 0–0.05 s

Full size image
Fig. 14
figure 14

The comparison of speed tracking with varying flux linkage: a speed response curve of 0–0.1 s, b transient speed response curve of 0–0.05 s

Full size image

5 Conclusion

In this paper, an adaptive fuzzy proportional integral and differential controller called AFPID is presented to control the speed of BLDCM, and the structure of AFPID is designed. AFPID consists of a conventional PID controller (C-DIP) and PI + PD architecture and a configurable fuzzy logic controller (C-PID-FLC). C-DIP and C-PID-FLC can realize adaptive switching according to the speed error and give full play to their advantages. AFPID and other controllers are simulated under different conditions. The results show that AFPID is superior to other control methods in terms of anti-interference ability, convergence time, overshoot/undershoot, response speed, steady-state error and robustness. And the sensitivity analysis of AFPID is carried out under the conditions according to the changes of mechanical parameters of the resistance, inductance, inertia, and flux linkage of the BLDCM. However, the proposed controller is still only a simulation test, the feasibility of practical application needs to be further verified, and we will build an experimental platform to verify its real-time performance in the next step. This paper intends to apply this research to the control unit of the robot arm joint motor and to carry out the research on the synchronous control method of the multi-joint motors in future.