1 Introduction

Magnetohydrodynamic (MHD) fluid flow through a porous medium has many significant roles in pure science, engineering, technological, and biomedical fields such as MHD power generators, MHD accelerators, blood flow measurements, electrolytes, ionized gases, traveling waves tubes, metal-working processes, propulsion units, and control fusion research. A porous medium is a substance that has pores. Numerous natural substances such as rocks, soil, wood, cork can be considered as porous media. The porous media is used in various science, engineering, and biomedical applications such as soil and rock mechanics, petroleum technology, the dying process, material science, human lungs, and small bold capillaries. Porous medium describes the two prompt properties, namely porosity and permeability. Porosity evaluates the amount of fluid tackled by the material, while permeability measures quantitatively the ability of the porous medium to permit fluid flow. In boundary layer flow problems, MHD controls the force and heat exchanged by the surface. Srinivas and Muthuraj [1] debilitated the homotopy analysis method to find an approximate solution for the MHD flow of viscous incompressible fluid with thermal radiation and porosity effects. Raftari and Vajravelu [2] investigated the magnetohydrodynamic viscoelastic fluid characteristic through a wall. Heat transfer for micropolar fluid embedded in a permeable medium was explored by Xinhui et al. [3]. Kothandapani and Prakash [4] have discussed the influence of chemical reactions, inclined magnetic fields, and thermal radiation over a vertical channel by using the method of homotopy perturbation. MHD flow over an exponentially stretching surface embedded by permeable medium with thermal radiation effect was elucidated by Sharma and Gupta [5]. Kumar et al. [6] examined the influences of a constant heat source on fractional exothermic reactions model with exponential, power, and Mittag–Leffler laws in a permeable medium. The boundary layer flow for viscous fluid over a flat sheet was evaluated by Sushila et al. [7].

In recent years, the analysis of Dufour and Soret effects has had great significance and attracted various scientific researchers due to its applications in engineering, industry, and geosciences such as hydrology, petrology, turbine blades, foam combustion, and gas-particle trajectories. The heat transfer and mass transfers caused by the concentration and the temperature gradient are said the Dufour effect and Soret effect, respectively. Soret and Dufour effects on steady MHD free convection and mass transfer flow through a semi-infinite vertical permeable sheet embedded in a permeable medium have been discussed by Alam and Rahman [8]. The transversely applied magnetic field effect on unsteady free convection and mass transport through an impulsively started infinite vertical permeable flat sheet in a permeable medium with Dufour and Soret effects has been explained by Alam and Rahman [9] (Fig. 1). The same problem in the case of MHD flow has been explained by Kafoussias and Williams [10]. They have completed their analytical studies by applying the Laplace transform method. The effect of thermal radiation and viscous dissipation on the two-dimensional MHD flow of viscoelastic Jeffrey fluid through the impermeable surface with heat generation/absorption effect has been discussed by Sharma and Gupta [11]. The effect of the chemical reaction and thermal radiation on three-dimensional MHD viscous and incompressible flow in the presence of Dufour and Soret effects has been investigated by Sharma and Bhaskar [12]. The two-dimensional unsteady squeezing Casson fluid flow between permeable channels along with viscous dissipation, cross-diffusion, chemical reaction, and radiation effects has been analyzed by Bhaskar and Sharma [13, 14]. Bhaskar and Sharma [13, 14] have investigated the effect of radiation and chemical reaction on the electrically conducting laminar flow incompressible mixed convective couple stress fluid, saturated past an upstanding passage in a permeable medium with Hall current, Joule heating, Dufour, and Soret effects. Nabil and Mahmoud [15] studied the effects of Dufour and Soret on the viscous fluid with mass and heat transfer flow past permeable medium on a shrinking plate. The effect of magnetic field and chemical reaction on unsteady free convection fluid flow through an infinite vertical permeable plate with thermal diffusion and diffusion-thermo effects have been also studied by Srinivasa Raju [16]. Further, the numerical results for the effects of thermal diffusion and diffusion-thermo on an unsteady free convection flow through an infinite vertical sheet with transverse magnetic field with thermal radiation and heat source have been observed by Srinivasa Raju et al. [16]. Saeed et al. [17] have examined the effect of heat generation/absorption and Joule heating on the transmission of thermal energy over a stretching cylinder theoretically. Also, they have investigated the entropy generation rate for spinning flow systems. Arshad Khan et al. [18, 19] have discussed the thermal analysis for bioconvection of hybrid nanofluid flowing upon a thin horizontally movable needle. They have also studied the influence of Brownian motion and thermophoretic forces on the flow system of the famous Buongiorno’s model. More recently, using the hybrid nanoparticles containing silver and copper oxide, the efficiency to conduct the distribution of heat transmission for fluid flow happens upon a thin-shaped hot needle with water as the base fluid has been studied by Arshad Khan et al. [18, 19]. The effect of thermal radiation on the multi slip conditions on the magnetohydrodynamic (MHD) mixed convection unsteady flow of micropolar nanofluids upon a shrinking/stretching plate with a heat source has been investigated by Abdal et al. [20]. Hussain et al. [21] have investigated the thermal radiation effect on the boundary layer flow and heat transfer aspects of a nanofluid on a permeable plate. Habib et al. [22] have considered a mathematical analysis for slip effects on MHD nanofluid in the presence of gyrotactic microorganisms and electromagnetic fields with thermal radiation and activation energy. The double-diffusion effects on free convective flow over a vertical stretching surface embedded in a permeable medium with radiation, Dufour and Soret effects, and a homogeneous first-order chemical reaction was explained by Abdelraheem et al. [23]. A numerical model for the effects of Soret number, Dufour number, and variable viscosity on MHD mixed convection and mass transfer flow of an exponentially stretching vertical surface embedded in a permeable medium was developed by Ahmed and Sibanda [24].

Fig. 1
figure 1

Physical model and coordinate system

Full size image

The main outcome of this present study is to consider the above problems through an infinite vertical permeable sheet keeping into account the effects of Dufour and thermal diffusion. The novelty of this work is increased further by considering the thermal radiation and chemical reaction with the Runge–Kutta Merson integration scheme which has not been discussed yet. Computations have been performed for the vast range of the non-dimensional numbers/parameters like suction parameter, magnetic number, Dufour number, Prandtl number, Soret number, and Schmidt number are discussed graphically. In addition to the skin friction coefficient, heat and mass transfer properties have been discussed with the tabular representations.

2 Governing equations

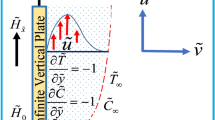
Let us consider an unsteady MHD free convection and mass transfer flow of the fluid of an electrically conducting viscous through an infinite vertical permeable sheet at \(y = 0\). We consider, the x-axis is along with the sheet in an upward direction and the plane of the sheet in the fluid is normal to the y-axis. Along the y-axis, the permeable sheet is assumed to be electrically non-conducting when a uniform magnetic field \({\varvec{B}}\) is imposedon the sheet. The induced magnetic field is negligible for considering small enough flow magnetic Reynolds number compare with one of the researches [25]. Then the magnetic force lines are adjusted comparative to the fluid and \({\varvec{B}} = \left( {0, B_{0} , \;0} \right)\). The charge conservation equation \(\nabla \cdot {\varvec{J}} = 0\) which gives us \(J_{y} =\) constant, where the density of current is \({\varvec{J}} = \left( {J_{x} , J_{y} , J_{z} } \right)\).The direction of propagation is considered only along the y-axis and does not have any variation along the y-axis and the derivative of \(J_{y}\) with respect to y, namely \(\frac{{\partial J_{y} }}{\partial y} = 0\). Since the sheet is electrically non-conducting, this constant is zero and hence \(J_{y} = 0\). The fluid is assumed to have constant properties except that the influence of the density variations with temperature and concentration, which are considered only in the body force term. Under the above assumptions, the physical variables are functions of y and t only.

The one-dimensional problem under the above assumptions and Boussinesq approximation can be put in the following form [Alam and Rahman [9]]:

The Continuity Equation:

$$\frac{\partial v}{{\partial y}} = 0$$
(1)

The Momentum Equation:

$$\frac{\partial u}{{\partial t}} + v\frac{\partial u}{{\partial y}} = \upsilon \frac{{\partial^{2} u}}{{\partial y^{2} }} + g\beta \left( {T - T_{\infty } } \right) + g\beta^{*} \left( {C - C_{\infty } } \right) - \frac{{\sigma^{\prime}B_{0}^{2} u}}{\rho }$$
(2)

The Energy Equation:

$$\frac{\partial T}{{\partial t}} + v\frac{\partial T}{{\partial y}} = \frac{k}{{\rho C_{{\text{p}}} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{D_{{\text{m}}} k_{{\text{T}}} }}{{C_{{\text{s}}} C_{{\text{p}}} }}\frac{{\partial^{2} C}}{{\partial y^{2} }}$$
(3)

The Concentration Equation:

$$\frac{\partial C}{{\partial t}} + v\frac{\partial C}{{\partial y}} = D_{{\text{m}}} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \frac{{D_{{\text{m}}} k_{{\text{T}}} }}{{T_{{\text{m}}} }}\frac{{\partial^{2} T}}{{\partial y^{2} }}$$
(4)

The associate boundary conditions for the present problem are

$$t > 0, \;u = U_{0} \left( t \right), \;v = v\left( t \right), \;T = T_{{\text{w}}} , C = C_{{\text{w}}} \;{\text{at}} y = 0$$
(5)
$$t > 0, \;u = 0, \;v = 0, \;T \to T_{\infty } ,\; C \to C_{\infty } \;{\text{at}} y \to \infty$$
(6)

where \(u\; {\text{and}}\; v\) are the velocity components in the \(x - {\text{axis and}} y - {\text{axis}}\), respectively. \(\rho\) is the fluid density, due to gravity \(g\) is the acceleration, \(\upsilon\) is the kinematic viscosity, \(\beta^{*}\) is the expansion volumetric coefficient with concentration, the volumetric expansion coefficient with temperature is \(\beta ,\;T\) is the fluid temperature,\(T_{{\text{w}}}\) is the wall temperature and \(T_{\infty }\) is the fluid temperature in the free stream, \(C\) is the fluid concentration, \(C_{{\text{w}}}\) is the wall concentration and \(C_{\infty }\) is the fluid concentration in the free stream, the thermal conductivity of the sheet is \(k\), \(C_{{\text{s}}}\) is the concentration susceptibility, at constant pressure \(C_{{\text{p}}}\) is the specific heat, \(T_{{\text{m}}}\) is the mean temperature of the fluid, the thermal diffusion ratio is \(k_{{\text{T}}}\), and \(D_{{\text{m}}}\) is the mass diffusivity coefficient.

Introducing a similarity parameter \(\sigma\) as

$$\sigma = \sigma \left( t \right)$$
(7)

where \(\sigma\) is the length scale with time-dependent. The solution of Eq. (1) is considered in terms of this length scale as follows:

$$v = v_{0} \frac{\upsilon }{\sigma }$$
(8)

here at the sheet, the dimensionless normal velocity is \(v_{0}\). If \(v_{0} > 0\) represents suction and \(v_{0} < 0\) represents blowing.

Upon introducing the following similarity variables

$$\eta = \frac{y}{\sigma } , \;f\left( \eta \right) = \frac{u}{{U_{0} }} ,\; \theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{{\text{w}}} - T_{\infty } }} , \;\phi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{{\text{w}}} - C_{\infty } }}$$
(9)

Applying Eqs. (7–9), Eqs. (1–4) are transformed into the non-dimensional coupled ordinary differential equations as follows:

$$f^{\prime\prime} + 2\xi f^{\prime} + G_{r} \theta + G_{{\text{m}}} \phi - Mf = 0$$
(10)
$$\theta^{\prime\prime} + 2\xi P_{r} \theta^{\prime} + P_{r} D_{f} \phi^{\prime\prime} = 0$$
(11)
$$\phi^{\prime\prime} + 2\xi S_{c} \phi^{\prime} + S_{c} S_{0} \theta^{\prime\prime} = 0$$
(12)

The transformed boundary conditions are as follows:

$$f = 1 , \theta = 1, \phi = 1 {\text{at}} \eta = 0$$
(13)
$$f = 0, \theta = 0, \phi = 0 {\text{at}} \eta \to \infty$$
(14)

where \(G_{r} = \frac{{g\beta \left( {T_{{\text{w}}} - T_{\infty } } \right)\sigma^{2} }}{{U_{0} \upsilon }}\) is the local Grashof number, the modified local Grashof number is \(G_{{\text{m}}} = \frac{{g\beta^{*} \left( {C_{{\text{w}}} - C_{\infty } } \right)\sigma^{2} }}{{U_{0} \upsilon }}\), Magnetic parameter is \(M = \frac{{\sigma^{\prime}B_{0}^{2} \sigma^{2} }}{\rho \upsilon }\), Prandtl number is \(P_{r} = \frac{{\rho \upsilon C_{{\text{p}}} }}{k}\), Dufour number is \(D_{f} = \frac{{D_{{\text{m}}} k_{{\text{T}}} \left( {C_{{\text{w}}} - C_{\infty } } \right)}}{{C_{{\text{s}}} C_{{\text{p}}} \upsilon \left( {T_{{\text{w}}} - T_{\infty } } \right)}}\), Soret number is \(S_{0} = \frac{{D_{{\text{m}}} k_{{\text{T}}} \left( {T_{{\text{w}}} - T_{\infty } } \right)}}{{\upsilon T_{{\text{m}}} \left( {C_{{\text{w}}} - C_{\infty } } \right)}}\), Schmidt number is \(S_{c} = \frac{\upsilon }{{D_{{\text{m}}} }}\) and \(\xi = \eta + \frac{{v_{0} }}{2}\).

The flow parameters are the Nusselt number, the Sherwood number, and local Skin friction coefficient as follows:

$$N_{u} \propto - \theta^{\prime} , S_{h} \propto - \phi^{\prime}, \tau \propto f^{\prime}$$
(15)

3 Numerical solution

The solutions of Eqs. (10, 11, and 12) with the boundary conditions (13–14) are obtained by using the superposition method (Na 1979). The boundary value problem reduces to an initial value problem by using this superposition method that can easily be integrated out by an initial value solver. Thus, to reduce Eqs. (10, 11, and 12) to an initial value problem the function \(\left( \eta \right)\), \(\theta \left( \eta \right)\) and \(\phi \left( \eta \right)\) are, respectively, decomposed to

$$f\left( \eta \right) = f_{1} \left( \eta \right) + \mu f_{2} \left( \eta \right) + \lambda f_{3} \left( \eta \right) + \delta f_{4} \left( \eta \right)$$
(16)
$$\theta \left( \eta \right) = \theta_{1} \left( \eta \right) + \mu \theta_{2} \left( \eta \right) + \lambda \theta_{3} \left( \eta \right) + \delta \theta_{4} \left( \eta \right)$$
(17)
$$\phi \left( \eta \right) = \phi_{1} \left( \eta \right) + \mu \phi_{2} \left( \eta \right) + \lambda \phi_{3} \left( \eta \right) + \delta \phi_{4} \left( \eta \right)$$
(18)

where \(\mu\), \(\lambda\), and \(\delta\) are constants, the physical significance of which is obtained later. Now substituting Eqs. (16–18) in Eqs. (10–12) and then equating the different coefficients to zero we obtain the following differential equations.

$$f_{1}^{^{\prime\prime}} + 2\xi f_{1}^{^{\prime}} - Mf_{1} + G_{r} \theta_{1} + G_{{\text{m}}} \phi_{1} = 0$$
(19)
$$f_{2}^{^{\prime\prime}} + 2\xi f_{2}^{^{\prime}} - Mf_{2} + G_{r} \theta_{2} + G_{{\text{m}}} \phi_{2} = 0$$
(20)
$$f_{3}^{^{\prime\prime}} + 2\xi f_{3}^{^{\prime}} - Mf_{3} + G_{r} \theta_{3} + G_{{\text{m}}} \phi_{3} = 0$$
(21)
$$f_{4}^{^{\prime\prime}} + 2\xi f_{4}^{^{\prime}} - Mf_{4} + G_{r} \theta_{4} + G_{{\text{m}}} \phi_{4} = 0$$
(22)
$$\theta_{1}^{^{\prime\prime}} + 2\xi P_{r} \theta_{1}^{^{\prime}} + D_{f} P_{r} \phi_{1}^{^{\prime\prime}} = 0$$
(23)
$$\theta_{2}^{^{\prime\prime}} + 2\xi P_{r} \theta_{2}^{^{\prime}} + D_{f} P_{r} \phi_{2}^{^{\prime\prime}} = 0$$
(24)
$$\theta_{3}^{^{\prime\prime}} + 2\xi P_{r} \theta_{3}^{^{\prime}} + D_{f} P_{r} \phi_{3}^{^{\prime\prime}} = 0$$
(25)
$$\theta_{4}^{^{\prime\prime}} + 2\xi P_{r} \theta_{4}^{^{\prime}} + D_{f} P_{r} \phi_{4}^{^{\prime\prime}} = 0$$
(26)
$$\phi_{1}^{^{\prime\prime}} + 2\xi S_{c} \phi_{1}^{^{\prime}} + S_{c} S_{0} \theta_{1}^{^{\prime\prime}} = 0$$
(27)
$$\phi_{2}^{^{\prime\prime}} + 2\xi S_{c} \phi_{2}^{^{\prime}} + S_{c} S_{0} \theta_{2}^{^{\prime\prime}} = 0$$
(28)
$$\phi_{3}^{^{\prime\prime}} + 2\xi S_{c} \phi_{3}^{^{\prime}} + S_{c} S_{0} \theta_{3}^{^{\prime\prime}} = 0$$
(29)
$$\phi_{4}^{^{\prime\prime}} + 2\xi S_{c} \phi_{4}^{^{\prime}} + S_{c} S_{0} \theta_{4}^{^{\prime\prime}} = 0$$
(30)

The initial values of the decomposed functions \(f_{1} \left( \eta \right), f_{2} \left( \eta \right),f_{3} \left( \eta \right),f_{4} \left( \eta \right), \ldots\) etc. are now obtained through the boundary conditions (13–14) as

$$f_{1} \left( \eta \right) = 1.0,\;f_{2} \left( \eta \right) = 0,\;f_{3} \left( \eta \right) = 0,\;f_{4} \left( \eta \right) = 0$$
(31)
$$\theta_{1} \left( \eta \right) = 1.0,\;\theta_{2} \left( \eta \right) = 0,\;\theta_{3} \left( \eta \right) = 0,\;\theta_{4} \left( \eta \right) = 0$$
(32)
$$\phi_{1} \left( \eta \right) = 1.0,\;\phi_{2} \left( \eta \right) = 0,\;\phi_{3} \left( \eta \right) = 0,\;\phi_{4} \left( \eta \right) = 0$$
(33)

Again as \(\eta \to \infty\), applying the boundary conditions (13, 14) in (16, 17, and 18) we get

$$\mu = - \frac{{f_{1} \left( {\theta_{3} \phi_{4} - \theta_{4} \phi_{3} } \right) + \theta_{1} \left( {f_{4} \phi_{3} - f_{3} \phi_{4} } \right) + \phi_{1} \left( {f_{1} \theta_{4} - f_{4} \theta_{1} } \right)}}{{f_{2} \left( {\theta_{3} \phi_{4} - \theta_{4} \phi_{3} } \right) + f_{1} \left( {f_{4} \phi_{3} - f_{3} \phi_{4} } \right) + \phi_{1} \left( {f_{1} \theta_{4} - f_{4} \theta_{1} } \right)}}$$
(34)
$$\lambda = - \frac{{f_{1} \left( {\theta_{4} \phi_{2} - \theta_{2} \phi_{4} } \right) + \theta_{1} \left( {f_{2} \phi_{4} - f_{4} \phi_{2} } \right) + \phi_{1} \left( {\theta_{2} f_{4} - \theta_{4} f_{2} } \right)}}{{f_{2} \left( {\theta_{3} \phi_{4} - \theta_{4} \phi_{3} } \right) + f_{1} \left( {f_{4} \phi_{3} - f_{3} \phi_{4} } \right) + \phi_{1} \left( {f_{1} \theta_{4} - f_{4} \theta_{1} } \right)}}$$
(35)
$$\delta = - \frac{{f_{1} \left( {\theta_{2} \phi_{3} - \theta_{3} \phi_{2} } \right) + \theta_{1} \left( {f_{3} \phi_{2} - f_{2} \phi_{3} } \right) + \phi_{1} \left( {\theta_{3} f_{2} - \theta_{2} f_{3} } \right)}}{{f_{2} \left( {\theta_{3} \phi_{4} - \theta_{4} \phi_{3} } \right) + f_{1} \left( {f_{4} \phi_{3} - f_{3} \phi_{4} } \right) + \phi_{1} \left( {f_{1} \theta_{4} - f_{4} \theta_{1} } \right)}}$$
(36)

In (16, 17, and 18) all the functional values are obtained as

$$\frac{\partial f\left( \eta \right)}{{\partial \eta }} = \frac{{\partial f_{1} \left( \eta \right)}}{\partial \eta } + \mu \frac{{\partial f_{2} \left( \eta \right)}}{\partial \eta } + \lambda \frac{{\partial f_{3} \left( \eta \right)}}{\partial \eta } + \delta \frac{{\partial f_{4} \left( \eta \right)}}{\partial \eta }$$
(37)
$$\frac{\partial \theta \left( \eta \right)}{{\partial \eta }} = \frac{{\partial \theta_{1} \left( \eta \right)}}{\partial \eta } + \mu \frac{{\partial \theta_{2} \left( \eta \right)}}{\partial \eta } + \lambda \frac{{\partial \theta_{3} \left( \eta \right)}}{\partial \eta } + \delta \frac{{\partial \theta_{4} \left( \eta \right)}}{\partial \eta }$$
(38)
$$\frac{\partial \phi \left( \eta \right)}{{\partial \eta }} = \frac{{\partial \phi_{1} \left( \eta \right)}}{\partial \eta } + \mu \frac{{\partial \phi_{2} \left( \eta \right)}}{\partial \eta } + \lambda \frac{{\partial \phi_{3} \left( \eta \right)}}{\partial \eta } + \delta \frac{{\partial \phi_{4} \left( \eta \right)}}{\partial \eta }$$
(39)

Then by setting the missing slopes.

\(\frac{\partial f\left( 0 \right)}{{\partial \eta }}, \frac{\partial \theta \left( 0 \right)}{{\partial \eta }}\) and \(\frac{\partial \phi \left( 0 \right)}{{\partial \eta }}\) as \(\frac{\partial f\left( 0 \right)}{{\partial \eta }} = \mu\), \(\frac{\partial \theta \left( 0 \right)}{{\partial \eta }} = \lambda\) and \(\frac{\partial \phi \left( 0 \right)}{{\partial \eta }} = \delta\).

The initial conditions for the slopes of the decomposed functions are obtained easily. The well known Runge-Kutta Merson integration scheme has been used as an initial value solver to integrate the above mentioned Eqs. (10, 11, and 12) and to obtain converged solutions which are presented graphically in Figs. 2, 3, and 4. The local values of the skin friction (\(\tau\)), Nusselt number (\(N_{u}\)), and Sherwood number (\(S_{h}\)) are proportional to \(- {\partial {\text{f}} \left( 0 \right)}/{{\partial \upeta }}\), \(- {\partial \uptheta \left( 0 \right)}/{{\partial \upeta }}\) and \(-{\partial \upphi \left( 0 \right)}/{{\partial \upeta }}\), respectively. The numerical values of the skin friction, Nusselt number and Sherwood number are sorted in Tables 1–3.

Fig. 2
figure 2

Velocity profiles for the variation of a \(v_{0}\), b M, c \(D_{f}\), d \(S_{0}\), e \(P_{r}\), and f \(S_{c}\)

Full size image
Fig. 3
figure 3

Temperature profile for the variation of a \(v_{0}\), b \(D_{f}\), c \(P_{r}\), and d \(S_{0}\)

Full size image
Fig. 4
figure 4

Concentration profiles for the variation of a \(v_{0}\), b \(P_{r}\) c \(S_{0} ,\) d \(D_{f}\), and e \(S_{c}\)

Full size image

4 Results and discussions

An investigation for unsteady MHD free convection and mass transfer flow through an infinite vertical permeable sheet has been investigated to analyze the effect of Dufour and thermal diffusion. The resulting initial value problems involving the set of ordinary differential equations (ODE) (10, 11, and 12) including the boundary conditions (13–14) are solved numerically by applying the superposition method through “Tec plot 9.6” software. The effects of suction parameter \(\left( {v_{0} } \right)\), the Dufour number \(\left( {D_{f} } \right)\), the magnetic parameter \(\left( M \right)\), the Prandtl number \(\left( {P_{r} } \right)\), the Soret number \(\left( {S_{0} } \right)\), the Schmidt number \(\left( {S_{c} } \right)\), and for constant values of local Grashof number \(\left( {G_{r} } \right)\) and modified local Grashof number \(\left( {G_{{\text{m}}} } \right)\) on velocity, temperature, and concentration distributions are plotted in Figs. (2, 3, and 4).The values 0.71, 1.0, and 7.0 are considered for \(P_{r}\) (0.71 for air at 200 and 1.0, 7.0 for water at 170). The values 0.22, 0.60, and 0.75 are also considered for \(S_{c}\)(0.75 for Oxygen, 0.60 for vapor water, and 0.22 for Hydrogen). The other parameter values are, however, chosen arbitrarily.

4.1 Velocity variation

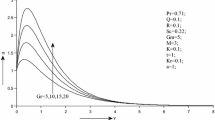
Figure 2a–f demonstrates the variation of fluid velocity for various values of the suction parameter \(\left( {v_{0} } \right)\),the magnetic parameter \(\left( M \right)\), the Dufour number \(\left( {D_{f} } \right)\), the Soret number \(\left( {S_{0} } \right)\), the Prandtl number \(\left( {P_{r} } \right)\) and the Schmidt number \(\left( {S_{c} } \right)\).It can be concluded from Fig. 2a that the velocity profiles decrease monotonically with the increase in the suction parameter \(\left( {v_{0} } \right)\) indicating the usual fact that suction stabilizes the boundary layer growth. It is seen from Fig. 2b that the velocity of the fluid reduces for uplifting values of magnetic parameter \(\left( M \right)\). A resistive type of force like a drag force is produced for increasing the values of the magnetic parameter, which name is Lorentz force. The nature of Lorentz force interrupts the force on the velocity which reduces its motion. Therefore, the velocity decreases with the increase in magnetic field parameter (M). Due to this physical phenomenon, the growing values for M decline axial velocity of the fluid. It is found from Fig. 2c that an increase in the Dufour number \(\left( {D_{f} } \right)\) causes a rise in the velocity throughout the boundary layer. However, a distinct velocity overshoot exists near the plate, and thereafter the profile falls to zero at the edge of the boundary layer. It is observed from Fig. 2d that the thermal boundary layer thickness becomes thinner for rising values of the Soret number. So that the velocity increases with an increase in the Soret number. It is noticed from Fig. 2e that with the increase in Prandtl number \(P_{r}\), the velocity profile decreases. Prandtl number is the ratio of momentum diffusivity to thermal diffusivity. An increase in \(P_{r} \;{\text{the}}\) fluid becomes more viscous and for a smaller value of \(P_{r}\) the momentum boundary layer thickness is increased which slows down the velocity of the fluid. With a rise in the Schmidt number \(\left( {S_{c} } \right)\), the velocity profile reduction is shown in Fig. 2f. Physically, the Schmidt number represents the relative thickness of the momentum boundary layer and mass concentration boundary layer. Therefore, as \(S_{c}\) increase, the momentum boundary layer is increased due to an increase in the kinematic viscosity of the fluid, and consequently, the fluid velocity decreases significantly.

4.2 Temperature variation

The temperature profile for varying values of the suction parameter \(\left( {v_{0} } \right)\), Dufour number \(\left( {D_{f} } \right),\) Prandtl number \(\left( {P_{r} } \right)\), and Soret number \(\left( {S_{0} } \right)\) is displayed in Fig. 3a–d. It is noticed from Fig. 3a that the thickness of the thermal boundary layer reduces for uplifting values of the suction parameter \(\left( {v_{0} } \right)\). As a result, the temperature decreases for rising the suction parameter. From Fig. 3 (b), it is observed that the thermal boundary layer thickness and the temperature distribution for uplifting the values Dufour number \(\left( {D_{f} } \right)\). Energy transfer takes place at a higher rate and, therefore, the temperature increases. It has been seen from Fig. 3c that the temperature decreases for enhancing the Prandtl number \(\left( {P_{r} } \right)\). When the Prandtl number increases, then the thermal diffusivity of fluid particles reduces, and hence its temperature reduces. It is noticed from Fig. 3d that the temperature profile reduces with a rise in Soret number \(\left( {S_{0} } \right)\). With an increase in the values of Soret number the thermal boundary layer thickness decrease, and, thus the temperature reduces.

4.3 Concentration variation

The effects of suction parameter \(\left( {v_{0} } \right)\), Prandtl number \(\left( {P_{r} } \right)\), Soret number \(\left( {S_{0} } \right)\), Dufour number \(\left( {D_{f} } \right)\), and Schmidt number \(\left( {S_{c} } \right)\) on the concentration profiles are plotted in Figs. 4a–e. The concentration decreases for rising the values of the suction parameter \(\left( {v_{0} } \right)\) is shown in Fig. 4a. Sucking decelerated fluid particles through the permeable wall reduces the growth of the fluid boundary layer as well as thermal and concentration boundary layers. It is seen from Fig. 4b that the larger values of Prandtl number \(\left( {P_{r} } \right)\) causes a reduction in the fluid particle’s concentration. Therefore, the nanoparticles concentration profile decreases with increases in \(P_{r}\). It is observed from Fig. 4c that the concentration of the fluid increases for growing values of Soret number. In the Soret phenomenon, temperature gradient affected the concentration distribution. So, higher values of the Soret number result in higher convective flow and, hence, concentration increases. It is evident from Fig. 4d that concentration decreases with a rise in Dufour number. The temperature difference between the fluid and the wall decreases with an increment in Dufour number, causing more heat to be transferred to the fluid which affects the fluid’s viscosity. Hence, the concentration profile decreases. It is determined from Fig. 4e that the concentration of fluid reduces for enhancing values of Schmidt number \(\left( {S_{c} } \right)\). In fact, when Sc increases then molecular/mass diffusivity of the fluid reduces that ultimately reduces the concentration of fluid particles.

4.4 Skin friction, heat and concentration rate

The various values of skin friction, rate of heat transfer, and rate of nanoparticle concentration have been presented in Tables 1, 2, and 3 for different values of mentioned parameters. From Table 1, it is observed that the skin friction reduces for moving suction parameter, Magnetic force number, Prandtl number, and Schmidt number but increases for uplifting values of Soret number and Dufour number. The heat transfer rate increases for increasing the suction parameter, Dufour number, Prandtl number, and Soret number is shown in Table 2. It is seen from Table 3 that the mass transfer rate increases for enhancing the values of the suction parameter, Magnetic force number, Soret number, and Prandtl number but decreases for Dufour number and Schmidt number.

Table 1 Computed values for the local skin friction, rate of heat transfer, and rate of mass transfer for different values of \(v_{0} \;{\text{and}}\;D_{f}\) taking \(G_{r} = 10.0, \;G_{{\text{m}}} = 5.0, \;M = 0.5, \;S_{0} = 0.5,\; P_{r} = 0.71 \;{\text{and}}\; S_{c} = 0.6\) as fixed
Full size table
Table 2 Computed values for the local skin friction, rate of heat transfer, and rate of mass transfer for different values of \(M \;{\text{and}}\;S_{0}\) taking \(G_{r} = 10.0, \;G_{{\text{m}}} = 5.0,\; v_{0} = 0.5, \;D_{f} = 0.5,\; P_{r} = 0.71\; {\text{and}}\; S_{c} = 0.6\) as fixed
Full size table
Table 3 Computed values for the local skin friction, rate of heat transfer, and rate of mass transfer for different values of \(P_{r} \;{\text{and}}\;S_{c}\) taking \(G_{r} = 10.0, \;G_{{\text{m}}} = 5.0,\; v_{0} = 0.5,\; D_{f} = 0.5,\; M = 0.5\; {\text{and}} \;S_{0} = 2.0\) as fixed
Full size table

5 Conclusions

A numerical investigation of unsteady MHD free convection and mass transfer flow through an infinite vertical permeable sheet has been performed under the Dufour and thermal diffusion effects. From the numerical simulations, the following conclusions may be drawn:

  • The skin friction coefficient increases about 5% and 14% due to increasing Dufour number (0.2–0.8) and Soret number (1.0–3.0), respectively. On the other hand, increasing the suction parameter (0.5–1.5), Magnetic force number (0.5–1.0), Prandtl number (0.71–1.0), and Schmidt number (0.22–0.75) decreases the skin friction by 38%, 23%, 18% and 10%, respectively.

  • Rising values of the suction parameter (0.5–1.5), Dufour number (0.2–0.8), Prandtl number (0.71–1.0), and Soret number (1.0–3.0) increases the heat transfer rate approximately 39%, 17%, 30%, and 6%, respectively.

  • Rate of mass transfer increases about 78% and 18% for suction parameter (0.5–1.5) and Prandtl number (0.71–1.0), respectively, but decreases about 38% and 30% for enhancing the Dufour number (0.2–0.5) and Schmidt number (0.22–0.75), respectively.

The outcome of this present research may be useful for paper production, suspensions, and coating, the technology of heat exchangers, exploiting of materials processing, drying, water body evaporation at the surface, etc.