1 Introduction

Convective heat transfer in many systems, including porous media, is of great importance for a large number of applications such as geothermal energy recovery, solid matrix heat exchangers, drying of iron ore pellets, pebble bed reactors, electronics cooling, solar collectors, and thus has attracted many researchers from a wide range of disciplines [1, 2]. Different approaches are proposed in the literature to enhance the heat transfer in industrial applications [3, 4], among which using porous media has drawn a lot of attention [5]. A complete filling of a pipe with porous media is shown to entail a high amount of pumping power, while it is not necessary for many applications [6]. Therefore, partial arrangements of porous media in pipes and channels are proposed in the literature to reach the heat transfer improvement without significantly increase the pressure drop across the pipe [7]. It also provides an opportunity to reach a compromise between an increase in heat transfer rate and pressure drop. A comprehensive review of analytical, numerical and experimental studies on heat transfer in a conduit partially filled with porous media is provided by Nield and Bejan [5]. The flow regimes inside the porous media and clear region are assumed to be laminar in most of these studies. However, it is found that the transition to turbulence in porous media occurs at a critical Reynolds number (defined based on pore diameter) of a few hundred [8]. As a result, the flow regime in many industrial applications that incorporate porous media shall be turbulent such as in strip casting [9], packed bed combustion [10], porous burners [11], drying of pellets [12], electronic components including data centers [13], solar heaters [14]. One of the areas in which turbulence in porous media plays an important role is in partially filled pipes incorporated in heat exchangers owing to the high velocity of heat transfer fluid in such applications. Thus many researchers, such as Kuznetsov [15] and Yang and Hwang [16], have numerically investigated the effects of turbulence on the Nusselt number in a pipe partially filled with a permeable media. It is found that including turbulence effects results in flatter velocity and temperature profiles and rectifies the under-prediction of Nusselt number in the laminar model. However, a laminar flow regime is considered in porous media in these studies due to the high resistance of porous media, and therefore, low pore-based Reynolds number of flow within the pores. Meanwhile, Nimvari et al. [17, 18] reported that the effects of turbulence within the permeable layer in a partially filled conduit are not negligible despite the low pore-based Reynolds number. The origin of these turbulence effects is observed to be from the turbulence generated at the interface of the porous layer and clear fluid and not the turbulence generation within the pores. Therefore, a modified turbulence model, proposed in Jouybari et al. [19], is used in their study in order to take into account the turbulence effects penetrated from the porous-fluid interface. The additional terms in the turbulent kinetic energy and dissipation rate equations arising due to generation of turbulence inside the pore structures of porous material reduce to zero with a reduction in Reynolds number in Jouybari et al.’s [19] model, which makes this model appropriate for the conditions described above. These additional terms are generally constant in earlier models and are calculated at high pore-based Reynolds number resulting in an overprediction of the turbulence effects in the cases where the pore-based Reynolds number is low within the porous layer, or the turbulence effects are originated from the boundaries.

Among the studies conducted on turbulent heat transfer analysis of conduits partially filled with a permeable layer, only a small number of them focused on the thermal performance of different porous layer configurations in turbulent regime. Nimvari et al. [17, 18] evaluated the heat transfer enhancement in a channel partially filled with porous media in two different configurations. They have used a turbulence model in porous media whose additional terms in turbulent kinetic energy and dissipation rate equations are calculated at high Reynolds number, and the coefficients in these additional terms are constant. As discussed above, such a modeling approach leads to an overprediction of Nusselt number, especially when the porous media is inserted close to the walls. Nimvari et al. [17, 18] also did not comment on the different mechanisms behind the thermal performance enhancement in the configurations of the porous layer in the partially filled channel. When it comes to laminar flow, more studies can be found in the literature that focused on the effect of porous layer configuration on heat transfer enhancement. An analytical investigation of heat transfer enhancement in parallel plate channels partially filled with porous media is reported in Bhargavi and Satyamurty [20]. They have considered three different geometries: (i) all of the porous material is inserted over one of the walls, (ii) equally distributed on both walls (iii) placed at the core of the channel. The maximum heat transfer per unit pressure drop is found in the third configuration, followed by the first and the second ones. Shokouhmand et al. [21] numerically investigated the effect of porous layer position on the heat transfer enhancement in a partially filled channel using the Lattice Boltzmann Method (LBM). They have considered two configurations of porous media in the channel: boundary arrangement and central arrangement corresponding to arrangements ii and iii in Bhargavi and Satyamurty [20]. It is shown that porous layer configuration highly affects the thermal performance of a partially filled channel. It is observed that the pressure drop calculated in the central arrangement is higher than that in the boundary arrangement and the required pumping power increases with a decrease in Darcy number. It is shown that using the boundary arrangement results in higher thermal performance when the thermal conductivity and Darcy number are high, while a higher Nusselt number is obtained in central arrangement for lower Darcy numbers. Yang et al. [22] analytically investigated forced convection in a tube partially filled with porous media at the core and over the wall. It is found that for low pumping powers, the heat transfer performance is higher when the porous layer is inserted at the core of the tube. Meanwhile, a higher thermal performance is observed in a high range of pumping power for the tube filled with porous media over the wall. The importance of porous layer position on the thermal performance is so high that it has been investigated in other heat transfer devices such as microchannel and double-tube heat exchangers. Jamarani et al. [23] studied the thermal performance of a double tube heat exchanger partially filled with porous media at two different configurations. They have reported that the permeability of porous media plays a more critical role when it is inserted at the core of the inner tube, while the effect of porous media thermal properties is more appreciable when the porous media is located over the wall. Akbarzadeh et al. [24] studied the optimized position of porous insert in a double-pipe heat exchanger in terms of the first and second laws of thermodynamics. The aim of their work was to maximize the heat transfer while the pressure drop and entropy generation is kept to a minimum. They have studied four different configurations of porous inserts. It is reported that the highest heat transfer rate occurs when the porous media is placed at the core in the inner tube and over the inner wall in the outer tube. Based on the discussion provided here, it can be seen that the appropriate position of porous insert in a heat transfer device and the mechanisms associated with heat transfer enhancement in each position are of high importance which is less addressed in the literature. Therefore, a detailed investigation of these mechanisms is necessary to reach the optimum flow and porous media parameters needed for highest possible heat transfer rate. The complexity of the problem is exacerbated when the flow regime inside the partially filled pipe is turbulent. Although the effect of different parameters including turbulence modeling [17], porous media parameters in channel [18] and double pipe heat exchanger [23] has been previously studied by the present authors, a detailed investigation of mechanisms that are behind the heat transfer enhancement in different configurations of porous media in a pipe is of interest to reach the best thermal performance in different applications.

Motivated by the foregoing, the present study is aimed to investigate in detail the effect of porous insert position on heat transfer enhancement and different mechanisms that help to this enhancement in a partially filled pipe in the presence of turbulence effects. A modified k–ε model is incorporated to account for the turbulence penetrating into the permeable layer from the porous-fluid interface. The additional terms in the TKE and dissipation rate equations in this turbulence model approaches zero for low pore-based Reynolds number, which enables to avoid the overprediction of Nusselt number, as it occurs in Nimvari et al. [17, 18]. To the best of the authors’ knowledge, such a comparison between different porous layer configurations in a pipe focusing on the investigation of heat transfer enhancement phenomena has been less processed in the literature despite its importance in different industrial applications such as double pipe heat exchangers. The effects of various parameters are investigated to determine their influence on the heat transfer performance of the pipe. It is observed that two completely different phenomena govern the heat transfer rate when the porous layers are inserted at the center and on the pipe’s walls. While the thermal conductivity of porous media is more important when the porous layer is located at the wall, the acceleration of flow in the non-porous region of the pipe or channeling effect plays a more critical role in the central arrangement. Finally, a comparison is carried out between the Nusselt number calculated with two porous configurations in the pipe with the same filling ratio, which helps to find the appropriate arrangement of porous layers when they occupy the cross-sectional area of the pipe.

2 Pipe geometry

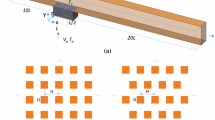
Figure 1 shows the two positions of the porous layer in the pipe used here to study the importance of porous layer configuration on the forced convection heat transfer in a partially porous pipe working in the turbulent regime. The diameter of the pipe is \(D = 2r_{0}\), and its length is considered 200D, which is long enough to reach the fully developed condition for both the velocity and temperature profiles. Only half of the pipe’s geometry is simulated because of the axisymmetric boundary condition at the pipe centerline, \({\text{r}} = 0\). The \(r_{p}\) represents the radius of porous/fluid interface. The non-dimensional porous layer radius is defined as \(R_{p} = {{r_{p} } \mathord{\left/ {\vphantom {{r_{p} } {r_{0} }}} \right. \kern-\nulldelimiterspace} {r_{0} }}\). The filling ratios in boundary and central arrangements are defined as \({{A_{p} } \mathord{\left/ {\vphantom {{A_{p} } A}} \right. \kern-\nulldelimiterspace} A} = 1 - R_{p}^{2}\) and \({{A_{p} } \mathord{\left/ {\vphantom {{A_{p} } A}} \right. \kern-\nulldelimiterspace} A} = R_{p}^{2}\), respectively. The heat transfer performances of two configurations are compared with the help of the Nusselt number (Nu), which is expressed as:

$$Nu = \frac{2}{{\left( {\theta_{w} - \theta_{m} (z)} \right)}}\left. {\frac{\partial \theta }{{\partial R}}} \right|_{wall}$$
(1)

where \(\theta_{m} (z)\) is the fluid temperature averaged over the pipe cross-section, defined as:

$$\theta = \frac{{T_{w} - T}}{{T_{w} - T_{in} }},\quad \theta_{m} (z) = \frac{{\int_{R = 0}^{R = 1} {U\theta RdR} }}{{\int_{R = 0}^{R = 1} {URdR} }}$$
(2)

where \(R = r/r_{0}\) and \(U = {u \mathord{\left/ {\vphantom {u {u_{in} }}} \right. \kern-\nulldelimiterspace} {u_{in} }}\) are the non-dimensional radius and non-dimensional velocity, respectively.

Fig. 1
figure 1

Porous media configurations: a central arrangement b boundary arrangement

Full size image

3 Governing equations and boundary conditions

The averaged equations for the flow through porous media are obtained by applying the volume averaging operator to the microscopic governing equations over a specific volume which is known as representative elementary volume. The volume-averaged Navier–Stokes equations for an incompressible flow through porous media are:

$$\nabla \cdot {\overline{\mathbf{u}}}_{D} = 0$$
(3)
$$\rho \nabla \cdot \left( {\frac{{{\overline{\mathbf{u}}}_{D} {\overline{\mathbf{u}}}_{D} }}{\phi }} \right) = - \nabla \left( {\phi \left\langle {\overline{P}} \right\rangle } \right) + \mu \nabla^{2} {\overline{\mathbf{u}}}_{D} + \nabla \cdot \left( { - \rho \phi \overline{{\left\langle {{\mathbf{u^{\prime}u^{\prime}}}} \right\rangle }}^{i} } \right) - \frac{\mu \phi }{K}\overline{u}_{D} - \frac{{c_{F} \phi \rho \left| {{\overline{\mathbf{u}}}_{D} } \right|{\overline{\mathbf{u}}}_{D} }}{\sqrt K }$$
(4)

where \({\overline{\mathbf{u}}}_{{\text{D}}}\) is the Darcian or filtration velocity, \({\overline{\mathbf{u}}}_{D} = \phi \left\langle {{\overline{\mathbf{u}}}} \right\rangle^{i}\), and \(\left\langle {{\overline{\mathbf{u}}}} \right\rangle^{{\text{i}}}\) identifies the intrinsic (liquid) average of the local time-averaged velocity vector \({\overline{\mathbf{u}}}\) [1]. The effect of forces inserted on the fluid when it passes through the solid structure of porous material is included in the momentum equation via two extra source terms in the momentum equation, Eq. (4), which are known as Darcy and Forchheimer terms and represent viscous and form drags, respectively [25]. In Eq. (4), \(\mu\) and \(K\) represent the viscosity and the permeability of porous material, respectively. The \(c_{{\text{F}}}\) in Eq. (4) is the non-linear Forchheimer coefficient and \(- \rho \phi \overline{{\left\langle {{\mathbf{u^{\prime}u^{\prime}}}} \right\rangle }}^{i}\) is the averaged Reynolds stress which is expressed as:

$$- \rho \left\langle \overline{\varvec{u}^{\prime}\varvec{u}^{\prime}} \right\rangle^{i} = \mu_{t\phi } 2\left\langle {\overline{\varvec{D}}} \right\rangle^{v} - \frac{2}{3}\phi \rho \left\langle k \right\rangle^{i} \varvec{I}$$
(5)

where the deformation tensor is defined as:

$$\left\langle {\overline{\varvec{D}}} \right\rangle^{v} = \frac{1}{2}\left[ {\nabla \left( {\phi \left\langle {\overline{\varvec{u}}} \right\rangle^{i} } \right) + \left[ {\nabla \left( {\phi \left\langle {\overline{\varvec{u}}} \right\rangle^{i} } \right)} \right]^{T} } \right]$$
(6)

In Eq. (5), \(\mu_{{{\text{t}}\varphi }}\) is turbulent viscosity and \(\left\langle k \right\rangle^{{\text{i}}}\) denotes the volume average of turbulent kinetic energy, \(k\). The turbulent viscosity in Eq. (5) is expressed as its counterpart in clear flow as: [1]:

$$\mu_{t\varepsilon } = \rho c_{\mu } \frac{{\left\langle k \right\rangle^{{i^{2} }} }}{{\left\langle \varepsilon \right\rangle^{i} }}$$
(7)

The volume averaged turbulent kinetic energy and dissipation rate equations in porous media are obtained by averaging their microscopic counterparts over a representative elementary volume, as:

$$\rho \nabla \cdot \left( {\overline{\varvec{u}}_{D} \left\langle k \right\rangle^{i} } \right) = \nabla \cdot \left[ {\left( {\mu + \frac{{\mu_{t\phi } }}{{\sigma_{k} }}} \right)\nabla \left( {\phi \left\langle k \right\rangle^{i} } \right)} \right] + P^{i} + G_{k}^{i} - \rho \phi \left\langle \varepsilon \right\rangle^{i}$$
(8)
$$\rho \nabla \cdot \left( {\overline{\varvec{u}}_{D} \left\langle \varepsilon \right\rangle^{i} } \right) = \nabla \cdot \left[ {\left( {\mu + \frac{{\mu_{t\varepsilon } }}{{\sigma_{\Phi } }}} \right)\nabla \left( {\phi \left\langle \varepsilon \right\rangle^{i} } \right)} \right] + c_{1} P^{i} \frac{{\left\langle \varepsilon \right\rangle^{i} }}{{\left\langle k \right\rangle^{i} }} + c_{2} \left( {G_{\varepsilon }^{i} - \rho \phi \frac{{\left\langle \varepsilon \right\rangle^{{i^{2} }} }}{{\left\langle k \right\rangle^{i} }}} \right)$$
(9)

The \(c_{1}\) and \(c_{2}\) in the above equations are the model constants and \(P^{i} = - \rho \left\langle {\overline{{{\mathbf{u^{\prime}u^{\prime}}}}} } \right\rangle^{i} :\nabla {\overline{\mathbf{u}}}_{D}\) represents the production of turbulent kinetic energy due to gradients in filtered velocity.

There are two additional source terms in the turbulent kinetic energy and dissipation rate equation as compared to a case without a porous media, \(G_{k}^{{\text{i}}}\) and \(G_{\varepsilon }^{i}\), which represent internal production of the turbulence kinetic energy and its dissipation rate due to the presence of solid matrix. A thorough review along with the relevant discussion on these models are provided in Vafai et al. [26] and Jouybari et al. [27]. The turbulence effects in porous media are modeled with a modified version of the Nakayama and Kuwahara’s model [28] proposed in Jouybari et al. [19] (Table 1). In general, two different ways are presented in the literature to study heat transfer in porous media. These two approaches are different in the way they treat solid and fluids energy equations. While the solid and fluid temperatures are considered to be identical in the Local Thermal Equilibrium model or the LTE approach, two energy equations for solid and fluid phases are solved in the Local Thermal Non-Equilibrium model (LTNE) model where the fluid and solid temperatures are considered to be different [29]. The LTE is found to be valid for the porous and flow parameters considered here [30]. In this condition, the energy equation is presented as:

$$(\rho c_{P} )_{f} \nabla \cdot \left( {{\overline{\mathbf{u}}}_{D} \left\langle {\overline{T}} \right\rangle^{i} } \right) = \nabla \cdot \left( {{\mathbf{K}}_{eff} \cdot \nabla \left\langle {{\overline{\text{T}}}} \right\rangle^{{\text{i}}} } \right)$$
(10)

where the effective conductivity tensor is expressed as:

$${\varvec{K}}_{{{\varvec{eff}}}} = \left[ {\phi k_{f} + \left( {1 - \phi } \right)k_{s} + \phi c_{Pf} \frac{{\mu_{t\varepsilon } }}{{\sigma_{T} }}} \right]_{eff}$$
(11)
Table 1 The \(k_{\infty }\) and \(\varepsilon_{\infty }\) expressions in the modified k–ε model
Full size table

The \(k_{f}\) is the fluid thermal conductivity, \(k_{s}\) denotes the solid thermal conductivity, and \(c_{Pf}\) is the specific heat of the fluid. In the cases of clear flow where the porosity is 1, the permeability tends to infinity in the above equations. For the non-unity values of \(\phi\), a porous media model is incorporated. The turbulence model and heat transfer constants in the above equations are similar to those in the clear media as:

$$c_{\mu } = 0.09,c_{1} = 1.44,c_{2} = 1.92,\sigma_{k} = 1.0,\sigma_{\varepsilon } = 1.3,\sigma_{T} = 0.9$$
(12)

3.1 Boundary conditions and numerical simulation

Fixed values of inlet velocity, turbulent kinetic energy, dissipation rate, and temperature are considered at the inlet, as:

$$u = u_{in} , v = 0, k = k_{in} = \frac{{3\left( {u_{in} I} \right)^{2} }}{2}, \Phi = \Phi_{in} = \frac{{k^{\frac{3}{2}} }}{{\lambda D_{h} }}, T = T_{in}$$
(13)

where I is the turbulence intensity, \(\lambda\) is the length scale constant and \(D_{h}\) is the hydraulic diameter. The no-slip boundary condition and constant temperature are applied over the impermeable wall along with the standard wall function to calculate the turbulent parameters adjacent to the wall. At the exit, the fully developed boundary condition is incorporated for all parameters. Only half of the pipe geometry is simulated with the axisymmetric boundary condition at \(r = 0\). The interface between porous media and the clear fluid is treated using Choi and Waller’s [31] single-domain approach, which takes into account the variation in the porous properties, as validated in several studies [32]. According to Chan et al. [32], the continuity of fluxes, shear stress, and velocities would be automatically satisfied across the fluid/porous interface without a need for any additional iterative procedure.

A FORTRAN code is developed to solve the equations governing the problem under study. A control-volume approach with a collocated grid is used in the simulations. The SIMPLE algorithm of Patankar [33] is used to handle the pressure–velocity coupling. The hybrid scheme based on the Upwind Differencing (UDS) and Central Differencing Schemes (CDS) is used to interpolate the convective fluxes and the second-order central difference scheme is used to discretize the diffusive terms. The details of the discretization scheme used in the present study can be explained using Fig. 2a, in which p denotes a general node in the domain. The points denoted by N, S, E, and W are its neighboring points (NP), while n, s, e, and w are the control surfaces (CS) located in the middle of P and NP. Considering φ as general property and taking its volume integral over the control volume of Fig. 2a, we have:

$$A_{p} \varphi_{p} = A_{N} \varphi_{N} + A_{S} \varphi_{S} + A_{E} \varphi_{E} + A_{W} \varphi_{W} + b{ , }A_{p} = A_{N} + A_{S} + A_{E} + A_{W} + {\text{ Extra terms}}$$
(14)

where

$$A_{I} = D{}_{i}A\left( {\left| {P_{i} } \right|} \right) + \max \left( { \pm F_{i} ,0} \right),\,F_{i} = \left( {\frac{{\rho_{f} {\text{u}}_{D} }}{\phi }} \right)_{i} \Delta X\Delta Y,\,D_{i} = \left( {\mu_{f} + \mu_{t\phi } } \right)\frac{{\Delta A_{c} }}{{\left( {\delta L} \right)_{i} }},\,P_{i} = \frac{{F_{i} }}{{D_{i} }}$$
(15)
Fig. 2
figure 2

a The control volume with the general node P, b variation of velocity along the pipe radius for the grid independency study

Full size image

In which \(i = n,s,e,w\). The coefficients \(b\), \(F_{i}\), \(D{}_{i}\) and \(\Delta A_{c}\) denote the source terms in above equations, the diffusion coefficient, the mass flow rate through the CS and the control volume cross-section, respectively. Depending on the scheme used for the discretization, the \(A\left( {\left| {P_{i} } \right|} \right)\) takes different values from 1 to \(1 - 0.5\left| {P_{i} } \right|\), respectively, in the cases of upwind and central differencing schemes or a value between these two if the hybrid scheme is incorporated. The SIP procedure is used to solve the individual algebraic equation sets where a maximum residue of \(10^{ - 6}\) is set for convergence check [34]. It should be noted that the oscillatory problem reported in the literature following the edge effects of thermal system is not observed using the numerical tool developed in the present study.

4 Grid independency and validation

The grid independency study is carried out in Fig. 2b, where the variation of velocity along the pipe radius is illustrated for five different grid numbers in boundary arrangement for \(R_{p} = 0.3\) and \({\text{Re}} = {{u_{in} D} \mathord{\left/ {\vphantom {{u_{in} D} \upsilon }} \right. \kern-\nulldelimiterspace} \upsilon }\) equal to 25,000. The grid structure used is non-uniform and it is refined at the vicinity of the walls and porous-fluid interface where the large gradients occur. As can be seen, no significant change can be observed in the results by increasing the grid numbers after \(300 \times 134\), and therefore, it is selected for all simulations. Based on the grid independence results in Fig. 2 the mesh size of \(300 \times 134\) is used for all computations. For validation purposes, the computed dimensionless turbulent viscosity is compared with the measured data reported in Prinos et al. [35]. As shown in Fig. 3, the present results successfully follow the microscopic results of Prinos et al. [35] in most parts of channel cross-section except the interface. However, Comparing the present and Prinos’s numerical results with experimental data reveals that the present model’s accuracy is higher in predicting the level of TKE close to the interface with a difference of nearly 1.5%. Further, the Dittus-Boelter equation [36] predicts the fully developed Nusselt number for turbulent flow in a pipe without porous material to be 165.5 in \({\text{Re}} = {25{,}000}\) which is nearly 0.5 percent smaller than that calculated in the present simulation, 166, supporting the validity of the present solver. This finding further validates the present numerical simulation. Figure 4 represents the validation of present results by comparing the Nu calculated in a flat plate solar collector filled with porous media with the experimental measurements of Saedodin et al. [37]. The offset between the two sets of the results changes from 5 to 10%, with an increase from the lowest to the highest flow rate. This level of difference is considered acceptable given the high number of uncertainties associated with the experimental measurements when porous media is inserted in the heater channel. One of the most important sources of these uncertainties is the surface of contact between porous media and the channel wall. While an ideal contact surface is considered in the numerical simulations, creating such an ideal contact is a complex task in the experiments. Further verification of the present results is carried out by comparing the computed Nusselt number with the analytical solution of Kaviany [38]. The analytical solution is presented for laminar flow in a channel completely filled with porous media bounded by isothermal walls. Table 2 illustrates an excellent agreement between the present numerical results and analytical solutions with a maximum difference of less than 0.5%.

Fig. 3
figure 3

A comparison of the macroscopic turbulent viscosity with the results of Prinos et al. [35]

Full size image
Fig. 4
figure 4

The calculated \(Nu\) number vs experimental results of Saedodin et al. [37]

Full size image
Table 2 The calculated \(Nu\) number vs analytical results of Kaviany [38]
Full size table

5 Results

5.1 Darcy number

An investigation of porous media permeability effects on fluid flow and heat transfer provides essential information on the heat transfer enhancement mechanisms in a partially filled pipe. To this end, the Darcy number, which is a non-dimensional number, is defined as the ratio of the permeability to the square of pipe radius. Figures 5 and 6 represent the velocity variation and TKE distribution as a function of Darcy number within the pipe partially filled with porous media in boundary and central configurations for \(R_{p} = 0.7\), \({{k_{s} } \mathord{\left/ {\vphantom {{k_{s} } {k_{f} }}} \right. \kern-\nulldelimiterspace} {k_{f} }} = 395\) and \({\text{Re}} = {25{,}000}\). The porous medium’s resistance against the fluid flow decreases with an increase in Da which leads to a higher flow rate passing through the permeable layer in both configurations. As shown in Fig. 5a for the boundary arrangement, filtered velocity slightly increases within the porous layer with an increase in Da resulting in higher velocity in the proximity of the wall and thus a better contact between the fluid and pipe wall, which is expected to enhance the heat transfer rate from the fluid to the pipe wall. However, a reverse trend is observed as will be discussed in the following of Fig. 13, which is due to counteracting of different phenomena affecting heat transfer in boundary arrangement, making the decision for heat transfer enhancement more complex in this configuration.

Fig. 5
figure 5

Variation of a velocity, b TKE with Da in boundary arrangement

Full size image
Fig. 6
figure 6

Variation of a velocity, b TKE with Da in central arrangement

Full size image

The velocity profiles calculated for central arrangement in Fig. 6a show a similar trend where the fluid’s velocity within the permeable layer increases with an increase in Da. As a result, the flow rate in the clear region decreases. The higher fluid velocity in the clear region in the form shown in Fig. 6a is called the channeling effect, and as can be observed, this effect is enhanced in the central arrangement with a decrease in the Da number. The channeling effect plays an important role in heat transfer enhancement when the porous media is located at the center through different mechanisms: (i) By increasing the fluid’s velocity in the clear region of the pipe, the convective heat transfer from the pipe wall is considerably enhanced (ii) a higher velocity in this region causes thinner boundary layer thickness over the wall which in turn decreases the resistance against the heat transfer between the wall the fluid flow (iii) a higher level of turbulence effects in this region, as shown in Fig. 6b, decreases even more the thickness of thermal boundary layer helping to increase the heat transfer rate in the pipe.

Another important phenomenon that affects the heat transfer rate in a pipe at high Re is the turbulence effects in the flow. The effect of Da on the TKE within the porous layer and the subsequent variation of TKE in the clear region of the pipe with boundary and central porous layer arrangements are presented in Figs. 5b and 6b. According to Fig. 6b, the TKE level inside the porous layer increases by increasing the Darcy number, while a reverse trend can be seen in the clear region. Increasing TKE in the clear region, with a decrease in Da, may be attributed to higher gradients of velocity at the interface between the porous layer and clear fluid and thus the larger production of turbulence. Meanwhile, the filtered velocity within the porous layer decreases with a decrease in Da, resulting in a lower TKE level inside the porous media since the TKE production term in Eq. (9), \(G_{k}^{{\text{i}}}\), is a direct function of filtered velocity inside the porous layer. In this condition, the aforementioned channeling effect would be even more enhanced, helping to increase the heat transfer rate as discussed in point (iii) above. While TKE variation in the clear region of boundary arrangement in Fig. 5b shows a similar trend, the TKE level within the porous layer away from the porous-fluid interface is negligible. Therefore, it can be concluded that the effects of turbulence do not significantly affect the heat transfer from the pipe wall in this arrangement.

The higher turbulence effects in the clear region in the central arrangement enhance the channeling effect resulting in a more uniform temperature profile in this region, as illustrated in Fig. 7. This channeling effect also increases the Nusselt number in the central arrangement, as shown in Fig. 8. Due to enhancing the channeling effect in the lower Da in the central arrangement, the maximum Nu increases up to \(\approx 400\) for \(Da = 10^{ - 4}\). Meanwhile, a non-uniform trend is observed for the variation of non-dimensional temperature and Nu with Da in the boundary arrangement. This non-uniform trend can be attributed to two counteracting mechanisms affecting the heat transfer rate in the boundary arrangement when the Da varies. As shown in Fig. 5(a), the fluid velocity within the porous layer increases with an increase in the Da, which positively affects the heat transfer from the pipe wall. However, as can be seen from Eq. (12), an increase in porosity, and therefore, Da decreases the effective thermal conductivity of porous media. From the Nu variation in the boundary arrangement in Fig. 8, it can be observed that the latter mechanism overwhelms the former when the Da is increased from \(Da = 10^{ - 4}\) to \(Da = 5 \times 10^{ - 4}\), and therefore, a drop in the Nu number can be observed. However, for a further increase in Da to \(Da = 2.5 \times 10^{ - 3}\), the increase of fluid velocity in the porous layer compensates some of the heat transfer attenuation due to lower effective thermal conductivity resulting in an increase in Nu.

Fig. 7
figure 7

Variation of non-dimensional temperature with Da for boundary (B) and central (C) arrangements

Full size image
Fig. 8
figure 8

Variation of Nu with Da for boundary (B) and central (C) arrangements

Full size image

5.2 Solid–fluid thermal conductivity ratio and Reynolds number

Figure 9 illustrates the solid to fluid thermal conductivity effect on the heat transfer performance of the partially porous pipe in the two configurations for \(Da = 5 \times 10^{ - 4}\) and \(R_{p} = 0.7\) in \({\text{Re}} = {25{,}000}\). It is observed that the higher thermal conductivity of solid matrix partially compensates for the the lower velocity and turbulence effects close to the pipe wall in boundary arrangement so that the Nu computed for \({{k_{s} } \mathord{\left/ {\vphantom {{k_{s} } {k_{f} = 669}}} \right. \kern-\nulldelimiterspace} {k_{f} = 669}}\) is about four times higher than that calculated for \({{k_{s} } \mathord{\left/ {\vphantom {{k_{s} } {k_{f} = 1}}} \right. \kern-\nulldelimiterspace} {k_{f} = 1}}\). These results indicate that attaching the porous layer to the pipe wall is justified only for a solid matrix with extremely high thermal conductivity, while the porous media at the core is preferred in a wide range of thermal conductivities. It can also be observed that increasing the solid–fluid thermal conductivity does not affect the Nu in central arrangement since the porous media is located away from the pipe wall in this configuration. The present results also illustrate that heat transfer in a partially porous pipe depends on porous layer configuration because of the role of different mechanisms in heat transfer enhancement in these configurations. While the channeling effect in the clear region is mainly responsible for the heat transfer enhancement in central arrangement, the conductivity of the solid matrix plays a more important role in a pipe filled with porous media at the wall. These findings are further confirmed by investigating the effect of Re on the Nu in central and boundary arrangements in Fig. 10 for \(R_{p} = 0.7\), \(Da = 5 \times 10^{ - 4}\) and \({{k_{s} } \mathord{\left/ {\vphantom {{k_{s} } {k_{f} }}} \right. \kern-\nulldelimiterspace} {k_{f} }} = 395\). As discussed previously, the Nu calculated for pipe partially filled with porous media at the core is higher than that obtained when porous media is attached to the wall. It is shown that the difference between Nu computed for these two arrangements increases with an increase in Reynolds number. For example, the difference between Nu increases from 223 to 327 for an increase in Re from 25,000 to 50,000. For central arrangement, an increase in Reynolds number results in higher maximum velocity and turbulent kinetic energy outside the porous layer, which highly enhances the heat transfer rate over the pipe wall. Whereas the increase of velocity and turbulence effects adjacent to the pipe wall in boundary arrangement is not as much as that observed in central arrangement owing to the porous media’s resistance against the flow.

Fig. 9
figure 9

Effect of solid–fluid thermal conductivity on Nu for boundary and central arrangements

Full size image
Fig. 10
figure 10

Effect of Re on Nu for boundary and central arrangements

Full size image

5.3 Filling ratio

The effect of porous layer thickness on the fluid flow and heat transfer in a pipe partially filled with porous media in central and boundary arrangements is illustrated in Figs. 11, 12 and 13 for \({{k_{s} } \mathord{\left/ {\vphantom {{k_{s} } {k_{f} }}} \right. \kern-\nulldelimiterspace} {k_{f} }} = 395\), \(Da = 5 \times 10^{ - 4}\) and \({\text{Re}} = 25{,}000\). The filling ratios for \(R_{p} = 0.5\), \(R_{p} = 0.6\) and \(R_{p} = 0.7\) in boundary arrangement are approximately equal to those for \(R_{p} = 0.86\), \(R_{p} = 0.8\) and \(R_{p} = 0.7\) in central arrangement, respectively. As shown in Fig. 11a, b, the trend of velocity variation with filling ratio is similar in two configurations. Increasing of filling ratio in both cases increases the filtered velocity within the permeable layer and maximum velocity outside this layer. The velocity increase in the clear region or the channeling effect in the central arrangement significantly enhances the heat transfer rate in the central arrangement because it occurs adjacent to the pipe wall. The effect of the filling ratio on TKE inside the porous media and clear regions is presented in Fig. 12a, b for both arrangements. It is observed that increasing the filling ratio results in an increase in TKE inside the porous media and clear region for both arrangements. Increasing of TKE in the clear region is due to the higher velocity gradients at the interface of the porous medium and clear fluid as well as inside the clear region at larger values of filling ratio, which enhances the production of TKE. In addition to velocity gradient, the \(G_{k}^{{\text{i}}}\) term in TKE equation (Eq. (9)) also plays an important role in TKE production within the permeable layer at larger velocities. Increasing the filtered velocity within the porous layer in larger filling ratios enhances the TKE production due to solid matrix (\(G_{k}^{{\text{i}}}\) term), which in turn increases the level of TKE inside the porous layer. Higher velocity and turbulence effects close to heat transfer surface result in higher Nu number at higher filling ratios in both arrangements, as illustrated in Fig. 13. However, the behaviors of Nu number variation with filling ratio are different in the two different configurations. While an initial jump is observed in the Nu number of central arrangement with an increase in filling ratio from 0.49 to 0.64, its variation is negligible with a further increase in filling ratio to 0.75. Meanwhile, the Nu number calculated in filling ratios of 0.51 and 0.64 are similar in the fully developed region of the pipe and only after an increase in filling ratio to 0.75 a slight increase is observed in boundary arrangement. The results presented in Fig. 13 suggest that the filling ratio in the central arrangement should be limited to the values around 0.8 since pressure drop increases significantly with a further increase in filling ratio without any considerable enhancement in heat transfer. However, an increase in the filling ratio affects the heat transfer mainly at larger filling ratios in the boundary arrangement, which can result in a significant increase in the pressure drop through the pipe. Therefore, based on the results obtained in this and previous sections, it is proposed that a thinner layer of porous media should be used in the boundary arrangement with high thermal conductivity.

Fig. 11
figure 11

Velocity profiles for different filling ratios in a central arrangement, b boundary arrangement

Full size image
Fig. 12
figure 12

Variation of TKE with filling ratio in a central arrangement, b boundary arrangement

Full size image
Fig. 13
figure 13

Variation of Nu with filling ratio in central and boundary arrangements

Full size image

5.4 Velocity and temperature distributions

Figure 14 illustrates the velocity distributions in a pipe partially filled with porous media in the two abovementioned configurations along with the corresponding velocity vectors. It should be noted that the region shown in the contours of Fig. 14 is only a small section of pipe at the downstream where the flow is fully developed. The channeling effect is clear in the case of central configuration where the fluid velocity highly increases as it is squeezed between the porous medium at the center of pipe and the pipe wall. As can be seen from the velocity vectors, the maximum velocity position is also deflected towards the pipe wall causing a reduction in the thickness of boundary layers resulting in higher heat transfer rate. On the contrary, placing the porous layer over the wall decreases the flow velocity in that region, and therefore, the only mechanism that contributes to the heat transfer enhancement is the heat conduction through the solid matrix in porous media. Using a material with a sufficiently large conductivity, it is possible to reach as nearly similar temperature distribution as in central arrangement (see Fig. 15). It is worth noting that the thermal parameters of porous media such as conduction heat transfer coefficient do not play an important role in heat transfer in the central arrangement suggesting that this arrangement is more appropriate for porous media with low thermal conductivity.

Fig. 14
figure 14

Velocity (m/s) distribution and vectors in a central arrangement, b boundary arrangement

Full size image
Fig. 15
figure 15

Temperature (K) distribution in a central arrangement, b boundary arrangement

Full size image

6 Conclusion

The effect of porous layer position on turbulent flow and heat transfer inside a pipe is numerically investigated in the present study. To this end, the effects of Da, solid/fluid thermal conductivity, Re and filling ratio on the heat transfer performance of partially filled pipe are examined in the two boundary and central arrangements. The present results suggest that the insertion of porous media at the center of the pipe enhances the heat transfer performances regardless of porous media thermal characteristics. Meanwhile, the porous medium’s thermal parameters play an important role in the heat transfer enhancement when it is located over the pipe’s wall. Therefore, it can be concluded that two entirely different mechanisms are behind the heat transfer enhancement in these two configurations. While the channeling effect raised from the increase in the fluid velocity and turbulent effects in the clear region causes an enhancement of the heat transfer rate in the central arrangement, it is the thermal conductivity of porous media which has a critical role in the variation of Nu in the boundary configuration. An innovative way to evaluate the superiority of different arrangements of porous media in a pipe is proposed in the present study by comparing the Nu calculated from different arrangements in a fixed filling ratio. It is observed that the values of Nu are larger in the same filling ratios for the pipe filled with porous media at the center. In order to investigate the pore scale mechanisms that cause the aforementioned heat transfer enhancement, a pore scale study of turbulent flow and heat transfer in a partially porous pipe is needed which is the topic of future studies. Having this information, it is possible to find the correlation between these pore scale mechanisms and their effect on the averaged results obtained in the present study. It is worth mentioning that since an averaged approach was used in the present study with a double-averaged k-ε model for turbulent simulations, an averaged effect of porous layer on the fluid flow was obtained. A detailed simulation of flow within the pores of porous media and its interaction with the fluid film layer forming over the porous layer is a topic of future studies.