1 Introduction

Spiral bevel gear (SBG) is applicable to transfer the torque between non-parallel high-speed axes. Durability and vibration are two main aspects in which researchers study interestingly. The vibration has affected the bending, pressure, and fatigue life of the gear systems [1].

Recently, researches on SBG are mainly focused on the tooth contact analysis to obtain the static transmission error (STE) which is marked as the main source of the vibration. A method to minimize vibration of the SBG is presented with the meshing impact model by Mu et al. [2]. Buzzoni et al. [3] investigated three different algorithms to discriminate proper contact patterns from improper ones with considering different speeds. Zolfaghari et al. [4] carried out a study on optimizing the straight bevel gear volume by means of a genetic algorithm. In their research, face width, module, and teeth number are considered as the design parameters for optimization. Chen et al. [5] achieved a new mathematical model of elastic ring squeeze film dampers (ERSFDs) based on the Reynolds equation and presented a semi-analytical method to estimate the elastic ring deformation of ERSFDs. Yavuz et al. [6] offered a nonlinear dynamic model for the SBG pair of a train with considering the effect of the shafts and the bearings stiffnesses. Motahar et al. [7] studied the optimization of straight bevel gear models by the Tredgold method. Kickbush et al. [8] presented two finite element models (two-dimensional and three-dimensional) to achieve mesh stiffness (MS) and derived a simple formula for calculating MS. Tang et al. [9] analyzed the effect of two different STEs on the dynamic response of SBG. The two considered STEs are predesigned parabolic function and the sine function. Lin and Wu [10] theoretically and experimentally showed that increasing the contact ratio has a significant effect on the vibration of helical curve-face gear pair.

Some researchers are focused on the effect of faults on the dynamic behavior of gear pairs [11,12,13]. Peng et al. [14] suggested a new idea of calculating the load transmission error (LTE) by considering the effect of the bearing supports. Wang et al. [15] investigated the time-varying mesh stiffness of the gear pair with cracked teeth, based on a finite element analysis method.

The main goals of this paper are to determine the effect of shaft stiffness by considering elastic deformation of gear and shaft, and periodic torque on the nonlinear dynamics of an SBG pair. It would be mentioned that the LTE is one of the sources of noise, and the elastic deformation is the primary source of strength. This study leads to a more accurate definition of the gear pair behavior in reality. In this study, nonlinearity and time-varying are perceived as two properties of the differential equation of motion due to the MS and backlash fluctuation. To investigate the dynamic behavior of gear-pair, a numerical method is applied according to the 4th order Runge–Kutta method. Two considered support locations, to change the shaft stiffness, are: (1) support located near the gear and (2) support located far from the gear. In order to illustrate the dynamic behavior of the considered SBG, bifurcation diagrams, Poincaré maps, and the root-mean-square (RMS) responses are utilized.

2 Model description

As it is mentioned, this study is done to scrutinize the effect of shaft stiffness and periodic input torques. So, this paper involves two parts: shaft stiffness and periodic torque. For the first part, the effect of the shaft stiffness in consideration of the elastic deformation, two different cases are as follows:

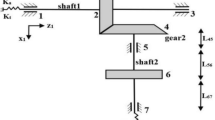
  • Case-1: The first one is the case that bearings are located near the gear and the pinion.

  • Case-2: The latter one is the case that one of the gear’s bearing is located far away from the gear.

To explain the conditions, Fig. 1. is brought. Figure 1a represents an SBG pair with the support located near the gear (case-1). Figure 1b shows the SBG pair with the support far from the gear (case-2, Fig. 1b). It is considered that SBG’s DOFs are restricted in all directions except the rotational DOF. These two support arrangements are utilized to present the effect of the shaft deformation on the LTE considering the elastic deformation evaluations. Consequently, these two support arrangement effects present on the dynamic response of the considered SBG. Note that the arrangement of the pinion remains constant.

Fig. 1
figure 1

Diagram of the supporting form a case-1 and b case-2

Full size image

For the second part, the effect of input torque for the case-1, two main different torques are considered: constant and periodic torque.

3 Governing equations

Based on the Lagrange formulation [7, 16, 17], the equations of motion are obtained (Eq. 1) as follows:

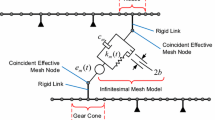
$$ \begin{array}{*{20}l} {I_{1} \ddot{\theta }_{1} + C_{m} r_{b1} \left( {r_{b1} \dot{\theta }_{1} - r_{b2} \dot{\theta }_{2} - \dot{e}} \right) + k_{m} r_{b1} f\left( {r_{b1} \theta_{1} - r_{b2} \theta_{2} - e} \right) = T_{1} } \hfill \\ {I_{2} \ddot{\theta }_{2} - C_{m} r_{b2} \left( {r_{b1} \dot{\theta }_{1} - r_{b2} \dot{\theta }_{2} - \dot{e}} \right) - k_{m} r_{b2} f\left( {r_{b1} \theta_{1} - r_{b2} \theta_{2} - e} \right) = - T_{2} } \hfill \\ \end{array} $$
(1)

To illustrate Eq. 1, Fig. 2 introduces the schematic diagram of the considered system in which the parameters, used in Eq. 1, are shown.

Fig. 2
figure 2

The dynamic model of a spiral bevel gear system with rotational degrees of freedom

Full size image

Geometric transmission error “\(e\left( t \right)\)” is the distance between mating teeth due to mounting and manufacturing error as well as free distance due to teeth profile modifications. The linear dynamic transmission error along the line of action is defined as \( \lambda = r_{{{\text{b}}1}} \theta_{1} - r_{{{\text{b}}2}} \theta_{2}\). Let \(n = r_{{{\text{b}}2}} /r_{{{\text{b}}1}}\), which is the speed ratio. Two equations in Eq. (1) are merged and the following equation obtain. In this equation, \(I_{eq} = (\frac{1}{{I_{1} }} + \frac{{n^{2} }}{{I_{2} }})^{ - 1}\), \(K_{eq} = kr_{b1}^{2}\), \(\lambda_{\theta } = \theta_{1} - n\theta_{2}\) and \(C_{eq} = {\text{c}}r_{b1}^{2}\).

$$ I_{eq} \ddot{\lambda }_{\theta } + C_{eq} \left( {\dot{\lambda }_{\theta } - {\dot{\text{e}}}_{\theta } } \right) + K_{eq} \left( t \right)f\left( {\lambda_{\theta } - e_{\theta } } \right) = T_{1} $$
(2)

Equation (2) presents the dimensional equivalent rotational displacement of the gear mesh and in this equation \(\lambda_{\theta }\) represents angular dynamic transmission error. \(f\left( {\lambda_{\theta } - e_{\theta } } \right) \) is the function of the rotational displacement, define as follows:

$$ f\left( {\lambda_{\theta } - e_{\theta } } \right) = \left\{ {\begin{array}{ll} {\lambda_{\theta } - e_{\theta } - \theta_{b} ,} \hfill & \quad{\lambda_{\theta } - e_{\theta } > \theta_{b} } \hfill \\ {0,} \hfill & \quad{ - \theta_{b} \le \lambda_{\theta } - e_{\theta } \le \theta_{b} } \hfill \\ {\lambda_{\theta } - e_{\theta } + \theta_{b} ,} \hfill &\quad {\lambda_{\theta } - e_{\theta } < - \theta_{b} } \hfill \\ \end{array} } \right. $$
(3)

\(K_{eq} \left( t \right)f\left( {\lambda_{\theta } - e_{\theta } } \right){ }\) returns the restoring force function [12, 18]. Whenever \({\uplambda }_{\theta } - e_{\theta }\) is between \(- \theta_{{b{ }}}\) and \(+ \theta_{{b{ }}}\) (\(\theta_{b}\): angular backlash), the contact loss happens [17]. For \({\uplambda }_{\theta } - e_{\theta } > \theta_{b}\), the contact occurs in forward face flank, while if \( {\uplambda }_{\theta } - e_{\theta } < - \theta_{b} ,\) backside contact happens; see Ref. [19]. Besides, the torsional GSOS is a time-varying function which is periodic with fundamental mesh frequency,\( \omega_{m}\).

$$ { } K_{eq} \left( t \right) = k_{0} + \mathop \sum \limits_{j = 1}^{S} a_{j} {\text{cos}}(j\omega_{m} t) + \mathop \sum \limits_{j = 1}^{S} b_{j} {\text{sin}}(j\omega_{m} t),\quad {\text{where}}:{ }\left\{ {\begin{array}{*{20}l} {\omega_{m} = \frac{2\pi }{{60}}N_{1} \gamma_{s} } \hfill \\ {S = \left( {N_{p} - 1} \right)/2} \hfill \\ \end{array} } \right. $$
(4)

In order to nondimensionalize the governing equation, new parameters are introduced as follows:

$$ \begin{array}{*{20}l} {\tau = \omega_{n} t,} \hfill & {\overline{\lambda }_{{{ }_{\theta } }} = \frac{{\lambda_{\theta } }}{{\theta_{b} }},} \hfill \\ \end{array} \begin{array}{*{20}l} { \omega_{n} = \sqrt {\frac{{k_{0} }}{{I_{eq} }}} ,} \hfill & {\overline{e}_{{{ }_{\theta } }} = \frac{{e_{\theta } }}{{\theta_{b} }},} \hfill & {\overline{\lambda ^{\prime}}_{{{ }_{\theta } }} = \frac{{d\overline{\lambda }_{{{ }_{\theta } }} }}{d\tau },} \hfill & {\overline{T}_{g} = \frac{{T_{1} }}{{\theta_{b} I_{eq} \omega_{n}^{2} }},} \hfill & {\zeta = \frac{{C_{m} }}{{2I_{eq} \omega_{n} }}} \hfill \\ \end{array} $$
(5)

Consequently, Eqs. (2, 3 and 4) can be rewritten as follows:

$$ \overline{\lambda }^{\prime\prime}_{{{ }_{\theta } }} + 2\zeta \left( {\overline{\lambda ^{\prime}}_{{{ }_{\theta } }} - \overline{e}^{\prime}_{{{ }_{\theta } }} } \right) + \overline{K}_{m} \left( \tau \right)f\left( {\overline{\lambda }_{{{ }_{\theta } }} - \overline{e}_{{{ }_{\theta } }} } \right) = \overline{T}_{g} $$
(6)
$$ f\left( {\overline{\lambda }_{{{ }_{\theta } }} - \overline{e}_{{{ }_{\theta } }} } \right) = \left\{ {\begin{array}{ll} {\overline{\lambda }_{{{ }_{\theta } }} - \overline{e}_{{{ }_{\theta } }} - 1} \hfill & \quad{\overline{\lambda }_{{{ }_{\theta } }} - \overline{e}_{{{ }_{\theta } }} > 1} \hfill \\ 0 \hfill \quad& { - 1 \le \overline{\lambda }_{{{ }_{\theta } }} - \overline{e}_{{{ }_{\theta } }} \le 1} \hfill \\ {\overline{\lambda }_{{{ }_{\theta } }} - \overline{e}_{{{ }_{\theta } }} + 1} \hfill & \quad{\overline{\lambda }_{{{ }_{\theta } }} - \overline{e}_{{{ }_{\theta } }} < - 1} \hfill \\ \end{array} } \right. $$
(7)
$$ \overline{K}_{m} \left( t \right) = 1 + \mathop \sum \limits_{j = 1}^{S} \frac{{a_{j} }}{{I_{eq} \omega_{n}^{2} }}{\text{cos}}(j\omega_{m} t) + \mathop \sum \limits_{j = 1}^{S} \frac{{b_{j} }}{{I_{eq} \omega_{n}^{2} }}{\text{sin}}(j\omega_{m} t) $$
(8)

Equation (6) presents the governing equation with the constant input torque. In some applications, the input torque consists of two parts, mean and ripple torque. Therefore, to analyze the dynamic behavior of a spiral bevel gear pair precisely, both parts should be considered. To achieve this goal, the Eq. (6) is modified. Actually, the calculation procedure of the motion equation for periodic input torque is approximately similar to the case with constant input torque [Eq. (6)]. The difference between these two conditions is related to input torques. Consequently, Eq. (6) is rewritten for the case with periodic torque as follows:

$$ \overline{\lambda }^{\prime\prime}_{{{ }_{\theta } }} + 2\zeta \left( {\overline{\lambda }^{^{\prime}}_{{{ }_{\theta } }} - \overline{e}^{^{\prime}}_{{{ }_{\theta } }} } \right) + \overline{K}_{m} \left( \tau \right)f\left( {\overline{\lambda }_{{{ }_{\theta } }} - \overline{e}_{{{ }_{\theta } }} } \right) = \overline{T}_{g} + n_{f} \overline{T}_{g} {\text{cos}}\left( {\frac{\omega }{{\omega_{n} }}\tau } \right) $$
(9)

In Eq. (9), \(n_{f}\) is used to determine the effect of ripple terms compare with the mean term. Equations (6) and (9) are the nondimensional nonlinear governing equations with time-varying coefficients. These equations are solved numerically by means of the 4th-order Runge–Kutta method. In order to achieve this goal, the dynamic models are solved in “RADAU algorithm” numerically [7, 20]. The accuracy of this code has been frequently confirmed in several published papers: [7, 11, 12, 20].

4 Characteristics of case study

The geometrical properties of the considered SBG pair are listed in Table 1. The RMS for each case is calculated and the bifurcation diagrams are presented by varying excitation frequency, i.e. pinion rotational speed [20]. Also, the Poincaré map is extracted from numerical results. The time response of the mentioned SBG nonlinear vibration is simulated for particular mesh frequencies. For each frequency, the transient part and steady-state part are separated.

Table 1 geometric parameters of the SBG pairs [14]
Full size table

5 Effect of shaft stiffness considering elastic deformation evaluations

To investigate the effect of shaft stiffness by considering the elastic deformation on gear pair dynamics, two different systems are considered: case-1 bearings are located close to the gear, and case-2 one bearing locates far away from the gear. In Fig. 3, a period of the time-varying GSOS for the gear with two different bearing supports is presented. Peng et al. [14] obtained transmission error of the gear pairs, utilized in this study, considering multiple elastic deformation evaluations under different supports conditions. The Fig. 3 portrays the pinion STE variation.

Fig. 3
figure 3

GSOS and Static Transmission Error, blue line—case-1, red line—case-2, dots present Fourier spots, Ref. [14]

Full size image

Figure 4 compares the RMS of oscillation for the considered SBG affected by different locations of support in terms of backward and forward simulations. Super-harmonic and primary harmonic responses are recognizable in these graphs. These results show that the dynamic response of the second case (the long-distance support) is higher than the dynamic response of the first case (the short-distance support). The RMS amplitude of the second case experiences higher amounts which are specified in Fig. 4: details views (a) and (b).

Fig. 4
figure 4

RMS diagram of forward and backward motions, black dot—case-1, red dot—case-2

Full size image

The presented results show that the vibrational behaviors for the two considered cases are similar; while the magnitudes of the vibration levels are different. For both cases, computed transmission error trends are similar; while, the peak-to-peak variation of the STE for the case-2 is 15% larger respect to the peak-to-peak variation of the STE for the case-1. This difference causes up to 67.5% differences in vibration RMS response; see Table 2 for details. The dynamic behavior of the gear pairs remains periodic, without any undesirable phenomena, for the two considered cases.

Table 2 The differences vibration level due to the support movement
Full size table

6 Effect of periodic torque

To scrutinize the dynamic behavior of gear pair, the input torque is considered as the main parameter which may result in chaos. The main goal of this part of the study is to investigate the gear-pair behavior in a nearly real circumstance. Consequently, it is considered that the input torque consists of two parts: a constant part and an oscillation part. By changing the ratio of the constant part to the periodic part, \(n_{f}\), the effect of periodic torque is determined. It would be mentioned that this parameter (\(n_{f}\)) could change from 0 to 1.

Figure 5 portrays the bifurcation diagram for the four cases. Actually, the \(n_{f}\) at each case has a different amount. As the results show, by increasing the amount of \(n_{f}\), the behavior of gear pair dynamics gets much worse. In other words, as \(n_{f}\) grows from 0 to 1, it is expected that the devastating phenomena are observed during monitoring the dynamic behavior of SBG. The results are presented for four cases: (a) \(n_{f} = 0\) which means the input torque is constant, (b) \(n_{f} = 0.5\), (c) \(n_{f} = 0.75\), and (d) \(n_{f} = 1\). To explain in detail, the bifurcation diagram for each case is divided into three parts: (1) The main diagram that \(0.1 \le \omega /\omega_{n} \le 1.1\), (2) Section (i) with red color that \(0.1 \le \omega /\omega_{n} \le 0.75\), and (3) Section (ii) with blue color that \(0.75 \le \omega /\omega_{n} \le 1.1\). For the case of constant excitation torque, \(n_{f} = 0\), the results show a periodic response (Fig. 5a) over the frequency ratio. However, by increasing the ratio of the constant part to the periodic part of the input torque, the probability of unwanted behavior, such as jumping or even chaos, rises.

Fig. 5
figure 5

Bifurcation diagram, a \( n_{f} = 0\), b \(n_{f} = 0.5\), c \(n_{f} = 0.75\), and d \(n_{f} = 1\)

Full size image

As mentioned, by increasing \(n_{f}\), the dynamic behavior of SBG gets much worse. To illustrate this point, Figs. 6 and 7 are brought. Figure 6 shows the bifurcation diagram for \(n_{f} = 1\), while the frequency ratio, \( \frac{\omega }{{\omega_{n} }}\), varies from 0.1 to 0.75. Similarly, Fig. 7 shows the bifurcation diagram for \(n_{f} = 0.75\). By investigating the bifurcation diagram, it could be found out that super-harmonic vibration is completely affected by the ratio of the constant part to the periodic part of the input torque, \(n_{f}\). And by passing from super-harmonic to sub-harmonic regime, the effect of \(n_{f}\) reduces. To investigate clearly, the results are brought in detail by means of the Poincaré map for three different frequency ratios: \(\omega_{A} /\omega_{n} = 0.23\), \(\omega_{B} /\omega_{n} = 0.52\), and \(\omega_{C} /\omega_{n} = 0.62\).

Fig. 6
figure 6

Bifurcation and corresponding Poincaré map for \(n_{f} = 1\)

Full size image
Fig. 7
figure 7

Bifurcation and corresponding Poincaré map for \(n_{f} = 0.75\)

Full size image

7 Discussion

Scrutinizing the results, it could be found out that increasing the proportion of shaft stiffness to GSOS leads to a rise in the nonlinearity of governing equation. In other words, the growth of shaft stiffness amplifies the softening behavior of gear-pair system. Also, by comparing the results of the two cases: bearings are located close to the gear and far away from the gear, going up the stiffness contributes to an increase the amplitude of vibration responses (RMS). Investigating the effect of stiffness on vibration behavior revealed that the gear-pair experienced four different jumping phenomena (refer to Fig. 2, RMS diagram) at \( \frac{\omega }{{\omega_{n} }} = 0.2, 0.25,0.34, 0.5\). By increasing the stiffness, the amount of jumping at \( \frac{\omega }{{\omega_{n} }} = 0.25\) and 0.5 are about 0.14; while the biggest one occurred at \( \frac{\omega }{{\omega_{n} }} = 0.34\) which is about 0.38.

Studying the input torque, it is concluded that considering the periodic torque significantly affects the rotational vibration. The more the proportion of ripple term increases, the more probability of unwanted phenomena such as chaos escalates. To determine the effect of ripple term compared with the mean term, a parameter is used which is named \(n_{f}\). By increasing the \(n_{f}\) from 0 to 1, the vibration behavior experienced some phenomena like period-doubling and chaos. Results show that (refer to Fig. 5, bifurcation diagram) for \(n_{f} = 0\) and 0.5, the solution is completely periodic; while for \(n_{f} = 1\), the period-doubling and chaos occurred frequently. Also, when \(n_{f} = 0.75\), the period-doubling and chaos happened once while \(0.52 \le \omega /\omega_{n} \le 0.61\) and \(0.62 \le \omega /\omega_{n} \le 0.64\) respectively. It would be mentioned that these devastating phenomena happened while \(\omega /\omega_{n}\) is lower than about one.

8 Conclusion

In this paper, the effect of different support locations by considering the effect of elastic deformation: the case with the short-distance support and the case with the long-distance support, on the dynamic behavior of the spiral bevel gears is investigated. Due to the time-varying GSOS and backlash, the nonlinear equation with variable coefficients is numerically solved by means of the Runge–Kutta method. The results of this manuscript show that by increasing the support distance from the gear, the trend of the static transmission error experiences no change. Consequently, the dynamic behavior of the gear-pair remains steady and periodic. Moreover, although increasing the distance between the supports causes higher levels of vibration, it is not a source of undesirable phenomena, e.g. chaos. While the peak-to-peak variation of the static transmission error for the case with long-distance support is 15% larger respect to the case with the short-distance support, the vibrational RMS response increases by up to 67.5% at the frequency ratio equal to 0.33. Also, by increasing the effect of ripple terms compared to the mean term, the probability of undesirable phenomena substantially rises.

Finally, it should be mentioned that there are some assumptions in order to drive the governing equations such as: no-friction, pure involute profile, dry contact, isothermal analysis, and one degree of freedom. Therefore, for further research it would be great if it is possible to investigate the dynamics of spiral bevel gear pairs without these simplifications and increase the number of degrees of freedom.