Piezoelectric relaxation of two-dimentional electron gas in InGaN/GaN heterostructures with quantum wells

Abstract

The article is devoted to the study of the mechanism of piezoelectric scattering of charge carriers in an InGaN/AlGaN/ GaN heterostructures with one filled quantum-confinement subband. The aim of the article is to create a mathematical model that can be used to estimate the kinetic parameters of a two-dimensional electron gas (2DEG) in the structure under study. The results of the calculation of the matrix scattering potentials demonstrated the reliability and consistency on the used model of industrial LED heterostructures with InGaN/GaN quantum wells. It is shown that mechanical stresses in the InGaN/GaN layers lead to an uneven distribution of the total electric field along the active layer. It has been established that the lifetime limiting the mobility of a two-dimensional electron gas in piezoelectric scattering is of the order of 10^–9 s.

1 Introduction

Modern InGaN/AlGaN/GaN heterostructures are widely used in semiconductor electronics in the production of high-frequency devices such as microwave detectors, ultra-bright LEDs and laser diodes [1, 2]. Such interest in group III-based compounds is determined by the fact that these semiconductor structures have a wide band gap, the size of which can be modified by varying the In concentration in the InGaN barrier layer. These features make possible to form transistors and monolithic schemes based on the InGaN/AlGaN/GaN heterostructures with high capacity and frequency characteristics (> 10 W/mm) [2].

This work examines samples grown by phase epitaxy at low pressure. In order to avoid formation of contamination and impurities in the process of layer-by-layer deposition of chemical reaction products, it is necessary to heat the sample continuously to high temperature in high vacuum. As a result, indium-doped delta layer is formed in the GaN barrier region. This layer influences the conductivity of two-dimensional electron gas (2DEG) [3]. In this work, we consider electronic gas to be two-dimensional. The thicknesses of the heterostructure layers are so thin that the motion of the electron gas occurs only in the plane of the layers. In the direction perpendicular to the plane, quantum-dimensional energy levels are realized.

Due to the above, it is necessary to take into account the delta layer when studying quantum-dynamic parameters of 2DEG in the active region of InGaN. The key parameters are concentration and mobility of 2DEG electrons in the active layer as they determine limit characteristics of instruments based on the InGaN/AlGaN/GaN heterostructures.

In epitaxy heterostructures studied in this work, the quantum wells are rather narrow, with the width of L = 4 nm. Due to this feature it is necessary to take into account the scattering mechanism of 2DEG on surface roughness under conditions of applied electric field. Additional, researches on InGaN/GaN heterostructures using scanning atomic-force microscopy has shown that the maximum size of irregularities that appear on heterointerface during epitaxy growth is d/3, d standing for characteristic thickness of the monoatomic layer GaN. Therefore scattering mechanism of 2DEG on InGaN/GaN interface roughness can be neglected, taking into account its insignificant contribution to the total relaxation channel.

Due to presence of internal mechanical tension in the layers of GaN hexagonal structure, piezoelectric fields appear on InGaN/GaN heterointerface. Worth note piezoelectric fields themselves do not cause scattering of two-dimensional carriers. Firstly, because they are closely related to the nodes of the crystal lattice of the GaN barrier. Secondly, because they have a periodic spatial distribution. Studies show that combined with defects in InGaN/GaN heterointerface, piezoelectric fields can lead to reduced mobility of 2DEG and can be considered as one of the relaxation channels [3]. Internal mechanical tension between the InGaN/GaN layers cause the deformation of the potential heterostructure profile and of the spatial distribution of two-dimensional charge carriers. Therefore, the overlap integration of wave functions is reduced and the proportion of leak-free electron transitions between the valence zone and the conductivity zone is increasing, which negatively affects the operation of quantum cascade lasers and LEDs [4].

The subjects studied in this study are LED samples based on InGaN/AlGaN/GaN heterostructures under conditions of applied external electric field. Purpose of the research is: (1) to create a mathematical model which allows to estimate the relaxation time and mobility of 2DEG under piezoelectric dispersion conditions; (2) to determine the aggregate value of electric field intensity and (3) to determine the distribution of electric field along the active layer.

2 Description of experimental samples

The high interest in InGaN/GaN-based LEDs is mainly due to the prospect of their use as highly efficient, environmentally friendly and durable lighting sources. Currently, blue LEDs from various manufacturers have achieved an efficiency of 63%, which exceeds the efficiency of not only incandescent lamps, but also fluorescent lamps. At the same time, the efficiency of the LED is determined by the product of its internal and external quantum output, which in turn depend on the mobility and concentration of 2DEG in the InGaN/GaN QE. The current global problems of LED development are to increase the radiation power of the device, increase the internal and external quantum output of the LED, increase the current at which the efficiency of the diode reaches a maximum. Therefore, the study of the features of recombination mechanisms in these structures allows us to find ways to increase the efficiency and power of LED radiation, which are of great interest for general lighting. Knowing the relaxation time and mobility of the 2DEG in the InGaN/GaN QE, it is possible to create powerful LEDs and lasers of the visible wavelength range, photodetectors, solar cells, resonant tunnel diodes and efficient quantum cascade lasers, high-speed transistors by selecting optimal layer parameters. This will lead to an increase in the performance of modern semiconductor optoelectronics.

The objects of this theoretical study are LED heterostructures with InGaN/GaN quantum wells in the p-n transition of GaN, grown by vapour phase epitaxy (VPE) on a sapphire substrate in the direction of [0001] [4].

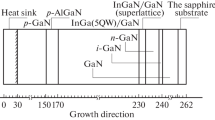
We used samples of InGaN/AlGaN/GaN/GaN heterostructures that were previously studied [4] with modular spectroscopy techniques. Parameters of the following LEDs were taken into account in calculation: «№CO1» and «№P1». The typical layer structure of the sample is shown in Fig. 1.

Fig. 1

InGaN/AlGaN/GaN/GaN semiconductor layer structure

Figure 1 shows that for InGaN/AlGaN/GaN heterostructures the first layers are the low-temperature layer and buffered layer of undoped i-GaN with thicknesses of 20 nm and 0.7 nm respectively. The next one is n-GaN layer doped by Si. With thickness of 3.6 nm for «№CO1» sample and 4.5 nm for «№P1» sample. Then follow buffer superlattice InGaN/GaN and an active zone consisting of 5 quantum wells (QW)/barriers In_xGa_1-xN/GaN. The thickness of the latter is 3/12 for «№CO1» sample and 4/4 nm for «№P1» sample. The last ones are p-AlGaN layer (thickness is 20 nm) doped by magnesium, and p-GaN layer (thickness is 120 nm). n-GaN layer is provided with an n-contact and p-GaN is provided with p-contact [5].

The concentration of 2DEG in InGaN/AlGaN/GaN heterostructures was determined by measuring of the Hall effect. The registration of temperature dependences of the Hall concentration and mobility of 2DEG were done on the device “HMS-3000” in magnetic fields up to 5 T in the dark in the range from 2 to 300 K (Fig. 2). The measurement data show that there is a non-monotonic dependence of the Hall concentration of 2DEG under the conditions of the studied temperature mode.

Fig. 2

Temperature dependences of the Hall concentration a and Hall mobility b of 2DEG for samples of heterostructures №CO1 and №P1. The arrows indicate the beginning of an abrupt increase in functional dependencies

It can be seen from Fig. 2a that in the low temperature region (40К $< T <$ 200К) there is a slight decrease in the Hall concentration with an average constant value of 2.0 $\cdot$ 10¹⁰ cm⁻² and 2.25 $\cdot$ 10¹⁰ cm⁻² for samples №CO1 and №P1, respectively. In the region of higher temperatures of $T >$ 200К, the Hall concentration of 2DEG increases sharply and reaches values of 2.15 $\cdot$ 10¹⁰ cm⁻² and 2.6 $\cdot$ 10¹⁰ cm⁻² in samples №CO1 and №P1. The functional dependencies obtained as a result of measurements can be explained as follows. The studied InGaN/AlGaN/GaN heterostructures are characterized by a wide band gap of 2.6 eV and a large concentration of the donor impurity of $N_{D} =$ 5 $\cdot$ 10¹⁸ cm⁻³. Therefore, in the studied temperature range, samples №CO1 and №P1 have impurity conductivity. The transition from impurity to intrinsic conductivity is possible at a temperature $T_{s} = E_{g} /k_{B} \ln (N_{c} N_{v} /N_{d}^{2} ),$ where $E_{g}$ is the band gap width, $N_{v} ,N_{c} ,\,N_{d} \,$ is the concentration of two-dimensional charge carriers in the valence band, in the conduction band and at the donor level, $k_{B}$ is the Boltzmann constant. Substituting the parameters of the InGaN/AlGaN/GaN heterostructures into the formula leads to a transition temperature of $T_{s} \sim$ 10⁴К. It follows from this that for the temperature range 90 K $< T <$ 170 K, the concentration of 2DEG is constant and is determined either by impurity conductivity or by carriers excited in 2DEG by femtosecond laser pulses.

The obtained temperature dependence of the Hall mobility of 2DEG is typical for InGaN/AlGaN/GaN heterostructures and is observed in the same way for samples №CO1 and №P1 (Fig. 2b). The mobility of two-dimensional carriers decreases with increasing temperature, which is explained by the strengthening of the 2DEG scattering mechanism on optical phonons at T = 85 K.

To determine the relaxation time of 2DEG in the heterostructure, the method of terahertz spectroscopy with time resolution (THz-TD) was used. Registration of the emission spectra of THz radiation for samples №CO1 and №P1 was carried out in the geometry for the passage (Fig. 3).

Fig. 3

Scheme of an experimental device for recording THz plasmon resonances in samples of InGaN/AlGaN/GaN heterostructures

The samples were excited by femtosecond laser pulses with time windows of 130 fs or 135 fs at a wavelength of 797 nm. The pulse repetition frequency of the femtosecond laser was 60 MHz with an average output power of 57 mW. A laser beam with a diameter of 1.8 mm passed through the optical system. To isolate the probing pulse, a femtosecond laser beam was directed through an optical delay system with a configurable pulse path length. The delay system consisted of mirrors 1, 2, lens 1 and a telescope, which contained a mirror 1 and 2 with an adjustable distance between them. The probing pulse was isolated for the purpose of strobing a detector sensitive to the electric field of THz pulses. Gating of the THz pulse detector in the time domain was carried out by changing the distance between mirrors 3 and 4. At the output of the sample, THz pulses excited in the 2DEG of the InGaN/GaN active region were focused by a lens 2 and mirrors 5, 6. THz radiation was recorded by a detector with a spectral resolution of 0.5 GHz and a spectral range of 6 THz. The emission spectra were visualized and processed using a personal computer. The reference $E_{off} (t)$ and modulated $E_{on} (t)$ signals passed through an empty cryostat and a cryostat with a sample, respectively, were studied. Figure 4a shows the time dependence of the detector signal for $E_{off} (t)$ and $E_{on} (t)$ sample №CO1.

Fig. 4

View of the output data of the THz pulse detector. The figure shows a the oscillograms of the electric field of the THz pulse signal in the time domain. Figure b shows the corresponding THz pulse waveform obtained by the fast Fourier transform. The spectrum was obtained for sample № CO1 at a temperature of 90 K

It can be seen from Fig. 4a that the main peak of the modulated signal transmitted through the cryostat with the sample is shifted on the time scale by an amount $\Delta t$ relative to the reference signal. The delay of the THz pulse beam recorded by the detector is due to the finite time of the 2DEG system adjustment. The delay time of THz radiation in the substrate could be neglected, since its thickness was 10 microns. Therefore, the pulse delay (Fig. 4a) in the time domain is a characteristic relaxation time $\tau$ of 2DEG in the InGaN/GaN QE. For samples №CO1, №P1, the relaxation time of 2DEG in the InGaN/GaN cell has values of $\tau =$ 5.7 ns and $\tau =$ 4.8 ns, respectively.

3 Theoretical model

Relaxation time of two-dimensional carriers in InGaN/AlGaN/GaN heterostructure with one filled subzone of the dimensional quantization within the piezoelectric scattering mechanism can be calculated using the Boltzmann general kinetic equation [6, 7]

$$ \sum {K_{ij} \tau_{ij} = E_{{F_{i} }} } , $$

(1)

$\tau_{ij}$ means the lifetime of two-dimensional carriers under conditions of the elastic scattering mechanism being studied,$E_{{F_{i} }} = E_{F} - E_{i}$ means the Fermi level in the i-th subzone,$E_{i}$ is the value of the energy level of the dimensional quantization. $K_{ij}$ stands for the components of 2DEG diffusion tensor, which determine the contribution of piezoelectric fields to the dominant conductivity channel. In the InGaN/GaN quantum wells, given its narrowness, only one energy level is realized. Therefore, interband transitions of 2DEG in the InGaN/GaN quantum wells are not observed. The indices i,j in the expression for mean the matrix elements that were calculated in this paper.$K_{ij}$ is calculated as below [8]:

$$ \begin{gathered} K_{ij} = \delta_{ij} \sum\limits_{l} {K_{ij}^{1} - } K_{ij}^{2} = \frac{{\vec{k}_{{F_{i} }} }}{2\pi \hbar } \times \left\{ {\int\limits_{0}^{\pi } {(\left| {\vec{k}_{{F_{i} }} } \right|\delta_{ij} \sum {\left| {V_{il} (q)} \right|}^{2} - \left| {\vec{k}_{{F_{j} }} } \right|\left| {V_{ij} (q)} \right|^{2} \cos \theta )d\theta } } \right\}, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,K_{ij}^{1} = \frac{{\vec{k}_{{F_{i} }}^{2} }}{2\pi \hbar }\int\limits_{0}^{\pi } {\left| {V_{il} (q)} \right|^{2} } d\theta ,\,\,\,\,\,\,\,\,\,K_{ij}^{2} = \frac{{\vec{k}_{{F_{i} }} \vec{k}_{{F_{j} }} }}{2\pi \hbar }\int\limits_{0}^{\pi } {\left| {V_{il} (q)} \right|^{2} \cos \theta } d\theta .\, \hfill \\ \end{gathered} $$

(2)

Taking into account the smooth potential created by scattering centers along the heterointerface and the increasing role of partial screening of potential by a 2DEG with increasing temperature, an additional condition needs to be imposed, where $K_{ij}^{2} = 0$. Therefore, the relaxation mechanism under investigation is elastic, so it is sufficient to use $K_{ij}^{1}$ elements to describe the kinetics of the process. The square of the matrix scattering potential under piezoelectric relaxation conditions is determined according to [8]:

$$ \left| {V_{il} (q)} \right|^{2} = \frac{{(eh_{\,\,14} )^{2} k_{B} T}}{2}\left(\sum\limits_{n,m} {(\varepsilon^{ - 1} )_{ij,nm} } \sqrt {\int {\left(\frac{{A_{l} }}{{c_{L} }} + 2\frac{{A_{\tau } }}{{c_{\tau } }}\right)} \frac{{\left| {i_{nm} (q_{z} )} \right|^{2} }}{{q_{ij}^{2} + q_{z}^{2} }}dq_{z} } \right)^{2} , $$

(3)

where, $h_{14}$ is a piezoelectric constant, $c_{L} ,\,c_{\tau }$ is constant elasticity at longitudinal and transverse deformations respectively, $k_{B}$ is a Boltzmann constant, T is temperature.

$$ \int {\left| {i_{{ii}} \left( {q_{z} } \right)} \right|^{2} dq_{z} = \int {dq_{z} \left( {\int {\phi _{i} \left( z \right)\exp \left( {iq_{z} z} \right)} \phi _{j} \left( z \right)dz} \right)\left( {\int {\phi _{i} \left( {z^{\prime}} \right)\exp \left( {iq_{z} z^{\prime}} \right)\phi _{j} } \left( {z^{\prime}} \right)dz^{\prime}} \right)} } $$

(4)

$$ q = \left(\left| {\vec{k}_{F}^{bef} } \right|^{2} + \left| {\vec{k}_{F}^{aft} } \right|^{2} - 2\left| {\vec{k}_{F}^{bef} } \right|^{2} \left| {\vec{k}_{F}^{aft} } \right|^{2} \cos \theta \right)^{1/2} , $$

(5)

$$ \varepsilon_{ij} (q) = \delta_{ij} + \frac{{q_{s} }}{q}H_{ij} (q)\chi (q), $$

(6)

where, $q$ is the variation of the wave vector with components before $\vec{k}_{F}^{bef}$ and after $\vec{k}_{F}^{aft}$ the scattering act respectively, $\varepsilon_{ij} (q)$ is the matrix of dielectric permeability in the approximation of Lindhard’s screening theory, which describes the acting scattering mechanism. $H_{ij} (q),\,\,\chi (q)$ Form-factor and static polarization of the atoms of the crystal lattice in the active layer InGaN. In the explicit form:

$$ H_{ij} (q) = \int\limits_{0}^{\infty } {dz\int\limits_{0}^{\infty } {dz^{\prime}\phi_{i} (z)\,\,\phi_{j} (z)\exp \left( - q\left| {z - z^{\prime}} \right|\right)\,} } \phi_{i} (z^{\prime})\,\,\phi_{j} (z^{\prime}),\, $$

(7)

$$ \chi (q) = 1 - \Theta \left( {q - 2\left| {\overrightarrow {k} _{F} } \right|} \right)\sqrt {\left( {1 - \left( {\frac{{2\left| {\overrightarrow {k} _{F} } \right|}}{q}} \right)^{2} } \right),\Theta } \left( {q - 2\left| {\overrightarrow {k} _{F} } \right|} \right) = \left\{ {\begin{array}{*{20}c} {1,} & {q > 2\left| {\overrightarrow {k} _{F} } \right|} \\ {0,} & {q < 2\left| {\overrightarrow {k} _{F} } \right|} \\ \end{array} } \right.. $$

(8)

Taking into account that the InGaN/AlGaN/GaN heterostructures were considered within one filled sub-zone of dimensional quantization, we introduced the following condition formula i = j. By applying matrix-shaped formalism of quantum theory to calculate the square of the scattering potential of 2DEG and the component of tensors under the conditions of the acting piezoelectric scattering mechanism, we get a formula for the relaxation time of 2DEG. This formula will be convenient for further mathematical modelling of the kinetic process and for evaluation of 2DEG dynamic parameters:

$$ \tau = \frac{1}{A + B}. $$

(9)

The relaxation time in the transverse $\tau_{T}$ and longitudinal $\tau_{L}$ directions can be calculated using the following expression

$$ \begin{gathered} A = \frac{1}{{\tau_{L} }} = \frac{{k_{B} T\alpha_{L} }}{{\pi \hbar \left| {\overrightarrow {k} } \right|^{2} }}\int\limits_{0}^{\pi } {q\left( {S\left( q \right)} \right)^{2} f_{L} \left( q \right)d\uptheta {,}} \hfill \\ B = \frac{1}{{\tau_{T} }} = \frac{{k_{B} T\alpha_{T} }}{{\pi \hbar \left| {\overrightarrow {k} } \right|^{2} }}\int\limits_{0}^{\pi } {q\left( {S\left( q \right)} \right)^{2} f_{T} \left( q \right)d\uptheta {.}} \hfill \\ \end{gathered} $$

(10)

According to the notations introduced in the above Eq. (10), we get

$$ \alpha_{L} = (eh_{\,\,14} )^{2} \frac{{9m^{*} }}{{128\hbar^{2} c_{L} }},\,\alpha_{T} = (eh_{\,\,14} )^{2} \frac{{13m^{*} }}{{256\hbar^{2} c_{T} }},\,\,\,S(q) = \frac{q}{{q + \frac{{2m^{*} e^{2} b(8b^{2} + 9bq + 3q^{2} )}}{{\varepsilon_{s} \hbar^{2} (b + q)^{3} }}}}\, $$

(11)

the dimensionless Form-factors, which determine considering the influence of particle sizes in the longitudinal and transverse channel of relaxation become:

$$ \begin{aligned} f_{T} (q) & = \frac{{13 + 78\left( {q/b} \right) + 72\left( {q/b} \right)^{2} + 82\left( {q/b} \right)^{3} + 36\left( {\left( {q/b} \right)^{4} + 6\left( {q/b} \right)^{5} } \right)}}{{13\left( {1 + \left( {q/b} \right)} \right)^{6} }}, \\ f_{L} (q) & = \frac{{1 + 6\left( {q/b} \right) + 12\left( {q/b} \right)^{2} + 2\left( {q/b} \right)^{3} }}{{\left( {1 + \left( {q/b} \right)} \right)^{6} }}. \\ \end{aligned} $$

(12)

Normalizing parameter b is a part of approximated Fang-Howard wave function ($\psi (z) = (b^{3} /2)^{1/2} z\exp ( - bz/2)$) [6]. Like any wave function, the squared module of the Fang-Howard wave function characterizes probability density distribution of a two-dimensional charge carrier localization in volume $dV = dxdydz$ in InGaN layer. In the approximation of a triangular potential profile we got an expression to evaluate the correlation parameter b, which is calculated as below

$$ b = \left(\frac{{33\pi m^{*} N}}{{2\varepsilon_{s} }}\right)^{1/3} \left(\frac{e}{\hbar }\right)^{2/3} , $$

(13)

where N is 2DEG concentration, $\hbar$- Planck's constant, $\varepsilon_{s}$ is dialectic constant, $m^{*} = \hbar^{2} (d^{2} E/dk^{2} )^{ - 1}$ is effective mass of two-dimensional carriers, which in general case is 2nd rank tensor in custom axis. However, diagonalization of a tensor and taking into consideration isotropy of InGaN layer convert the expression for effective mass of 2DEG in scalar value.

The additional equation below used to evaluate b parameter can also help in determination of the plausibility of parameters estimated in formula (13)

$$ b = \eta (N)^{1/3} , $$

(14)

where $\eta$ is a normalizing value.

Taking into consideration the fact, that the shift value of energy level within the i-th quantum well will take different values, the relaxation time of 2DEG also has a variation of values along the complete active InGaN layer. Relaxation time of 5 quantum wells ensemble under the dominant piezoelectric scattering mechanism will be recorded as below:

$$ \tau = \tau_{i}^{piz} \pm \Delta \tau , $$

(15)

where, acceptable size of standard interval is defined as

$$ \Delta \tau = \frac{{\sqrt {\sum\nolimits_{i = 1}^{5} {(\tau_{i} - \left\langle \tau \right\rangle )^{2} } } }}{2}. $$

(16)

2DEG mobility for one quantum well in InGaN active layer can be estimated using the expression

$$ \mu = e\tau /m^{*} . $$

(17)

One of the purpose of this work is to study uneven distribution of the built-in electric field along the active layer caused by defects on the heteroboundaries and fluctuations of the In molar fraction in GaN. Within the model, we derived the below formula and estimated the total electric field stress, which consists of a built-in and external electric field component.

$$ \left| {\vec{E}^{i} } \right| = \left| { - \frac{{\hbar \vec{k}^{i} mL^{2} E^{i}_{g} }}{{\mu m^{*} (mL^{2} E^{i}_{g} + \pi^{2} \hbar^{2} (1 + m^{*} /m)^{2} )}} + \vec{E}_{i}^{W} } \right|, $$

(18)

where, L is the width of quantum well InGaN, i = 1,2…K, where K is the number is quantum wells (for InGaN/GaN, K = 5), $E^{i}_{g}$ is the width of band gap in i-th QW area, $\left| {\vec{E}_{i}^{W} } \right|$ is intensity module of applied electric field, $\vec{k}^{i}$ is wave vector of two-dimensional carriers localized on the first sub-zone of size quantization. This parameter also takes different module values within the i-th QW.

The width of the $E_{g}$ band gap was calculated on the basis of empirical expression, In molar concentration in the InGaN layer was also taken into account [4]

$$ E_{g} = 1.7\,x + 3.45(1 - x) - 1.3x(1 - x), $$

(19)

where, x is In mole part.

The energy spectrum of particles in QW InGaN/GaN can be calculated by solving the transcendental equation numerically or graphically:

$$ k_{1} L = \pi n - 2\arcsin (\hbar k_{1} /\sqrt {2m^{*} U_{0} } ),\,\,n = 1,\,2,\,3 $$

(20)

where, L is QW width, $k_{1} = \sqrt {\frac{{2m^{*} E}}{{\hbar^{2} }}}$ is a wave vector that determines discrete values of energy levels of 2DEG in InGaN/GaN quantum wells, $U_{0}$ is the height of potential barrier. The formula (20) was obtained by solving the Schrödinger equation (see e.g. [9]) for a particle in two dimentional QW of final height and serves to determine its energetical spectrum.

An important issue to consider is the degree of the degeneration of 2DEG in InGaN/GaN quantum wells caused by the identity of quantum particles. To make an appropriate assessment, we calculated the temperature of degeneration $T_{0}$, which characterizes 2DEG degeneration degree in composite structures. According to the physical meaning, quantum size effects result from undistinguishable two-dimensional carriers in InGaN/GaN QW and occur when the average distance between particles $\left\langle a \right\rangle \sim \lambda$(here, $\lambda$ is de Broglie wave length), and the temperatures being studied are in the $T < T_{0}$ range. If these conditions are met, the two-dimensional electronic gas degenerates and is subject to Fermi–Dirac statistics. For $T > T_{0}$ temperatures, the gas submits the classical Boltzmann distribution. For semiconductors, 2DEG degeneration temperature is the Fermi temperature, which can be estimated using the below formula:

$$ T_{F} = \frac{{\hbar^{2} }}{{2m^{*} k_{B} }}(3\pi^{2} N)^{2/3} . $$

(21)

Inserting universal constant $k_{B} = 1.38 \cdot 10^{ - 23}$ J $\cdot$ K⁻¹ and 2DEG concentration (~ 10¹³ cm⁻²) gives degeneration temperature value equal to $T_{F} = 2.5 \cdot 10^{3}$ K which is significantly more than the studied temperatures. It should be noted that for semiconductors $T_{F}$ increases in case the effective particles mass decreases and 2DEG density increases in QW.

Internal mechanical tension in the hexagonal structure of GaN are known to result in built-in piezoelectric fields. Together with the externally applied electric field, they distort the profile of the potential InGaN/AlGaN/GaN heterostructure and cause the Stark effect [10, 11], which appears in the shift of energy levels of the valence zone and the conductivity zone. The size of the shift is determined by the different values of the local superpositions of the built-in and applied electric fields and will be different within the i-th QW (Fig. 5). It is also known that the influence of electric fields results in the description of two-dimensional carriers in QW being done using Airy wave functions for the triangular potential barrier. Figure 5 illustrates these features; two zone diagrams of the InGaN/AlGaN/GaN heterostructure; Franz–Keldysh effect, which appears in the shift of the inter-zone absorption boundary into the longwave region. Spontaneous polarization has not been considered in the course of research.

Fig. 5

A scheme of a zone diagram of an active layer consisting of 5 InGaN/GaN quantum wells: a With no applied electric field and without taking into account built-in fields. EV, EC are the maximum possible efficiency of the valence zone and the lowest possible efficiency of conductivity zone, respectively; b When reverse bias of p-n transition is applied. The oscillations and the Franz–Keldysh effect are shown within 1 QW. Square modules of wave functions of holes $\psi_{1}^{h}$ and electrons $\psi_{1,2}^{e}$ respectively in the valence region and in the conductivity zone

4 Results and discussion

An analytical study of the 2DEG electron dynamics in InGaN/AlGaN/GaN heterostructures under the piezoelectric scattering mechanism allowed us to obtain a mathematical model, helping to estimate important parameters such as the relaxation time and the 2DEG mobility. The stated theoretical model made it possible to establish, based on the calculated values of the relaxation time, the distribution of the total electric field strength modulus within the active layer. The initial empirical constants in the SGS system, the values of which were used in the calculations and characterized the mechanical and conductive properties of InGaN/AlGaN/GaN semiconductor heterostructures, are presented in Table 1.

Table 1 Initial parameters of InGaN/AlGaN/GaN heterostructure

The above mathematical model, based on the application of the matrix form of quantum calculations, for the first time was given a numerical estimation of the 2DEG relaxation time during $\tau^{pz}$ piezoelectric scattering in the InGaN active layer. As shown by theoretical calculations, the value obtained at room temperatures (T = 300 K) amounts to 10^–9 s in order of magnitude. Consequently, the available evidence suggests that the scattering mechanism in question is the defining one and significantly extent limits of the relaxation time of 2DEG electrons.

The research allowed us to estimate the values of the first $E_{V}^{1}$ and the second $E_{V}^{2}$ size quantization levels, as well as the $E_{g}$ band gap within the i-th QW (Table 2). It should be noted that the calculated values are in good agreement with those obtained by the authors [4] while interpreting the transmission spectra taken from InGaN/AlGaN/GaN heterostructure samples at different p-n junction reverse biases (Table 3). This fact speaks of a good alignment between the theory and the experiment. The results of the calculations carried out within the framework of the theoretical model are presented in Table 2.

Table 2 2DEG parameters in InGaN/AlGaN/GaN heterostructure

Table 3 Values of quantum size energy levels in the active layer InGaN/GaN

Numerous studies [12, 13] show that built-in piezoelectric fields have a significant influence on the mobility of two-dimensional carriers. In this regard, this work is biased towards estimating the distribution of the total value of the electric field along the active layer, since this factor determines the frequency characteristic of radiative and non-radiative recombination for interband transitions. Formula (18) includes the distribution of the external electric field strength $\left| {\vec{E}_{i}^{W} } \right|$ along the active layer InGaN, which was obtained during the experimental stage of the present research. Table 4 presents the molar mass of In (x) in the layer GaN [4], the average mobility over the ensemble of quantum wells, the concentration of two-dimensional carriers N, and the magnitude of the wave vector $\left| {\vec{k}} \right|$ of the charge carrier localized in the QW within the first subband. Table 2 shows the $\left| {\vec{E}_{i} } \right|$ values calculated during the research for all 5 QWs.

Table 4 Analytical 2DEG data obtained through calculations for a series of heterostructure samples InGaN/AlGaN/GaN

Tables 4 and 2 make it clear that piezoelectric scattering is characterized by high mobility and short relaxation periods of two-dimensional charge carriers. It appears from this that the researched mechanism turns up to be dominant and also affects the nature of the transitions of two-dimensional carriers between the allowed energy bands. The high mobility of 2DEG contributes to a high frequency of radiative transitions; however, the short relaxation period under conditions of piezoelectric scattering leads to other than zero frequency of non-radiative recombination. It should be emphasized that the frequency of such transitions is determined by the value of the reverse bias of the p–n junction and the concentration of 2DEG in the semiconductor.

The simulation of the temperature dependence of the relaxation period was carried out on the basis of expression (10) with the preliminary defining of the integral.

The corresponding temperature dependence of the mobility was obtained by substituting the result of defining the integral (10) into formula (17) (Fig. 6). The interpolation of the obtained analytical values by the method of Least Squares (LS) leads to the fact that the temperature dependence of the relaxation period is described by the exponential law, whereas the corresponding dependence of the mobility is described by the linear law.

Fig. 6

Temperature relationships of relaxation time and electron mobility 2DEG for a series of InGaN/AlGaN/GaN heterostructure samples

In the case of a degenerated 2DEG, the corresponding temperature dependences of the mobility longitudinal components and the average value of the relaxation time are characterized by the expression [8]

$$ \mu_{||} \sim T^{{\beta_{i} }} ,\,\,\,\left\langle {\tau^{pz}_{||} } \right\rangle \sim \left(1 - \exp \left(\frac{ - N}{{N_{c} }}\right)\right)^{ - 1} , $$

(22)

where $N_{c} = \frac{{k_{B} Tm^{*} }}{{\pi d\hbar^{2} }}$ stands for the effective density of 2DEG states in the dimensional quantization subband, $d = a + b$ is a period of layers of an active field consisting of quantum wells and barriers of the width a and b accordingly, $\beta_{i} \cong 1$ is the coefficient arising from bringing to the average value the longitudinal component of the relaxation time over temperature (50 < T < 300) in the approximation of a power-law dependence.This is what determines the linear and the exponential form of the obtained dependences. The transverse components of the mobility and relaxation time show a low degree of dependence on the temperature and do not contribute to the overall relaxation channel.

According to the formulas (17) and (22), the temperature dependence of the mobility is mainly determined by the temperature dependence of the relaxation time of 2DEG in the semiconductors under study. Thus an increase in temperature within the selected range should lead to an exponential decrease in the mobility of 2DEG. However, in the case of InGaN/AlGaN/GaN heterostructures with 5 impurity-doped quantum wells, the situation of $N \ge N_{c}$ takes place, which gives an opportunity to decompose the expression (22) with an exponential into a series in a small parameter. This results in linear temperature dependence of the longitudinal component of the mobility in the formula (22), which we bring to the average according to the statistical ensemble of two-dimensional carriers in the QW.

The graphs made as a result of modeling using the method of Least Squares (Fig. 6) correspond to the fundamental dependences (22), which indicates the correspondence between the proposed model and the kinetics of the studied processes. It is clear from the graphs that the maximum values of the mobility and relaxation time are achieved at low temperatures which ensure the low intensity of the piezoelectric scattering mechanism. It is worth noting that a similar dependence for the mobility is observed in the case of changing the width L of the quantum well. The upper limit for L is limited by the value which still allows to realize quantum-well energy levels in the active layer InGaN. The lower limit corresponds to the minimum value of the mobility [7].

As a rule, the mobility of 2DEG at room temperatures under conditions of an applied electric field is deter-mined mainly by piezoelectric scattering. Along with this, it is important to note that the mechanisms of scattering by polar acoustic and optical phonons also produce a significant effect on the dynamics of 2DEG electrons in semiconductor heterostructures InGaN/AlGaN/GaN [14, 15]. However, these mechanisms appear to be dominant in the extremely low and in extremely high temperature areas, therefore they were not taken into account during the modeling.

2DEG transfer processes in the investigated samples of heterostructures. It should also be mentioned that the filling of two dimensional quantization subbands should lead to the need to take into account the interband channel relaxation [7], which makes a significant contribution to the total relaxation time. However, in this case, when the quantum well is narrow enough (L = 4 nm) and has high potential barriers, the distance between quantum-well energy levels is quite long. Therefore, with a QW width of 4 nm, the interband scattering is insignificant, so it is reasonable to pay no attention to the effect of the second subband on the relaxation channel. Despite this, the corresponding values $E_{V}^{2}$ are demonstrated in Table 2 in order to evaluate the size of the gap between energy levels.

Based on the calculated relaxation time values under piezoelectric scattering dominating mechanism and also based on the Eq. (18), we got an estimate of the total electric field stress value in InGaN/AlGaN/GaN heterostructure. Table 2 shows the results of these calculations.

Data in Table 2 suggests that distribution of the total field along the entire InGaN/GaN active layer is nonuniform, which is appears in different values of $\left| {\vec{E}^{i} } \right|$ within the i-th QW. One of the reasons may be that the built-in piezoelectric field, which is caused by mechanical stresses and the disjunction of crystal lattices on the InGaN/GaN heterointerface, also has a gradient distribution along the active layer. According to E. Rubel principle, the area in the middle of the active layer compensates for the external influence most intensively due to maximum built-in piezoelectric fields.

As a result, this type of compensation for external application causes the resulting electrical field to have the lowest modular value in the central area of the active layer (Fig. 7). In another research [4] the authors give a different explanation of uneven distribution of the electric field based on Kerr effect. Figure 7 shows module distribution of electric field total value along the active layer. The shift of energy levels reaches its maximal value in quantum wells bordering n-GaN and p-GaN layers, which can be seen in Fig. 7 below.

Fig. 7

Distribution of electric field superposition tension value along the active InGaN/AlGaN/GaN heterostructure layer

As noted previously, Stark effect value is different for all five QW and is defined as the total value of the built-in and external electric field components within the i-th QW. Calculations show that this value reaches its minimum in the third quantum well, within which the Stark effect value is minimal.

It should be noted that under piezoelectric scattering relaxation time correlation with 2DEG energy in the active area is significantly different from the corresponding correlation for bulk semiconductors of which it is composed. In general cases the energetic dependence of relaxation time under piezoelectric relaxation is defined as below [14]

$$ \frac{1}{{\tau_{pz} (E)}} = \frac{1}{{\tau {}_{0}(E)}}G_{i} (E), $$

(23)

where, $\tau {}_{0}(E) = (a\sqrt {k_{x}^{2} + } k_{y}^{2} )\tau (E)$, $\tau (E)$ is the corresponding dependence for three-dimensional samples; $G_{i} (E)$ is a function, the parameters of which are QW width, concentration of 2DEG and active layer period; $k_{x} ,k_{y}$ are the components of the wave vector. The correlation between relaxation time and energy in the approximation of a two-dimensional electronic gas as opposed to a three-dimensional gas becomes the below power function

$$ \left\langle {\tau_{||}^{pz} } \right\rangle \sim E_{F}^{{\beta_{i} + 1/2}} , $$

(24)

where, $E_{F}$ is Fermi level. This largely explains the dynamics of 2DEG, according to which the decrease in relaxation time occurs in parallel with the increase of the Stark effect within QW along GaN active layer. Furthermore, another work [4] experimentally confirms the gradient distribution of the electric field along InGaN/GaN active layer, which indicates that the mathematical model is well agreed with the experiment.

The data calculated on the basis of the mathematical model are consistent with the experimental data obtained during the registration of THz spectra and measurements of the Hall effect. Therefore, we can talk about a good agreement between theory and experiment.

5 Conclusions

It was found that one of the dominant mechanisms in the InGaN/AlGaN/GaN heterostructure is piezoelectric scattering of two-dimensional charge carriers. In the course of the work, it was possible to simulate the 2DEG dynamics and show the consistency of the model as applied to the composite InGaN/AlGaN/GaN heterostructures under analysis.

One of the findings is the estimation of the 2DEG relaxation time under piezoelectric scattering, which amounts to 10^–9 s in order of magnitude. For each quantum well, the relaxation time and mobility take on different values and are mainly determined by the strength of the total electric field. The smallest relaxation times have two-dimensional carriers localized in the region of the third quantum well. This is due to the large value of mechanical tension that lead to the spatial distribution of 2DEG and form scattering centres located in the immediate vicinity of the 2DEG. Thus, together with heterointerface defects, piezoelectric fields represent one of the relaxation channels that must be taken into account when simulating the 2DEG dynamics, since this factor determines the character and frequency of intersubband transitions.

In the course of the work, we were able to estimate the mobility of two-dimensional carriers, which, due to the small life time, is about 2000–3000 cm² /V $\cdot$ s. It is shown that the total value of the electric field has a gradient distribution along the active layer with a minimum in 3 QW. The performed calculation of the 2DEG relaxation time, taking into account the filling of one dimensional quantization subband in InGaN/AlGaN/GaN, provided an opportunity to study the kinetics of 2D electrons. It has been established that the model under analysis authentically describes the 2DEG effects in the active layer of the heterostructure with triangular potential profile.