1 Introduction

The heat exchangers (HE) are presented in several engineering applications such as automotive, aerospace industry, electronics devices, and chemical engineering. Some examples of HE applications include condensation and evaporation for refrigeration, cooling of fluids in power plants, the radiator of cars, cogeneration, and steam generation. However, design this type of equipment with a smaller possible size, higher heat transfer, and lower pressure drop penalty remains a great challenge for engineers and researchers, encouraging them to develop studies to find innovation to increase the performance of HE [1, 2]. In the same way, solar water heaters (SWH) are HE that converting solar radiation into thermal energy. However, this type of device has low conversion efficiency and, therefore, a lot of researches have been conducted their works to improve the performance of these systems [3]. Moreover, solar thermal systems can generate thermal and electrical energy, which is useful for domestic, hospital, and industry sectors. Therefore, it is associated with economic development, technological advances, and human well-being. The management of affordable energy such as solar sources is a global concern, mainly in nations that do not have a secure supply of energy or indiscriminately consume fossil fuel, rising environmental pollution due to pollutant emissions. Hence, these issues could create instability for several countries which have a single principal resource of energy, increasing the importance to find alternatives to improve the performance of thermal systems such as solar thermal devices to provide useful and ecology alternative [4,5,6,7].

Several works have investigated the enhancement heat transfer by active and passive techniques. The passive method is effective for convective heat transfer enhancement without the aid of external equipment [8]. Recent investigations have been done to study the potential applications of different inserts including wire coils [9, 10], vortex generators [11,12,13,14], and twisted tapes [15,16,17,18] for several solar thermal applications. However, few researchers have investigated the optimal configurations of inserts applied to SWH at the moderate temperature of the working fluid [19,20,21].

In order to promote the heat transfer enhancement with low/moderate pressure drop penalty, longitudinal vortex generators (LVGs) have been applied as a promising passive technique for internal flow [22]. The potential of the LVG could be investigated through Computational fluid dynamic (CFD) coupled to optimization methods that allow greater flexibility of investigation, which is possible to evaluate several geometric parameters with low computational and time cost. As shown by our previous work [13], robust results can be found through numerical simulation and the effect of different shapes of the LGVs on heat transfer enhancement for laminar flow in a circular tube of SWH. The thermal–hydraulic performance of SWH is increased by using LGVs since the mixing of the hot and cold fluid is enhanced due to the swirling motion by longitudinal vortices, flow destabilization, and the detachment of the dynamic and thermal boundary layers [22, 23]. Furthermore, the longitudinal vortices are very persistent downstream for the laminar and turbulent flow [24, 25].

Zheng et al. [26] investigated the optimum design parameters of conical strip vortex generators into a circular tube to find the maximum heat transfer with minimum pressure drop penalty. Response Surface Methodology (RSM) and Genetic Algorithm (GA) were applied by the authors. The results showed that both the heat transfer rate and pressure drop increased with an increment of Reynolds number and strip filling ratio and reduction in the pitch. However, the pressure drop penalty was more sensitive to these design parameters than heat transfer [26]. Sun et al. [27] investigated the turbulent thermal–hydraulic performance in circular tubes with multiple rectangular-winglet vortex generators, where they concluded that a better flow mixing due to multi-longitudinal vortices. Chtourou et al. analyzed the laminar (Re 200–800) counterflow inside a small channel heat exchanger fitted with devices as LVG works. The authors investigated the influence of geometrical parameters on thermal–hydraulic performance. The results show an enhancement of 1.44 and 2.66 times of smooth tubes for different kinds of devices [28]. Moreover, several works have investigated the optimal LVG for compact heat exchanger and solar air heater [29,30,31,32,33].

Overall, considering the potential of the longitudinal vortex generators applied to enhance the heat transfer with low/moderate-pressure drop penalty at low Reynolds number, this work investigates the optimal geometrical parameters of a stamped LGVs applied on Solar Water Heater (SWH) through a 3D periodical numerical simulation based on the Finite Volume Method coupled to an optimization method called NSGA-II (Non-dominated Sorting Genetic Algorithm II [34]). The present research is an immediate continuation of our previous work [13] since no previous works have been found to address the optimization of the vortex generator inside a circular tube. The longitudinal vortex generators were stamped over a flat plate inserted inside a smooth tube operating under a typical residential application at Reynolds numbers of 300, 600, and 900. The optimization problem was set as an unconstrained single-objective function defined as a relation between the heat transfer (performed by Nusselt number, Nu) and pressure drop penalty (performed by Friction factor, f). The geometric parameters submitted to the optimization procedure are the angle of attack, front/rear height, and length of the longitudinal vortex generator.

2 Computational methodology

2.1 Governing equations

Considering an active thermal solar system, the numerical modeling of the heat transfer and fluid flow inside a circular tube is assumed to be three-dimensional and incompressible flow, laminar, and steady-state [35,36,37,38]. The buoyancy term is neglected since the Richardson Number is lower than 0.1 [13]. For a Newtonian fluid with constant properties, the equations of Continuity, Momentum, and Energy are, respectively:

$$\frac{\partial }{{\partial x_{j} }}\left( {\rho u_{j} } \right) = 0$$
(1)
$$\frac{\partial }{{\partial x_{j} }}\left( {\rho u_{j} u_{i} - \tau_{ij} } \right) = - \frac{\partial p}{{\partial x_{j} }}$$
(2)
$$\frac{\partial }{{\partial x_{j} }}\left( {\rho u_{j} h - k\frac{\partial T }{{\partial x_{j} }}} \right) = - u_{j} \frac{\partial p}{{\partial x_{j} }} + \tau_{ij} \frac{{\partial u_{i} }}{{\partial x_{j} }}$$
(3)

A Third-Order discretization scheme, called MUSCL (Monotone Upstream-Centered Schemes for Conservation Laws [39]) is used for convection terms. The pressure–velocity coupling is performed by the Coupled Algorithm, which solves simultaneously the Momentum and pressure-based Continuity Equations. The Gradient Evaluation Green-Gauss Node-based is used following the approach proposed by [40, 41]. The computational convergence is ensured for residuals lower than 10–5 for the Momentum equation and 10–8 for the Energy equation.

2.2 Thermal–hydraulic parameters

The fluid flow (water) inside a circular tube is characterized by the Reynolds number, based on tube diameter, Eq. (4). The parameters to calculate the heat transfer and pressure loss are expressed by the Nusselt number and friction factor, respectively, defined by Eq. (5) and Eq. (6).

$$Re = \frac{{\rho uD_{h} }}{\mu }$$
(4)
$$Nu = \frac{{hD_{h} }}{k}$$
(5)
$$f = \frac{{2\Delta p_{ch} }}{{\rho u^{2} }}\frac{{D_{h} }}{{L_{ch} }}$$
(6)

The average pressures and temperatures, pressure drop and convective heat transfer coefficient were performed following our previous work [13].

2.3 Computational domain and boundary conditions

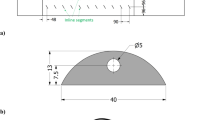
The computational domain was built-in the commercial software ANSYS 19.2. An approach considering a periodic zone is defined, which corresponds nearly 0.2 of the full-domain related to tube length of 1000 mm and 9.52 mm of diameter. This numerical approach allows a high-quality mesh hence the results of the convective heat transfer and flow simulations could be better characterized with suitable computational and time cost. There are ten vortex generators on a flat plate inside the elevation tube of a solar water heater, five above and five bellows, similarly as evaluated by Silva et al. [13]. Figure 1 shows the full-domain with periodic zone, the longitudinal vortex generator, and the flat plate where the passive devices were stamped. The plate is positioned exactly in the middle of the tube only to support the vortex generators.

Fig. 1
figure 1

Heat exchanger tube and periodic zone

Full size image

A periodic condition defined at the inlet and outlet of Fig. 2 is considered for a mass flow rate corresponding to the Reynolds number of 300, 600, and 900. A constant heat flux of 750 W/m2 is set on the tube wall which is an average value verified for solar radiation in Brazil, since for an active solar system different values for this boundary condition not change the enhanced heat transfer since the thermosyphon effect is not modeled, as discussed by Silva et al. [13]. Therefore, an absorber plate is not considered herein since this would only change the boundary condition. Figure 2 shows all the boundary conditions and a periodical computational domain with the stamped vortex generators and flat plate inside a circular elevation tube. The boundary condition on the walls is considered no-slip.

Fig. 2
figure 2

Computational domain and boundary conditions

Full size image

2.4 Grid independence and numerical validation

The mesh density study (with LVG) was evaluated by Grid Convergence Index (GCI) proposed by Roache [42]. This method allows comparing the discretization error for different objective functions for different mesh densities. The mesh features were defined by scale size in order to build refined meshes to meet the refinement factor (r) indicated by Roache [42]. Figure 3 shows the 2D elements over the tube and an approximated highlight of 3D Grid 2 inside the tube, besides the prism layer to better define the boundary layer. Table 1 shows the three mesh densities evaluated considering the Nusselt number and Friction factor as objective functions.

Fig. 3
figure 3

2D and 3D elements for Grid 2

Full size image
Table 1 Grid densities and refinement factor
Full size table

Roache [42] suggests that the Refinement factor (r) should be higher than 1.30, which is satisfied in the present work, Table 1. It was considered the angle of attack of 45 deg for the LVG and Reynolds number of 900. The discretization error found is 2.44% for the Nusselt number (Nu) and 0.10% for the Friction factor (f). Therefore, with these low values of error the grid independence is achieved, and Grid 2 can be used for the numerical simulation for the optimization procedure described in Fig. 5.

Numerical validation is evaluated through a comparison between the numerical and theoretical values of the Nusselt number and Friction factor. According to Incropera et al. [43], the Nusselt number is 4.36 for a laminar fully developed fluid flow in a circular tube with constant flux on the surface, and the Friction factor is f = 64/Re. This approach was also experimentally proved by Bashir et al. [44] for the Reynolds number range of 400–6000 with constant heat flux. Figure 4 shows that the maximum error between theoretical values and simulation is 1.62% and 2.16% for the Nusselt number at Reynolds number of 900 and the Friction factor at Reynolds number of 600, respectively, which indicates the numerical approach is reliable and robust.

Fig. 4
figure 4

Numerical validation

Full size image

3 Optimization process

An optimization problem consists of the task to find an optimal design of the vortex generators which increase the heat transfer (Nusselt number) with a lower value of pressure drop penalty (Friction factor). The geometric parameters of the LVG submitted to the optimization procedure were rear/front heights (a, b), the length (c), and the angle of attack (θ) for the superior and inferior vortex generators stamped on the flat plate inside the tube. Figure 5 shows those parameters submitted to the optimization procedure and the angle of attack is shown from the top view. Table 2 presents the ranges and steps for each input parameter. The input parameters a and b define the shape of the LVG, where an optimal shape of the LVG could be similar to a delta-winglet, rectangular-winglet or intermediate between them. The input parameter c defines the aspect ratio of the LVG while the angle of attack maintains an important interaction with a, b and c, during optimization convergence. For the optimization procedure, the angle of attack for each LVG (superior and inferior) is assumed independent while the shape parameters (a, b and c) are equals for each LVG.

Fig. 5
figure 5

The geometric parameters of the LVG submitted to the optimization procedure

Full size image
Table 2 Input parameters ranges applied
Full size table

The optimization algorithm used is NSGA-II (Non-dominated Sorting Genetic Algorithm II [34]), which is defined for the present work since can avoid stalling and detect global and multiple local extremes [45]. This algorithm is robust and extensive used for similar researches, which was applied for heat transfer augmentation, pressure drop penalty, and LVG applications [26, 31, 46,47,48].

Figure 6 presents a flowchart of the direct optimization for the present work similar as proposed by Salviano et al. [46]. An optimization method is defined through integrator software, and an initial population is built considering the number of input parameters. The pre-processing CFD is performed to generate 3D mesh and set the boundaries conditions. After running the CFD solution, pressure and temperatures are taken to calculate the Nusselt number (Nu) and Friction factor (f). Since the hydraulic parameters are performed, a single-objective function (Nu/Nu0)/(f/f0) is evaluated and the convergence of the optimization procedure is checked. If the convergence is not reached the optimization solver generates new candidates through the genetic operator (crossover and mutation) up to convergence of the single-objective function is reached. This single-objective function is defined since it is a direct relation between heat transfer and pressure drop.

Fig. 6
figure 6

Flowchart for direct optimization

Full size image

For the present work, according to defined by Rao [49], the optimization statement for an unconstrained problem can be defined as follow:

$${\text{Find}}\;Z = \left[ {\begin{array}{*{20}c} a \\ b \\ c \\ {\theta_{{LGV_{1} }} } \\ {\theta_{{LGV_{2} }} } \\ \end{array} } \right]{\text\,{which\, maximize}}\frac{{\left( {\frac{Nu}{{Nu_{0} }}} \right)}}{{\left( {\frac{f}{{f_{0} }}} \right)}}$$
(7)

4 Results and discussion

The optimal parameters of the longitudinal vortex generators are found to enhance the heat transfer with low/moderate pressure drop penalty for Reynolds number of 300, 600, and 900, which represents a typical operating condition of a solar water heater in Brazil. Table 3 shows the optimal values of the geometrical parameters of the LGVs after NSGA-II optimization for each Reynolds number evaluated.

Table 3 Optimal geometric parameter values for each Reynolds number
Full size table

For the optimization procedure, the angles of attack for each stamped LVG on the plate are independent. However, the optimal configurations for each Reynolds number indicate small variation, indicating that the angle of attack could be constant in the entire tube. It is important to point out that these found optimal configurations are for a periodic zone and the optimal configurations considering the entrance region could be different from those shown in Table 3. Therefore, the angle of attack of the vortex generator 1 and 2 should be considered equals which reduces the time for convergence of the optimization procedure. Figure 7 shows the optimal design of LVG for Reynolds number of 300, 600, and 900.

Fig. 7
figure 7

Optimal design of vortex generator for each Reynolds number evaluated

Full size image

For Reynolds number of 300 and 600 the shape of the optimal LVG were equals and similar to rectangular winglet, which is associated with the difficulty to enhance the convective heat transfer at low Reynolds number. Rectangular shapes take up a bigger area into the tube and increase the fluid velocity near the wall increasing the thermal exchanges for a conjugate problem. For Reynolds number of 900 the shape of LGVs is similar to a trapezoidal winglet. This configuration promotes decreases the pressure drop penalty as compared to rectangular winglet. Figure 8 shows the increased heat transfer and pressure drop penalty by the Nusselt number (Nu) and Friction factor (f), respectively. The Nu0 and f0 are the reference values for the smooth tube (without LVG and plate).

Fig. 8
figure 8

The ratio for configuration with/without LVG, a Nusselt number b Friction factor

Full size image

The heat transfer for Reynolds number 900 is increased by 62%. Although the difficult to increase the convective heat transfers at low Reynolds number, it was obtained an intensification of 51% for Reynolds number of 300. The pressure drop is 3 times higher than the smooth tube for Reynolds number of 900, which was the worst penalty verified. A small variation of the pressure drop is observed between Reynolds number of 300 and 600 (2.0%), increasing between the Reynolds number of 600 and 900 (8.0%). Such characteristics are important during the optimization convergence to find an optimal vortex generator shape, justifying the reduction in the frontal area of the LVG for Reynolds number of 900 in order to decrease the associated pressure drop. Figure 9 shows the ratio between heat transfer intensification and the associated pressure drop.

Fig. 9
figure 9

Relationship between the increase of Nusselt number and friction factor

Full size image

Although the optimal design of the LVG at Reynolds number of 900 showed a higher value for heat transfer, the value of the friction factor is also higher, decreasing the trade-off between heat transfer and pressure drop. The best performance was found at Reynolds number of 600, in which the heat transfer intensification represents 55% of the pressure drop penalty. Moreover, the value at Reynolds number of 300 is closer to the best performance. These results are different from those conclusions verified in our previous work [13], reinforcing the great potential of the optimization procedure to find the optimal shape of the LVG. The input parameters submitted to optimization could have interaction among them and a parametric analysis could suggest limited conclusions. Longitudinal planes for velocity and temperature contours of water fluid are shown in Figs. 10 and 11.

Fig. 10
figure 10

The velocity contours at the longitudinal planes

Full size image
Fig. 11
figure 11

The temperature contours at the longitudinal planes

Full size image

Stamped vortex generators decrease the low-pressure zone behind the LVG. This phenomenon is due to the fluid from the underside of the plate is flowing to the low-pressure zone behind the vortex generator at the upper side of the plate, thus this dynamic flow contributes to decreasing the pressure drop behind the vortex generators and increasing the mix between cold and hot streams after the generated longitudinal vortex. The fluid flow near the wall, with higher temperatures, is mixed with the flow stream closer to the plate. The average temperature keeps almost the same, however, the mix is better as the Reynolds numbers increase since the temperature near the wall is highest for Reynolds number of 300.

Figures 12 and 13 show the velocity and temperature contours, respectively, for the smooth tube, while Figs. 13 and 14 are those for SWH with LVG. The transversal planes allow evaluating the flow behavior before (x/L = 0.22 and 0.72) and after (x/L = 0.28 and 0.88) of the LGVs. Intermediate positions (x/L = 0.38 and 0.88) are also evaluated since the longitudinal vortex are persistent on downstream.

Fig. 12
figure 12

Velocity contours along the smooth tube for a longitudinal direction

Full size image
Fig. 13
figure 13

Temperature contours along the smooth tube for a longitudinal direction

Full size image
Fig. 14
figure 14

Velocity contours along the tube with LVG

Full size image

As well known, a viscous flow inside a smooth tube has a parabolic profile with higher velocity at the center of the tube and no-slip on the wall. The temperature of the fluid is higher near the wall due to the constant heat flux boundary condition imposed on the tube surface.

The vortex generator impact on the flow dynamic is evident at position x/L = 0.28 and 0.78. The LVG increases the velocity close to the wall and higher distortion in the fluid flow. This modification is due to the creation of a secondary flow toward the longitudinal direction. Therefore, the dynamic and thermal boundary layer thickness decrease which determine high gradients of property, increasing the convection heat transfer coefficient and, consequently, the pressure drop penalty. Figure 15 also shows the mix of the hot and cold fluid streams which is evidenced by planes at the positions x/L = 0.22 and 0.88 for all Reynolds number evaluated. Figure 16 shows the fluid streamlines which characterize the vortex at each transversal planes.

Fig. 15
figure 15

Temperature contours along the tube with LVG

Full size image
Fig. 16
figure 16

Streamlines along the tube with optimal LVG

Full size image

The secondary flow is persistent on downstream along the tube which is verified at position x/L = 0.88, although the distance between the LVG is not considered an input parameter for the optimization procedure. At the positions x/L = 0.28 and 0.78, it is possible to see the corner vortex at Reynolds number of 900, which is an important phenomenon to enhance the convective heat transfer with higher pressure drop penalty. At Reynolds number of 600 and 300, the corner vortex is not strong, but it is possible to identify this longitudinal vortex at the position x/L = 0.38 and 0.88, which indicates that the corner vortex is not generated immediately after the LVG but it is generated as the main vortex is propagated on downstream.

5 Conclusions

The present research evaluated by optimization procedure the impact of the geometric parameters of the LVG on the heat transfer for a solar water heater inserted in a circular tube. The performance of the heat transfer and pressure drop was numerically evaluated through the software ANSYS Fluent 19.2 coupled to Genetic Algorithm for optimization procedure. The geometric parameters of the LVG submitted to the optimization procedure are both front/rear heights, the chord, and the angle of attack. The flow condition investigated corresponds to Reynolds number of 300, 600, and 900, which represent some typical operating conditions of a SWH.

  • The results showed that the application of LVG to enhance heat transfer is an effective passive technique.

  • For the two lower Reynolds number evaluated (300 and 600) the shape of the LGVs is similar to rectangular delta-winglet, varying only the aspect ratio, while at Reynolds number of 900 the shape of the LGV is trapezoidal.

  • The highest augmentation of Nusselt number compared with the smooth tube was finding at Reynolds number of 900, which indicates an increase of 60%.

  • The pressure drop penalty is 3 times higher more than for the smooth tube. Therefore, the best thermo-hydraulic efficiency value is identified at Reynolds number of 600, where the heat transfer enhancement represented 55% of the pressure drops penalty.

  • The vortex characterization showed at Reynolds number of 300 the intensity of the secondary flow was not enough to propagate for all computational domain.

  • The corner vortex at Reynolds number of 300 and 600 is generated downstream due to synergy between the main vortex and the tube wall, while at Reynolds number of 900 this phenomenon is generated immediately after the LGVs.

  • The higher distortion at Reynolds number of 900 justifies the best values of heat transfer augmentation. Therefore, suggests at a low Reynolds number the distance between the LGVs should be considered, thus the quantity of LGVs necessary along the entire tube could be determined.

Finally, the results have proven the use of longitudinal vortex generation to improve the heat transfer with moderate pressure drop penalty at low Reynold number and laminar flow. That kind of investigation has extensive importance when it is applied in a solar water heater, considering the recent advances are observed only for solar air heater.