1 Introduction

The plate heat exchanger (PHE) is a device that transfers heat between fluids (liquid or gaseous) through an energy interaction. Indeed, the hot fluid gives part of its enthalpy to cold fluid. The PHE is characterized by its great diversity. First, it can be classified according to the transfer mode type. In addition, it can be categorized according to the contact type as direct contact and indirect contact. Moreover, Mota et al. [1]classified it according to the plate corrugations type as herringbone plate, zigzag plate protrusions and depression plate and washing board plate. Also, they showed that the PHE can be classified according to the flow arrangement type. Besides, this heat exchanger type can be classed according to its design.

Pirozfam and et al. [2]investigated the influence of the channel geometrical parameters on the PHE performance. Therefore, they simulated the hydrodynamics and thermal behavior of different forms of obstacles which were placed in the channel into a counter flow. The numerical result was obtained in a laminar flow by CFD software. They demonstrated that obstacles, improve the heat transfer. Indeed, the rectangular shape ensured the highest heat transfer rate with a great turbulence. It increased the Nusselt number and the friction factor due to its sharp corners. Also, they found that increasing the wave form of the corrugated plate can improve the heat transfer. Also, Ruoxu et al. [3] analyzed a counter flow parallel plate heat exchanger using the CFD software Comsol. They simulated a laminar flow with low Reynolds number in smooth ducts. A numerical and theoretical investigation of a counter flow parallel flow and multilayered plate heat exchangers were performed by Vera and Linan [4]. They developed analytical approximations and expressions for a laminar flow for the fully developed in a long PHE. Besides, Hossain and Islam [5]studied the thermal behavior of an internal cooling in different channel shapes. They showed the flow characteristics in 3 wavy channels (triangular, sine shaped, and arc shaped). In addition, the channel geometry influence on the counter flow thermal and hydraulic performance was carried out by Hassan and et al. [6]. A numerical simulation of different channel shapes such as trapezoidal, circular, rectangular, square and iso-triangular was conducted. They found that the increase of the channel number leads to the increase of pressure drop and the heat transfer. Also, the decrease of the channel volume can enhance the heat transfer. Their research showed that the circular shape has the best thermal performance. In addition, Zhan et al. [7] investigated numerically the effect of the channel geometrical factors on the thermal effectiveness and the counter flow system capacity. They validated their model experimentally. A new counter flow heat exchanger was developed by Kragh et al. [8]. They analyzed experimentally and theoretically its thermal efficiency. Moreover, Kim and Kim [9] developed a numerical procedure to find an optimal channel design with angled ribs. Four non-dimensional variables were chosen to optimize the internal cooling heat transfer. The numerical results were validated with experimental studies. Kim and Lee [10] studied an ideal conception of an obstacle placed in a cross flow with V-shaped ribs. Also, Mckillops and Dunkley [11] developed a correlation between the Nusselt number and the Reynolds number. They showed the effect of the channel geometry on the heat transfer coefficient. In order to the best configuration, Yilmaz et al. investigated a micro channel heat exchanger. Besides, Chamanroy et al. [12] investigated numerically the heat transfer characteristics and the pressure drop for a laminar flow in the wavy miniature heat sink (WMHS) and the straight miniature heat sink (SMHS) fitted with straight and wavy pin-fins. For a Reynolds number range Re 100–1000, the thermal performances are enhanced compared to the smooth cases. Due to the presence of wavy pin-fins, the heat transfer rate increases from 0.05 to 2.5 times and the pressure drop intensifies from 2.6 to 13.6 times compared to the smooth cases. They found that the WMHS equipped with wavy pin-fins and the SMHS fitted with straight pin-fins are the best configurations which provide the maximum the heat transfer and the minimum pressure loss. They validated experimentally their results. In addition, Hosseinirad et al. [13] studied numerically the presence of the Straight splitter and the Arched splitter Wavy splitter effect on the thermal hydraulic performance of the plate-pin–fin heat sinks (PPFHSs). They analyzed and investigated the impact of the arrangement and the shapes (square, rectangular) of the splitters on the thermal behavior with a Reynolds number Re range 50–250. They validated their numerical simulations with experimental. They discovered that with the arched and forward arrangement, the heat transfer rate is maximized. Indeed, they provide a thermal performance index enhancement with 36%. The effect of the pin- longitudinal-pitch and length on the thermal and hydraulic performance of the pin–fin heat sin was carried out by Rezaee et al. [14]. Different configurations such as PL-LH (variable-pin-length-with-low-to-high-arrangement), PL-HL (variable-pin-length-with-high-to-low arrangement), LP-LH (variable-longitudinal-pitch-with-low-to high-arrangement) and LP-HL (variable-longitudinal-pitch-with-high-to-low-arrangement) were investigated numerically and experimentally. Compared to the smooth cases, the Nusselt number Nu and skin friction factor Cf enhanced. They found that the PL-HL and LP-HL are the best configurations which provide the optimum hydro-thermal performance.

The heat transfer enhancement of the PHE is based on increasing the fluid turbulence and the heat transfer area. The obstacles introduction in the channels creates the turbulence in the flow. Therefore, the researchers searched for an optimal design of PHE which ensures a high heat transfer rate (HTR). In this work, the impact of the geometrical parameters (shapes and rib pitch p) of the Y and C shape obstacles on the thermal behavior and the hydrodynamic performance of the PHE is studied numerically in terms of CFD simulation.

This paper covers a computational fluid dynamics examination of small channels PHE. It includes three significant steps: the pretreatment, the problem resolution and the post treatment. In the first step, the computational domain was defined and developed. Then, the mesh was conducted based on a refinement grid investigation. After that, the boundary conditions and the initial conditions were determined and defined. Also, the solid and fluid properties were specified. In the second level, based on the solution methods and convergence criteria, the differential equations are transformed into linear algebraic equations. At last, the post treatment is the evaluation and the analysis of the numerical results. This work displays the flow characteristics (the effect of the Reynolds number Re and the impact of the rib pitch p) and the performance characteristics in terms of Nusselt number Nu, Friction factor Cf and Thermo-Hydraulic Performance Parameter THPP.

2 CFD analysis of a counter flow plate heat exchanger

Three-dimensional CFD analysis of a counter flow through PHE fitted with Y and C shaped obstacles is conducted with Ansys Fluent. For this evaluation, the counter flow works under steady state conditions. The flow is considered as incompressible, single phase. It is thermally fully developed. The thermal and the physical properties of the working fluid and the plate material are maintained as constant. Besides, in the channel there are no slip boundary conditions. The channels are separated by insulated walls [3]. Ansys includes different tools such as the geometry construction, the mesh creation, the simulation (Fluent) and the post-processing. It is a volume modeler.

2.1 The computational model

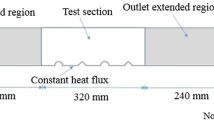
For this examination, the computational domain is maintained the same of the previous works [2, 3]. The conjugate model studied is a counter flow parallel PHE. It was created by Solidworks 2017, CAD software. The computational domain consists of two square channels (hot and cold) separated by a plate which have the different forms of obstacles. Each channel dimensions are the same of the previous works [2, 3]. The internal cross-section of the duct is 20 × 20mm2 where the obstacles are placed, as indicates the Fig. 1. All geometrical parameters of the computational channels are indicated in the Table 1 [2, 3]. The obstacles placed on the duct are assumed with constant rib height e and a variable rib pitch p, Fig. 2.

Fig. 1
figure 1

Computational domains a: without obstacles b: with obstacles

Full size image
Table 1 Geometrical parameters of the computational channels
Full size table
Fig. 2
figure 2

Y and C configurations with different rib pitch p a: Y shaped ribs b: C shaped ribs

Full size image

The height e of the Y or C ribs is maintained at 5 mm [2]. The relative roughness height is maintained constant at e/D = 0.25. Between two adjacent Y or C ribs, the pitch p is chosen at 10 mm, 15 mm, 20 mm, 25 mm. Then, the relative roughness pitch is kept variable with range of 2 < p/e < 5. The hydraulic diameter of the counter flow is D = 20 mm. Both of the hot fluid and the cold fluid flow with different temperature and velocity. Different configurations of the Y roughness employed in the CFD simulation and examination are shown in Fig. 2. Their parameters are indicated in the Table 2.

Table2 Geometrical parameters of different configurations used in the small channels PHE
Full size table

2.2 Grid generation

The most importing step in the CFD examination is the grid generation. It divides the fluid domain into sub domains called elements (Tetrahedron, Hexahedron…). In order to ensure the simulation accuracy, the meshing should be with a high quality. Since, it influences the rate convergence and the computational time.

An-uniform meshing is employed. Gird independence is carried aiming to investigate the flow characteristics and the heat transfer. Six different grids are performed with different meshing elements number as indicated in the Table 3. The meshing sensibility investigation shows that the meshing bigger than 544,768 elements provides the same average Nusselt number Nu as indicates the Fig. 3. The Tetrahedral [2], Hexahedral [15] meshing were chosen for the previous analysis. While, in our case, we choose to work with prismatic meshing with 544,768 elements as shown the Fig. 4. This selected meshing grid provides accurate results with the minimum calculation time.

Table 3 Different meshing grids independence for the CFD simulations
Full size table
Fig. 3
figure 3

Grid independence results for the average Nusselt number Nu

Full size image
Fig. 4
figure 4

Uniform grid for the computational domain of the small channels PHE

Full size image

2.3 Governing equations

In order to solve the steady state problem for a fully developed flow, the fundamental physical principals are resolved. For a three-dimensional analysis, the governing equations can be written in a Cartesian tensor as,

Continuity equation:

$$\begin{gathered} \frac{{\partial u_{j} }}{\partial x} + \frac{{\partial v_{j} }}{\partial y} + \frac{{\partial w_{j} }}{\partial z} = 0 \hfill \\ \hfill \\ \end{gathered}$$
(1)

Momentum equation:

$$u_{j} \frac{{\partial u_{j} }}{\partial x} + v_{j} \frac{{\partial u_{j} }}{\partial y} + w_{j} \frac{{\partial u_{j} }}{\partial z} = \frac{\mu }{\rho }\left( {\frac{{\partial^{2} u_{j} }}{{\partial x^{2} }} + \frac{{\partial^{2} u_{j} }}{{\partial y^{2} }} + \frac{{\partial^{2} u_{j} }}{{\partial z^{2} }}} \right) - \frac{1}{\rho }\frac{{\partial p_{j} }}{\partial x}$$
(2)
$$u_{j} \frac{{\partial v_{j} }}{\partial x} + v_{j} \frac{{\partial v_{j} }}{\partial y} + w_{j} \frac{{\partial v_{j} }}{\partial z} = \frac{\mu }{\rho }\left( {\frac{{\partial^{2} v_{j} }}{{\partial x^{2} }} + \frac{{\partial^{2} v_{j} }}{{\partial y^{2} }} + \frac{{\partial^{2} v_{j} }}{{\partial z^{2} }}} \right) - \frac{1}{\rho }\frac{{\partial p_{j} }}{\partial y} + g$$
(3)
$$u_{j} \frac{{\partial w_{j} }}{\partial x} + v_{j} \frac{{\partial w_{j} }}{\partial y} + w_{j} \frac{{\partial w_{j} }}{\partial z} = \frac{\mu }{\rho }\left( {\frac{{\partial^{2} w_{j} }}{{\partial x^{2} }} + \frac{{\partial^{2} w_{j} }}{{\partial y^{2} }} + \frac{{\partial^{2} w_{j} }}{{\partial z^{2} }}} \right) - \frac{1}{\rho }\frac{{\partial p_{j} }}{\partial z}$$
(4)

Energy equation [16,17,18]: The conservation equation of energy is defined in a steady heat flow [16],

$$k_{s} \nabla^{2} T + q = 0$$
(5)

At the interface Solid–fluid, the heat flux is defined with the Newton law of heating and cooling.

$$- k\frac{\partial T}{{\partial y}}|_{y = wall} = h\left( {T_{wall} - T_{m} } \right)$$
(6)

Afzal et al. [16] assumed in their evaluation that at the interface Solid–Fluid bodies, the temperatures are the same. Besides, they supposed that heat flux is continued. Where Tw is the wall temperature and Tm is the fluid domain mean temperature. Hence, the energy equation for the fluid domain is determined as,

$$u_{j} \frac{{\partial T_{j} }}{\partial x} + v_{j} \frac{{\partial T_{j} }}{\partial y} + w_{j} \frac{{\partial T_{j} }}{\partial z} = \frac{{k_{j} }}{{\rho_{j} Cp_{j} }}\left( {\frac{{\partial^{2} T_{j} }}{{\partial x^{2} }} + \frac{{\partial^{2} T_{j} }}{{\partial y^{2} }} + \frac{{\partial^{2} T_{j} }}{{\partial z^{2} }}} \right)$$
(7)

While for the solid wall, the energy equation can be defined as,

$$\frac{{\partial^{2} T_{s} }}{{\partial x^{2} }} + \frac{{\partial^{2} T_{s} }}{{\partial y^{2} }} + \frac{{\partial^{2} T_{s} }}{{\partial z^{2} }} = 0$$
(8)

j = c for cold channel and j = h for hot channel. Where ρ is density, g is gravitational acceleration, μ is dynamic viscosity, Cp is the heat capacity, T is the temperature, p is pressure u, v, w are respectively the velocity components in x, y, z directions and q is the heat generation. The flow velocity depends on the Reynolds number Re which indicated,

$${\text{Re}} = \frac{\rho \times V \times D}{\mu }$$
(9)

Between the following water stream in the square duct and the separated plate, the average value of Nusselt Number Nu is calculated by using the following equation:

$$Nu = \frac{h \times D}{k}$$
(10)
$$Q = h \times (T_{w} - T_{bulk} )$$
(11)
$$\to Nu = \frac{Q \times D}{{k \times (T_{w} - T_{bulk} )}}$$
(12)

It is non-dimensional parameter which is a ratio between the convective transfer and the conductive transfer [25]. It characterizes the flow heat transfer intensity. Where Q is the total surface heat flux, Tw is the temperature of wall and Tbulk is the average temperature cross the section of the laminar flow, h is the convective coefficient of heat transfer (W/m2K), k is the thermal conductivity and Dh is the hydraulic diameter. It is a ratio between the cross-sectional area A and the wetted perimeter of the cross section P. It can be written as the following equation,

$$D_{h} = \frac{4A}{P}$$
(13)

The second important parameter is the skin friction factor Cf which investigates the flow characteristics. It is written as,

$$Cf = \frac{2 \times \Delta P \times D}{{\rho \times L \times V^{2} }}$$
(14)

To evaluate the heat transfer enhancement of shaped ribs in small channels PHE, Kamali and Binesh [19], Kumar and Saini [20], Webb and Eckert [21], Promvonge and Thianpong [22], defined the thermal enhancement factor TEF or the thermo-hydraulic performance parameter THPP. It is a comparison between the results obtained with shaped ribs and with the smooth duct. It is computed as,

$$THPP = \frac{{\frac{Nu}{{Nu_{s} }}}}{{\left( {\frac{Cf}{{Cf_{s} }}} \right)^{\frac{1}{3}} }}$$
(15)

2.4 Boundary conditions

The computational domain of a counter flow PHE is a square duct with inlet, outlet, symmetry and walls as indicates the Fig. 5. It can be assumed as a conjugate model. In the upper channel, the cold fluid enters with temperature of 300 K and in the lower channel, the hot fluid enters with temperature of 330 K [2]. The separated plate has obstacles which are located in the both hot and cold channels. The upper and the lower walls are assumed symmetries. The others walls are maintained isolated.

Fig. 5
figure 5

Boundary conditions of the small channels PHE

Full size image

The water is considered as working fluid for both hot and cold channels [2]. The fluid enters with a constant velocity which depends on the Reynolds number Re. This numerical simulation was conducted with a Reynolds number Re range of 200–800. The no slip boundary condition is assumed for all solid surfaces constituting the channels. \((u_{c} = v_{c} = w_{c} = 0)\) At the inlet of the hot and the cold channels, the velocities are imposed \((w_{c} = w_{ci} )\) or \((w_{h} = w_{hi} )\). Furthermore, to model the flow exists, the pressure outlet boundary in Ansys Fluent are used. The thermal boundary conditions for heat transfer calculations are resumed in the table below (Table 4) [16, 17]. The thermal properties of the working fluids are mentioned in the Table 5.

Table 4 Mathematical formulations of the applied boundary conditions
Full size table
Table 5 Thermo-physical properties of the hot and the cold fluids
Full size table

2.5 Solution method

In order to investigate the heat transfer and the fluid flow, the computational fluid dynamics CFD code is used [23]. It is based on the finite volume method FVM [24]. It allows to convert the governing equations to the algebraic equations. Therefore, Ansys Fluent, CFD software, is chosen to solve the Navier Stokes equations. Then, it allows visualizing the velocity, the pressure and the temperature distribution. The simple algorithm is employed in order to solve the conservation of mass, momentum and energy [21]. The convergence solutions for the residuals of mass, energy, and momentum conservation equations are selected as constant and equals, respectively to 10–3, 10–6, 10–6 [2].

Afzal et al. [18] announced that the obtaining of significant and accuracy results needs an important computational time, millions of mesh elements. They confirmed that the increase in the computational domain size produces an increment in the simulation time. Then, it is necessary to employ a CPU with powerful performance. The evaluation of these small channels PHE (conjugate model) with the CFD code requires high informatics performance (computer capacity and memory). Due to the computing technology progress, the simulation was conducted using a computing station with 20Go RAM and Intel i7 4770 processor.

3 Results and discussions

3.1 Validation with a simple smooth channel

A smooth duct with the same dimensions of the channel was considered as a validation model. It is a laminar flow over a smooth duct with a low Reynolds number Re. The air as working fluid enters with a constant velocity of 0.146 m/s and a temperature of 250 K. The walls of the channel are maintained isothermal with a temperature of 400 K. The accuracy of the simulation is presented in terms of the velocity and the Nusselt Number profiles for a fully developed flow. Handbook of heat transfer [25] indicates that for a laminar flow in square duct, with isothermal walls, the Nusselt number Nu for fully developed is assumed a constant equal to 2.98.

Laminar velocity profile The accuracy of the numerical method is ensured by the velocity field flow evolution in the smooth duct with a laminar flow. The velocity profiles at the midpoint of the smooth channel and at the inlet are mentioned in the Fig. 6. Indeed, at the inlet of the channel, the velocity is constant and equals to 0.146 m/s (Re = 200). At the midpoint of the channel, after the entrance zone, the velocity profile has the parabolic aspect. The flow is hydro dynamically fully developed for Re < 2300. The fully developed begins at 200 mm. That’s why the channel dimensions are 20 × 20 \(\times\) 200 mm3.

Fig. 6
figure 6

Velocity profiles at the midpoint of the smooth channel and at the inlet for a simple smooth channel

Full size image

Nusselt number Nu and the friction factor f profiles At the inlet, in the entrance zone, the Nusselt number Nu is higher as shown the Fig. 7. Then, in the fully developed zone, it established an asymptotic value equal to 2.95.

Fig. 7
figure 7

Nusselt number Nu profile for simple smooth channel

Full size image

3.2 Validation with Ruoxu et al. [3] work

It is a comparison between the present work and the previous numerical study of Ruoxu jia et al. [3]. In this case, it is a CFD examination of a laminar counter flow through Smooth Square two ducts with length of 200 mm. The computational domain and the boundary conditions are maintained the same as Ruoxu et al. [3]. The hot fluid enters with a temperature of 330 K and the cold fluid enters with 300 K. The temperature profiles in the centerline according to the duct length are indicated in the Fig. 8a. The Fig. 8b represents the temperature evolutions in both hot and cold domains.

Fig. 8
figure 8

Temperature profiles a: in the centerline according to the duct length b: in both hot and cold domain according to Y

Full size image

While, the Fig. 9a and b describe the temperature and the velocity distributions according to the various planes parallel to the inlet and the outlet. There is a good agreement between the present work and the previous numerical work in terms of the temperature and velocity contours. Therefore, the numerical model is more reliable.

Fig. 9
figure 9

Temperature and velocity distributions according to the various planes parallel to the inlet and the outlet a: temperature distribution b: velocity distribution

Full size image

3.3 Validation with Piroozfam et al. [2] work

To ensure the accuracy of the CFD results, we tried to validate the previous analysis work of Piroozfam [2]. The previous numerical work was validated by the previous experimental work of Wie [26]. A laminar counter flow with rectangular obstacles placed on the separated plate was numerically simulated. The same dimensions and the same boundary conditions as Piroozfam[2] were performed. The Fig. 10 confirmed the validity of the CFD tool analysis. There is a good agreement between the previous work [2] and our CFD present simulation. The maximal deviation between the previous numerical work and the present CFD work differences is 1.46%.

Fig. 10
figure 10

Numerical results for rectangular obstacles using the CFD code (Fluent)

Full size image

3.4 Flow characteristics

In this part, CFD analysis are performed in order to evaluate the pressure drop and the heat transfer through small channels PHE fitted with Y and C shaped obstacles. The numerical method is validated by the previous numerical results of Piroozfam et al. [2]. In this evaluation, a cold fluid with a temperature of 300 k, a hot fluid with 330 k and a Reynolds number range of 200–800 are employed for counter laminar and single phase flow.

The Figs. 11 and 12 present the temperature and the velocity distribution in the hot and the cold sides for respectively Y and C shaped obstacles (rib pitch P of 15 mm) with a Reynolds number Re of 200 at different planes parallel to the plane (x–z). For both Y and C shaped obstacles, the heat transfer area is increased and the heat transfer is enhanced. Besides, as shown in the velocity contours, the thermal boundary layer is interrupted.

Fig. 11
figure 11

Temperature and Velocity distributions in the cold and the hot sides at different planes of Y shaped ribs Y515 (rib pitch P of 15 mm) with Reynolds number Re of 200

Full size image
Fig. 12
figure 12

Temperature and Velocity distributions in the cold and the hot sides at different planes with C shaped ribs C515 (rib pitch P of 15 mm) with Reynolds number Re of 200

Full size image

Following the expected path, the fluid enters in the channels. The trajectory of the fluid is parallel to the walls. As, it encounters the obstacles Y or C, the fluid diverges and the fluid velocity increases. Around the obstacles, the fluid flow turbulence intensity is augmented. At the walls of the channels, the velocity is zero. Away from the walls, it increases progressively. At the level of the obstacles, the thermal boundary layer is broken and destabilized [27, 28]. Due to the Y and C obstacles, the turbulence in the flow is created. Besides, the increase of heat transfer area leads to the increase of the heat transfer rate. These obstacles play the role of the generator of vortexes.

3.5 Effect of Reynolds number Re

The presence of the obstacles in the duct creates turbulence in the fluid flow. Therefore, the heat transfer is enhanced. These obstacles have the role of generators of vortexes. Indeed, around them, the flow is separated and the laminar sub layer is broken. The local mixing of the flow is immersed. Then, the disturbances are created in the flow. In fact, the flow pressure cross the duct is increased. Besides, the fluid flow resistance is intensified also. Therefore, the pumping power is augmented. The only goal is to obtain the maximum heat transfer and the minimum flow resistance.

Figures 13, 14, 15 and 16 represent the temperature and the velocity distribution in the mid plane parallel to the plane (y–z) respectively for the Y and C shapes obstacles with a Reynolds number Re range of 200–800. Indeed, with a constant rib pitch P of 10 mm, the increase of the Reynolds number Re leads to the increment of the fluid velocity cross the flow. Therefore, the heat transfer enhancement is increased. Moreover, the laminar sublayer thickness is decreased by the augmentation of the Reynolds number Re. In fact, around the obstacles, the vortices are created. Then, the increase of the velocity provides the intensification of the flow turbulence. At the regions next to the Y and C shapes obstacles, the temperature variation is maximum as indicated in the temperature contours. As can be seen, with the Y shape obstacles, the laminar sub layer is more broken than the flow with the C shape obstacles.

Fig. 13
figure 13figure 13

Temperature distributions in the mid plane parallel to the plane (y–z) with Y shapes obstacles for Reynolds number range of 200–800 and a constant rib pitch P of 10 mm (configuration Y510)

Full size image
Fig. 14
figure 14figure 14

Temperature distributions in the mid plane parallel to the plane (y–z) with C shapes obstacles for Reynolds number range of 200–800 and a constant rib pitch P of 10 mm (configuration C510)

Full size image
Fig. 15
figure 15figure 15

Velocity distributions in the mid plane parallel to the plane (y–z) with Y shapes obstacles for Reynolds number range of 200–800 and a constant rib pitch P of 10 mm (configuration Y510)

Full size image
Fig. 16
figure 16figure 16

Velocity distributions in the mid plane parallel to the plane (y–z) with C shapes obstacles for Reynolds number range of 200–800 and a constant rib pitch P of 10 mm (configuration Y510)

Full size image

3.6 Effect of pitch between two successive ribs:

The effect of the pitch between two successive ribs on the velocity distribution is presented in two different mid planes as show the Figs. 17 and 18. With a constant Reynolds number Re of 600, various configurations are numerically investigated with rib pitch range of [10, 15, 20, 25] mm. The Y and C shape obstacles fitted in the mid plate of the small channel PHE influence the fluid motion. Then, these affect the thermal displacement phenomenon. This variation affects strongly the velocity distribution for the Y shape obstacles more than the C shape obstacles.

Fig. 17
figure 17figure 17

Velocity distributions with the Y shapes obstacles for pitch P range of [10 15 20 25] mm and Reynolds number Re of 600 in the mid plane parallel to the plane (y–z))

Full size image
Fig. 18
figure 18figure 18

Velocity distributions with the Y shapes obstacles for pitch range of [10 15 20 25] mm and Reynolds number Re of 600 in the mid plane parallel to the plane (x–y)

Full size image

The increase of the rib pitch from 15 to 25 mm with a constant Reynolds number Re of 600, leads to the decrease of velocity cross the duct. Indeed, the intensification of the pitch from 10 to 15 mm causes the increase of the flow velocity. The flow becomes detached when the distance between two successive ribs increased. Then, it attached to the walls again. Near the Y obstacles, the vortexes are forms. Therefore, the flow turbulence increased and the average heat transfer coefficient enhanced. The shapes of the vortexes have a direct impact on the heat transfer improvement.

The presence of the shaped obstacles in the small channels as generators vortexes, affects the flow path. Near the obstacles, the hydrodynamic and thermal boundary layer is cut and again reformed. Then, the heat transfer increased and the thermal resistance reduced.

In the plane median parallel to plane (x–y), the velocity contours (Figs. 17, 18) show that the thermal boundary layer is interrupted around the obstacles Y and C. The presence of Y and C ribs as obstacles on the separated plate will generate turbulence in the flow. Indeed, the flow is dispersed around the obstacles. The hydrodynamic and thermal boundary layers are distributed. It has been cut and reformed. Then, the heat transfer rate is improved. Therefore the vortexes generators change the flow structure and primary profile [27,28,29]. At the level of the obstacles, the flow becomes interrupted and tortuous. Then, the flow shear stress is enhanced. Indeed, the raise of the Reynolds number Re causes the augmentation of velocity and the diminish of the temperature distribution progression in both hot and cold channels. The heat transfer enhancement of the PHE is based on the passive techniques as, the introduction of the geometrical disruptive in the flow. This last works as generator vortex. Fiebig et al. [30,31,32] affirmed that the generator vortexes disrupt the flow and modify the flow structure. Therefore the flow turbulence intensity increased and the heat transfer rate growths. In both the hot and the cold channels, the fluid distribution over the separated plate is non-uniform. In fact, this last affects the heat transfer rate and the thermal performance in the PHE. The Fig. 19 indicates that the presence of the obstacles in the channels enhanced the heat transfer between the cold and the hot fluids. Indeed, on the side of the hot small channel, the Y shape obstacles lead to a significant decrease in the temperature.

Fig. 19
figure 19

Temperature distributions with the Y and C shapes obstacles for a constant rib pitch of 25 mm and Reynolds number Re of 800 in different planes

Full size image

3.6.1 The non-dimensional parameters

3.6.1.1 Nusselt number Nu

The average Nusselt number Nu for different configurations Y and C ribs are indicated in Figs. 20 and 21. They describe the Nusselt number Nu evolution for various configurations. The parameter Nu can be calculated by the expression.

$$Nu = \frac{hD}{k}$$
(16)
Fig. 20
figure 20

Average Nusselt number Nu with the Y configuration according to Reynolds number Re range of 200–800 for different rib pitch P = 10–15-20–25 mm

Full size image
Fig. 21
figure 21

Average Nusselt number Nu with the Y configuration according Reynolds number Re range of 200–800 for different rib pitch P = 10–15-20–25 mm

Full size image

where, D is the Hydraulic diameter, k is the fluid thermal conductivity and h is the convective heat transfer coefficient. For a constant rib pitch, the increase of the Reynolds number Re leads to the augmentation of the Nusselt number Nu due to the intensification of the velocity. The counter flow through small plate heat exchanger with a pitch of 10 mm for Y ribs and a pitch of 25 mm for C ribs, have the maximum value of the non-dimensional parameter Nusselt number Nu with a Reynolds number Re range of 200–800. The maximum value of the factor Nu of Y ribs and C ribs are found respectively about 16.43 and 15.7 with a Reynolds number Re of 800.

3.6.1.2 Skin friction factor Cf

The Fig. 22 and 23 show the average skin friction factor Cf evolution according to Reynolds number range of 200–800, with Y and C ribs. It is calculated by the following expression,

$$Cf = \frac{2 \times \Delta P \times D}{{L \times \rho \times V^{2} }}$$
(17)
Fig. 22
figure 22

Average Skin friction factor Cf with the Y configuration according to Reynolds number Re range of 200–800 for different rib pitch P = 10–15-20–25 mm

Full size image
Fig. 23
figure 23

Average Skin friction factor Cf with the C configuration according to Reynolds number Re range of 200–800 for different rib pitch P = 10–15-20–25 mm

Full size image

where, ΔP is the pressure drop, L is the length of the channel, ρ is the fluid density and V is the mean flow velocity.

The presence of the Y and C shapes obstacles in the small channel, not only enhance the heat transfer but also, it causes an increase in the pressure drop in the small channels. it affects the flow path. In fact, the increase of the Reynolds number Re leads to the decrease of the skin friction factor Cf. For a constant Reynolds number Re, the increase of the rib pitch causes the decrease of average friction factor Cf. Comparing to smooth duct, the minimum value of average friction factor Cf is obtained with Reynolds number Re of 800 and a pitch of 25 mm for the Y ribs and 20 mm for C ribs as indicated in Figs. 22 and 23.

3.6.1.3 Thermo-hydraulic performance parameter THPP

In order to discover the overall heat exchanger performance, the parameter thermo-hydraulic performance THPP is employed. It is expressed as following [2, 19,20,21]

$$THPP = \tfrac{{\frac{Nu}{{Nu_{s} }}}}{{\left( {\frac{Cf}{{Cf_{s} }}} \right)^{\frac{1}{3}} }}$$
(18)

The Figs. 24 and 25 present the impact of the Reynolds number Re on the thermo-hydraulic performance parameter THPP. They describe the THPP evolution for both Y and C ribs with rib pitch range of 10–25 mm and a Reynolds number Re range 200–800. Indeed, the index THPP increases with the raise of Reynolds number Re. Beyond a critical Reynolds Number Rec, the factor THPP decreases.

Fig. 24
figure 24

Thermo hydraulic performance parameter THPP with the Y configuration according to Reynolds number Re range of 200–800 for different rib pitch P = 10–15-20–25 mm

Full size image
Fig. 25
figure 25

Thermo hydraulic performance parameter THPP with the C configurations according to Reynolds number Re range of 200–800 for different rib pitch P = 10–15-20–25 mm

Full size image

For Y rib configuration, the maximum value of the thermo-hydraulic performance parameter THPP is about 1.44 and achieved with the Reynolds number Re of 800 and the rib pitch of 10 mm. For the C rib configuration, the thermal efficiency factor THPP is maximized with Reynolds number Re of 600 and a rib pitch of 20 mm. It is about 2.6 times the smooth duct.

The Fig. 26, presents a comparison of the thermal performance between the Y ribs and the C ribs with the same rib pitch, and geometrical parameters. The thermo-hydraulic performance parameter THPP is maximized with Reynolds number of 800 for the Y ribs and a Reynolds number Re of 600 for the C ribs. With Reynolds number inferior to 400, the C ribs configuration has the highest thermal efficiency. While, beyond the Reynolds number Re of 400, the Y ribs has the best overall thermal performance.

Fig. 26
figure 26

Thermo hydraulic performance parameter THPP with the Y and C configurations according to Reynolds number Re range of 200–1000 with a constant rib pitch P = 10 mm

Full size image

The Fig. 27, describes the effect of the Reynolds number Re on the thermo-hydraulic performance parameter THPP. It presents a comparison between the THPP evolution for both Y ribs and C ribs and the previous works [2] for a Reynolds number Re range 200–800.

Fig. 27
figure 27

Thermo-hydraulic performance parameter THPP according to Reynolds number Re range of 200–800 for C and Y ribs configurations

Full size image

The maximum value of the thermo-hydraulic performance parameter THPP for the C rib with a rib pitch of 10 mm is 1.399 with a Reynolds number Re 400. In fact, the thermo-hydraulic performance parameter THPP increase until a Reynolds number 400 then, it decreases. While for the Y ribs configuration, the maximum value of the thermo-hydraulic performance parameter THPP is 1.44 with a Reynolds number Re of 800.

Indeed, the increase of Reynolds number Re leads to the decrease of the thermo-hydraulic performance parameter THPP for Reynolds number superior to 400. The presence of the Y and C shaped ribs in the counter flow leads to more thermo-hydraulic performance parameter THPP than the previous works (rectangular which is the best configuration in their analysis). Hence, the heat transfer is enhanced, and the thermal performance of the small channel PHE is improved. Therefore, the new proposed designs Y and C ribs provide the highest performance.

4 Conclusion

The presence of the obstacles in a laminar counter flow through small channels enhances the thermal and the hydraulic performance of a plate heat exchanger. The influence of the shape obstacles, the rib pitch on the thermal efficiency and the heat transfer enhancement is studied numerically with a Reynolds number range 200–800. The Y and C shaped obstacles which are placed on the separated plate, cause modification on the flow direction and structure. Indeed, the profile of the flow is perturbed. Moreover, the thermal boundary layer is interrupted. Therefore, the heat transfer is enhanced. The CFD evaluation and examination can be summarized,

  • The average Nusselt number Nu increases with the increase of Reynolds number Re with a constant rib pitch P. While, the average skin friction factor Cf decreases with the increment of the Reynolds number Re.

  • Up to the critical Reynolds number Re, the thermo-hydraulic performance parameter THPP intensifies with the augmentation of the Reynolds number Re. Beyond the critical Reynolds number Re, the factor THPP decreases. The maximum value of the thermo-hydraulic performance parameter THPP for the Y ribs configuration is about 1.44 times of smooth duct with Reynolds number Re of 800 and a rib pitch of 10 mm. For the C rib channel, with Reynolds number Re of 600 and a rib pitch of 20 mm the thermo-hydraulic performance parameter THPP is maximized with a value of 2.6 times the smooth duct.

  • The CFD analysis show that the small channel plate heat exchanger fitted with Y shape obstacles is the optimum configuration. It procures the highest thermo-hydraulic performance by providing the maximum heat transfer rate, and the minimum pressure drop. Indeed, the Y shape obstacles are inspired by the human respiratory system structures [33]. That’s why, these new proposed designs Y and C shaped obstacles (Vortex generators VG) enhance the thermal and hydrodynamic efficiency of the PHE.

In the future research, the impact of the geometrical parameters such as the rib height h, the transversal pitch Pt, the longitudinal pitch Pl, the fractal steps number N… and the working fluid nano-fluid (Al2O3/water, Fe3O4/water…) on the novel PHE thermal efficiency can be studied and evaluated.