1 Introduction

Rainfall is a measure (indicator) of an ecosystem's water availability and has strong relationships with the productivity of a region [1, 2]. Variables related to precipitation such as average, maximum and annual variability, among others, are important for explaining spatial patterns of anomalies, as well as allowing assessments of climate change by increasing the frequency of extreme events [2], Al‐Yaari et al.[3]). Its monitoring makes it possible to understand the hydrological cycle that influences ecological and environmental dynamics, also affecting economic and social activities (Morales and Araujo [4]).

The analysis of climatic variables essentially consists of two stages: an exploratory one, using descriptive statistics in order to verify the normality of the data and to discard the need for transformation in the set and also to identify the existence of possible outliers; and the second, which is based on the adjustment of mathematical statistical models to the data, which can study the phenomena with different approaches, as well as the occurrence of extreme values [5,6,7], temporal distribution (Pereira Britto, Barletta and Mendonça [8]), spatial distribution [9], intensity of the phenomenon [10], among others.

According to Pereira Britto et al. [8], even though the state of Rio Grande do Sul is industrially developed, its economy is dependent on agriculture, and despite the great advances that have taken place in this sector during the last years, agricultural activity and crop yields depend on the occurrence of rainfall. The state has a large part of its territory in the La Plata Basin, which has a sparse and irregular rainfall network [11]. Therefore, in order to have knowledge about the regime or behavior of precipitation in these locations, it is necessary to spatially distribute the precipitation. In this situation, it is essential to apply a spatial interpolation process where points with known values are used to estimate unknown values at other points.

Geostatistics began in the 1960s with a series of publications by Georges Matheron with theoretical bases on a method of spatial interpolation called Kriging developed by South African Daniel G. Krige [12]. Geostatistics is a set of statistical methods appropriate for analyzing an attribute of a phenomenon with continuous distribution over a geographic area.

Among the various methods of interpolation are the inverse distance weighted (IDW), Kriging, closest neighbor, spline and top-to-raster methods. According to Chirinos & Mallqui [13], the most used interpolators are Kriging, inverse distance and spline. The results obtained in each of the methods may be different for the same set of data. The inverse distance weighted is a univariate weighted interpolator that uses the distance between the points sampled to estimate an attribute of interest and has been highlighted by the ease of its applicability. Several studies prove its applicability. However, simulation studies involving these methods to investigate the influence of the number of points on the accuracy of the estimates are uncommon [14, 15]. The number of points used to obtain estimates through interpolators is directly related to the algorithm's execution time, representing a significant concern from the computational point of view[16], Das et al. [17]).

The Kriging using a continuous covariance function, which explains the behavior of the variable in space, stands out in the literature for presenting non-biased estimates and the minimum variance associated with the estimated value [18].

Choosing interpolators for climate data is not a simple task and the end result does not just depend on the interpolator. The interpolation process requires knowledge about the nature of the data to be interpolated and the spatial distribution of the samples [19].

Spatial analyzes involving climatic events are rare and require simulation studies [20]. In studies of this type, it is desirable that the random variables have a symmetrical distribution in order to satisfy the first- and second-order stationarities. From a practical point of view, in the meteorological studies, other statistics such as maximum and median are usual, their probability distributions are not necessarily symmetrical, and more complex geostatistical methodologies are required [21, 22].

In the state of Rio Grande do Sul, Brazil, the analysis of spatial events has been based on specific regions [23, 24]. Understanding the spatial distribution of data from phenomena that occur in space today constitutes a major challenge for the elucidation of central issues in several areas of knowledge [9]. In order to analyze the spatial distribution of rain, we usually use interpolators that can be classical or geostatistical. The interpolation methods are used to evaluate the spatial variability of a given attribute based on sample data located in a locality of interest (Gardiman [25]. According to Nashwan & Shahid [26], although there is a certain degree of reliability in the analyzes using grid data, the uncertainty in the results is still a considerable problem and arises mainly due to factors, such as the interpolation of observed data, the model used for data generation, the number of stations used for the development of models, in addition to the quality of the observed data.

Because the state of Rio Grande do Sul is a region of high importance for the economy of Brazil and has most of its activities dependent on the occurrence of rains, it is important to know the spatial behavior of different variables related to annual precipitation. In addition, there are no studies for this region, indicating (analyzing) different techniques used in the spatial analysis of rainfall in order to have more accurate and accurate results. Given these facts, the main objective of the present work is to evaluate the performance of different interpolation methods in the estimation of spatially dependent annual rainfall levels in the state of Rio Grande do Sul. Therefore, it sought to answer the following questions: (i) which interpolation method is best suited to estimate spatially dependent annual rainfall levels in the state of Rio Grande do Sul? (ii) how do the interpolators behave in the use of different statistics (mean, median and maximum)? (iii) to predict spatially, more precisely, rainfall, how many neighboring points are needed?

2 Materials and methods

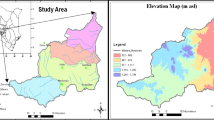
Rio Grande do Sul is located in the extreme south of Brazil (Fig. 1), with a territorial area of 281,737.888 km2 [27]. The relief is represented by plateaus of the Paraná Basin, Peripheral Depression, Eastern Plateau of Rio Grande do Sul and Patos and Mirim lagoons plains (Ross [28]). According to Sartori [29],

Due to its location in a transition zone, the climate of Rio Grande do Sul reflects the participation of Extratropical Atmospheric Systems (polar masses and fronts) and intertropical (Tropical masses and Disturbed Currents), although the first control the types of weather in 90% of the days of the year, providing also the monthly and annual distribution of rainfall.

Fig. 1
figure 1

a Location of the state of Rio Grande do Sul, Brazil; b Location of the 18 weather stations in the state

Full size image

According to the Kõppen system, Rio Grande do Sul falls into the fundamental temperate zone, denoted by "C", and humid, denoted by "Cf". Due to the altimetric differences, the state's climate split into "Cfa" and "Cfb". The oceanic climate, with mild summers (Cfb), occurs in the mountains of the southeast and northeast, where the average temperatures of the summer months are below 22 °C, and the Cfa type, or humid subtropical climate, occurs in the other regions, where the average temperature is warmer, exceeding 22 °C in the month with high temperatures [30].

The data set was obtained from the meteorological database for teaching and research (BDMEP) provided by National Institute of Meteorology (INMET). Information from 18 conventional monitoring stations were used and cover the period from 1961 to 2017, totaling 56 years of analysis (Table 1). The variable considered was the monthly cumulative rainfall, the data were separated by year and the maximum, mean and median of each season were extracted, thus forming a subset with the annual averages, medians and maximums values of each weather station. The georeferenced points that form the polygon of Rio Grande do Sul were extracted from a file of the type Shapefile made available by the Brazilian Institute of Geography and Statistics (IBGE). The percentage of failures was calculated by the ratio between the number of monthly records in which there was no reading and the total number of monthly records. We emphasize that the choice for the stations, as mentioned above, was because they are the stations with the most considerable amount of records available in the state according to the BDMEP.

Table 1 Data from the meteorological stations evaluated in the state of Rio Grande do Sul, Brazil, as well as the beginning and end dates of the series and percentage of failures
Full size table

2.1 Inverse Distance Weighted (IDW)

The IDW method, univariate interpolator, is a classical interpolator that uses the distance between the points sampled to determine the value of the points of interest. Thus, to estimate a point not sampled at a given location, we used Eq. (1) described by

$$Z\left( {u_{i} } \right) = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \frac{{Z\left( {u_{i} } \right)}}{{d_{i}^{p} }}}}{{\mathop \sum \nolimits_{i = 1}^{n} \frac{1}{{d_{i}^{p} }}}}$$
(1)

where \({d}_{i}\) is the distance between the observation pairs (\({u}_{i}\)), p is a power parameter generally equal to two and n represents the number of sampled points used for the estimation [10]. In Eq. (1), more significant power parameters emphasize closer points, making the result less smooth. Smaller power parameters emphasize more distant points, making the result smoother but less accurate (Marcuzzo, Andrade and Melo [31]). As the distance increases, weights diminish significantly when the value of the power parameter rises. Nearby stations have a heavier weight more influence on the estimation [32].

2.2 Kriging methods

Kriging is a geostatistical method based on the Theory of Regionalized Variables, which assumes that phenomenon variation depends on its location. A semivariogram quantifies the spatial variation in the Kriging method. The semivariogram is, in turn, calculated by Eq. (2).

$$2\hat{\gamma }\left( h \right) = \frac{1}{N\left( h \right)}\mathop \sum \limits_{i = 1}^{n} \left[ {Z\left( {u_{i} } \right) - Z\left( {u_{i} + h} \right)} \right]$$
(2)

in which, \(h\) is the vector distance between pairs of observations, \(N\left(h\right)\) is the number of ordered pairs and Z (\({u}_{i}\)) and Z (\({u}_{i}+h\)) are values observed at respective locations.

The empirical semivariogram estimated by \(\widehat{\gamma }\left(h\right)\) provides a graph to which a function fits, thus generating a theoretical semivariogram. This function should best represent the behavior of \(\widehat{\gamma }\left(h\right)\). Omnidirectional semivariograms were used.

Three theoretical semivariogram models were considered: spherical, exponential and Gaussian models. All of these models have as parameters: range (a), distance within which the samples are spatially correlated; partial sill (C) is the maximum value of the semivariogram within its range; effect nugget (C0) is the value of semivariogram for distance zero.

The adjustment of the theoretical models was done by the methods of ordinary least squares (ols) and weighted least squares (wls), to determine which would best fit the graph generated by \(\widehat{\gamma }\left(h\right)\). The choice of the best semivariogram was aided by the Cambardella criterion, which quantifies the degree of spatial dependence [33]. The degree of dependence is obtained by expressing the nugget effect as a percentage of the partial sill, so semivariograms with a nugget effect ≤ 25% of the partial sill are considered with strong spatial dependence, moderate dependence when the nugget effect is between 25 and 75% and weak dependence nugget effect is ˃ 75%.

The ordinary Kriging method (OK) is used when the regionalized average of the data is unknown. In order to estimate the amount of annual rainfall at a non-sampled location (\(\widehat{Z\left({u}_{i}\right)}\)), the following ordinary Kriging estimator was used,

$$\widehat{{Z\left( {u_{i} } \right)}} = \mathop \sum \limits_{i = 1}^{n} \lambda^{{{\text{KM}}}} Z\left( {u_{i} } \right) + \mathop \sum \limits_{i = 1}^{n} \lambda^{{{\text{OK}}}} \left[ {Z\left( {u_{i} } \right) - \mathop \sum \limits_{i = 1}^{n} \lambda^{{{\text{KM}}}} Z\left( {u_{i} } \right)} \right]$$
(3)

where \(Z\left( {u_{i} } \right)\) is the observed value, \(\lambda^{OK}\) refers to the weights calculated on the basis of n data \(Z\left( {u_{i} } \right)\) and \(\mathop \sum \nolimits_{i = 1}^{n} \lambda^{KM} Z\left( {u_{i} } \right)\) is the estimator of the average for each region. Further details on the estimation of the mean can be seen in Yamamoto [12].

The universal Kriging (UK) is used to model a trend in rainfall in longitude and/or latitude, when this happens to occurs. Instead of considering the regional average \(m\left(u\right)\) unknown, which can be estimated by an average around a region with the n closest points (ordinary Kriging), a first-order or higher-order polynomial for the trend and/or covariates is set (E. j Pebesma and Bivand [34]). Assuming that we have a first-degree bias in n points, then

$$m\left( u \right) = \beta_{0} + \beta_{1} x\left( u \right)$$
(4)

where x may be the direction of the trend. Similarly, if a covariate (secondary variable) is analyzed joint with the annual rainfall, the co-ordinary Kriging (COK) estimator can be considered and is given by

$$\widehat{{Z\left( {u_{i} } \right)}} = \mathop \sum \limits_{i = 1}^{n} \lambda^{OK} Z\left( {u_{i} } \right) + \mathop \sum \limits_{{j_{i} = 1}}^{m} \beta_{{j_{i} }}^{OK} S_{k} \left( {u_{{j_{1} }} } \right)$$
(5)

where \(S_{k} \left( {u_{{j_{1} }} } \right)\) is the observed value from secondary variable and \(\beta_{{j_{i} }}^{OK}\) are the ordinary Kriging weights. We used the k = 1 case for altitude as secondary variable.

The influence of the neighboring points in the prediction of non-sampled points is verified through the maps of the IDW and Kriging methods constructed considering fractions of points near the ones that will be estimated, given by 10, 20, 30, 50, 70 and 100% of the set of points data. The fractions formed by the 18 points are equivalent to 2, 4, 6, 9, 13 and 18 neighbors.

2.3 Evaluation of the models

The quality of the estimates was evaluated by the leave-one-out method, which is a particular case of k-fold, also known as cross-validation. According to Andriotti [35], the leave-one-out method consists of taking a sample point from the data set and calculating the estimate for that point. Repeating the procedure for all points in the sample set and at the end comparing the known point with the estimate gives the mean square error (MSE) of these discrepancies. In this sense, five methods were used to evaluate the residuals calculated by the cross-validation, MSE (6), R2 (7), square root of the MSE (RMSE) and modified Willmott's concordance index (md) (8),

$${\text{MSE}} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {Z\left( {u_{i} } \right) - \widehat{{Z\left( {u_{i} } \right)}}} \right)}}{n}$$
(6)
$$R^{2} = 1 - \frac{{{\text{SQR}}}}{{{\text{SQT}}}} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {Z\left( {u_{i} } \right) - \widehat{{Z\left( {u_{i} } \right)}}} \right)}}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {Z\left( {u_{i} } \right) - \overline{Z}\left( {u_{i} } \right)} \right)^{2} }}$$
(7)
$${\text{md}} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left| {Z\left( {u_{i} } \right) - \widehat{{Z\left( {u_{i} } \right)}}} \right|}}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\left| {Z\left( {u_{i} } \right) - \overline{Z}\left( {u_{i} } \right)} \right| + \left| {\widehat{{Z\left( {u_{i} } \right)}} - \overline{Z}\left( {u_{i} } \right)} \right|} \right)}},$$
(8)

where \(\overline{Z}\left( {u_{i} } \right)\) is the mean and \(\widehat{{Z\left( {u_{i} } \right)}}\) is the fitted value. The md index is less sensitive to the presence of outliers and has a range between 0 and 1, where values close to 1 better indicate the model's performance in the prediction [36].

We conducted a computational simulation study to evaluate the performance of the geostatistical and classical methods used. The Monte Carlo simulation method was used, which consists of making several achievements of a phenomenon according to pre-established parameters. At the end of these simulations, we can calculate the mean and standard deviation of the simulations, and these represent measures of accuracy and precision, respectively [37, 38]. Thus, two scenarios are considered:

  1. 1.

    Random fields generated considering spatial dependence structure according to the best result of the geostatistical method;

  2. 2.

    Random fields generated considering the spatial dependence structure different from the best results obtained by the geostatistical method.

In the proposed methodology we use, the R version 4.0.0 [39], the packages geoR [40], gstat (E. J. [41], sp (E. j Pebesma and Bivand [34]), rgdal (Bivand and Keitt [42]), hydroGOF [43] and ggplot2 [44].

3 Results

All rainfall series are homogeneous by Levene's test considering 1% as significance level (Fig. 2). The size of the dataset is an essential issue in the analysis of the data. As shown in Table 1, there is an imbalance in the amount of data among the weather stations. The occurrence of technical problems at the stations has meant that many other stations in the state have a much lower number of records than our work, which is similar in quantity to the work of Alvares et al. [30]. Given these considerations and given the focus of the work, we analyze annual rainfall data. However, we emphasize that this approach constitutes one possibility of analysis, and others such as monthly, seasonal and/or cumulative annual analysis could be considered [11, 32, 45, 46]. The plots of the exploratory analyses are shown in Fig. 3. In the mean and median histograms, it is possible to notice a slight negative asymmetry, −0.231671 and −0.230965, respectively, while for the maximum, the asymmetry is positive 0.583762. This result suggests that the data may not follow a normal distribution. However, it is possible to assume the normality of the data before the results of the Shapiro–Wilk test [47], 1% of significance, with the following p values: for a maximum of 0.5466, for a mean of 0.3167 and a median of 0.06111.

Fig. 2
figure 2

Box plots of the daily rainfall series in each weather station evaluated according to Table 1 and Levene's homogeneity test (p-value)

Full size image
Fig. 3
figure 3

Histograms of annual rainfall in mm. a Histogram of the mean; b histogram of the median; c histogram of the maximum

Full size image

Figure 4 shows the relation between the rainfall variable with the latitude and longitude coordinates, where it is possible to verify that there is no trend around the longitude for any of the measures under study. For latitude, the mean and median tend as the coordinates increase the observed values. This behavior indicates that the trend can be modeled.

Fig. 4
figure 4

Plots of mean a, median b and maximum c annual rainfall with latitude and longitude coordinates

Full size image

Table 2 shows the semivariogram fitted values, and Fig. 5 shows the plots. We analyzed the degree of spatial dependence calculated by Cambardella and the square root of the mean square error to choose the method and model that best fits the empirical semivariogram. The values of the Cambardella test are all within the same range of less than 25%, indicating strong spatial dependence [33]. For the variables analyzed in OK, the Gaussian model is the one that presented the lowest value of the RMSE for the mean and the median, fitted by the weighted least squares (wls) method. For the maximum, the exponential model fitted by ordinary least squares (ols) was the best. In the UK, the mean was adjusted by the spherical model by wls, and the median with the Gaussian model by ols.

Table 2 Estimates of the parameters (Co), contribution (C) and range (a) of the semivariograms by the ordinary (ols) and weighted (wls) least squares methods and results of the Cambardella criterion and root mean squared error (RMSE)
Full size table
Fig. 5
figure 5

Fitted theoretical semivariograms to the empiricals. a semivariogram of the mean for ordinary Kriging (OK), b semivariogram of the median for OK, c semivariogram of the maximum for OK, d semivariogram of the mean for universal Kriging (UK), e semivariogram of the median for UK, f semivariogram of the maximum for UK, g semivariogram of the mean for co-ordinary Kriging (COK), h semivariogram of the median for COK, i semivariogram of the maximum for COK

Full size image

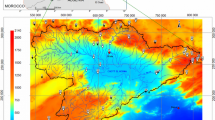
Figure 6 shows the generated maps for IDW and Kriging. It is possible to notice that the estimation surfaces provided by the IDW show some regions of rainfall well delimited generating some islands or points located in the vicinity of the sampling points. The maps provided by Kriging have smoother surfaces and evidence of transition zones between different levels of rainfall.

Fig. 6
figure 6

Prediction maps of annual rainfall levels. a Map of the mean generated with the IDW using 50% of the data set; b map of the mean generated with co-ordinary Kriging (COK) using 50% of the data set; c map of the median generated with the IDW using 50% of the dataset; d map of the median generated with co-ordinary Kriging using 50% of the data set; e map of the maximum generated with the IDW using 50% of the data set; f map of the maximum generated with co-ordinary Kriging using 50% of the data set

Full size image

The rainfall variable has no relation with the longitude coordinates. It was possible to verify that there is no trend around the longitude for any of the measures under study. For latitude, the mean and median have a trend as the coordinates increase the observed values, indicating that the trend can be modeled. The universal Kriging was used to adjust the first-degree polynomial, explaining this feature in the rainfall estimates.

Table 3 shows the cross-validation results for the mean and median. For the mean, the models presented the lowest MSE with 50% of the data set, which equals nine points. According to Andriotti [35], the number of neighboring samples required depends on the configuration of locations sampled and the degree of anisotropy, and for irregularly spaced samples is 10 samples. OK presented the best result with a 3.1 mm error in relation to IDW, corresponding to 31.62%, lower than the IDW and a determination coefficient of 84.12%.

Table 3 Results of cross-validation for mean, median and maximum, mean squared error (MSE), root mean squared error (RMSE), determination coefficient (R2) and modified Willmott's index of agreement (md) for the evaluated methods (OK—ordinary Kriging, UK—universal Kriging, COK—co-ordinary Kriging, IDW—inverse distance weighted)
Full size table

This study shows a slight difference in the MSE values, indicating OK as the most appropriate for the mean. Analyzing the values of the RMSE it is possible to notice that the difference of the OK and UK errors is of 0.88 mm of rainfall. This result indicates that considering the assumed modeling trend did not bring substantial improvement in Kriging estimates, which leads to consider the equivalence between them. Thus, the trend observed in the data may have more relation with other variables such as altitude. This result is in agreement with Baratto & Wollmann [48] who studied the rainfall profile of state of Rio Grande do Sul. According to the authors, it is possible to trace two profiles in the state, one in the south–north direction and the other in the west-northeast direction, and conclude that rainfall is influenced by orography and this influence is more significant in the north–south direction between Santa Maria and Júlio de Castilho cities. The results for COK were better than OK and UK, which shows that considering the covariate altitude for rainfall has brought substantial improvements in decreasing the prediction error (Table 3).

Concerning the median, the interpolators diverged on the ideal number of neighboring neighbors. The MSE lowest value for OK was obtained with 70% of the points. The best MSE results were obtained for the UK using 100% of the set. In IDW, the lowest RMSE was with 50% of the data set, but for other numbers of points, there were no significant discrepancies between the RMSE, showing that for the median, the IDW showed approximately consistent results (Table 3).

The values of the determination coefficient (R2) related to the best results of Kriging, ordinary and universal, of the mean and median are more significant than 0.7. This value of R2 means that the choice of the number of points is correctly determined. The R2 values of the IDW, 0.6975 for mean and 0.6828 for median, indicate that the estimated values are moderately close to the real ones.

The modified Willmott's index of agreement shows that the co-ordinary Kriging approach is more appropriate in all predictions evaluated, unless in the case of the maximum, as md < 0.6, as pointed out by Da Silva Moraes et al. [49], for all approaches.

Three points not sampled in different regions of the state were chosen to verify if the estimates for these locations are within the mean error margin of the OK and COK models. For the city of Itaqui, located on the western border, considering the mean annual rainfall between January and December 2019, the model underestimated the rainfall by 4.05 and 2.04 mm. In same way, for the city located in the south of the state, Jaguarão, the observed rainfall refers to the period from 2019, was underestimated at 2.59 mm (OK) and 2.49 mm (COK). Federico Westphalen at the north at 7.86 mm (OK) and 10.11 mm (COK). In this case, both models slight overestimate the mean annual rainfall (Table 4).

Table 4 Annual mean rainfall estimates by ordinary Kriging (OK) and co-ordinary Kriging (COK) for non-sampled points in Rio Grande do Sul state, Brazil, to the period from January 2018 to December 2020 at Jaguarão, Frederico Westphalen and Itaqui
Full size table

The annual maximum rainfall analysis presented high values for the MSE (Table 3). The lowest result for MSE was obtained using the IDW method using 50% of the data set equivalent to the nine points closest to the estimated point. The RMSE expresses the error in the same proportion of the variable. Thus, the best fit presented an average error of 85.37 mm of rainfall. The low values for the coefficient of determination (R2) are direct results of the MSE values and, at most, can explain 0.2295 of the rainfall that occurred.

Since R2 values are far below 0.7, it is clear that the models do not apply to maximum values. These values can be approached by other probability distributions that are not considered in this work (Table 3). It should be noted that since Fig. 4 does not provide an indicative trend for maximum rainfall in the direction of latitude or longitude, we did not perform the universal Kriging for this variable. These results may be associated with the inherent difficulties in the process of forecasting extreme values. Ferro [50] points out that, due to the extreme values being at the tail of the distribution, there is a difficulty in verifying the forecast of these events, as this fact causes only a small number of events to be observed and this generates great variation in the verification measures and, therefore, great uncertainty about the quality of the forecast. More information must be incorporated into the modeling To reduce this uncertainty, as highlighted by Cox et al. [51]. When discussing some theoretical and practical aspects in the analysis of extreme values related to torrential rainfalls and floods, they concluded that, in order to obtain more accurate and reliable estimates, are needed models that take into account as much information as possible, such as trend, dispersion and temporal and spatial dependence.

The Kriging model with the fitted semivariograms used was satisfactory for the mean and median rainfall. We can then test this model for other variables using algorithms that simulate their behavior in the same sample space of this study, thus determining the level of robustness or evidencing the sensitivity of the model to the different sample situations.

Monte Carlo method is used to simulate different scenarios to evaluate the interpolators' behavior before a new data set is introduced, as mentioned in Sect. 2.3. The simulation results (Table 5) point out that the Gaussian random field for the OK presented greater accuracy and precision for all sets of simulated samples. This greater accuracy and precision provide to be robust when submitted to a different data set from which it was modeled.

Table 5 Monte Carlo simulation results for scenario 1, best results for the methods, ordinary Kriging (OK) and inverse distance weighted (IDW), with random field generated under the assumption of spatial dependence by the Gaussian semivariogram, nugget C0 = 40.07, contribution C = 2065.703 and range a = 7.623926, in different sample sizes N. In similar way, scenario 2, from Monte Carlo simulation for the best results of the methods, ordinary Kriging (OK) and inverse of the weighted distance (IDW), with random field generated in the assumption of spatial dependence by the exponential semivariogram, nugget C0 = 1 contribution C = 0 and range a = 0.1, in different sample sizes N. The results are in terms of mean squared error (MSE) and square root mean squared error (RMSE). In both scenarios, 50% of the data set was considered for calculating the MSE and RMSE
Full size table

Random fields were generated under the hypothesis of an Exponential random field with parameters C0, C and chosen randomly to analyze the interpolators' behavior when submitted to scenario 2. The results of Table 5 show that with the lowest number of samples, 100 observations, the IDW method presented better performance, being more accurate, since it presented lower Monte Carlo mean of the MSE, and more accurate, with lower standard deviation Monte Carlo of the MSE, that the ordinary Kriging. For the other sample sizes, this result did not maintain. Therefore, Kriging is the most accurate and precise.

As for computational efficiency, in a laptop computer core i7 CPU, 2.2 GHz, 8 GB RAM, the execution time for 1 simulation by ordinary Kriging using the parameters established in Table 5 for N = 750 was 48.3 s considering 50% of the data set to perform spatial estimates. Considering 100% of the data set, the time was 99.64 s. We can see that time has practically doubled. Regarding our application, the computation time was approximately 0.2 s considering 50% of the data set and 0.26 s considering 100% of data set.

4 Discussion

For Marcuzzo et al. [31] the formation of islands is a feature of the IDW and are formed because as the distance between the interpolated point and the sampling point tends to zero, the weight attributed to the influence of the sampled point on the interpolated tends to infinity thus points esteemed many close to an observed suffer influence practically only of him. However, among classic interpolators, it cannot be said that this is the best among them, as shown by Lyra et al. [15] with the use of splines. Still, there may be situations in which the IDW may perform better, as pointed out by Qiao et al. [52], in the study of maximum and minimum concentrations of heavy metals in the ground. Lu and Wong [53] when studying rainfall data for Taiwan, and because the data are limited to support Kriging (such as problems with the spatial correlation structure), IDW was shown to be a logical and viable alternative.

Interpolators require the number of points as a hyper-parameter to calculate spatial estimates. As shown in Table 2, the ideal number of points to estimate the average using ordinary Kriging corresponds to 50% of the data set. In large data sets, reducing data to make estimates is an important concern from a computational perspective. Geostatistical methods based on machine learning are considered in some situations [54,55,56,57]. However, in these studies, this parameter has not been explored.

Carvalho et al. [58] concluded in their study that the weighted least squares method allows the estimation of model parameters with greater precision. This greater precision reflects in the smallest sum squared residuals, as occurred in the present study. Hatvani et al. [59] used geostatistics resources to predict isoscape areas, consisting of water isotopes preserved in ice bodies in Antarctica. They concluded that the range parameter of the adjusted Gaussian semivariogram estimated that the area of influence of the referred isotopes is 350 km. In our paper, this semivariogram showed the most negligible sums of squares of the residuals.

Medeiros et al. [60] point out that universal Kriging was the one with the lowest prediction error being the most appropriate for the region of the state of Rio Grande do Norte. It should be noted that these authors make a uniquely visual analysis of the Kriging and Kriging variance maps to arrive at this conclusion.

For Lundgren et al. [61], cross-validation provides estimates of errors consistent with genuine errors in irregularly spaced samples, and when R2 ≥ 0.7 can be used as the determinant of the best number of points. Several studies show that IDW performed worse than geostatistical methods [62, 63]. Cross-validation is widely used to assess the quality of the geostatistical and classical method and simulation studies are rare. In the present work, in addition to the one done with cross-validation, we present simulation results and show the consistency of our results.

More complex models of Kriging can be considered when, for example, variables cause some trend in the spatially dependent variable, as reported Collardos-Lara et al. [45], who used regression Kriging and external drift Kriging to relate rainfall to elevation. The latter, also known as universal Kriging, was also used in the work of Lado et al. [64], who found slightly better results than ordinary Kriging in terms of RMSE in the analysis of the concentration of heavy metals in the soil. Kizza [65] used two interpolation methods were used for generating the gridded rainfall dataset and the universal Kriging method performed slightly better than the inverse distance weighting method. However, there is no guarantee that modeling external drift can increase the accuracy of rainfall estimates [66]. Furthermore, for Haberlandt [67], the extra value of a variable's information, such as elevation, can be influenced by the time interval and the type of rainfall considered. In multivariate analysis, data obtained from satellites as an additional variable have greater relevance. Our results indicate an advantage for ordinary and co-ordinary Kriging.

Co-Kriging is a viable method to be applied. However, there is no guarantee that the results in terms of RMSE will be better than those achieved by ordinary Kriging [62, 68]. Many applications have been used to improve the accuracy of expensive-to-measure properties (sparsely sampled) using one or more spatially interdependent, cheaper-to-measure properties. This is because the benefits of co Kriging are maximized when the secondary data are related to the primary data and the amount of secondary data is considerably larger than the primary data. In this respect, remotely sensed data provide cheap, intensively sampled spatial information for use with this technique. According to Cunha et al. [46], the improvement in the prediction accuracy is conditioned to the covariate to be used and they verified that the altitude allows better performance of the interpolation by co-Kriging of the rainfall than the distance from the sea. Slightly better results with co-Kriging were also found by Hoshmand & Delghandi [69], but note that ordinary Kriging can also be used to estimate water salinity parameters. Our results indicate that using altitude as a covariate has brought about a substantial improvement in the annual rainfall accuracy for the mean, median and maximum, corroborating with studies by Ma et al. [70], who, by using altitude as a covariate, reduced errors in the generation of rainfall grid in the Tibetan Plateau (TP). However, even with the best global indicators of fit quality point out that the geostatistical methods considered and classic are not suitable in the study of maximum annual rainfall. Possibly, for situations involving maximums, methods for analyzing extreme events are more suitable [71, 72].

Our application is a small size data set because it is longitudinal records, so computing time is relatively short. In the simulation studies, we observed that larger sample sizes demand more computation time, which was already expected, and that using half of the data provides results as good as the whole. In addition, more complex models and large data sets, such as big data, pose a challenge concerning modeling (Gárate-Escamilla, El Hassani, and Andres [73]; Das et al. [17]).

We can make a point regarding missing data. We decided to work with original data and not to embed artificial data since we have a long series of data for each weather station. Given the objective of the work and part of the results, it is evident the importance of considering statistics when analyzing climatological data. It is possible to verify that the models used managed, in a certain way, to capture the behavior of the series, since the margin of error was low and variable depending on the year (Table 4). This study may have ramifications such as those carried out by Barrios, Trincado, and Garreaud [74] in monthly precipitation records and Aieb et al. [75] to daily rainfall considering data imputation methods such as an artificial neural network (ANN), multiple linear regression (MLR), among others.

All Kriging techniques use ordinary Kriging as opposed to simple Kriging because of the underlying assumption made that the rainfall process is stationary only within local neighborhoods, and hence, the mean's population is unknown [68]. For this reason, we prefer not to address simple Kriging. On the other hand, we explore the number of neighboring points that must be used to make spatial estimates. We found the surprising result that it is not necessary to use the entire data set to obtain accurate spatial estimates, which in none of the papers presented was discussed. It should be noted that, as presented, there are many other promising methodologies for spatial analysis and that we do not address in this paper. Issues such as simulation of random fields with the presence of external and / or covariable drift are not well established at the moment but constitute possibilities for future work. Thus, the simulation results of this work are restricted to the absence of external or secondary influence, as shown in Table 5.

5 Conclusions

The geostatistical method was the one that best represented the spatial distribution of the annual rainfall in the state of Rio Grande do Sul with the estimates that were closer to those observed. Minimum error for non-sampled point was 2.04 mm.

For the mean, Kriging methods presented the slightest mean square error using only nine points (50% of the dataset) for the calculus, representing a decrease in the computational cost. Our results indicate that using altitude as a covariate has brought about a substantial improvement the mean, median and maximum annual rainfall accuracy. Among the Kriging methods, co-ordinary Kriging resulted in the best goodness of fit indicators, which indicates that the inclusion of the altitude covariate increased the accuracy of the predictions. If this information were not available, ordinary Kriging would still be a viable method to be applied. Our results points out those conventional Kriging methods are not suitable when analyzing maximum rainfall events. For situations that involves maximum events (or extreme events), methods for modeling extreme events could be considered.

The simulation results show that Kriging is the interpolator with the highest degree of reliability in the annual rainfall estimates according to the scenarios evaluated. Sample sizes greater than 500 points and using 50% of the data set indicate that both MSE and RMSE tend to stabilize. The spatial interpolators methods used in this study were not suitable for analysis of maximum annual rainfall data.