1 Introduction

For a range of decades, MHD has been handled to quest the Arcanum of unknown astrophysical and geophysical cruxes. The investigation on thermal diffusion effects of MHD flows is fruitful since thermal impermanence has large scale importance in separation processes, in nature, in chemical operations, and various industrial processes. The induced magnetic field and thermal radiation have important applications in several biomedical and medical fields. MHD flows have umpteen effective applications in the field of power generation, biomechanics processes, and aerodynamics, etc. A significant number of engineering problems are concerned with thermally radiating flows such as glass production, design of the furnace, and propulsion procedures. Chemical processing industries have many operative uses of heat transfer and mass transfer phenomena.

A well-deliberated thought was developed by Soundalgekar and Pop [1] on the approximate solutions of the mean and fluctuating flow with viscous dissipation. The skin friction phase with amplitude has also been enquired through the research work. Influences of Hall current on flow due to natural convection with a boundary of the infinitely oriented plate were analyzed by Ram [2]. With a negligible assumption of the Joule heating term, they found similar results for velocity with Raptis et al. [3] for steady motion. The concept of this study varied with the angle between the transverse magnetic field and vertical direction. Frictional heating effect along with heat generation/absorption in heat transfer flow with PST and PHF cases by concerning suction/blowing velocity was carried out by Vajaravelu and Hadjinicolaou [4]. In this inspection, Kumer’s functions have been employed to enumerate temperature and heat transfer rates. They observed that for smaller estimations of the Prandtl number, the type of BL solutions may not happen. Labroopulu et al. [5] studied the oblique flow adopting suction or blowing, and it is also noticed that the fluid penetration occurred for the causation of suction while blowing shifted the stagnation point. El-Hakim [6] reckoned unsteady non-scattering gray fluid flow with the engagement of thermal radiation via a highly saturated porous medium. The surface absorbing velocity for the inquiry was uniform in magnitude and the velocity for outward BL has been assumed in a vibration about a constant estimation. Singh et al. [7] employed a perturbation technique in the analysis of MHD vertical flow by adopting fluctuating permeability of porous medium and suction. Chen [8] deliberated the MHD vertical flow problem for the reveal of dissipative and Ohmic heating impacts through a conducting fluid by the employment of implicit FDM. This study concluded a decrement in all the embedded physical quantities due to the introduction of the magnetic field. Zhang et al. [9] established the DTM-BF solutions for Cu, Al2O3, and Ag nanoparticles based flow of MHD heat transfer and radiating fluid by incorporating the single order chemical reaction and varying nature surface flux for heat. They found a close agreement of their DTM-BF based results with the numerical results which have mentioned in the same study. Reddy et al. [10] numerically investigated the situation of both the homogenous-heterogeneous chemical reaction-based MHD flow under the controlling of nonlinear type thermal radiation. The rising tendency of the temperature, i.e. thermal BL has been checked with the hiking variations of nonlinear radiation, also the fluid concentration has been affected significantly for the assumption of homogenous-heterogeneous reaction. Reddy [11] had taken an endeavor to analyze the three-dimensional unsteady MHD flow phenomena with Hall current by taking suction flow velocity under an impulsively moving infinite plate. A Galerkin’s FEM has been employed for the numerical estimations of the flow equations where the author marked retardation in flow velocity with rotational parameter whereas Hall current causes acceleration to flow velocity. Iva et al. [12] took an endeavor to analyze the BL heat source and suction-based flow of MHD fluid with a rotating system under the influence of the Hall effect. This study was dealt with FDM solving structure with time-domain consideration, i.e. for the unsteady solutions. They alluded that, with the development of time, all the basic profiles are increasing in features. Kafoussias et al. [13] and Alam et al. [14] numerically computed the impacts of Dufour and Soret numbers on MHD flow with or without suction. Alam et al. [15] executed a substantial numerical inquiry on MHD mixed convective flow with the appearance of magnetic field induction along with the Soret effect. Specifically, this study was a take on regular fluids e.g. water and air along with some regular diffusing mass species by the choice of Schmidt number. Raju et al. [16] have taken varying suction velocity criteria to understand the MHD flow nature of radiationally responding fluid by the assumption of thermal diffusion occurrence. An exponential and small perturbation law was considered to govern free stream velocity. They decided on an increment in the fluid velocity with the Soret number and Grashof number of thermal buoyancy term. An efficient study was conducted by Das et al. [17] on the heat source effects of conducting MHD flow with porosity by involving fluctuating natured permeability over time and oscillatory suction. The key remarks of this perturbation technique based study were the observation of deceleration of velocity with diffusing Schmidt number and magnetic parameter while the acceleration happened for buoyancy mass and heat transfer parameters, the medium porosity term, and heat source parameter. Shamshuddin et al. [18] researched the non-linear type of steady flow of micropolar radiating fluid by considering the inclusion of a heat source/sink inside the BL. The increasing estimations of suction/injection parameters are the factor to the causation of decrement in velocity and the microrotation of the micropolar fluid of interest while the electric field occurred increment in velocity. Jha et al. [19] analyzed the steady-state flow behavior through a vertical channel with thermal radiation by employing a numerical procedure. They found a proportionality relation to achieve a steady-state situation with the Prandtl number. The analysis on the influences of the cross magnetic field on micropolar fluid flow wielded in the inner zone circumscribed by two vertically oriented porous plates has been done by Umavathi et al. [20]. The DTM method based solutions have also been verified for accuracy by the numerical procedure of RKSM and trusted compliance was found among them. They found that for both the suction and injection cases, a diminution occurred for skin friction and couple stress with the rise of micropolar fluid term and magnetic parameter. The steady-state MHD flow of fluid with suction/injection was analyzed by Verma and Gupta [21]. This study is concerned with the Brinkman equation-based flow with suction and injection.

Space science, liquid metals, and high-temperature plasmas are significantly controlled in many situations by the radiation effects. Polymer processing sectors are depending sometimes on heat transfer involving thermal radiation to ensure a fine quality of produced products. Despite being so effective, a little knowledge is gathered on thermal radiation. Keeping the importance of thermal radiation in mind, the repercussions of radiative heat flux on MHD flow has been analyzed in different circumstances on different fluids behavior by refs. [22,23,24,25,26,27,28,29].

Majeed et al. [30] addressed the multiple slips on the MHD flow by the incorporation of numerical simulation along with activation energy. Their observation concluded retardation in the fluid velocity due to the hiking of porosity parameter and magnetic parameter. The numerical procedure on the MHD cooling problem with the involvement of the magnetic induction profile was computed by Islam et al. [31]. Recently, Mollah et al. [32] substantially conducted a numerical investigation on channel flow of Bingham fluid with MHD phenomena. Several flow structures of Casson fluid and/or Walters’-B fluid model have been analyzed with or without the employment of fractional derivatives of Caputo-Fabrizio type in refs. [33,34,35]. Deep investigations with perturbation techniques have been performed to quest the effects of Joule heating, Soret number by employing Hall currents on MHD rotating flow by Veera Krishna et al. [36]. Ellahi et al. [37] dealt with the flow of nanofluids for an electro-osmotic field to establish an innovative model. They observed a decrement in the velocity estimations under the influence of magnetic parameter while the temperature went through an increasing estimation. Islam and Islam [38] established the MHD micropolar flow criteria over a porous wedge, which is stretching in nature by applying the iteration procedure of Natcheim-Swigert type with Joule heating force. Hasan et al. [39] noticed an interaction between the steady solutions and the secondary flow on their investigations about the heat transfer flow. Several substantial types of research have been performed recently on the criteria of induced magnetic field on several different flow nature estimations some are worth mentioning, refs. [40,41,42,43,44].

The above literature represents several studies on the MHD flow of different fluids with or without induced magnetic field. Pondering the importance of thermal radiation and induced magnetic field in different field of applied sciences, a new investigation is presented on the steady-state solution of unsteady MHD viscous incompressible radiating and conducting fluid flow wielded over an infinite vertical plate with the involvement of thermal diffusion, constant suction, and induced magnetic field by taking constant heat and mass fluxes into account. After completing the mathematical model establishment, the system of PDEs is gone through further simplification under usual transformations and, then the new retrieved system is solved numerically. Necessary mechanical descriptions of the BL flow structures have been given through plots by discussing relevant embedded parameters physically.

2 Physical model

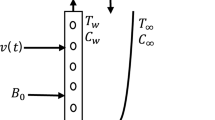
The numerical solution for viscous, electrically conducting, incompressible, and radiating optically thin MHD heat and mass transfer flow past an electrically non-conducting infinite plate of vertical orientation with the engagement of exalted concentration of mass of foreign type has been determined. The fluid is driven under the governance of constant suction velocity and viscous dissipation. The wall heat and concentration mass fluxes are respectively taken as \(\left( { - \kappa \frac{{\partial \tilde{T}}}{{\partial \tilde{y}}}} \right) = q_{f}\) and \(\left( { - D_{m} \frac{{\partial \tilde{C}}}{{\partial \tilde{y}}}} \right) = \Gamma_{f}\), as in Alam et al. [15]. The orientation of the \(\tilde{x}\)-axis is planned in the plate direction, and the \(\tilde{y}\)-axis is occupied a normal direction to it.

A magnetic field is applied in 90ο alignment on the plate. Let \(\tilde{H}_{{\tilde{x}}}\) and \(\tilde{H}_{{\tilde{y}}}\) be the components of the induced magnetic field in \(\tilde{x}\) and \(\tilde{y}\) directions respectively. Dufour and Soret impacts are taken into account by the assumption that the foreign mass concentration is high enough. Considering, the temperature and solute concentration of the fluid as \(\tilde{T}\) and \(\tilde{C}\) whereas the uniform temperature of the free stream is \(\tilde{T}_{\infty }\); the uniform concentration of the free stream is \(\tilde{C}_{\infty }\). Due to the consideration of infinite plate, the quantity \(\frac{{\partial \tilde{u}}}{{\partial \tilde{x}}} = 0\) and thus the continuity equation becomes \(\frac{{\partial \tilde{v}}}{{\partial \tilde{y}}} = 0\) i.e. \(\tilde{v} = - v_{0}\) (constant). The thermal radiation is used in a form that can be approximated under the Rosseland approximation [45] of radiative heat flux with Taylor series expansion. The whole system of flow mechanism is represented in Fig. 1. with respective coordinates.

Fig. 1
figure 1

Schematic model and flow coordinates

Full size image

Under these assumptions that are narrated above, the achievement of the governing equations with appropriate BL approximations are ([15, 46]):

2.1 The continuity equation

$$\tilde{v} = - v_{0} = {\text{constant}}$$
(1)

2.2 The momentum equation

$$\left\{ \begin{gathered} \frac{{\partial \tilde{u}}}{{\partial \tilde{t}}} - v_{0} \frac{{\partial \tilde{u}}}{{\partial \tilde{y}}} = \upsilon \frac{{\partial^{2} \tilde{u}}}{{\partial \tilde{y}^{2} }} + g\beta (\tilde{T} - \tilde{T}_{\infty } ) + g\beta^{*} (\tilde{C} - \tilde{C}_{\infty } ) \hfill \\ \, + \frac{{\mu_{e} }}{\rho }\tilde{H}_{0} \frac{{\partial \tilde{H}_{{\tilde{x}}} }}{{\partial \tilde{y}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered} \right\}$$
(2)

2.3 The magnetic induction equation

$$\frac{{\partial \tilde{H}_{{\tilde{x}}} }}{{\partial \tilde{t}\,}} - v_{0} \frac{{\partial \tilde{H}_{{\tilde{x}}} }}{{\partial \tilde{y}}} = \tilde{H}_{0} \frac{{\partial \tilde{u}}}{{\partial \tilde{y}}} + \frac{1}{{\sigma \mu_{e} }}\frac{{\partial^{2} \tilde{H}_{{\tilde{x}}} }}{{\partial \tilde{y}^{2} }}$$
(3)

2.4 The energy equation

$$\left\{ \begin{gathered} \frac{{\partial \tilde{T}}}{{\partial \tilde{t}\,}} - v_{0} \frac{{\partial \tilde{T}}}{{\partial \tilde{y}}} = \frac{\kappa }{{\rho C_{p} }}\frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{y}^{2} }} + \frac{1}{{\rho C_{p} \sigma }}\left( {\frac{{\partial \tilde{H}_{{\tilde{x}}} }}{{\partial \tilde{y}}}} \right)^{2} \hfill \\ + \frac{\upsilon }{{C_{p} }}\left( {\frac{{\partial \tilde{u}}}{{\partial \tilde{y}}}} \right)^{2} + \frac{{D_{m} k_{{\tilde{T}}} }}{{C_{s} C_{p} }}\frac{{\partial^{2} \tilde{C}}}{{\partial \tilde{y}^{2} }}{ + }\frac{{16\sigma^{ * } \tilde{T}_{\infty }^{3} }}{{3k^{ * } \rho C_{p} }}\frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{y}^{2} }} \,\,\,\,\hfill \\ \end{gathered} \right\}$$
(4)

2.5 The concentration equation

$$\frac{{\partial \tilde{C}}}{{\partial \tilde{t}\,}} - v_{0} \frac{{\partial \tilde{C}}}{{\partial \tilde{y}}} = D_{m} \frac{{\partial^{2} \tilde{C}}}{{\partial \tilde{y}^{2} }} + \frac{{D_{m} k_{{\tilde{T}}} }}{{\tilde{T}_{m} }}\frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{y}^{2} }}$$
(5)

The corresponding initial and boundary settings for the flow scheme are:

$$\left\{ {\tilde{t} \le 0: \, \tilde{u} = 0, \, \tilde{H}_{{\tilde{x}}} = 0, \, \tilde{T} \to \tilde{T}_{\infty } , \, \tilde{C} \to \tilde{C}_{\infty } {\text{ everywhere}}} \,\,\,\right\}$$
(6)
$$\left\{ \begin{gathered} \tilde{t} > 0:\, \tilde{u} = 0, \, \tilde{H}_{{\tilde{x}}} = \tilde{H}_{w} , \, \frac{{\partial \tilde{T}}}{{\partial \tilde{y}}} = - \frac{{q_{f} }}{\kappa }, \, \frac{{\partial \tilde{C}}}{{\partial \tilde{y}}} = - \frac{{\Gamma_{f} }}{{D_{m} }},{\text{ at }}\tilde{y} = 0; \\\hfill \hfill\hfill \,\tilde{u} = 0, \,\, \tilde{H}_{{\tilde{x}}} = 0, \,\, \tilde{T} \to \tilde{T}_{\infty } , \,\, \tilde{C} \to \tilde{C}_{\infty } ,\,{\text{ at }}\tilde{y} \to \infty ; \,\,\,\,\,\,\hfill \\ \end{gathered} \right\}$$
(7)

To ensure a dimensional agreement through the governing equations, a set of non-dimensional variables have been used and those are:

$$\left\{ \begin{gathered} t = \frac{{\upsilon \tilde{t}}}{{L^{2} }},x = \frac{{\tilde{x}}}{L},y = \frac{{\tilde{y}}}{L},u = \frac{{\tilde{u}L}}{\upsilon },T = \frac{{\tilde{T} - \tilde{T}_{\infty } }}{{\frac{{q_{f} L}}{\kappa }}}, \\\hfill C = \frac{{\tilde{C} - \tilde{C}_{\infty } }}{{\frac{{\Gamma_{f} L}}{{D_{m} }}}},H_{x} = \sqrt {\frac{{\mu_{e} }}{\rho }} \frac{{\tilde{H}_{{\tilde{x}}} L}}{\upsilon } \hfill\hfill \\ \end{gathered} \right\}$$
(8)

With the help of the above non-dimensional assumptions, the governing Eqs. (1)–(5) can be converted into non-linear PDEs as in the following equations:

$$\frac{\partial u}{{\partial t\,}} - S\frac{\partial u}{{\partial y}} = \frac{{\partial^{2} u}}{{\partial y^{2} }} + T + C + M\frac{{\partial H_{x} }}{\partial y}$$
(9)
$$\frac{{\partial H_{x} }}{\partial t\,} - S\frac{{\partial H_{x} }}{\partial y} = M\frac{\partial u}{{\partial y}} + P_{m} \frac{{\partial^{2} H_{x} }}{{\partial y^{2} }}$$
(10)
$$\left\{ \begin{gathered} \frac{\partial T}{{\partial t}} - S\frac{\partial T}{{\partial y}} = \left( {\frac{{1 + R^{*} }}{{P_{r} }}} \right)\frac{{\partial^{2} T}}{{\partial y^{2} }} + E_{c} P_{m} \left( {\frac{{\partial H_{x} }}{\partial y}} \right)^{2} \\\hfill\hfill\hfill \,\,\,\,\,\,+ \,E_{c} \left( {\frac{\partial u}{{\partial y}}} \right)^{2}\, + \,D_{u} \frac{{\partial^{2} C}}{{\partial y^{2} }} \hfill \,\,\,\,\,\,\,\,\, \end{gathered} \right\}$$
(11)
$$\frac{\partial C}{{\partial t}} - S\frac{\partial C}{{\partial y}} = \frac{1}{{S_{c} }}\frac{{\partial^{2} C}}{{\partial y^{2} }} + S_{o} \frac{{\partial^{2} T}}{{\partial y^{2} }}$$
(12)

The non-dimensional process requires that the characteristic length \(L\) can be taken as:

$$L = \left( {\frac{{\upsilon^{2} }}{{g\beta \left( {\frac{{q_{f} }}{\kappa }} \right)}}} \right)^{\frac{1}{4}} = \left( {\frac{{\upsilon^{2} }}{{g\beta^{*} \left( {\frac{{\Gamma_{f} }}{{D_{m} }}} \right)}}} \right)^{\frac{1}{4}}$$
(13)

The respective settings for dimensionless initial and boundary conditions are:

$$\left\{ {t \le 0: \, u = 0, \, H_{x} = 0, \, T \to 0, \, C \to 0{\text{ everywhere}}} \,\right\}$$
(14)
$$\left\{ \begin{gathered} t > 0:u = 0, \, H_{x} = d = 1, \, \frac{\partial T}{{\partial y}} = - 1, \, \frac{\partial C}{{\partial y}} = - 1,{\text{ at }}y = 0; \\\,\, u = 0, \, H_{x} = 0, \, T \to 0, \, C \to 0,{\text{ at }}y \to \infty ; \hfill \\ \end{gathered} \right\}$$
(15)

where \(d = \frac{{\tilde{H}_{w} L}}{\upsilon }\sqrt {\frac{{\mu_{e} }}{\rho }}\) (say), \(S = \frac{{v_{0} L}}{\upsilon }\) (suction parameter), \(M = \frac{{\tilde{H}_{0} L}}{\upsilon }\sqrt {\frac{{\mu_{e} }}{\rho }}\) (magnetic parameter), \(P_{m} = \frac{1}{{\upsilon \sigma \mu_{e} }}\) (magnetic Prandtl number), \(P_{r} = \frac{{\upsilon c_{p} \rho }}{\kappa }\) (Prandtl number), \(R^{*} = \frac{{16\sigma^{*} \tilde{T}^{3}_{\infty } }}{{3\kappa k^{*} }}\) (radiation parameter), \(E_{c} = \frac{{\upsilon^{2} }}{{C_{p} \left( {\frac{{q_{f} L}}{\kappa }} \right)L^{2} }}\) (Eckert number),\(D_{u} = \frac{{D_{m} k_{{\tilde{T}}} \left( {\frac{{\Gamma_{f} L}}{{D_{m} }}} \right)}}{{\upsilon C_{s} C_{p} \left( {\frac{{q_{f} L}}{\kappa }} \right)}}\) (Dufour number), \(S_{c} = \frac{\upsilon }{{D_{m} }}\) (Schmidt number) and \(S_{o} = \frac{{D_{m} k_{{\tilde{T}}} \left( {\frac{{q_{f} L}}{\kappa }} \right)}}{{\upsilon \tilde{T}_{m} \left( {\frac{{\Gamma_{f} L}}{{D_{m} }}} \right)}}\) (Soret number).

3 Declaration of quantities of engineering curiosity

Shear stress and current density are the physically exigent quantities of engineering necessity. The shear stress (skin friction coefficient) features the layer of the fluid vicinity to the plate. The dimensional form of the local shear stress at the plate is, \(\tau = \mu \left( {\frac{{\partial \tilde{u}}}{{\partial \tilde{y}}}} \right)_{{\tilde{y} = 0}}\) and the dimensional form of the local current density is, \(J = - \left( {\frac{{\partial \tilde{H}_{{\tilde{x}}} }}{{\partial \tilde{y}}}} \right)_{{\tilde{y} = 0}}\). where \(\mu\) is the dynamic viscosity of the governing fluid. In the dimensionless form, the local shear stress and local current density expose relation as \(\tau_{L} = \left( {\frac{\partial u}{{\partial y}}} \right)_{y = 0}\) and \(J_{L} = - \left( {\frac{{\partial H_{x} }}{\partial y}} \right)_{y = 0}\) respectively.

4 Computational technique

This section is basically for a brief understanding of the explicit FDM solution [12] operation on the regulatory Eqs. (9) to (12). The flow regime is furcated into some grid of lines normal to the \(y\)-direction. This furcation leads us to have some simultaneously discretized finite difference equations in both time and space. The BL flow region is discretized by using backward differencing for 1st order derivatives and central differencing for derivatives that have order more than one. Here an assumption has been made that the free stream region is occurred at \(y_{\max } \left( { = 20} \right)\). This is an arbitrary choice to identify the \(y \to \infty\) region i.e. free stream region. By trialing some random values of meshes, the estimation \(n = 400\) has been selected to execute the computation for numerical schemes. Visualization of this mesh space creation is presented in Fig. 2. Under the consideration of a wee time difference

Fig. 2
figure 2

Visualization of mesh layout

Full size image

\(\Delta t = 0.0001\), the constant mesh size in \(y\) direction is made as \(\Delta y = 0.05\left( {0 \le y \le 20} \right)\). Let \(u^{ * } ,\) \(H_{x}^{ * } ,\) \(T^{ * }\) and \(C^{ * }\) exhibit the values of \(u,\) \(H_{x} ,\) \(T,\) and \(C\) at the final time-step respectively. Incorporating the explicit FDM approach, a collection of discretized equations have been established as follows:

$$\left\{ \begin{gathered} \frac{{u_{j}^{ * } - u_{\,j} }}{\Delta t} - S\frac{{u_{j} - u_{\,j - 1} }}{\Delta y} = \frac{{u_{\,j + 1} - 2u_{j} + u_{j - 1} }}{{\left( {\Delta y} \right)^{2} }} + T_{j} + C_{j} \hfill \\ \, + M\frac{{H_{{x_{j} }} - H_{{x_{j - 1} }} }}{\Delta y} \hfill \\ \end{gathered} \right\}$$
(16)
$$\left\{ \begin{gathered} \frac{{H_{{x_{j} }}^{ * } - H_{{x_{j} }} }}{\Delta t} - S\frac{{H_{{x_{j} }} - H_{{x_{j - 1} }} }}{\Delta y} = M\frac{{u_{j} - u_{\,j - 1} }}{\Delta y} \hfill \\ \, + P_{m} \frac{{H_{{x_{j + 1} }} - 2H_{{x_{{_{\,j} }} }} + H_{{x_{j - 1} }} }}{{\left( {\Delta y} \right)^{2} }} \hfill \\ \end{gathered} \right\}$$
(17)
$$\left\{ \begin{gathered} \frac{{T_{{_{j} }}^{ * } - T_{j} }}{\Delta t} - S\frac{{T_{j} - T_{j - 1} }}{\Delta y} = \left( {\frac{{1 + R^{ * } }}{{P_{r} }}} \right)\frac{{T_{\,j + 1} - 2T_{j} + T_{j - 1} }}{{\left( {\Delta y} \right)^{2} }} \hfill \\ \, + E_{c} P_{m} \left( {\frac{{H_{{x_{j} }} - H_{{x_{j - 1} }} }}{\Delta y}} \right)^{2} + E_{c} \left( {\frac{{u_{j} - u_{\,j - 1} }}{\Delta y}} \right)^{2} \hfill \\ \, + D_{u} \frac{{C_{\,j + 1} - 2C_{j} + C_{j - 1} }}{{\left( {\Delta y} \right)^{2} }} \hfill \\ \end{gathered} \right\}$$
(18)
$$\left\{ \begin{gathered} \frac{{C_{{_{j} }}^{ * } - C_{j} }}{\Delta t} - S\frac{{C_{j} - C_{j - 1} }}{\Delta y} = \frac{1}{{S_{c} }}\frac{{C_{\,j + 1} - 2C_{j} + C_{j - 1} }}{{\left( {\Delta y} \right)^{2} }} \hfill \\ \, + S_{o} \frac{{T_{\,j + 1} - 2T_{j} + T_{j - 1} }}{{\left( {\Delta y} \right)^{2} }} \hfill \\ \end{gathered} \right\}$$
(19)

The FDM schemes generate the initial and boundary conditions as:

$$\left\{ {u_{j}^{0} = 0, \, H_{{x_{j} }}^{0} = 0, \, T_{j}^{0} \to 0, \, C_{j}^{0} \to 0{\text{ everywhere}}} \right\}$$
(20)
$$\left\{ \begin{gathered} \begin{gathered} u_{L}^{p} = 0,H_{{x_{L} }}^{p} = 1,\frac{{T_{L}^{p} - T_{L - 1}^{p} }}{\partial y} = - 1,\frac{{C_{L}^{p} - C_{L - 1}^{p} }}{\partial y} = - 1, \, {\text{ at L}} = 0; \\ \end{gathered} \\ u_{L}^{p} = 0,H_{{x_{L} }}^{p} = 0,T_{L}^{p} = 0,C_{L}^{p} = 0{\text{ at L}} \to \infty ; \hfill\hfill\hfill\hfill\hfill\hfill\hfill \\ \end{gathered} \right\}$$
(21)

The subscript notation \(j\) denotes the nodal points regarding \(y\) coordinate and the superscript notation \(p\) denotes a time iteration value where, \(t = p\Delta t\) with some integer values \(p = 0,1,2,3.........\)

5 Criteria of convergence

The general assumptions for the quantities \(u,\) \(H_{x} ,\) \(T,\) and \(C\) in terms of Fourier’s expansion [32] allow us to determine the converging and stable criteria for the solutions. The smaller time step and the mesh step values are the ingredients for the whole stability computational procedure. The converging restrictions for the FDM solution schemes are,

$$\frac{2\Delta t}{{\left( {\Delta y} \right)^{2} }} - S\frac{\Delta t}{{\Delta y}} \le 1$$
(22)
$$P_{m} \frac{2\Delta t}{{\left( {\Delta y} \right)^{2} }} - S\frac{\Delta t}{{\Delta y}} \le 1$$
(23)
$$\left( {\frac{{1 + R^{*} }}{{P_{r} }}} \right)\frac{2\Delta t}{{\left( {\Delta y} \right)^{2} }} - S\frac{\Delta t}{{\Delta y}} \le 1$$
(24)
$$\frac{1}{{S_{c} }}\frac{2\Delta t}{{\left( {\Delta y} \right)^{2} }} - S\frac{\Delta t}{{\Delta y}} \le 1$$
(25)

The values \(\Delta t = 0.0001\) and \(\Delta y = 0.05\) as well as the initial conditions generate the converging and stable constraints materially as \(S \ge - 484\) \(0.04 \le P_{m} \le 24\) \(0.07 \le P_{r} \le 30.50\) and \(S_{c} \ge 0.04\) with a smaller estimation of Eckert number as \(E_{c} = 0.01\).

6 Results with explications

The prevailing nonlinear PDEs for the Dufour and thermal diffusion effects on MHD heat and mass transfer dissipative and radiating fluid flow past an infinitely long vertical plate with the impact of an induced magnetic field have been solved numerically and the numerical computations are attained through the explicit FDM technique. The foremost formulated equations have been simplified by the utilization of competent BL assumptions and also normalized for calculations under non-dimensional analysis. An insight of the physical parameters have been demonstrated by understanding the effectiveness and significance of the magnetic parameter, Prandtl number, radiation parameter, magnetic Prandtl number, suction parameter, Dufour number, Eckert number, Schmidt number, and Soret number on velocity, induced magnetic field, thermal energy, and concentration outlines along with these analyses, the local current density, and local shear stress have also been reckoned and tabulated. The numerical computations are supported by the mesh and time sensitivity test. The graphical outputs for the numerical values have been graphed by using MATLAB R2015a and also verified with the aid of Studio Developer FORTRAN 6.6a. A comparative analysis of the referred results is shown in graphical and tabular form with published results.

6.1 Questing appropriate mesh

With the successive trials of several mesh sizes, appropriate mesh size is planned for the flow model inside the BL flow zone. Three of the trial values are \(n = 360,\) \(n = 400,\) and \(n = 440\). The approach is conducted in a trial and error manner, i.e. after using a trial, a valid variation is compared with the next trial assumption. The graphical output for this trial has been illustrated in Fig. 3(a, b) for velocity and induced magnetic field with the parameters as \(S = 1.30,\) \(M = 1.00,\) \(P_{m} = 2.00,\) \(P_{r} = 0.71,\) \(R^{ * } = 0.20,\) \(D_{u} = 0.50,\) \(S_{o} = 0.20,\) \(E_{c} = 0.01\) and \(S_{c} = 0.60\) at time \(t = 60\)(steady-state). Exposure of the sleekness and converging nature of the reported graphs leads us to come to a decision that the mesh size \(n = 400\) can be considered for the numerical calculations.

Fig. 3
figure 3

Justification of meshes for (a) velocity; (b) induced magnetic field

Full size image

6.2 Questing steady-state

With the successive trials of several time values, a steady-state situation is gained for the flow model equations. The steady-state calculations for velocity, induced magnetic field, temperature, and concentration for the time estimations \(t = 10,20,30,40,50,60,70\) and \(80\) are presented in Fig. 4(a, b, c, d), with \(S = 1.30,\) \(M = 1.00,\) \(P_{m} = 2.00,\) \(P_{r} = 0.71,\) \(R^{ * } = 0.20,\) \(D_{u} = 0.50,\) \(S_{o} = 0.20,\) \(E_{c} = 0.01\) and \(S_{c} = 0.60\). Now precise observations show that the temperature and concentration profiles express minor variation after \(t = 10\) while magnetic field induction and velocity profiles express minor change after \(t = 40\). The concentration and temperature exhibit almost ineffective variations immediately after \(t = 20\), likewise the ineffective variation for the induced magnetic field and velocity profiles are confirmed after \(t = 60\). Analyzing this status, the time value \(t = 60\) has been thought of as a materialistic steady-state for all the mentioning profiles. The steady-state behavior for temperature and concentration is substantially rapid than velocity and induced magnetic field.

Fig. 4
figure 4

Justification of steady-state for (a) velocity; (b) induced magnetic field; (c) temperature and (d) concentration

Full size image

6.3 Verification of codes via different simulation tools

The repercussion of the velocity profile under the suction parameter \(\left( S \right)\) is computed through MATLAB R2015a and Studio Developer FORTRAN 6.6a. The consequences for both the simulation tools are identical, which assures the exactitude of the numerical computations. This experimentation has been illustrated through Fig. 5(a, b), with \(S = 1.30,\) \(M = 1.00,\) \(P_{m} = 2.00,\) \(P_{r} = 0.71,\) \(R^{ * } = 0.20,\) \(D_{u} = 0.50,\) \(S_{o} = 0.20,\) \(E_{c} = 0.01\) and \(S_{c} = 0.60\) at time \(t = 60\)(steady-state).

Fig. 5
figure 5

Justification of codes with the suction parameter \(\left( S \right)\) for (a) velocity in MATLAB R2015a; (b) velocity in Studio Developer FORTRAN 6.6a

Full size image

6.4 Verification of codes with published result

Excellent agreement has been found between the published result of Pandit et al. [47] and the present result. The comparing output has been depicted in Fig. 6(a, b). This comparison has been carried out by the impact of time on concentration inside the BL.

Fig. 6
figure 6

Time variation for concentration in (a) present study; (b) Pandit et al. [47]

Full size image

6.5 Effects of parameters

For the purpose of digging out the physical insight of the flow scheme, the varying estimations of various pertinent parameters such as magnetic parameter \(\left( M \right)\), Prandtl number \(\left( {P_{r} } \right)\), radiation parameter \(\left( {R^{ * } } \right)\), magnetic Prandtl number \(\left( {P_{m} } \right)\), suction parameter \(\left( S \right)\), Dufour number \(\left( {D_{u} } \right)\), Eckert number \(\left( {E_{c} } \right)\), Schmidt number \(\left( {S_{c} } \right)\), and Soret number \(\left( {S_{o} } \right)\) on velocity, induced magnetic field, thermal energy, and concentration outlines along with the local current density and local shear stress have been reckoned, graphed and/or tabulated through Figs. 6, 7, 8, 9, 10 and 11 and Table 1 with a common assumption of

Fig. 7
figure 7

Features of velocity for (a) suction parameter \(\left( S \right)\); (b) magnetic parameter \(\left( M \right)\)

Full size image
Fig. 8
figure 8

Features of velocity for (a) Prandtl number \(\left( {P_{r} } \right)\); (b) magnetic Prandtl number \(\left( {P_{m} } \right)\); (c) radiation parameter \(\left( {R^{ * } } \right)\) and (d) Soret number \(\left( {S_{o} } \right)\)

Full size image
Fig. 9
figure 9

Features of the induced magnetic field for (a) suction parameter \(\left( S \right)\) and (b) magnetic parameter \(\left( M \right)\)

Full size image
Fig. 10
figure 10

Features of induced magnetic field for (a) Prandtl number \(\left( {P_{r} } \right)\); (b) magnetic Prandtl number \(\left( {P_{m} } \right)\); (c) radiation parameter \(\left( {R^{ * } } \right)\) and (d) Eckert number  \(\left( {E_{c} } \right)\)

Full size image
Fig. 11
figure 11

Features of temperature field for (a) suction parameter \(\left( S \right)\); (b) Prandtl number \(\left( {P_{r} } \right)\); (c) radiation parameter \(\left( {R^{ * } } \right)\); (d) Eckert number \(\left( {E_{c} } \right)\); (e) Dufour number \(\left( {D_{u} } \right)\) and (f) Soret number \(\left( {S_{o} } \right)\)

Full size image

\(S = 1.30,\) \(M = 1.00,\) \(P_{m} = 2.00,\) \(P_{r} = 0.71,\) \(R^{ * } = 0.20,\) \(D_{u} = 0.50,\) \(S_{o} = 0.20,\) \(E_{c} = 0.01\) and \(S_{c} = 0.60\) at time the \(t = 60\)(steady-state). Incorporating some widely used fluid likewise air \(\left( {P_{r} = 0.71} \right)\), water \(\left( {P_{r} = 7.00} \right)\), salt water \(\left( {P_{r} = 1.00} \right)\), and some broadly used diffusing species likewise Helium \(\left( {S_{c} = 0.30} \right)\), carbon dioxide \(\left( {S_{c} = 0.94} \right)\), water vapor \(\left( {S_{c} = 0.60} \right)\), and propyl-benzene \(\left( {S_{c} = 2.62} \right)\). The other relevant parameters are chosen by the guidance of stability and convergence criteria.

Table 1 Local current density \(\left( {J_{L} } \right)\) and local shear stress \(\left( {\tau_{L} } \right)\)
Full size table

Figure 7(a, b) delineates the velocity pattern with the variation of suction and magnetic parameters. Evidently, it is marked that, the increment in the suction parameter \(\left( S \right)\) causes the momentum BL corrugation, i.e. the flow substantially decelerates within the BL zone (see Fig. 7-a). The suction velocity is the reason behind the minimization of the fluid density within The BL, which resultant the deceleration in velocity. For small estimations of \(y\), i.e. \(0 \le y \le 2.5\)(approximately), the velocity retards and after that, velocity develops for larger values of \(y\), with the amplifying values of the magnetic parameter \(\left( M \right)\)(see Fig. 7-b).

The impacts of Prandtl number \(\left( {P_{r} } \right)\), magnetic Prandtl number \(\left( {P_{m} } \right)\), radiation parameter \(\left( {R^{ * } } \right)\), and Soret number \(\left( {S_{o} } \right)\) on fluid velocity have been witnessed from Fig. 8(a, b, c, d). Figure 8-a witnesses that, the causation of velocity downfall happens with the rising values of the Prandtl number \(\left( {P_{r} } \right)\). Strong counting of Prandtl number \(\left( {P_{r} } \right)\) has a proclivity to reduce momentum BL. This happening occurs because the kinematic viscidity criteria develop with the strengthening of Prandtl number \(\left( {P_{r} } \right)\), which causes diminution on heat diffusivity. Figure 8-b implies that the fluid momentum decelerates on strengthening the magnetic Prandtl number \(\left( {P_{m} } \right)\).The sketch for velocity with different values of radiation parameter \(\left( {R^{ * } } \right)\) is plotted in Fig. 8-c, and the observation implies that the thermal radiation boosts the velocity up, i.e. prolong momentum BL. Again the wideness of momentum BL comes into view with the increasing amount level of thermal-diffusion consideration, i.e. for high estimations of Soret number \(\left( {S_{o} } \right)\), the velocity boosts up (see Fig. 8-d). Remarkable peak hiking is observed as well.The graphical sketches of induced magnetic fields under the counting of suction and magnetic parameters are portrayed through Fig. 9(a, b). Starting from the highest positive value, the induced magnetic field tends to the negative direction inside the BL regime, i.e. the feature of magnetic induction reverses to attain a smooth cusp through the negative direction and then decreases to the null value towards the free streamflow. Negative cusping of the induced magnetic field usually occurs in the BL regime [15, 48]. This responsive phenomenon is observed for all the permutations of pertinent parameters on the induced magnetic field (see Figs. 9(a, b) and  10(a, b, c, d). A tiny decrement has happened in magnetic field induction for a very short value of \(y\), i.e. the nearest zone of the plate (wall) under an increased formation of suction parameter \(\left( S \right)\) and thereafter with relative increment in \(y\) the induced magnetic field elevates (see Fig. 9a). The magnetic parameter \(\left( M \right)\) causes a cut down on the induced magnetic field as sketched in Fig. 9b.

The visualization of the induced magnetic field under the hiking impacts of Prandtl number \(\left( {P_{r} } \right)\), magnetic Prandtl number \(\left( {P_{m} } \right)\), radiation parameter \(\left( {R^{ * } } \right)\), and Eckert number \(\left( {E_{c} } \right)\) have been depictured in Fig. 10(a, b, c, d). The escalation on the profile of magnetic field induction is perceived for all the inward BL transverse distance \(y\) with the hiking magnitudes of the Prandtl number \(\left( {P_{r} } \right)\) (see Fig. 10-a). Materially, it can be comprehended that water \(\left( {P_{r} = 7.00} \right)\) induces more magnetic strength than air \(\left( {P_{r} = 0.71} \right)\) throughout the BL regime. The responding nature of the induced magnetic field with the developing values of the magnetic Prandtl number \(\left( {P_{m} } \right)\) is comprised in Fig. 10-b. It is marked from that particular sketch that, from the zero value of \(y\) to a relatively broader value \(y \le 12\) (approximately), the induced magnetic field profile prolongs with magnetic Prandtl number \(\left( {P_{m} } \right)\) whereas, it becomes a little clumsy in the sense of consecutive changes for the rest of the BL distance \(12 \le y \le 20\) (approximately). A propensity of declination on the induced magnetic field is checked in Fig. 10-c with the rising prescribed values of the radiation parameter \(\left( {R^{ * } } \right)\). Thus there happens a negative enhancing of induced magnetic flux for enhancement of radiation parameter \(\left( {R^{ * } } \right)\). A negatively rising estimation of the magnetic field induction profile is obvious for relatively larger estimations of dissipative effect, i.e. Eckert number \(\left( {E_{c} } \right)\) (see Fig. 10-d). This causes an enhancing reversal in the induced magnetic field within the BL zone for the whole transverse space \(y\).

The parceling of energy throughout the BL flow territory have been discerned for the suction parameter \(\left( S \right)\), Prandtl number \(\left( {P_{r} } \right)\), radiation parameter \(\left( {R^{ * } } \right)\), Eckert number \(\left( {E_{c} } \right)\), Dufour number \(\left( {D_{u} } \right)\), and Soret number \(\left( {S_{o} } \right)\) with the view of Fig. 11(a, b, c, d, e, f). A growth in suction parameter \(\left( S \right)\) notifies a thermal BL slenderness which causes subdue in thermal energy of the fluid as depicted in Fig. 11-a. The uplifting estimations of the Prandtl number \(\left( {P_{r} } \right)\) from 0.71 to 7.00 downtrend the temperature profile (see Fig. 11-b). The internal energy development has occurred for the existence of radiative heat flux, i.e. the fluid becomes warmer. Likewise, rising repercussions of temperature profile have been counted from Fig. 11-c for an upward tendency of radiation parameter \(\left( {R^{ * } } \right)\). The uptrend of thermal BL occurs for the enhancing estimations of the radiation parameter \(\left( {R^{ * } } \right)\). An evident prolongation in temperature is introduced for escalating estimations of the Eckert number \(\left( {E_{c} } \right)\) (see Fig. 11-d. This happening follow the presumption, as positive uplifting values of Eckert number \(\left( {E_{c} } \right)\) set forth, a plate cooling nature and therefore the fluid temperature develops by absorbing the heat left by the plate. The Dufour number \(\left( {D_{u} } \right)\) naturally aids the acceleration of the convective process of heat transfer. Evidently, with the hiking estimations of the Dufour number \(\left( {D_{u} } \right)\), an escalation of the temperature of the fluid within BL is perceived as demonstrated in Fig. 11-e. It is also perceived that the BL for temperature expands towards the free stream zone for the accelerating multiple values of the Dufour number \(\left( {D_{u} } \right)\). In Fig. 11-f, the Soret number \(\left( {S_{o} } \right)\) depicts a gradual enhancing response on the fluid temperature versus the transverse distance \(y\).

Implications of the suction parameter \(\left( S \right)\), Prandtl number \(\left( {P_{r} } \right)\), Schmidt number \(\left( {S_{c} } \right)\), and Soret number \(\left( {S_{o} } \right)\) on fluid concentration have been plotted in Fig. 12(a, b, c, d). Downtrend indications of the concentration profile have been estimated through Fig. 12-a when the suction parameter \(\left( S \right)\) boosts up in magnitudes. The obviousness of this phenomenon is because of the emaciation of momentum BL with the rising estimations of the suction parameter \(\left( S \right)\). A consequence of the Prandtl number \(\left( {P_{r} } \right)\) on the fluids concentration profile is depicted in Fig. 12-b, which reveals a wee falling tend with the Prandtl number \(\left( {P_{r} } \right)\). The concentration medium depicts a declining behavior when the application of the Schmidt number \(\left( {S_{c} } \right)\) develops (see Fig. 12-c). This feature has been encountered because Schimdt number occurs decrement on buoyancy effects of concentration which as well retards the fluid velocity. The flow is carried out for some regular diffusing species under the Schmidt number \(\left( {S_{c} = 0.30,0.60,0.94,2.62} \right)\) respectively for helium, water vapor, carbon dioxide, and propyl benzene. The enhancing response of thermal diffusion, i.e. Soret number \(\left( {S_{o} } \right)\), implies an uptrend on concentration level as illustrated in Fig. 12-d.

Fig. 12
figure 12

Features of concentration for (a) suction parameter \(\left( S \right)\); (b) Prandtl number \(\left( {P_{r} } \right)\); (c) Schmidt number \(\left( {S_{c} } \right)\) and (d) Soret number \(\left( {S_{o} } \right)\)

Full size image

The responsive behavior of local current density and local shear stress versus the dimensionless time \(t\) with all the flow ruling parameters have been tabulated in Table 1. Interestingly, the local shear stress diminishes when the magnetic parameter \(\left( M \right)\) and suction parameter \(\left( S \right)\) have been increasingly applied to that. The transverse magnetic field has an instinctive feature to produce a flow opposing force known as Lorentz force which, consequently downtrends the local skin friction coefficient. Increasing estimations of Prandtl number \(\left( {P_{r} } \right)\) boost up the decaying nature of the temperature field for the total range of transverse distance \(y\) which contributes to the diminution of local shear stress. The local shear stress coefficient also expresses enhancing characteristics for the uplifting values of magnetic Prandtl number \(\left( {P_{m} } \right)\), radiation parameter \(\left( {R^{ * } } \right)\), Eckert number \(\left( {E_{c} } \right)\), Dufour number \(\left( {D_{u} } \right)\), and Soret number \(\left( {S_{o} } \right)\) while Schmidt number \(\left( {S_{c} } \right)\) substantially deny this criterion. The local current density of the induced magnetic field exhibit rising nature when the suction parameter \(\left( S \right)\) and Schmidt number \(\left( {S_{c} } \right)\) enhance on contrary the magnetic Prandtl number \(\left( {P_{m} } \right)\) tends the local current density uplift. A small decreasing impact on local current density is marked for the magnetic parameter \(\left( M \right)\), radiation parameter \(\left( {R^{ * } } \right)\), Eckert number \(\left( {E_{c} } \right)\), Dufour number \(\left( {D_{u} } \right)\), and Soret number \(\left( {S_{o} } \right)\).

6.6 Comparison

The subsequent table (Table. 2) brings out a comparative qualitative understanding of the reported work with some published works. The prime focus of this article is to make out the numerical solution of unsteady MHD heat and mass transfer flow of dissipative and radiating fluid with the incorporation of an induced magnetic field and thermal diffusion phenomena by expressing unchanged heat and mass fluxes along an infinitely defined vertical plate while Alam et al. [46] studied steady MHD flow criteria of conducting fluid by taking heat and mass transfer phenomena with the magnetic field induction along with the presumption of constant heat and mass fluxes along the vertical plate; Khan et al. [48] prescribed numerical methods to quest the nature of heat generation on MHD flow by the acting of the induced magnetic field; Iva et al. [12] analyzed the BL heat source and suction-based flow of MHD fluid with a rotating system under the influence of the Hall effect. The study was basically dealt with an FDM-solving structure with time-domain consideration, i.e. for the unsteady solutions.

Table 2 Comparison of the present study with several published studies
Full size table

7 Concluding remarks

MHD heat and mass transfer flow of an electrically conducting, thermally radiating, and viscous incompressible fluid with magnetic field induction, thermal diffusion and constant wall suction by the concern of constant wall (plate) heat and mass fluxes have been investigated. It is worth alluding that the diffusion-thermo effect is also an ingredient of this current analysis. Depending on the tabular and graphical consequences which have figured out earlier, some symptomatic and decisive facts of the study are mentioned below:

  1. 1.

    The dimensionless steady-state time has been gotten at \(t = 60\).

  2. 2.

    Numerical FDM procedures have been conveyed for \(400\) meshes.

  3. 3.

    The flow controlling parameters have been steered as \(S \ge - 484,\) \(0.40 \le P_{m} \le 24,\) \(0.00 \le R^{ * } \le 87.50,\) \(0.07 \le P_{r} \le 30.50\) and \(S_{c} \ge 0.04\)

  4. 4.

    The fluid concentration superiority is marked for rising estimations of \(S_{o}\) while \(S_{c}\) shows the opposite nature.

  5. 5.

    The velocity accelerates when the estimations of \(R^{ * }\) and \(S_{o}\) is in an uptrend vibe while velocity decelerates with the increase of \(S,\) \(P_{m}\) and \(P_{r}\).

  6. 6.

    The local shear stress marks up for extending estimations of \(R^{ * } ,\) \(P_{m} ,\) \(E_{c} ,\) \(D_{u}\) and \(S_{o}\) while \(S,\) \(S_{c}\) and \(P_{r}\) dictate a decrement in local shear stress.

  7. 7.

    Enlarging effects of \(S,\) \(P_{m}\) and \(P_{r}\) amplify the induced magnetic field on the contrary \(R^{ * } ,\) \(E_{c}\) and \(M\) pointing out a diminution on the induced magnetic field.

  8. 8.

    The local current density exhibit a rising nature when \(S,\) and \(S_{c}\) enhance on contrary \(P_{m}\) tends the local current density uplift.

  9. 9.

    The temperature profile rises with the rise of \(R^{ * } ,\) \(E_{c} ,\) \(D_{u}\) and \(S_{o}\) while it reduces with the rise of \(S\) and \(P_{r}\).

In the future, the authors wish to analyze the non-uniform heat source impacts on MHD vertical flow with the induced magnetic field.