Thermal analysis of airway mucus clearance by ciliary activity in the presence of inertial forces

Abstract

In this study heat transfer effects on cilia induced mucus flow in human airways is presented. The elliptic wave pattern of cilia tips produces metachronal wave which enables the transportation of highly viscous mucus with nonzero inertial forces. Upper Convective Maxwell model is considered as mucus. The governing partial differential equations are transformed from the fixed frame to the wave frame by using Galilean transformation and viscous dissipation is also incorporated in the energy equation. The non-linear governing equations are evaluated by the perturbation technique by using software “MATHEMATICA” and pressure rise is computed by numerical integration. The impact of interested parameters on temperature profile, velocity, pressure rise and pressure gradient are plotted by the graphs. The comparison of velocities due to symplectic and antiplectic metachronal wave are also achieved graphically.

1 Introduction

Due to the presence of toxic chemicals, dust particles, pathogens and viruses in inhaled air, lungs are abnormally resistant to environmental injury. Lungs resistance based on strong defence delivered by the airway mucus made up of water and mucin and ciliary beating helps to transport the inhaled toxin out of the lungs trapped in airways mucus. The weak clearance and thick mucus add pathogenesis of airway diseases and causes to failure of mucus clearance that results in abnormal lung function which is mentioned in Ref. [1]. Cilia play an important role for mucus clearance that is essential for normal lung function. Muco ciliary clearance can only be functional if cilia beat frequency is normal. Moisture and humidity (depending upon temperature gradient) present in environment is necessary to regulate ciliary beat frequency. Lee et al. [2] studied the muco-ciliary transport by considering the Newtonian fluid model in both PCL and mucus layers and investigated the factors affecting this transportation and underlying the diseases related to respiratory tract due to defects in ciliary systems such as cystic fibrosis. Results are obtained by the immersed boundary method combined with the projection method and concluded that the factors which affect the muco-ciliary transport include number of cilia, cilia beat frequency and the depth of PCL. Mercke et. al [3] performed the experiments on rabbit’s trachea and concluded that relationship between metachronal wave movements and temperatures ranging from 20° and 40 °C is linear. Clary et. al [4] studied the effect of temperature on ciliary beat frequency and concluded that cilia beat with higher frequencies when temperature rises. Kilgour et al. [5] experimentally determined that a fall in environmental temperature causes to reduce in ciliary beat frequency and a decreases the mucus speed. Diesel et al. [6] also found a similar linear relationship between environmental temperature and mucus velocity in respiratory tract. Furthermore different researchers studied the effect of temperature and vapour pressure on rate of muco ciliary clearance. Also Hatanaka et al. [7]. discussed the effect of temperature difference on ciliated epithelium present in the respiratory tract and found that by the modification of temperature (temperature gradient) cilia beat frequency can be regulated for the increase velocity of ciliary tips required for the muco ciliary clearance.

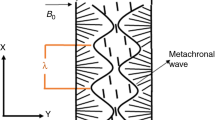
Cilia motion plays important role in many physiological processes including, respiration and reproduction [8]. Single cycle of ciliary motion consists of forward and backward strokes. During power stroke cilia starts its motion towards base of cilium shaft and returned back to its initial position until the start of second ciliary beat [9]. A cilia beat with a constant phase difference with one another, a large curvature in the cilium is present at its base which helps to move very rapidly through the fluid medium with a whip-like motion called the metachronism. This collective ciliary motion of cilia has been studied in many biological studies [10]. Cilia are present in the human airways where foreign matters out of lungs. The moving cilia which are responsible for muco-ciliary clearance exhibit a coordinated and periodic pattern due to phase difference in their beat and are characterized by metachronal waves. The interaction between cilia and airways mucus is considered very sophisticated hydrodynamic-structural interaction. Many researchers [11, 12] studied the interaction between cilia and mucus by using different mathematical and computational models. Two types of approaches are present in literature for the motion of cilia tips, the first one is the sub-layer and second is envelope model approach [13]. Cilia consists of two strokes i.e. power and recovery strokes, therefore ciliary motion have been studied by using different mathematical models. If the direction of propagation of metachronal wave is towards forward stroke, symplectic beat pattern is produced whereas, when it propagates in opposite direction, antiplectic wave pattern is produced. These both types of beat patterns are observed in mucus clearance and other biological functions. Many researchers [14,15,16] studied different ciliary beat patterns and diseases related to ciliary activity. Lauga [17] much later has also shown that dynamics of tracheal cilia features sympletic waves used to propel viscoelastic mucus. There are also cases where the metachronal waves may propagate oblique to the effective stroke.

Mucus is considered as non-Newtonian gel at macroscale and it is different from classical solids and liquids by its response to shear stress and shear rate.and it is considered as fluid with low viscosity at nanoscale. Mucus is a heterogeneous mixture mainly composed by water (∼95%), mucins (up to ∼5%), and other minority components such as cellular debris, fragments of genetic material, lipids, etc. Vasquez et al. [18] considered the viscous fluid model as mucus depending upon ciliary beat frequency and temperature. Many researchers studied mucus as different fluid models including Sisko model [19], Jeffery model [20], Maxwell model [21] and Williamson model [22]. To make the problem less complicated, we choose the simplest viscoelastic fluid constitutive equation, i.e., one that is linear and which has only one “relaxation time” i.e., the simplest spring-and-dashpot models analogous with the Maxwell fluid model.

The inertia has two effects on ciliay flow. First, the momentum diffusion from the cilia at the boundary into the channel is delayed. Second, the energy input into the fluid in the effective stroke is retained beyond its duration. Khaderi et al. [23] discussed that at moderate Reynolds numbers, the high energy input into the fluid by the fast recovery stroke creates a large flow in the direction of the recovery stroke. Furthermore, some representative studies on cilia motion with different fluid models have been carried out in literature with long wavelength approximation and without inertial effects [24]. However the study of Maxwell fluid flow induced by the ciliary movement with heat transfer under the effect of inertial forces has not been studied in literature. Therefore, to make the fast process of mucociliary clearance inertial and thermal effects are considered for the Maxwell fluid flow. In this research mathematical model has been developed for cilia induced mucus flow in human respiratory system with the effect of heat transfer at moderate Reynolds. The UC Maxwell model is considered as mucus flow which to the authors’ knowledge has not yet been studied explicitly in ciliated propulsion with heat transfer. This model has several unique features not available in other viscoelastic models. Also, it is a generalization of the Maxwell linear model for large deformations and is formulated using the upper-convected time derivative. Although the UC Maxwell model successfully incorporates the first difference of normal stresses it cannot predict the second difference of the normal stresses. It does however predict that for simple shear, shear stress is proportional to the shear rate and the first difference of normal stresses and reasonably approximates mucus rheology over a wide range of shear rates. The Upper Convective Maxwell model has been studied in biological fluid mechanics for endoscopic flows by Abbasi et al. [25] and embryological transport by Narla et al. [26]. But no one has described the inertial and thermal effects on the mucus flow (Maxwell fluid model) due to the ciliary activity which is beneficial for the muco ciliary clearance required for the normal functioning of lungs.

The present study is organized in five sections; introduction and literature review is added in section one, mathematical modelling of thermal analysis of airway mucus clearance by ciliary activity in the presence of inertial forces by the help of mass, momentum and energy conservation is presented in section two. Results regarding the velocity, stream function, pressure gradient and temperature are calculated by perturbation method in section three. In section four graphical results for the pressure gradient, velocity and temperature are plotted and effects of Maxwell rheological parameter (relaxation time) and Reynolds’ number are discussed. In the last section results are summarized with critical observation.

2 Mathematical model

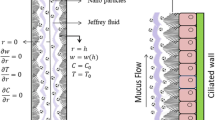
The geometrical model for mucus clearance is presented in Fig. 1. We have considered the effects of heat transfer of an Upper-Convective Maxwell (UCM) fluid (mucus) flowing in ciliated tube. Due to presence of continuously beating cilia at the boundaries of cylinder, metachronal wave is produced which moves in the direction of z-axis with speed c. The temperature at the boundaries is taken as ${T}_{1}.$ In this research envelop model approach [27] is used for elliptic motion of ciliary tips. The continuity, momentum and energy equations for convective flow of Upper-Convective Maxwell (UCM) fluid (mucus) flowing through the cylindrical tube can be written as

$$ \nabla \cdot {\varvec{V}} = 0, $$

(1)

$$ \rho \frac{{d{\varvec{V}}}}{Dt} = div{\varvec{T}}, $$

(2)

$$ \rho c_{p} \frac{dT}{{dt}} = k\nabla^{2} T + trace\left( {{\varvec{S}}.{\varvec{L}}} \right) $$

(3)

stress tensors for the Upper-Convective Maxwell model can be written as [28]

$$ {\varvec{T}} = - p{\varvec{I}} + {\varvec{S}}, $$

(4)

$$ {\varvec{S}} + \lambda_{1} \left( {\frac{dS}{{dt}} - {\varvec{L}}^{{\varvec{T}}} {\varvec{S}} - {\varvec{SL}}} \right) = \mu {\varvec{A}}_{1} . $$

(5)

Fig. 1

Geometry of the flow problem

The velocity vector is defined as

$$ {\varvec{V}} = \left[ {u\left( {r,z,t} \right),0,w\left( {r,z,t} \right)} \right] $$

(6)

Substituting in Eqs. (4), (5) into the Eqs. (1) and (2), the partial differential takes the following form:

$$ \frac{1}{r}\frac{\partial }{\partial r}\left( {ru} \right) + \frac{\partial w}{{\partial z}} = 0, $$

(7)

$$ \rho \frac{du}{{dt}} = - \frac{\partial p}{{\partial r}} + \frac{1}{r}\frac{\partial }{\partial r}\left( {rS_{rr} } \right) + \frac{{\partial S_{rz} }}{\partial z} - \frac{{S_{\theta \theta } }}{r} $$

(8)

$$ \rho \frac{dw}{{dt}} = - \frac{\partial p}{{\partial z}} + \frac{1}{r}\frac{\partial }{\partial r}\left( {rS_{zr} } \right) + \frac{{\partial S_{zz} }}{\partial z}, $$

(9)

$$ \rho c_{p} \frac{dT}{{dt}} = k\left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial T}{{\partial r}}} \right) + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right) + S_{rr} \frac{\partial u}{{\partial r}} + S_{rz} \left( {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right) + S_{zz} \frac{\partial w}{{\partial z}}. $$

(10)

where $\frac{d}{dt} = \frac{\partial }{\partial t} + u\frac{\partial }{\partial r} + w\frac{\partial }{\partial z}.$

Here the stresses satisfy the following expressions:

$$ S_{rr} + \lambda_{1} \left( {\nabla S_{rr} - 2\frac{\partial u}{{\partial r}}S_{rr} - 2\frac{\partial u}{{\partial z}}S_{rz} } \right) = 2\mu \frac{\partial u}{{\partial r^{\prime } }} $$

(11)

$$ S_{rz} + \lambda_{1} \left( {\nabla S_{rz} - \left( {\frac{\partial w}{{\partial z}} + \frac{\partial u}{{\partial r}}} \right)S_{zr} - \frac{\partial u}{{\partial z}}S_{zz} - \frac{\partial w}{{\partial r}}S_{rr} } \right) = \mu \left( {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right), $$

(12)

$$ S_{zz} + \lambda_{1} \left( {\nabla S_{zz} - 2\frac{\partial w}{{\partial r}}S_{rz} - 2\frac{\partial w}{{\partial z}}S_{zz} } \right) = 2\mu \frac{\partial w}{{\partial z}}. $$

(13)

where $\nabla = u\frac{\partial }{\partial r} + w\frac{\partial }{\partial z}.$

Axisymmetric flow states the following boundary condition at the center of the regime

$$ \frac{\partial w}{{\partial r}} = 0, \frac{\partial T}{{\partial r}} = 0 at r = 0 $$

(14a)

No slip condition due to the metachronal wave generated by the ciliary tip suggests the following condition as given in [27]

$$ w = w\left( h \right) = \frac{{ - \left( {\frac{2\pi }{\lambda }} \right)\left[ {\varepsilon a\alpha c\sin \frac{2\pi }{\lambda }z} \right]}}{{1 - \left( {\frac{2\pi }{\lambda }} \right)\left[ {\varepsilon a\alpha \cos \frac{2\pi }{\lambda }z} \right]}} $$

(14b)

$$ u = u\left( h \right) = \frac{{\left( {\frac{2\pi }{\lambda }} \right)\left[ {\varepsilon a\alpha c\sin \frac{2\pi }{\lambda }z} \right]}}{{1 - \left( {\frac{2\pi }{\lambda }} \right)\left[ {\varepsilon a\alpha \cos \frac{2\pi }{\lambda }z} \right]}}, T = T_{1} $$

(14c)

at

$$ r = \pm h\left( z \right) = \pm \left[ {a + \varepsilon \alpha a\cos \frac{2\pi }{\lambda }z} \right]. $$

Following non-dimensional parameters and transformation from fixed to wave frame given in Ref. [27] are introduced to normalize the above equations,

$$ \begin{gathered} z^{*} = \frac{z}{\lambda }, r^{*} = \frac{r}{a}, u^{*} = \frac{u}{\beta c},w^{*} = \frac{w}{c}, h^{*} = \frac{h}{a},p^{*} = \frac{a\beta }{{c\mu }}p, \hfill \\ \beta = \frac{a}{\lambda }, S_{ij}^{*} = \frac{a}{\mu c}S_{ij} , \lambda_{1}^{*} = \frac{{c\lambda_{1} }}{a},{\text{Re}} = \frac{\rho ac}{\mu }, \theta = \frac{{T - T_{0} }}{{T_{1} - T_{0} }} , \hfill \\ \Pr = \frac{{\mu c_{p} }}{k} , Ec = \frac{{c^{2} }}{{c_{p} \left( {T_{1} - T_{0} } \right)}}, Br = \Pr . Ec. \hfill \\ \end{gathered} $$

(15)

After using Eq. (15), Eqs. (7)–(14) take the following form

$$ \frac{\partial u}{{\partial r}} + \frac{u}{r} + \frac{\partial w}{{\partial z}} = 0, $$

(16)

$$ Re\beta^{3} \left[ {\nabla u} \right] = - \frac{\partial p}{{\partial r}} + \frac{\beta }{r}\frac{\partial }{\partial r}\left( {rS_{rr} } \right) + \beta^{2} \frac{{\partial S_{zr} }}{\partial z} - \beta \frac{{S_{\theta \theta } }}{r}, $$

(17)

$$ Re\beta \left[ {\nabla w} \right] = - \frac{\partial p}{{\partial z}} + \frac{1}{r}\frac{\partial }{\partial r}\left( {rS_{zr} } \right) + \beta \frac{{\partial S_{zz} }}{\partial z}, $$

(18)

$$ \begin{aligned} \beta {\text{Re}} \Pr \left[ {\nabla \theta } \right] = & \left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial \theta }{{\partial r}}} \right) + \beta^{2} \frac{{\partial^{2} \theta }}{{\partial z^{2} }}} \right) \\ & + Br\left( {\beta S_{rr} \frac{\partial u}{{\partial r}} + \beta^{2} S_{rz} \frac{\partial u}{{\partial z}} + S_{zr} \frac{\partial w}{{\partial r}} + \beta S_{zz} \frac{\partial w}{{\partial z}}} \right). \\ \end{aligned} $$

(19)

$$ S_{rr} + \lambda_{1} \beta \left[ {\nabla S_{rr} - 2\frac{\partial u}{{\partial r}}S_{rr} - 2\beta \frac{\partial u}{{\partial z}}S_{zr} } \right] = 2\beta \frac{\partial u}{{\partial r}}, $$

(20)

$$ S_{rz} + \lambda_{1} \left( {\beta \nabla S_{rz} - \beta \left( {\frac{\partial w}{{\partial z}} + \frac{\partial u}{{\partial r}}} \right)S_{zr} - \beta^{2} \frac{\partial u}{{\partial z}}S_{zz} - \frac{\partial w}{{\partial r}}S_{rr} } \right) = \beta^{2} \frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}, $$

(21)

$$ S_{zz} + \lambda_{1} \left[ {\beta \nabla S_{zz} - 2\frac{\partial w}{{\partial r}}S_{rz} - 2\beta \frac{\partial w}{{\partial z}}S_{zz} } \right] = 2\beta \frac{\partial w}{{\partial z}}. $$

(22)

The non-dimensional boundary conditions can be written as

$$ \frac{\partial w}{{\partial r}} = 0, \frac{\partial \theta }{{\partial r}} = 0 at r = 0 $$

(23a)

$$ w = w\left( h \right) = - \left( {1 + 2\pi \varepsilon \alpha \beta \cos \left( {2\pi z} \right)} \right), $$

(23b)

$$ u = u\left( h \right) = \pm 2\pi \varepsilon \left( {\sin \left( {2\pi z} \right)} \right) + \beta 2\pi \varepsilon \alpha \sin \left( {2\pi z} \right)\cos \left( {2\pi z} \right), \theta = 1 $$

(23c)

at

$$ r = \pm h\left( z \right) = \pm \left[ {a + \varepsilon \alpha a\cos \left( {2\pi z} \right)} \right], $$

Introducing stream functions to reduce number of unknowns

$$ u = \frac{ - 1}{r}\frac{\partial \psi }{{\partial z}}, \quad w = \frac{1}{r}\frac{\partial \psi }{{\partial r}} $$

(24)

Equation (16) is identically satisfied and Eqs. (17) to (23) are transformed to:

$$ \begin{gathered} {\text{Re}} \beta^{3} \left( {\left( {\frac{ - 1}{r}\frac{\partial \psi }{{\partial z}}} \right)\frac{\partial }{\partial r}\left( { - \frac{1}{r}\frac{\partial \psi }{{\partial z}}} \right) + \left( {\frac{1}{r}\frac{\partial \psi }{{\partial r}}} \right)\frac{\partial }{\partial z}\left( { - \frac{1}{r}\frac{\partial \psi }{{\partial z}}} \right)} \right) = - \frac{\partial p}{{\partial r}} + \frac{\beta }{r}\frac{\partial }{\partial r}\left( {rS_{rr} } \right) \hfill \\ \quad + \beta^{2} \frac{{\partial S_{zz} }}{\partial z} - \beta \frac{{S_{\theta \theta } }}{r}, \hfill \\ \end{gathered} $$

(25)

$$ \beta Re\left( {\left( {\frac{ - 1}{r}\frac{\partial \psi }{{\partial z}}} \right)\frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{\partial \psi }{{\partial r}}} \right) + \left( {\frac{1}{r}\frac{\partial \psi }{{\partial r}}} \right)\frac{\partial }{\partial z}\left( {\frac{1}{r}\frac{\partial \psi }{{\partial z}}} \right)} \right) = - \frac{\partial p}{{\partial z}} + \frac{1}{r}\frac{\partial }{\partial r}\left( {rS_{rz} } \right) + \beta \frac{{\partial S_{zz} }}{\partial z}, $$

(26)

$$ \begin{gathered} \beta RePr\left[ {\left( {\frac{ - 1}{r}\frac{\partial \psi }{{\partial z}}} \right)\frac{\partial \theta }{{\partial r}} + \left( {\frac{1}{r}\frac{\partial \psi }{{\partial r}}} \right)\frac{\partial \theta }{{\partial z}}} \right] = \left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial \theta }{{\partial r}}} \right) + \beta^{2} \frac{{\partial^{2} \theta }}{{\partial z^{2} }}} \right) \hfill \\ \quad + Br\left( {\beta S_{rr} \frac{\partial }{\partial r}\left( {\frac{ - 1}{r}\frac{\partial \psi }{{\partial z}}} \right) + \beta^{2} S_{rz} \frac{\partial }{\partial z}\left( {\frac{ - 1}{r}\frac{\partial \psi }{{\partial z}}} \right) + S_{zr} \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{\partial \psi }{{\partial r}}} \right) + \beta S_{zz} \frac{\partial }{\partial z}\left( {\frac{1}{r}\frac{\partial \psi }{{\partial r}}} \right).} \right) \hfill \\ \end{gathered} $$

(27)

Taking cross derivative and subtracting to eliminae the axial $\frac{\partial p}{{\partial z}}$ and radial pressure gradients $\frac{\partial p}{{\partial r}}$ from Eqs. (25)-(26) yields:

$$ \begin{gathered} \beta^{3} Re\frac{\partial }{\partial z}\left( {\frac{ - 1}{r}\frac{\partial \psi }{{\partial z}}\frac{\partial }{\partial r}\left( { - \frac{1}{r}\frac{\partial \psi }{{\partial z}}} \right) + \left( {\frac{1}{r}\frac{\partial \psi }{{\partial r}}} \right)\frac{\partial }{\partial z}\left( { - \frac{1}{r}\frac{\partial \psi }{{\partial z}}} \right)} \right) \hfill \\ \quad - \beta Re\frac{\partial }{\partial r}\left( {\frac{ - 1}{r}\frac{\partial \psi }{{\partial z}}\frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{\partial \psi }{{\partial r}}} \right) + \left( {\frac{1}{r}\frac{\partial \psi }{{\partial r}}} \right)\frac{\partial }{\partial z}\left( {\frac{1}{r}\frac{\partial \psi }{{\partial r}}} \right)} \right) \hfill \\ = \frac{\partial }{\partial z}\left( {\frac{\beta }{r}\frac{\partial }{\partial r}\left( {rS_{rr} } \right) + \beta^{2} \frac{{\partial S_{zz} }}{\partial z} - \beta \frac{{S_{\theta \theta } }}{r}} \right) - \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {rS_{rz} } \right) + \beta \frac{{\partial S_{zz} }}{\partial z}} \right), \hfill \\ \end{gathered} $$

(28)

Here:

$$ \begin{gathered} S_{rr} + \lambda_{1} \beta \left[ {\frac{1}{r}\left( { - \frac{\partial \psi }{{\partial z}}\frac{\partial }{\partial r} + \frac{\partial \psi }{{\partial r}}\frac{\partial }{\partial z}} \right)S_{rr} + 2\beta \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{\partial \psi }{{\partial z}}} \right)S_{rr} + 2\beta^{2} \frac{\partial }{\partial z}\left( {\frac{1}{r}\frac{\partial \psi }{{\partial z}}} \right)S_{rz} } \right] \hfill \\ \quad = - 2\beta \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{\partial \psi }{{\partial z}}} \right), \hfill \\ \end{gathered} $$

(29)

$$ \begin{gathered} S_{rz} + \lambda_{1} \beta \left[ {\frac{1}{r}\left( { - \frac{\partial \psi }{{\partial z}}\frac{\partial }{\partial r} + \frac{\partial \psi }{{\partial r}}\frac{\partial }{\partial z}} \right)S_{rz} - \beta \left( {\frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{\partial \psi }{{\partial z}}} \right) - \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{\partial \psi }{{\partial z}}} \right)} \right)S_{rz} + \beta^{2} \frac{\partial }{\partial z}\left( {\frac{1}{r}\frac{\partial \psi }{{\partial z}}} \right)S_{zz} - \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{\partial \psi }{{\partial r}}} \right)S_{rr} } \right] \hfill \\ \quad = \beta^{2} \frac{\partial }{\partial r}\left( {\frac{ - 1}{r}\frac{\partial \psi }{{\partial z}}} \right) + \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{\partial \psi }{{\partial r}}} \right), \hfill \\ \end{gathered} $$

(30)

$$ \begin{gathered} S_{zz} + \lambda_{1} \left[ {\frac{\beta }{r}\left( { - \frac{\partial \psi }{{\partial z}}\frac{\partial }{\partial r} + \frac{\partial \psi }{{\partial r}}\frac{\partial }{\partial z}} \right)S_{zz} - 2\frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{\partial \psi }{{\partial r}}} \right)S_{rz} - 2\beta \frac{\partial }{\partial z}\left( {\frac{1}{r}\frac{\partial \psi }{{\partial r}}} \right)S_{zz} } \right] \hfill \\ \quad = 2\beta \frac{\partial }{\partial z}\left( {\frac{1}{r}\frac{\partial \psi }{{\partial r}}} \right). \hfill \\ \end{gathered} $$

(31)

The volumetric flow rate can be defined in the inertial frame as:

$$ Q\left( {Z, t} \right) = 2\pi \mathop \int \limits_{0}^{h} RW\left( {R, Z, t} \right)dR, $$

(32)

After transforming volume flow rate in wave frame we get

$$ q = 2\pi \mathop \int \limits_{0}^{h} rw\left( {r, z} \right)dr, $$

(33)

Using Eqs. (16), (32) and (33), we obtain:

$$ Q\left( {Z, t} \right) = q + c\pi h^{2} , $$

(34)

The mean-time volume flow rate can be written as:

$$ Q^{*} = \frac{1}{T}\mathop \int \limits_{0}^{1} Qdt = q + a^{2} c\pi \left( {1 + \frac{{\varepsilon^{2} }}{2}} \right), $$

(35)

Defining $\overline{Q} = \frac{{Q^{*} }}{{2a^{2} c\pi }}$ and $F = \frac{Q}{{2a^{2} c\pi }}$ it follows that dimensionless mean-time volumetric flow rate:

$$ \overline{Q} = F + \left( {1 + \frac{{\varepsilon^{2} }}{2}} \right). $$

(36)

If we select ψ = 0 at r = 0 (tube centreline); then ψ = F at r = h (distance from centreline to the cilia tip): Thus, the boundary conditions are:

$$ \psi = 0,\;\frac{\partial \theta }{{\partial r}} = 0{ }\quad {\text{by}}\;{\text{convension}} $$

(37a)

$$ \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{\partial \psi }{{\partial r}}} \right) = 0\quad {\text{by}}\;{\text{symmetry}}\;{\text{at}}\;r = 0 $$

(37b)

$$ \left( {\frac{1}{r}\frac{\partial \psi }{{\partial r}}} \right) = w\left( h \right)\quad {\text{by}}\;{\text{no}}\;{\text{slip}}\;{\text{condition}} $$

(37c)

$$ \psi = F, \theta = 1\quad {\text{at}}\;r = h $$

(37d)

3 Perturbation solutions for velocity profile

The Eqs. (25) to (31) are higher order non-linear partial differential equations therefore it is impossible to find the closed form solution so.to find the solution perturbation technique [29] is applied for small wave number.

$$ \psi = \psi_{0} + \beta \psi_{1} + \beta^{2} \psi_{2} \ldots \ldots \ldots \ldots $$

(38a)

$$ p = p_{0} + \beta p_{1} + \beta^{2} p_{2} \ldots \ldots \ldots \ldots $$

(38b)

$$ S = S_{0} + \beta S_{1} + \beta^{2} S_{2} \ldots \ldots \ldots \ldots $$

(38c)

$$ F = F_{0} + \beta F_{1} + \beta^{2} F_{2} \ldots \ldots \ldots \ldots $$

(38d)

$$ \theta = \theta_{0} + \beta \theta_{1} + \beta^{2} \theta_{2} \ldots \ldots \ldots \ldots $$

(38e)

3.1 Zeroth order system

$$ \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial r}} \right)} \right)} \right) = 0, $$

(39a)

$$ \frac{{\partial p_{0} }}{\partial z} = \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial r}} \right)} \right), $$

(39b)

$$ \frac{{\partial p_{0} }}{\partial r} = 0, $$

(39c)

$$ \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial \theta_{0} }}{\partial r}} \right) = - Br\frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial r}} \right)S_{0rz} $$

(39d)

$$ S_{0rr} = 0, $$

(39e)

$$ S_{0rz} = \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial r}} \right), $$

(39f)

$$ S_{0zz} = 2\lambda_{1} \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial r}} \right)S_{0rz} . $$

(39g)

$$ S_{0\theta \theta } = 0 $$

(39h)

The associated boundary conditions are:

$$ \psi_{0} = 0, \quad \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial r}} \right) = 0,\quad \frac{{\partial \theta_{0} }}{\partial r} = 0\quad {\text{at}}\;r = 0 $$

(40a)

$$ \psi_{0} = F_{0} ,\quad \frac{{\partial \psi_{0} }}{\partial r} = w\left( h \right),\quad \theta_{0} = 1\quad {\text{at}}\;r = h $$

(40b)

Pressure rise per wavelength can be calculated as:

$$ {\Delta }p_{{\lambda_{0} }} = \int \frac{{\partial p_{0} }}{\partial z}dz $$

(41)

3.2 First Order SYSTEM

$$ \begin{gathered} Re\frac{\partial }{\partial r}\left( { - \frac{1}{r}\frac{{\partial \psi_{0} }}{\partial z}\frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial r}} \right) + \left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial r}} \right)\frac{\partial }{\partial z}\left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial z}} \right)} \right) \hfill \\ = \frac{\partial }{\partial z}\left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {rS_{0rr} } \right) - \frac{{S_{0\theta \theta } }}{r}} \right) - \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {rS_{1rz} } \right) + \frac{{\partial S_{0zz} }}{\partial z}} \right) \hfill \\ \end{gathered} $$

(42a)

$$ \frac{{\partial p_{1} }}{\partial z} = - Re\left( {\left( {\frac{ - 1}{r}\frac{{\partial \psi_{0} }}{\partial z}} \right)\frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial r}} \right) + \left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial r}} \right)\frac{\partial }{\partial z}\left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial r}} \right)} \right) + \frac{1}{r}\frac{\partial }{\partial r}\left( {rS_{1rz} } \right) + \frac{{\partial S_{0zz} }}{\partial z} $$

(42b)

$$ \begin{gathered} \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial \theta_{1} }}{\partial r}} \right) = - \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial \psi_{1} }}{\partial r}} \right)S_{0rz} - \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial r}} \right)S_{1rz} - \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial r}} \right)S_{0zz} \hfill \\ + {\text{Re}} \Pr \left( {\left( {\frac{ - 1}{r}\frac{{\partial \psi_{0} }}{\partial z}} \right)\frac{{\partial \theta_{0} }}{\partial r} + \left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial r}} \right)\frac{{\partial \theta_{0} }}{\partial z}} \right), \hfill \\ \end{gathered} $$

(42c)

$$ \frac{{\partial p_{1} }}{\partial r} = 0, $$

(42d)

$$ S_{1rr} = - 2\frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial z}} \right), $$

(42e)

$$ \begin{aligned} S_{1rz} = & \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial \psi_{1} }}{\partial r}} \right) - \lambda_{1} \left[ {\left( { - \frac{1}{r}\frac{{\partial \psi_{0} }}{\partial z}\frac{\partial }{\partial r} + \frac{1}{r}\frac{{\partial \psi_{0} }}{\partial r}\frac{\partial }{\partial z}} \right)} \right]S_{0rz} \\ & - S_{1rr} \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial r}} \right) - \left[ {\frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial z}} \right) + \frac{\partial }{\partial z}\left( {\frac{1}{r}\frac{{\partial \psi_{0} }}{\partial r}} \right)} \right]S_{0rz} \\ \end{aligned} $$

(42f)

The relevant boundary conditions are:

$$ \psi_{1} = 0,\quad \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial \psi_{1} }}{\partial r}} \right) = 0,\quad \frac{{\partial \theta_{1} }}{\partial r} = 0\quad {\text{at}}\;r = 0 $$

(43a)

$$ \psi_{1} = F_{1} ,\quad \frac{1}{r}\frac{{\partial \psi_{1} }}{\partial r} = 0,\quad \theta_{1} = 0\quad {\text{at}}\;r = h $$

(43b)

Integrating Eq. (42b) we get pressure rise

$$ {\Delta }p_{{\lambda_{1} }} = \int \frac{{\partial p_{1} }}{\partial z}dz $$

(44)

To solve the zeroth and first order system for velocity profile, stream function, shear stress and temperature profile, we use the symbolic software “MATHEMATICA”. The expressions of zeroth and first order solutions are included in “Appendix” and their analyses are constructed through the graphs.

4 Graphical results and discussion

As suggested by Wu et al. [30], heat transfer in airway mucus by ciliary activity in the presence of inertial forces energy and momentum equations are modelled. As the mucus flow depends on temperature, speed and pressure exerted by the ciliary movement, therefore results for pressure gradient, velocity and temperature profile are calculated by the software MATHEMATICA and impact of inertial force and relaxation time is presented through graphs. As the mucus flow in the airway has relevance with the physiological process [31], therefore, we have assumed $\alpha =0.4, \beta =0.1, \varepsilon =0.2, Re=1 and {\lambda }_{1}=0.1$ from the previous study of mucus flow (Maxwell fluid model) under the inertial effects [23].

The muco ciliary clearance causes a significant increase in the movement of cilia by the pressure forces also the pressure gradient in the airway cause liquid flow down and up during inhalation and exhalation, it is also mentioned in the Ref. [32] pressure gradient helps to propel the mucus out of the airways (muco ciliary clearance). The metachoronal wave allows the changes in the pressure drop which also depends on the movement of the mucus and its viscosity therefore in this research we discuss the pressure gradient for the different values of Reynolds number and relaxation time.

Figure 2a shows that pressure gradient reduces for the increasing values of Reynolds number near the centre of tube but it increases near the ciliary tip, therefore for the muco ciliary clearance near the ciliary tip inertial forces are required. Therefore in Fig. 2b it is shown that near the centre of tube pressure gradient increases with increasing values of relaxation time, whereas contrary response is computed near the ciliary tip as the mucus viscosity near the ciliary tip rises by the increasing values of relaxation time, hence for the mucociliary clearance more pressure change is required. It is also previously discussed in Ref. [27] that the propulsion of mucus is quite sensitive for the mucus formation and pressure gradient increase with increasing relaxation times.

Fig. 2

Axial pressure gradient versus axial coordinate for various values of Reynolds number (Re) and Maxwell parameter (${\lambda }_{1}$)

As the mucus flow is generated by the metachronal wave in the axial and radial direction of the tube therefore velocity field is described through the Fig. 3 and Fig. 4. Figure 3(a, b) shows the axial velocity for different values of Reynolds number (Re) and relaxation time (λ₁). These figures show that the increasing values of Reynolds number clearly indicates that the effect of inertial forces is dominate over the viscous force, so mucus flow increases. Similarly, by increasing relaxation time deceleration is produced in the flow. Thus it is concluded that mucus having weak viscoelastic property generates maximum flow and make the fast process of muco ciliary in the airways. Figure 4(a, b) present the velocity distributions in radial direction for various values of Reynolds number (Re) and relaxation time (λ₁) parameter. It is observed through these graphs that the increasing values of Reynolds number make the fast mucus flow in the radial direction across the entire cross-section. Whereas, by increasing relaxation time considerable resistance is produced in the mucus flow since elastic forces make the mucus thick by which the resistive property of mucus enhances which makes the slow flow.

Fig. 3

Axial velocity versus radial coordinate for various values of Reynolds number (Re) and Maxwell parameter (${\lambda }_{1}$)

Fig. 4

Radial velocity versus radial coordinate for various values of Reynolds number (Re) and Maxwell parameter (${\lambda }_{1}$)

For the high flow of mucus metachoronal wave pattern is important so in this study the comparison of symplectic and antiplectic wave patterns are presented in Fig. 5(a-b). The velocity of mucus comprising on a gel material shows that with the increasing values of relaxation time both axial and radial velocities decreases but the magnitude of velocity is high in symplectic wave pattern, so the symplectic wave is more effective than antiplectic wave that is claimed in the first section.

Fig. 5

Comparison of velocity profile of mucus with symplectic and antiplectic wave pattern

The heat transfer analysis of airway-boundary yielded the mucus layer temperature that allowed to predict temperature distributions in the airway as suggested in [24]. In this study the energy and momentum equation is modelled under the inertial effects and elastic property of the fluid. The momentum and energy equation collectively give the expression of temperature distribution of the mucus layers that changes by under the inertial forces and relaxation time. The temperature distribution can be visualized by the Fig. 6(a, b) under different values of Reynolds number (Re) and relaxation parameter (λ₁). Figure (6a) shows that by increasing Reynolds number (Re) temperature distribution reduces as inertial forces make the mucus thin and the process of heat transfer become slow due to reduction in bounding forces within mucus. The reduction in temperature distribution may affect the ciliary beat frequency that will make problem in muco ciliary clearance. Figure (6b) shows that by increasing relaxation time (λ₁) the temperature distribution in the mucus flow increases, because the fluid become thick and attractive force between the molecules enhances which helps to transfer the heat transfer in mucus. Thermal analysis shows that for the mucocilairy clearance the normal temperature is required that is equivalent to the body temperature (37⁰) and in this study it can be controlled by the inertial forces and relaxation time.

Fig. 6

Variation of temperature profile versus radial for various values of Reynolds number (Re) and Maxwell parameter (${\lambda }_{1}$)

5 Conclusions

In this research mathematical model has been developed for cilia induced mucus flow in human respiratory system with the effect of heat transfer at moderate Reynolds number. Upper Convective model is considered as mucus. The governing partial differential equations are transformed from the fixed frame to the wave frame by using Galilean transformation and resulting differential equations are solved by perturbation method considering small wave number. The effects of various parameters i.e. Reynolds number (Re) and relaxation time (λ₁) for specified values of wave number have been shown in graphs. If $Re\to 0$, $\beta \to 0$ and ${\lambda }_{1}\to 0$ the Maxwell fluid model reduces to the viscous fluid model and our results are matching precisely with the existing results [27]. This study has shown following features:

• I. With increasing Reynolds number there is an elevation in axial and radial velocity and

• II. With increasing values of relaxation time there is a substantial enhancement in axial pressure gradient and also a strong retardation in the axial and radial flow.

• III. The graphical results show that with the increasing values of fluid parameter axial velocity decreases which indicates that high viscoelasicty effect the efficiency of ciliary activity that results to reduce the axial flow (horizontal velocity).

• IV. It is analyzed that symplectic wave dominate over the antiplectic wave for the mucociliary clearance in the airways.

• V. Magnitude of temperature profile decreases by increasing Reynolds number and rises by the mounted values of Maxwell parameter.

• VI. The mathematical analysis is precisely matching with the experimental studies [33] in which it has been shown that for rise in viscosity and elasticity of mucus alters the efficiency of propulsion of mucus in the trachea which may be due to respiratory infections. In this study it is also analysed that the flow rate increases for the low values of relaxation time which make the fluid more elastic also the inertial forces help to accelerate the flow which reduces the viscosity of the mucus.

This study shows that mucociliary clearance in the airway can be controlled by the viscosity and elasticity of the mucus in the presence of temperature and inertial effects. The present study will hopefully provide significant applications in bioengineering, medical sciences, and medical equipment for the clearance of viscoelastic fluid from dust and viruses.

In this study we have considered the single layer of mucus in the trachea but near the shaft of cilium and at the center of tube mucus has different viscosity, so in future two layer approach of ciliary motion can be considered.

Appendix

$$ \psi_{0} = \frac{{r^{2} }}{2}w\left( h \right) - \frac{{\left( {2F_{0} - h^{2} w\left( h \right)} \right)\left( {r^{4} - 2r^{2} h^{2} } \right)}}{{2h^{4} }} $$

$$ w_{0} = \frac{{ - 2\left( {2F_{0} - h^{2} w\left( h \right)} \right)}}{{h^{4} }}\left( {r^{2} - h^{2} } \right) + w\left( h \right) $$

$$ u_{0} = \frac{{r^{3} \left( { - 8{\text{F}}_{0} {\text{h}}_{z} + 2h^{2} w\left( h \right){\text{h}}_{z} - h^{3} w_{z} \left( h \right)} \right)}}{{2h^{5} }} + \frac{{r\left( {8{\text{F}}_{0} h^{2} h_{z} + h^{5} w_{z} \left( h \right)} \right)}}{{2h^{5} }} $$

$$ \theta_{0} = 1 - \frac{{Br\left( {2F_{0} + h^{2} w\left( h \right)^{2} } \right)}}{{h^{8} }}\left( {r^{4} - h^{4} } \right) $$

$$ \frac{{\partial p_{0} }}{\partial z} = \frac{{ - 8\left( {2F_{0} - h^{2} w\left( h \right)} \right)}}{{h^{4} }}, $$

$$ \begin{aligned} \psi_{1} = & \frac{{a_{11} }}{6}\left( {\frac{{r^{5} }}{5} - \frac{{r^{2} h^{3} }}{2}} \right) + \frac{{a_{12} }}{32}\left( {\frac{{r^{6} }}{6} - \frac{{r^{2} h^{4} }}{2}} \right) + \frac{{a_{13} }}{15}\left( {\frac{{r^{7} }}{7} - \frac{{r^{2} h^{5} }}{2}} \right) + \frac{{a_{14} }}{180}\left( {\frac{{r^{8} }}{8} - \frac{{r^{2} h^{6} }}{2}} \right) \\ & - \frac{4}{{h^{4} }}\left( {\frac{{r^{4} }}{4} - \frac{{r^{2} h^{2} }}{2}} \right)\left( {F_{1} + \frac{{3h^{5} }}{60}a_{11} } \right) \\ & - \frac{4}{{h^{4} }}\left( {\frac{{r^{4} }}{4} - \frac{{r^{2} h^{2} }}{2}} \right)\left( {\frac{{h^{6} }}{90}a_{12} + \frac{{h^{7} }}{210}a_{13} + \frac{{h^{8} }}{480}a_{14} } \right), \\ \end{aligned} $$

$$ \begin{gathered} w_{1} = \frac{{a_{11} }}{6}\left( {r^{3} - h^{3} } \right) + \frac{{a_{12} }}{32}\left( {r^{4} - h^{4} } \right) + \frac{{a_{13} }}{15}\left( {r^{5} - h^{5} } \right) + \frac{{a_{14} }}{180}\left( {r^{6} - h^{6} } \right) \hfill \\ - \frac{4}{{h^{4} }}\left( {r^{2} - h^{2} } \right)\left( {F_{1} + \frac{{3h^{5} }}{60}a_{11} } \right) - \frac{4}{{h^{4} }}\left( {r^{2} - h^{2} } \right)\left( {\frac{{h^{6} }}{90}a_{12} + \frac{{h^{7} }}{210}a_{13} + \frac{{h^{8} }}{480}a_{14} } \right). \hfill \\ \end{gathered} $$

$$ a_{11} = \frac{{ - 2\left( { - 2F_{0} + h^{2} w\left( h \right)} \right)\left( { - 8F_{0} \lambda_{1} h + 8F_{0} h_{x}^{2} + h^{3} \left( {2\lambda_{1} w\left( h \right) + w_{x} \left( h \right)} \right)} \right)}}{{h^{7} }} $$

$$ \begin{aligned} a_{12} = & \frac{{8\left( {256F_{0}^{2} \lambda_{1} + {\text{Re}} h^{6} w\left( h \right)^{2} + 8F_{0} h^{2} \left( {2F_{0} {\text{Re}} - F_{0} \lambda_{1} - 24\lambda_{1} w\left( h \right)} \right)} \right)}}{{h^{9} }} \\ & + 4h^{4} w\left( h \right)\left( { - 2F_{0} {\text{Re}} + F_{0} \lambda_{1} + 8\lambda_{1} w\left( h \right)} \right)h_{x} \\ & + h^{3} \left( \begin{gathered} 64F_{0} \lambda_{1} + \left( { - {\text{Re}} + \lambda_{1} } \right)h^{4} w\left( h \right) \hfill \\ + h^{2} \left( { - 24{\text{Re}} - 2F_{0} \lambda_{1} + 8 - 32\lambda_{1} w\left( h \right)} \right) \hfill \\ \end{gathered} \right)w_{x} \left( h \right) \\ \end{aligned} $$

$$ a_{13} = \frac{{6\left( { - 2F_{0} h^{2} w\left( h \right)} \right)\left( { - 8F_{0} \lambda_{1} h + 40F_{0} h_{z} - 10h_{z} h^{2} w\left( h \right)} \right) + h^{3} \left( {4\lambda_{1} w\left( h \right) + 5w_{z} \left( h \right)} \right)}}{{h^{9} }} $$

$$ a_{14} = \frac{{8\left( {Re - \lambda_{1} } \right)\left( { - 2F_{0} + h^{2} w\left( h \right)} \right)\left( {\left( {8F_{0} - 2h_{z} h^{2} w\left( h \right)} \right) + h^{3} w_{z} \left( h \right)} \right)}}{{h^{9} }} $$

$$ \begin{gathered} \theta_{1} = \frac{{a_{15} }}{4}\left( {r^{2} - h^{2} } \right) + \frac{{a_{16} }}{16}\left( {r^{4} - h^{4} } \right) + \frac{{a_{17} }}{25}\left( {r^{5} - h^{5} } \right) + \frac{{a_{18} }}{36}\left( {r^{6} - h^{6} } \right) + \frac{{a_{19} }}{49}\left( {r^{7} - h^{7} } \right) \hfill \\ + \frac{{a_{20} }}{64}\left( {r^{8} - h^{8} } \right) \hfill \\ \end{gathered} $$

where the constants are calculated by software “MATHEMATICA”

$$ \begin{aligned} \frac{{\partial p_{1} }}{\partial z} = & \frac{{8\left( { - 2F + h^{2} w\left( h \right)} \right)}}{{h^{4} }} + \frac{1}{{315h^{9} }}\beta (10080F^{2} r^{2} \left( { - 4 + 5r} \right)\lambda_{1} h + 2016F^{2} r^{2} (100 - 25r\left( {5 + \lambda_{1} } \right) \\ &+ r^{2} \left( {{\text{Re}} + 4\lambda_{1} } \right))h_{z} - 56Fh^{2} (2F(90r^{2} \lambda_{1} - 135r\left( {1 + 2\lambda_{1} } \right) + 4(45 + 256\lambda_{1} )) + 27r^{2} \left( {100 - 25r\left( {5 + \lambda_{1} } \right) + r^{2} \left( {{\text{Re}} + 4\lambda_{1} } \right)} \right)w\left( h \right))h_{z} + 4h^{4} ( - 864F^{2} \lambda_{1} \\ & + 7(8F^{2} \left( {19{\text{Re}} + 10\lambda_{1} } \right) + 6F\left( {60 + 512\lambda_{1} + 30r^{2} \lambda_{1} - 45r\left( {1 + 2\lambda_{1} } \right)} \right)w\left( h \right) \\ & + 9r^{2} \left( {100 - 25r\left( {5 + \lambda_{1} } \right) + r^{2} \left( {{\text{Re}} + 4\lambda_{1} } \right)} \right)w\left( h \right)^{2} )h_{z} ) - 35(5{\text{Re}} \\ & + 4\lambda_{1} )]^{9} w\left( h \right)w_{z} \left( h \right) - 8h^{8} w\left( h \right)\left( {w\left( h \right)\left( {234\lambda_{1} + 7\left( {5{\text{Re}} + 3\lambda_{1} } \right)h_{z} } \right) + 387w_{z} \left( h \right)} \right) \\ & -8h^{6} \left( {1792\lambda_{1} w\left( h \right)^{2} h_{z} + Fw\left( h \right)\left( { - 684\lambda_{1} - 7\left( {{\text{Re}} - 14\lambda_{1} } \right)h_{z} } \right) - 774Fw_{z} \left( h \right)} \right) \\ & + h^{7} ( - 90w\left( h \right)^{2} \left( {7\left( { - 4 + 3r} \right)\lambda_{1} - 80h_{z} } \right) + 28F\left( {19{\text{Re}} + 10\lambda_{1} } \right)w_{z} \left( h \right) + 7(90r^{2} \lambda_{1} \\ & -135r\left( {1 + 2\lambda_{1} } \right) + 4\left( {45 + 256\lambda_{1} } \right))w\left( h \right)w_{z} \left( h \right)) - 36Fh^{3} (280r^{2} \left( { - 4 + 5r} \right)\lambda_{1} w\left( h \right) \\ & -1376Fh_{z} + 7(20F\left( { - 4 + 3r} \right)\lambda_{1} - r^{2} (100 - 25r\left( {5 + \lambda_{1} } \right) + r^{2} ({\text{Re}} + 4\lambda_{1} ))w_{z} \left( h \right))) + 2h^{5} (1260r^{2} ( - 4 \\ & +5r)\lambda_{1} w\left( h \right)^{2} - 7F\left( {90r^{2} \lambda_{1} - 135r\left( {1 + 2\lambda_{1} } \right) + 4\left( {45 + 256\lambda_{1} } \right)} \right)w_{z} \left( h \right) - 9w\left( h \right)(2176Fh_{z} \\ &+ 7(30F(4 - 3r)\lambda_{1} + r^{2} (100 - 25r(5 + \lambda_{1} ) + r^{2} ({\text{Re}} + 4\lambda_{1} ))w_{z} (h))))) \\ \end{aligned} $$