1 Introduction

Evaluating the functionality of mucus flow is important as the first defensive mechanism against pathogens and viruses (Xu and Jiang 2019). Trapping and transferring harmful particles toward the stomach using the mucus flow is the so-called mucociliary clearance phenomenon (MCC) (Shang et al. 2019). Investigation of different aspects of MCC process has led to extensive researches including experimental inspections (Xu and Jiang 2019; Shang et al. 2019; Chen et al. 2018; Lubkin et al. 2007; Sedaghat et al. 2016a; Smith et al. 2008; Vasquez et al. 2016; Quraishi et al. 1998), mathematical models (Guo, et al. 1708; Cortez et al. 2005; Eloy and Lauga 2012; Osterman and Vilfan 2011; Gueron and Liron 1992), and numerical simulations (Chen et al. 2018; Sedaghat et al. 2016a; Chatelin et al. 2017).

Exploring modern therapy methods encountered severe challenges in remedying airway diseases due to mucus flow (Quraishi et al. 1998). The limitation of measurement devices, continuous production of mucins through goblet cells, and the effects of boundary conditions on the mucus flow make the issue more complicated. Some experimental investigations addressed the effects of boundary conditions on the mucus flow in human bronchial epithelial (HBE) cell cultures using a rotational cylinder (Vasquez et al. 2016). The others investigated transferring viscoelastic and Newtonian mucus by cilia beating in cell cultures (Lubkin et al. 2007; Dillon et al. 2007; Mitran 2007; Sedaghat et al. 2016b; Lee et al. 2011).

The rate of MCC was specified by the Saccharin test (Shang et al. 2019). The saccharin test was a standard method where a saccharin particle was located 1 cm behind the anterior end of the inferior turbinate and the time was taken until the patient comprehended a sweet taste from the saccharin. Moreover, the variation of MCC rate against diseases including cystic fibrosis caused difficulties in local therapy of nasal airway diseases (Derichs et al. 2011). Cystic fibrosis was one of the most widely recognized genetic diseases (Farrell 2008) which increased and decreased the mucus accumulation and surface liquid volume inside the nasal respiratory system, respectively (Derichs et al. 2011). MCC was in a high order of dependency with cilia beating frequency (Xu and Jiang 2019; Shang et al. 2019; Sedaghat et al. 2016a; Gizurarson 2015). Therefore, an evaluation of the effects of cilia movement on mucus flow was performed to develop multilayer models for MCC rate (Snyder et al. 1988; Hollenberg 1986).

Inspired by biological explorations, the development of different mathematical models was performed to understand the details of the underlying mechanisms of MCC process (Fauci and Dillon 2006; Lauga and Powers 2009). Mathematical models were developed to determine the formation of metachronal waves (rhythmic back-and-forth movement), conditions for the stability of the metachronal wave, the cilium mechanism to generate force for propelling the mucus, and the efficiency of MCC. The simple mathematical models were developed by studying the wavelike motion in polychaete worm (Gray 1939) and sea-urchin spermatozoa (Gueron and Liron 1992; Gray and Hancock 1955). These studies neglected the effects of fluid flow on cilia motion. The further models were established based on resistance theory (Xu and Jiang 2019) which considered the effects of fluid flow in modeling cilia (Eloy and Lauga 2012; Osterman and Vilfan 2011; Blake 1972, 1971; Barton and Raynor 1967). The metachronal wave led to a movement of the mucus layer with an average velocity of 5 mm min−1 (Illum 2003; Mistry et al. 2009). Therefore, to consider the effects of mucus flow on the cilia motion the inertia terms were neglected and the Navier–Stokes equations turned to Stokes equations. In this way, the Stokeslet method which was developed based on the slender body theory (Dusenbery 2009) used to solve the equations.

By using mathematical models, a variety of numerical investigations were conducted in different categories. The cilia beating frequency, the interaction between mucus flow and cilia, and the interaction between the airway surface liquid (ASL) layer and macroscale were different aspects of numerical simulations (Shang et al. 2019; Chen et al. 2018; Sedaghat et al. 2016a, b). The effects of cilia beating frequency were evaluated on MCC rate by Sedaghat et al. (Sedaghat et al. 2016a). The linear relation between MCC and cilia beating frequency was obtained as the result. Furthermore, the porosity effects on viscoelastic cilia-driven flow in a divergent channel were evaluated by Javid et al. (Javid et al. 2021), numerically. They analyzed 2D cilia-driven flow under different physical parameters and observed boundary layer phenomena in the velocity profile by increasing porosity and relaxation time. Moreover, increasing the porosity and viscoelastic effects led to the reduction of trapped bolus magnitude in the divergent channel. The effects of heat transfer and induced magnetic field were also inspected on the cilia-driven flow analytically by Ishtiaq et al. (Ishtiaq et al. 2022). It was concluded the velocity and magnetic fields were in opposite directions than the eccentricity parameter of the cilia equations. Furthermore, the temperature profile was increased for Prandtl and Eckert number, while it was decreased due to thermal radiation. The development of multilayer models for MCC was reviewed in another line of studies based on the interaction between mucus flow and cilia beating frequency (Shang et al. 2019; Sedaghat et al. 2016b). Moreover, the effects of different nasal cavities on the rate of MCC were inspected by many researchers (Gizurarson 2015; Pires et al. 2009; Corbo et al. 1989). It was concluded simulation of mucus flow inside 3D shell surface models provided a closer rate of MCC against experimental data (Shang et al. 2019).

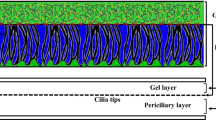
Modeling the ASL layer as a single or two-layer model was one of the differences between numerical simulations. Based on the hypotonic-defensin hypothesis, the ASL layer was a single layer (Shang et al. 2019; Vasquez et al. 2016; King et al. 1993; Satir and Sleigh 1990; Sleigh 1977), while the modern hypothesis stated that it was a two-layer model (Sedaghat et al. 2016a, b; Ross and Corrsin 1974; Matar et al. 2002; Zhu 2019). The other difference was related to the boundary condition at the lower boundary of the ASL layer. The common boundary conditions were constant (Shang et al. 2019) and continuous cyclic (sine or cosine) (Sedaghat et al. 2016a, b) velocities. However, the real boundary condition was neither constant nor continuous cyclic and should be applied at the mucus–periciliary interface (Vasquez et al. 2016). The last difference was the use of different fluids as mucus including viscoelastic (Sedaghat et al. 2016a, b; Vasquez et al. 2016), power law (Chatelin et al. 2017), and Newtonian fluids (Shang et al. 2019; Vasquez et al. 2016). On the other hand, the use of the free-slip condition at the upper boundary of the mucus layer was a common feature of numerical simulations.

Nowadays, the dangers of COVID-19 epidemic are plaguing most researchers all over the world to find different methods to prevent the penetration of viruses into the respiratory system (Zanin et al. 2016; Khashkhosha and Elhadi 2020; Sundararaman 2020; Chowdhury 2020). The impacts of COVID-19 on the respiratory system were discussed by Chowdhury et al. (Chowdhury 2020). Since the first defensive shield of the body against pathogens is the ASL layer (Sundararaman 2020), obtaining adequate knowledge is essential about the structure of the ASL layer under the influence of different conditions.

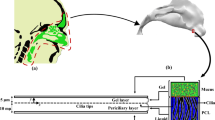
In the present study, two types of non-Newtonian fluids including power law and thixotropic are considered as the nasal mucus. Although the existence of cilia is neglected, their motion is replaced with four velocity profiles at the lower boundary of the mucus layer. The cyclic boundary conditions are continuous constant effective stroke, discrete constant effective and recovery strokes, continuous cyclic effective stroke, and discrete cyclic effective stroke along with constant recovery stroke. Moreover, the upper boundary of the mucus layer is exposed to free shear stress. The squared part in Fig. 1 is modeled using two infinite parallel plates to simulate mucus flow inside the nasal cavity.

Fig. 1
figure 1

Modeling of MCC structure inside the nasal cavity with two infinite parallel plates

Full size image

2 Governing equations

The fluid flow is evaluated by the sets of continuity and momentum equations along with an extra constitutive equation related to the shear stress as follows:

$$ \nabla \,{\mathbf{.u}} = 0 $$
(1)
$$ \rho \left( {\frac{{\partial {\mathbf{u}}}}{\partial t} + {\mathbf{u}}{\mathbf{.}}\nabla {\mathbf{u}}} \right) = \nabla {\mathbf{.}}\,{{\varvec{\upsigma}}} $$
(2)

where u, t, ρ, and σ are the velocity vector, time, density, and the Cauchy stress tensor, respectively. The Cauchy stress tensor is calculated by:

$$ {{\varvec{\upsigma}}} = - p{\mathbf{\rm I}} + {{\varvec{\uptau}}} $$
(3)

where τ, I, p denote the extra stress tensor, the unit tensor, and the pressure, respectively. In this study, two different types of fluids including power law and thixotropic are considered as the mucus layer. The deviatoric stress tensor can be expressed as:

$$ \left\{ \begin{gathered} {{\varvec{\uptau}}} = \left( {k\dot{\gamma }^{n - 1} + \frac{{\tau_{0} }}{{\dot{\gamma }}}} \right){\dot{\mathbf{\gamma }}}\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,\,\tau > \tau_{0} \hfill \\ \dot{\gamma } = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,\,\,\tau \le \tau_{0} \hfill \\ \end{gathered} \right. $$
(4)

where τ0, n, k, and \({\dot{\mathbf{\gamma }}}\) are the yield stress, the power index, the consistency index, and the deformation rate tensor, respectively. Moreover, τ and \(\dot{\gamma }\) are the magnitudes of τ and \({\dot{\mathbf{\gamma }}}\), respectively. The yield stress is equal to zero for the power law fluid.

Thixotropic fluid deals with the microstructure of materials which evolves with the time of flowing. The evolution of microstructure is modeled by the definition of a structural parameter λ ranging from 0 to 1 (Bui and Ho 2020). The lower and upper limits correspond to completely broken and fully recovered states of the microstructure, respectively. The constitutive equation to calculate the rate of evolution for λ is determined by:

$$ \frac{\partial \lambda }{{\partial t}} + {\mathbf{u}}{\mathbf{.}}\nabla \lambda = K_{1} \left( {1 - \lambda } \right)^{m} - K_{2} \lambda^{n} $$
(5)

where m and n are the rate indices and K1 and K2 are the rate parameters. The recovery and breakdown rates correspond to the first and second terms on the RHS of Eq. (5), respectively. In the present study, Burgos’s (Burgos et al. 2001), thixotropic fluid is considered as the mucus layer with the following evolution equation for λ.

$$ \frac{\partial \lambda }{{\partial t}} + {\mathbf{u}}{\mathbf{.}}\nabla \lambda = \alpha \left( {1 - \lambda } \right) - \beta_{1} \lambda \dot{\gamma }\exp \left( {\beta_{2} \dot{\gamma }} \right) $$
(6)

where α1, β1, and β2 are the recovery, breakdown, and breakdown exponent parameters, respectively.

3 Physiology of the ASL layer

The polymeric structure of ASL consists of two different fluids (Sedaghat et al. 2016a; Quraishi et al. 1998): Newtonian and non-Newtonian (Quraishi et al. 1998). The Newtonian fluid (periciliary layer) is placed at the bottom of the non-Newtonian fluid (mucus) and provides one-way movement for the mucus layer (Blake 1971; Brennen 1974). The non-Newtonian mucus moves on the lower fluid by cilia beating which is the main mechanism for transporting pathogens and harmful substances (Blake 1971; Brennen 1974). Cilia beating is a composition of two different strokes: effective and recovery strokes (Xu and Jiang 2019). In the effective stroke, cilia penetrate the mucus layer and push it toward the esophagus (MCC) (Blake 1971; Brennen 1974) then detach from the mucus layer and move back through the periciliary layer in the recovery stroke. This type of cilia movement leads to unilateral movement of the mucus layer. Cilia are surrounded by the periciliary layer (Blake 1971, 1975; Brennen 1974; Brennen and Winet 1977) and perform rhythmic back-and-forth movement (metachronal wave) (Blake 1971; Brennen 1974). The structure of the mucus layer is different in micro- and macroscales which behaves like a low viscous fluid and non-Newtonian one, respectively (Lai et al. 2009). Mucus constituents are 0.02% DNA, 1% lipids, 1% mineral, 2–3% glycoproteins and proteins, and 95% water (Potter et al. 1967; Matthews et al. 1963). The total height of mucus layers is 15 µm (Gizurarson 2015) which 33% is related to the thickness of the mucus layer (Shang et al. 2019), and the rest belongs to the periciliary layer (Quraishi et al. 1998). At the resting rate secretion of mucus is about 0.5–1 ml cm−2 mucus over 24 h which moves toward the posterior of the nasopharynx (Quraishi et al. 1998) with the rate of 5–10 mm min−1 (Illum 2003; Mistry et al. 2009; Lale et al. 1998; Rusznak et al. 1994). The rate of mucus flow is in a high order of dependency with the cilia beating frequency (Xu and Jiang 2019; Shang et al. 2019; Sedaghat et al. 2016a; Gizurarson 2015) and the evaluated frequencies are 15 Hz (T = 1/15 s) and 30 Hz (T = 1/30 s) (Cornaz and Buri 1994; Ugwoke et al. 2001; Sanderson and Sleigh 1981) in the present study. The density of goblet cells specifies the mucus secretion which is about 5700–11,000 cells per ml (Dalhamn 1956) in adults. When the rate of mucus secretion exceeds the normal state (Rhinorrhea) (Myon et al. 2010), the mucus is directed out of the respiratory tract due to the disability of the cilia in transferring extra mucus. Furthermore, respiratory mucosa contains enzymes including lysozyme that play a key role in eliminating harmful particles (Singh et al. 2002).

4 Boundary conditions

Simulation of mucus flow is performed between two parallel plates with a length-to-the hydraulic diameter ratio (L/Dh) of 300. Dh is the hydraulic diameter and defined using Eq. (7).

$$ D_{h} = {4}A/P $$
(7)

where A and P are the flow cross section and wetted perimeter of the cross section, respectively (Kahramanoglu et al. 2017).

The applied boundary conditions to the computational domain are the free shear stress at the top of the mucus layer, atmospheric pressure at the outlet boundary, and different velocity profiles at the lower bound of the mucus layer. The different patterns of velocity profiles are exposed on the bottom plate shown in Fig. 2.

Fig. 2
figure 2

Different velocity profiles exert on the mucus–periciliary interface a continuous constant effective stroke, b discrete constant effective and recovery strokes, c continuous cyclic effective stroke, d discrete cyclic effective stroke along with constant recovery stroke

Full size image

As the first step in mucus flow simulation, the assumption of permanent contact of cilia and the mucus layer (constant effective stroke) is investigated (profile (a)). By applying the recovery stroke to profile (a), the effects of both effective and recovery strokes are examined on the mucus layer variations (profile (b)).

In the second step, the effect of gradual effective stroke is evaluated by substituting profile (a) with profile (c). Furthermore, to consider a more realistic motion for cilia beating the combination of the gradual effective and recovery strokes is used for further numerical simulations (profile (d)). Figure 3 indicates different flow times to examine velocity variations of the mucus layer.

Fig. 3
figure 3

Different flow times to examine velocity variations of the mucus layers

Full size image

5 Numerical procedure

Incompressible and unsteady 2D Navier–Stokes equations are solved numerically to obtain variations of the mucus velocity field. Due to the high viscosity of the mucus layer and the cilia metachronal wave, the mucus movement is generally from the anterior to the posterior of the nasal cavity and there is nearly no lateral mucus movement (Xu and Jiang 2019; Gsell et al. 2020; Schneiter et al. 2021). Therefore, the mucus movement in the third direction is neglected. The high order of viscous forces against the inertia forces inside the mucus layer (Re  ≪ 1) leads to discretize the convection terms with the central scheme. To accelerate the convergence rate of the solution, multi-grid method is applied to the equations. Furthermore, to handle the pressure–velocity coupling the PIMPLE algorithm (Roohi et al. 2016) is used and the flow variables are stored using the arrangement of a collocated grid (Round 1980; Flórez-Orrego et al. 2012). By setting the time step size to 10–5, the courant number (uΔt/Δx) is controlled during the numerical solutions less than one. To obtain the convergence stability for the solution, the residuals of all variables are set to less than 10–9. All numerical solutions are accomplished using OpenFOAM 7 packages.

The grid independency test and uncertainty of grid discretization are evaluated using the grid convergence index (GCI) (Celik et al. 2008). The grid size of 5 × 104 results in the GCI factor less than 2% for the velocity variations inside the mucus layer all over the computational domain.

6 Results and discussion

Velocity variations inside the mucus layer are discussed using two different approaches: power law and thixotropic in the following subsections. A variety of different boundary conditions are applied on the lower bound of the computational domain as cilia motion to evaluate the response of the mucus layer. Furthermore, the effects of different parameters including the power index, the consistency index, and the recovery and breakdown parameters on the behavior of the mucus layer are examined using two different fluids, separately. The duration of each simulation is 5 s equivalent to 150 and 75 cycles for cilia oscillating frequencies 30 and 15 Hz, respectively, and the results are extracted from the last cycle. Figure 4 shows the validation of numerical results against the available in Ref (Chatelin and Poncet 2016), and dML and dASL are the depth of mucus and ASL layers, respectively.

Fig. 4
figure 4

Validation of numerical results against the available data (Chatelin and Poncet 2016)

Full size image

6.1 Power law mucus layer

The power index is less than one (n < 1) to save the shear-thinning property of the mucus layer. The effects of different power and consistency indexes are investigated separately. The power and consistency indexes are 0.482 and 0.355 for a healthy mucus layer, respectively (Chatelin et al. 2017). Therefore, all the numerical simulations are performed for the effects of different power and consistency indexes at k = 0.355 and n = 0.482, respectively.

Figure 5 indicates the velocity variation of the mucus layer affected by profile (a) for a range of power and consistency indexes (n = 0.2–0.8 and k = 10–4–10). The constant effective stroke provides sufficient time for the mucus flow to adjust the changes from the bottom plate, and the mucus layer characteristics become independent of the changes in fluid indexes. Therefore, the velocity field all over the layer is the same as the velocity at the lower bound.

Fig. 5
figure 5

Velocity variations of the mucus layer using profile (a) along with zero shear stress on the upper bound of the mucus layer for different power and consistency indexes

Full size image

6.1.1 Influence of the consistency index (k)

By applying profile (b) to the lower bound of the mucus layer, the effects of different consistency indexes are determined on the mucus velocity field in the recovery stroke (Fig. 6). Increasing the consistency index leads to an increment of the adaptation rate of the mucus layer with the changes from the bottom plate. Adaptation rate describes the response rate of mucus layer velocity to the changes from the mucus–periciliary interface velocity. According to Fig. 6, variations of the mucus layer become independent of the changes in the consistency index for values greater than 0.01 (k ≥ 10–2). The changes in the mucus layer are consistent with the changes in the bottom plate and are independent of the fluid indexes when the constant effective stroke of profiles (a) and (b) is applied to the lower bound, because the mucus flow has enough time to respond to the changes from the bottom plate.

Fig. 6
figure 6

Velocity variations of the mucus layer using profile (b) in the recovery stroke along with zero shear stress on the upper bound of the mucus layer for different consistency indexes with n = 0.482

Full size image

Substituting profile (a) with profile (c) (gradual effective stroke) provides transient variations for the mucus flow, and there is not enough time to adapt to the changes from the bottom plate. Figure 7 shows the mucus velocity at different times using profile (c). Although the adaptation rate increases with the increment of the consistency index, the rate of adaptation increases and decreases over time, repeatedly (Table 1). The maximum adaptation rate is taken into account using Eq. (8).

$$ {\text{Adaptation rate}} = 100 - \frac{{\left| {\left( \frac{u}{U} \right)_{{{\text{interface}}}} - \left( \frac{u}{U} \right)_{{{\text{mucus}}}} } \right|}}{{\left( \frac{u}{U} \right)_{{{\text{interface}}}} }} \times 100 $$
(8)
Fig. 7
figure 7

Velocity variations of the mucus layer using profile (c) affected by zero shear stress on the upper bound of the mucus layer for different consistency indexes with n = 0.482 a t/T = 1/8, b t/T = 2/8, c t/T = 3/8

Full size image
Table 1 Maximum adaptation rates for a range of consistency indexes using profile (c)
Full size table

The differences between acceleration rates at periods (t/T = 0 to t/T = 1/8) and (t/T = 1/8 to t/T = 2/8) and deceleration rates at periods (t/T = 2/8 to t/T = 3/8) and (t/T = 3/8 to t/T = 4/8) cause differences between adaptation rates (Fig. 8). The rates of acceleration and deceleration at periods (t/T = 0 to t/T = 1/8) and (t/T = 3/8 to t/T = 4/8) are more than (t/T = 1/8 to t/T = 2/8) and (t/T = 2/8 to t/T = 3/8) periods, respectively. Therefore, at periods (t/T = 0 to t/T = 1/8) and (t/T = 3/8 to t/T = 4/8) the adaptation rate of the mucus flow is less than (t/T = 1/8 to t/T = 2/8) and (t/T = 2/8 to t/T = 3/8) periods. The differences between adaptation rates at two times t/T = 1/8 and t/T = 3/8 relate to the acceleration rate at period (t/T = 0 to t/T = 1/8) and the deceleration rate at period (t/T = 2/8 to t/T = 3/8), respectively. The acceleration rate at period (t/T = 0 to t/T = 1/8) is more than the deceleration rate at period (t/T = 2/8 to t/T = 3/8). Therefore, mucus flow adapts faster with the changes from the bottom plate at period (t/T = 2/8 to t/T = 3/8) than the periods (t/T = 0 to t/T = 1/8).

Fig. 8
figure 8

Different acceleration and deceleration rates over time

Full size image

By imposing a complete pattern of cilia motion (profile (d)) at the bottom plate, the obtained results for the effective stroke are the same as those obtained using profile (c), because the mucus flow ceases completely in the recovery stroke. The results of recovery stroke are similar to those obtained using profile (b); however, the adaptation rate and the order of velocities are more and lower than the values using profile (b), respectively (Fig. 9), because the mucus flow enters the recovery stroke with the velocity close to zero.

Fig. 9
figure 9

Velocity variations of the mucus layer using profile (d) in the recovery stroke along with zero shear stress on the upper bound of the mucus layer for different consistency indexes with n = 0.482

Full size image

6.1.2 Influence of the power index (n)

The independence of the mucus layer variations from changes in power index is shown in Figs. 10 and 11. Although different boundary conditions (profiles (a)–(d)) are imposed at the bottom plate, there are no changes in the velocity field using different power indexes. It is concluded that the mucus velocity is independent of the indexes variations and has enough time to adjust the changes from the bottom plate, while k ≥ 0.01 and 0.2 ≤ n < 1. Figures 10 and 11d show the mucus velocity under the influence of recovery stroke using profiles (b) and (d), respectively. The lower order of velocity filed in the recovery stroke using profile (d) is related to the velocity close to zero at the end of the effective stroke. The same variation of the mucus velocity in the effective stroke using both profiles (c) and (d) is presented in Fig. 11a–c, and the maximum adaptation rates are given in Table 2.

Fig. 10
figure 10

Velocity variations of the mucus layer using profile (b) in the recovery stroke along with zero shear stress on the upper bound of the mucus layer for different power indexes with k = 0.355

Full size image
Fig. 11
figure 11

Velocity variations of the mucus layer using profiles (c) and (d) affected by zero shear stress on the upper bound of the mucus layer for different power indexes with k = 0.355 a t/T = 1/8, b t/T = 2/8, c t/T = 3/8, d t/T = 5/8 (recovery stroke of profile (d))

Full size image
Table 2 Maximum adaptation rates for a range of power indexes using profile (c)
Full size table

Similar to Table 1, the differences in adaptation rates are due to differences in the acceleration and deceleration rates at different times. According to the results presented in Figs. 5, 6, 7, 8, 9, 10 and 11 and Tables 1 and 2, changes in power law fluid indexes were ineffective on the mucus velocity field. Figure 12a and b shows comparisons between high viscous Newtonian (12 Pa s) and power law fluids for the mucus layer in the effective and recovery strokes that there are no differences between the fluids. Therefore, the power law mucus could be substituted with a high viscous (12 Pa s) Newtonian mucus (Shang et al. 2019; Puchelle et al. 1987).

Fig. 12
figure 12

Comparison of mucus layer velocity using both Newtonian and power law fluids affected by profile (d) and zero shear stress on the upper bound of the mucus layer for different power and consistency indexes a effective stroke, b recovery stroke

Full size image

6.2 Thixotropic mucus layer

To investigate the effects of time-varying viscosity, power law fluid is replaced with thixotropic fluid. In the present study, Burgos’s thixotropic model is used as the mucus fluid and the effects of different parameters including recovery, breakdown, and breakdown exponent parameters are evaluated, separately. The evaluation ranges for recovery, breakdown, and breakdown exponent parameters are (10–3 − 1), (10–3 − 1), and (5 × 10–4 − 1), respectively.

Figure 13 shows the mucus velocity field affected by profile (a) and effective stroke of profile (b) for all fluid parameters in the aforementioned ranges. Although all flow parameters have changed, the effect of boundary conditions is such that the fluid has ample opportunity to adapt to the bottom plate changes. Therefore, uniform distribution is observed all over the mucus layer.

Fig. 13
figure 13

Velocity variations of the mucus layer using profile (a) along with zero shear stress on the upper bound of the mucus layer for different recovery, breakdown, and breakdown exponent parameters

Full size image

6.2.1 Influence of the recovery parameter (α)

The effects of different recovery parameters (α = 10–3 − 1) in the presence of β1 = 0.05 and β2 = 0.05 are indicated in Fig. 14 for the recovery stroke. For small recovery parameters, the structural parameter (λ) is small and the effect of the breakdown parameter (β1 = 0.05) is greater, i.e., the structure of the fluid is broken. When the fluid microstructure is broken, the behavior of the flow tends to low viscous liquid flow. However, when α → 1, λ increases, and the effect of the breakdown parameter decreases, thus the structure of the flow is recovered. Increasing the recovery parameter leads to an increase in the recovery rate of the fluid structure, and the mucus flow tends to a solid state. Therefore, with the decline of α the rate of adaptation increases, and the mucus adjusts to the changes from the bottom plate faster.

Fig. 14
figure 14

Velocity variations of the mucus layer using profile (b) in the recovery stroke along with zero shear stress on the upper bound of the mucus layer for different recovery parameters with β1 = 0.05 and β2 = 0.05

Full size image

Regardless of α values, the mucus flow has stopped completely in the recovery stroke and it does not affect the mucus flow pattern in the effective stroke. Therefore, the results using profile (c) and the effective part of profile (d) are the same. Figure 15 shows the variation of mucus flow in the effective stroke for different values of α over time. By increasing time, the rate of adaptation due to the effects of acceleration and deceleration rates over time increases and decreases, repeatedly. As a result, the effects of the recovery parameter on the mucus velocity field are negligible against the rates of acceleration and deceleration over time for the effective stroke (see the previous section). The rates of acceleration and deceleration are related to the frequency and amplitude of the profiles (c) and (d). However, when the bottom plate encounters zero velocity in the recovery stroke (there are no acceleration and deceleration rates), the effects of the recovery parameter become more visible on the mucus flow. The maximum adaptation rates for different recovery parameters are given in Table 3.

Fig. 15
figure 15

Velocity variations of the mucus layer using profiles (c) and (d) affected by zero shear stress on the upper bound of the mucus layer for different recovery parameters with β1 = 0.05 and β2 = 0.05 a t/T = 1/8, b t/T = 2/8, c t/T = 3/8, d t/T = 5/8 (recovery stroke of profile (d))

Full size image
Table 3 Maximum adaptation rates for a range of recovery parameters using profile (c)
Full size table

6.2.2 Influence of the breakdown parameter (β 1)

Investigation of breakdown parameter (β1 = 10–3 − 1) on the mucus flow in the presence of α = 0.05 and β2 = 0.05 is shown in Figs. 16 and 17. Figure 16 is related to the mucus velocity variations in the recovery stroke by increasing the breakdown parameter. According to Fig. 16, increasing the breakdown parameter causes the mucus flow to react slower to the changes from the bottom plate. Increasing breakdown parameter causes the reduction of fluid structural parameter, and fluid behaves as a low viscous liquid. In the recovery stroke in which the mucus flow completely ceases, the adaptation rate increases as the β1 parameter decreases.

Fig. 16
figure 16

Velocity variations of the mucus layer using profile (b) in the recovery stroke along with zero shear stress on the upper bound of the mucus layer for different breakdown parameters with α = 0.05 and β2 = 0.05

Full size image
Fig. 17
figure 17

Velocity variations of the mucus layer using profiles (c) and (d) affected by zero shear stress on the upper bound of the mucus layer for different breakdown parameters with α = 0.05 and β2 = 0.05 a t/T = 1/8, b t/T = 2/8, c t/T = 3/8, d t/T = 5/8 (recovery stroke of profile (d))

Full size image

Variation of mucus velocity field over time is shown in Fig. 17 for the effective stroke. During the effective stroke, by increasing β1 parameter the fluid structure is broken more than it recovered, and adjust the changes slowly. Similar to α parameter, the effects of β1 parameter are negligible against the acceleration and deceleration rates. The reduction of acceleration rate at period (t/T = 1/8 to t/T = 2/8) against (t/T = 0 to t/T = 1/8) period causes the mucus flow to obtain sufficient time to adapt to the variations over time (Fig. 17a and b). Thus, the effects of β1 parameter are small at period (t/T = 1/8 to t/T = 2/8) and then become significant at t/T = 3/8 and t/T = 5/8 due to deceleration rate (Fig. 17c and d). Table 4 shows the adaptation rates over time which are taken into account using Eq. 8.

Table 4 Maximum adaptation rates for a range of breakdown parameters using profile (c)
Full size table

6.2.3 Influence of the breakdown exponent parameter (β 2)

The influence of the breakdown exponent parameter (β2) is similar to the breakdown parameter (β1), except that it is more effective on the mucus flow. Figures 18 and 19 show the mucus flow under the influence of β2 variations. The evaluation range for β2 is (5 × 10–4 − 1) with α = 0.05 and β1 = 0.05. The effects of β2 become important, while the value of the recovery parameter is more than β1 parameter. In this section due to the equal values for α and β1 parameters, the role of β2 parameter is clear. Figure 18 illustrates the variation of velocity for different β2 parameters in the recovery stroke which adapts to the bottom plate changes slower when β2 → 1.

Fig. 18
figure 18

Velocity variations of the mucus layer using profile (b) in the recovery stroke along with zero shear stress on the upper bound of the mucus layer for different breakdown exponent parameters with α = 0.05 and β1 = 0.05

Full size image
Fig. 19
figure 19

Velocity variations of the mucus layer using profiles (c) and (d) affected by zero shear stress on the upper bound of the mucus layer for different breakdown exponent parameters with α = 0.05 and β1 = 0.05 a t/T = 1/8, b t/T = 2/8, c t/T = 3/8, d t/T = 5/8 (recovery stroke of profile (d))

Full size image

The effects of β2 parameter on the velocity field over time are shown in Fig. 19. Similar to the previous section, by increasing β2 the mucus flow adjusts to the changes slowly, but the rate of adaptation is different over time. By tending to the maximum velocity, the effect of β2 decreases due to the reduction of acceleration rate and increases in the deceleration rates (Fig. 19a–d). The maximum rates of adaptation are given in Table 5 for different β2 parameters over time.

Table 5 Maximum adaptation rates for a range of breakdown exponent parameters using profile (c)
Full size table

Inspection of the velocity field using three different recovery, breakdown, and breakdown exponent parameters shows the mucus flow variations are independent of all values of α, β1, β2 in the effective stroke. However, independence of the mucus flow variations occurs for α, β1, β2 ≤ 0.05 in the recovery stroke. To examine the replacement of the thixotropic fluid with a high viscous Newtonian fluid, variations of the mucus velocity for different fluid parameters are investigated (Fig. 20a and b). The maximum difference between Newtonian and thixotropic fluids is 1% for the effective stroke, while it is more than 98.5% for the recovery stroke. Differences are calculated using Eq. (9).

$$ \frac{{\left| {\left( \frac{u}{U} \right)_{{{\text{Newtonian}}}} - \left( \frac{u}{U} \right)_{{{\text{Thixotropic}}}} } \right|}}{{\left( \frac{u}{U} \right)_{{{\text{Thixotropic}}}} }} \times 100 $$
(9)
Fig. 20
figure 20

Comparison of mucus layer velocity using both Newtonian and thixotropic fluids affected by profile (d) and zero shear stress on the upper bound of the mucus layer for different recovery, breakdown, and breakdown exponent parameters a effective stroke, b recovery stroke

Full size image

Based on the results obtained for the velocity field, it is concluded that the replacement of thixotropic fluid with Newtonian fluid is only acceptable in the effective stroke. However, the difference between results is so great in the recovery stroke that the replacement of the thixotropic fluid with a Newtonian fluid is invalid. The velocity using thixotropic fluid (7 × 10–5) is at least two orders of magnitude higher than Newtonian fluid (10–6).

7 Concluding remarks

The velocity variations of the mucus layer were evaluated using power law and thixotropic fluids under different cyclic boundary conditions. The effects of changes in the fluid model parameters were examined on the mucus velocity field. The results showed differences were negligible due to replacing the power law fluid with the Newtonian fluid. Therefore, replacing the power law fluid with the Newtonian fluid was acceptable when zero shear stress was applied on the upper bound of the mucus layer. However, the substitution of thixotropic fluid with the Newtonian fluid was acceptable only for the effective stroke (maximum difference value was 1%), because both fluids have a high order of differences (98.5%) in the recovery stroke. On the other hand, the rates of adaptation indicated the mucus flow had ample opportunity to adapt to the changes resulting from the bottom plate. Thus, the mucus flow ceased completely in the recovery stroke and it did not affect the velocity field in the effective stroke. The maximum adaptation rate was taken into account for each case, and it was concluded the rate of acceleration and deceleration had significant effects on the adaptation rate. It was observed that the effects of recovery, breakdown, and breakdown exponent parameters on the mucus flow variations were the same for the effective stroke and led to similar adaptation rates. However, velocity variations showed the effects of the exponent parameter were more than the other two parameters in the recovery stroke. In the continuation of the present work, the viscoelastic effects can be studied using the 5-mode nonlinear Giesekus model. Moreover, the effects of movement induced by the separation of cilia from the mucus layer in the recovery stroke can be investigated, because in the current study the recovery stroke is zero, while in the real model it is opposite to zero. It is also better to use real cilia motion in connection with the mucus layer than a movement plate to obtain more accurate information about the mucus flow in the nasal airway system.