1 Introduction

Depending upon the shape and cross-section of the duct, the fluid has various velocity distribution. Ducts with different shapes such as rectangular, circular, trapezoidal and triangular are commonly used in several applications particularly heat exchangers (such as trapezoidal cross-section [1, 2], circular cross-section [3], and elliptic cross-section [4]), cooling systems (like microscale cooling [5], vortex cooling [6], and circular cooling [7]) and microchannels (for example arbitrary cross-section [8, 9], trapezoidal cross-section [10, 11], circular cross-section [12, 13]).

Plenty of studies on the different shape of the duct cross-section have been conducted during the decades. Yuan et al. [14] simulated fully developed laminar flow and heat transfer in fuel cell, numerically. They considered rectangular and trapezoidal cross-section. They applied finite volume method (FVM) for solving the problem. They reported that the aspect ratio has significant effect on the thermal-hydrualic parameters.

The efficiency dependency of the coolant on the channel’s cross-section in microchannels is provided by Sharma et al. [15]. They analyzed the performance of trapezoidal (with two configurations A and V-type) and rectangular microchannels. They modeled and solved the problem by FVM using FLUENT. They concluded that for the same flow rate for all geometries, one type of trapezoidal configuration offers an appropriate choice.

Zhang [16] provided an investigation on transient heat and mass transfer in a hexagonal cross-section duct. He investigated the problem both numerically and experimentally. He observed that the thickness of wall has notable effects unlike steady-state heat transfer tube.

Ciofalo and Di Liberto [17] employed Computational Fluid Dynamics (CFD) to investigate heat transfer in serpentine pipes for laminar and fully developed flow. They picked various curvature and curvature radius for each geometry. The numerical results were compared with experimental results.

Navardi et al. [18] yielded some correlations in a noncircular cross-section for velocity profiles and flow resistance. They discussed how to drive an analytical solution describing the flow profile for geometries like triangles or trapeziums or rectangles.

Letelier et al. [19] solved a steady laminar viscoelastic fluid flow in a straight tube with arbitrary cross-section. They used the mapping method to model the cross-section geometry. They applied the asymptotic series for expanding the variables. The temperature distributions for each cross-section were provided.

Heat transfer and flow characteristics of heat exchangers with different trapezoidal ducts was examined by Zhang et al. [20]. They observed that the temperature difference distribution and pressure drop in trapezoidal ducts are better than that of in rectangular ducts. Thus, the heat transfer enhances.

Moorthi and Sharma [21] examined the fully developed laminar fluid flow and heat transfer in non-circular sub-channel geometries. The aforementioned geometries are representing a typical nuclear fuel bundle. They simulated the problem numerically in COMSOL multi physics code as classical PDEs. The effect of different aspect ratio on fRe, flow and temperature distributions. Moreover, correlations are provided to estimate flow and heat transfer characteristics as a function of p/d ratio for non-circular sub-channels by least square regression analysis.

Here we motivated from the authors’ previous work [22], and aim to apply both sine and cosine transform functions to investigate the influence of round edge on the fluid flow through a duct. Furthermore, the velocity distribution correlation in both Cartesian and Cylindrical coordinates will be obtained.

In the following sections, the problem is described, the governing equations and boundary conditions are defined, then using the dimensionless parameters, the equations are transformed into dimensionless form. Afterward, the solution methodology is defined and applied, then the validation of the results is presented, and in the next, the results and discussions are provided.

2 Description of problem

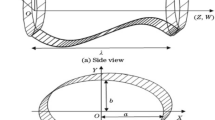
In this paper, we consider a fully developed, laminar, incompressible, Newtonian fluid flow in a ducts. We are going to investigating the impact of the duct edge on the flow. Because of the simplicity of the super-ellipse function toward other similar functions like hyper-ellipsoid function, it is preferred for modeling the duct edge. Generally, super-ellipse in Cartesian coordinates is defined as [23, 24]:

$${\left|\frac{x}{A}\right|}^{m}+{\left|\frac{y}{B}\right|}^{m}=1$$
(1)

where m, A and B are positive numbers. Replacing x = rcosθ and y = rsinθ, the super-ellipse function can be represented in cylindrical coordinates as:

$$\frac{1}{{A}^{m}}\left({\left(r\mathit{cos}\theta \right)}^{m}+\frac{{\left(r\mathit{sin}\theta \right)}^{m}}{{\varepsilon }^{m}}\right)=1$$
(2)

where \(\varepsilon =\frac{B}{A}\). Therefore, the radius of the cross-section, according to θ can be obtained as:

$$r=\frac{A}{{\left({\left(\mathit{cos}\theta \right)}^{m}+{\left(\frac{\mathit{sin}\theta }{\varepsilon }\right)}^{m}\right)}^\frac{1}{m}}$$
(3)

In the present research, we have chosen different m to produce different edges as illustrated in Figs. 1 and 2.

Fig. 1
figure 1

Ducts produced with different m

Full size image
Fig. 2
figure 2

Edges produced with different m value

Full size image

3 Governing equation

Considering aforementioned assumption, the momentum equation is introduced as:

3.1 Cartesian coordinate

$$ \frac{1}{\mu }\;\frac{\partial P}{{\partial x^{*} }} = \left( {\frac{{\partial^{2} u^{*} }}{{\partial y^{*2} }} + \frac{{\partial^{2} u^{*} }}{{\partial z^{*2} }}} \right) $$
(4)

3.2 Cylindrical coordinate

$$ \frac{1}{\mu }\;\frac{\partial P}{{\partial z^{*} }} = \left( {\frac{1}{{r^{*} }}\;\frac{{\partial v_{z}^{*} }}{{\partial r^{*} }} + \frac{{\partial^{2} v_{z}^{*} }}{{\partial r^{*2} }} + \frac{1}{{r^{*2} }}\;\frac{{\partial^{2} v_{z}^{*} }}{{\partial \theta^{2} }}} \right) $$
(5)

Introducing the dimensionless parameters as:

$$x=\frac{{x}^{*}}{h}, y=\frac{{y}^{*}}{h}, r=\frac{{r}^{*}}{R}, u(y,z)=\frac{\mu {u}^{*}}{{h}^{2}\left(-\frac{dP}{d{x}^{*}}\right)} , u(r,\theta )=\frac{\mu {v}_{z}^{*}}{{R}^{2}\left(-\frac{dP}{d{z}^{*}}\right)}$$
(6)

Equations 4–6 can be transformed into the dimensionless form, respectively, as:

$$\frac{{\partial }^{2}}{\partial {y}^{2}}u\left(y,z\right)+\frac{{\partial }^{2}}{\partial {z}^{2}}u\left(y,z\right)=-1$$
(7)
$$\frac{{\partial }^{2}}{{\partial r}^{2}}u(r,\theta )+\frac{1}{r}\frac{\partial }{\partial r}u(r,\theta )+\frac{1}{{r}^{2}}\frac{{\partial }^{2}}{{\partial \theta }^{2}}u(r,\theta )=-1$$
(8)

In addition, we consider the no-slip condition on the walls as boundary conditions.

4 Methodology

4.1 Sine and cosine transform functions

The momentum equation in both coordinates is solved analytically with the aid of sine and cosine transform functions. These functions help us to convert the partial differential equation (PDE) form into the ordinary differential equation (ODE) form; hence, the solving becomes convenient. In the following both of them are demonstrated.

4.1.1 Applying sine transform

Using the sine transform function [25, 26] on Eq. (7), we have:

$${S}_{n}\left(\frac{{\partial }^{2}}{{\partial y}^{2}}u\left(y,z\right)+\frac{{\partial }^{2}}{{\partial z}^{2}}u\left(y,z\right)\right)={S}_{n}\left(-1\right)$$
$${S}_{n}\left[\frac{{\partial }^{2}}{{\partial y}^{2}}u\left(y,z\right)\right]=-{\left(\frac{n\pi }{2d}\right)}^{2}{S}_{n}\left(z\right)+\left(\frac{2n\pi }{2d}\right)\left[u\left(0,z\right)+{\left(-1\right)}^{n}u\left(2h,z\right)\right]$$
(9)
$${S}_{n}\left[\frac{{\partial }^{2}}{{\partial z}^{2}}u\left(y,z\right)\right]={S}_{n}^{"}\left(z\right)$$
$${S}_{{\varvec{n}}}\left[-1\right]=-\left(\frac{2}{2d}\left(\frac{\left(1-{\left(-1\right)}^{n}\right)}{n\pi /2d}\right)\right)$$

Considering the non-slip boundary condition, we can write:

$${S}_{n}\left[\frac{{\partial }^{2}}{{\partial y}^{2}}u\left(y,z\right)\right]=-{\left(\frac{n\pi }{2d}\right)}^{2}{S}_{n}\left(z\right)$$
(10)

Consequently, Eqs. (9) and (10) reduce to:

$$ S_{n}^{\prime \prime } \left( Z \right) - \left( {\frac{n\pi }{{2d}}} \right)^{2} S_{n} \left( Z \right) = - \frac{{2\left( {1 - \left( { - 1} \right)^{n} } \right)}}{n\pi },\;n = 1,\;3,\;5,\; \ldots $$
(11)

By solving Eq. (11); subsequently, applying the invers sine transform, the dimensionless velocity distribution in Cartesian coordinate is obtained as follow:

$$ u\left( {y,z} \right) = \sum\limits_{n = 1}^{\infty } {S_{n} \left( Z \right) \cdot {\text{Sin}} \left( {\frac{n\pi y}{2}} \right),\;n = 1,3,5, \ldots } $$
(12)

4.1.2 Applying cosine transform

We can employ similar procedure for Eq. (8) for cosine transform function [25, 26]; accordingly, we obtain:

$${C}_{n}\left(\frac{{\partial }^{2}}{{\partial r}^{2}}u\left(r,\theta \right)+\frac{1}{r}\frac{\partial }{\partial r}u\left(r,\theta \right)+\frac{1}{{r}^{2}}\frac{{\partial }^{2}}{{\partial \theta }^{2}}u\left(r,\theta \right)\right)={C}_{n}\left(-1\right);$$
$${C}_{n}\left[\frac{{\partial }^{2}}{{\partial r}^{2}}u\left(r,\theta \right)\right]={C}_{n}^{\prime\prime}\left(r\right)$$
$${C}_{n}\left[\frac{1}{r}\frac{\partial }{\partial r}u\left(r,\theta \right)\right]=\frac{1}{r}{C}_{n}^{{^{\prime}}}\left(r\right)$$
(13)
$${C}_{n}\left[\frac{1}{{r}^{2}}\frac{{\partial }^{2}}{{\partial \theta }^{2}}u\left(r,\theta \right)\right]=\frac{1}{{r}^{2}} \left[{\left(4n\right)}^{2}{C}_{n}\left(r\right)-\frac{8}{\pi }\left({u}_{\theta }\left(r.0\right)-{\left(-1\right)}^{n+1}{u}_{\theta }\left(r.\frac{\pi }{2}\right)\right)\right]= \frac{{\left(4n\right)}^{2}}{{r}^{2}}{C}_{n}(r)$$
$${C}_{n}\left[-1\right]=\left\{\begin{array}{c}-1 n=0\\ 0 n\ne 0\end{array}\right.$$

Note that considering symmetry, we get:

$$ C_{0}^{\prime \prime } \left( r \right) + \frac{1}{r}C_{0}^{\prime } \left( r \right) + 1 = 0,\;for\;n = 0 $$
(14)
$$ C_{n}^{\prime \prime } \left( r \right) + \frac{1}{r}C_{n}^{\prime } \left( r \right) - \frac{{\left( {4n} \right)^{2} }}{{r^{2} }}C_{n} \left( r \right) = 0,\;for\;n = 1,\;2,\;3, \ldots $$
(15)

To obtain the dimensionless velocity distribution in cylindrical coordinate, Eq. (14) and (15) are solved, and we have:

$$u\left(r,\theta \right)=-\frac{1}{4}{r}^{2}+A+2\sum_{n=1}^{10}{B}_{n}{r}^{4n}\mathit{cos}\left(4n\theta \right)$$
(16)

where the values of A and Bn can be obtained using no-slip condition.

It is worth to note that due to using the cartesian coordinate for the rectangular cross-section, the no-slip condition can be applied (zero velocity on the walls). However, for non-circular cross-sections, the cylindrical coordinate and the symmetric condition at 0 and π/2 angles have been used deliberately. In other words, the condition of velocity differentiation in respect to θ has been used at these two points. Also, it can be seen that for m = 400 (big m), the results of sine transformation for cartesian and cosine transformation for cylindrical has become the same.

5 Results and discussion

In Fig. 3, the comparison of sine transforms results with other conventional analytical methods introduced in ref. [27] is depicted. It can be seen that the sine transform method results are in reasonable agreement with the analytical method.

Fig. 3
figure 3

Comparison of Sine transform method with analytical method

Full size image

In Fig. 4, we show 3D dimensionless velocity distributions for various m. Accordingly, the maximum velocity occurred at r = 0, or at the center of the cross-section in all angles. Figure 5, depicts the impact of dimensionless velocity distribution contours of the whole cross-section. In this figure, since the cross-section is too small, the velocity distribution intensifies near the center.

Fig. 4
figure 4

3D velocity distribution for different m value

Full size image
Fig. 5
figure 5

Velocity contour for different m value

Full size image

The velocity distribution in the duct at different angles on the cylindrical coordinates by cosine transform function for various m is illustrated in Fig. 6. Further, the velocity distribution in the duct at different radius on by cosine transform function for various m is presented in Fig. 7. It can be seen when the value of m decreases, the slope of the velocity profiles near the wall increases, the value velocity for different θ tends to be the same; hence, the velocity profiles overlap. Besides, as the value of m reduces, the velocity profile in different r becomes uniform, therefore, we have less fluctuation in the velocity distribution. It means that the round edge leads to more uniform velocity distribution.

Fig. 6
figure 6

velocity profile in the duct at different angles by cosine transform function for various m

Full size image
Fig. 7
figure 7

velocity profile in the duct at different angles by cosine transform function for various m

Full size image

Figure 8 shows the variation of flow velocity distributions for radius from 0 to 1 and various m value. We can observe due to less effect of the duct wall on the flow, the velocity remains unchanged at the center of the cross section (r = 0) for all m value. The value of the velocity differs, however for m = 400, 200, 100 are almost equal.

Fig. 8
figure 8

Comparison of velocity profiles for different r

Full size image

Also, it can be seen that the velocity for m = 400, 200, 100 (rectangular cross section) has the highest value, but when the edge round becomes completely circular (m = 2), it becomes minimum. This can be interpreted that the wall shear stress of a circular cross-section is larger than a rectangular cross-section profile. It can be found that as the edge shape changed from the rectangular cross-section into the circular one, roundness of the cross-section influences the flow velocity, and the value of it becomes smaller.

The flow velocity distributions of the duct for various m and angles from θ = 0 to π/2 is demonstrated in Fig. 9. It is demonstrated for θ = 0 and π/2, the velocity values at the wall (r = 1) are zero in all cases; however, at other angles and with a constant radius it is not zero. In that case, you move away from the wall, depending on the cross-section shape (Fig. 2); thus, the velocity becomes non-zero.

Fig. 9
figure 9

Comparison of velocity profiles for different θ

Full size image

The minimum and maximum value of the velocity occur at m = 2 and m = 400, 200, 100, respectively for all θ, and the maximum velocity values (r = 0) in each shape differ from another, due to differences in cross-section. Moreover, near the round corner (θ = π/4), the velocity values increase more than other points, due to roundness effect of that point. Besides, it should be noted that for m = 2 (circular shape), the velocity profile remains unchanged at different angles.

The dimensionless value of the average velocity in different m is plotted in Figs. 10 and 11. When m increases, the values of maximum velocity (Vmax) and the average one (Vav) is increased. However, in m ≥ 4, the values of maximum velocity and the average velocity almost equal. Also, it can be seen that when the identical pressure difference is applied, by increasing m, the average velocity enhances; thus, the mass flow increases.

Fig. 10
figure 10

comparison of maximum velocity (Vmax) and average velocity (Vav) in different m

Full size image
Fig. 11
figure 11

Variation of average velocity (Vav) in various m

Full size image

6 Conclusion

The purpose of this research is to investigate the effect of the round edge on the fluid flow through the duct. Using the super-ellipse function, the cross-section of the duct changes from rectangular into circular configuration. The sine and cosine transform function is applied to transform the momentum governing equation into the ODE form and the analytical expression for the velocity distribution is obtained for both Cartesian and Cylindrical coordinates. The effect of round edge on the flow velocity profile was analyzed and discussed. It was revealed when the cross-section becomes circular, the velocity becomes more uniform toward the rectangular and round edge cross-section. Besides, it was concluded that at different angles of circular cross-section, the velocity profiles remain constant; whereas, for the round edge and rectangular cross-sections, velocity profile was changed. Furthermore, the maximum and minimum value of the velocity was observed in m = 2 and 400, respectively.