Pressuremeter test in unsaturated soils: a numerical study

Abstract

The paper presents a numerical analysis of pressuremeter test in unsaturated cohesive soils. In practice, pressuremeter is commonly expanded up to 10–15% cavity strains. At these strains, limit pressure is not usually reached, and its value is estimated by extrapolation. Accordingly, authors suggest using cavity pressure at 10% strain (P₁₀) for the interpretation of pressuremeter test rather than limit pressure. At this strain, it is also assured that plastic strain occurs around the cavity, which is crucial for the interpretations. In unsaturated soils, the moisture at which a soil is tested has a noticeable influence on the pressuremeter cavity pressure, and consequently, on the magnitude of P₁₀. In this paper, unsaturated soil behaviour has been captured by Barcelona basic model (BBM), and the influence of each BBM parameter on the P₁₀ value is explored. Next, relative weight analysis technique is performed to investigate the relative importance of BBM parameters in prediction of P₁₀. Artificial intelligence technique of genetic programming is used to develop a relationship to predict the P₁₀ value in unsaturated soils from BBM parameters. Finally, the application of the proposed equation is shown through illustrative examples.

1 Introduction

The innovative technology of pressuremeter was introduced in the 1950s by Ménard. Pressuremeter test (PMT) can provide useful data for estimation of soil parameters to be used in geotechnical design. One of the main advantages of PMT is its robust theoretical background due to its similarity to cylindrical cavity expansion phenomenon. In the past few decades, extensive researches have focused on developing theoretical expressions for cavity expansion in dry or saturated soils [1,2,3,4]. Partially saturated soils are often encountered in practical engineering applications; however, very few contributions have been made to investigate the cavity expansion in unsaturated soils. The pioneer researches for interpreting pressuremeter in unsaturated soils were done by Consoli et al. [5]. Miller and Muraleetharan [6] illustrated the notable influence of matric suction on the pressuremeter limit pressure. Suction-monitored pressuremeter test (SMPMT) results in unsaturated granite residual soils conducted by Schnaid et al. [7] proved the significant influence of suction on pressure cavity expansion curve. Tan [8] conducted mini-pressuremeter tests (MPMT) in a calibration chamber containing unsaturated soils. Russell and Khalili [9] solved the cavity expansion problem in unsaturated soils utilizing a bounding surface plasticity model along with the similarity technique. Collins and Miller [10] investigated the influence of moisture content and matric suction on the field results of the pressuremeter test to establish a framework to interpret PMT results in unsaturated soils. Yang and Russell [11] presented a cavity expansion analysis for unsaturated silty sand exhibiting hydraulic hysteresis. In this paper, a numerical simulation of PMT in unsaturated cohesive soils is performed using Barcelona basic model (BBM). BBM is not a built-in constitutive law in FLAC, and therefore it has been implemented into the FLAC software in this study to capture the behaviour of unsaturated soils. Despite its simplicity in comparison with other unsaturated soil constitutive models, this model is capable of predicting the main aspects of the mechanical response of an unsaturated fine-grained soil. BBM parameters of different types of soils required for numerical modelling are also measured and reported in the literature. In addition, BBM is applied in the numerical studies of some former researchers [12,13,14]. Therefore, it is possible to validate the numerical solutions obtained in this study with the ones obtained by previous researchers. Sensitivity analyses have been conducted to explore the effect of each BBM parameter on the pressuremeter cavity expansion curve. A large number of numerical analyses of PMT in unsaturated cohesive soil with various BBM properties are conducted, and values of cavity pressure at 10% cavity strain (P₁₀) for each analysis are deduced. Relative weight analysis (RWA) technique is performed to compare the relative importance of BBM parameters in prediction of P₁₀. A new relationship between the P₁₀ value in unsaturated soils and BBM parameters is provided with the aid of genetic programming method. Finally, the accuracy of the developed relationship is evaluated, and applications of the proposed relationship are also discussed.

2 The Barcelona basic model for unsaturated soils

The pioneer work of Alonso et al. [15] led to one of the most popular elastoplastic constitutive models for unsaturated soils known as the Barcelona basic model (BBM). BBM is capable of reproducing the main aspects of the stress–strain response of an unsaturated soil including the variation in shear strength and preconsolidation pressure with suction and the occurrence of reversible swelling and irreversible collapse strains during wetting at low and high confining stresses, respectively. The state variables of this model are as follows: the mean net stress, p, deviator stress, q, and suction, s. The suction, denoted by the symbol s is defined as s = u_a − u_w, where u_a and u_w are the pore air and pore water pressure, respectively. The yield curve at constant suction is defined in terms of stress invariants by Eq. (1):

$$q^{2} = M^{2} (p + p_{{\text{s}}} )(p_{0} (s) - p)$$

(1)

where M is the slope of the critical state line in the (p, q) plane at constant suction and p_s (apparent tensile strength) is defined as:

$$p_{s} = ks$$

(2)

where k is a constant parameter. The parameter p₀(s) is the isotropic preconsolidation stress at suction s defined as:

$$p_{0} (s) = p^{{\text{c}}} \left[ {\frac{{p_{0} (0)}}{{p^{{\text{c}}} }}} \right]^{{\frac{\lambda (0) - \kappa }{{\lambda (s) - \kappa }}}}$$

(3)

where λ(s) and λ(0) are the slopes of the normal compression lines at suctions equal to s and 0, respectively, κ is the slope of the swelling lines with respect to changes of mean net stress, p₀(0) is the isotropic preconsolidation stress at suction equal to 0, and p^c is a reference pressure. Equation (3) indicates the relationship between the isotropic preconsolidation stress and suction in the (p, s) plane at q = 0 and is referred to as the loading-collapse (LC) yield curve. The isotropic normal compression lines for unsaturated soils with various suction values are defined by:

$$v = N(s) - \lambda (s){\text{ln}}\left( {\frac{p}{{p^{{\text{c}}} }}} \right)$$

(4)

where v is the specific volume and the variation in intercept N(s) with suction is described as:

$$N(s) = N(0) - \kappa_{{\text{s}}} {\text{ln}}\frac{{s + p_{{{\text{atm}}}} }}{{p_{{{\text{atm}}}} }}$$

(5)

where N(0) is the value of N(s) at zero suction, κ_s is the elastic stiffness parameter for changes in suction, and p_atm is the atmospheric pressure. In addition, the variation in λ(s) with suction can be shown as follows:

$$\lambda (s) = \lambda (0)\left[ {r + (1 - r){\text{exp}}( - \beta s)} \right]$$

(6)

where r and β are soil constants.

The elastic volumetric and deviatoric strain increments are given by:

$${{\rm d}}\varepsilon_{{\text{v}}}^{{\text{e}}} = \frac{\kappa }{v}\frac{{{{\rm d}}p}}{p} + \frac{{\kappa_{{\text{s}}} }}{v}\frac{{{{\rm d}}s}}{{s + P_{{{\text{atm}}}} }}$$

(7)

$${{\rm d}}\varepsilon_{{\text{s}}}^{{\text{e}}} = \frac{G}{3}{{\rm d}}q$$

(8)

where G is the elastic shear modulus. The volumetric plastic strain increments can be given by:

$${{\rm d}}\varepsilon_{{\text{v}}}^{{\text{p}}} = \frac{\lambda (0) - \kappa }{v}\frac{{dp_{0} (0)}}{{p_{0} (0)}}$$

(9)

Assuming an associative flow rule in the (p, q) plane, increments of plastic deviatoric and volumetric strains can be related as follows:

$$\frac{{{{\rm d}}\varepsilon_{{\text{s}}}^{{\text{p}}} }}{{{{\rm d}}\varepsilon_{{\text{v}}}^{{\text{p}}} }} = \frac{2q}{{M^{2} (2p + p_{{\text{s}}} - p_{0} (s))}}$$

(10)

It should be noted that a second yield curve, known as the suction-increase (SI) yield curve is introduced in BBM. In this paper, however, the existence of the SI yield curve is neglected. The reason for this neglecting lies in the assumption of constant suction during cavity expansion. This is discussed in the following section.

3 Numerical modelling

3.1 Material model

BBM is implemented and used for all of the analyses performed in this study via FLAC program. Although this is a simple constitutive model for unsaturated soils, it has been widely used especially for fine-grained soils, excluding those containing highly expansive clay minerals [14]. In addition, in most of the pressuremeter tests in unsaturated soils available in the literature, only the BBM parameters have been reported, and therefore this constitutive model is employed in the numerical analyses of this study to validate the procedure with available measurements or numerical studies found in the literature. Three different drainage conditions (constant suction, constant moisture content and constant contribution of suction to the effective stress) may be encountered during the expansion of a pressuremeter in soil. The results of suction-monitored pressuremeter tests (SMPMT) presented by Schnaid et al. [7] showed that suction remains constant around the cavity, while Anderson et al. [16] indicated that the water pressure, and consequently, soil suction may vary along the radius of the soil around the pressuremeter. In this study, it is assumed that the value of suction remains constant during the test. This assumption is used for the sake of simplicity in that considering suction changes requires additional model parameters. Model parameters used for the numerical analyses will be discussed in later sections.

3.2 Validation of the BBM implementation

To validate the BBM implementation in FLAC, a single-element axisymmetric triaxial test is simulated. The BBM parameters as used in this test are listed in Table 1. The initial specific volume of the soil is assumed 1.9. An unsaturated soil with an initial suction value of 200 kPa has experienced two different paths. In Path 1, a soil sample with an initial mean net stress of 150 kPa is isotropically compressed up to a mean net stress of 600 kPa. In Path 2, the same soil sample is first exposed to a suction reduction until full saturation condition is reached. This suction reduction results in an elastic swelling of the soil. After that, the sample is isotropically compressed up to a mean net stress of 600 kPa. The stress paths experienced by the samples in the (s, p) plane are illustrated in Fig. 1. In Fig. 2, the volumetric deformations of the samples are plotted against the mean net stresses. It is evident that the results of this study are in close agreement with those provided by Alonso et al. [15]. Several other validations with Alonso et al. [15] are also performed in this study, and the agreement between the numerical results and measurement reported by Alonso et al. [15] is found to be satisfactory.

Table 1 BBM parameters used for validation of implementation [15]

Fig. 1

Stress paths of the samples in the (s, p) plane [15]

Fig. 2

Variation in the specific volume with net mean stress

3.3 BBM parameters used in the present study

One of the main steps in a numerical modelling is determination of appropriate ranges for each of the parameters associated with the constitutive law. In the numerical analyses of this study, p varied from 30 to 500 kPa, p₀(0) varied from 15 to 500 kPa, and p^c varied from 2 and 480 kPa. Bowels [17] suggested that elastic Young’s moduli of clays typically range from 5 to 25, 15 to 50 and 50 to 100 MPa for soft, medium and hard clays, respectively. According to Bowels [17], Poisson’s ratio of 0.3 is assumed for unsaturated clay, which corresponds to shear moduli in the range of 2–38 MPa. A wider range of 2–50 MPa is chosen for the shear moduli values to cover the stiffness characteristics of most clayey soils. The parameter M (slope of the critical state line in the (p, q) plane) varied from 0.4 to 1.3 corresponding to the friction angles of 10°–32°, respectively. This range of friction angle for cohesive soils in drained conditions is in accordance with Look [18]. From the BBM parameters collected by Abed [12] from published literature, λ(0) values for cohesive soils vary from 0.06 to 0.24. Additionally, it is known that κ falls in the range of λ(0)/10 to λ(0)/5. Therefore, the minimum and maximum values for κ are 0.006 and 0.048, respectively. As a result, the applied ranges chosen for λ(0) and κ are 0.05–0.3 and 0.005–0.05, respectively. Authors propose that the effect of parameters s, r and β be taken into consideration by the ratio of λ(s) to λ(0) described as:

$$x = \lambda (s){/}\lambda (0) = [r + (1 - r){\text{exp}}( - \beta s)]$$

(12)

The minimum value of x (ratio of λ(s) to λ(0)) is taken to be 0.5. Smaller values of x may result in large values of p₀(s) at high suctions (see Eq. 3) leading to elastic behaviour of surrounding soil at 10% strain (see Eq. 1). In addition, the maximum value of x equals to 1 occurring at saturated or zero suction condition. Several researchers such as Frydman and Baker [19] showed that the soil suction varies from 1 to 10⁶ kPa. However, numerical analyses in this study indicated that for the suction values higher than 400 kPa, results are not further influenced by the suction. Hence, matric suction was changed from 0 to 400 kPa. In all of the analyses, parameters of Eq. (3) and p are chosen such that the ratio of p₀(s)/p (i.e., overconsolidation ratio) falls in the range of 1–30, which is a typical range for cohesive soils as suggested by Look [18].

Toll [20] and Toll and Ong [21] proposed the following equation for the parameter controlling the increase in apparent cohesion with suction (k):

$$k = \frac{{6{\text{cos}}\phi }}{{3 - {\text{sin}}\phi }}{\text{tan}}\phi^{{\text{b}}}$$

(13)

where ϕ^b is the friction angle associated with matric suction. By assuming the friction angle value to lie in the range of 10°–32°:

$$k \approx 2{\text{tan}}\phi^{{\text{b}}}$$

(14)

According to Fredlund and Rahardjo [22], ϕ^b varies from 12.6° to 21.7° for cohesive soils; consequently, k varies from 0.45 to 0.8. Nevertheless, a k value equal to 1.2 is also reported in the literature [12]. In this paper, k parameter is chosen to be in a range of 0.4–1.2. From the foregoing, it can be noted that the parameter p_s varies from 0 to 480 kPa. Finally, N(s) is taken to be in the range of 1.6–2.4. This range can be inferred from the common void ratio values for various cohesive soils presented by Das and Sobhan [23].

3.4 PMT model specifications

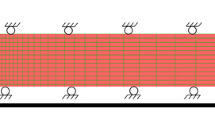
PMT has been simulated using the FLAC software. The type of the test modelled is a self-boring pressuremeter (SBPM) test. The length and diameter of the SBPM are 500 and 80 mm, respectively, the same as the Cambridge SBPM instrument. This gives a height-to-diameter ratio of 6.25, which exceeds the recommended value of 6 needed for the plane strain behaviour [24]. The mesh grid and boundary conditions of the axisymmetric model are shown schematically in Fig. 3. The ratio of r_m/r₀ (ratio of model radius to cavity radius) is set to be 100 so that the outside boundaries would have no influence on the numerical results. Further information concerning the numerical modelling is given by Ahmadi and Keshmiri [25].

Fig. 3

Mesh grid and boundary conditions of the axisymmetric model

3.5 Stress distribution around an expanding cavity

To evaluate the stress distribution in soils with various suctions surrounding an expanding cavity, the horizontal net stresses were examined away from the cavity wall for soil properties of Table 2. Shown in Fig. 4 are horizontal stress–distance curves at the cavity strain of 10%. Normalized distance is denoted by r/r₀ (ratio of radial distance from cavity wall to cavity radius). As shown in Fig. 4, the presence of suction in unsaturated soil increased the induced horizontal stress around the expanding cavity. For all of the suctions, the induced horizontal stress remained constant at and beyond a radial distance approximately 15 times the cavity radius. The radius of the plastic zone formed around the pressuremeter is also investigated at the cavity strain of 10%. On this purpose, the normalized radii of the plastic zone (normalized to the cavity radius) for different suction values are depicted by vertical dashed lines in Fig. 4. It can be noted that as the suction increases, the plastic zone radius decreases since according to Eq. (3), suction increase leads to increase in isotropic preconsolidation stress. As a result, less amount of soil around the cavity experiences plastic strains.

Table 2 BBM parameters to examine the horizontal stress distribution

Fig. 4

Horizontal stress–distance curves at cavity strain of 10%

4 Verification of the numerical model used in this study

Zhang et al. [13] proposed a method for determination of parameter values in the Barcelona basic model (BBM) by inverse analysis of the experimental cavity pressure–cavity strain curve from pressuremeter tests in unsaturated soils. They utilized parallel-modified particle swarm optimization (PSO) algorithm to match the cavity pressure–cavity strain curves calculated by finite element (FE) models to the field measurements. Table 3 represents the BBM parameters obtained from the inverse analysis of the SMPMT curve (reported by Schnaid et al. [7]) using the PSO algorithm. It is important to bear in mind that the parameters of Table 3 may not be realistic and attributable to a specific natural soil. The same values of model parameters were used in this numerical model, and the results of this study, field measurements of Schnaid et al. [7] and those achieved by FE model of Zhang et al. [13] are shown in Fig. 5 for two suction values of 0 and 43 kPa. As observed in Fig. 5, the difference in cavity pressure between the results of this study and those proposed by Zhang et al. [13] falls below 7% and 3% for the suctions of 0 and 43 kPa, respectively.

Table 3 BBM parameters from the inverse analysis of SMPMT [13]

Fig. 5

Verification of the numerical model in this study with the results of Zhang et al. [13]

5 Sensitivity analysis

As noted by Ahmadi and Keshmiri [25], the cavity pressure at 10% strain can be used instead of limit pressure for the interpretation of PMT results. Soil moisture conditions change depending on the season in which they are tested. Therefore, the soil parameters deduced from PMT are dependent on the soil saturation condition during the test period. As a result, it is important to estimate the cavity pressure (P₁₀) of the pressuremeter test for different suction (saturation) conditions. At first, it is instructive to survey the effect of each soil property of BBM on the value of P₁₀. A series of numerical analyses were carried out in which only one soil property was changed, while all other soil properties were kept constant. Soil parameters used for each sensitivity analysis are given in Table 4. Parameters are normalized to the average of their maximum and minimum values of their typical ranges (see Sect. 3.3) to better compare their influence on P₁₀. Figures 6 and 7 represent the variation in P₁₀ with parameters M, p, p₀(0), N(s), G, κ and p_s. As these parameters increase, the value of P₁₀ increases. Figure 8 represents the variation in P₁₀ with parameters x, p^c and λ(0). As these parameters decrease, the value of P₁₀ decreases. Results of Figs. 6, 7 and 8 lead to the conclusion that parameters p₀(0) and κ are the most and least influential parameters on P₁₀, respectively.

Table 4 Soil properties used for the sensitivity analyses

Fig. 6

Normalized BBM parameters (M, p, p₀(0), and N(s)) having increasing effect on P₁₀

Fig. 7

Normalized BBM parameters (G, κ, and p_s) having increasing effect on P₁₀

Fig. 8

Normalized BBM parameters (x, p^c, and λ(0)) having decreasing effect on P₁₀

6 Relative weight analysis technique

Sensitivity analyses introduced in the previous section suffer from the following major flaws in determining the relative importance of each parameter on P₁₀:

• 1. They were performed based on a limited number of numerical modelling results.

• 2. The influence of one independent or predictor variable (soil parameter) on the dependent variable (P₁₀) may depend on another one. In other words, interrelated influence of parameters on P₁₀ is ignored.

In a regression analysis, various methods are developed and used by researchers to realize the relative contribution (importance) of each independent variable in calculating the value of the dependent variable. One of these methods is relative weight analysis (RWA). In RWA, the total variance predicted in a regression model (R²) is decomposed into weights that properly reflect the proportional contribution of the various independent variables in estimation of the dependent variable. The interested reader is directed to Johnson [26] for further information concerning relative weight. In this regard, Tonidandel and LeBreton [27] designed an interactive website to perform RWA. RWA-Web is available at http://relativeimportance.davidson.edu/. In this study, a large number of numerical analyses of PMT with various BBM parameters are conducted and values of cavity pressure at 10% cavity strain (P₁₀) are deduced to be used in RWA. In these analyses, each of the BBM parameter was changed from its minimum to maximum value regarding the ranges discussed in Sect. 3.3. It should be noted that some combinations of these parameters result in unrealistic and incompatible soil properties, but their analyses are necessary to find a precise weight for each parameter. As previously shown in the preceding section, effect of κ on P₁₀ has proved negligible. Thus, a common value of 0.01 is taken for this parameter in all of the analyses to preserve simplicity. Results of the RWA are presented in Table 5. The column labelled “Raw Weight” provides an estimate of the importance of each parameter (variable). These weights represent an additive decomposition of the total model R², and can be interpreted as the proportion of contribution of each parameter in prediction of P₁₀. By summing the raw weights, we obtain the total model R² = 0.884 (i.e., 0.0926 + 0.0414 + 0.0653 + 0.4459 + 0.1029 + 0.0690 + 0.0126 + 0.0540 + 0.0001 = 0.8838). The values listed under the “Rescaled Weight” column were achieved by dividing each raw relative weight by the model R². As is evident from the results, p₀(0) and N(s) are the most and least important variables in prediction of P₁₀ with rescaled weights of approximately 50% and 0.01%, respectively.

Table 5 Results of the RWA analyses

7 Proposed relationship for P ₁₀

It can be inferred from the previous sections that nine parameters including p, G, M, p₀(0), p^c, x, λ(0), p_s and N(s) are sufficient to estimate the P₁₀ value. Sensitivity analyses indicate that the variation in P₁₀ versus each parameter can be approximated by an nth degree polynomial. Thus, a relationship in the following form can be assumed to predict the P₁₀ value:

$$P_{10} = \frac{{\overline{p } \times \overline{G } \times \overline{M} \times \overline{{p_{0} (0)}} \times \overline{{p_{{\text{s}}} }} \times \overline{N(s)} + a_{i} }}{{ \overline{{p^{c} }} \times \overline{x} \times \overline{\lambda (0)} + a_{j} }} + a_{k}$$

(15)

where a_i, a_j and a_k are constants and $\overline{p}$, $\overline{G}$, $\overline{M}$, $\overline{{p_{0} (0)}}$, $\overline{{p^{{\text{c}}} }}$, $\overline{x}$, $\overline{\lambda (0)}$, $\overline{{p_{s} }}$ and $\overline{N(s)}$ are the nth degree polynomials associated with p, G, M, p₀(0), p^c, x, λ(0), p_s and N(s), respectively. To exemplify, the fourth-degree polynomial of p is:

$$\overline{p} = a_{1} p^{4} + a_{2} p^{3} + a_{3} p^{2} + a_{4} p + a_{5}$$

(16)

where p is a normalized parameter or variable (net mean stress) and a₁ to a₅ are constants. As seen in Eq. (15), the variables increasing the P₁₀ value are located in the numerator of the fraction and the ones decreasing the P₁₀ value are placed in the denominator of the fraction. A large database of the P₁₀ values resulting from the numerical analyses (described in the preceding section) is employed to determine the appropriate degree for each polynomial and optimized values for each constant with the aid of genetic programming (GP). Genetic programming is an extension of the genetic algorithm [28]. GP is especially useful in the problems where the exact form of the solution is not known in advance or an approximate solution is acceptable (possibly because finding the exact solution is very difficult) [29]. In this study, the main objective of the GP process is to find the appropriate degree for each polynomial and optimized values for each constant so that the fitness criterion (F.C) is minimized. Authors define the fitness criterion as the summation of relative errors in prediction of P₁₀:

$$F.C = \sum {\frac{{|P_{10} - P_{10}^{\prime} |}}{{P_{10} }}}$$

(17)

where P₁₀ is deduced from the numerical analyses, and $P_{10}^{\prime}$ is predicted from Eq. (15). It is assumed that the degree of the polynomial corresponding to each variable can take a value between 1 and 6. All of the parameters (variables) used in GP are normalized to the average of their maximum and minimum values. It was realized that normalizing the P₁₀ value according to the following expression gives better accuracy in the results (less values of fitness criterion):

$$P_{{{10}}}^{*} = \frac{{P_{10} + p_{0} (0)}}{{p^{c} }}$$

(18)

It should be clarified that in Eq. (18), p₀(0) and p^c are not normalized values. The appropriate degrees for each polynomial found from the GP optimization process are displayed in Table 6. In addition, the optimized constants for each polynomial are presented in Table 7. Three missing constants in Table 7 including a_i, a_j and a_k in Eq. (15) are equal to 9.139, − 5.082, 0.562, respectively. In Fig. 9, values of $P_{10}^{\ast}$ calculated from Eq. (15) are compared to those achieved from numerical analyses. As can be noticed, trend line has been fitted to the predicted values with coefficient of determination of 0.998. It can be observed that most of the data points are located between the dashed lines implying that the relative errors of the estimation are less than 20%. Moreover, the average relative error of the estimation is about 5%. In Figs. 10 and 11, the values of $P_{10}^{\ast}$ calculated from Eq. (15) are compared to those achieved from numerical analyses for the soil properties used for the sensitivity analyses of G and M, respectively (see Table 4). As can be seen, the trends of variation in $P_{10}^{\ast}$ with respect to G and M parameters are well captured by Eq. (15). Besides, in these figures, the error introduced between the predicted and numerical values of $P_{10}^{\ast}$ is not more than 5%.

Table 6 Degree of the polynomial for each variable

Table 7 Constants for each polynomial

Fig. 9

Predicted versus numerical values of $P_{10}^{\ast}$; dashed lines indicate ± 20% difference between predicted and numerical values of $P_{10}^{\ast}$

Fig. 10

$P_{10}^{\ast}$ values plotted against normalized G values

Fig. 11

$P_{10}^{\ast}$ values plotted against normalized M values

8 Evaluation of the predicted P ₁₀

It is necessary to evaluate the reliability of Eq. (15) for soil properties not involved in the analyses. To this end, 25 numerical analyses with soil parameters different from those used to establish Eq. (15) are performed. Figure 12 exhibits the variation in $P_{10}^{\ast}$ values calculated from Eq. (15) versus those gained from the numerical analyses. As can be noticed, trend line has been fitted to the predicted values with coefficient of determination of 0.993, and the error band for most of the data points is about ± 20%. These results lead to the conclusion that the established relationship gives satisfactory predictions of $P_{10}^{\ast}$ values.

Fig. 12

Evaluation of the proposed relationship; dashed lines indicate ± 20% difference between predicted and numerical values of $P_{10}^{\ast}$

9 Examples and applications

Example 1

This example describes the required calculations to estimate the P₁₀ value in unsaturated soils. Consider soil properties given in Table 1. By assuming a value of 200 kPa for suction, parameters required in Eq. (15) to calculate $P_{10}^{\ast}$ value are as follows: p = 150 kPa, G = 10 MPa, M = 1, p₀(0) = 200 kPa, p^c = 100 kPa, x = 0.77, λ(0) = 0.2, p_s = 120 kPa and N(s) = 2. The values of the parameters normalized to the average of their maximum and minimum values are found to be: p = 0.57, G = 0.38, M = 1.18, p₀(0) = 0.78, p^c = 0.41, x = 1.03, λ(0) = 1.14, p_s = 0.5 and N(s) = 1. By putting these normalized values in Eq. (15), and making use of the constants presented in Table 7, $P_{10}^{\ast}$ is computed to be 6.77. By using Eq. (18), P₁₀ is found to be 449 kPa. Comparing this value of P₁₀ with the one gained from the numerical analysis (483 kPa), it is concluded that the relative error of the proposed relationship is approximately 7%.

Example 2

This example indicates the inverse analysis of the proposed relationship to predict soil parameters. It is recognized that the parameter most influential on P₁₀ value can be predicted from inverse analysis with better accuracy. Therefore, it is intended to find the p₀(0) parameter by knowing the P₁₀ value. Consider soil properties given in Table 2. By assuming a value of 400 kPa for suction, P₁₀ value from the numerical analysis is found to be 610 kPa. This value corresponds to a $P_{10}^{\ast}$ value of 5.4. Normalized parameters required in Eq. (15) to calculate the $P_{10}^{\ast}$ value are as follows: p = 0.75, G = 0.38, M = 1.18, p^c = 0.62, x = 0.67, λ(0) = 1.14, p_s = 1 and N(s) = 1. The normalized p₀(0) value is changed so that the $P_{10}^{\ast}$ value achieved from Eq. (15) equals to 5.4. This iteration process leads to the normalized p₀(0) value of 0.69 corresponding to a p₀(0) value of 178 kPa. This value is in close agreement with the p₀(0) value used in the numerical analysis (200 kPa).

10 Discussion

In the last several sections and paragraphs, a method is suggested to predict the P₁₀ value of pressuremeter test in unsaturated soils, provided the soil parameters are known. Nevertheless, the applicability of the method for field PMT results in unsaturated soil cannot be explored, since BBM parameters of the soil tested in the field are not measured or reported in the literature. In addition, the reliability of the method depends on the constitutive model (i.e., BBM) employed for the numerical analyses. As mentioned earlier, BBM is a common constitutive law for unsaturated soil and has been widely used in the literature. Nevertheless, this model has some shortcomings as well. A number of researchers have outlined these shortcomings as follows:

• 1. BBM is formulated in terms of the net stress and suction. The direct influence of the degree of saturation on the mechanical behaviour is not taken into account in this model. This is especially important for unsaturated soils exhibiting noticeable hydraulic hysteresis during drying and wetting.

• 2. According to Eq. (2), the apparent tensile strength increases with suction and BBM expressed a linear increase in apparent tensile strength with suction. However, in accordance with Mehndiratta and Sawant [30], the apparent tensile strength generally increases nonlinearly with suction.

• 3. The BBM loading-collapse yield curve increases monotonically with suction (Eq. 3). However, Sheng et al. [31] state that this curve should reduce at an angle of 45° until the point of air entry value.

• 4. The experimental results of Alonso et al. [15] support a decreasing slope of λ(s) with increasing suction (Eq. 6), whereas Wheeler and Sivakumar [32] proposed an increasing slope of λ(s) with increasing suction, and Josa et al. [33] proposed a more complicated relationship between λ(s) and suction. Therefore, it is a worthy effort to propose a more unified explanation for the variation in λ(s) with suction.

In spite of the fact that some researchers [30, 31, 34,35,36,37,38] have tackled most of the aforementioned issues via modifying BBM or proposing new constitutive models for unsaturated soils, these models require more parameters in comparison with BBM. Also, reports on the calibration of these models are inadequate in the literature. In addition, BBM is applied in the numerical studies of some former researchers [12,13,14]. Therefore, it is possible to validate the later numerical studies with the ones obtained previously. These reasons would justify the application of this model in this study. Finally, it is worth emphasizing that the main assumption made in this study is that the suction remains constant along the radius of the soil around the pressuremeter.

11 Conclusion

A new method was established for the interpretation of PMT using the results of numerical modelling. It is realized that the cavity pressure at 10% strain (P₁₀) can applied for interpretation of PMT. A large number of numerical analyses were conducted in unsaturated soil with different BBM parameters, and the values of P₁₀ were deduced. In all of the analyses, suction was assumed to be constant in the soil around the pressuremeter. Relative importance of BBM parameters in prediction of P₁₀ value was explored with the aid of relative weight analysis (RWA). Results of RWA indicate that the most influential parameter on P₁₀ is p₀(0) (isotropic preconsolidation stress under saturated conditions). Based on genetic programming approach, a new relationship is developed for the interpretation of PMT results from the cavity pressure at 10% cavity wall strain (P₁₀). By the comparison of the predicted values of P₁₀ from the proposed relationship and those achieved from numerical analyses, it is concluded that the proposed relationship produces reliable predictions of P₁₀. In addition, it is indicated that unsaturated soil properties can be inferred by the inverse analysis of the proposed relationship.