Adapting ant colony optimization of compliant structures using elements with linearly varying cross-sections

Abstract

This work addresses the design of miniature compliant displacement amplifiers. The optimum design of the compliant mechanism is generated through topology optimization of two-node frame elements with linearly varying cross sections using the Ant Colony Optimization technique. First, stiffness matrices that account for the change in the cross-section dimensions are formulated. Then, each element is assigned 5 independent ants that represent its design variables defined as the width and thickness of each of the two peripheral cross-sections in addition to the material density. Three case studies with customized cost functions are furnished; the first maximizes the amplification ratio, the second maximizes the output displacement, while the third maximizes both amplification ratio and output displacement simultaneously. The resulting micro-compliant amplifiers are more compact in volume and surpass their constant cross-section counterparts in terms of amplification ratio and output displacement while keeping relatively low internal stresses. The performances of all optimized topologies are verified through ANSYS.

1 Introduction

A compliant mechanism is an interconnected structure that deflects due to its material’s elastic properties. These flexible mechanisms contain less number of parts than their corresponding rigid counterparts delivering the same task. In addition, complaint mechanisms have great advantages over their rigid counterparts in terms of friction and wear elimination as they lack joints within their structure. Being joint-less, compliant mechanisms are noticeably reputable for the ease in miniaturization that makes them applicable in advanced robotics and micro-electro-mechanical systems, MEMS [1].

The main challenge lies in the topology design of complaint mechanisms since their behavior is not clearly defined as compared to rigid linkages. Synthesis of compliant mechanisms is usually classified by two categories; pseudo-rigid body model (PRBM) [2] which leads to partially compliant mechanisms and topology optimization which generates fully compliant mechanisms [3].

Optimization of compliant mechanisms is of three levels: topology, shape and size. Topology optimization is used to generate material layout concepts. Once the structure’s topology is defined, shape optimization refines and improves the topology within the desired concept whereas size optimization identifies the optimal parameters, such as cross-section and thickness dimensions [1].

Topology optimization was first applied to compliant mechanisms using the homogenization method [4]. It defines the material layout and thus its distribution between the input and output nodes in the design space leading to a joint-less mechanism that gains its flexibility from the structure’s elastic deformation. Topology optimization is either ground structure parameterization or continuous material density parameterization. In the first approach, or the binary approach, the design space is divided into elements that are given the values of either zero (no material), or 1 (full material) for the normalized modulus of elasticity of the material [5]. However, the second approach distributes materials in the design space based on their densities, thus, observing white and black contour regions as well as grey regions modeling softer materials [4]. At the end of either approach, a complete view of the mechanism is formulated in terms of the material distribution.

In the past decade, topology optimization for various applications using swarm intelligence techniques has prospered including compliant and rigid mechanisms. Kaveh and Shahrouzi [6, 7] elaborated a new algorithm called hybrid ant strategy that mixed between the Genetic Algorithm (GA) and the Ant Colony Optimization (ACO) to enhance convergence efficiency. Later, Kaveh and Talatahari [8] introduced a new concept of Improved Ant Colony Optimization (IACO) to solve problems using the sub-optimization mechanism (SOM) at maximum accuracy with higher convergence rates. Wu et al. [9] proposed a modified ACO algorithm to find the optimal design by evaluating the accumulated pheromone on the finite elements. Their proposed algorithm provides a swap technique of optimization with a higher probability of finding the optimal topology of a structure as compared to genetic algorithms and typical ACO methods. Kim et al. [10] suggested the modified ant colony optimization (MACO) to obtain stable and optimal topology for geometrically linear and non-linear compliant mechanisms. To overcome the weakness of the ACO in low target volume problems, MACO is developed depending on results of Kosaka and Swan [11]. Their approach was based on comparing three objective functions and defining the fitness ratio where they modeled stiffness and flexibility in the objective function as mutual strain energy and strain energy ratio respectively. Yoo and Han [12] introduced a new variable, “element contribution significance”, which reflects the significance of each finite element and consequently adapted a new form of the classical ACO algorithm. Sharma and Grover [13] integrated another MACO to set the optimum energy efficient path of sensor nodes in signal transmission. Liu et al. [14] implemented MACO algorithm where their technique excluded nodes enclosed by low density elements from the mesh. Si and Wei [15] categorized the ants in their work into scout, search and worker ants each with different specified tasks. The same categorization concept was implemented by Diab and Smaili [16] where their modified ant search (MAS) algorithm intended to optimize the performance of the algorithm with dynamic enter/exit strategies between exploration and exploitation phases.

Designing for compliant mechanisms that balance the stiffness-flexibility criterion while allowing for large deformations is a challenging task that recent research work is addressing. Lately, many researchers have streamlined their efforts for optimum design of compliant amplifiers. Clark et al. [17] studied optimized topologies using bridge structures to maximize output displacement of flexure based mechanisms. They introduced new cost functions to approximate the output displacement in the direction normal to the input load. The optimized designs generated bridge-element topologies with variable thicknesses and additional sideways connections that enhanced the displacement amplification. Iqbal et al. [18] tested the effect of different geometric parameters, namely length of flexure hinges and flexure angle, on the amplification ratio of the optimized flexure mechanisms. Cao et al. [19] applied topology optimization of compliant mechanisms using a hybrid mesh of flexure hinges and beam elements. The former allow for high flexibility while the latter give the overall topology its stiffness. Since flexure hinges store strain energy when deformed, Zhao et al. [20] proposed near-zero stiffness rotational flexural pivots to cut down on the rotational stiffness of the overall compliant structure while allowing for relatively large deformations. For multi-input/multi-output compliant mechanisms that allow for large displacements, Zhu et al. [21] implemented fully decoupled flexible mechanisms by adding several constraints to suppress the undesirable outputs due to each input through a coupling index. Diab and Smaili [22] conducted four case studies on topology optimization of compliant mechanisms through four different objective functions using two node frame elements with constant cross sections. In their work, the authors postulated new objective functions for modeling output displacements and amplification ratios of micro-compliant mechanisms.

In this work, the ACO algorithm is implemented for topology optimization of a micro-compliant displacement amplifier. The objective of this study is twofold. Firstly, unlike previous work in literature [6,7,8,9,10,11,12,13,14,15,16], the ACO technique adopted in this study redeemed ants from crossing physical node-to-node elements into a more flexible and conceptual perception of optimization. This unique approach paves the way for geometry (dimensions of the tapered elements) and topology (material layout) optimization by assigning an ant to each design variable irrespective of the existence of physical paths for the ants. Secondly, in addition to the aforementioned unique adaptation of ACO to optimum design of topology optimization, the current study targets to enhance the performance of micro-compliant amplifiers by manipulating the geometry and topology of its frame elements without the limitations and undesirable effects of flexure hinges (i.e. strain energy storage) and bridge type mechanisms (i.e. output displacement is normal to input force) as presented in [17,18,19,20,21]. The performance of the optimum compliant mechanisms obtained in this paper are benchmarked with those in [1] and [22] to highlight the effect of tapering mesh elements over constant-cross-sections.

In what follows, the finite element formulation of frame elements with tapered cross-sections is furnished followed by the problem formulation and the ACO algorithm. The study concludes with 3 case studies that address different objectives of the miniature compliant amplifier.

2 FEA formulation

A basic step in reaching the objective of this work is to formulate the stiffness matrices of the two node frame elements with variable cross section. These elements are the stones of constructing the mechanism’s topology. It is believed that a tapered cross-section has more flexibility compared to its constant cross-section counterpart and this will be tested by benchmarking the results obtained in this work with those in [22]. The two-node frame element is a superposition of the two-node bar element and the two-node beam element. Bar or truss elements are spring-like elements that only withstand axial loading as shown in Fig. 1.

Fig. 1

Loaded bar element

Therefore, they behave like springs and their stiffness matrix ($k_{bar}$) is given as [24]:

$$\begin{aligned} k_{bar}=\int _{0}^{L}\frac{A_{area}E}{L^2} \quad \begin{bmatrix} 1 &{} -1 \\ -1 &{} 1 \end{bmatrix} \end{aligned}$$

(1)

where

$$\begin{aligned} A_{area}=bh \end{aligned}$$

(2)

is the cross sectional area of the bar with b defined as the out-of-plane width and h defined as the in-plane thickness, E is the modulus of elasticity, and L is the length of the bar. For a constant cross section, the stiffness matrix of the bar element derived from (1) is as follows:

$$\begin{aligned} k_{bar,cst}= \quad \begin{bmatrix} \frac{AE}{l} &{} -\frac{AE}{l} \\ -\frac{AE}{l} &{} \frac{AE}{l} \end{bmatrix} \end{aligned}$$

(3)

However, if we assume b and h to be linearly varying across the length L between nodes 1 and 2 (Fig. 2), the equations of their cross-sectional variations will be as follows:

$$\begin{aligned} b= & {} \frac{b_{2}-b_{1}}{L}x+b_{1} \end{aligned}$$

(4)

$$\begin{aligned} h= & {} \frac{h_{2}-h_{1}}{L}x+h_{1} \end{aligned}$$

(5)

Fig. 2

Tapered rectangular two node element

Thus, substituting (4) and (5) in (1) gives the new stiffness matrix of a bar with linearly variable cross section:

$$\begin{aligned} k_{bar,var}=E \quad \begin{bmatrix} \frac{2b_{1}h_{1}+b_{1}h_{2}+b_{2}h_{1}+2b_{2}h_{2}}{6L} &{} -\frac{2b_{1}h_{1}+b_{1}h_{2}+b_{2}h_{1}+2b_{2}h_{2}}{6L} \\ -\frac{2b_{1}h_{1}+b_{1}h_{2}+b_{2}h_{1}+2b_{2}h_{2}}{6L} &{} \frac{2b_{1}h_{1}+b_{1}h_{2}+b_{2}h_{1}+2b_{2}h_{2}}{6L} \end{bmatrix} \end{aligned}$$

(6)

On the other hand, beam elements are subjected to transverse loading which implies bending and shear in the beam as shown in Fig. 3.

Fig. 3

Loaded beam element

Thus, the stiffness matrix ($k_{beam}$) of a constant cross-section beam element is as follows:

$$\begin{aligned} k_{beam}=\int _{0}^{L}\frac{EI_{inertia}}{L^4}M_{x}dx \end{aligned}$$

(7)

where

$$M_{x}= \begin{bmatrix} 12\frac{x}{L}-6 \\ 6x-4L \\ 6-12\frac{x}{L} \\ 6x-2L \end{bmatrix} \quad\quad \begin{bmatrix} 12\frac{x}{L}-6&6x-4L&6-12\frac{x}{L}&6x-2L \end{bmatrix}$$

(8)

$$\begin{aligned}&I_{Inertia}=\frac{1}{12}bh^{3} \end{aligned}$$

(9)

Developing $M_{x}$ into one matrix gives (only upper triangular matrix is listed due to symmetry):

$$\begin{aligned}&M_{x}= \quad \begin{bmatrix} (12\frac{x}{L}-6)^2 &{} (12\frac{x}{L}-6)(6x-4L) &{} (12\frac{x}{L}-6)(6-12\frac{x}{L}) &{} (12\frac{x}{L}-6)(6x-2L) \\ sym &{} (6x-4L)^2 &{} (6-12\frac{x}{L})(6x-4L) &{} (6x-2L)(6x-4L) \\ sym &{} sym &{} (6-12\frac{x}{L})^2 &{} (6-12\frac{x}{L})(6x-2L) \\ sym &{} sym &{} sym &{} (6x-2L)^2 \end{bmatrix} \end{aligned}$$

(10)

For a constant cross-section, (7) through (10) give the stiffness matrix of a beam element as:

$$\begin{aligned} k_{beam,cst}= E \quad \begin{bmatrix} \frac{12I}{L^{3}} &{} \frac{6I}{L^{2}} &{} -\frac{12I}{L^{3}} &{} \frac{6I}{L^{2}}\\ \frac{6I}{L^{2}} &{} \frac{4I}{L} &{} -\frac{6I}{L^{2}} &{} \frac{2I}{L}\\ -\frac{12I}{L^{3}} &{} -\frac{6I}{L^{2}} &{} \frac{12I}{L^{3}} &{} -\frac{6I}{L^{2}}\\ \frac{6I}{L^{2}} &{} \frac{2I}{L} &{} -\frac{6I}{L^{2}} &{} \frac{4I}{L} \end{bmatrix} \end{aligned}$$

(11)

However, for a beam element with linearly varying cross-sections, the stiffness matrix can be formulated by substituting b and h from Eqs. 4 and 5 into Eq. (7) through (10) to obtain:

$$\begin{aligned} k_{beam,var}= & {} \frac{E}{L^{4}}\int _{0}^{L}IM_{x}dx = \frac{E}{L^{4}}\nonumber \\&\int _{0}^{L}\frac{1}{12} \left( \frac{\varDelta bx}{L} + b_{1}\right) \nonumber \\&\left( \frac{\varDelta hx}{L} + h_{1}\right) ^3 M_{x} dx \nonumber \\= & {} E \quad \begin{bmatrix} {\hat{A}} &{} {\hat{B}} &{} {\hat{C}} &{} {\hat{D}} \\ {\hat{B}} &{} {\hat{E}} &{} {\hat{F}} &{} {\hat{G}} \\ {\hat{C}} &{} {\hat{F}} &{} {\hat{H}} &{} {\hat{I}} \\ {\hat{D}} &{} {\hat{G}} &{} {\hat{I}} &{} {\hat{J}} \end{bmatrix} \end{aligned}$$

(12)

where

$$\begin{aligned} \begin{aligned} {\hat{A}}&=-{\hat{C}}={\hat{H}}=\frac{44b_{1}h_{1}^3 + 5b_{1}h_{2}^3 + 5b_{2}h_{1}^3 + 44b_{2}h_{2}^3 + 6b_{1}h_{1}h_{2}^2 + 15b_{1}h_{2}h_{1}^2 + 15b_{2}h_{1}h_{2}^2 + 6b_{2}h_{2}h_{1}^2}{140L^3} \\ {\hat{B}}&=-{\hat{F}}=\frac{94b_{1}h_{1}^3 + 4b_{1}h_{2}^3 + 11b_{2}h_{1}^3 + 38b_{2}h_{2}^3 + 9b_{1}h_{1}h_{2}^2 + 33b_{1}h_{2}h_{1}^2 + 12b_{2}h_{1}h_{2}^2 + 9b_{2}h_{2}h_{1}^2}{420L^2} \\ {\hat{D}}&=-{\hat{I}}=\frac{38b_{1}h_{1}^3 + 11b_{1}h_{2}^3 + 4b_{2}h_{1}^3 + 94b_{2}h_{2}^3 + 9b_{1}h_{1}h_{2}^2 + 12b_{1}h_{2}h_{1}^2 + 33b_{2}h_{1}h_{2}^2 + 9b_{2}h_{2}h_{1}^2}{420L^2} \\ {\hat{E}}&=\frac{68b_{1}h_{1}^3 + 2b_{1}h_{2}^3 + 9b_{2}h_{1}^3 + 12b_{2}h_{2}^3 + 8b_{1}h_{1}h_{2}^2 + 27b_{1}h_{2}h_{1}^2 + 6b_{2}h_{1}h_{2}^2 + 8b_{2}h_{2}h_{1}^2}{420L} \\ {\hat{G}}&=\frac{26b_{1}h_{1}^3 + 2b_{1}h_{2}^3 + 2b_{2}h_{1}^3 + 26b_{2}h_{2}^3 + b_{1}h_{1}h_{2}^2 + 6b_{1}h_{2}h_{1}^2 + 6b_{2}h_{1}h_{2}^2 + b_{2}h_{2}h_{1}^2}{420L} \\ {\hat{J}}&=\frac{12b_{1}h_{1}^3 + 9b_{1}h_{2}^3 + 2b_{2}h_{1}^3 + 68b_{2}h_{2}^3 + 8b_{1}h_{1}h_{2}^2 + 6b_{1}h_{2}h_{1}^2 + 27b_{2}h_{1}h_{2}^2 + 8b_{2}h_{2}h_{1}^2}{420L} \end{aligned} \end{aligned}$$

Finally the frame element, which is a superposition of a bar and a beam, holds three degrees of freedom at each node. As shown in Fig. 4, the frame element can bear axial loads along with shear forces and bending moments.

Fig. 4

Loaded frame element

Hence the stiffness matrix ($k_{frame,cst}$) of the frame element is the superposition of that of a bar and that of a beam. So, superimposing matrices stated in (3) and (11) yields to the stiffness matrix of the frame element with constant cross section as:

$$\begin{aligned} k_{frame,cst}= E \quad \begin{bmatrix} \frac{A}{L} &{} 0 &{} 0 &{} -\frac{A}{L} &{} 0 &{} 0 \\ 0 &{} \frac{12I}{L^3} &{} \frac{6I}{L^2} &{} 0 &{} -\frac{12I}{L^3} &{} \frac{6I}{L^2} \\ 0 &{} \frac{6I}{L^2} &{} \frac{4I}{L} &{} 0 &{} -\frac{6I}{L^2} &{} \frac{2I}{L} \\ -\frac{A}{L} &{} 0 &{} 0 &{} \frac{A}{L} &{} 0 &{} 0 \\ 0 &{} -\frac{12I}{L^3} &{} -\frac{6I}{L^2} &{} 0 &{} \frac{12I}{L^3} &{} -\frac{6I}{L^2} \\ 0 &{} \frac{6I}{L^2} &{} \frac{2I}{L} &{} 0 &{} -\frac{6I}{L^2} &{} \frac{4I}{L} \\ \end{bmatrix} \end{aligned}$$

(13)

And superimposing matrices in (6) and (12) gives the stiffness matrix of a frame element with linearly changing cross-section as:

$$\begin{aligned} k_{frame,var}= E \quad \begin{bmatrix} \frac{2b_{1}h_{1} + b_{1}h_{2} + h_{1}b_{2} + 2h_{2}b_{2}}{6l} &{} 0 &{} 0 &{} -\frac{2b_{1}h_{1} + b_{1}h_{2} + h_{1}b_{2} + 2h_{2}b_{2}}{6l} &{} 0 &{} 0 \\ 0 &{} {\hat{A}} &{} {\hat{B}} &{} 0 &{} {\hat{C}} &{} {\hat{D}} \\ 0 &{} {\hat{B}} &{} {\hat{E}} &{} 0 &{} {\hat{F}} &{} {\hat{G}} \\ -\frac{2b_{1}h_{1} + b_{1}h_{2} + h_{1}b_{2} + 2h_{2}b_{2}}{6l} &{} 0 &{} 0 &{} \frac{2b_{1}h_{1} + b_{1}h_{2} + h_{1}b_{2} + 2h_{2}b_{2}}{6l} &{} 0 &{} 0 \\ 0 &{} {\hat{C}} &{} {\hat{F}} &{} 0 &{} {\hat{H}} &{} {\hat{I}} \\ 0 &{} {\hat{D}} &{} {\hat{G}} &{} 0 &{} {\hat{I}} &{} {\hat{J}} \end{bmatrix} \end{aligned}$$

(14)

After considering each element’s stiffness matrix individually, the elements are assembled into a global stiffness matrix for the whole mesh where elements have different orientations. Figure 5 shows a general element in the mesh inclined at an angle theta ($\theta$) with the horizontal axis.

Fig. 5

Inclined frame element

In order to rectify the orientations of the elements into the global axes (x, y) for the apt of assembly, the transformation matrix T is multiplied by the local stiffness matrix of every element to get its global stiffness matrix K:

$$\begin{aligned} K= T'KT \end{aligned}$$

(15)

where T is given by:

$$\begin{aligned} T= \quad \begin{bmatrix} cos(\theta ) &{} -sin(\theta ) &{} 0 &{} 0 &{} 0 &{} 0 \\ sin(\theta ) &{} cos(\theta ) &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} cos(\theta ) &{} -sin(\theta ) &{} 0 \\ 0 &{} 0 &{} 0 &{} sin(\theta ) &{} cos(\theta ) &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \end{bmatrix} \end{aligned}$$

(16)

After assembling the global stiffness matrix of all two node frame elements, the global load matrix is then formulated with axial forces (A), shear forces (V) and bending moments (M) at both nodes. So, the load vector for a single frame element is:

$$\begin{aligned} f= [A_{1} \ V_{1} \ M_{1} \ A_{2} \ V_{2} \ M_{2}] \end{aligned}$$

(17)

Along with that, the displacement vector for a frame element, that includes the axial displacement u, the transverse displacement v and rotation about the element w, is as follows:

$$\begin{aligned} d= [u_{1} \ v_{1} \ w_{1} \ u_{2} \ v_{2} \ w_{2}] \end{aligned}$$

(18)

where the equation of static equilibrium for each frame element is given as [24]:

$$\begin{aligned} f=ku \end{aligned}$$

(19)

where f, k and u are the local force, stiffness and displacement matrices respectively.

The global equation of static equilibrium is:

$$\begin{aligned} F=KU \end{aligned}$$

(20)

where F, K and U are the global force, stiffness and displacement matrices respectively.

3 Problem formulation

The objective or the performance function is what governs the behavior of the optimization process. Depending on the type of problem or the task intended from this mechanism, the objective function is set. The major challenge in formulating the objective function of topology optimization problems is the compromise between the stiffness and flexibility of the structure. The strain energy and the mutual strain energy have been found to have a great effect on the compliance of the mechanism [25]. The stiffness is measured by the strain energy (SE) defining the elastic energy stored in the structure while the flexibility is measured by the mutual strain energy (MSE) resembling the energy at the output port [4]. Howell [1] found that the total strain energy for all elements, in its discretized form, is:

$$\begin{aligned} SE=\frac{1}{2}U^{T}KU \end{aligned}$$

(21)

And the mutual strain energy can be measured as:

$$\begin{aligned} MSE=D^{T}KU \end{aligned}$$

(22)

where D is the displacement field due to a dummy load.

Based on what preceded, Howell [1] revealed the energy-based objective function that seeks a stiff yet flexible mechanism by minimizing SE and maximizing MSE:

$$\begin{aligned} Minimize: \frac{MSE}{SE} \end{aligned}$$

(23)

The above objective function eventually maximizes the amplification ratio (AR) defined as the ratio of the output to the input displacements:

$$\begin{aligned} Maximize: AR = \frac{\delta _{output}}{\delta _{input}} \end{aligned}$$

(24)

Diab and Smaili [22] elaborated a new objective function in order to maximize the displacement at the output port yet keeping the topology in physically feasible conditions. To prevent misleading outcomes, they postulated a new objective function that hooked the output displacement to the maximum tensile and compressive stresses that the topology is subjected to:

$$\begin{aligned}&Minimize: \frac{MSE}{SE} \left( log_{10} \left( \mid \sigma _{max,ten} \mid \right) \nonumber \right. \\&\quad \left. + log_{10} \left( \mid \sigma _{max,comp} \mid \right) \right) \end{aligned}$$

(25)

where $\sigma _{max,ten}$ and $\sigma _{max,comp}$ are the maximum tensile and maximum compressive stresses in the structure. These normal stresses are computed from the bending-moment (M) and axial forces (A) generated within each frame element as listed in (17). The logarithmic scale is used to account objectively for relative changes in stresses and $\frac{MSE}{SE}$.

Five design variables, of discrete and continuous nature, are allocated to each frame element. The cross-sectional dimensions of each element represented by the continuous variables $b_1$, $h_1$, $b_2$ and $h_2$ in Fig. 2 can take any value between an upper and lower limit as listed in Sect. 5. In addition, the normalized material density En is the discrete design variable that can take values of 0 or 1 indicating the existence or non-existence of a material element respectively.

4 Ant colony optimization

Swarm intelligence is a family of optimization stochastic algorithms that uses the novelty of living organisms like insects’ colonies such as ants and bees, bird flocks, fish schools and microbes in connecting their home with the food source. First proposed by Dorigo and Caro [23], ant colony optimization was found to be an efficient tool in designing fully compliant mechanisms and thus gaining huge attention in research.

Researchers were able to imitate the natural ants’ behavior through artificial “simulated” ants. Their performance is coded into a mathematical approach of numerical equations and notations. Resembling the search space, a design space of a compliant mechanism is the room where artificial ants roam to intend the optimal path between two points. These points, representing the home and food source, are considered as the input and the output ports of the mechanism.

Since an individual ant is not multitasking and it searches for only one variable, multi-variable problems require an ant assigned to each variable. In this work, the ACO algorithm is adapted in a unique approach where the ants’ paths are no longer confined by the finite elements, as real physical node-to-node paths; however, each ant path represents an independent design variable. Upon randomly changing one of the variables and if the objective function is improved, this will be decoded as “an ant crossing an imaginary path” and thus pheromone is layed over that path. Increasing the pheromone deposit on that trail will consequently affect the no-change probability (P) and thus increase the probability of saving this change for the coming few iterations:

$$\begin{aligned} P_{i} = \frac{\tau _{i}}{\tau _{avg}} \end{aligned}$$

(26)

where $\tau _{i}$ is the pheromone intensity for ant i and $\tau _{avg}$ is the average pheromone intensity for all ants. This value is compared to a random number (s) generated between 0 and 1; if $P_{i}$ is less than s then the variable is randomly changed (i.e. ant is allowed to cross the path) and the objective function is recalculated. If an improvement is detected, the variable is updated by its new value otherwise the old value is retained. This probability test will ensure low chances of change on variables that revealed improvement and higher chances for less frequent paths. And since not all improvements have the same contribution in reaching the optimal solution, the pheromone update $\varDelta {\tau }$ is a function of the objective function change:

$$\begin{aligned} \varDelta {\tau _{iter}} = \frac{f_{iter-1} - f_{iter}}{f_{iter-1}} \end{aligned}$$

(27)

where $f_{iter-1}$ and $f_{iter}$ are the objective function values at iterations $iter-1$ and iter respectively. Furthermore, the pheromone evaporation rate $\rho$ at the end of each iteration is uniform for all ants. Thus, the total pheromone update is given by:

$$\begin{aligned} \tau _{iter+1} = (1-\rho )\tau _{iter} + \varDelta {\tau _{iter}} \end{aligned}$$

(28)

In this work, 5 ants are assigned to each frame element in the topology layout, 4 of them representing the geometric design variables and 1 representing the normalized modulus of elasticity (En). Accordingly, for a compliant topology with n frame elements, the total number of ants involved in the ACO algorithm is 5n. The imaginary paths of the ACO algorithm represent the possible change in the values of the design variables. Therefore, when an ant crosses over an imaginary path, this is translated as a successful change in the value of the design variable that improves the objective function. The pheromone intensity laid over each path represents the driving force of motion for the corresponding ant as formulated by the no-change probability P in 26. The objective functions stated in (23) and (25) will be used herein to present three case studies. A comparison between two types of frame elements, constant and variable cross section, will be casted. The results are tested using ANSYS under the same conditions as illustrated in the coming section.

5 Case studies

In this section, three case studies are tested for different objective functions to address the miniature displacement amplifier first introduced by Howell [1] Unlike the study in [22] where the design domain was meshed with constant cross-section two node frame elements, in this work, the elements have linearly changing cross-sections. As mentioned earlier, the number of ants used in this work is 5n where n is the number of elements. The initial amount of pheromones (ph) associated to each ant has a minimal effect on the convergence of the solution as it will only differentiate between the pheromone intensities during the first few iterations. Accordingly, each ant is initialized with a unit pheromone (ph=1). For the pheromone evaporation rate ($\rho$), 50$\%$ is deemed most appropriate as it presents a compromise between fast convergence to local minima and very slow convergence to the global minimum.

The design domain is a rectangular 2D space, 200 by 100 $\mu m$, meshed according to the pattern shown in Fig. 7. The mesh consists of 154 elements and 59 nodes. The four corner nodes (1, 7, 53 and 59) are constrained, the input force ($F_{in}$) is applied to node 4 and the desired output displacement ($\delta _{out}$) is at node 56. Each of the elements shown in Fig. 6 is of two nodes with a linearly changing cross section as illustrated in Fig. 2. The material used is plastic ABS as reported by Howell [1] which can withstand compressive and tensile stresses up to 38MPa and 52MPa respectively.

Fig. 6

Design space for the displacement amplifier problem

The elements are considered as Euler-Bernoulli beams where the length is much greater than b and h (aspect ratio greater than 10). The modulus of elasticity (E), is 160GPa and $F_{in}$ is $500 \mu N$ acting upward. The optimizer may omit or keep some elements by giving it a normalized modulus of elasticity (En) of either 0 (void) or 1 (material). For comparison purposes with the previous work in [1] and [22], $h_{1}$ and $h_{2}$ are fixed to 0.053$\mu m$ and b varies within the bounds of 0.01$\mu m$ and 5$\mu m$. The termination criteria for the optimizer is reached when the pheromone values for all ants drop below a threshold value ($\tau _{th}$=$10^{-6}$) which indicates that the objective function has stabilized.

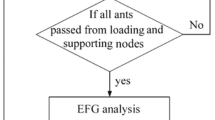
The proposed methodology is summarized in Fig. 7 with a flowchart that streamlines the flow of steps in adapting ACO to optimum synthesis of a micro-compliant displacement amplifier.

Fig. 7

Flowchart of the ACO methodology for optimum synthesis of micro-compliant amplifiers

5.1 Case 1

The objective function used in this section is to minimize $\frac{MSE}{SE}$ and thus maximize the amplification ratio. Table  1 shows the values of $b_{1}$ and $b_{2}$ for each element in the optimized topology where elements that are not listed in the table are simply void with $E_{n}$ = 0. The AR of the optimized mechanism is 90.464. Table 2 summarizes the performance of the optimized mechanism and compares its performance to that obtained in [22]. Figure 8 shows the optimized compliant mechanisms for maximizing the amplification ratio where the solid and dashed lines represent the un-deformed and deformed topologies respectively.

Table 1 Element Specifications for case 1 as obtained by the ACO

Table 2 Comparison of results obtained in all 3 cases

Fig. 8

Un-deformed/deformed topology of case 1

To validate the results obtained from the topology optimization approach of case 1, the topology parameters listed in Table 1 are used in the finite element solver ANSYS and the un-deformed/deformed topologies are shown in Fig. 9. The performance criteria of the optimized design mechanism (output displacement, AR, maximum stresses, and material volume) as obtained through ANSYS are also listed in Table 2 for comparison.

Fig. 9

Displacement of the topology in case 1 as obtained in ANSYS

Figure 10 displays the convergence curves of the ACO algorithm for 5 different runs of case study 1. Each run starts from a different value of the objective function depending on the initial solution vector of the design variables, however all runs converge to the optimum value of the cost function as listed in Table 2. Plateaus in the convergence curves represent iterations with no improvement in the objective function.

Fig. 10

Convergence curves of the ACO for case 1

5.2 Case 2

In this case, the objective is to maximize the output displacement. Thus, the objective function stated in 25 is used. Table 3 shows the values of $b_{1}$ and $b_{2}$ for the optimized topology where the maximum output displacement is found to be 0.992 m. The elements that are not listed in Table 3 are the ones with $E_{n}$= 0 and consequently represent void elements.

Table 3 Element specifications for case 2 as obtained by the ACO

Figure 11 shows the un-deformed and deformed topologies of case 2 represented through the solid and dashed lines respectively. The same elements’ parameters listed in Table 3 are inserted to ANSYS FEA solver under the same loads and constraints and the un-deformed/deformed topologies are shown in Fig. 12. The optimized topology performance (output displacement, AR, maximum stresses, and material volume) as calculated from ANSYS is also furnished in Table 2.

Fig. 11

Un-deformed/deformed topology of case 2

Fig. 12

Displacement of the topology in case 2 as obtained in ANSYS

Figure 13 displays the convergence curves of the ACO algorithm for 5 different runs of case study 2 where all runs converge to the optimum value of the objective function listed in Table 2.

Fig. 13

Convergence curves of the ACO for case 2

5.3 Case 3

The objective of this case study is to maximize the output displacement and the amplification ratio (AR) simultaneously. Consequently, the objective function to be used in this case is the superposition of those previously presented in cases 1 and 2. Thus the objective function is formulated as follows:

$$\begin{aligned}&Minimize: \frac{MSE}{SE} \left( log_{10} \left( \mid \sigma _{max,ten} \mid \right) \nonumber \right. \\&\quad \left. + log_{10} \left( \mid \sigma _{max,comp} \mid \right) \right) + \frac{MSE}{SE} \end{aligned}$$

(29)

The elements’ specifications ($b_{1}$ and $b_{2}$) for the optimized topology (Fig. 14) of case 3 are listed in Table 4. The amplification ratio and output displacement are found to be 46.374 and $0.663 \mu m$ respectively as listed in Table 2 in addition to the maximum internal stresses and material volume used.

Table 4 Element specifications for case 3 as obtained by the ACO

Fig. 14

Un-deformed/deformed topology of case 3

The same optimized mechanism is modeled in ANSYS and the deformed topology is shown in Fig. 15. Comparison between the results obtained through the ACO algorithm and that of ANSYS is listed in Table 2.

It is worth noting that the hanging elements in all three cases do not affect the performance of the overall topology but were kept there to show the exact output of the ACO algorithm. The stiffness matrices of such elements do not enter into the formulation of the global stiffness matrix of the overall topology. Such elements can be easily removed via a post-processing phase without interfering with the physical feasibility of the mechanism.

Fig. 15

Displacement of the topology in case 3 as obtained in ANSYS

Figure 16 displays the convergence curves of the ACO algorithm for 5 different runs of case study 3 where all runs converge to the optimum value of the objective function listed in Table 2.

Fig. 16

Convergence curves of the ACO for case 3

5.4 Discussion of results

By looking at Table 2 and comparing the results obtained through the ACO algorithm for linearly variable cross-sections (current work) to constant cross-sections previously presented in literature, the following interpretations can be emphasized. In case 1, the main goal was to maximize the amplification ratio AR of the micro-displacement amplifier. An amplification ratio of 90.464 is reported in this work as compared to 40.13 for constant cross-section frame elements. Therefore, compared to the work in [22], AR was increased by $55.64\%$ with a decrease of $25.2\%$ and $25.36\%$ in maximum tensile and compressive stresses respectively along with $15.91\%$ cut down on the total material volume used. In case 2, the output displacement is to be maximized. The optimized topology in this case study produced an output displacement of $0.991 \mu m$ compared to $0.29 \mu m$ and $0.9232 \mu m$ in [1] and [22] respectively. Therefore, compared to constant cross-section elements [22], the linearly varying cross-section topology have shown an increase in $\delta _{out}$ by $6.945\%$ with $18\%$ less tensile and compressive stresses with a reduction of $41.989\%$ on material volume. In case 3, both the output displacement and the AR were to be maximized. The optimized topology in this work generated an output displacement of $0.6631 \mu m$ and an amplification ratio of 46.3744 as compared to an output displacement of $0.6276 \mu m$ and an amplification ratio of 31.8525 in the optimum constant cross-section topology. Therefore, an output displacement increase by $5.356\%$ and an amplification ratio increase by $31.31\%$ is achieved. Moreover, the optimum topology in case 3, as compared to that in [22], achieved a decrease of $43.28\%$ and $43.39\%$ in maximum tensile and compressive stresses respectively and $41.007\%$ drop in total material volume. The stress values obtained in all the case studies are less than the tensile (52MPa) and the compressive (38MPa) yield strengths of the ABS plastic used, ensuring the mechanism is deforming within its elastic limits.

6 Conclusions

The objective of this work is to optimally design compliant mechanisms using frame elements with linearly varying cross-sections. New stiffness matrices are derived to account for the linear change in an element’s cross-section. Three case studies are presented to optimize for amplification ratio, output displacement and the combination of both. The ACO algorithm is applied to optimize for the element specifications and consequently the whole topology. The performances of the 3 optimally designed topologies are compared to those previously reported in [1] and [22] for elements with constant cross-sectional areas. In addition, the performance of all optimized topologies are validated through ANSYS. Results show that the performance of a compliant structure with variable cross-sections surpasses that of its constant cross-section counterpart for all three cases. The variable cross-section topologies have more flexibility at the output port and more rigidity at the input port as reflected in the larger output displacements and amplification ratios. Moreover, the variable cross-section topologies are subjected to lower levels of compressive and tensile stresses and can be manufactured using less material volume. For future work, node positions can be added as design variables such that the locations of the nodes are variable. In addition, non-linear cross section variations are to be investigated where the tapering between the two nodal areas of an element is non-linear (ex: parabolic). The material density, $E_{n}$ currently restricted to 0 or 1 (i.e. void or material), can be released to have any material density and thus obtain grey elements of intermediate densities other than black (i.e. full material) and white (i.e. void). The current work focused on frame elements however, the topology optimization approach presented herein can be easily extended to 3D structures.