State consistence of data-driven reduced order models for parametric aeroelastic analysis

Abstract

This paper investigates the state consistence of parametric data-driven reduced order models (ROMs) in a state-space form obtained by various system identification methods, including autoregressive exogenous (ARX) and subspace identification (N4SID), for aeroelastic analysis in varying flight conditions. The target flight envelop is first partitioned into discrete grid points, on each of which an aerodynamic ROM is constructed using system identification to capture the dependence of the generalized aerodynamic force on the generalized displacement of structural modes. High-fidelity aeroelastic modal perturbation simulations are used to generate the ROM training and verification data. Aerodynamic ROMs not on the grid point are obtained by interpolating those at neighboring grid points. Through a thorough analysis of the model coefficients and pole migration, it is found that only the ARX-based aerodynamic ROM preserves the state consistence, and hence, allowing direct interpolation of system matrices at the non-grid point and rapid aerodynamic ROM database development in the entire flight parameter space. In contrast, N4SID-based ROM destroys the state consistence and yields physically meaningless results when ROMs are interpolated. The origin of the difference in the state consistence caused by both methods is also discussed. The interpolated ARX aerodynamic ROMs coupled with the structural ROM for parametric aeroelastic analysis exhibit excellent agreement with the high fidelity full order model (mostly <5% relative error) and salient computational efficiency.

1 Introduction

The modern design of aerospace vehicles utilizes state-of-the-art lightweight and flexible materials that push the limits to enhance maneuverability, endurance, and performance, and hence, is more prone to complex dynamics, stability, and durability issues. The ability of data-driven reduced order models (ROMs) to accurately predict aeroelasticity and flutter conditions is of foremost importance for developing safe and high-performance vehicles and has been well demonstrated in the limit cycle oscillations, flutter, and gust load alleviation analysis. Data-driven ROM is a non-intrusive method that extracts predictive models from response or training maneuver data and can be classified into several categories [1], including indicial response functions, Volterra series, state space models, and surrogate models.

Indicial response functions are constructed using the output response of a system due to a unit step change of inputs. Then the system responses to arbitrary inputs can be obtained through the convolution of the indicial response function. Ghoreyshi, Jirask, and Cummings [2] proposed a grid-movement method that uses computational fluid dynamics (CFD) simulation to generate the response data of a step function, and more importantly, allows to uncouple the input parameters, e.g., the angle of attack (AoA) and pitch rate. It then was used to predict the aerodynamic load through convolution step functions with the derivative of the input. Van Rooij et al. [3] employed the indicial response function and grid motion techniques to obtain the nonlinear ROM for unmanned combat air vehicles.

Volterra series is a ROM technique used to model a nonlinear and time-invariant system by a series of polynomial linear and nonlinear terms based on multidimensional convolution integrals [4, 5]. Raveh, Yuval Levy, and Karpel [6] developed a ROM methodology based on the nonlinear Volterra series to predict the nonlinear generalized aerodynamic force (GAF) in the transonic flow regime for flutter analysis, in which a time-domain CFD simulation was performed subjected to a modal step excitation of each structural mode to collect the response data for Volterra kernel extraction. Silva [4] proposed to use the analytical form of Volterra series and CFD simulation to develop computationally efficient aeroelastic ROM (AE-ROM). Balajewicz and Dowell [5] presented an approach to construct a sparse representation of the Volterra series to reduce the identification cost of high-order Volterra kernels for modeling flutter and limit-cycle oscillations.

A state space model is a mathematic representation of a dynamic system using a set of input, output, and state variables and has found widespread use in modern control engineering and aeroservoelastic analysis. The state space model is obtained through system identification of response data generated by input excitation, and the most widely used system identification techniques include Eigensystem Realization Algorithm [7, 8], Observer/Kalman Filter Identification [9], Numerical Algorithm for Subspace State Space System Identification (N4SID) [10, 11], among others. Kim [12] modified the classical eigensystem realization algorithm and presented an efficient system identification method in discrete time-domain using multiple inputs of statistically independent random samples, which significantly accelerates the ROM construction process. Silva [13] proposed a method for simultaneous excitation of multiple structural modes in CFD simulation to expedite data generation for ROM generation. Four types of input signals, including lagged step, block pulse, Haar, and Walsh functions, were evaluated, and the results showed excellent agreement with the one-mode-at-a-time approach. Winter, Heckmeier, and Breitsamter [14] used the linear system identification to construct a time-domain ROM and considered the parameter-varying structural model that approximates the mode shapes at different parameters through radial basis function and two-dimensional Chebyshev polynomials. Chen et al. [15] developed an autoregressive model with exogenous input (ARX) and took into account CFD-induced uncertainties in aerodynamic ROM (A-ROM) development. Mannarino and Dowell [16] proposed an approach to identify a nonlinear state space ROM for unsteady aerodynamic responses in aeroelasticity. The ROM is obtained through a two-step procedure, viz., subspace projection to identify the linear part and output error minimization to fit the coefficients of the nonlinear terms that are a function of aerodynamic states. The procedure was then modified by Quan et al. [17] who only added the nonlinear term of the aerodynamic states in the output equation, and by Huang et al. [18] and Yang et al. [19] where the nonlinear terms of aerodynamics states and inputs were added into both the state equation and the output equation to achieve lower state space orders. Huang, Hu, and Zhao [20] developed a nonlinear A-ROM consisting of a finite sum of Wiener-type cascade models, and each component model includes a linear dynamic state-space element followed by a single-layer neural network (NN) model. The approach computes the model coefficients through optimization to minimize the prediction residual from the previous component model.

Surrogate modeling for A-ROM constructs a black-box function that establishes a direct mapping between the vehicle motion and aerodynamic responses. Grauer and Morelli [21] proposed a multivariate orthogonal function approach to build a functional relationship between the flight rigid motion and aerodynamic responses, which tailors the regressor terms based on Gram-Schmidt orthogonalization and captures the nonlinearities in aerodynamics while keeping the regressors sparse, and hence, effectively mitigating the overfitting issues [22]. In contrast, most aerodynamic surrogate models are based on the formulation of Nonlinear AutoRegressive Moving Average with eXogenous input (NARMAX) or implicit function theorem, which evaluates the output vector at a time instant as a function of its historical values of inputs and outputs [1], and is also termed surrogate-based recurrent model. Glaz, Liu and Friedmann [23] developed a Kriging-based recurrent ROM that accounts for flow unsteadiness, time-history effects, and nonlinearities at a constant or varying Mach number to predict unsteady lift, moment, and drag coefficients of a rotating airfoil. The Kriging-based surrogate model was utilized by Li, Jin, and Zhou [24] to obtain unsteady and nonlinear A-ROM for active flow-based synthetic jet control. Liu et al. [25] also developed a Kriging-based ROM to predict aeroelastic responses (pitch angle and plunge displacement) of a NACA 64A010 airfoil in transonic flow with varying Mach numbers. Zhang et al. [26] developed radial basis function-based neural network ROM to predict aerodynamic responses subjected to nonlinear flow caused by large-scale shock motion, and the ROM is then used to investigate limited cycle oscillation behavior in the transonic flow regime. The approach was later improved by the width determination technique [27] and the center selection via the proper orthogonal decomposition (POD) technique [28], and their combinations [29]. Ghoreyshi, Jirasek, and Cummings [30] developed a radial basis function NN and extended the approach to multifidelity recurrent surrogate modeling to incorporate secondary data (Euler simulation) that is cheaper to obtain relative to the primary data (Reynolds-averaged Navier–Stokes simulation). The nonlinear functional dependence is enhanced by adding the predicted aerodynamic responses into the input. The similar idea was also applied to generate flight dynamics aerodynamic tables using CFD simulations [31]. It should be noted that some surrogate models can be transformable to the state space model through its companion form. For example, Cowan, Arena, and Gupta [32] developed a discrete-time aerodynamic model based on the autoregressive moving average model and proposed a 3-2-1-1 input profile, which allowed simultaneous excitation of the multiple structural modes to reduce CFD simulation cost. The explicit aerodynamic model and the structural model were then coupled and recast into the state space form.

Another active research area of A- and AE-ROM is to extend it from a single flight condition (e.g., Mach number, AoA) to a range of varying parameters, i.e., parametric model. It should be noted that there are two kinds of definitions currently in the ROM community for “parametric”: one from the statistical modeling perspective refers to the model that directly establishes the functional representation of the system inputs and outputs without the need for an explicit functional form [1, 33]; and the other defines the varying operational conditions of the model [34, 35]. In this paper, the latter definition is adopted.

In general, there are two approaches to consider the parametric effects in the data driven model. In the first one, the flight condition is treated as an additional input and included in the surrogate model along with the delayed aerodynamic force vectors and motion vectors. For example, Kou and Zhang [36] embedded the flight parameters into their recursive NN to consider the effect of varying Mach numbers and structural parameters on time- and frequency-domain analysis and limit cycle oscillation analysis in a range of transonic flows. Glaz et al. [23, 37] included freestream Mach number and its change rate into their Kriging model and trained it using high-fidelity simulation data of multiharmonic inputs at several flight conditions to predict the aerodynamic load of rotor blades. Liu et al. [25] reported efficient parametric ROMs that included free-stream Mach numbers and mean AoA in their Kriging-based recurrent surrogate model for unsteady aerodynamic load prediction to analyze the aeroelastic problem of a NACA 64A010, and hence, eliminating the need to reconstruct ROMs when flight parameters are changed. Skujins et al. [38] presented a single ROM applicable to multiple Mach regimes by combining linear convolution with a nonlinear correction factors. Winter and Breitsamter [39] extended the recurrent surrogate modeling to aircraft with flexible structures and presented an A-ROM based on the recurrent local linear neurofuzzy method to predict the GAF, and the Mach number is incorporated into the NARMAX model as an additional input to account for the flow condition. The ROM was tested and verified in a broad flight regime from subsonic to supersonic. Chen et al. [40] presented a support vector machine-based A-ROM to investigate limit cycle oscillation in the 2-DOF aeroelastic system for the NACA 64A10 airfoil in the transonic regime.

In contrast, another method to parameterize ROM is the gridded domain [41, 42], in which the targeted flight regime is partitioned by grid points. At these grid points, a parametric database of local state-space ROMs is constructed, and each local ROM only captures the aerodynamic or aeroelastic behavior at that flight condition. Specifically, the state-space ROM at the non-grid location where the ROM is not available initially can be obtained by interpolating the system matrices of those at the grid points [43]. The advantages of this method are: firstly, it only entails one-time interpolation at the non-grid location whenever the new ROM is needed for use, which allows fast and accurate ROM construction at a new, non-grid flight condition and eliminates the need for system identification for online applications. Second, the flight controller can be synthesized offline at the grid points, and the control law at non-grid points can be generated through interpolation. Lastly, the database can be easily expanded or locally refined without modifying ROMs at existing grid points, which is desirable for developing control law and aeroservoelastic analysis across a broad flight regime. Therefore, this parameterization approach is mostly adopted with the state-space ROMs for flight control and design engineering [44,45,46,47].

Both methods and their applications are different. A-ROM parameterization through the surrogate model is a global modeling method, i.e., a single mathematical function predicting aerodynamics in a wide range of flight parameters. Flight parameters and inputs (e.g., motion variables) are combined together, and their interactions are depicted through nonlinear surrogate functions. Because modern control engineering is predominantly built on the state-space formulation and techniques, parameterization through local state-space ROM and interpolation is broadly used for aeroelastic and aeroservoelastic analysis and control law design for vehicle stability and maneuverability improvement. However, state-space ROMs at different flight conditions usually suffer from a state inconsistency issue, which is further illustrated in Fig. 1. To construct the aerodynamic state-space ROM, the data of aerodynamic responses ${\mathbf{Y}}_{f}$ subjected to a prescribed input profile of motion ${\mathbf{Y}}_{sc}$ is generated by physics-based simulation, such as CFD and is also flight condition dependent. System identification is then applied onto the discrete data set to extract the state space model at each grid point

$$\begin{gathered} {\mathbf{x}}^{p} \left( {k + 1} \right) = {\mathbf{A}}^{p} {\mathbf{x}}^{p} \left( k \right) + {\mathbf{B}}^{p} {\mathbf{Y}}_{sc} \left( k \right) \hfill \\ {\mathbf{Y}}_{f} \left( k \right) = {\mathbf{C}}^{p} {\mathbf{x}}^{p} \left( k \right) + {\mathbf{D}}^{p} {\mathbf{Y}}_{sc} \left( k \right) \hfill \\ \end{gathered}$$

(1)

where x is the state vector, [A, B, C, D] are the system matrices of the state space model, and superscript p is the p^th grid point in the flight regime. Essentially system identification truncates less important information in the data and captures key dynamics in ROM. However, the information truncated depends on the location of the grid points and the methods used. For methods that rely on singular value decomposition (SVD) to extract $\left[ {{\mathbf{A}}^{p} , {\mathbf{B}}^{p} , {\mathbf{C}}^{p} , {\mathbf{D}}^{p} } \right]$, such as N4SID, the basis vectors of the oblique projection of Hankel matrices are computed and re-ordered according to the significance of their singular values. Therefore, the definition of the state vector x is solely from a mathematical perspective and non-physical and will be different at various grid points p. In other words, the state representation of the ROM is cast in different coordinate systems, which makes direct interpolation of system matrices meaningless. This can be illustrated by a simple example of a 2-state system at the bottom of Fig. 1, where x^j and x^k are, respectively, the coordinate systems of the states at the jth and kth grid point obtained through system identification, and subscript 1 and 2 denote the two coordinates of the state-space ROM at the grid point. Apparently, x^j and x^k do not align with each other spatially, and any given state vector x when expressed in x^j and x^k, will have completely different meanings, viz., state inconsistency. As a result, at a non-grid location adjacent to the jth will have completely and kth grid, its system matrices [A, B, C, D] cannot be obtained through the interpolation of those at grid points. It should also be noted that the state inconsistence is different from the issue associated with identifiability that is caused by the ill-posedness and solution stability of the inverse problems, and can be mitigated through ‘a priori’ knowledge about constraints or penalty-regularization [48]. In contrast, the state consistence in the present investigation refers to the expression of the identified parameters in the same/consistent coordinate systems. The state inconsistence issue is also clearly revealed in Fig. 2a, which displays the vectorized elements in the “A” matrix of the state-space ROM obtained by N4SID, over a Mach domain and a AoA parameter space, and the matrix elements vary randomly and dramatically without a pattern across the parameter space. As a result, ROM interpolation directly on the “A” matrices between neighboring grid points is erroneous and creates physically meaningless results in aeroelastic responses. Fig. 2b depicts an example of aeroelastic responses, viz., the generalized displacement (GD) and GAF of the ROM at Mach = 0.65. The ROM is obtained by interpolating those at Mach = 0.6 and 0.7. No correlation is observed between real CFD data and the interpolated ROM prediction.

Fig. 1

Schematic of the gridded domain methodology and the issue of state inconsistency in state-space ROM

Fig. 2

3D view of vectorized “A” matrix elements over a section of (a-1) Mach domain; and (a-2) AoA domain from the N4SID model; and (b) Comparison of GD in aeroelastic response between interpolated ROM (obtained by N4SID) and real FOM/CFD data at Mach = 0.65, and Mach step size of 0.1 is used for interpolation

State inconsistence of the state space model is well recognized in the research of projection-based model order reduction [35, 49,50,51], but less studied in the data-driven ROM. One workaround to this issue of the state-space ROM is to interpolate on the output [42], i.e., ${\mathbf{Y}}_{f}$ (instead of system matrices) in Eq. (1) because it has the physical meaning of aerodynamic responses, i.e., GAF regardless of state representation. For example, Liu et al. [42] developed parametric ROMs to consider varying Mach numbers in the transonic regime and predict unsteady GAFs for an elastic wing with the control surface. The GAF output data predicted by the precomputed ROMs at adjacent grid points is then interpolated to attain GAF at the Mach where the ROM is not available. In this approach, two or multiple ROMs at surrounding grid points need to be computed simultaneously in each time step during ROM simulation, leading to enormous computational costs.

Therefore, a fundamentally state consistent parametric ROM is desirable for practical use. The present effort addresses this by investigating and comparing the aerodynamic ROMs obtained by two common system identification methods, ARX and N4SID, in aeroelastic analysis with respect to state consistency. Our hypothesis is that ARX should preserve the state consistency better because it directly establishes the least squares relationship between the physical inputs and outputs, and its state space ROM is constructed by its companion form, in which the definition of states is physical and represents a vector of GAFs and GDs, and hence, enhancing state consistence. To prove this hypothesis, the AE-ROM that combines the aerodynamic state-space ROM generated by ARX and the structural ROM (S-ROM) is thoroughly inspected in two separate one-dimensional parameter spaces encompassing the Mach number and the AoA. First, for each parameter space, state-space ROMs are generated and verified at each grid point. Second, different aspects of ARX ROMs are examined, such as state consistence for varying flight conditions and system poles and accuracy of interpolated ROMs. Third, the state consistence of new models obtained by ROM interpolation is examined using independent high-fidelity aeroelastic CFD data sets.

The key novelties that distinguish the present effort from existing research are: (1) unveiling the state inconsistence issue of the state-space ROM that is critical for data-driven parametric ROM development but has been overlooked; (2) through analysis of the model coefficients and pole migration, it is found that in contrast to other system identification techniques, the definition of states in ARX-based A-ROM is physical, and indeed maintains state consistence naturally without need for additional remedies. Hence, it allows direct model interpolation and coverage of the broad flight parameter space; (3) the construction of state consistent ROMs in the gridded parameter space enables the development of a parametric A- and AE-ROM database for the targeted flight envelop; and (4) it is also found that the local grid refinement in the parameter space will dramatically improve the state consistence between grid points and increase the accuracy of the interpolated ROMs. Therefore, a strategy of adaptive grid refinement is necessary for the progressive construction of a parametric ROM database with minimal efforts/costs. Potentially, the parametric ROM databased can be used as the plant model for control law design and aeroservoelastic analysis.

It should be emphasized that the focus of the present effort is not on ROM interpolation but rather identifying a system identification method that could produce a consistent state-space ROM amenable to direct interpolation of system matrices and investigating the rationale. ROM interpolation only serves as a means to examine the state consistence. Indeed, with state consistence preserved, any interpolation method can be used to generate ROMs at non-grid points. The present research is also distinctly different from the work on interpolation in the space tangent to the Grassmann manifold in two aspects: (1) this paper studies how to preserve the consistence of ROM states (i.e., coordinate systems in Fig. 1) to enable direct system matrix interpolation at non-grid points, while the latter proposes an approach to interpolate the basis vectors of an orthonormal projection subspace at the non-grid points [35]. In fact, as discussed in [35], the state consistence is required prior to interpolation of basis vectors in Grassmann manifold (e.g., through congruence transformation); and (2) the state inconsistence of ROMs investigated by the present research is not caused by difference in basis vectors of projection at various grid points because in our work the distributed aerodynamic forces are projected on the structural modal shapes that are invariant with the flight conditions. Instead, the inconsistence arises from the system identification process that relies on SVD of the oblique projection of Hankel matrices and uses non-physical states, and then casts the state-space model in different coordinate systems. It should be noted that although initially proposed for projection-based linear parametric ROMs [35], the interpolation approach for Grassmann manifold is also applicable to nonlinear ROMs obtained through local reduced order basis [52] and hyper-reduction for system approximation [53] and even data-driven ROM [54].

The present work also distinguishes from the POD-based [34, 55,56,57,58,59] and dynamic mode decomposition (DMD)-based [11, 60] methods for dynamic modeling. POD is a L2-optimal low-rank matrix approximation approach. Since it is completely data-driven, its main utility is to extract dominant basis vectors of snapshot data and to predict distributed field variables, such as surface pressure. DMD is a dimensionality reduction technique that distills a set of normal modes from snapshot data, each with a constant frequency. When combined with Koopman theory, it can be used for constructing data-driven, non-intrusive ROM with inputs and outputs (i.e., dynamic mode decomposition with inputs and outputs, IODMD) [11, 60]. Our A-ROM is distinctly different from both POD- and DMD-based methods in the following: (1) our ROM aims to establish a functional mapping directly between the input of GD and the output of GAF, and physical modal shapes of elastic structures are used as the subspace for projecting the distributed aerodynamic force. However, in the POD-ROM and IODMD-ROM, basis vectors of snapshot data are used as the projection subspace, and POD modal coefficients are used as the output or states for ROM, respectively; and (2) the focus of the present study is on aeroelastic analysis rather than prediction of distributed aerodynamic responses/loads. It is rational to directly select GAF as the output of our A-ROM rather than POD modal coefficient as this will eliminate an additional step of POD to reconstruct the distributed aerodynamic forces during aeroelastic analysis.

The paper is organized as follows. The model formulation and methodology including the A-ROM, S-ROM, ROM coupling and interpolation is first described in Section 2. Next, the case studies to verify the AE-ROMs and investigate the state consistence along with the results and discussion are presented in Sect 3. The paper concludes with a summary of the scientific findings and insights gained from the modeling and case studies in Sect 4.

2 Model formulation and methodology

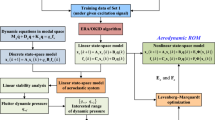
In this section, we present the methodology of the system identification-based state-space ROM for aeroelastic analysis. As shown in Figs. 3 and 4, the entire ROM process includes three key steps: (1) Aerodynamic ROM: A set of local aerodynamic ROMs (abbreviated as A-ROM hereafter) are constructed at selected flight conditions (i.e., grid points) in the flight envelop using the data generated by the full order model (FOM) of aerodynamic CFD simulation. The local A-ROMs describe the mapping relationship between the GAF ${\mathbf{Y}}_{f}$ and the GD of structure ${\mathbf{Y}}_{sc}$ at the grid points and will be obtained through system identification (see Sect 2.1 below). The A-ROM at any non-grid location within the flight envelope is obtained by interpolating the system matrices of the A-ROMs at the neighboring grid points attained in the previous step. Since interpolated ROMs are based on locally optimal ROMs of low dimensions, in which only local aerodynamic characteristics needs to be captured, it may potentially yield more compact model structure and faster simulation speed; (2) Structural ROM: The structural ROM (abbreviated as S-ROM hereafter) is based on the modal equations of structure dynamics. That is, the spatial distribution of the structural displacement is projected onto mode shapes, yielding the GD of structure ${\mathbf{Y}}_{sc}$. Thus, the S-ROM uses ${\mathbf{Y}}_{f}$ as the input and outputs ${\mathbf{Y}}_{sc}$; and (3) ROM assembly. The interpolated A-ROM at non-grid location then can be integrated with the S-ROM for coupled aeroelastic analysis as shown in Fig. 3. The results of the interpolated AE-ROM, such as GAF and GD responses and pole migration will serve as an effective means to evaluate the state consistence of the constructed A-ROM database at grid points. It also should be noted that separation of the flight parameters from aeroelastic variables (${\mathbf{Y}}_{f}$ and ${\mathbf{Y}}_{sc}$), i.e., gridded domain and local ROM method, leads to simple ROM model structure, database organization, maintenance, and extension.

Fig. 3

Data-driven parametric ROMs for aeroelastic analysis

Fig. 4

Meshes used in simulation in the volume and along the wing surface.

2.1 Aerodynamic reduced order modeling

A-ROMs take the GD ${\mathbf{Y}}_{sc}$ as inputs in the time domain and outputs the GAF ${\mathbf{Y}}_{f}$, which can be described as

$$\begin{gathered} {\tilde{\mathbf{Y}}}_{f} = {\tilde{\mathbf{Y}}}_{f}^{0} + {\mathbf{N}}\left( {{\tilde{\mathbf{Y}}}_{sc} - {\tilde{\mathbf{Y}}}_{sc}^{0} } \right) \hfill \\ {\mathbf{Y}}_{f} = {\mathbf{N}}\left( {{\mathbf{Y}}_{sc} } \right) \hfill \\ \end{gathered}$$

(2)

where superscript “0” denotes the quantities at the equilibrium state, e.g., modal displacements ${\tilde{\mathbf{Y}}}_{sc}^{0}$ due to asymmetric GAF loads ${\tilde{\mathbf{Y}}}_{f}^{0}$ arising from non-zero AoAs and non-symmetric geometry. ${\mathbf{Y}}_{f} = {\tilde{\mathbf{Y}}}_{f} - {\tilde{\mathbf{Y}}}_{f}^{0}$ and ${\mathbf{Y}}_{sc} = {\tilde{\mathbf{Y}}}_{sc} - {\tilde{\mathbf{Y}}}_{sc}^{0}$ are, respectively, the variation/perturbation in the GD and GAF relative to the equilibrium state. N is the functional relationship between them and can be described by a linear function when the perturbation is small. In this paper, N is built using the multi-input and multi-output system identification method with training data generated by a high-fidelity CFD simulation [13]. The entire process of constructing A-ROM is summarized in pseudo-Algorithm 1 and elucidated as follows:

• Step 1: The flight parameter space is uniformly sampled with grid points P. In this paper, two separate one-dimensional parameter spaces (Mach number and AoA) domain are given in Table 1, and those for AoA are given in Table 2

• Step 2: The training data is generated based on the modal perturbation/excitation technique presented in [13, 61], which are briefly summarized here for the sake of completeness. It consists of three sub-steps:

  • Step 2.1 The simulation is initialized using a converged steady-state CFD simulation assuming a rigid structure to provide an estimation of the main bulk flow and an initial condition for the next simulation;

  • Step 2.2 For any scenario involving a nonzero initial displacement (due to nonzero asymmetric loads on the top and bottom surface of the wing, such as nonzero AoA or an asymmetric wing shape), a static aeroelastic simulation is run to find the aeroelastic equilibrium with respect to the mean flow. This is a time accurate, fully coupled aeroelastic simulation but uses large structural damping with a value of 0.99 to mitigate dynamic transients and quickly converge to the aeroelastic equilibrium, ${\tilde{\mathbf{Y}}}_{f}^{0}$ and ${\tilde{\mathbf{Y}}}_{sc}^{0}$ [13, 61]. These static aeroelastic quantities are then used to initialize the next simulation;

  • Step 2.3 A dynamic aerodynamic response simulation is performed. A perturbation of ${\mathbf{Y}}_{sc}$ around ${\tilde{\mathbf{Y}}}_{sc}^{0}$ following a prescribed time-dependent input profile is imposed throughout the transient CFD simulation that collects the GAF responses ${\mathbf{Y}}_{f}$ arising from the perturbation. Several input profiles capable of capturing wide frequency contents were proposed and widely used for training data generation for aeroelastic modeling, including Walsh functions [53]; random-like and noisy sweep signal [16]; filtered white Gaussian noise [17]; and 3-2-1-1 profile [15, 32]. In this paper, the 3-2-1-1 profile verified by our previous work [62] is used, which is able to excite a relatively broad frequency range that accommodates the targeted frequency in this study. In this simulation, a realistic and conservative value (zero) of structural damping is used [61, 63]. The data of ${\mathbf{Y}}_{sc}$ and ${\mathbf{Y}}_{f}$ form $N_{t}$ input-output pairs for system identification and A-ROM construction, where $N_{t}$ is the number of time steps in the simulation.

  • The training simulation procedure above will be performed at specified grid points P within the flight parameter space. For symmetric wings (e.g., ARARD 445.6 in this study) at AoA = 0°, step 2.2 for static aeroelastic simulation is not needed.

• Step 3 : Given the data pair (${\mathbf{Y}}_{sc}$ and ${\mathbf{Y}}_{f}$) from the training simulation, the mapping relationship N above at a single grid point can be obtained using a variety of system identification methods, including the Volterra series [58], eigenvalue realization algorithm [12, 64], and regression [15, 32, 40]. Specifically, in this paper, two methods based on ARX [65] and N4SID [10] are adopted and investigated in terms of state consistence of the state-space ROM. In the ARX model, the GAF ${\mathbf{Y}}_{f}$ is expressed as a sum of the previous outputs and the present and previous inputs ${\mathbf{Y}}_{sc}$ in a discrete time-domain

  $${\mathbf{Y}}_{f} \left( k \right) = \mathop \sum \limits_{i = 1}^{{n_{a} }} {{\varvec{\upalpha}}}_{i} {\mathbf{Y}}_{f} \left( {k - i} \right) + \mathop \sum \limits_{j = 0}^{{n_{b} - 1}} {{\varvec{\upbeta}}}_{j} {\mathbf{Y}}_{sc} \left( {k - j} \right) + {\mathbf{e}}\left( k \right)$$

  (3)

where k is the k^th time step; $n_{a}$ is the number of the previous inputs included in the model; and $n_{b}$ is the total number of the present and previous inputs. ${{\varvec{\upalpha}}}_{i}$ and ${{\varvec{\upbeta}}}_{i}$ are the model parameter matrices and can be obtained by the least-squares regression, and e is the error between the model-predicted GAF output and the actual output of the k^th data point. Eq (3) can be transformed into a vector form, defined as:

$${\mathbf{Y}}_{f} \left( k \right) = {\mathbf{\varphi }}^{{\text{T}}} \left( k \right) {{\varvec{\uptheta}}}$$

(4)

where ${\mathbf{\varphi }}^{{\text{T}}} \left( k \right)$ is the set of vectors consisting of $\left[ {{\mathbf{Y}}_{f} \left( {k - 1} \right), \ldots ,{\mathbf{Y}}_{f} \left( {k - n_{a} } \right), {\mathbf{Y}}_{sc} \left( k \right),{\mathbf{Y}}_{sc} \left( {k - 1} \right), \ldots , {\mathbf{Y}}_{sc} \left( {k - n_{b} } \right)} \right]$, and ${{\varvec{\uptheta}}}$ is a set of vector made up of $\left[ {{{\varvec{\upalpha}}}_{1} , \ldots , {{\varvec{\upalpha}}}_{{n_{a} }} , {{\varvec{\upbeta}}}_{0} ,{{\varvec{\upbeta}}}_{1} , \ldots , {{\varvec{\upbeta}}}_{{n_{b} }} } \right]^{{\text{T}}}$. By stacking up the data of ${\mathbf{\varphi }}^{{\text{T}}} \left( k \right)$ for each time instant k = 1, …, $N_{t}$ during the training simulation, ${{\varvec{\uptheta}}}$ can be computed using the least-squares method. Once θ is determined, the ARX model in Eq. (3) can be transformed into the state-space representation, i.e., Eq. (1) by introducing a state-vector ${\mathbf{x}}\left( k \right)$ as follows [15, 32]:

$${\mathbf{x}}\left( k \right) = \left[ {\begin{array}{*{20}c} {y\left( {k - 1} \right)} \\ \vdots \\ {y\left( {k - n_{a} } \right)} \\ {u\left( {k - 1} \right)} \\ \vdots \\ {u\left( {k - n_{b} + 1} \right)} \\ \end{array} } \right]$$

(5)

Table 1 ARX-based Aeroelastic ROM verification for the Mach parameter space (AoA = 0°)

Table 2 ARX-based Aeroelastic ROM verification for the AoA parameter space (Mach = 0.5)

and [A, B, C, D] of the identified system matrices are given by

$$\begin{gathered} \hfill \\ \begin{array}{*{20}c} {{\mathbf{A}} = \left[ {\begin{array}{*{20}c} {{{\varvec{\upalpha}}}_{1} } & {{{\varvec{\upalpha}}}_{2} } & \ldots & {{{\varvec{\upalpha}}}_{{n_{a} - 1}} } & {{{\varvec{\upalpha}}}_{{n_{a} }} } & {{{\varvec{\upbeta}}}_{1} } & {{{\varvec{\upbeta}}}_{2} } & \ldots & {{{\varvec{\upbeta}}}_{{n_{b} - 2}} } & {{{\varvec{\upbeta}}}_{{n_{b} - 1}} } \\ {\mathbf{I}} & 0 & \ldots & 0 & 0 & 0 & 0 & \ldots & 0 & 0 \\ 0 & {\mathbf{I}} & \ldots & 0 & 0 & 0 & 0 & \ldots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \ldots & {\mathbf{I}} & 0 & 0 & 0 & \ldots & 0 & 0 \\ 0 & 0 & \ldots & 0 & 0 & 0 & 0 & \ldots & 0 & 0 \\ 0 & 0 & \ldots & 0 & 0 & {\mathbf{I}} & 0 & \ldots & 0 & 0 \\ 0 & 0 & \ldots & 0 & 0 & 0 & {\mathbf{I}} & \ldots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \ldots & 0 & 0 & 0 & 0 & \ldots & {\mathbf{I}} & 0 \\ \end{array} } \right]} & {{\mathbf{B}} = \left[ {\begin{array}{*{20}c} {{{\varvec{\upbeta}}}_{0} } \\ 0 \\ 0 \\ \vdots \\ 0 \\ I \\ 0 \\ 0 \\ \vdots \\ 0 \\ \end{array} } \right]} \\ {{\mathbf{C}} = \left[ {\begin{array}{*{20}c} {{{\varvec{\upalpha}}}_{1} } & {{{\varvec{\upalpha}}}_{2} } & \ldots & {{{\varvec{\upalpha}}}_{{n_{a} - 1}} } & {{{\varvec{\upalpha}}}_{{n_{a} }} } & {{{\varvec{\upbeta}}}_{1} } & {{{\varvec{\upbeta}}}_{2} } & \ldots & {{{\varvec{\upbeta}}}_{{n_{b} - 2}} } & {{{\varvec{\upbeta}}}_{{n_{b} - 1}} } \\ \end{array} \user2{ }} \right]} & {{\mathbf{D}} = \left[ {{{\varvec{\upbeta}}}_{0} } \right]} \\ \end{array} \hfill \\ \end{gathered}$$

(6)

The A-ROM can also be identified using the N4SID technique. It constructs the Hankel matrix consisting of the past inputs/outputs and the future inputs/outputs. The Hankel matrix is then processed by the oblique projection, and SVD of the oblique projection determines the system order and the state vector, which then can be used to identify [A, B, C, D] in the state-space form. N4SID is capable of extracting the GAF response using simultaneous excitation of multiple structural modes with arbitrary input functions, and hence, is efficient for training data generation and ROM development. More details about N4SID are given in "Appendix 1" , and in this paper MATLAB’s built-in function ‘n4sid’ in the system identification toolbox was used.

2.2 Structural dynamics reduced order modeling

The full-order governing equation of the structural dynamics for the elastic structure is given by

$${\mathbf{M}}{\ddot{\mathbf{z}}} + {\mathbf{E}}\dot{z} + {\mathbf{K}}z = {\mathbf{F}}$$

(7)

where ${\mathbf{M}}$, ${\mathbf{E}}$, and ${\mathbf{K}}$ are the matrices describing the mass, damping, and stiffness of the structure, respectively; ${\mathbf{F}}$ is the vector of distributed forces acting on the structure; ${\ddot{\mathbf{z}}}$, ${\dot{\mathbf{z}}}$, and ${\mathbf{z}}$ are the acceleration, velocity, and displacement of the structure, respectively. An S-ROM can be formulated based on the principle of the modal superposition, that is, the displacement of the structure is treated as a superposition of leading modal shapes ${\mathbf{z}}\user2{ }$=${\varvec{\Phi}}{\mathbf{Y}}_{sc}$, in the range of target frequency, where ${\varvec{\Phi}}$ is a low-dimensional mode shape subspace obtained from the structurally undamped system, and ${\mathbf{Y}}_{sc}$ is the GD of modes. Substituting ${\mathbf{z}}\user2{ }$=${\varvec{\Phi}}{\mathbf{Y}}_{sc}$ into Eq. (7) and pre-multiplying by ${{\varvec{\Phi}}}^{{\text{T}}}$ yields

$${{\varvec{\Phi}}}^{{\text{T}}} {\mathbf{M}} {\varvec{\Phi}} {\ddot{\mathbf{Y}}}_{sc} + {{\varvec{\Phi}}}^{{\text{T}}} {\mathbf{C}}{\varvec{\Phi}}{ \dot{\mathbf{Y}}}_{sc} + {{\varvec{\Phi}}}^{{\text{T}}} {\mathbf{K}}{\varvec{\Phi}} {\mathbf{Y}}_{sc} = {{\varvec{\Phi}}}^{{\text{T}}} {\mathbf{F}} \Rightarrow {\mathbf{\ddot{Y}}}_{sc} + 2\xi {\varvec{\omega}} {{ \dot{\mathbf{Y}}}}_{sc} + {\mathbf{\Omega}}{\mathbf{Y}}_{sc} = q{\mathbf{Y}}_{f}$$

(8)

where ${\mathbf{Y}}_{f}$ = ${{\varvec{\Phi}}}^{{\text{T}}} {\mathbf{F}}/q$ is the GAF mentioned above; q is the dynamic pressure; $\xi$ is the critical damping ratio (a scalar); and ${\varvec{\omega}}$ are the natural frequencies of the structure in free vibration arranged as diag(ω₁, ω₂, …, ω_n). A linear structural damping and stiffness is assumed in Eq. (8). The property of the orthogonality of the modes is used in deriving Eq. (8): ${{\varvec{\Phi}}}^{{\text{T}}} {\mathbf{M}}{\varvec{\Phi }} = {\mathbf{I}}$; ${{\varvec{\Phi}}}^{{\text{T}}} {\mathbf{C}}{\varvec{\Phi }} = 2\xi {\varvec{\omega}}$; and ${{\varvec{\Phi}}}^{{\text{T}}} {\mathbf{K}}{\varvec{\Phi}} ={\varvec{\Omega}} =$ diag(ω₁², ω₂², …, ω_n²). In computational flutter studies, the damping ratio $\xi$ is set to 0 in an effort to be conservative following the previous studies [61, 63]. Eq. (8) is a second-order ordinary differential equation (ODE) set, and can be reduced by introducing the rate of the GD (i.e., modal velocity ${\dot{\mathbf{Y}}}_{sc}$),

$${\mathbf{x}}_{s} = \left[ {\begin{array}{*{20}c} {{\mathbf{Y}}_{sc} } \\ {{\dot{\mathbf{Y}}}_{sc} } \\ \end{array} } \right] {\text{and }} {\dot{\mathbf{x}}}_{s} = \left[ {\begin{array}{*{20}c} 0 & {\mathbf{I}} \\ { - {{\varvec{\Omega}}}} & 0 \\ \end{array} } \right]{\mathbf{x}}_{s} + q\left[ {\begin{array}{*{20}c} 0 \\ {\mathbf{I}} \\ \end{array} } \right]{\mathbf{Y}}_{f}$$

(9)

Eq. (9) can be numerically solved in two ways: directly integrating by ODE solvers (e.g., ode15s in MATLAB) or discretization using the same time step as that in CFD simulation for A-ROM training, yielding the state-space model of the discrete systems $\left[ {{\mathbf{A}}_{s} , {\mathbf{B}}_{s} ,{\mathbf{C}}_{s} ,{\mathbf{D}}_{s} } \right]$.

2.3 Reduced order model coupling

The A-ROM and S-ROM can be coupled and solved iteratively. Specifically, the coupling is expressed as an overall equation set

$$\left\{ {\begin{array}{*{20}c} {x\left( {k + 1} \right) = Ax\left( k \right) + B{\mathbf{Y}}_{sc} \left( k \right)} \\ {{\mathbf{Y}}_{f} \left( k \right) = Cx\left( k \right) + D{\mathbf{Y}}_{sc} \left( k \right)} \\ \end{array} } \right.\user2{ }{\text{and }}\left\{ {\begin{array}{*{20}c} {{\mathbf{x}}_{s} \left( {k + 1} \right) = {\mathbf{A}}_{s} {\mathbf{x}}_{s} \left( k \right) + {\mathbf{B}}_{s} {\mathbf{Y}}_{f} \left( k \right)} \\ {{\mathbf{Y}}_{sc} \left( k \right) = {\mathbf{C}}_{s} {\mathbf{x}}_{s} \left( k \right) + {\mathbf{D}}_{s} {\mathbf{Y}}_{f} \left( k \right)} \\ \end{array} } \right.$$

(10)

where the subscript s corresponds to the quantities of S-ROM. Eq. (10) shows that A-ROM takes ${\mathbf{Y}}_{sc}$ as the input and outputs ${\mathbf{Y}}_{f}$ and S-ROM takes ${\mathbf{Y}}_{f}$ as the input and calculates ${\mathbf{Y}}_{sc}$. Therefore, the equation forms closure for direct integration in the time domain. The coupled aeroelastic ROM is supplied only with an initial condition, and then left to respond spontaneously. Since A-ROM is developed using system identification of CFD-generated training data, it has to use the same time step as CFD, which typically is a constant. In order to harness advanced adaptive time stepping techniques of ODEs for further computational acceleration, the discrete A-ROM can also be converted into a continuous state-space model in the form of ODEs.

2.4 Aerodynamic reduced order model interpolation

The A-ROM described above is only applicable to a single flight condition because the CFD training data is generated at that specific condition. To attain an AE-ROM at a non-grid location within the flight envelop, system matrices ([A, B, C, D]) of A-ROMs at the neighboring grid points are interpolated if their state consistence is preserved. Since in this study, the S-ROM is assumed flight condition-independent, and interpolation of the S-ROM is not necessary. Interpolation of the system matrices only needs to be undertaken once at the beginning of the simulation, which is computationally efficient and allows a new model to be explicitly obtained at each flight condition while keeping the ROM size the same as those at the grid points.

The parameter space P could be extended to include multiple dimensions. In the present paper two flight parameters, Mach number and Angle of Attack (AoA) are considered individually. Also, if the system initially has asymmetric aerodynamic loads as discussed in Sect 2.1 the initial conditions ${\tilde{\mathbf{Y}}}_{f}^{0}$ and ${\tilde{\mathbf{Y}}}_{sc}^{0}$ at grid points P will need to be similarly interpolated at the non-grid point. A key requirement of system matrices interpolation is that each A-ROM needs to have matrices of the same size, and more importantly, the state vectors x in the neighboring points must have the same state representation as discussed in Sect 1 above. In this paper, the state consistence of A-ROMs across varying flight parameters obtained using N4SID and ARX is investigated and compared by observing the trends of the vectorized matrix elements and the pole migration of the interpolated ROMs. According to the analysis above, we will show that ARX better preserves the state consistence, and hence, the local ROM can be interpolated to new grid points, which however is not true for N4SID.

2.5 Error quantification

A cumulative error metric is also defined to compare ROM and full order model (FOM) results using the following equation:

$$Err = \frac{{\parallel {\mathbf{Y}}_{{_{{ROM}} }} - {\mathbf{Y}}_{{_{{FOM}} }} \parallel _{2} }}{{\parallel {\mathbf{Y}}_{{_{{FOM}} }} \parallel _{2} }}$$

(11)

where FOM represents the results of using CFD model for GAF computation, which is coupled with the modal solver of structure (i.e., Eq. (8)) within the FUN3D package; ${\mathbf{Y}}_{ROM}$ and ${\mathbf{Y}}_{FOM}$, respectively, denote the aeroelastic results (GAF and GD) computed by the ROM and the FOM. The comparison can be performed at the grid point or non-grid flight condition where the ROM is obtained through interpolation. In addition to ROM evaluation, the comparison and error metric can also be used for identifying the location within the parameter space for grid refinement.

3 Results and discussion

Next the case studies to generate and verify ARX ROM are performed. State consistence of the ROM is examined, and ROM results and their comparison against the FOM/CFD model at both the grid and the non-grid point in the flight parameter space are presented using the widely studied AGARD 445.6 wing.

3.1 High fidelity simulation

As discussed above, two separate one-dimensional parameter spaces (Mach number and AoA) are considered in the present work. At each grid point, training data is generated using the A-ROM training simulation following the procedure summarized in Sect 2.1. Such a process generates input-output data pairs of ${\mathbf{Y}}_{sc}$ and ${\mathbf{Y}}_{f}$ that are processed by system identification above to extract A-ROM. In the verification simulation, given an initial modal velocity perturbation, the A-ROM and S-ROM respond spontaneously, which is different from the training simulation where GDs are prescribed throughout the time accurate simulation. Each grid point and interpolation point within the flight parameter space is verified using these data sets.

Two case studies are evaluated in this paper. In the first one that investigates the effect of the Mach number, an AoA = 0° is assumed. This simplifies the simulation initialization because the AGARD 445.6 wing is symmetric in geometry, and therefore with AoA = 0° the initial steady-state deflection is 0. This means the aeroelastic equilibrium step of the training simulation in Sect 2.1 can be skipped. The second case study aims to evaluate the effect of AoA, and the A-ROM is trained about the aeroelastic equilibrium points as described by Eq. (2) above. Both the training and verification data for all cases is obtained using NASA’s research code FUN3D [66]. The aerodynamics is simulated by solving the inviscid Euler equations, and a moving mesh algorithm is used to accommodate the surface deformation (See "Appendix 2"). In all the simulations, the wing root is fixed while the rest is allowed to deform freely. The first four structural modes of the wing are used to calculate the deformation and the GAF and the GD of the wing. Their modal frequencies are 60.31, 239.80, 303.78, and 575.19 rad/s, respectively. Note that these are the same modal frequencies and mode shapes that are used for the S-ROM. The numbers of the meshes used in the simulation are given as follows: 2,381,922 cells and 430,866 nodes in volume and 50,827 nodes along the wing surface in CFD of aerodynamic flow. 121 nodes are used to describe the modal shapes of the wing structure. FUN3D has the functionality to directly output the modal forces rather than the distributed force vector F at the structural nodes for ROM construction. In other words, FUN3D exports ${\varvec{\Phi}}^{{\text{T}}} {\mathbf{F}}$ in Eq. (8), viz., the force vector F projected onto the modal shapes to yield the GAF. A 3-2-1-1 multistep function for the prescribed GDs in Fig. 5a is adopted, which carries excellent harmonic contents and wide bandwidths at the low end of the frequency spectrum [67]. Another widely used input profile, a Walsh function offering orthogonality among individual inputs, is also applicable [13]. Fig. 5b illustrates the four corresponding GAFs subjected to the prescribed GDs. In the training runs of the nonzero AoA cases, the prescribed GDs are of the same magnitude added to the nonzero GD equilibrium values.

Fig. 5

A 3-2-1-1 multistep input profile for training simulation: (a) GD and (b) GAF response to prescribed GDs

3.2 State consistence

As discussed above, the system matrices $\left[ {{\mathbf{A}}^{{\mathbf{P}}} , {\mathbf{B}}^{{\mathbf{P}}} , {\mathbf{C}}^{{\mathbf{P}}} , {\mathbf{D}}^{{\mathbf{P}}} } \right]$ of the A-ROM at surrounding grid points P will be interpolated to attain the A-ROM at the target non-grid condition. However, the requirement for system matrix interpolation is that the states at varying flight conditions need to have consistent representation, i.e., coordinates of the states as discussed in Sect 1. In other words, the physical meaning of the states in the ROMs remains the same across the flight envelop [41]. In this section, the state consistence of the ROM obtained by ARX and N4SID is examined by two means: the change of the system matrix elements and the poles with varying flight parameters.

Figure 6a shows the vectorized elements in the “A” matrix of the ARX state-space ROM over a Mach domain. It is clear that the elements of the A matrix in the ARX ROM vary continuously and smoothly with the Mach number, while those for the N4SID ROM illustrate significant inconsistence (Fig. 2). Therefore, ARX ROM enhances state consistence relative to N4SID and should be more amenable to system matrix interpolation of ROMs. The trends shown for the “A” matrix hold true for the other matrices as well, i.e., B, C, and D (results not shown). Similar plots can be seen for the AoA dimension in Fig. 6b, and state consistence of AoA in the ARX plot is similar to the Mach parameter and is better than that of N4SID in Fig. 2b. It is interesting to note that the A matrix changes more dramatically at the low AoA range, and therefore, more grid refinement (i.e., adaptive grid sampling) is needed to improve the interpolation accuracy there, e.g., at AoA = 1° and 2°.

Fig. 6

3D view of vectorized “A” matrix elements over a section of (a) Mach domain; and (b) AoA domain from the ARX model

A more direct approach to examine the state consistence of the parametric state-space ROM for system matrix interpolation is to examine the pole migration of the interpolated ROM [41, 68]. If the poles of the interpolated ROM migrate smoothly within the parameter space and follow similar patterns of those at the grid points, the state consistence of ROMs is confirmed, and vice versa. It should be noted that smooth pole migration of ROMs at the grid points is not sufficient for state consistence confirmation [41]. This is because the pole distribution is a dynamic characteristic of the system, while consistence refers to the coordinates used to express the states of the dynamic system. ROMs at two grid points that have similar dynamic behavior but cast in different coordinates (by a coordinate rotation) can still exhibit similar pole locations, which however is not true for ROMs interpolated between them. Figure 7a and b, respectively, show the pole migration of the ROMs at the grid points obtained by ARX and the interpolated ROMs using adaptive step sizes. That is, a larger step size of 0.1 is used in the lower Mach range and a smaller step size of 0.01 towards the flutter regime. Due to the wide range of the pole values, the region at the lower frequency including that of the positive poles is enlarged to facilitate visualization, in particular, around the stable/unstable transition. It is clear that the poles of the interpolated ROMs match very well the ROMs directly constructed using the FOM training data, and the agreement in the frequency domain then translates to the comparison in time response as shown in the next sections. Figure 8a and b show the pole migration of the ROMs at the grid points obtained by N4SID and the corresponding interpolated ROMs, respectively. There are two interesting observations: (1) the poles of the former change smoothly across the Mach number similar to that by ARX in Fig. 7a, which confirms that the dynamic behavior of the system and its dependence on Mach is accurately captured; and (2) the distribution of poles of the interpolated ROM scatters almost randomly without any pattern as a result of inconsistent state representation of the ROMs at the grid points. This also verifies the statement above, i.e., only pole migration of the interpolated ROMs (rather than those at the grid points) is a convincing indicator of state consistence. Figure 9 shows the pole plots of the ROMs at the grid points and the interpolated ROMs across the AoA using a step size of 0.25 degrees throughout. It can be seen that the poles of the interpolated ROMs are in the similar trend and pattern as those of ROMs at the grid points although they are not exactly the same and the individual pole of the interpolated ROM seems to vary in a wider range, which may be caused by the abrupt changes in the aerodynamic behavior due to non-zero AoAs, and an even finer AoA step size is needed for enhanced state consistence between neighboring grid points. This is another confirmation of the slightly less consistent matrices as shown in the Fig. 6b above. Since it is already verified that ROMs extracted by N4SID are not consistent in the Mach range, their results along the AoA are not shown for the sake of paper conciseness.

Fig. 7

ARX system poles throughout Mach range for (a) ROMs constructed directly using CFD/FOM data at grid points; and (b) interpolated ROMs

Fig. 8

N4SID system poles throughout Mach range for (a) ROMs constructed directly using CFD/FOM data at grid points; and (b) interpolated ROMs

Fig. 9

ARX system poles throughout AoA range for (a) ROMs constructed directly using CFD/FOM data at the grid points; and (b) interpolated ROMs

A further analysis can identify the root of difference in state consistence of both ROM methods. In N4SID, the physical meaning of the states of the ROM is dictated by the SVD that ranks and reorders the basis vectors according to significance of the singular values, and the information truncated is not the same among the ROMs. Therefore, the dominant bases of each ROM and state representation in the model for various flight conditions are different, and the system matrices cannot be directly interpolated by this method. Normally, N4SID ROMs need to be converted to a global reference states through transformation (rotation) or a canonical form [41, 44, 68], prior to ROM interpolation, which however may not be an excellent remedy as the information truncated at varying flight conditions is not consistent. In contrast, the ARX method is not a subspace identification method. Instead, it relies on the least squares method to build the relationship between the physical inputs and outputs of consistent meanings, and the state-space ROM is constructed by its companion form in which the states are also physical, and hence, preserving better state consistency. This fundamental difference is the reason for the enhanced interpolatability of ARX state-space ROM.

3.3 Aeroelastic ROM validation at grid points

Each grid point ROM must be validated before it can be used in the parametric ROM. This section presents the verification of the AE-ROM in the time domain at discrete grid points throughout the two parameter spaces. Since N4SID ROM cannot produce state consistent ROM, their results will not be presented hereafter. Figure 10 shows the results of comparing the FOM/CFD and ARX ROM in terms of GAF and GD at Mach = 0.85. We can see that FOM and ROM match very well, and the discrepancy is almost indistinguishable.

Fig. 10

Comparison of (a) GAFs and (b) GDs in aeroelastic response between ARX ROM and real FOM/CFD at Mach = 0.85

Table. 1 illustrates the quantitative comparison in the Mach range 0.5-0.95 with an increment of 0.05 (while holding AoA = 0°), and Table 2 does the same for AoA ranging from 0°-5.5° with an increment of 0.25° at constant Mach = 0.5. All aeroelastic ROMs exhibit excellent agreement with FOMs in the specified Mach range. As discussed previously for matrix interpolation, all the model matrices must be the same size, which corresponds to the fit order. Therefore, the fit orders of all the ARX ROM at different grid points are the same. It can also be seen that in the AoA range the ROMs and FOMs match very well, although towards the higher AoA the ROM generally becomes worse. This can be attributed to the fact that at the higher AoA the governing equations being used (Euler solver) do not accurately represent the aerodynamics of the system, such as flow separation.

3.4 Aeroelastic ROM validation at Non-grid points

Next the ROMs at the non-grid points obtained by interpolating ROMs at grid points are examined. Cubic splines are used to interpolate the system matrices of the ROM. Likewise, matrix interpolation is also attempted for N4SID AE-ROMs, and the results are physically meaningless. Therefore, interpolated AE-ROM presented in the varying flight conditions only includes ARX ROM. The results for the Mach parameter space will be presented first, followed by the AoA parameter space. In addition, since A-ROM and S-ROM are coupled in the aeroelastic analysis, only GAF results are presented graphically in this section to avoid redundancy.

3.4.1 Mach parameter space

Figure 11 illustrates the GAF results of the aeroelastic ROM at the non-grid point of Mach = 0.65 that is obtained by interpolating those at the grid points with a Mach step size of 0.1 based on the ARX method. That is, AE-ROMs at Mach = 0.6 and Mach = 0.7 are interpolated to obtain the AE-ROM at Mach = 0.65. Table 3 lists the prediction error of the interpolated AE-ROM compared against FOM/CFD simulation with the Mach step size of 0.1. It shows good agreement from the subsonic to transonic regime with the ARX method. However, when approaching the flutter regime (around Mach = 0.85-0.95), where aerodynamics behavior exhibits strong nonlinear dependence on the flight parameters, the performance of system matrix interpolation begins to deteriorate. In particular, the error of the GAF and GD predicted by the AE-ROM relative to the FOM reaches 10%. This is clearly shown in Fig. 12 by comparing the FOM with the interpolated ROM at Mach = 0.85 in terms of GAF, and the ROM is obtained by interpolating those at Mach = 0.8 and 0.9 with the step size of 0.1. The attempt to use system matrix interpolation for N4SID models quickly shows unstable behavior in Fig. 2, yielding non-physical results, confirming the lack of state consistence and difficulty of direct interpolation for the N4SID-based parametric aeroelastic ROM.

Fig. 11

Comparison of GAF in aeroelastic response between interpolated ARX ROM and FOM/CFD at Mach = 0.65 with a Mach step size of 0.1 for interpolation

Table 3 Prediction errors of interpolated AE-ROM (ARX) with a Mach step size of 0.1

Fig. 12

Comparison of GAF in aeroelastic response between interpolated ARX ROM and FOM/CFD at Mach = 0.85 with a Mach step size of 0.1 for interpolation

An effective avenue to address the strong dependence of ROM state consistence and interpolation on flight parameters is to decrease the grid spacing at the flutter regime. Figure 13 shows the results of the interpolated ROM at Mach = 0.85 using the Mach step size of 0.05, viz., ROMs at the grid point of Mach = 0.825 and 0.875 are used for interpolation to enhance state consistence among neighboring points. It is evident that the ROM prediction accuracy is dramatically improved. However, it can be seen in Table 4 that even with the Mach step size of 0.05, the error between the ROM and FOM/CFD at Mach = 0.925 is still appreciable and reaches up to 27.7%. To further boost ROM state consistence between grid points and interpolation accuracy, the local flight regime (i.e., the flutter regime) is again refined with a smaller Mach step size of 0.01, viz., interpolating ROMs at the grid point of Mach = 0.92 and 0.93. Table 5 shows the results of the new interpolated ROM and its comparison against the FOM in GAF. We can see that while only the local range (around Mach = 0.92) is refined, the state consistence and interpolation accuracy is improved significantly. This confirms that an accurate parametric ROM at non-grid points can be achieved through the adaptation and refinement of offline ROM database grid spacing and improvement in state consistence. Table 4 also shows that below the flutter regime the implementation of a finer grid to a Mach step size of 0.05 is adequate for interpolation to construct ROMs at non-grid points, while the GAF and GD results are not plotted here to avoid being repetitive Fig. 14.

Fig. 13

Comparison of GAF in aeroelastic response between interpolated ARX aeroelastic ROM and FOM/CFD at Mach = 0.85 with a Mach step size of 0.05 for interpolation

Table 4 Prediction errors of interpolated AE-ROM (ARX) with a Mach step size of 0.05

Table 5 Prediction errors of interpolated AE-ROM (ARX) with a Mach step size of 0.01

Fig. 14

Comparison of GAF in aeroelastic response between interpolated AE-ROM and FOM/CFD at AoA = 2° with an AoA step size of 2°

It should be noted that while system matrix interpolation is desirable and has been shown to be effective with grid refinement, it is observed in Tables 3 and 4 that it is a fairly sensitive method, meaning it potentially requires a fine grid spacing. This is because each element in the matrix has an individual contribution to the fundamental characteristics of the system (such as eigen-frequency, poles, and others) with respect to the other matrix elements. This means that some of the characteristics may be notably sensitive to particular matrix elements or combinations of elements (and interpolation on those elements), leading to sensitive prediction errors. This is particularly important when dealing with the ARX ROM matrices. Since they are very similar to each other over the Mach range, a small variation of a particular element could have a significant impact on the results.

3.4.2 Angle of attack parameter space

Next, a similar interpolation and grid refinement scheme is carried out for the second parameter, AoA. As mentioned previously, this is a one-dimensional parameter space, holding Mach = 0.5 while varying AoA from 0° to 5.5°. Figure 14 shows the results of the ROM obtained by system matrix interpolation at an AoA of 2° using a step size of 2°. That is, ROMs at AoA = 1° and 3° are used to interpolate to obtain ROM at AoA = 2°. Table 6 shows the results for the whole grid resolution and step size. First it is clear that the step size is too large for matrix interpolation as the results are non-physical indicated by divergence of both GAFs and GDs, which again is attributed to the fact that matrix interpolation is sensitive to the step size of interpolation as elements in system matrices contribute differently to dynamics and modal characteristics of the interpolated ROM. Table 7 shows the interpolation errors in the parameter space of AoA using a step size of AoA = 1°. It again shows that resolving the grid spacing increases accuracy. However, using a step size of 1° is still inadequate to resolve the local aeroelastic behavior around AoA = 1°, and a second refinement is required. Note that the interpolation error is not necessarily always trending higher at higher AoAs. This is because aeroelasticity of the system does not become more nonlinear as AoA increases towards a specific point as it does with the Mach parameter space towards flutter. In fact, as shown in Fig. 15, the system actually becomes more damped as AoA increases. This is likely due to larger initial equilibrium load and displacement at the larger AoAs. This artificially stiffens the system in terms of perturbations about the equilibrium point because not only does the displacement have less distance to go before it reaches its restoring point, but it is more difficult to return to equilibrium (or go past it) due to the increased force on the wing. The locations of the high error are likely due to the slightly less consistent matrix elements observed in Fig. 6b.

Table 6 Prediction errors of interpolated AE-ROM (ARX) with an AoA step size of 2°

Table 7 Prediction errors of interpolated AE-ROM (ARX) with an AoA step size of 1°

Fig. 15

AoA downrange view of the first GD about the aeroelastic equilibrium point

Figures 16 and 17 show the second grid refinement used to improve state consistence and interpolation accuracy, in particular, at AoA = 1° and 2°. We can see that the interpolated ROM and FOM/CFD match very well in GAF. Table 8 shows the interpolation errors with a step size of 0.5° throughout the parameter space. The error at AoA = 5° is still notable, however, the parameter space of AoA = 0°−4.75° is resolved reasonably well. As with the Mach parameter space, there are local areas that may not require uniform spacing, which can be accomplished with adaptive sampling. This will be explored in future work. In terms of computational performance, our coupled AE-ROM engines demonstrated excellent accuracy with relative error generally <5%.

Fig. 16

Comparison of GAF in aeroelastic response between interpolated AE-ROM and FOM/CFD at AoA = 1° with an AoA step size of 0.5°

Fig. 17

Comparison of GAF in aeroelastic response between interpolated AE-ROM and FOM/CFD at AoA = 2° with an AoA step size of 0.5°

Table 8 Prediction errors of interpolated AE-ROM (ARX) with an AoA step size of 0.5°

The computational time for CFD training simulation (Step 2.1-2.3 in Sect 2.1), ROM construction (Step 3), verification simulation using CFD or ROM is listed in Table 9. Due to the license and the ITAR-requirements of the software, CFD simulation and ROM are conducted on different computing platforms. Although a direct comparison in speedup is not made, it is apparent that ROM can be simulated at a very fast speed. It should be noted that CFD training simulation is a one-time cost. The generated ROM can be simulated with different model configurations and scenarios, such as different initial conditions, physical simulation time, and controller design. The established ROM database can also be used to obtain ROMs at non-grid flight conditions where the ROM is not initially available.

Table 9 Computational time of CFD training simulation, ROM construction, and CFD and ROM verification simulation

4 Conclusions

The state consistence of the data-driven parametric ROMs in the state-space form obtained by different system identification methods for coupled aeroelastic analysis within a broad flight regime is systematically studied. In order to construct parametric ROMs, the flight regime is first partitioned using grid points, where high-fidelity CFD simulation is conducted to generate training and verification data. Local A-ROMs at grid points capturing the relationship between the GAFs and GD are then built using two different system identification methods for comparison, such as the N4SID and ARX, yielding a parametric A-ROM database that covers the entire flight parameter space. The A-ROM at any location (non-grid point) within the flight envelope is obtained by interpolating the system matrices [A, B, C, D] of the ROMs at the neighboring grid points. The interpolated A-ROM is then coupled with the mode-based S-ROMs in the form of the state-space model for coupled aeroelastic analysis under various flight conditions.

The case studies to evaluate the state consistence of ROMs are carried out. Although both N4SID and ARX construct accurate A-ROMs and AE-ROMs at the grid point, it is found that ARX exhibits salient state consistence, which is confirmed by the continuous variation of the matrix elements and smooth migration of the interpolated ROM poles across flight parameter space. In contrast, N4SID ROM cannot generate state consistent A-ROMs and yield physically meaningless interpolation. It can be attributed to the nature of these methods, specifically, ARX uses the least squares to directly capture the relationship between physical inputs and outputs without intermediate basis vector computation or ranking/sorting steps, and the state-space model obtained from the companion form that uses physical GAF and GD as the states, which is fundamentally different from the approaches based on SVD, such as N4SID. Therefore, ARX allows direct interpolation of model system matrices to generate A-ROMs at non-grid flight conditions. In terms of parametric AE-ROM construction, it is noted that the demand for the grid points to resolve non-uniform aerodynamic behavior depends on the flight regime. When approaching the flutter or transonic regime, more grid points (and offline ROM construction) would be needed therein to enhance state consistence between them for accurate construction of parametric ROMs. Also, although desirable and efficient for online ROM computation and control engagement. For the benchmark cases presented, our coupled AE-ROMs demonstrate excellent accuracy with relative error <5%, and in general the AE- ROM only takes ~0.01-0.03 seconds.

This effort provides a path forward to optimally train and construct a parametric aeroelastic ROM database with state consistence. The future work will focus on (1) extending the state consistent aeroelastic ROM to higher-dimensional parameter space and more complex vehicles; and (2) develop adaptive sampling scheme and error estimator to automatically select the flight regimes for adaptive grid refinement.

Appendices

Appendix 1: Numerical Algorithm for Subspace State Space System Identification (N4SID)

The state-space model of the combined deterministic-stochastic system used in N4SID is defined as:

$$\begin{gathered} {\mathbf{x}}\left( {k + 1} \right) = {\mathbf{Ax}}\left( k \right) + {\mathbf{Bu}}\left( k \right) + {\mathbf{v}}\left( k \right) \hfill \\ {\mathbf{y}}\left( k \right) = {\mathbf{Cx}}\left( k \right) + {\mathbf{Du}}\left( {{k}} \right) + {\mathbf{w}}\left( k \right) \hfill \\ \end{gathered}$$

(12)

where ${\mathbf{v}}\left( k \right)$ and ${\mathbf{w}}\left( k \right)$ are the process and the measurement noise at the $k$-th time instance with covariance matrices $E\left[ {{\mathbf{v}}_{k} {\mathbf{v}}_{k}^{{\text{T}}} } \right] = {\mathbf{Q}}$, $E\left[ {{\mathbf{w}}_{k} {\mathbf{w}}_{k}^{{\text{T}}} } \right] = {\mathbf{R}}$, and $E\left[ {{\mathbf{v}}_{k} {\mathbf{w}}_{k}^{{\text{T}}} } \right] = {\mathbf{S}}$ [69]. The first step of N4SID arranges the input ${\mathbf{Y}}_{sc}$ and output data into Hankel signal matrices ${\hat{\mathbf{Y}}}_{sc}^{p}$, ${\hat{\mathbf{Y}}}_{sc}^{f}$, ${\hat{\mathbf{Y}}}_{f}^{p}$, and ${\hat{\mathbf{Y}}}_{f}^{f}$, where the superscript $p$ and $f$ denote the past and future, respectively. The oblique projection method is first applied to ${\hat{\mathbf{Y}}}_{sc}^{p}$, ${\hat{\mathbf{Y}}}_{sc}^{f}$, ${\hat{\mathbf{Y}}}_{f}^{p}$, and ${\hat{\mathbf{Y}}}_{f}^{f}$

$${\mathbf{W}}: = {\hat{\text{P}}}_{{{\hat{\mathbf{Y}}}_{sc}^{f} }}^{{{\hat{\mathbf{Y}}}_{f}^{f} }} \left( {\left[ {\begin{array}{*{20}c} {{\hat{\mathbf{Y}}}_{f}^{p} } \\ {{\hat{\mathbf{Y}}}_{sc}^{p} } \\ \end{array} } \right]} \right)$$

(13)

Note that the operator ${\hat{\text{P}}}_{{\mathbf{a}}}^{{\mathbf{b}}} \left( {\mathbf{q}} \right)$ indicates the oblique projection of ${\mathbf{q}}$ along ${\mathbf{a}}$ onto ${\mathbf{b}}$. The singular value decomposition (SVD) of ${\mathbf{W}}$ yields:

$${\mathbf{W}} = {\mathbf{U\Sigma V}}^{{\text{T}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{U}}_{1} } & {{\mathbf{U}}_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{{\varvec{\Sigma}}}_{1} } & 0 \\ 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{V}}_{1}^{{\text{T}}} } \\ {{\mathbf{V}}_{2}^{{\text{T}}} } \\ \end{array} } \right] = {\mathbf{U}}_{1} {{\varvec{\Sigma}}}_{1} {\mathbf{V}}_{1}^{{\text{T}}}$$

(14)

where ${\mathbf{U}}$ is the matrix consisting of left-singular vectors; ${{\varvec{\Sigma}}}$ is the diagonal matrix of singular values; ${\mathbf{V}}$ is the matrix for right-singular vectors; and the subscript 1 means the retained components in ${\mathbf{U}}$, ${{\varvec{\Sigma}}}$, and ${\mathbf{V}}$ of SVD corresponding to non-zero singular values ${{\varvec{\Sigma}}}$. The state vector then can be estimated by:

$${\mathbf{x}} = {{\varvec{\Sigma}}}_{1}^{1/2} {\mathbf{V}}_{1}^{{\text{T}}}$$

(15)

Through Eq. (15), the state sequences can be determined as

$${\overline{\mathbf{x}}}_{k + 1} = \left[ {{\mathbf{x}}\left( {k + 1} \right),{ } \ldots ,{ }{\mathbf{x}}\left( {k + N_{t} - 1} \right)} \right],\user2{ }{\overline{\mathbf{x}}}_{k} = \left[ {{\mathbf{x}}\left( k \right), \ldots ,{\mathbf{x}}\left( {k + N_{t} - 2} \right)} \right]{\overline{\mathbf{Y}}}_{sc,k} = \left[ {{\mathbf{Y}}_{sc} \left( k \right), \ldots ,{\mathbf{Y}}_{sc} \left( {k + N_{t} - 2} \right)} \right],\user2{ }{\overline{\mathbf{Y}}}_{f,k} = \left[ {{\mathbf{Y}}_{f} \left( k \right), \ldots ,{\mathbf{Y}}_{f} \left( {k + N_{t} - 2} \right)} \right]$$

where $N_{t}$ is the number of the data points used in the system identification. The matrices of the state-space model ${\mathbf{A}}$, ${\mathbf{B}}$, ${\mathbf{C}}$, and ${\mathbf{D}}$ are estimated after forming a set of linear equations, and the solution can be obtained by applying the least-square regression

$$\left[ {\begin{array}{*{20}c} {{\overline{\mathbf{x}}}_{k + 1} } \\ {{\overline{\mathbf{Y}}}_{f,k} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\mathbf{A}} & {\mathbf{B}} \\ {\mathbf{C}} & {\mathbf{D}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\overline{\mathbf{x}}}_{{\varvec{k}}} } \\ {{\overline{\mathbf{Y}}}_{sc,k} } \\ \end{array} } \right]$$

(17)

Appendix 2: Moving Mesh Algorithm

In FUN3D, the general aerodynamic and aeroelastic CFD simulation package developed by NASA, the general mesh deformation algorithm is formulated as a linear elasticity problem for the varying geometry. From the definition of the linear elasticity equations where body forces are neglected, Gauss Theorem in a differential form of a control volume is written as

$${\mathbf{R}}_{{{\mathbf{el}}}} ({\mathbf{z}}) = \oint_{\partial V} \kappa \frac{{\partial z_{i} }}{{\partial x_{i} }}\overline{\overline{{\mathbf{I}}}} \cdot {\hat{\mathbf{n}}} dS + \oint_{\partial V} \mu \left( {\frac{{\partial z_{i} }}{{\partial x_{j} }} + \frac{{\partial z_{j} }}{{\partial x_{i} }}} \right) \cdot {\hat{\mathbf{n}}} dS = 0$$

(18)

where ${\mathbf{z}}$ represents the displacement vector, i.e., ${\mathbf{z}} = \left[ {z_{1} , z_{2} ,z_{3} } \right]^{{\text{T}}}$, $\kappa$ and $\mu$ are the material properties define as a function of Young’s modulus and Poisson’s ratio [70], and $\mathop {\mathbf{I}}\limits^{ = }$ denotes the identity tensor. Then,

$$\frac{{\partial {\mathbf{R}}_{{{\text{el}}}} }}{{\partial {\mathbf{z}}}}{\Delta }{\mathbf{z}} = - {\mathbf{R}}_{{{\text{el}}}} \left( {{\mathbf{z}}_{0} } \right)$$

(19)

${\mathbf{z}}$ here is expressed by the sum of an initial guess and displacement, i.e., ${\mathbf{z}} = {\mathbf{z}}_{0} + {\Delta }{\mathbf{z}}$; $\frac{{\partial {\mathbf{R}}_{{{\text{el}}}} }}{{\partial {\mathbf{z}}}}$ is the Jacobian matrix independent of ${\mathbf{z}}$. The generalized minimum residual method is utilized to obtain the solution of Eq. (19), which is the displacement vector. Then, a CFD mesh is updated for deformation.