1 Introduction

Stability studies are among the main issues of any system. Since the 1990s, hybrid systems have been the subject of research by control theorists, computer scientists, and applied mathematical scientists, motivated mainly by the critical applications of the hybrid system theory in various fields [1, 2]. Generally, hybrid systems are a category of dynamic systems with continuous and discrete variables in their structure.

It is generally accepted that switchable systems are one of the most commonly used subsets of hybrid systems as they can model an extensive range of physical systems, including electronic power systems, chemical processes, network control systems, and automobile industries [3,4,5]. Switching systems are classified into arbitrary and restricted categories according to the switching signal. Stability testing methods of these systems vary according to the type of switching system, but like other linear and nonlinear systems, they are usually based on the selection of the Lyapunov function [6, 7]. Because of the switching property and creation of complex behavior in switchable systems, their stability assessment is essential to researchers, and thus, they have investigated various methods for switched systems including stability analysis [8], observability analysis [9, 10], H∞ control [11,12,13], and optimal control [16, 17].

Robust Control, H∞, is a strategy for designing control systems that emphasizes the robustness and stability of control systems against disturbances. The design of such systems aims to create a control system under which changes in system conditions have the least impact on the output. In other words, the main objectives of designing robust control systems include increased system reliability, improved performance or stability in the presence of uncertainties, and non-modeled dynamics or disturbing factors such as turbulence and unwanted inputs. Recently, the H∞ control problem for switched systems has gained traction among researchers because of the efficiency of the H∞ index in control synthesis of practical systems [16,17,18].

A hyperchaotic secure communication scheme for non-ideal communication channels is designed in [19]. The proposed approach employs the Takagi–Sugeno (TS) fuzzy model and linear matrix inequality (LMI) technique to design a controller that synchronizes the hyperchaotic transmitter and receiver systems. An H∞ performance for a chaotic based secure communication scheme for a non-ideal transmitting public channel is suggested in [20]. The presented approach employs the polynomial representation and numerical SOS convex optimization technique to design a novel polynomial synchronizer for hyper (chaotic) systems. Sadeghi and Vafamand in [21] present an optimal approach for more relaxed stability analysis conditions and controller design for Takagi–Sugeno fuzzy systems. The optimal selection of the upper bounds by employing the LMI approach leads to conservative conditions. A Takagi–Sugeno (TS) fuzzy model is also proposed in [22] to further decrease the conservativeness instability analysis condition and controller design. The stability condition proved by using a non-quadratic Lyapunov function in terms of LMI.

Indeed, choosing the right switching signal plays a crucial role in stabilizing the system as applying an appropriate switching signal to a switched system with unstable subsystems could lead to system stability. Similarly, a wrong switching signal may cause instability of a switched system with stable sub-systems. Designing suitable switching signals for the asymptotic stability of switchable systems has, thus, encouraged many researchers to invest and study-related fields [23,24,25]. On the other hand, given the fact that a switchable system consists of unstable sub-systems; thus, system states tend to diverge. Therefore, there is a need to design an efficient switching signal that can stabilize a switchable system with unstable subsystems. [26] designed a state dependent switching law that obeys a dwell time constraint and guarantees the stability of a switched linear systems.

In the past two decades, a significant class of state-dependent switching signals known as variable structures (VSs), have been investigated extensively for application in switched systems [27,28,29]. The VS method modifies the dynamic of a nonlinear system by applying a high frequency switching control and switches from one smooth condition to another. Therefore, the structure of the control rule differs relative to the position of the state trajectory, in a sense that it switches from one smooth control rule to another, and perhaps at higher speeds. In [30], an output feedback variable structure control was suggested for a set of continuous-time switched linear systems in the presence of parametric uncertainties. Moreover, sliding surfaces were created using the LMI method. Moreover, Zhao et al. [28] proposed the adaptive control problem for a set of continuous-time switched linear systems by proposing a VS switching rule and sliding sector.

Adaptive control is considered an effective way of dealing with uncertain systems. Interestingly, adaptive control is utterly distinct from robust control. That is, contrary to robust control, and adaptive control does not entail prior knowledge of the boundaries of uncertainties or time-varying parameters, but rather, it is concerned with control rules modifying themselves to adapt to the parameters. Over the last decade, adaptive control has received much attention in many fields, primarily when undesired chattering exists while the control system is in the sliding mode. In fact, the chattering phenomenon can play an undesirable role in reducing system performance since it may increase high-frequency dynamics, leading to instability. The boundary layer technique is usually adopted to eliminate the chattering; meanwhile, many adaptation methods have been introduced and extended to tune the control gain [28, 29]. A common sliding surface is constructed for the proposed nonlinear switched system, and an adaptive sliding mode controller is developed to adapt the unknown parameters and guarantee reachability to state trajectories [31]. Zhu and Khayati aimed to enhance accuracy and smooth the chattering phenomenon [32]. Also, the switching gain adaptation rule was analyzed, and an alternative design was proposed. A new adaptive robust control was proposed in [33] for uncertain switched EL systems which reduces the complexity of control design. Furthermore, the adaptive tracking control problem of uncertain switched linear systems was proposed in [34].

In contrast to previous research works [12, 28, 35, 36], the present study takes the state-dependent switching signal as a sliding surface, ensuring the stability of the switched nonlinear system in the presence of disturbance by introducing an adaptive controller. In addition, the proposed approach can be generalized to most nonlinear systems. Indeed, the turning point of the present paper is to apply a convex combination of unstable subsystems in such a way to end up with stable states of the system.

In this paper, a controller with an adaptive approach and a variable structure switching rule were utilized to stabilize a nonlinear switched system in the presence of disturbances. This was achieved using the Lyapunov function theory and the sliding sector method. In this paper, the problem of stabilization and stability for nonlinear switched systems was investigated by introducing a new class of switching signals in a continuous-time setting. A new adaptive controller, a state feedback control, and a VS switching rule with a sliding sector were developed to ensure that the H∞ control problem for a class of nonlinear switched systems is solvable in the condition where all subsystems are unstable.

This paper organized as follows: Sect. 2 states the problem of adaptive control of switched nonlinear systems. In Sects. 3 and 4, stabilization and H∞ control conditions for switched nonlinear systems with and an adaptive approach and a VS switching rule are proposed. The simulation results are presented in Sect. 5 to verify the effectiveness of the proposed controller and Sect. 7 concludes the paper.

2 Descriptions and Preliminaries

Here, we have a class of continuous-time nonlinear switched systems that can be represented by the following model:

$$\begin{aligned} \dot{x}(t) & = A_{\sigma (t)} x(t) + B_{\sigma (t)} f_{\sigma (t)} (x(t))\, + \xi (t)\theta \\ & + D_{\sigma (t)} u(t) + E_{\sigma (t)} \omega (t)\, \to \,\,\,r \in M = \left\{ {1,2,...,m} \right\} \\ y(t) & = C_{\sigma (t)} x(t) \\ \end{aligned}$$
(1)

where \(\sigma (t):\left[ {0, + \infty } \right) \to M = \left\{ {1,2,...,m} \right\}\) is the switching signal, which is a piecewise time-dependent constant function, \(x \in R^{n}\) is the state vector, \(f_{i} (x(t)) \in (R^{n} \to R^{n} )\) denotes a nonlinear term of the system, \(u(t) \in R^{m}\) and \(y(t) \in R^{q}\) stand for the control input of the ith subsystem and the control output, respectively. Signal \(\omega (t) \in L_{2} \left[ {0,\infty } \right)\) represents the disturbance input. \(\theta \in R^{l}\) is a constant unknown parameter vector and \(A_{r} ,B_{r} ,C_{r} ,D_{r} ,E_{r} ,r \in M\) are known constant matrices with proper dimensions. \(\xi (t)\) denotes the matrices of known signals considered as being piecewise-differentiable and uniformly bounded in time. Although the system matrices may not satisfy the Hurwitz stability criterion, it is assumed that there exists a positive constant \(\alpha_{r} ,r \in M\), which contains \(\alpha_{r} \in [0,1][0,1]\), \(\sum\nolimits_{r = 1}^{m} {\alpha_{r} } = 1\) and Hurwitz stable matrices \(A_{0} \in R^{n \times n}\), \(D_{0} \in R^{n \times m}\), \(E_{0} \in R^{n \times d}\) such that \(\forall r \in m\)

$$A_{0} = \sum\limits_{r = 1}^{m} {\alpha_{r} A_{r} } ,\,D_{0} = \sum\limits_{r = 1}^{m} {\alpha_{r} D_{r} } ,\,E_{0} = \sum\limits_{r = 1}^{m} {\alpha_{r} E_{r} }$$
(2)

Remark 1

With respect to this point that all the system matrices \(A_{r} ,r \in M\) are probably unstable, the condition Real \(\left( {\lambda_{i} \left( {\sum\nolimits_{r = 1}^{m} {\alpha_{r} A_{r} } } \right)} \right) < 0,\,\,, \, i \, = 1, \ldots ,n\) is necessary here.

Lemma 1

(Young’s Inequality) [37] For the matrices X and Y with proper dimensions, for every symmetric positive definite matrix S and scalar ε > 0, we have:

$$X^{T} Y + Y^{T} X \le \varepsilon X^{T} SX + \frac{1}{\varepsilon }Y^{T} S^{ - 1} Y$$
(3)

Lemma 2

(Schur’s lemma) [30] Let Q1, Q2, and Q3 be three matrices of proper dimensions to the extent that \(Q_{1} = Q_{1}^{T}\) and \(Q_{3} = Q_{3}^{T}\). Then, \(Q_{3} < 0\) and \(Q_{1} - Q_{2}^{T} Q_{3}^{ - 1} Q_{2} < 0\) if and only if.

$$\left[ {\begin{array}{*{20}c} {Q_{1} } & {Q_{2}^{T} } \\ {Q_{2} } & {Q_{3} } \\ \end{array} } \right] < 0$$
(4)

Assumption 1

[38] The Lipschitz condition for all \(x \in R^{n}\) and \(y \in R^{n}\) is as:

$$\begin{gathered} \left\| {f(y) - f(x)} \right\| \le \delta \left\| {y - x} \right\| \hfill \\ f(x):\Omega \to {\mathbf{\mathbb{R}}}\, \hfill \\ x \in \Omega \hfill \\ \end{gathered}$$
(5)

in which \(\delta\) is the Lipschitz constant. Meanwhile, inequality (5) is exemplified as follows:

$$(f(y) - f(x))^{T} (f(y) - f(x)) \le \delta^{2} (x - y)^{T} (x - y)$$
(6)

Definition 1

[35] The H∞ control problem for System (1) can be specified because it gives a constant \(\gamma > 0\), and then designs an adaptive state feedback controller \(u_{r} ,\,r \in M\) for each subsystem and a switching rule \(r = \sigma (t)\) to the extent that:

  1. (1)

    If \(\omega (t) = 0\), the closed-loop system will be asymptotically stable;

  2. (2)

    For all feasible uncertainties, System (1) has an H∞ performance index \(\gamma\) from \(\omega (t)\) to y(t), i.e., the following is held:

    $$\int_{0}^{\infty } {y(t)^{T} y(t)} dt \le \gamma^{2} \int_{0}^{\infty } {w(t)^{T} w(t)} dt$$
    (7)

If it holds that for \(x_{0} = 0\).

The following discussion aims to assist in the design of an adaptive feedback controller (u(t)) for dealing with uncertainties.

3 Primary result

3.1 Stabilization for a nonlinear switched system

Here, we focus on stabilization for the switched nonlinear system (1) when \(\omega (t) = 0\). This paper emphasized designing an adaptive controller as its highest priority in achieving asymptotical stability in System (1). First, we must define a sliding sector for future derivations. Regarding the switched linear system, all of the system matrices \(A_{r} ,r \in M\) might be unstable as defined in the preceding section. Here, we have the following inequality:

$$x^{T} (t)(A_{r}^{T} P + PA_{r} )x(t) \le - x^{T} (t)Qx(t)\,\,\,,\,\,r = 1,2, \ldots ,m$$
(8)

that might not appear to be true for any given positive matrix P and non-negative matrix Q. Nevertheless, for each subsystem, we can break the state space down to two sections in a way that one section satisfies the condition for some of the elements \(x \in {\mathbf{\mathbb{R}}}^{n}\)

$$x^{T} (t)(A_{r}^{T} P + PA_{r} )x(t) > - x^{T} (t)Qx(t)\,\,,\,\,r = 1,2, \ldots ,m$$
(9)

while another part satisfies the condition for other elements \(x \in {\mathbf{\mathbb{R}}}^{n}\).

$$x^{T} (t)(A_{r}^{T} P + PA_{r} )x(t) \le - x^{T} (t)Qx(t)\,\,,\,\,r = 1,2, \ldots ,m$$
(10)

Definition 2

[28] For each subsystem of the nonlinear switched system.

\(\dot{x}(t) = A_{\sigma (t)} x(t) + B_{\sigma (t)} f_{\sigma (t)} (x(t))\, + \xi (t)\theta + D_{\sigma (t)} u(t)\), the corresponding sliding sector is defined in the state space \({\mathbf{\mathbb{R}}}^{n}\) as:

$$S_{\sigma } = \left\{ \begin{gathered} x^{T} (t)\left[ \begin{gathered} (A_{\sigma (t)} + D_{\sigma (t)} K)^{T} P + P(A_{\sigma (t)} + D_{\sigma (t)} K) \hfill \\ + \gamma^{ - 2} PB_{\sigma (t)} B_{\sigma (t)}^{T} P + \gamma^{2} \delta^{2} I \hfill \\ \end{gathered} \right]x(t) \hfill \\ \,\,\,\,\,\,\, \le \, - x^{T} (t)Qx(t)\,\,,\,\,\forall x(t) \in {\mathbb{R}}^{n} \hfill \\ \end{gathered} \right\}\,$$
(11)

in which P is a positive matrix, \(Q\) is a negative matrix, and \(\gamma\) and \(\delta\) are positive constants. The amount of energy for the corresponding Lyapunov function, \(V(x(t)) = x^{T} (t)Px(t) + \tilde{\theta }^{T} \tilde{\theta }\), reduces and satisfies the above condition.

Remark 2

For either stable and unstable systems, a sliding sector can be defined in the state space.

Theorem 1

Consider \(\omega (t) = 0\); in this case, all the subsystem matrices of the nonlinear switched system (1) might be unstable. For a positive constant \(\alpha_{r}\), \(\alpha_{r} \in [0,1]\) and \(\sum\nolimits_{r = 1}^{m} {\alpha_{r} } = 1\), \(r \in M\). If there exists a positive matrix P, a non-negative matrix Q, and Hurwitz matrices \(B_{0} \in R^{n \times n}\), \(D_{0} \in R^{n \times m}\), a Hurwitz stable matrix \(A_{0} \in R^{n \times n}\) and \(\overline{B}\) have appropriate dimensions, such that:

$$\begin{gathered} (A_{0} + D_{0} K)^{T} P + P(A_{0} + D_{0} K) \hfill \\ \quad + \gamma^{ - 2} P\overline{B}\overline{B}^{T} P + \gamma^{2} \delta^{2} I + Q \le 0 \hfill \\ \end{gathered}$$
(12)

By Applying the LMI method, we have

$$\left[ {\begin{array}{*{20}c} {XA_{0}^{T} + A_{0} X + D_{0} Y + Y^{T} D_{0}^{T} + \gamma^{ - 2} \overline{B}\overline{B}^{T} } & {\gamma \delta X} & X \\ {\gamma \delta X} & { - I} & 0 \\ X & 0 & { - Q^{ - 1} } \\ \end{array} } \right] \le 0$$
(13)
$$A_{0} = \sum\limits_{r = 1}^{m} {\alpha_{r} A_{r} } ,\,D_{0} = \sum\limits_{r = 1}^{m} {\alpha_{r} D_{r} } ,\,\overline{B} = \left[ {\begin{array}{*{20}c} {\sqrt {\alpha_{1} } B_{1} } & {\sqrt {\alpha_{2} } B_{2} } & \cdots & {\sqrt {\alpha_{m} } B_{m} } \\ \end{array} } \right]$$
(14)

where

$$X = P^{ - 1} > 0$$
(15)
$$Y = KP^{ - 1} = KX$$
(16)

Considering the subsequent switched adaptive controller, VS control rule, and adaptive law, the switched system (1) would be asymptotically stable as follows:

$$u(t) = Kx(t) - D_{{^{\sigma (t)} }}^{ - 1} \xi (t)\hat{\theta }(t)$$
(17)
$$\dot{\hat{\theta }}(t) = \xi (t)Px(t)$$
(18)
$$\sigma (t) = r\,\,,\,\,r \in \left\{ {1,2, \ldots ,m} \right\}\,\,{\text{when}}\,\,x(t) \in S_{r}$$
(19)

where \(D_{{^{r} }}^{ - 1}\) is the generalized right inverse of the matrix \(D_{r}\), \(\hat{\theta }\) is the estimate of θ, and \(S_{r}\) is the sliding sector outlined in (11).

Proof

For the \(r\) subsystem of the system (1), when \(\omega (t) = 0\), the Lyapunov functional candidate is constructed as follows:

$$V(x(t)) = x^{T} (t)Px(t) + \tilde{\theta }^{T} \tilde{\theta }$$
(20)

in which P is a positive matrix and \(\tilde{\theta } = \hat{\theta }(t) - \theta\). Then, for every nonzero state, x(t), V(x(t)) is positive. V(x(t)) can be derived with reference to t along with the solution of the system (1). Thus, we have:

$$\begin{aligned} \dot{V}(x(t)) & = \dot{x}^{T} (t)Px(t) + x^{T} (t)P\dot{x}(t) + \dot{\hat{\theta }}^{T} \tilde{\theta } + \tilde{\theta }^{T} \dot{\hat{\theta }} \\ & = \left[ {(A_{r} + D_{r} K)x(t) - \xi (t)\tilde{\theta } + B_{r} f_{r} (x(t))} \right]^{T} Px(t) \\ & \quad + x^{T} (t)P\left[ {(A_{r} + D_{r} K)x(t) - \xi (t)\tilde{\theta } + B_{r} f_{r} (x(t))} \right] \\ & \quad + x^{T} (t)P\xi (t)\tilde{\theta } + \tilde{\theta }^{T} \xi (t)Px(t) \\ & = x^{T} (t)\left( {(A_{r} + D_{r} K)^{T} P + P(A_{r} + D_{r} K)} \right)x(t) \\ & \quad + x^{T} (t)PB_{r} (f_{r} (x(t)) + f_{r} (x(t))^{T} B_{r}^{T} Px(t) \\ \end{aligned}$$
(21)

from Lemma 1 and Assumption 1, we have

$$\begin{aligned} & \dot{V}(x(t)) \le x^{T} (t)\left( {(A_{r} + D_{r} K)^{T} P + P(A_{r} + D_{r} K)} \right)x(t) \\ & \quad + \gamma^{2} f_{r}^{T} (x)f_{r} (x) + \gamma^{ - 2} x^{T} (t)PB_{r} B_{r}^{T} Px(t) < 0 \\ & \dot{V}(x(t)) \le x^{T} (t)\left( \begin{gathered} (A_{r} + D_{r} K)^{T} P + P(A_{r} + D_{r} K) \hfill \\ + \gamma^{ - 2} PB_{r} B_{r}^{T} P \hfill \\ \end{gathered} \right)x(t) \\ & \quad + \gamma^{2} \delta^{2} x^{T} (t)x(t) < 0 \\ & \dot{V}(x(t)) \le x^{T} (t)\left( \begin{gathered} (A_{r} + D_{r} K)^{T} P + P(A_{r} + D_{r} K) \hfill \\ + \gamma^{ - 2} PB_{r} B_{r}^{T} P + \gamma^{2} \delta^{2} I \hfill \\ \end{gathered} \right)x(t) < 0 \\ \end{aligned}$$
(22)

As with all the system matrices \(A_{r} + D_{r} K\),\(r \in M\) that are likely to be unstable, the variable structure control method is applied to stabilize the corresponding nonlinear switched system. Therefore, the Lyapunov function is defined for the autonomous system \(\dot{x}(t) = (A_{0} + D_{0} K)x + \overline{B}f_{r} (x(t))\) as:

$$\tilde{V}(x(t)) = x^{T} (t)Px(t)$$
(23)

From (12) and (23), for \(\forall x \in {\mathbb{R}}^{n}\), we can derive:

$$\begin{aligned} \dot{\tilde{V}}(x(t)) & \le x^{T} (t)\left( \begin{gathered} (A_{0} + D_{0} K)^{T} P + P(A_{0} + D_{0} K) \hfill \\ + \gamma^{ - 2} P\overline{B}\overline{B}^{T} P + \gamma^{2} \delta^{2} I \hfill \\ \end{gathered} \right)x(t) \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & \, \le - x^{T} (t)Qx(t) \\ \end{aligned}$$
(24)

From (14) and (24), it can be easily obtained:

$$\begin{aligned} & = x^{T} (t)\left( \begin{gathered} (A_{0} + D_{0} K)^{T} P + P(A_{0} + D_{0} K) \hfill \\ + \gamma^{ - 2} P\overline{B}\overline{B}^{T} P) \hfill \\ \end{gathered} \right)x(t) \\ & \quad + x^{T} (t)(\gamma^{2} \delta^{2} I + Q)x(t) \\ \end{aligned}$$
(25)

Thus, there must be a scalar \(r \in \left\{ {1,2,...,m} \right\}\) where \(\forall x \in S_{r}\)

$$\begin{aligned} \dot{V}(x(t)) & \le x^{T} (t)\left( \begin{gathered} (A_{r} + D_{r} K)^{T} P + P(A_{r} + D_{r} K) \hfill \\ + \gamma^{ - 2} PB_{r} B_{r}^{T} P + \gamma^{2} \delta^{2} I \hfill \\ \end{gathered} \right)x(t) \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & \, \le - x^{T} (t)Qx(t) \\ \end{aligned}$$
(26)

when \(\omega (t) = 0\), we can stabilize the nonlinear switched system (1) using the proposed VS control rule in (19).

Remark 3 In Theorem 1, the adaptive controller u(t) is designed to accommodate the uncertainties. On the other hand, to stabilize the underlying system, the VS control approach with the sliding sector is investigated using a designed switching signal. To summarize, the proposed control design method is not only flexible but may also be capable of reducing the complexity and cost of the combination.

4 An H ∞ control designed for nonlinear switched system

Here, the H∞ problem is investigated for the nonlinear switched system (1), when \(\omega (t) \ne 0\). Therefore, a definition is offered for the sliding sector as follows:

Definition 3

Consider the sliding sector for the nonlinear switched system (1) in the state space \({\mathbb{R}}^{n}\). For every subsystem, we have:

$$S_{\sigma } = \left\{ \begin{gathered} x^{T} (t)\left[ \begin{gathered} (A_{\sigma (t)} + D_{\sigma (t)} K)^{T} P + P(A_{\sigma (t)} + D_{\sigma (t)} K) + \gamma^{2} \delta^{2} I \hfill \\ + \gamma^{ - 2} PB_{\sigma (t)} B_{\sigma (t)}^{T} P + \gamma^{ - 2} PE_{\sigma (t)} E_{\sigma (t)}^{T} P + C_{\sigma (t)}^{T} C_{\sigma (t)} \hfill \\ \end{gathered} \right]x(t) \hfill \\ \,\,\,\,\, \le \, - x^{T} (t)Qx(t)\,\,,\,\,\forall x(t) \in {\mathbb{R}}^{n} \hfill \\ \end{gathered} \right\}\,$$
(27)

in which P is a positive matrix, \(Q\) is a negative matrix, \(\gamma\) and \(\delta\) are positive constants.

Theorem 2

Consider the nonlinear switched system (1), when \(\omega (t) \ne 0\), in which all the subsystem matrices are probably unstable. For the given positive scalar \(\alpha_{r}\), in which \(\alpha_{r} \in [0,1]\), \(\sum\nolimits_{r = 1}^{m} {\alpha_{r} } = 1\), \(p \in M\). If there exists a scalar \(\gamma > 0\), \(\delta > 0\), a positive matrix P, a non-negative matrix Q, and Hurwitz matrices \(A_{0} \in R^{n \times n}\), \(D_{0} \in R^{n \times m}\), \(E_{0} \in R^{n \times d}\) with appropriate dimensions, such that:

$$\left[ {\begin{array}{*{20}c} \begin{gathered} XA_{0}^{T} + A_{0} X + D_{0} Y \hfill \\ + Y^{T} D_{0}^{T} + \gamma^{ - 2} \overline{B}\overline{B}^{T} \hfill \\ \end{gathered} & {\overline{E}} & {X\overline{C}^{T} } & {\gamma \delta X} & X \\ {\overline{E}^{T} } & { - \gamma^{2} I} & 0 & 0 & 0 \\ {\overline{C}X} & 0 & { - I} & 0 & 0 \\ {\gamma \delta X} & 0 & 0 & { - I} & 0 \\ X & 0 & 0 & 0 & { - Q^{ - 1} } \\ \end{array} } \right] \le 0$$
(28)
$$\begin{gathered} A_{0} = \sum\limits_{r = 1}^{m} {\alpha_{r} A_{r} } ,\,D_{0} = \sum\limits_{p = 1}^{m} {\alpha_{r} D_{r} } ,\,\overline{B} = \left[ {\begin{array}{*{20}c} {\sqrt {\alpha_{1} } B_{1} } & {\sqrt {\alpha_{2} } B_{2} } & \cdots & {\sqrt {\alpha_{m} } B_{m} } \\ \end{array} } \right] \hfill \\ \overline{C} = \left[ {\begin{array}{*{20}c} {\sqrt {\alpha_{1} } C_{1} } & {\sqrt {\alpha_{2} } C_{2} } & \cdots & {\sqrt {\alpha_{m} } C_{m} } \\ \end{array} } \right],\,\overline{E} = \left[ {\begin{array}{*{20}c} {\sqrt {\alpha_{1} } E_{1} } & {\sqrt {\alpha_{2} } E_{2} } & \cdots & {\sqrt {\alpha_{m} } E_{m} } \\ \end{array} } \right] \hfill \\ \end{gathered}$$
(29)

where

$$X = P^{ - 1} > 0$$
(30)
$$Y = KP^{ - 1} = KX$$
(31)

Therefore, the nonlinear switched system (1) is considered asymptotically stable according to the switched adaptive controller, adaptive rule, and VSC rule with the H∞ performance index γ,

$$u(t) = Kx(t) - D_{{^{\sigma (t)} }}^{ - 1} \xi (t)\hat{\theta }(t)$$
(32)
$$\dot{\hat{\theta }}(t) = \xi (t)Px(t)$$
(33)
$$\sigma (t) = r\,\,,\,\,r \in \left\{ {1,2, \ldots ,m} \right\}\,{\text{when}}\,x(t) \in S_{r}$$
(34)

in which \(D_{{^{r} }}^{ - 1}\) is the generalized right inverse of the matrix \(D_{r}\), Sp is the sliding sector, and \(\hat{\theta }\) is an estimate of θ, as described in (27).

Proof

Based on Lemma 2 and the sliding sector (27), we have:

$$\begin{gathered} \overline{C}^{T} \overline{C} + (A_{0} + D_{0} K)^{T} P + P(A_{0} + D_{0} K) \hfill \\ + \gamma^{ - 2} P\overline{B}\overline{B}^{T} P + \gamma^{ - 2} P\overline{E}\overline{E}^{T} P + \gamma^{2} \delta^{2} I + Q \le 0 \hfill \\ \end{gathered}$$
(35)

and, from the definition of \(A_{0} ,D_{0} ,\overline{C},\overline{B},\overline{E}\), we can obtain the following relationship:

$$\begin{aligned} & \sum\limits_{p = 1}^{m} {\alpha x^{T} (t)\left( \begin{gathered} (A_{r} + D_{r} K)^{T} P + P(A_{r} + D_{r} K) \hfill \\ + C_{r}^{T} C_{r} + \gamma^{ - 2} PB_{p} B_{p}^{T} P + \gamma^{ - 2} PE_{r} E_{r}^{T} P \hfill \\ \end{gathered} \right)x(t)} \\ & \quad + x^{T} (t)(\gamma^{2} \delta^{2} I + Q)x(t) \le 0 \\ \end{aligned}$$
(36)

Then, \(\forall x \in S_{r}\) we have:

$$x^{T} (t)\left( \begin{gathered} (A_{r} + D_{r} K)^{T} P + P(A_{r} + D_{r} K) + C_{r}^{T} C_{r} \hfill \\ + \gamma^{ - 2} PB_{r} B_{r}^{T} P + \gamma^{ - 2} PE_{r} E_{r}^{T} P + \gamma^{2} \delta^{2} I \hfill \\ \end{gathered} \right)x(t) \le 0$$
(37)

Thus, the above inequality can be maintained provided the discrete switching signal \(\sigma (t) = r\) is selected observing \(x(t) \in S_{r}\). Furthermore, consider the Lyapunov function when \(\omega (t) \ne 0\):

$$V(x(t)) = x^{T} (t)Px(t) + \tilde{\theta }^{T} \tilde{\theta }$$
(38)

in which P is a positive matrix, and \(\tilde{\theta } = \hat{\theta }(t) - \theta\). Taking the derivative of V(t) along the trajectory of System (1), we can obtain the following relationship:

$$\begin{aligned} \dot{V}(x(t)) & = \dot{x}^{T} (t)Px(t) + x^{T} (t)P\dot{x}(t) + \dot{\hat{\theta }}^{T} \tilde{\theta } + \tilde{\theta }^{T} \dot{\hat{\theta }} \\ & = \left( \begin{gathered} A_{r} x + D_{r} Kx + B_{r} f_{r} (x(t)) \hfill \\ - \psi (t)\tilde{\theta } + \psi (t)\theta + E_{r} \omega (t) \hfill \\ \end{gathered} \right)^{T} Px(t) \\ & \quad + x^{T} (t)P\left( \begin{gathered} A_{r} x + D_{r} Kx + B_{r} f_{r} (x(t)) \hfill \\ - \psi (t)\tilde{\theta } + \psi (t)\theta + E_{r} \omega (t) \hfill \\ \end{gathered} \right) + \dot{\hat{\theta }}^{T} \tilde{\theta } + \tilde{\theta }^{T} \dot{\hat{\theta }} \\ = x^{T} (t)\left( {(A_{r} + D_{r} K)^{T} P + P(A_{r} + D_{r} K)} \right)x(t) \\ & \quad + x^{T} (t)PB_{r} f_{r} (x(t)) + f_{r} (x(t))^{T} B_{r}^{T} Px(t) \\ & \quad + x^{T} (t)PE_{r} \omega (t) + \omega^{T} (t)E_{r}^{T} Px(t) \\ & \le x^{T} (t)\left( \begin{gathered} (A_{r} + D_{r} K)^{T} P + P(A_{r} + D_{r} K) \hfill \\ + \gamma^{ - 2} PB_{r} B_{r}^{T} P + \gamma^{2} \delta^{2} I \hfill \\ \end{gathered} \right)x(t) \\ & \quad + x^{T} (t)PE_{r} \omega (t) + \omega^{T} (t)E_{r}^{T} Px(t) \le - x^{T} (t)Qx(t)\, \\ \end{aligned}$$
(39)

So, we have:

$$\begin{aligned} \dot{V}(x(t)) & \le x^{T} (t)\left( \begin{gathered} (A_{r} + D_{r} K)^{T} P + P(A_{r} + D_{r} K) \hfill \\ + \gamma^{ - 2} PB_{r} B_{r}^{T} P + \gamma^{2} \delta^{2} I + Q \hfill \\ \end{gathered} \right)x(t) \\ & \quad + x^{T} (t)PE_{r} \omega (t) + \omega^{T} (t)E_{r}^{T} Px(t) \le 0 \\ \end{aligned}$$
(40)

Now, for the nonlinear switched system (1), consider:

$$\begin{gathered} J = \int_{0}^{\infty } {\left( {y(t)^{T} y(t) - \gamma^{2} \omega (t)^{T} \omega (t)} \right)} dt \hfill \\ \,\,\,\,\, = \int_{0}^{\infty } {\left( {y(t)^{T} y(t) - \gamma^{2} \omega (t)^{T} \omega (t) + \dot{V}(t)} \right)} dt - \left( {V(\infty ) - V(0)} \right) \hfill \\ \end{gathered}$$
(41)

Therefore, from the time derivative of V(t) and (40), we have:

$$\begin{aligned} & y(t)^{T} y(t) - \gamma^{2} \omega (t)^{T} \omega (t) + \dot{V}(t) \\ & \quad = \left[ {\begin{array}{*{20}c} {x^{T} (t)} & {\omega^{T} (t)} \\ \end{array} } \right]\varphi_{1} \left[ {\begin{array}{*{20}c} {x(t)} \\ {\omega (t)} \\ \end{array} } \right] \\ \end{aligned}$$
(42)

where

$$\varphi_{1} = \left( {\begin{array}{*{20}c} \begin{gathered} (A_{0} + D_{0} K)^{T} P + P(A_{0} + D_{0} K) \hfill \\ + \gamma^{ - 2} P\overline{B}\overline{B}^{T} P + \overline{C}^{T} \overline{C} + \gamma^{2} \delta^{2} I + Q \hfill \\ \end{gathered} & {P\overline{E}} \\ {\overline{E}^{T} P} & { - \gamma^{2} I} \\ \end{array} } \right) \le 0$$
(42)

and

$$\begin{gathered} \varphi_{1} = \left( {\begin{array}{*{20}c} \begin{gathered} (A_{0} + D_{0} K)^{T} P + P(A_{0} + D_{0} K) \hfill \\ + \gamma^{ - 2} P\overline{B}\overline{B}^{T} P \hfill \\ \end{gathered} & {P\overline{E}} \\ {\overline{E}^{T} P} & { - \gamma^{2} I} \\ \end{array} } \right) \hfill \\ + \left[ {\begin{array}{*{20}c} {\overline{C}^{T} } & {\gamma \delta I} & I \\ 0 & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} I & 0 & 0 \\ 0 & I & 0 \\ 0 & 0 & {Q^{ - 1} } \\ \end{array} } \right]^{ - 1} \left[ {\begin{array}{*{20}c} {C^{T} } & 0 \\ {\gamma \delta I} & 0 \\ I & 0 \\ \end{array} } \right] \hfill \\ \end{gathered}$$
(43)

According to Lemma 2:

$$\varphi_{2} = \left[ {\begin{array}{*{20}c} \begin{gathered} A_{0}^{T} P + PA_{0} + PD_{0} Y \hfill \\ + Y^{T} D_{0}^{T} P + \gamma^{ - 2} P\overline{B}\overline{B}^{T} P \hfill \\ \end{gathered} & {P\overline{E}} & {\overline{C}^{T} } & {\gamma \delta I} & I \\ {\overline{E}^{T} P} & { - \gamma^{2} I} & 0 & 0 & 0 \\ {\overline{C}} & 0 & { - I} & 0 & 0 \\ {\gamma \delta I} & 0 & 0 & { - I} & 0 \\ I & 0 & 0 & 0 & { - Q^{ - 1} } \\ \end{array} } \right]$$
(44)

However, to find of \(\varphi_{2} < 0\), the obtained condition is altered by some manipulations, pre- and post-multiplication \(\varphi_{2}\) by diagonal matrix \(\sum = {\text{diag}}\left[ {\begin{array}{*{20}c} {P^{ - 1} } & I & I & I \\ \end{array} } \right]\) and introducing \(X = P^{ - 1} > 0\),\(Y = KP^{ - 1} = KX\) results in (28). Then, the system (1) based on the sliding sector, the switched adaptive controller, adaptive law, and VSC rule is uniformly asymptotically stable with an L2-gain smaller than γ.

5 Numerical simulations

In this section, we present a numerical example that attempts to validate the proposed method. Considering the Rossler system [39] as a subsystem (1), it is described as follows:

$$\left\{ \begin{gathered} \dot{x}_{1} = - x_{2} - x_{3} \hfill \\ \dot{x}_{2} = x_{1} + a_{1} x_{2} \hfill \\ \dot{x}_{3} = b_{1} + x_{3} (x_{2} - c_{1} ) \hfill \\ \end{gathered} \right.$$
(45)

where \(a_{1} = b_{1} = 0.2\,\) and \(c_{1} = 5.7\) are three real constants, and the Newton-Leipnik system [40] as subsystem (2) is described as follows:

$$\left\{ \begin{gathered} \dot{x}_{1} = - a_{2} x_{1} + x_{2} + 10x_{2} x_{3} \hfill \\ \dot{x}_{2} = - x_{1} - 0.4x_{2} + 5x_{1} x_{3} \hfill \\ \dot{x}_{3} = b_{2} x_{3} - 5x_{1} x_{2} \hfill \\ \end{gathered} \right.$$
(46)

where \(a_{2} = 0.4\,\) and \(b_{2} = 0.175\) are the system parameters. The state-space model comprises two subsystems and is described as follows:

$$\begin{aligned} \dot{x}(t) & = A_{\sigma (t)} x(t) + B_{\sigma (t)} f_{\sigma (t)} (x(t))\, \\ \,\,\,\,\,\,\,\,\,\, & \quad \, + \xi (t)\theta + D_{\sigma (t)} u(t) + E_{\sigma (t)} \omega (t)\, \\ y(t) & = C_{\sigma (t)} x(t) \\ \end{aligned}$$
(47)

where the system matrices are:

$$\begin{aligned} A_{1} & = \left[ {\begin{array}{*{20}c} 0 & { - 1} & { - 1} \\ 1 & {0.2} & 0 \\ 0 & 0 & { - 5.7} \\ \end{array} } \right],\,A_{2} = \left[ {\begin{array}{*{20}c} { - 0.4} & 1 & 0 \\ { - 1} & { - 0.4} & 0 \\ 0 & 0 & {0.175} \\ \end{array} } \right],\,B_{1} = B_{2} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right], \\ f_{1} (x(t)) & = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {b + x_{1} x_{3} } \\ \end{array} } \right],\,f_{2} (x(t)) = \left[ {\begin{array}{*{20}c} {10x_{2} x_{3} } \\ {5x_{1} x_{3} } \\ { - 5x_{1} x_{2} } \\ \end{array} } \right],\,D_{1} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right],\,D_{2} = \left[ {\begin{array}{*{20}c} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \\ \end{array} } \right] \\ C_{1} & = \left[ {\begin{array}{*{20}c} 1 & 0 & 1 \\ \end{array} } \right],\,C_{2} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ \end{array} } \right],\,E_{1} = E_{2} = \left[ {\begin{array}{*{20}c} {0.1} \\ {0.2} \\ {0.1} \\ \end{array} } \right],\,\xi (t) = \left[ {\begin{array}{*{20}c} {\varphi_{1} (t)} & 0 & 0 \\ 0 & {\varphi_{2} (t)} & 0 \\ 0 & 0 & {\varphi_{3} (t)} \\ \end{array} } \right] \\ \omega (t) & = 10\sin (2\pi t)e^{ - 0.5t} \\ \end{aligned}$$

Although the eigenvalue of A1 and A2 are not Hurwitz stable, the associated Hurwitz stable convex combination with \(\alpha_{1} = 0.2\) and \(\alpha_{2} = 1 - \alpha_{1}\) can be obtained as follows:

$$A_{0} = \sum\limits_{p = 1}^{m} {\alpha_{r} A_{r} } = \alpha_{1} A_{1} + \alpha_{2} A_{2} = \left[ {\begin{array}{*{20}c} { - 0.32} & {0.6} & { - 0.2} \\ { - 0.6} & { - 0.28} & 0 \\ 0 & 0 & { - 1} \\ \end{array} } \right]$$

and

$$D_{0} = \sum\limits_{p = 1}^{m} {\alpha_{r} D_{r} } = \alpha_{1} D_{1} + \alpha_{2} D_{2} = \left[ {\begin{array}{*{20}c} {1.8} & 0 & 0 \\ 0 & {1.2} & 0 \\ 0 & 0 & {1.8} \\ \end{array} } \right]$$

Furthermore, by choosing \(\gamma = 0.8\), \(\delta = 0.3\), and \(Q = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\),

a feasible solution for the system (47) is obtained as follows:

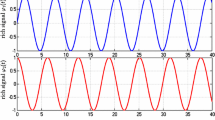
$$\begin{gathered} P = \left[ \begin{gathered} {1}{\text{.9189 - 0}}{.0009 - 0}{\text{.0005}} \hfill \\ { - 0}{\text{.0009 1}}{.0552 0}{\text{.0006}} \hfill \\ { - 0}{\text{.0005 0}}{.0006 1}{\text{.0543}} \hfill \\ \end{gathered} \right], \hfill \\ K = \left[ \begin{gathered} { - 2}{\text{.5034 - 0}}{.1000 0}{\text{.0924}} \hfill \\ { - 0}{\text{.1835 - 0}}{.5844 - 0}{\text{.0115}} \hfill \\ { 0}{\text{.1675 - 0}}{.0116 - 0}{\text{.4233}} \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered}$$

As seen in Fig. 1, the specified signals are chosen as \(\varphi_{1} (t) = \sin t\), \(\varphi_{2} (t) = \cos t\), and

$$\varphi_{3} (t) = e^{ - 2\sin 2\pi t} .$$
Fig. 1
figure 1

Known signals \(\varphi_{1} ,\,\varphi_{2} \,{\text{and}}\,\varphi_{3}\)

Full size image

Accordingly, the system parameters are set to \(\theta_{1} = 2\), \(\theta_{2} = 5\), and \(\theta_{3} = 9\). Moreover, to demonstrate the effectiveness of the presented control in Figs. 2, 3, and 4, the initial values of the estimated parameters are \(\hat{\theta }(0) = \left[ {\begin{array}{*{20}c} 1 & 6 & {11} \\ \end{array} } \right]^{T}\), and the initial condition of state trajectories are considered to \(x(0) = \left[ {\begin{array}{*{20}c} {0.349} & 0 & { - 0.16} \\ \end{array} } \right]^{T}\). As seen in the figures, the H∞ problem is solved by the proposed controller with acceptable performance. Figures 2 and 3 depict the time response of adaptive rule \(\hat{\theta }(t)\), and the state variable of the nonlinear switched system (47) under the variable control rule as well as the control input u(t) are illustrated in Fig. 4. Evidently, the designed reliable controller with H∞ performance not only leads to a globally asymptotical stable closed-loop system but also consistently offsets the associated uncertainties.

Fig. 2
figure 2

Adaptive laws

Full size image
Fig. 3
figure 3

State trajectory of a nonlinear switched system under variable control law

Full size image
Fig. 4
figure 4

Control inputs

Full size image

6 Conclusion

This paper attempted to solve the adaptive control problem for a class of nonlinear switched systems. To do so, first, the sufficient condition of the system stability was satisfied using the adaptive controller to adapt to system uncertainties, a convex combination method, and the switching signal. Then, considering that the subsystems are possibly unstable, an adaptive controller and VS switching rule were applied to ensure the globally asymptotical stability. Thereby, the H∞ control problem of the nonlinear switched system was solved with regard to linear matrix inequalities. Lastly, a numerical example was offered to reveal the unique and practical approach developed through the designed controller and the proposed switching strategy.

Qualities of high accuracy, the rapid convergence of states toward zero, attenuation of disturbance and reduction of its effect on the nonlinear system are the advantages of our proposed method. As a future work, the authors seek to develop a new adaptive controller along with a switching sliding sector in the presence of parametric uncertainty and disturbance to maintain the states at desired values.