1 Introduction

Study of algal bloom is classical and widely recognized for the wealth of marine ecosystem. The research to investigate the mechanisms behind such phenomena is still important to understand the plankton dynamics and ultimately for other marine animals. In food web interaction infochemical, kairomones and pheromones used by an individual can exploit such chemical for searching prey or to avoid predator. Phytoplankton deterrents by producing infochemical may decrease the grazing rate on the producing species in marine environment [1]. Algae species are extremely flexible in their growth from production of toxic substance, biochemical composition and deterrent compounds [2]. Microzooplankton is an important grazer of bacteria and phytoplankton, and their ability to respond on infochemical cues confers a strong selective advantage [3]. The chemicals released by phytoplankton work as a defense mechanism and decrease the grazing pressure, but it also enhances the searching ability of zooplankter [4, 5]. Resulting grazing-induced release of infochemical in multi-tropic interaction attracts carnivorous predators that reduce the grazing pressure on primary producer [6]. Recently, the models investigating the effect of toxin-producing phytoplankton (TPP) received much attention [7,8,9,10,11]. But grazing-induced toxic deterrents have received less attention. Inclusion of such toxic deterrents plays an important role for understanding and restructuring the dynamics of plankton bloom. Mathematical models describing the interaction between the toxic phytoplankton and other aquatic species have been discussed by many authors. Bairagi et al. [12] have proposed interacting nutrient–plankton dynamics and suggested that interactions among these species are very complex and situation specific. Model for interacting toxin-producing phytoplankton, non-toxic phytoplankton and zooplankton observed that the populations are independent of the magnitude of the steady-state component [13]. A two zooplankton and one phytoplankton model with toxicity observed that coefficient of toxin plays an important role for existence of Hopf bifurcation around the interior equilibrium [14]. Chatterjee and Pal [15] studied the effect of toxin in nutrient–plankton model and observed that toxic phytoplankton may change the steady-state behavior. De Silva and Jang [16] observed that the mutual interference of zooplankton diminishes harmful blooms.

Many researchers have used the predator–prey interaction models to study the spatiotemporal dynamics in plankton system [10, 17,18,19,20]. Spatiotemporal patterns in plankton dynamics with the sequence of chaotic spiral, strip and spot patterns were studied by Rao [21]. Wang et al. [22] observed that the direction of cross-diffusion influences the spatial distribution. Sekerci and Petrovskii [23] studied the oxygen–plankton model system in pattern formation and observed (for somewhat different initial conditions) irregular spatiotemporal patterns, simple spirals, double spirals or “mushroom-like” structures and “snake-like” structures. Thakur et al. [11] have proposed diffusive three species plankton models with toxic effect for wetland ecosystem. Chaudhuri et al. [24] studied toxic phytoplankton-induced spatiotemporal patterns observed that the populations become inhomogeneous in the presence of toxin-producing phytoplankton. Sekerci and Petrovskii [25] have proposed coupled plankton–oxygen model with effect of global warming. Sekerci [26] has studied theoretically by considering a coupled of the oxygen–plankton model where planktons habitat changes and beachhead as a response to climate change. Recently, some mathematical models exploring the dynamics of interaction between infochemical-producing phytoplankton and microzooplankton have been studied by [1, 3, 5, 27,28,29,30,31]. Study shows that the inclusion of grazing-induced infochemical term acts as attractor of predatory copepods which can stabilize the system [27]. Inclusion of such term may promote plankton bloom [33]. Hence, DMS acts as principal promoter of multi-trophic interaction [6]. With this motivation, our objective is to understand the effect of grazing-induced DMS and spatiotemporal evolution on system dynamics. The organization of the paper is as follows. Section 2 deals with model formulation, and stability analysis is discussed in Sect. 3. Section 4 describes numerical results. Discussion and conclusion are discussed in Sect. 5 and Sect. 6, respectively.

2 Model formulation

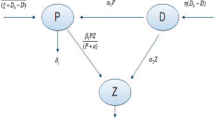
We present interacting plankton system where microzooplankton M(x; t) grazes on two competing phytoplanktons: \(P_1(x; t)\) infochemical-producing phytoplankton (IPP) and \(P_2(x; t)\) non-infochemical-producing phytoplankton (NIP) at any location x and time t. Both phytoplankton species grow logistically with their intrinsic growth rates \(r_1, r_2\) and carrying capacities \(K_1\) and \(K_2,\) respectively. The growth of phytoplankton is limited by availability of nutrients and light. Phytoplankton growth is also limited by an interspecific competition term, where \(\alpha _1\) is the competitive effect of non-infochemical producers on infochemical producers and \(\alpha _2\) is the vice versa. The \(\alpha\) terms are assumed to represent growth limiting factors such as nutrient depletion and/or shading by the other species [34]. The relationship between \((P_1, P_2, M)\) is defined by Holling type II or BD-type functional response. Microzooplankton predates non-infochemical-producing phytoplankton (NIP) at a rate of \(w_1\) with the maximum conversion rate \(\gamma _1\) and predates infochemical-producing phytoplankton (IPP) at a rate of \(w_2\) with the reduction rate \(\gamma _2,\) respectively, while k is the half-saturation constant. A key point to note is that although copepods are not explicitly modeled here, the effect of copepod predation is accounted for in the microzooplankton mortality terms in Eq. (2.1). Contrary to studies on toxic phytoplankton [8], DMS has no toxic effects on microzooplankton grazers [31, 32], and therefore, IPP has no direct adverse effect on microzooplankton, but their mortality is indirectly increased by a factor \(\lambda\) proportional to grazing on IPP [1]. The mortality term m represents any mortality incurred by microzooplankton in the absence of infochemicals and the interspecific competition coefficients (\(\delta\)) of microzooplankton that express the self-limitation of microzooplankton. With this assumption, we propose the model given by:

$$\begin{aligned} \begin{aligned} \frac{\partial P_1}{\partial t}&=r_1P_1\bigg (1-\frac{P_1+\alpha _1P_2}{K_1}\bigg )\\&\quad -\frac{w_1P_1M}{k+P_1+P_2}+D_1\nabla ^2 P_1,\\ \frac{\partial P_2}{\partial t}&=r_2P_2\bigg (1-\frac{P_2+\alpha _2P_1}{K_2}\bigg )\\&\quad -\frac{w_2P_2M}{k+P_1+P_2}+D_2\nabla ^2 P_2,\\ \frac{\partial M}{\partial t}&=\frac{(\gamma _1-\lambda )w_1P_1M+\gamma _2w_2P_2M}{k+P_1+P_2}\\&\quad -mM-\delta M^2+D_3\nabla ^2 M, \end{aligned} \end{aligned}$$
(2.1)

non-vanishing initial conditions

$$\begin{aligned} P_1(x,0)>0, ~P_2(x,0)>0, ~M(x,0)>0,\,\, x\in [0,R], \end{aligned}$$
(2.2)

and the zero-flux boundary conditions

$$\begin{aligned} \begin{aligned} {\frac{\partial P_1}{\partial x}\mid _{x\in [0,R]} = \frac{\partial P_2}{\partial x}\mid _{x\in [0,R]} = \frac{\partial M}{\partial x}\mid _{x\in [0,R]}=0.} \end{aligned} \end{aligned}$$
(2.3)

where \(D_1, \ D_2\) and \(D_3\) are the diffusion coefficients of IPP, NIP and microzooplankton populations, respectively. \(\nabla ^2= \frac{\partial ^2}{\partial x^2}\) denotes the 1D Laplacian operator, whereas \(\nabla ^2= \frac{\partial ^2}{\partial x^2} + \frac{\partial ^2}{\partial y^2}\) denotes the 2D Laplacian operator (Table 1).

Table 1 Definition of the parameters used in the model system (2.1)
Full size table

3 Analytical methodologies

3.1 Stability analysis of temporal model system

In this subsection, we have discussed the nonnegative equilibrium points and their stability properties of the model system in the absence of diffusion. The reduced system of ordinary differential equation is as follows:

$$\begin{aligned} \begin{aligned} \frac{dP_1}{ dt}&=r_1P_1\bigg (1-\frac{P_1+\alpha _1P_2}{K_1}\bigg )-\frac{w_1P_1M}{k+P_1+P_2},\\ \frac{dP_2}{dt}&=r_2P_2\bigg (1-\frac{P_2+\alpha _2P_1}{K_2}\bigg )-\frac{w_2P_2M}{k+P_1+P_2},\\ \frac{dM}{dt}&=\frac{(\gamma _1-\lambda )w_1P_1M+\gamma _2w_2P_2M}{k+P_1+P_2}-mM-\delta M^2, \end{aligned} \end{aligned}$$
(3.1)

with

$$\begin{aligned} P_1(0)>0, ~P_2(0)>0, ~M(0)>0. \end{aligned}$$
(3.2)

Lemma 1

The set

$$\begin{gathered} A = \{ (P_{1} (t),P_{2} (t),M(t)):0 \le P_{1} (t) \le K_{1} ,0 \le P_{2} (t) \le K_{2} , \hfill \\ \quad 0 \le M(t) \le \frac{{\gamma _{1} w_{1} K_{1} + \gamma _{2} w_{2} K_{2} }}{{\delta (k + K_{1} + K_{2} )}}\} \hfill \\ \end{gathered}$$

is a positively invariant set and attracts all solutions initiating in the interior of the positive octant.

The proof of this lemma can be obtained by simple calculation and hence omitted.

The non-spatial model system (3.1) possesses seven nonnegative real equilibrium points:

  1. (i)

    The trivial equilibrium point \(E_0 = (0, 0, 0)\) always exists.

  2. (ii)

    The axial equilibrium point \(E_1 = (K_1, 0, 0)\) exists on the boundary of the first octant.

  3. (iii)

    The axial equilibrium point \(E_2 = (0, K_2, 0)\) exists on the boundary of the first or second octant.

  4. (iv)

    The planar equilibrium point \(E_3 = (\hat{P}_{1}^{'},\hat{P}_{2}^{'}, 0)\) exists on the \(P_1P_2\)-plane, where \(\hat{P}_{1}^{'}=\dfrac{(K_1-\alpha _1K_2)}{(1-\alpha _1\alpha _2)}\), \(\hat{P}_{2}^{'}=\dfrac{(K_2-\alpha _1K_1)}{(1-\alpha _1\alpha _2)}\), if \(\alpha _1<\dfrac{K_1}{K_2}<\dfrac{1}{\alpha _2}.\)

  5. (v)

    The planar equilibrium point \(E_4 =(\bar{P}_{1},0,\bar{M})\) exists on the \(P_1M\)-plane. \(\bar{P}_{1}\) and \(\bar{M}\) are the positive solution of the following equations:

    $$\begin{aligned}&r_1\bigg (1-\frac{P_1}{K_1}\bigg )-\frac{w_1M}{k+P_1}=0, \end{aligned}$$
    (3.3)
    $$\begin{aligned}&\frac{(\gamma _1-\lambda )w_1P_1}{k+P_1}-m-\delta M=0. \end{aligned}$$
    (3.4)

    From Eq. (3.3), we have

    $$\begin{aligned} M=\dfrac{r_1}{w_1}\bigg (1-\dfrac{P_1}{K_1}\bigg )(k+P_1). \end{aligned}$$
    (3.5)

    Putting the value of M from Eq. (3.5) into Eq. (3.4), we get

    $$\begin{aligned} \begin{aligned}&\delta r_1 P_1^3+\delta r_1(2k-K_1)P_1^2+\{w_1K_1((\gamma _1-\lambda )w_1-m)\\&\quad +\delta r_1k(k-2K_1)\}P_1-kK_1(mw_1+\delta r_1k)=0. \end{aligned} \end{aligned}$$
    (3.6)

    According to Descartes rule of sign, Eq. (3.6) has a unique positive real root if

    $$\begin{aligned} K_1<2k. \end{aligned}$$
    (3.7)

    It may be noted that for \(\bar{M}\) to be positive, we must have

    $$\begin{aligned} \bar{P}_{1}<K_1. \end{aligned}$$
    (3.8)

    This shows that \(E_4 =(\bar{P}_{1},0,\bar{M})\) exists under conditions (3.7) and (3.8).

  6. (vi)

    The planar equilibrium point \(E_5 =(0,\tilde{P}_{2},\tilde{M})\) exists on the \(P_{2}M\)-plane. \(\tilde{P}_{2}\) and \(\tilde{M}\) are the positive solution of the following equations:

    $$\begin{aligned}&r_2\big (1-\frac{P_2}{K_2})-\frac{w_2M}{k+P_2}=0, \end{aligned}$$
    (3.9)
    $$\begin{aligned}&\frac{\gamma _2w_2P_2}{k+P_2}-m-\delta M=0. \end{aligned}$$
    (3.10)

    From Eq. (3.9), we have

    $$\begin{aligned} M=\dfrac{r_2}{w_2}\bigg (1-\dfrac{P_2}{K_2}\bigg )(k+P_2). \end{aligned}$$
    (3.11)

    Putting the value of M from Eq. (3.11) into Eq. (3.10), we get

    $$\begin{aligned} \begin{aligned}&\delta r_2P_2^3+\delta r_2(2k-K_2)P_2^2+\{w_2K_2(\gamma _2w_2-m)\\&\quad +\delta r_2k(k-2K_2)\}P_2-kK_2(mw_2+\delta r_2k)=0. \end{aligned} \end{aligned}$$
    (3.12)

    According to Descartes rule of sign, Eq. (3.12) has a unique positive real root if

    $$\begin{aligned} K_2<2k. \end{aligned}$$
    (3.13)

    It may be noted that for \(\tilde{M}\) to be positive, we must have

    $$\begin{aligned} \tilde{P}_{2}<K_2. \end{aligned}$$
    (3.14)

    This shows that \(E_5 =(0,\tilde{P}_{2},\tilde{M})\) exists under the condition (3.13) and (3.14).

  7. (vii)

    Existence of interior equilibrium point \(E_6 = (P_1^*,P_2^*,M^*)\) has been established below after following [35]. In this case, \(P_1^*,P_2^*\) and \(M^*\) are the positive solutions of following equations:

    $$\begin{aligned}&r_1\big (1-\frac{P_1+\alpha _1P_2}{K_1})-\frac{w_1M}{k+P_1+P_2}=0, \end{aligned}$$
    (3.15)
    $$\begin{aligned}&r_2\big (1-\frac{P_2+\alpha _2P_1}{K_2})-\frac{w_2M}{k+P_1+P_2}=0, \end{aligned}$$
    (3.16)
    $$\begin{aligned}&\frac{(\gamma _1-\lambda )w_1P_1+\gamma _2w_2P_2}{k+P_1+P_2}-m-\delta M=0. \end{aligned}$$
    (3.17)

    From Eq. (3.15), we get

    $$\begin{aligned} M=\dfrac{r_1}{w_1}\bigg (1-\dfrac{P_1+\alpha _1P_2}{K_1}\bigg )(k+P_1+P_2), \end{aligned}$$
    (3.18)

    clearly \(M>0\) if \(K_1>(P_1+\alpha _1P_2).\)

    Putting the value of M from Eq. (3.18) in Eqs. (3.16) and (3.17), we get

    $$\begin{aligned} F(P_1, P_2)&= r_2\bigg (1-\frac{P_2+\alpha _2P_1}{K_2}\bigg )\nonumber \\&\quad -\dfrac{w_2r_1}{w_1}\bigg (1-\frac{P_1+\alpha _1P_2}{K_1}\bigg )=0, \end{aligned}$$
    (3.19)
    $$\begin{aligned} G(P_1, P_2)&=\frac{(\gamma _1-\lambda )w_1P_1+\gamma _2w_2P_2}{k+P_1+P_2}-m-\nonumber \\&\quad \dfrac{\delta r_1}{w_1}\bigg (1-\frac{P_1+\alpha _1P_2}{K_1}\bigg )(k+P_1+P_2)=0. \end{aligned}$$
    (3.20)

    From Eq. (3.19), when \(P_2 = 0,\) then \(P_1 = P_{1a}\) where

    $$\begin{aligned} P_{1a}&=\dfrac{\bigg (1- \dfrac{ w_2r_1}{w_1r_2}\bigg )}{\bigg (\dfrac{\alpha _2}{K_2}-\dfrac{w_2r_1}{w_1r_2 K_1}\bigg )},\nonumber \\&\quad P_{1a}>0~~ \mathrm{if}~~ w_1r_2>w_2r_1 \,\, \mathrm{and}\,\, \alpha _2w_1r_2K_1>w_2r_1K_2. \end{aligned}$$
    (3.21)

    From Eq. (3.19), when \(P_1 = 0,\) then \(P_2 = P_{2a}\) where

    $$\begin{aligned} P_{2a}=\dfrac{\bigg (1-\dfrac{w_2r_1}{w_1r_2}\bigg )}{\bigg (\dfrac{1}{K_2}-\dfrac{\alpha _1w_2r_1}{K_1w_1r_2 }\bigg )}. \end{aligned}$$

    From the above equation, \(P_{2a}>0\) if

    $$\begin{aligned} w_1r_2>w_2r_1 \,\, \mathrm{and}\,\, K_1w_1r_2>\alpha _1w_2r_1K_2. \end{aligned}$$
    (3.22)

    Also, we have

    $$\begin{aligned} \frac{dP_1}{dP_2}=-\frac{\partial F}{\partial P_2}/\frac{\partial F}{\partial P_1}. \end{aligned}$$

    We noted that \(\frac{dP_1}{dP_2}<0,\) if

    $$\begin{aligned} \begin{aligned}&\mathrm{either}~~(i) \frac{\partial F}{\partial P_1}>0~~\mathrm{and} ~~\frac{\partial F}{\partial P_2}>0,\\&\quad \mathrm{or}~~(ii) \frac{\partial F}{\partial P_1}<0~~\mathrm{and} ~~\frac{\partial F}{\partial P_2}<0, \end{aligned} \end{aligned}$$
    (3.23)

    holds.

    From Eq.(3.20), when \(P_2=0\), then \(G(P_1, 0)=0\) has a root \(P_{1b}\), which is the solution of the following equation

    $$\begin{aligned} \begin{aligned}&\dfrac{\delta r_1}{w_1K_1}P_1^3-\dfrac{\delta r_1}{w_1}\bigg (1-\dfrac{2k}{K_1}\bigg )P_1^2-\bigg \{\dfrac{\delta r_1k}{w_1}\bigg (2-\dfrac{k}{K_1}\bigg )+\\&\quad (m-(\gamma _1-\lambda )w_1)\bigg \}P_1-k\bigg (m+\dfrac{\delta r_1k}{w_1}\bigg )=0. \end{aligned} \end{aligned}$$
    (3.24)

    Hence, \(P_{1b}\) is a unique positive root of Eq.(3.24) if

    $$\begin{aligned} K_1<2k. \end{aligned}$$
    (3.25)

    From Eq.(3.20), when \(P_1=0\), then \(G(0, P_2)=0\) has a root \(P_{2b}\), which is the solution of the following equation

    $$\begin{aligned} \begin{aligned}&\dfrac{\delta r_1\alpha _1}{w_1K_2}P_2^3-\dfrac{\delta r_1}{w_1}\bigg (1-\dfrac{2\alpha _1 k}{K_2}\bigg )P_2^2-\bigg \{\dfrac{\delta r_1k}{w_1}\bigg (2-\dfrac{\alpha _1k}{K_2}\bigg )+\\&\quad (m-\gamma _2w_2)\bigg \}P_2-k\bigg (m+\dfrac{\delta r_1k}{w_1}\bigg )=0. \end{aligned} \end{aligned}$$
    (3.26)

    Hence, \(P_{2b}\) is a unique positive root of Eq.(3.26) if

    $$\begin{aligned} K_2<2\alpha _1k. \end{aligned}$$
    (3.27)

    Also, we have

    $$\begin{aligned} \frac{dP_1}{dP_2}=-\frac{\partial G}{\partial P_2}/\frac{\partial G}{\partial P_1}. \end{aligned}$$

    We noted that \(\frac{dP_1}{dP_2}>0,\) if

    $$\begin{aligned} \begin{aligned}&\mathrm{either}~~\mathrm{(i)}~~ \frac{\partial G}{\partial P_1}>0~~\mathrm{and} ~~\frac{\partial G}{\partial P_2}<0,\\&\quad \mathrm{or}~~\mathrm{(ii)}~~ \frac{\partial G}{\partial P_1}<0~~\mathrm{and} ~~\frac{\partial G}{\partial P_2}>0, \end{aligned} \end{aligned}$$
    (3.28)

    holds.

We noted that the two isoclines given by Eqs. (3.19) and (3.20) intersect at a unique point \((P_1^*, P_2^*)\) if in addition to the conditions given in Eqs. (3.22), (3.23), (3.25) and (3.28), the inequality \(P_{1b}<P_{1a}\) holds.

The local stability of each equilibrium point is now discussed by deriving the variance matrices and using the Routh–Hurwitz criterion. The findings were obtained below:

  1. (i)

    \(E_0(0, 0, 0)\) is a saddle point.

  2. (ii)

    \(E_1(K_1, 0, 0)\) is locally asymptotically stable if \(\dfrac{K_2}{\alpha _2}<K_1<\dfrac{mk}{(\gamma _1-\lambda )w_1-m},\,\, \gamma _1w_1>\lambda w_1+m.\)

  3. (iii)

    \(E_2(0, K_2, 0)\) is locally asymptotically stable if \(\dfrac{K_1}{\alpha _1}<K_2<\dfrac{mk}{\gamma _2w_2-m},\, \gamma _2w_2>m\).

  4. (iv)

    \(E_3(\hat{P}_{1}^{'}, \hat{P}_{2}^{'}, 0)\) is stable or unstable in the positive direction orthogonal to the \(P_1P_2\)-plane, i.e., M-direction depending on whether \(\bigg ( \dfrac{(\gamma _1-\lambda )w_1\hat{P}_{1}^{'}+\gamma _2 w_2\hat{P}_{2}^{'}}{k+\hat{P}_{1}^{'}+\hat{P}_{1}^{'}}-m \bigg )\) is negative or positive, respectively.

  5. (v)

    \(E_4(\bar{P}_{1}, 0, \bar{M})\) is stable or unstable in the positive direction orthogonal to the \(P_1M\)-plane, i.e., \(P_2\)-direction depending on whether \(\bigg (r_2-\dfrac{\alpha _2r_2\bar{P}_{1}}{K_2}-\dfrac{(k+\bar{P}_{1})w_2\bar{M}}{(k+\bar{P}_{1})^2} \bigg )\) is negative or positive, respectively, if \(K_1w_1\bar{M}< r_1(K+\bar{P}_{1})^2.\)

  6. (vi)

    \(E_5 =(0,\tilde{P}_{2},\tilde{M})\) is stable or unstable in the positive direction orthogonal to the \(P_2M\) -plane, i.e., \(P_1\)-direction depending on whether \(\bigg (r_1-\dfrac{\alpha _1r_1\tilde{P}_{2}}{K_1}-\dfrac{(k+\tilde{P}_{2})w_1\tilde{M}}{(k+\tilde{P}_{2})^2}\bigg )\) is negative or positive, respectively, if \(K_2w_2\tilde{M}< r_2(K+\tilde{P}_{2})^2.\)

  7. (vii)

    The variational matrix along \(E_6(P_1^*, P_2^*, M^*)\) is given by

    $$\begin{aligned} \begin{aligned} W&=\begin{pmatrix} a_{11} &{} a_{12} &{} a_{13} \\ a_{21} &{} a_{22}&{} a_{23}\\ a_{31} &{} a_{32} &{} a_{33}\end{pmatrix}\\&= \small { \begin{pmatrix} P_1^*\bigg (-\dfrac{r_1}{K_1}+\dfrac{w_1M^*}{(k+P_1^*+P_2^*)^2}\bigg ) &{} -\dfrac{\alpha _1r_1P_1^*}{K_1}+\dfrac{w_1P_1^*M^*}{(k+P_1^*+P_2^*)^2} &{} \dfrac{-w_1P_1^*}{(k+P_1^*+P_2^*)}\\ \\ -\dfrac{\alpha _2r_2P_2^*}{K_2}+\dfrac{w_2P_2^*M^*}{(k+P_1^*+P_2^*)^2} &{} P_2^*\bigg (-\dfrac{r_2}{K_2}+\dfrac{w_2M^*}{(k+P_1^*+P_2^*)^2}\bigg ) &{} \dfrac{-w_2P_2^*}{(k+P_1^*+P_2^*)} \\ \\ \dfrac{(k+P_2^*)(\gamma _-\lambda )w_1M^*-\gamma _2w_2P_2^*M^*}{(k+P_1^*+P_2^*)^2} &{}~~~~ \dfrac{(k+P_1^*)\gamma _2w_2M^*-(\gamma _1-\lambda )w_1P_1^*M^*}{(k+P_1^*+P_2^*)^2}&{} -\delta M^* \end{pmatrix}}. \end{aligned} \end{aligned}$$

    The characteristic equation for the above matrix W is given by

    $$\begin{aligned} \nu ^3+A_1\nu ^2+A_2\nu +A_3=0, \end{aligned}$$

    where

    $$\begin{aligned} {\text{A}}_{1} & = - \left({\text{a}}_{11} + {\text{a}}_{22} + {\text{a}}_{33}\right), \\{\text{A}}_{2} & = {\text{a}}_{22}{\text{a}}_{33}-{\text{a}}_{23}{\text{a}}_{32}+ {\text{a}}_{11}{\text{a}}_{33} -{\text{a}}_{13}{\text{a}}_{31}+ {\text{a}}_{11}{\text{a}}_{22}-{\text{a}}_{12}{\text{a}}_{21},\\{\text{A}}_{3} & = - {\text{a}}_{11}{\text{a}}_{22}{\text{a}}_{33} + {\text{a}}_{11}{\text{a}}_{23}{\text{a}}_{32}+{\text{a}}_{12}{\text{a}}_{21}{\text{a}}_{33}- {\text{a}}_{12}{\text{a}}_{23}{\text{a}}_{31}- {\text{a}}_{13}{\text{a}}_{21}{\text{a}}_{32} +{\text{a}}_{13}{\text{a}}_{22}{\text{a}}_{31} \\ \end{aligned}$$

Theorem 1

Assume that the \(E_6(P_1^*, P_2^*, M^*)\) is positive equilibrium point of the system (3.1). Therefore, the equilibrium point \(E_6(P_1^*, P_2^*, M^*)\) is locally asymptotically stable when \(A_1>0, A_3>0\) and \(A_1A_2-A_3>0\) are satisfied.

The proof of the theorem follows from the Routh–Hurwitz criterion, hence omitted.

Theorem 2

Let the following inequalities hold in \(\varLambda\)

$$\begin{aligned}&w_1K_1M^*<r_1k(k+P_1^*+P_2^*), \end{aligned}$$
(3.29)
$$\begin{aligned}&w_2K_2M^*<r_2k(k+P_1^*+P_2^*), \end{aligned}$$
(3.30)
$$\begin{aligned}&\bigg (\frac{(c_1w_1+c_2w_2)M^*}{k(k+P_1^*+P_2^*)} -\frac{c_1r_1\alpha _{1}}{K_1}-\frac{c_2r_2\alpha _{2}}{K_2}\bigg )^2<c_1c_2\nonumber \\&\quad \bigg (\frac{r_1}{K_1}-\frac{w_1M^*}{k(k+P_1^*+P_2^*)}\bigg )\bigg (\frac{r_2}{K_2} -\frac{w_2M^*}{k(k+P_1^*+P_2^*)}\bigg ). \end{aligned}$$
(3.31)

Then, the positive equilibrium \(E_6\) is globally asymptotically stable with regard to all solutions within the positive octant.

Proof

We take into account the positive definite function of the positive equilibrium \(E_6(P_1^*,P_2^*,M^*)\) as,

$$\begin{aligned} \begin{aligned}&V(P_1,P_2,M)=c_{1}\bigg (P_1-P_1^*-P_1^*\ln \frac{P_1}{P_1^*}\bigg )+c_{2}\bigg (P_2-P_2^*\\&\quad -P_2^*\ln \frac{P_2}{P_2^*}\bigg )+\bigg (M-M^*-M^*\ln \frac{M}{M^*}\bigg ), \end{aligned} \end{aligned}$$
(3.32)

where \(c_{1}\) and \(c_{2}\) are positive constant to be chosen suitably. Differentiating Eq. (3.32) with respect to time t along the solution of the model system (3.1), after some algebraic manipulations we get

$$\begin{aligned} \begin{aligned} \frac{dV}{dt}=&-\frac{1}{2}m_{11}(P_1-P_1^*)^2+m_{12}(P_1-P_1^*)(P_2-P_2^*)\\&-\frac{1}{2}m_{11}(P_1-P_1^*)^2+m_{13}(P_1-P_1^*)(M-M^*)\\&-\frac{1}{2}m_{22}(P_2-P_2^*)^2+m_{23}(P_2-P_2^*)(M-M^*)\\&-\frac{1}{2}m_{22}(P_2-P_2^*)^2-\frac{1}{2}m_{33}(M-M^*)^2\\&-\frac{1}{2}m_{33}(M-M^*)^2, \end{aligned} \end{aligned}$$
(3.33)

where

$$\begin{aligned} \begin{aligned} m_{11}&= c_1\bigg (\frac{r_1}{K_1}-\frac{w_1M^*}{(k+P_1+P_2)(k+P_1^*+P_2^*)}\bigg ),\\ m_{12}&= \bigg (\frac{(c_1w_1+c_2w_2)M^*}{(k+P_1+P_2)(k+P_1^*+P_2^*)}-\frac{c_1r_1\alpha _{1}}{K_1}-\frac{c_2r_2\alpha _{2}}{K_2}\bigg ),\\ m_{13}&=\bigg (\frac{(\gamma _1-\lambda )w_1(k+P_2^*)-\gamma _2w_2P_2^*}{(k+P_1+P_2)(k+P_1^*+P_2^*)}-\frac{c_{1}w_{1}}{k+P_{1}+P_{2}}\bigg ),\\ m_{22}&=c_2\bigg (\frac{r_2}{K_2}-\frac{w_2M^*}{(k+P_1+P_2)(k+P_1^*+P_2^*)}\bigg ),\\ m_{23}&=\frac{\gamma _2w_2(k+P_1^*)-w_1(\gamma _1-\lambda )P_1^*}{(k+P_1+P_2)(k+P_1^*+P_2^*)}-\frac{c_2w_2k}{(k+P_1+P_2)},\\ m_{33}&=\delta . \end{aligned} \end{aligned}$$

Sufficient condition for \(\frac{dV}{dt}\) to be negative is that the following inequalities hold:

$$\begin{aligned}&m_{11}>0, \end{aligned}$$
(3.34)
$$\begin{aligned}&m_{22}>0, \end{aligned}$$
(3.35)
$$\begin{aligned}&m_{33}>0, \end{aligned}$$
(3.36)
$$\begin{aligned}&m^2_{12}<m_{11}m_{22}, \end{aligned}$$
(3.37)
$$\begin{aligned}&m^2_{13}<m_{11}m_{33}, \end{aligned}$$
(3.38)
$$\begin{aligned}&m^2_{23}<m_{22}m_{33}. \end{aligned}$$
(3.39)

By choosing \(c_{1}=\frac{\left( \gamma _{1}-\lambda \right) w_{1}\left( k+P_2^* \right) -\gamma _{2}w_{2}P_2^* }{w_{1}\left( k+P_1^*+P_2^*\right) }\), we note that \(m_{13}=0\), and condition (3.38) holds automatically. If we choose \(c_{2}=\frac{\gamma _{2}w_{2} \left( k+P_1^*\right) -\left( \gamma _{1}-\lambda \right) w_{1}P_1^*}{w_{2}\left( k+P_1^*+P_2^*\right) }\), the condition (3.39) holds automatically. The condition (3.36) holds automatically. It is easy to see that conditions (3.29) \(\Rightarrow\) (3.34), (3.30) \(\Rightarrow\) (3.35) and (3.31) \(\Rightarrow\) (3.37). \(\square\)

3.2 Stability analysis of spatial model system

In this section, we discuss the stability of interior equilibrium of the diffusive model system. In order to derive the condition of stability, we linearized the model system (2.1) about \(E_6(P_1^*, P_2^*, M^*)\) with small perturbation X(x, t), Y(x, t) and Z(x, t) as \(P_{1}=P_1^*+X(x,t), P_{2}=P_2^*+Y(x,t)\) and \(M=M^*+Z(x,t)\). The linearized form of model system is obtained as:

$$\begin{aligned} \begin{aligned} \frac{\partial X}{\partial t} =a_{11}X+a_{12}Y+a_{13}Z+D_1 \frac{\partial ^2 X}{{\partial x}^2}\\ \frac{\partial Y}{\partial t} =a_{21}X+a_{22}Y+a_{23}Z+D_2 \frac{\partial ^2 Y}{{\partial x}^2}\\ \frac{\partial Z}{\partial t} =a_{31}X+a_{32}Y+a_{33}Z+D_3 \frac{\partial ^2 Z}{{\partial x}^2} \end{aligned} \end{aligned}$$
(3.40)

Let us assume the solution of system (3.40) is given by

$$\begin{aligned} \left( \begin{array}{l} X \\ Y \\ Z \\ \end{array} \right) = \left( \begin{array}{l} l \\ m \\ n \\ \end{array} \right) \exp (\sigma t)\cos (\sqrt{{\mu _i}} x). \end{aligned}$$
(3.41)

The characteristic equation of the linearized system is given by

$$\begin{aligned} {\sigma }^3+\rho _1{\sigma }^2+\rho _2{\sigma }+\rho _3=0, \end{aligned}$$
(3.42)

where

$$\begin{aligned} \begin{aligned} \rho _1&=(D_1+D_2+D_3)\mu _i+A_1,\\ \rho _2&=A_2-((a_{22}+a_{33})D_1+(a_{11}+a_{33})+(a_{11}+a_{22}))\mu _i\\&\quad +(D_1D_2+D_2D_3+D_3D_1)\mu _i^2,\\ \rho _3&=A_3+((a_{22}a_{33}-a_{23}a_{32})D_1+(a_{11}a_{33}-a_{13}a_{31})D_2\\&\quad +(a_{11}a_{22}-a_{12}a_{21})D_3)\mu _i\\&\quad -(a_{33}D_1D_3+a_{22}D_1D_3+a_{11}D_2D_3)\mu _i^2+D_1D_2D_3\mu _i^3. \end{aligned} \end{aligned}$$
(3.43)

Theorem 3

The positive equilibrium point \(E_6(P_1^*, P_2^*, M^*)\) is locally asymptotically stable in the presence of diffusion if and only if:

(i) :

\(\rho _1>0\),

(ii) :

\(\rho _3>0\),

(iii) :

\(\rho _1\rho _2-\rho _3>0\).

From Eq. (3.42) and using the Routh–Hurwitz criterion, the above theorem follows immediately.

Theorem 4

If the positive equilibrium point \(E_6\) of the model system (3.1) is globally asymptotically stable, then corresponding uniform steady state of model system (2.1) remains globally asymptotically stable.

Proof

For stability behavior of the system (2.1), we define a positive definite function \(V_{1}(t)\), given by

$$\begin{aligned} V_1(t)=\int _{0}^{R} V(P_1,P_2,M)dx, \end{aligned}$$
(3.44)

where \(V(P_1,P_2,M)\) is given in Eq. (3.32). Differentiating Eq. (3.44) with respect to time t along the solution of model system (2.1), we obtain

$$\begin{aligned} \small {\frac{dV_1}{dt}=I_1+I_2, } \end{aligned}$$
(3.45)

where

$$\begin{aligned} \begin{aligned} I_1&=\dfrac{dV}{dt}, \\ I_2&=-D_1\int _{0}^{R}\frac{c_{1}P_1^*}{P_1^2} \bigg (\frac{\partial P_1}{\partial x}\bigg )^2dx\\&-D_2\int _{0}^{R}\frac{c_{2}P_2^*}{P_2^2} \bigg (\frac{\partial P_2}{\partial x}\bigg )^2dx\\&-D_3\int _{0}^{R}\frac{M^*}{M^2}\bigg (\frac{\partial M}{\partial x}\bigg )^2dx. \end{aligned} \end{aligned}$$
(3.46)

From Eq. (3.46), we can see that if \(\frac{dV}{dt}<0\), then \(\frac{dV_{1}}{dt} <0\). Thus, the theorem follows. \(\square\)

3.3 Turing instability

In this subsection, we have derived the required conditions for the existence of Turing instability of the spatial phytoplankton–microzooplankton system (2.1). Due to spatial diffusion, the occurrence of Turing instability changes the stable equilibrium to the unstable one. Mathematically, Turing instability requires at least one of the roots of the characteristic (3.42) which has a nonnegative or nonnegative real part or on the other hand, \(Re(\sigma ) >0\) for some \(\mu _i>0\). Irrespective of the sign of \(\rho _1\) and \(\rho _2\), the diffusion-induced instability occurs when \(\rho _3=P(\mu _i)<0.\) Hence, the condition for diffusive instability is given by

$$\begin{aligned} P(\mu _i)=b_0\mu _i^3+b_1\mu _i^2+b_2\mu _i+A_3<0, \end{aligned}$$
(3.47)

where

\(b_0=D_1D_2D_3,\)

\(b_1=-a_{11}D_2D_3-a_{22}D_1D_3-a_{33}D_1D_2,\)

\(b_2=D_1(a_{22}a_{33}-a_{23}a_{32})+D_2(a_{11}a_{33}-a_{13}a_{31})\)

\(+D_3(a_{11}a_{22}-a_{12}a_{21}).\)

P is cubic polynomial in \(\mu _i\). The critical value of \(P(\mu _i)\) occurs at the \(\mu _i=\mu _{icr}\), where

$$\begin{aligned} \mu _{icr}=\frac{-b_1 + \sqrt{ b_1^2-3b_0b_2}}{3b_0}. \end{aligned}$$
(3.48)

For positive value of critical points \(\mu _i=\mu _{icr}\), we require:

$$\begin{aligned} b_1^2-3b_0b_2>0~and~ b_1<0 ~or~ b_2<0. \end{aligned}$$
(3.49)

Now, we have taken the set of parameter values from Lewis et al. [1]. The parameter values given here are fixed unless otherwise stated. These values were taken from parameter ranges found in the literature to give biologically reasonable results.

Fig. 1
figure 1

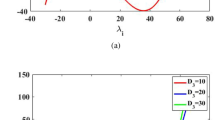
The graph of the function \(P(\mu _i)\) for the set of parameter values given in Eq. (3.50) with \(D_1=D_2=0.0001\), \(D_3=5, 10, 15\)

Full size image

We have chosen the diffusion coefficients on the basis of the values reported in [18, 36,37,38]. Instabilities of the spatially uniform distribution can obtain if the species move with different velocities regardless of which one is faster [37]. If we take the diffusion coefficient of microzooplankton \(D_3\) which is greater than the diffusion coefficients of infochemical-producing phytoplankton \(D_1\) and non-infochemical-producing phytoplankton \(D_2,\) then Turing instability will prevail in ecological sense (c.f. Fig. 1).

$$\begin{aligned} \begin{aligned}&r_1=0.4425,r_2=0.4632, K_1=505,\\&\quad K_2=505, w_1=3.9925,\\&w_2=0.585, \alpha _1=0.001,\alpha _2=0.002, k=30, \gamma _1=0.25,\\&\gamma _2=0.25, m=0.109, \lambda =0.1, \delta =0.001. \end{aligned} \end{aligned}$$
(3.50)

At this set of parameter values as given in Eq. (3.50), the equilibrium point is given by \(E_6( P_1^*, P_2^*, M^*) =(25.6430\), 437.9112, 51.8768). The equilibrium point \(E_6( P_1^*, P_2^*, M^*)\) is stable without diffusion. In the presence of \(D_1=D_2=0.0001, D_3=5\),  \(\rho _3=P(\mu _{i})\) changes its sign with \(\mu _{i}\) as shown in Fig. 1. At above set of parameter values, the critical value is \(\mu _{icr}=13.4515\) and corresponding value of \(P(\mu _{icr})=-0.0278\) (c.f., Fig. 1). In this case, Turing instability is possible.

4 Results

In this section, we have performed numerical simulation of the spatial model system (2.1) for one and two dimensions. We have also described the bifurcation diagram and plot of time vs population density for model system (3.1). To investigate the spatiotemporal dynamics of the model system (2.1), we have taken the set of parameter values as given in Eq. (3.50).

Fig. 2
figure 2

Bifurcation diagram of NIP and microzooplankton for the model system (3.1) with respect to \(w_2\). Rest of the parameters are the same values as in (3.50). Here, the red line represents the upper limit of the oscillation cycle and blue line represents the lower limit of the oscillation cycle

Full size image
Fig. 3
figure 3

Bifurcation diagram of NIP and microzooplankton for the model system (3.1) with respect to \(\delta\). Rest of the parameters are the same values as in (3.50). Here, the red line represents the upper limit of the oscillation cycle and blue line represents the lower limit of the oscillation cycle

Full size image

Figures 2 and 3 depict the bifurcation diagram of model system (3.1), taking \((w_2)\) and \((\delta )\) as bifurcation parameters, respectively. The successive variation of NIP and microzooplankton has been considered in the ranges \(0\le P_2\le 600\) and \(0\le M\le 150,\) respectively, as a function of \((w_2)\) which is in the range \(0.5\le w_2\le 1.3\). All other parameter values are same as in Eq. (3.50). Under the bifurcation analysis of model system (3.1), we observe that the higher value of \(w_2\) is responsible for the limit cycle oscillations and at the lower value of \(w_2\), the dynamics shows the stable behavior, and similarly, we observe that the higher value of \((\delta )\) is responsible for the stable dynamics and at the lower value of \((\delta )\), the dynamics shows the limit cycle oscillations. From Figs. 2(a)-2(b), it can be seen that initially, the model system shows the stable behavior but when we take the value \((w_2)>0.849,\) the system dynamics becomes oscillatory behavior. Thus, it can say that \(w_{2c}=0.849\) is the critical value \((w_2)\) for occurrence of bifurcation. Similarly, in Fig.3 we have observed the effect of \((\delta )\) on the system dynamics through bifurcation diagram. System dynamics of model (3.1) becomes stable to oscillatory behavior after the critical value \(\delta =\delta _{c}=0.00019\). We have observed the effect of \((w_2)\) on the dynamical behavior of the model system (3.1) through Fig. 4. In Fig. 4, the plot (time versus population densities) has been obtained. We observe that the increasing value of the \((w_2)\) system shows stable to oscillatory behavior of model system (c.f., Fig. 4(a)-4(b)). In Figs. 5 and 6, the spatiotemporal patterns reflect the effect of different parameter values at both spatial and temporal scales. Figure 5 depicts the effect of \(w_2\) on spatiotemporal dynamics of model system (2.1) with one-dimensional diffusion. From Fig. 5, we can see that when we increase the values of \(w_2,\) the system goes stable to oscillatory dynamics, whereas in Fig. 6, increasing the values of \(\delta\) the system becomes stable behavior. Figure 7 depicts the effect of diffusion coefficient of microzooplankton \(D_{3}\) and time evolution of model system (2.1) in two-dimensional case. Initially, at \(D_{3}=2.0\) the density of microzooplankton is distributed in the form of patches of spots.

Fig. 4
figure 4

Time series (first column) and phase portrait (second column) of the model system (3.1) at (a) \(w_2=0.585\), (b) 1.09

Full size image
Fig. 5
figure 5

Spatiotemporal pattern of IPP, NIP and microzooplankton of the model system (2.1) at different values of (a) \(w_2= 0.585\), (b) \(w_2= 0.9\), (c) \(w_2= 1.09\), with \(D_{1}=D_{2}=0.0001,~ D_{3}=5.0\)

Full size image
Fig. 6
figure 6

Spatiotemporal pattern of IPP, NIP and microzooplankton of the model system (2.1) at different values of a \(\delta =0.0001\), b \(\delta =0.0005\), c \(\delta =0.001\), with \(w_2=0.585\) and \(D_{1}=D_{2}=0.0001,~ D_{3}=5.0\)

Full size image
Fig. 7
figure 7

Spatial distribution of microzooplankton in \(x-y\) plane of model system (2.1) for \(D_1=D_2=0.0001\) and a \(D_3=2.0,~ \mathbf{b} ~ 3.0,~ \mathbf{c} ~ 4.0\) at t=3000

Full size image
Fig. 8
figure 8

Spatial distribution of microzooplankton in \(x-y\) plane of model system (2.1) for \(D_1=D_2=0.0001\) and \(D_3=1.5\) at a \(t=5000\), b \(t=7000\), c \(t=9000\)

Full size image

Higher density (red) acquires more region in the domain of consideration. But when we increase the value of \(D_{3}=3.0\) from \(D_{3}=2.0\), patches of spots move away from each other. Same scenario can be observed at \(D_{3}=4.0\). The upper bound of microzooplankton decreases with increase in diffusion coefficient of microzooplankton. In Fig. 8, we have described the effect of time evolution on density distribution of microzooplankton. Density distribution of microzooplankton forms of spot-like pattern an upper bound increases with increase in time evolution t.

5 Discussion

The microzooplankton grazing selectivity is investigated through a simple mathematical competition model under the consideration of infochemical. The infochemical produced by phytoplankton has directly influenced the feeding as well as selectivity nature of zooplankton. Additionally, grazing-induced DMS infochemicals for multi-trophic interaction are considered for microzooplankton susceptibility. The competition factor between the phytoplanktons is taken that limited their growth. Here, we have taken one more important factor, i.e., intraspecific competition coefficient of microzooplankton \(\delta,\) which expresses the self-limitation of microzooplankton in the form \(\delta M^2\). All the needful comparison with past studies of the study is summarized below:

  1. (i)

    A three-species plankton model with competition is studied by Lewis et al. [1], but the effect of spatial variability on the population dynamics has been avoided. Assuming spatial variability in the form of diffusion fascinated our study.

  2. (ii)

    Thakur et al. [11] investigated a diffusion-based competing plankton system for Sundarban mangrove system and mainly focused on the role of reduction rate of zooplankton, but infochemical term in phytoplankton has been ignored in the model formulation. Therefore, this term has been taken in the third equation of the system (2.1).

  3. (iii)

    The Turing Instability in the case of without diffusion is well obtained for the appropriate set of parameters (c.f., Fig. 1).

  4. (iv)

    Without diffusion, the role of \(w_2\) and \(\delta\) is explored. The increasing value of \(w_2\) makes a stable system to unstable, whereas the increasing value of \(\delta\) makes an unstable system to stable one.

  5. (v)

    Spatiotemporal patterns are plotted for different values of \(w_{2}\) and δ. A stable to oscillatory temporal pattern is observed for different values of  \(w_{2}\), whereas a stable temporal pattern is observed for different value of δ. A similar kind of temporal pattern is also found by Thakur et al. [10].

  6. (vi)

    Spatial distribution for different diffusion coefficients of \(D_3\) and time intervals are plotted. An irregular patchy pattern is observed for microzooplankton species.

6 Conclusions

In this paper, we have investigated a nonlinear diffusive three species food chain models interacting IPP, NIP and microzooplankton with the effect of grazing-induced DMS infochemicals in multi-tropic interaction. We have implicitly incorporated the parameter \(\lambda\) to understand the sensitivity of predators to infochemicals signals that enhance grazing rates of microzooplankton by copepod. Production of DMS releases the grazing pressure on IPP and allows to reach its densities equivalent to plankton bloom. We first proved the boundedness of the model system which shows that the model system is biologically well behaved. Analytically, we have discussed the stability of non-trivial equilibrium and existence of Turing instability and observed that higher value of diffusion coefficient of microzooplankton leads to occurrence of Turing instability (c.f., Fig. 1). With the help of numerical simulation, we tried to understand the extent to which infochemical influences the tropic interaction and spatiotemporal patterns in heterogeneous marine environment. We have taken weak competition between planktons (i.e., \(\alpha _{1}<\alpha _{2}\)) and infochemicals as grazing attractors (i.e., \(w_{1}>w_{2}\)). Here, we have taken IPP which has lower intrinsic growth rate than the NIP (i.e., \(r_{1}<r_{2}\)) that corresponds to cost of production of infochemicals. Firstly, we have carried out the bifurcation analysis to understand the microzooplankton grazing selectivity and its intraspecific interference (c.f., Figs. 2 and 3). Figure. 2 shows that increasing value of \(w_{2}\) leads to oscillatory dynamics and system may become stable with increasing intraspecific competition (\(\delta\)). Further, we have studied the spatiotemporal pattern to understand the effect of \(w_2\) and \(\delta\). Increasing the value of \(w_2\) and observed stable to oscillatory system dynamics (c.f., Fig. 5) and increasing \(\delta\) and observed stable behavior (c.f., Fig. 6). Finally, patch distribution of microzooplankton is studied with the help of snapshots and observed that increasing diffusion coefficients and time evolution show lowering the patch densities (c.f., Figs. 7 and 8). Our result shows that increasing predation of NIP or grazing refuse of IPP (due to grazing-induced infochemicals cue that attracts predatory copepods) destabilizes the system dynamics. Our study may be useful for better understanding of plankton bloom in the ecology of marine food webs.