Design of event-driven control strategy for spoofing attacks in wireless sensor networks

Abstract

In this study, an event-driven control strategy is developed to counter the spoofing attacks in wireless sensor networks which is considered as a control strategy in stochastic system. We have also devised the corresponding spoofing-proof event-driven transmission mechanism. For this, first, an event-driven state estimator for the underlying stochastic system is designed. Then, using the stochastic stability theory, the event-triggered state estimator gain is derived by means of the stochastic Laypunov function, so that the corresponding state estimation mean square error is compensated. The estimator’s output error is used to suppress the related spoofing attack. The devised event-driven transmission strategy applies some approximate quadratic performance indicators to ensure a measured balance between estimation error, data communication rate and sensor battery life time. Finally, numerical examples are presented to verify the validity of the theoretical results.

1 Introduction

Wireless sensor network (WSN) comprises a collection of sensor nodes employed to monitor and record the status of the physical environment and organize the gathered data at a central location. The research on wireless sensor networks has made a great progress in recent years, where many solutions have been proposed to address various problems arose these architectures. One of the main concerns of wireless multimedia sensor networks (WMSNs) is the huge data size causing the higher energy consumption in transmission. The high energy consumption is a critical problem for lifetime of network includes sensor nodes with limited battery [1]. In [2], presents a deep learning based distributed data mining (DDM) model to achieve energy efficiency and optimal load balancing at the fusion centre of WSN. Peng et al. [3] consider a linear all-transmission scenario where the intermediate clusters act not only as forwarding clusters but also transmitting clusters. Database applications in wireless sensor networks very often demand data collection from sensor nodes of specific target regions. Design and development of spatial query expressions and energy-efficient query processing strategy are important issues for sensor network database systems [4, 5]. In a wireless sensor network (WSN), the usage of resources is usually highly related to the execution of tasks which consume a certain amount of computing and communication bandwidth [6]. Consumed life time monitoring of a structure during operation is a topic of increasing interest [7, 8]. Localization technology is crucial in wireless sensor networks (WSN) by forming the basis of various WSN applications. With the advancements of WSN, WSN attacks for node localization have increasingly become an important security issue [9]. Location based access in wireless sensor networks (WSN) are vulnerable to location spoofing attacks [10]. However, sensor nodes are equipped with limited-capacity batteries due to their small form factor requirements. This necessitates frequent battery replenishments, i.e., maintenance tasks to be performed, which becomes impractical for some cases/deployment areas. As a corollary of this issue, event-driven transmission mechanisms have recently attracted a great deal of attention from both the control and the communication network communities due to reduces the number of transmissions so the overall power consumption of the network, which significantly prolongs the network lifetime [11,12,13].

Meanwhile, a communication channel is shared between the various physical devices in the network. Due to the high openness of these shared networks, there is no security guarantee for the data transmission between the varied sensors, especially in networks where some data is transmitted in plaintext, and the problem is particularly serious. In this environment, the attackers can easily interfere to the information flow in the network and thereby destroy the control system. In recent years, such behaviors have received significant attention by, whereby considerable contribution has been made by the researchers [14]. It should be noted that the attackers with deceptive behavior are the most dangerous as they often inject the wrong data to destroy the control system. For example, in [15], an algorithm has been proposed to protect the system against such erroneous data transmission behavior, and its main research has been supplemented in [16]. The datasets in [17] are produced to evaluate the ability of intrusion detection systems to detect attacks that emulate normal non-periodical messages, at differing attack occurrence rates. In [18], author develop a spoofing process equation (SPE) that can be used to calculate the tracking point of the delay lock loop (DLL) at regular chip intervals for the entire spoofing process. Paper [19] presents a new approach to estimate the true position of an unmanned aerial vehicle (UAV) in the conditions of spoofing attacks on global positioning system (GPS) receivers. It is proposed the position/velocity-fusion-based integration system in Ref. [20], it can detect both MEAC and LOA attacks with high probability using the IMU error compensations. Paper [21] primarily details the step-by-step implementation of a low-cost GPS spoofing and high-level spoofing data collection apparatus to model a simplistic spoofing attack that could be implemented with limited resources. At the same time, when the system is in a spoofed attack condition, the node tend to generate high-frequency transmitting signals, thereby consuming a large amount of power and reducing the node’s life time. To our knowledge, a corresponding security control strategy has not been proposed in the current literature, especially under the event-driven transmission scenarios.

This paper studies the event-driven control strategy to counter spoofing attacks. To devise an event-driven transmission control strategy aiming at detecting the anomalous events caused by spoofing attacks, the state estimator gain triggered by the event is derived by means of a stochastic Laypunov function using stochastic stability theory. Thus, the corresponding state estimation mean square erroris compensated and the corresponding spoofing attack is suppressed using the output error of the estimator. The corresponding event-driven transmission strategy is designed with the aid of approximate secondary performance indicators.

The main contributions of this paper include the following:

• 1. A new scheme is proposed to detect fraudulent node behavior in wireless sensor networks, including spoofing attacks and processes by estimating and measuring the stochastic system state under attack conditions.

• 2. Taking advantages of the stochastic mean square stability theory, the corresponding sufficient conditions are derived for the upper bound of the exponential mean square estimation error as $k \to \infty$, using which the stability of the designed estimator is proved. Additionally, the optimal estimator gain to suppress the corresponding spoofing attack is obtained via the linear estimator inequality.

• 3. An event-driven transmission strategy is proposed using some quadratic approximate system performance indexes. The purpose is to make a measured balance between estimation error, data communication rate and sensor battery life. In order to verify the effectiveness of the estimator-based event-driven attack prevention mechanism, a target tracking application is modeled.

2 Problem statement

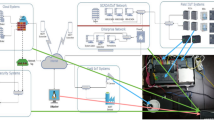
In Fig. 1, the state estimation based on the measurement process by a battery-powered sensor is shown. A remote estimator receives measurements over the wireless channel, and it can observe current sensor measurements as well as current estimates. When an event is triggered, the current sensor measurement is sent to the remote estimator. Since there is a correlation between the spoofing attack measurements and the estimation error, the standard Kalman filter will no longer be applicable. Hence, the event-driven estimation mechanism is applied to reduce the data transmission of the sensor nodes, thereby achieving both energies saving and bandwidth reduction.

Fig. 1

The event-triggered state estimator driving the plan of sensor

Figure 2 shows that the lithium battery powered controller can detect the tracked object and the remote actuator can obtain the control information over the wireless channel.

Fig. 2

Transmission scheme with external attacks

Symbols: $\mathcal{N}$ and $\mathcal{R}$ are collection of natural and real numbers, respectively. $\text{R}_{{}}^{m \times n}$ denotes a real value matrix of $m \times n$, and ${\text{R}}^{n}$ is the abbreviation for ${\text{R}}^{n \times 1}$. $\text{R}_{ + }^{n \times n}$ and $\text{R}_{ + + }^{n \times n}$ is the positive semidefinite matrix and positive definite matrix of $n \times n$. When $X \in \text{R}_{ + }^{n \times n}$, we simply write $X \ge 0$ or $X > 0$. For $X \in \mathcal{R}^{m \times n}$, $X^{\text{T}}$ denotes the transpose of X, $E\left[ \cdot \right]$ denotes the mathematical expectation, and $\left\| \cdot \right\|$ is the Euclidean norm.

The process dynamics and sensor measurement equations are assumed to be as in the following:

$$\begin{aligned} & x_{k + 1} = A_{1} x_{k} + u_{c,k} + D_{1} d_{k} + w_{k} \\ & y_{k} = Cx_{k} + D_{2} d_{k} \\ \end{aligned}$$

(1)

In the equation, $x_{k} \in \text{R}^{n}$ is the system state, $y_{k} \in \text{R}^{m}$ is the system output, $u_{c,k} \in R^{n}$ is the control input, $c$ is the control entity, $k \to \infty$ is time, and $d_{k} \in \mathcal{R}^{n}$ is the spoofing attack input. It is assumed that the random variable $\left\{ {w_{k} } \right\}$ stands for spoofing attack behavior with zero mean and variance of $Q_{w}$. When $x_{k}$ needs to be transmitted to the remote controller, the event-driven algorithm decides whether to send it to the executor. It is assumed that the matrix $A_{1}$, $D_{1}$, $D_{2}$ and $C$ are known. We consider $\gamma_{k}$ as a decision variable: when $\gamma_{k} = 1$, it indicates that $u_{c,k}$ is sent; and when $\gamma_{k} = 0$, it means $u_{c,k}$ is not sent. Therefore, only when $\gamma_{k} = 1$, the actuator will know the true value of $u_{c,k}$. Besides, we assume that the spoofing attack size and at the same time, the energy are both bounded: $\left\| {d_{k} } \right\| \le \bar{d}$, $\sum\nolimits_{k = 0}^{\infty } {d_{k}^{T} d_{k} \le \rho }$.

When the network does not have node protection measures, spoofing attacks may occur. The mathematical model for such attack is considered as follows:

$$u_{a,k} = u_{k} + \varepsilon_{k}$$

(2)

where $u_{k}$ is the event-driven controller, $\varepsilon_{k}$ is unknown but bounded signals that satisfy the $\left\| {\varepsilon_{k} } \right\| \le \varepsilon$, the $\varepsilon > 0$ is known, and can be estimated by security requirements.

In actual applications, the behavior of an attacker is often unpredictable due to the nonlinearity of the physical device construction, bandwidth constraints and signal quantization, and physical constraints and randomness. The effects of such constructs should be added to the attack model. Doing so, the actual $u_{c,k}$ obtained by the actuator is as follows:

$$u_{c,k} = u_{k} + \alpha_{k} \varGamma u_{a,k}$$

(3)

where the matrix $\varGamma$ satisfying $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \le \varGamma \le \bar{\varGamma }$, where $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }$ and $\bar{\varGamma }$ are respectively its upper and lower bounds, which satisfy the following nonlinear relations

$$\left\{ {\begin{array}{*{20}c} {\varGamma u_{a,k} = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } u_{a,k} + \phi_{k} } \\ {\phi_{k}^{T} \left( {\phi_{k} - \tilde{\varGamma }u_{a,k} } \right) \le 0} \\ \end{array} } \right.$$

(4)

where $\tilde{\varGamma } \triangleq \bar{\varGamma } - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } > 0$. In addition, $\alpha_{k}$ is a random variable obeying the Bernoulli distribution, where its probability satisfies

$$\begin{aligned} & {\text{Prob}}\left\{ {\alpha_{k} = 1} \right\} = \alpha \\ & {\text{Prob}}\left\{ {\alpha_{k} = 0} \right\} = \alpha_{1} = 1 - \alpha \\ \end{aligned}$$

(5)

where $\alpha_{k}$ has nothing to do with random variable $\left\{ {w_{k} } \right\}$, $\gamma_{k}$.

Next, the event-driven controller form [7] is given as follow:

$$u_{k} = \left\{ {\begin{array}{*{20}l} {BKx_{k} BKx_{k} } \hfill & {\gamma_{k} = 1} \hfill \\ 0 \hfill & {\gamma_{k} = 0} \hfill \\ \end{array} } \right.$$

(6)

Then the closed-loop system $x_{k}$ satisfies the following

$$\begin{aligned} x_{k + 1} & = A_{1} x_{k} + \gamma_{k} u_{c,k} + D_{1} d_{k} + w_{k} \\ & = A_{1} x_{k} + \gamma_{k} \left( {\left( {1 - \alpha_{k} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } } \right)u_{k} + \alpha_{k} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} + \alpha_{k} \phi_{k} } \right) + D_{1} d_{k} + w_{k} \\ & = \left( {A_{1} + \gamma_{k} \left( {1 - \alpha_{k} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } } \right)BK} \right)x_{k} + \gamma_{k} \left( {\alpha_{k} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} + \alpha_{k} \phi_{k} } \right) + D_{1} d_{k} + w_{k} \\ \end{aligned}$$

(7)

Lemma 1

(Lemma 1 [8]) Define $V\left( {e_{k} } \right)$ as a Lyapunov function. If there exist $\varepsilon_{1} \ge 0$, $\varepsilon_{2} > 0$, $\varepsilon_{3} > 0$ and $0 < \varepsilon_{4} \le 1$, then

$$\varepsilon_{2} \left\| {e_{k} } \right\|^{2} \le V\left( {e_{k} } \right) \le \varepsilon_{3} \left\| {e_{k} } \right\|^{2}$$

(8)

and

$$\text{E} \left\{ {V\left( {e_{k + 1} \left| {e_{k} } \right.} \right)} \right\} - V\left( {e_{k} } \right) \le \varepsilon_{1} - \varepsilon_{4} V\left( {e_{k} } \right)$$

(9)

Then the mean $e_{k}$ square is bounded. As shown in

$$\text{E} \left\{ {\left\| {e_{k} } \right\|^{2} } \right\} \le \frac{{\varepsilon_{3} }}{{\varepsilon_{2} }}\left\| {e_{0} } \right\|^{2} \left( {1 - \varepsilon_{4} } \right)^{k} + \frac{{\varepsilon_{1} }}{{\varepsilon_{2} \varepsilon_{4} }}\sum\limits_{i = 1}^{k} {\left( {1 - \varepsilon_{4} } \right)^{k} }$$

(10)

Next, defining $T \in \text{N}$ as the time domain, and selecting $J$ as a cost function, we get

$$J = \mathop { \limsup }\limits_{T \to \infty } \frac{1}{T}\sum\limits_{k = 0}^{T - 1} \text{E} \left( {b\left( {e_{k} } \right)} \right)$$

(11)

where the $b\left( {e_{k} } \right) = e_{k}^{\text{T}} He_{k} + \theta \gamma_{k}$, the system weight $H > 0$ and the communication weight $\theta > 0$.

The cost given by Formula (11) is called the approximate quadratic performance index [9]. Design in accordance with the secondary form defined by $H$ and through setting the number of $\gamma_{k} = 1$ transmitting times. The main tool used to determine the upper bound is given by the following lemma.

Lemma 2

(Theorem 1 [10]) Suppose there is a Markov sequence that satisfies the state space $X$. Suppose that: $f :\;X \to \text{R}$, $b :\;X \to \text{R}$. Definition:

$$J = \mathop {\text{lim sup}}\limits_{T \to \infty } \frac{1}{T}\sum\limits_{k = 0}^{T - 1} \text{E} \left( {b\left( {x_{k} } \right)} \right)$$

(12)

If there is $c \in \text{R}$ which satisfies

$$m\left( x \right) \ge c\quad x \in X,$$

(13)

then it can be concluded that

$$J \le \mathop { \sup }\limits_{\vartheta \in X} \left( {b\left( \vartheta \right) + \text{E} \left( {m\left( {\left. {x_{k + 1} } \right)\left| {x_{k} = \vartheta } \right.} \right.} \right) - m\left( \vartheta \right)} \right)$$

(14)

It can be seen that the corresponding sufficient conditions can make the system to reach a state of bounded exponential mean square error in $k \to \infty$, which proves the stability of the designed estimator. The event-driven mechanism is applied in the remote state estimation to reduce the data transmission of the sensor nodes and to ensure the performance of the remote state estimation simultaneously, thereby achieving the purpose of both energies saving and bandwidth reduction.

3 Design of event-driven controller

Here, the $\gamma_{k} = 1$ controller gain $K$ is derived by Lemma 1 to make the state $x_{k}$ mean square convergence and suppress the effect of $d_{k}$.

Theorem 1

If $\gamma_{k} = 1$ is given a positive number $\gamma_{1}$, $P > 0$ is assumed to be a symmetric matrix, and the following linear inequality is satisfied

$$\begin{aligned} \varOmega &= \left[ {\begin{array}{*{20}c} { - X} & 0 & 0 & {X^{T} C^{T} D_{2} } \\ * & { - I} & 0 & 0 \\ * & * & { - I} & 0 \\ * & * & * & { - \gamma_{1}^{2} I + D_{2}^{T} D_{2} } \\ * & * & * & * \\ * & * & * & * \\ * & * & * & * \\ \end{array} } \right. \hfill \\ &\left.\quad{\begin{array}{*{20}c} {X^{T} A_{1}^{T} + R^{T} B^{T} S^{T} } & { - R^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} } & {X^{T} C^{T} } \\ {\alpha \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} } & {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} } & 0 \\ I & I & 0 \\ {D_{1}^{T} } & 0 & 0 \\ X & 0 & 0 \\ * & {\alpha_{2}^{ - 1} X} & 0 \\ * & * & { - I} \\ \end{array} } \right] < 0 \hfill \\ \end{aligned}$$

(15)

then, the mean square of the state $x_{k}$ is bounded when $d_{k} = 0$. In addition, when $d_{k} \ne 0$, under the initial condition of 0, the output satisfies: $\left\| {y_{k} } \right\| \le \gamma_{1} \left\| {d_{k} } \right\| + \varepsilon + trace\left( {Q_{w} P} \right)$.

The Controller Gain $K = RX^{ - 1}$.

Proof

To satisfy the condition (8) of Lemma 1, we select the following Lyapunov function

$$V\left( {x_{k} } \right) = x_{k}^{T} Px_{k} ,$$

where $P > 0$ is a symmetric matrix. When $d_{k} = 0$, by substituting formula (7) into the above formula

$$\begin{aligned} \Delta V_{k} & = \text{E} \left\{ {\left( {V_{{_{k + 1} }} \left| {x_{k} , \ldots ,x_{0} } \right.} \right)} \right\} - V_{k} \left( {x_{k} } \right) = x_{k}^{T} \left( {\left( {A_{1} + SBK} \right)^{T} P\left( {A_{1} + SBK} \right) - P} \right)x_{k} \\ & \quad + \alpha^{2} \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} + \alpha^{2} \phi_{k}^{T} P\phi_{k} \\ & \quad + 2\alpha x_{k}^{T} \left( {A_{1} + \left( {1 - \alpha \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } } \right)BK} \right)^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} \\ & \quad + 2\alpha x_{k}^{T} \left( {A_{1} + \left( {1 - \alpha \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } } \right)BK} \right)^{T} P\phi_{k} + \alpha^{2} \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\phi_{k} \\ & \quad + \alpha_{2} K^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } BK + \alpha_{2} \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} + \alpha_{2} \phi_{k}^{T} P\phi_{k} \\ & \quad + 2\alpha_{2} K^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} + 2\alpha_{2} K^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\phi_{k} \\ & \quad + 2\alpha_{2} \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\phi_{k} + trace\left( {Q_{w} P} \right) \\ & \le x_{k}^{T} \left( {\left( {A_{1} + SBK} \right)^{T} P\left( {A_{1} + SBK} \right) - P} \right)x_{k} \\ & \quad + \alpha^{2} \varepsilon_{k}^{T} \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } - I} \right)\varepsilon_{k} + \alpha^{2} \phi_{k}^{T} \left( {P - I} \right)\phi_{k} \\ & \quad + 2\alpha x_{k}^{T} \left( {A_{1} + \left( {1 - \alpha \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } } \right)BK} \right)^{T} P\phi_{k} \\ & \quad + \alpha^{2} \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\phi_{k} \\ & \quad + \alpha_{2} x_{k}^{T} K^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } BKx_{k} + \alpha_{2} \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} \\ & \quad + \alpha_{2} \phi_{k}^{T} P\phi_{k} \\ & \quad + 2\alpha_{2} x_{k}^{T} K^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} + 2\alpha_{2} x_{k}^{T} K^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\phi_{k} \\ & \quad + 2\alpha_{2} \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\phi_{k} \\ & \quad + 2\alpha x_{k}^{T} \left( {A_{1} + \left( {1 - \alpha \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } } \right)BK} \right)^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} - \phi_{k}^{T} \tilde{\varGamma }Kx_{k} \\ & \quad + \phi_{k}^{T} \tilde{\varGamma }\varepsilon_{k} + \varepsilon + trace\left( {Q_{w} P} \right) \\ & = \eta_{k}^{T} \varOmega \eta_{k} + \varepsilon + trace\left( {Q_{w} P} \right) \\ \end{aligned}$$

(16)

where the $S = 1 - \alpha \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }$, the $\eta_{k} = \left[ {\begin{array}{*{20}c} {x_{k}^{T} } & {\varepsilon_{k}^{T} } & {\phi_{k}^{T} } \\ \end{array} } \right]^{T}$ in order to satisfy the condition of Lemma 9, if $\varOmega < 0$, the above formula can be simplified as

$$\begin{aligned} \text{E} \left\{ {\left( {V_{{_{k + 1} }} \left| {x_{k} , \ldots ,x_{0} } \right.} \right)} \right\} - V_{k} \left( {x_{k} } \right) & = \eta_{k}^{T} \varOmega \eta_{k} + \varepsilon + trace\left( {Q_{w} P} \right) \\ & \le - \lambda_{\hbox{min} } \left( { - \varOmega } \right)\eta_{k}^{T} \eta_{k} + \varepsilon + trace\left( {Q_{w} P} \right) \\ & < - \sigma_{11} x_{k}^{T} x_{k} + \varepsilon + trace\left( {Q_{w} P} \right). \\ \end{aligned}$$

(17)

where the $0 < \sigma_{11} < \hbox{min} \left\{ {\lambda_{\hbox{min} } \left( { - \varOmega } \right),\;\lambda_{\hbox{max} } \left( P \right)} \right\}$, $\lambda_{\hbox{min} } \left( \cdot \right)$ and $\lambda_{\hbox{max} } \left( \cdot \right)$ refer to minimum and maximum eigenvalues of the matrix, respectively.

By using Lemma 1 and Inequality (15), the above formula can be summarized as

$$\begin{aligned} \text{E} \left\{ {\left\| {x_{k} } \right\|^{2} } \right\} & \le \frac{{\lambda_{\hbox{max} } \left( P \right)}}{{\lambda_{\hbox{min} } \left( P \right)}}\left\| {x_{0} } \right\|^{2} \left( {1 - \sigma_{11} } \right)^{k} + \frac{{\varepsilon + trace\left( {Q_{w} P} \right)}}{{\lambda_{\hbox{min} } \left( P \right)\sigma_{11} }}\sum\limits_{i = 1}^{k} {\left( {1 - \sigma_{11} } \right)^{k} } \\ & \le \frac{{\lambda_{\hbox{max} } \left( P \right)}}{{\lambda_{\hbox{min} } \left( P \right)}}\left\| {x_{0} } \right\|^{2} \left( {1 - \sigma_{11} } \right)^{k} + \frac{{\varepsilon + trace\left( {Q_{w} P} \right)}}{{\lambda_{\hbox{min} } \left( P \right)\sigma_{11} }}. \\ \end{aligned}$$

(18)

Therefore, it is verified that when $d_{k} = 0$ and $\gamma_{k} = 1$, $x_{k}$ is mean-square bounded.

Next, assuming $d_{k} \ne 0$ we reformulate $\Delta V_{k}$ as

$$\begin{aligned} \Delta V_{k} & \le x_{k}^{T} \left( {\left( {A_{1} + SBK} \right)^{T} P\left( {A_{1} + SBK} \right) - P} \right)x_{k} \\ & \quad + \alpha^{2} \varepsilon_{k}^{T} \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } - I} \right)\varepsilon_{k} + \alpha^{2} \phi_{k}^{T} \left( {P - I} \right)\phi_{k} \\ & \quad + 2\alpha x_{k}^{T} \left( {A_{1} + \left( {1 - \alpha \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } } \right)BK} \right)^{T} P\phi_{k} + \alpha^{2} \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\phi_{k} \\ & \quad + \alpha_{2} x_{k}^{T} K^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } BKx_{k} + \alpha_{2} \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} + \alpha_{2} \phi_{k}^{T} P\phi_{k} \\ & \quad + 2\alpha_{2} x_{k}^{T} K^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} + 2\alpha_{2} x_{k}^{T} K^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\phi_{k} + 2\alpha_{2} \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\phi_{k} \\ & \quad + 2\alpha x_{k}^{T} \left( {A_{1} + \left( {1 - \alpha \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } } \right)BK} \right)^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} - \phi_{k}^{T} \tilde{\varGamma }Kx_{k} + \phi_{k}^{T} \tilde{\varGamma }\varepsilon_{k} \\ & \quad + d_{k}^{T} D_{1}^{T} PD_{1} d_{k} + 2x_{k}^{T} \left( {A_{1} + \left( {1 - \alpha \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } } \right)BK} \right)^{T} PD_{1} d_{k} + trace\left( {Q_{w} P} \right) \\ & \quad + 2\alpha \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} PD_{1} d_{k} + 2\alpha \phi_{k}^{T} PD_{1} d_{k} \\ \end{aligned}$$

(19)

Introducing performance index $H_{\infty }$ to suppress the effect of unknown inputs $d_{k}$, we get

$$J_{1} = \text{E} \left\{ {\sum\limits_{k = 0}^{\infty } {y_{k}^{T} y_{k} } } \right\} - \gamma_{1}^{2} \text{E} \left\{ {\sum\limits_{k = 0}^{\infty } {d_{k}^{T} d_{k} } } \right\}$$

(20)

Under the initial conditions of 0, $J_{1}$ is substituted in $\Delta V_{k}$, as

$$J_{1} \le \text{E} \left\{ {\sum\limits_{k = 0}^{\infty } {\left( {\left( {\begin{array}{*{20}c} {x_{k}^{T} } & {d_{k}^{T} } \\ \end{array} } \right)\varOmega \left( {\begin{array}{*{20}c} {x_{k} } \\ {d_{k} } \\ \end{array} } \right)} \right)} } \right\} + \varepsilon$$

(21)

If $\varOmega < 0$, then the following inequality can be obtained

$$\text{E} \left\{ {\sum\limits_{k = 0}^{\infty } {y_{k}^{T} y_{k} } } \right\} - \gamma_{1}^{2} \text{E} \left\{ {\sum\limits_{k = 0}^{\infty } {d_{k}^{T} d_{k} } } \right\} \le \varepsilon$$

(22)

Therefore, we can conclude the following

$$\left\| {y_{k} } \right\| \le \gamma_{1} \left\| {d_{k} } \right\| + \varepsilon$$

(23)

With Schur complement, we can get the following matrix inequality constraints

$$\varOmega = \left[ {\begin{array}{*{20}c} { - P + C^{T} C} & 0 & 0 & {C^{T} D_{2} } & {A_{1}^{T} + K^{T} B^{T} S^{T} } & { - K^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} } \\ * & { - I} & 0 & 0 & {\alpha \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} } & {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} } \\ * & * & { - I} & 0 & I & I \\ * & * & * & { - \gamma_{1}^{2} I + D_{2}^{T} D_{2} } & {D_{1}^{T} } & 0 \\ * & * & * & * & {P^{ - 1} } & 0 \\ * & * & * & * & * & {\alpha_{2}^{ - 1} P^{ - 1} } \\ \end{array} } \right] < 0$$

(24)

By multiplying both end sides of $diag\left\{ {P^{ - 1} ,I} \right\}$:

$$\begin{aligned} \varOmega = \left[ {\begin{array}{*{20}c} { - P^{ - 1} + \left( {P^{ - 1} } \right)^{T} C^{T} CP^{ - 1} } & 0 & 0 \\ * & { - I} & 0 \\ * & * & { - I} \\ * & * & * \\ * & * & * \\ * & * & * \\ \end{array} } \right. \hfill \\ \left. {\quad \quad \begin{array}{*{20}c} {\left( {P^{ - 1} } \right)^{T} C^{T} D_{2} } & {A_{1}^{T} + \left( {P^{ - 1} } \right)^{T} K^{T} B^{T} S^{T} } & { - \left( {P^{ - 1} } \right)^{T} K^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} } \\ 0 & {\alpha \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} } & {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} } \\ 0 & I & I \\ { - \gamma_{1}^{2} I + D_{2}^{T} D_{2} } & 0 & 0 \\ * & {P^{ - 1} } & 0 \\ * & * & {\alpha_{2}^{ - 1} P^{ - 1} } \\ \end{array} } \right] < 0 \hfill \\ \end{aligned}$$

(25)

Again using Schur to complement

$$\begin{aligned} \varOmega &= \left[ {\begin{array}{*{20}c} { - X} & 0 & 0 & {X^{T} C^{T} D_{2} } \\ * & { - I} & 0 & 0 \\ * & * & { - I} & 0 \\ * & * & * & { - \gamma_{1}^{2} I + D_{2}^{T} D_{2} } \\ * & * & * & * \\ * & * & * & * \\ * & * & * & * \\ \end{array} } \right. \hfill \\ &\left. \quad{ \begin{array}{*{20}c} {X^{T} A_{1}^{T} + R^{T} B^{T} S^{T} } & { - R^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} } & {X^{T} C^{T} } \\ {\alpha \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} } & {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} } & 0 \\ I & I & 0 \\ {D_{1}^{T} } & 0 & 0 \\ X & 0 & 0 \\ * & {\alpha_{2}^{ - 1} X} & 0 \\ * & * & { - I} \\ \end{array} } \right] < 0 \hfill \\ \end{aligned}$$

(26)

where the $X = P^{ - 1}$, the $R = KX$.

The proof is completed.

The method described so far uses the linear matrix inequality to obtain the corresponding estimator gain values, thus achieving high accuracy in suppressing the corresponding spoofing attack.

4 Design of event-driven strategy

In this section, we derive the event-driven transmission strategy by using Lemma 2 to prove the upper bound of the approximate quadratic performance.

Theorem 2

Given $H > 0$ as the system weight, $\theta > 0$ as communication weight. Suppose $M > 0$ is a symmetric matrix. If:

$$\varLambda = \left[ {\begin{array}{*{20}c} { - M + H} & 0 & 0 & 0 & {A_{1}^{T} + K^{T} B^{T} S^{T} M^{T} } & { - K^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} M^{T} } \\ * & { - I} & 0 & 0 & {\alpha \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} M^{T} } & {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} M^{T} } \\ * & * & { - I} & 0 & {M^{T} } & {M^{T} } \\ * & * & * & { - \bar{d}^{2} I} & {D_{1}^{T} M^{T} } & 0 \\ * & * & * & * & { - M} & 0 \\ * & * & * & * & * & { - \alpha_{2}^{ - 1} M} \\ \end{array} } \right] < 0$$

(27)

and meet the following event-driven conditions

$$\gamma_{k} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {if\;\vartheta^{\text{T}} \left( {A_{1}^{T} MA_{1} - \varPsi^{\text{T}} M\varPsi } \right)\vartheta \le \tilde{\theta } + trace\left( {MQ_{w} } \right)} \hfill \\ 1 \hfill & {otherwise} \hfill \\ \end{array} } \right.$$

(28)

where the $\varPsi = A_{1} + SBK$, the $\tilde{\theta } = \varepsilon + \bar{d} + \theta$, then the approximate quadratic performance function satisfies

$$J \le \mathop {\sup }\limits_{{\vartheta \in \mathcal{R}^{n} }} g\left( \vartheta \right) \le trace\left( {MQ_{w} } \right) + \tilde{\theta }$$

(29)

Proof

Choose a function $m\left( {x_{k} } \right) = x_{k}^{T} Mx_{k}$. It is easy to see that there is an upper bound, $m\left( {x_{k + 1} } \right)$ can be calculated by (7)

$$x_{k + 1} = \left\{ {\begin{array}{*{20}l} {A_{1} x_{k} + w_{k} } \hfill & {\gamma_{k} = 0,} \hfill \\ {\left( {A_{1} + SBK} \right)x_{k} - \left( {\alpha_{k} - \alpha } \right)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } BKx_{k} } \hfill & {} \hfill \\ {\quad + \alpha \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} + \alpha \phi_{k} + \left( {\alpha_{k} - \alpha } \right)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} } \hfill & {} \hfill \\ {\quad + \left( {\alpha_{k} - \alpha } \right)\phi_{k} + D_{1} d_{k} + w_{k} } \hfill & {\gamma_{k} = 1.} \hfill \\ \end{array} } \right.$$

(30)

Then the following formula can be obtained as

$$\begin{aligned} & \text{E} \left( {m\left( {x_{k + 1} } \right)\left| {x_{k} = \vartheta } \right.} \right) \\ & \quad = \left\{ {\begin{array}{*{20}l} {\vartheta^{\text{T}} A_{1}^{T} MA_{1} \vartheta + trace\left( {MQ_{w} } \right)} \hfill & {\gamma_{k} = 0,} \hfill \\ {\vartheta_{k}^{T} \left( {\left( {A_{1} + SBK} \right)^{T} M\left( {A_{1} + SBK} \right)} \right)\vartheta_{k} } \hfill & {} \hfill \\ { +\, \alpha^{2} \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} + \alpha^{2} \phi_{k}^{T} P\phi_{k} + 2\alpha x_{k}^{T} \left( {A_{1} + \left( {1 - \alpha \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } } \right)BK} \right)^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} } \hfill & {} \hfill \\ { +\, 2\alpha x_{k}^{T} \left( {A_{1} + \left( {1 - \alpha \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } } \right)BK} \right)^{T} P\phi_{k} + \alpha^{2} \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\phi_{k} } \hfill & {} \hfill \\ { +\, \alpha_{2} K^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } BK + \alpha_{2} \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} + \alpha_{2} \phi_{k}^{T} P\phi_{k} } \hfill & {} \hfill \\ { +\, 2\alpha_{2} K^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} + 2\alpha_{2} K^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\phi_{k} } \hfill & {} \hfill \\ { +\, 2\alpha_{2} \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\phi_{k} + trace\left( {MQ_{w} } \right)} \hfill & {} \hfill \\ {} \hfill & {\gamma_{k} = 1.} \hfill \\ \end{array} } \right. \\ \end{aligned}$$

(31)

Define the function $g$:

$$g\left( \vartheta \right) = b\left( \vartheta \right) + \mathcal{E}\left( {m\left( {x_{k + 1} } \right)\left| {x_{k} = \vartheta } \right.} \right) - m\left( \vartheta \right)$$

(32)

Substituting the above formula, we get:

$$g\left( \vartheta \right) = \left\{ {\begin{array}{*{20}l} {\vartheta^{\text{T}} A_{1}^{T} MA_{1} \vartheta + trace\left( {MQ_{w} } \right) - \vartheta^{\text{T}} M\vartheta + \vartheta^{\text{T}} H\vartheta } \hfill & {\gamma_{k} = 0 ,} \hfill \\ {\vartheta_{k}^{T} \left( {\left( {A_{1} + SBK} \right)^{T} M\left( {A_{1} + SBK} \right) - M + H} \right)\vartheta_{k} } \hfill & {} \hfill \\ {\quad +\, \alpha^{2} \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} + \alpha^{2} \phi_{k}^{T} P\phi_{k} + 2\alpha x_{k}^{T} \left( {A_{1} + \left( {1 - \alpha \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } } \right)BK} \right)^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} } \hfill & {} \hfill \\ {\quad +\, 2\alpha x_{k}^{T} \left( {A_{1} + \left( {1 - \alpha \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } } \right)BK} \right)^{T} P\phi_{k} + \alpha^{2} \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\phi_{k} } \hfill & {} \hfill \\ {\quad +\, \alpha_{2} K^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } BK + \alpha_{2} \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} + \alpha_{2} \phi_{k}^{T} P\phi_{k} } \hfill & {} \hfill \\ {\quad +\, 2\alpha_{2} K^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } \varepsilon_{k} + 2\alpha_{2} K^{T} B^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\phi_{k} } \hfill & {} \hfill \\ {\quad +\, 2\alpha_{2} \varepsilon_{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma }^{T} P\phi_{k} + trace\left( {MQ_{w} } \right) + \theta } \hfill & {} \hfill \\ {} \hfill & {\gamma_{k} = 1.} \hfill \\ \end{array} } \right.$$

(33)

In order to derive Lemma 2, we need to calculate the upper bound. First, when $\gamma_{k} = 1$, we get

$$g(\vartheta ) \le \tilde{\vartheta }^{T} \varLambda \tilde{\vartheta } + trace(MQ_{w} ) + \varepsilon + \theta + \bar{d}$$

(34)

where the $\tilde{\vartheta }_{k} = \left[ {\begin{array}{*{20}c} {\vartheta_{k}^{T} } & {\varepsilon_{k}^{T} } & {\phi_{k}^{T} } & {d_{k}^{T} } \\ \end{array} } \right]^{T}$. Considering $\varLambda < 0$, we get

$$g\left( \vartheta \right) \le trace\left( {MQ_{w} } \right) + \varepsilon + \theta + \bar{d}$$

(35)

Next, when $\gamma_{k} = 0$, $g\left( \vartheta \right)$ is rewritten as follows

$$g\left( \vartheta \right) - trace\left( {MQ_{w} } \right) = \vartheta^{\text{T}} \left( {A_{1}^{T} MA_{1} - M + H} \right)\vartheta$$

(36)

Since $\gamma_{k} = 0$, the event-driven mechanism becomes

$$\vartheta^{\text{T}} \left( {A_{1}^{T} MA_{1} - \varPsi^{\text{T}} M\varPsi } \right)\vartheta \le \theta + trace\left( {MQ_{w} } \right) + \varepsilon + \bar{d}$$

(37)

where by $\varPsi = A_{1} + SBK$ we can infer

$$g\left( \vartheta \right) - trace\left( {MQ_{w} } \right) = \vartheta^{\text{T}} \left( {A_{1}^{T} MA_{1} - M + H} \right)\vartheta < \theta + \bar{d} + \varepsilon$$

(38)

If the assumption (16) can be established, the following conclusions can be drawn

$$J \le \mathop {\sup }\limits_{{\vartheta \in \mathcal{R}^{n} }} g\left( \vartheta \right) \le trace\left( {MQ_{w} } \right) + \tilde{\theta }$$

(39)

where the $\tilde{\theta } = \varepsilon + \bar{d} + \theta$.

The proof is completed.□

This section proposes a corresponding event-driven transmission strategy based on quadratic approximate system performance indicators. The event-driven transmission strategy is obtained by balancing the remote estimation error and the energy consumption of the sensors. This is performed by deriving an upper bound for a class of performance indicators, which provides a good balance between estimation error, data communication rate, and sensor battery life.

5 Simulation

System (1) has the following parametric form:

$$A_{1} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - 2} & { - 3} \\ \end{array} } \right],\quad B = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right],\quad D_{1} = D_{2} = \left[ {\begin{array}{*{20}c} {0.115} \\ {0.12} \\ \end{array} } \right],\quad C = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right]$$

This example has been discussed in [11, 12]. In addition, suppose the $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varGamma } = 0.2$, the $\bar{\varGamma } = 1.2$, the $\bar{d} = \rho = \varepsilon = 0.15$, the $\gamma_{1} = 0.7$, the variance $Q_{w} = \left[ {\begin{array}{*{20}c} {0.12} & 0 \\ 0 & {0.17} \\ \end{array} } \right]$ for spoofing attack $w_{k}$, and spoofing attack $d_{k} = 0.013e^{ - 0.5k}$.

Solving the corresponding LMI in Theorems 1 and 2 through the LMI toolbox of MATLAB:

$$P = \left[ {\begin{array}{*{20}c} {1.0128} & 0 \\ 0 & {2.9180} \\ \end{array} } \right],\quad K = \left[ {\begin{array}{*{20}c} { 2. 0 0 0 0} & { 2. 9 5 5 4} \\ \end{array} } \right]$$

Furthermore, the error weighted value, the transmission weighted value and the event-driven gain are calculated by Theorem 2, where we get

$$H = \left[ {\begin{array}{*{20}c} 3 & 2 \\ 2 & 1 \\ \end{array} } \right],\quad \theta = 11,\quad M \approx \left[ {\begin{array}{*{20}c} {0.8761} & 0 \\ 0 & {0.834} \\ \end{array} } \right].$$

In order to simplify the simulation complexity, the average approximate quadratic performance index is given in this paper:

$$J_{avg} = \frac{1}{T}\sum\limits_{k = 0}^{T - 1} {\left( {\left( {x_{k} - \hat{x}_{k} } \right)^{T} H\left( {x_{k} - \hat{x}_{k} } \right) + \lambda \gamma_{k} } \right)}$$

The system simulations are implemented in MATLAB environment. Each scenario is repeated 50 times starting in the initial zero state and performs a periodical control according to the standard procedures. Figures 3 and 4 show the periodic state, event-driven transmission and spoofing attacks. It can be seen from these figures that the difference between the event-driven transmission mechanism under the spoofing attack, and the periodic transmission under the ordinary event-driven strategy is small, that is, the system performance is not greatly affected by the attack.

Fig. 3

The evolution of the state × 1

Fig. 4

The evolution of the state × 2

The corresponding event-driven transmission mode is plotted in Fig. 5, reflecting the actual transmission of data throughout the process. During the entire process, the sensor node sends 28 rounds of data, which is reduced to 22 rounds by the event-driven mechanism. That is to say, the resource usage is reduced by about 35% relative to the periodic transmission mechanism.

Fig. 5

Event-triggered transmission mode

Under this performance indicator, by changing the transmission weight value $\lambda$, the upper performance limit of the estimator is shown in Fig. 6. Figure 7 shows the results of comparison with the standard Kalman estimator. It can be seen that the performance of the standard Kalman filter is similar to the estimator we designed, which further proves that the transmission strategy of this paper can well balance the estimated performance and communication rate compared to periodic transmission.

Fig. 6

The limit of the $J_{\text{avg}}$

Fig. 7

Compared with the $J_{\text{avg}}$ of Kalman filter

6 Conclusion

In this paper, an event-driven state estimator for a stochastic wireless sensor system under spoofing attacks is designed. Since the spoofing attack affects the state at time $k + 1$ in the state model, a spoofing attack is defined as a process spoofing attack at time $k$ and a measurement spoofing attack at time $k + 1$. First of all, the quadratic Lyapunov function is chosen, and using the results of the stochastic Lyapunov stability theory, the homotopic boundedness of the error dynamics equation is derived. Second, considering the case where the spoofing attack is not zero, and using the classic $H_{\infty }$ performance indicator, the impact of spoofing attacks is suppressed. Furthermore, the corresponding estimator gain is derived by means of linear matrix inequalities, thereby ensuring the stability of the mean square error when there are no spoofing attacks; while in the case of deceitful attacks, the performance indicators based on the mean square output error are used to resist the impact of spoofing attacks. Subsequently, an event-driven sensor transmission mechanism is derived to determine when to transmit the data by a sensor.