1 Introduction

With the rapid development of weapons and ammunition, a variety of concrete structures and protective facilities are facing more and more serious threat of projectile impact, such as the concrete protective walls of nuclear power plant and concrete shelters of protective engineering [1, 2]. As concrete is easy to crack or fracture under projectile impact, it has been a critical issue to improve the strength, ductility and toughness of concrete under impact loading [3], in which steel-tube-confined concrete (STCC) is one of the effective ways [4, 5]. STCC targets show excellent penetration resistance in comparisons with unconfined concrete targets. The penetration tests performed by Wan et al. [4] revealed that steel tube could restrict the radial displacement of the in-filled concrete and development of radial cracks, and the concrete damage was restrained within the steel tube of STCC targets when impacted by projectiles; the depth of penetration (DOP) of STCC targets can be reduced by 10–20% than that of semi-infinite targets. Therefore, proposing an appropriate DOP model for STCC targets is of significant importance to conveniently and efficiently expand the application of STCC to protective structures.

DOP models based on spherical or cylindrical cavity-expansion approximation model have been extensively used [6, 7]. The spherical cavity-expansion (SCE) approximation model is shown to be suitable to deep penetration problems of semi-infinite targets impacted by ogival nose rigid projectiles [8, 9], while the cylindrical cavity-expansion (CCE) approximation model is more applicable to perforation problems with ductile hole-growth and deep penetration problems of semi-infinite targets impacted by rigid conical or other sharp-nosed projectiles or [10,11,12]. The CCE approximation model has been employed to solve the penetration problems of dry porous rock [13, 14], soil [15] and concrete [16,17,18] targets. Mastilovic and Krajcinovic [19] proposed CCE approximation model for semi-infinite targets on the assumption that the target is divided into elastic, process (damaged), crushed (comminuted) and cavity zones, and material in crushed (comminuted) zone yields according to the Mohr–Coulomb criterion. Forrestal and Tzou [20] also used the Mohr–Coulomb criterion to capture the mechanical performance of concrete in the comminuted zone.

Macek and Duffey [21] regarded the targets as incompressible materials, and proposed a finite SCE approximation model for the analysis of rigid ogival-nose projectiles obliquely penetrating into geological medium to consider the effect of free surface at the initial stage. On the basis of incompressible Mohr–Coulomb material and the SCE approximation model for semi-infinite targets proposed by Forrestal and Tzou [20], Warren et al. [22, 23] proposed a dynamic finite spherical cavity-expansion (FSCE) approximation model for the targets obliquely impacted by projectiles. With targets treated as incompressible Mohr–Coulomb material, Fang et al. [24] constructed a decay function to include the free-surface effect for geological targets by assuming that plastic-cracked-elastic response region exists during the cavity-expansion process. Chen et al. [25] proposed a fast algorithm to predict penetration trajectory in simulation of a rigid steel projectile obliquely penetrating into a limestone target and the effect of cratering and free surface, and separation-reattachment phenomenon were involved. However, the models mentioned above do not include the influence of lateral free boundary and also do not account for the confinement effect of restraints imposed on the target material. Zhen et al. [26] established a finite cylindrical cavity-expansion (FCCE) approximation model for perfect elastic–plastic compressible and incompressible materials with the inclusion of the influence of the lateral free boundary. On the basis of assumptions of incompressible material and the Modified-Griffith criterion [27, 28], which shows the same form with the Hoek–Brown criterion [29, 30], Meng et al. [31] proposed a dynamic FSCE approximation model and DOP model for confined concrete targets normally impacted by rigid projectile. The results showed that under high confinement, the empirical constant m in the Modified-Griffith criterion was recommended to be above 15 on the basis of triaxial experiments. However, in the practical application to calculation of DOP for armor piercing projectile (APP) with conical core normally penetrating into STCC targets in Ref. [4], the calculated results with m ranged between 6 and 8 agree well with the test results, i.e., the value of m in Ref. [31] is lower than the recommended values. The reason is that under conditions that there is no coarse aggregate within concrete of the targets in Ref. [4] and the penetration resistance is overestimated by the FSCE approximation model. Moreover, the geometric shape of an STCC target with finite lateral dimensions and tunneling cavity response is approximately cylindrical when the STCC target is normally penetrated by rigid conical or other sharp-nosed projectiles, which is close to the basic assumptions of the FCCE models.

On the basis of the above backgrounds and problems, a dynamic FCCE approximation model is proposed to analyze the stress distribution during the penetration process and predict the DOP of STCC targets normally impacted by rigid conical or other sharp-nosed projectiles. Firstly, a dynamic FCCE approximation model is established for STCC targets with the Hoek–Brown criterion and incompressible material, and the equations of stresses and displacements in STCC targets are also proposed. Moreover, formula of the DOP for STCC targets based on the dynamic FCCE approximation model is developed. Lastly, the relevant penetration tests of STCC targets are employed to validate the proposed DOP model.

2 Dynamic FCCE model for STCC targets

2.1 Simplification of penetration problems

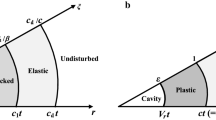
The penetration process of projectiles into STCC targets includes the cratering and tunneling stages [4], as shown in Fig. 1a. Generally, the DOP in the cratering stage (H1) is based on empirical formula according to experimental results, while the DOP in the tunneling stage (H2) is usually calculated by analytical models based on cavity-expansion approximation models. Like the results of cavity-expansion approximation model for semi-infinite targets [8,9,10,11,12], FCCE approximation model is expected to be more applicable to analyze the penetration problem of STCC targets normally penetrated by rigid conical or other sharp-nosed projectiles.

Fig. 1
figure 1

Schematic diagram for FCCE models

Full size image

For FCCE approximation model, the STCC targets can be idealized as infinitely thin layers normal to the impacting direction and particles of the target material move in a radial direction during the penetration process shown in Fig. 1a. Therefore, the penetration analysis can be simplified to one dimensional problem, as shown in Fig. 1b.

Like the dynamic FSCE approximation model for confined concrete targets proposed by Meng et al. [31], some assumptions are further employed to establish the dynamic FCCE approximation model for STCC targets.

(1) Target concrete is a fully incompressible material with Poisson’s ratio υ = 0.5. By ignoring the compressibility and strain-softening of concrete, the cavity-expansion pressure would be overestimated; and if shear dilatancy, strain-rate, strain-hardening of concrete are not included, the cavity-expansion pressure would be underestimated. Therefore, under low and medium penetration velocity, the above effects of concrete material generally offset each other, which indicates the incompressible material assumption of target concrete is reasonable [31,32,33]. Additionally, incompressible material assumption excludes the effect of stress wave and thus greatly simplifies the problem with possible analytical solutions.

(2) Confinement effect of steel tube to concrete is equivalent to a series of linear radial springs with stiffness (K) shown in Fig. 1b. As for the circular STCC targets, the equivalent confining stiffness (K) is shown in Eq. (1) [4].

$$ K = \frac{{E_{s} \delta }}{{r_{0}^{2} }} $$
(1)

where Es, δ and \( r_{0} \) are the elastic modulus, thickness and internal radius of steel tube, respectively.

(3) Finite cavity-expansion is assumed as a concentric cylindrical cavity expanding at a constant velocity \( \dot{r}_{c} \) from initial radius zero to the radius of r0. Under low and medium penetration velocity, elastic, cracked and comminuted regions generally appear in the STCC targets [31]. A typical finite cavity-expansion process includes three phases, i.e., “elastic-cracked-comminuted”, “cracked- comminuted” and “completely comminuted” phases, as shown in Fig. 2. In Fig. 2, rc, rcr and rp are the cavity radius, radius of the interface between the elastic and cracked zones and radius of the interface between the cracked and comminuted zones, respectively.

Fig. 2
figure 2

Schematic diagram of a typical cavity-expansion process

Full size image

For “elastic-cracked-comminuted” phase shown in Fig. 2a, the elastic zone is surrounded by the radius r0 of core concrete as the outer boundary. When the cracked zone expands to the outer boundary of core concrete (rcr= r0), the elastic zone disappears; and the first phase comes to end (rc= rc1, rc1 is a critical cavity radius).

For “cracked-comminuted” phase shown in Fig. 2b, the cracked zone takes the radius r0 of core concrete as the outer boundary, i.e., rcr≡ r0; when the comminuted zone reaches the outer boundary of the core concrete, the cracked zone disappears, then the second phase ends (rp= r0, rc= rc2, rc2 is another critical cavity radius and larger than rc1).

For “completely comminuted” phase shown in Fig. 2c, the external radius of the comminuted zone is r0, i.e., rp≡ r0; and the third phase ends when the elastic constraint fails.

Moreover, in cracked zone, the radial stress of the incompressible target concrete is continuous with the circumferential stress σθ= 0, and the radial stress gets to equal the uniaxial compressive strength (σu) at the interface between the comminuted and cracked zones. In elastic zone, the circumferential stress is equal to the uniaxial tensile strength (σt) at the elastic-cracked interface.

(4) As strength performance of confined concrete is similar to that of the surrounding rock, the nonlinear Hoek–Brown criterion is used to describe the confined concrete in comminuted region under triaxial compression [31]. The equation of the Hoek–Brown criterion is Eq. (2) for intact rock [29, 30].

$$ \frac{{\sigma_{1} }}{{\sigma_{u} }} = \frac{{\sigma_{3} }}{{\sigma_{u} }} + \sqrt {m\frac{{\sigma_{3} }}{{\sigma_{u} }} + 1} $$
(2)

where σu, σ1 and σ3 are the uniaxial compressive strength, first and third principal stresses respectively, measured positive in compression; and m is an empirical constant.

For cylindrical coordinate system, equilibrium equation of axial stress (σz) is shown in Eq. (3) and further simplified according to assumption (1) (υ = 0.5).

$$ \sigma_{z} =\upupsilon\left( {\sigma_{r} + \sigma_{\theta } } \right) = \frac{1}{2}\left( {\sigma_{r} + \sigma_{\theta } } \right),\;\quad \sigma_{r} > \sigma_{\theta } $$
(3)

where σz, σr and σθ are the axial, radial and circumferential stresses, respectively, and taken positive in compression.

Generally, the three principal stresses in cylindrical coordinate system meet relationship of Eq. (4).

$$ \sigma_{1} = \sigma_{r} ,\sigma_{2} = \sigma_{z} ,\sigma_{3} = \sigma_{\theta } $$
(4)

Transforming Eq. (2) into the function of σr can give Eq. (5).

$$ \frac{{\sigma_{\theta } }}{{\sigma_{u} }} = \frac{{\sigma_{r} }}{{\sigma_{u} }} + \frac{m}{2} - \sqrt {m\frac{{\sigma_{r} }}{{\sigma_{u} }} + n} $$
(5)

where n = m2/4 + 1.

2.2 Basic equations

For solutions of FCCE approximation model, as the density of concrete keeps constant according to assumption (1), the equations of momentum and mass conservation and the relations between particle velocity and displacement in the cylindrical coordinates are as follows [12].

$$ \frac{{\partial \sigma_{r} }}{\partial r} + \frac{{\sigma_{r} - \sigma_{\theta } }}{r} = - \rho \left( {\frac{\partial v}{\partial t} + v\frac{\partial v}{\partial r}} \right) $$
(6)
$$ \frac{{\partial \left( {r - u} \right)^{2} }}{\partial r} = 2r $$
(7)

where u and v are displacement and velocity of particle, respectively, with outward motion considered positive; ρ is the density of material.

The particle velocity can be obtained by time derivative of the particle displacement.

$$ v = \frac{\partial u}{\partial t} + v\frac{\partial u}{\partial r} $$
(8)

At cavity wall (r = rc), the particle displacement (u) is equal to the cavity radius (r = rc), and integral of Eq. (7) would get

$$ \left( {r - u} \right)^{2} = r^{2} - r_{c}^{2} $$
(9)

Derivation of time from Eq. (9) gets

$$ v = \frac{{r_{c} }}{r}\dot{r}_{c} $$
(10)

At the interface between concrete and steel tube (\( r = r_{0} \)), the boundary conditions can be expressed as

$$ \sigma_{r} \left( {r = r_{0} } \right) = Ku_{0} ,\quad u_{0} = u\left( {r = r_{0} } \right) = r_{0} - \sqrt {r_{0}^{2} - r_{c}^{2} } $$
(11)

According to assumption (3) about the elastic-cracked and cracked-comminuted interfaces, the stresses at the interfaces are

$$ \sigma_{\theta } \left( {r = r_{cr}^{ + } } \right) = - \left| {\sigma_{t} } \right| $$
(12)
$$ \sigma_{r} \left( {r = r_{p}^{ - } } \right) = \sigma_{u} $$
(13)

On the basis of assumption (3) with a constant cavity-expansion velocity (\( \dot{r}_{c} \)), integrating Eq. (10) with Eq. (6) obtains

$$ \frac{{d\sigma_{r} }}{dr} + \frac{{\sigma_{r} - \sigma_{\theta } }}{r} = - \rho \dot{r}_{c}^{2} \left( {\frac{1}{r} - \frac{{2r_{c}^{2} }}{{r^{3} }}} \right) $$
(14)

Furthermore, when compressibility of concrete is ignored according to assumption (1), the continuous conditions at interface are obtained as follows [19].

$$ u_{2} = u_{1} ,\;v_{2} = v_{1} ,\;\sigma_{r2} = \sigma_{r1} $$
(15)

Where figure subscripts (1 and 2) represent the front and rear of the interfaces, respectively.

2.3 Solutions of dynamic responses of concrete

2.3.1 Elastic-cracked-comminuted phase (r c< r c1)

In the elastic region (rcr≤ r≤r0, rc≪ r), relationships between strain and displacement can be described with Eq. (16) under the conditions of small deformation.

$$ \varepsilon_{r} = - \frac{\partial u}{\partial r},\quad \varepsilon_{\theta } = - \frac{u}{r} $$
(16)

Derivative of r for Eq. (9) and in combination with Eq. (16) could gain the relationship between strain and displacement.

$$ \varepsilon_{r} - \varepsilon_{\theta } = - \left( {\frac{\partial u}{\partial r} - \frac{u}{r}} \right) = \left( {\frac{{r_{c} }}{r}} \right)^{2} \left( {1 - \frac{{r_{c}^{2} }}{{r^{2} }}} \right)^{{ - \frac{1}{2}}} $$
(17)

Using the Hooke law with assumption (1) (υ = 0.5) and ignoring the high-order terms of Eq. (17) get

$$ \sigma_{r} - \sigma_{\theta } = \frac{2E}{3}\left( {\frac{{r_{c} }}{r}} \right)^{2} $$
(18)

At the elastic-cracked interface (r = rcr), substituting Eq. (12) into Eq. (18) gets

$$ \sigma_{r} = \frac{2E}{3}\frac{{r_{c}^{2} }}{{r_{cr}^{2} }} - \left| {\sigma_{t} } \right| $$
(19)

Combining Eq. (14) with Eq. (18) can obtain

$$ \frac{{d\sigma_{r} }}{dr} = - \frac{2E}{3}\frac{{r_{c}^{2} }}{{r^{3} }} - \rho \dot{r}_{c}^{2} \left( {\frac{1}{r} - \frac{{2r_{c}^{2} }}{{r^{3} }}} \right) $$
(20)

Integral of Eq. (20) with the boundary conditions of Eq. (11) gains the radial stress (σr).

$$ \sigma_{r} = \frac{E}{3}\left( {\frac{{r_{c}^{2} }}{{r^{2} }} - \frac{{r_{c}^{2} }}{{r_{0}^{2} }}} \right) - \rho \dot{r}_{c}^{2} \left( {{ \ln }\frac{r}{{r_{0} }} + \frac{{r_{c}^{2} }}{{r^{2} }} - \frac{{r_{c}^{2} }}{{r_{0}^{2} }}} \right) + Kr_{0} \left[ {1 - \left( {1 - \frac{{r_{c}^{2} }}{{r_{0}^{2} }}} \right)^{{\frac{1}{2}}} } \right] $$
(21)

The circumferential stress (σθ) in elastic region is gotten by combining Eq. (21) and Eq. (18).

$$ \sigma_{\theta } = - \frac{E}{3}\left( {\frac{{r_{c}^{2} }}{{r^{2} }} + \frac{{r_{c}^{2} }}{{r_{0}^{2} }}} \right) - \rho \dot{r}_{c}^{2} \left( {{ \ln }\frac{r}{{r_{0} }} + \frac{{r_{c}^{2} }}{{r^{2} }} - \frac{{r_{c}^{2} }}{{r_{0}^{2} }}} \right) + Kr_{0} \left[ {1 - \left( {1 - \frac{{r_{c}^{2} }}{{r_{0}^{2} }}} \right)^{{\frac{1}{2}}} } \right] $$
(22)

Combining Eq. (21) with Eq. (19) can gain the equation of interface radius (rcr).

$$ \frac{E}{{3\sigma_{u} }}\left( {\frac{{r_{c}^{2} }}{{r_{cr}^{2} }} + \frac{{r_{c}^{2} }}{{r_{0}^{2} }}} \right) - \frac{{\left| {\sigma_{t} } \right|}}{{\sigma_{u} }} = \frac{{Kr_{0} }}{{\sigma_{u} }}\left[ {1 - \left( {1 - \frac{{r_{c}^{2} }}{{r_{0}^{2} }}} \right)^{{\frac{1}{2}}} } \right] - \frac{{\rho \dot{r}_{c}^{2} }}{{\sigma_{u} }}\left( {\ln \frac{{r_{cr} }}{{r_{0} }} + \frac{{r_{c}^{2} }}{{r_{cr}^{2} }} - \frac{{r_{c}^{2} }}{{r_{0}^{2} }}} \right) $$
(23)

The critical cavity radius rc1 is gained by definition of rcr = r0 in Eq. (23). The “elastic-cracked-comminuted” phase would come to end if rcr= r0, and then Eq. (23) can be further simplified as

$$ \frac{{Kr_{0} }}{{\sigma_{u} }}\left[ {1 - \left( {1 - \frac{{r_{c1}^{2} }}{{r_{0}^{2} }}} \right)^{{\frac{1}{2}}} } \right] + \frac{{\left| {\sigma_{t} } \right|}}{{\sigma_{u} }} = \frac{2E}{{3\sigma_{u} }}\frac{{r_{c1}^{2} }}{{r_{0}^{2} }} $$
(24)

It can be seen from Eq. (24) that rc1/r0 is only related to the parameters of the targets (Kr0/σu,|σt|/σu and E/σu) but independent of the cavity-expansion velocity.

In the cracked region (rp≤ r≤rcr), according to assumption (3), there is no circumferential stress, i.e., σθ= 0, and then integral of Eq. (14) gains

$$ \sigma_{r} = \frac{C}{r} - \rho \dot{r}_{c}^{2} \left( {1 + 2\frac{{r_{c}^{2} }}{{r^{2} }}} \right) $$
(25)

where C is the integral constant.

Moreover, on the basis of the continuous conditions of the radial stress (σr) related to Eq. (15), substituting Eq. (19) into Eq. (25) can provide C as

$$ C = r_{cr} \left[ {\frac{2E}{3}\left( {\frac{{r_{c} }}{{r_{cr} }}} \right)^{2} - \left| {\sigma_{t} } \right| + \rho \dot{r}_{c}^{2} \left( {1 + 2\frac{{r_{c}^{2} }}{{r_{cr}^{2} }}} \right)} \right] $$
(26)

The integral constant (C) can be further simplified by substituting Eq. (13) into Eq. (25).

$$ C = r_{p} \left[ {\sigma_{u} + \rho \dot{r}_{c}^{2} \left( {1 + 2\frac{{r_{c}^{2} }}{{r_{p}^{2} }}} \right)} \right] $$
(27)

Integration of Eqs. (26) and (27) gains the relationship between rp and rcr, as shown in Eq. (28).

$$ r_{cr} \left[ {\frac{2E}{3}\left( {\frac{{r_{c} }}{{r_{cr} }}} \right)^{2} - \left| {\sigma_{t} } \right| + \rho \dot{r}_{c}^{2} \left( {1 + 2\frac{{r_{c}^{2} }}{{r_{cr}^{2} }}} \right)} \right] = r_{p} \left[ {\sigma_{u} + \rho \dot{r}_{c}^{2} \left( {1 + 2\frac{{r_{c}^{2} }}{{r_{p}^{2} }}} \right)} \right] $$
(28)

Interface radii rcr and rp can be solved by combining Eq. (23) and Eq. (28).

If the cracked zone is absent during the FCCE process, by definition of rcr= rp in Eq. (28), it gets

$$ \frac{{r_{c} }}{{r_{cr} }} = \frac{{r_{c} }}{{r_{p} }} = \sqrt {\frac{{3\left( {\sigma_{u} + \left| {\sigma_{t} } \right|} \right)}}{2E}} $$
(29)

Integration of Eqs. (23) and (29) can gain the cavity-expansion velocity (\( \dot{r}_{c,\hbox{max} } \)) for response mode exchange, i.e., \( \dot{r}_{c,\hbox{max} } \) is the maximum cavity-expansion velocity for the “elastic-cracked- comminuted” phase during the FCCE process; and there is no cracked zone in targets at initial expansion if cavity-expansion velocity exceeds \( \dot{r}_{c,\hbox{max} } \), which belongs to hypervelocity penetration problems.

$$ \dot{r}_{c,\hbox{max} } = \left\{ {\frac{{\frac{E}{{3\sigma_{u} }}\left( {\frac{{r_{c} }}{{r_{0} }}} \right)^{2} + \frac{{\sigma_{u} - \left| {\sigma_{t} } \right|}}{{2\sigma_{u} }} - \frac{{Kr_{0} }}{{\sigma_{u} }}\left[ {1 - \left( {1 - \frac{{r_{c}^{2} }}{{r_{0}^{2} }}} \right)^{{\frac{1}{2}}} } \right]}}{{\frac{{r_{c}^{2} }}{{r_{0}^{2} }} - { \ln }\frac{{r_{c} }}{{r_{0} }} + \frac{1}{2}{ \ln }\frac{{3\left( {\sigma_{u} + \left| {\sigma_{t} } \right|} \right)}}{2E} - \frac{{3\left( {\sigma_{u} + \left| {\sigma_{t} } \right|} \right)}}{2E}}}\frac{{\sigma_{u} }}{\rho }} \right\}^{{\frac{1}{2}}} $$
(30)

It can be seen from Eq. (30) that \( \dot{r}_{c,\hbox{max} } \) is related to the geometric and mechanical parameters of the targets.

Then, combining Eq. (25) with Eq. (26) gets

$$ \sigma_{r} = \frac{{r_{cr} }}{r}\left[ {\frac{2E}{3}\left( {\frac{{r_{c} }}{{r_{cr} }}} \right)^{2} - \left| {\sigma_{t} } \right| + \rho \dot{r}_{c}^{2} \left( {1 + 2\frac{{r_{c}^{2} }}{{r_{cr}^{2} }}} \right)} \right] - \rho \dot{r}_{c}^{2} \left( {1 + 2\frac{{r_{c}^{2} }}{{r^{2} }}} \right) $$
(31)

In the comminuted region (rc≤ r≤rp), transformation of Eq. (5) gives

$$ \sigma_{r} - \sigma_{\theta } = \sigma_{u} \left( {\sqrt {m\frac{{\sigma_{r} }}{{\sigma_{u} }} + n} - \frac{m}{2}} \right) $$
(32)

Combining Eq. (32) with Eq. (14) provides

$$ \frac{{d\sigma_{r} }}{dr} = \frac{{\sigma_{u} \left( {\frac{m}{2} - \sqrt {m\frac{{\sigma_{r} }}{{\sigma_{u} }} + n} } \right)}}{r} - \rho \dot{r}_{c}^{2} \left( {\frac{1}{r} - \frac{{2r_{c}^{2} }}{{r^{3} }}} \right) $$
(33)

Equation (33) is a nonlinear ordinary differential equation, and could be solved by Runge–Kutta method with the boundary conditions of Eq. (13).

2.3.2 Cracked-comminuted phase (r c1 ≤ r c< r c2)

In the cracked region (rp≤ r≤r0), radial stress (σr) can still be obtained by Eqs. (25) and (27). The equation of boundary conditions is still Eq. (11) at r = r0, and then the integral constant C in Eq. (25) can be gained by combination of Eqs. (25) and (11).

$$ C = r_{0} \left[ {Kr_{0} \left[ {1 - \left( {1 - \frac{{r_{c}^{2} }}{{r_{0}^{2} }}} \right)^{{\frac{1}{2}}} } \right] + \rho \dot{r}_{c}^{2} \left( {1 + 2\frac{{r_{c}^{2} }}{{r_{0}^{2} }}} \right)} \right] $$
(34)

The radial stress (σr) can be gained by substituting Eq. (34) into Eq. (25).

$$ \sigma_{r} = \frac{{r_{0} }}{r}\left[ {Kr_{0} \left[ {1 - \left( {1 - \frac{{r_{c}^{2} }}{{r_{0}^{2} }}} \right)^{{\frac{1}{2}}} } \right] + \rho \dot{r}_{c}^{2} \left( {1 + 2\frac{{r_{c}^{2} }}{{r_{0}^{2} }}} \right)} \right] - \rho \dot{r}_{c}^{2} \left( {1 + 2\frac{{r_{c}^{2} }}{{r^{2} }}} \right) $$
(35)

In the comminuted region (rc≤ r≤rp), the solution procedure of the control equation Eq. (33) with the boundary conditions of Eq. (13) is similar to that in the “elastic-cracked-comminuted” phase.

At the cracked-comminuted interface, the Eq. (36) is gotten by integrating Eqs. (27) with (34).

$$ \frac{{Kr_{0} }}{{\sigma_{u} }}\left[ {1 - \left( {1 - \frac{{r_{c}^{2} }}{{r_{0}^{2} }}} \right)^{{\frac{1}{2}}} } \right] + \frac{{\rho \dot{r}_{c}^{2} }}{{\sigma_{u} }}\left( {1 + 2\frac{{r_{c}^{2} }}{{r_{0}^{2} }}} \right) = \frac{{r_{p} }}{{r_{0} }}\left[ {1 + \frac{{\rho \dot{r}_{c}^{2} }}{{\sigma_{u} }}\left( {1 + 2\frac{{r_{c}^{2} }}{{r_{p}^{2} }}} \right)} \right] $$
(36)

When the “cracked-comminuted” phase ends, the comminuted region has just reached the outer boundary of the targets. Therefore, the critical cavity radius (rc2) is obtained by definition of rp= r0, and then Eq. (36) can be transformed into

$$ \left( {\frac{{r_{c2} }}{{r_{0} }}} \right)^{2} = 1 - \left( {1 - \frac{{\sigma_{u} }}{{Kr_{0} }}} \right)^{2} $$
(37)

It is shown in Eq. (37) that rc2/r0 is correlated closely with dimensionless confinement stiffness Kr0/σu, which can reflect the confinement effect of the outer tube to concrete to a certain degree. The applicable maximum confinement (Kr0)max can be obtained by the substitution of the critical condition rc1 = rc2 into Eqs. (24) and (37).

$$ \frac{{\sigma_{u} }}{{\left( {Kr_{0} } \right)_{\hbox{max} } }} = 1 - \sqrt {1 - \frac{{3\left( {\sigma_{u} + \left| {\sigma_{t} } \right|} \right)}}{2E}} $$
(38)

There will be no “cracked-comminuted” phase if Kr0 > (Kr0)max, and the cavity-expansion process just includes “elastic-cracked-comminuted” and “completely comminuted” phases.

2.3.3 Completely comminuted phase (r c≥ r c2)

In the completely comminuted phase, the comminuted zone has reached the outer boundary of the targets, i.e., rp≡ r0. The boundary conditions and control equation would be Eqs. (11) and (33) respectively, and the solution procedure of radial stress σr is also similar to the “elastic-cracked-comminuted” phase.

As equations of stresses for the three possible phases of FCCE models are complex, numerical solutions of the radial stress and circumferential stress at the cavity wall can be solved by Runge–Kutta method according to a standardized and classified procedure shown in Fig. 3, which is similar to the procedure for FSCE models reported by Meng et al. [31]. The procedure generally includes five steps: (1) Collecting and defining the initial conditions; (2) Discussing the applicability of the dynamic FCCE model; (3) Calculating the two critical cavity radii; (4) Determination of the response phases; (5) Solving the stresses at cavity wall at different phases, as shown in Fig. 3.

Fig. 3
figure 3

Flowchart and steps for calculation of pressure at cavity wall

Full size image

3 DOP model of STCC targets penetrated by rigid projectiles

3.1 DOP formula of STCC targets

The penetration process of the STCC targets normally penetrated by rigid projectiles includes the cratering and tunneling stages [4] and the formula of total DOP (H) is

$$ H = H_{1} + H_{2} $$
(39)

where H1 is the DOP of the cratering stage with H1 = kd, k is an empirical constant and d is the diameter of projectile; H2 is the DOP of the tunneling stage obtained by the FCCE model.

For the confined concrete targets, the tunneling stage DOP (H2) can be calculated by Eq. (40) according to Ref. [31]

$$ H_{2} = \frac{2M}{{\pi d^{2} \rho NB}}{ \ln }\left( {1 + \frac{{NB\rho V_{1}^{2} }}{{A\sigma_{u} }}} \right),\quad V_{1}^{2} = \frac{{4MV_{0}^{2} - Ak\pi d^{3} \sigma_{u} }}{{4M + k\pi d^{3} \rho NB}} $$
(40)

where N is the shape factor of the projectile nose [34, 35]; V1 is the velocity of projectile at beginning of the tunneling stage, which is equal to the impact velocity of projectile (V0) for APP [31]; A and B are constants, obtained by curve-fitting of the numerical solutions of the dynamic FCCE governing equations with Eq. (41) between a series of σrc and the given \( \dot{r}_{c} \).

$$ \frac{{\sigma_{rc} }}{{\sigma_{u} }} = A + B\frac{{\rho \dot{r}_{c}^{2} }}{{\sigma_{u} }} $$
(41)

where σrc is calculated with the FCCE model described above. Therefore, the total DOP (H) is the sum of H1 and H2.

$$ H = H_{1} + H_{2} = kd + \frac{2M}{{\pi d^{2} \rho NB}}\ln \left( {1 + \frac{{NB\rho V_{1}^{2} }}{{A\sigma_{u} }}} \right) $$
(42)

3.2 Validation of the DOP model

Penetration tests of STCC targets in Ref. [36] were selected to validate the DOP model in the Sect. 3.1. In Ref. [36], 9 specimens were designed, as shown in Table 1. All the tubes of the targets had the same dimension and the diameter, wall thickness and length of the tubes were 140 mm, 3.5 mm and 350 mm, respectively. Self-compacting concrete was filled in the steel tube and the unconfined compressive strength and splitting tensile strength of the standard specimens at the time of test (age 35 d) were 56.3 MPa and 5.66 MPa, respectively.

Table 1 Damage parameters of targets in Ref. [36]
Full size table

The test set-ups, procedures and methods were also the same as those in Ref. [4]. The damage parameters of the STCC targets were are summarized in Table 1. Where, Δd is the distance from the center of ballistic crater to the center of target, r0 is the radius of confined concrete, as shown in Fig. 1; VL is the volume of the crater volume, which is measured by sand-filling method; H is the total DOP; H1 is the depth of the funneled crater and correlated with the diameter of projectile. Based on the tested H1, the empirical constant k is deduced by rounding the numbers of the averaged values according to the designed penetration velocity range. The results show that for the 12.7 mm APP, k is related closely to the impact velocity V0, approximately, k = 4 for V0 = 820 m/s–830 m/s, k = 3 for V0 = 700 m/s–710 m/s and k = 2 for V0 = 600 m/s–610 m/s.

The hard core of 12.7 mm APP is considered to be rigid during the penetration process and the velocity loss of hard core during the cratering stage is neglected [4, 36]. Therefore, the parameters of projectile of the DOP model is replaced by those of the hard core during the tunneling stage, i.e., d = dw and V1 = V0 in Eq. (40), where dw is the diameter of hard core. The relevant parameters of the 12.7 mm APP and STCC targets in Ref. [36] are as follows: d = 12.7 mm, dw= 7.5 mm, M = 19.8 g, N = 0.26; Es= 198 GPa; \( {{Kr_{0} } \mathord{\left/ {\vphantom {{Kr_{0} } {\sigma_{u} }}} \right. \kern-0pt} {\sigma_{u} }} \) = 192, \( \delta \) = 3.5 mm, r0 = 66.5 mm, rc= dw/2 = 3.75 mm, σu= 54.3 MPa, \( \left| {\sigma_{t} } \right| \) = 5.66 MPa, \( E = 3375 \times \sqrt {\sigma_{u} } \) = 24869.9 MPa, ρ = 2420 kg/m3; the constant of k is valued according to the deduced results in Table 2.

Table 2 Resistance coefficient and DOP of FCCE model for STCC targets
Full size table

As m between 8 and 26 is recommended in Ref. [31], m = 10, 15, 20 and 25 are tentatively selected and the corresponding constant coefficients A and B were fitted with Eq. (41) as described in Sect. 3.1. One of the fitted results for m = 25 is shown in Fig. 4, and the fitted parameters A and B are 4.96 and 9.44, respectively, with the correlation coefficient (R2) 0.998. And then, the tested DOP (the DOP and impact velocity are averaged for the specimens with valid measured results) and calculated DOP are compared as shown in Table 2. The results in Table 2 show that the relative error decreases with the increasing values of m, and the optimal values are gained with m = 25 where the relative error is about 8% except that of the targets with the impact velocity about 600 m/s (The possible reason is that the projectiles do not completely normally impact the STCC targets under the lower impact velocity [36]).

Fig. 4
figure 4

Curve-fitting of coefficients A and B (m = 25)

Full size image

The comparisons of several DOP models for STCC targets including Li–Chen model [34, 35], FSCE model [31] and FCCE model in this paper, are shown in Fig. 5. As for Li–Chen model, in cratering stage, H1 = 2d, and d is replaced with dw in tunneling stage; H2 is calculated by Eq. (40) with V1 = V0, B = 1, σu= fc, A = S and S = 72f −0.5c . For FSCE model and FCCE model, m = 25 is selected.

Fig. 5
figure 5

Comparison between the predicted models and tested results in Ref. [36]

Full size image

As shown in Fig. 5, the results of DOP calculated by Li–Chen model are much larger than those of tests with the relative error as high as 23.7–57.5%, while the results of DOP calculated by FSCE model are smaller than those of tests with the relative error of 5.9–25.1%. However, the relative error between the results calculated by Eq. (42) in this paper and the tested data is less than 8% except that the targets with the impact velocity about 600 m/s. Generally, it is shown that the DOP of STCC targets calculated by engineering model based on the Hoek–Brown criterion and FCCE model is obviously superior to that of the Li–Chen model. It is because that the constraint effect of the steel tube on concrete is not considered in Li–Chen model. It should point out that all the DOP of the engineering models are discrete with the impact velocity about 600 m/s, which may be due to the oblique penetration of the projectiles [36].

In order to further testify the applicability of the DOP model in this paper, Table 3 presents the comparison between the DOP model based on FCCE model and the tests in Ref. [4]. The parameters of penetrators, i.e., 12.7 mm APP, are identical to those in Ref. [36]. The parameters of STCC targets in Ref. [4] are as follows: \( \sigma_{u} = 35.8 \) MPa, \( \left| {\sigma_{t} } \right| = 5.9 \) MPa, \( E_{s} = 198 \) GPa, \( \delta = 3.5 \) mm (4.5 mm) and r0 = 53.5 mm (52.5 mm). Since the in-filled concrete of targets was designed without coarse aggregate, the value of m should be smaller than that of concrete with coarse aggregate in Ref. [36]. Therefore, m (10, 15 and 20) is tentatively selected for that concrete without coarse aggregate in Ref. [4]. The tested (the DOP and impact velocity are averaged for the specimens with valid measured results) and calculated DOP data are compared as shown in Table 3.

Table 3 Resistance coefficients and DOP for STCC targets in Ref. [4]
Full size table

It can be seen from Table 3 that when m = 15, the calculated results of the FCCE model are generally consistent with the experimental data in Ref. [4], with the maximum disparity of 10.0%. And the comparison results further shows that the DOP model based on the dynamic FCCE models can predict the DOP of the STCC targets normally impacted by rigid conical nosed projectile.

Furthermore, the comparisons of DOP models based on the dynamic FSCE model [31] and FCCE model (m = 15) for STCC targets with r0 = 53.5 mm and δ = 3.5 mm in Ref. [4] normally impacted by 12.7 mm APP ranging from 600 m/s to 830 m/s are shown in Fig. 6. It is shown that the DOP obtained by FCCE model are 26%–29% higher than that obtained by FSCE model with impact velocity ranging from 600 m/s to 830 m/s. Especially, for the tested STCC targets (D6#, D7#) in Ref. [4] normally impacted by 12.7 mm APP ranging from 822.7 m/s to 829.1 m/s, the DOP obtained by FCCE model agrees well with tested results with the maximum relative error about 1%, while the relative error between tested results and the DOP obtained by FSCE model is about -25%. Therefore, the DOP model based the dynamic FCCE model is more applicable to predict the DOP of STCC targets penetrated by rigid conical projectiles with a proper value of m.

Fig. 6
figure 6

Comparison of the predicted models with tested results in Ref. [4]

Full size image

4 Conclusions

Based on the assumptions of incompressibility and H-B criterion, a dynamic FCCE model has been developed to analyze the penetrating process and stresses at cavity wall of the STCC targets, followed by a DOP model of STCC targets normally penetrated by rigid sharp-nosed projectiles. And the relevant penetration tests of STCC targets by 12.7 mm APP were used to validate the DOP model based on the FCCE model. The results of DOP for the STCC targets based on the dynamic FCCE model show the optimal consistence with those of the relevant penetration experiments in comparisons with the results based on the dynamic FSCE and Li–Chen models. It is shown that under the conditions of a proper m, the DOP model based on the dynamic FCCE model is more applicable to predict the DOP of STCC targets penetrated by rigid conical or other sharp-nosed projectiles with an impact velocity below 830 m/s.