1 Introduction

Nowadays, flexible manipulators are very important due to their varying and versatile uses [1]. Compared to heavy rigid manipulators, flexible ones grant faster operational displacement and higher payload-to-manipulator-weight ratios as well as lower energy consumption [2]. However, since their links are flexible, subsequent operations are often delayed due to residual vibration, and particular care should be taken with regard to their control strategies [3]. Thus, numerous active vibration control researches have been motivated trying to achieve the desired trajectory tracking along with residual vibration elimination, especially when they are subject to unknown disturbances such as environmental interaction forces in different technical applications  [4].

Several studies [5, 6] have discussed the modeling issues and active control strategies of flexible manipulators, and both, rigid body and flexible motion are always considered either for their modeling or for their control/observation schemes setting up [7]. In order to model a flexible manipulator, it is more convenient to use the energy approach via the assumptions of a Newton–Euler beam. The expression of the Lagrange-Euler equations or the use of the Hamilton principle provides the equations of motion, and the elastic motion is generally approximated using either the assumed modes or the finite element methods [8].

Unfortunately, the implementation of an active vibration controller requests, most of the time, the flexible manipulator full state feedback which is, often unjustifiably, assumed available. In practice, either the required variables are too much noised to be used, or they are outright not measurable, and consequently, state reconstruction is of great importance.

To estimate states variables and external disturbances or parameters variation, many observers have targeted the one link flexible manipulator. A first order sliding mode observer was derived and confronted to the classical full-order Luenberger one regarding the estimation of the state vector for a flexible one-link manipulator under parameters variation [9]. Another variant of robust sliding mode observer has been employed to accurately estimate the state of a single one link flexible manipulator subject to unmodeled disturbance and modal uncertainties [10]. In [11], a high-order sliding mode differentiator has been proposed in order to estimate both, the state and the unknown input for a highly nonlinear one link flexible manipulator. The higher-order sliding mode approach has been examined in [12], where a controller has been derived based on a disturbance observer for a two-link flexible manipulator. Also, a disturbance observer-based vibration controller, with constrained output has been developed for an infinite dimensional flexible link manipulator in [13] and [14]. Besides, extended and unscented Kalman filtering algorithms have been successfully implemented to give a fast an accurate state estimation for a flexible manipulator [15] and a two degree of freedom rigid flexible one [16].

In this paper, a robust SOSM observer is carried out using dSPACE DS1104. The main contribution is the estimation of the state and the external perturbation for a highly nonlinear one-link flexible manipulator. The Euler–Bernoulli assumption is used to describe the flexible link, while the residual vibration is expressed using the assumed modes method. The system equations are derived using Hamilton’s principle.

The remainder of this paper is structured as follows. Section 2 presents the dynamic modeling of the targeted one link flexible manipulator, and Sect. 3 details the observer formulation and the algorithm used to identify the external disturbance. Simulation results are illustrated and discussed to prove the effectiveness of the proposed observer in Sect. 4, the conclusion and future perspective are provided in Sect. 5.

2 Dynamic model of single link flexible manipulator

2.1 The flexible manipulator system

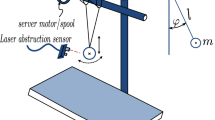
The single-link flexible manipulator considered in this study is shown in Fig. 1, it consists of a clamped-free Euler–Bernoulli beam moved on horizontal plane and is rigid in vertical flexion and torsion. One of its rigidity is attached to the rigid hub driven by a Dc servo-motor, the other is free.

Fig. 1
figure 1

Schematic representation of one link flexible manipulator

Full size image

The relative motion of the beam is described by the rotation of rigid body \(\theta (t)\) and an elastic deflection \(w(x,t)\) .

$$y(x,t) = x\theta (t) + w(x,t)$$
(1)

The Lagrange method is the common method used for modeling of flexible manipulators. It is necessary then to define the kinetic and the potential energy of the system. The effect of rotational inertia and shear deformation of a flexible link is neglected by applying Euler–Bernoulli’s beam theory. The kinetic energy of the system can be written as follows [17]:

$$E_{T} = \frac{1}{2}I_{H} \dot{\theta }\left( t \right)^{2} + \frac{\rho A}{2}\mathop \smallint \limits_{0}^{L} \left( {\dot{\theta }^{2} w^{2} + \dot{w}^{2} + \dot{\theta }^{2} x^{2} + 2\dot{\theta }\dot{w}x} \right)dx$$
(2)

Note that the first term of Eq. (2) is related to the inertia of the hub, and a second term is due to the rotation of the manipulator with respect to the origin.

The potential energy of the system is related only to the flexion of the beam. Since the height of the manipulator is much greater than its thickness, the effects of shear displacement are negligible. The potential energy of the manipulator can be written as follows [18]:

$$E_{p} = \frac{1}{2}EI\int\limits_{0}^{L} {\left( {\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }}} \right)^{2} dx} .$$
(3)

Where \(\rho\), \(A\) and \(I\) are respectively the mass density of the beam, its cross section area and its moment of inertia, and \({\text{E}}\) is the Young’s modulus of the beam,

The elastic defluxion of the end tip \(w\left( {x,t} \right)\) was approximated using the assumed mode method, will written in terms of the modal coordinates \(a_{i} \left( t \right)\) and the modes shapes \(\phi_{i} \left( x \right)\) :

$$w(x,t) = \sum\limits_{i = 1}^{N} {\phi_{i} \left( x \right).a_{i} \left( t \right)}$$
(4)

Where

$$\phi_{i} (x) = \cos (\beta_{i} x) - \cosh (\beta_{i} x) - \sigma \left( {\sin (\beta_{i} x) - \sinh (\beta_{i} x)} \right)$$

And

$$\sigma = \frac{{\cos (\beta_{i} L) + \cosh (\beta_{i} L)}}{{\sin (\beta_{i} L) + \sinh (\beta_{i} L)}}$$

And \(\beta_{i}\) satisfy

$$\cos (\beta_{i} L)\cosh (\beta_{i} L) + 1 = 0$$

Only the first proper mode of vibration is considered to achieve the system’s response, due to its most significant contribution to the overall behavior of the system

2.2 Dynamic equation of motion

The manipulator motion equations are derived using Hamilton’s extended principle [19]:

$$\int\limits_{{t_{0} }}^{{t_{f} }} {\left( {\delta E_{T} - \delta E_{p} + \delta w} \right)dt} = 0$$
(5)

where \(w\) is the non-conservative work for the input torque \(\tau\).

Then Hamilton’s Principle can be simplified into Lagrange’s Equation:

$$\frac{d}{dt}\frac{\partial L}{{\partial \dot{q}_{i} }} - \frac{\partial L}{{\partial q_{i} }} = Q_{i} \;{\text{for}}\;i = 1 \ldots N + 1$$
(6)

Where \(L = E_{T} - E_{p}\) it’s the Lagrange function of the system, \(Q_{i}\) is the \(ith\) element of the vector of generalized forces, \(q_{i}\) is the \(ith\) element of the vector of generalized coordinates.

All the elements of the vector of generalized forces are zero, except for the first element, which is equal to the torque applied by the servomotor.

The Hamilton principle provides the following equations:

$$\begin{aligned} \left[ {EI\int\limits_{0}^{L} {\frac{{\partial^{4} \phi_{1} \left( x \right)}}{{\partial x^{4} }}dx} } \right]q_{1} & + \rho A\frac{{L^{2} }}{2}\ddot{\theta } + \left[ {\left( {\rho A\int\limits_{0}^{L} {\phi_{1} \left( x \right)dx} } \right)} \right. \\ & - \left. {\left( {\rho I\int\limits_{0}^{L} {\frac{{\partial^{2} \phi_{1} \left( x \right)}}{{\partial x^{2} }}dx} } \right)} \right]\ddot{q}_{1} - \left[ {\left( {\rho A\int\limits_{0}^{L} {\phi_{1} \left( x \right)dx} } \right)q_{1} } \right]\dot{\theta }^{2} = 0 \\ \end{aligned}$$
(7)
$$\begin{aligned} \left( {I_{H} + \rho A\frac{{L^{3} }}{3} + \rho IL} \right)\ddot{\theta } & + \left[ {\left( {\rho A\int\limits_{0}^{L} {x\phi_{1} \left( x \right)dx} } \right) + \left( {\rho I\int\limits_{0}^{L} {\frac{{\partial \phi_{1} \left( x \right)}}{\partial x}dx} } \right)} \right]\ddot{q}_{1} \\ & + \left[ {\left( {\rho A\int\limits_{0}^{L} {\phi_{1}^{2} \left( x \right)dx} } \right)q_{1}^{2} } \right]\ddot{\theta } + 2\left[ {\left( {\rho A\int\limits_{0}^{L} {\phi_{1}^{2} \left( x \right)dx} } \right)q_{1} \dot{q}_{1} } \right]\dot{\theta } = \tau \, \\ \end{aligned}$$
(8)

Rearrange (7) and (8), these equations can be expressed in matrix form as follows

$$M\left( q \right)\ddot{q} + h\left( {q,\dot{q}} \right) + Kq = u(t)$$
(9)

Here, \(q = \left[ {\begin{array}{*{20}c} \theta & {a_{1} } \\ \end{array} } \right]\) is the vector of generalized coordinates which formed by the rigid coordinates \(\theta\) and the elastic modal coordinates \(a_{1}\),\(M\left( q \right)\) is the mass matrix, \(h\left( {q,\dot{q}} \right)\) is the vector of Coriolis and centrifugal forces, \(K\left( q \right)\) is the stiffness matrix and \(u\left( t \right)\) is the vector of external forces given by:

$$u = \left[ {\begin{array}{*{20}c} \tau & 0 \\ \end{array} } \right]^{T}$$
(10)

The effect of the Servomotor viscous friction and the structural damping of the beam can be integrated in the model by means of a viscous damping matrix \(H_{d}\) given by:

$$H_{d} = \left[ {\begin{array}{*{20}c} {B_{m} } & 0 \\ 0 & {2\xi_{1} m_{22} w_{1} } \\ \end{array} } \right]$$
(11)

Where \(w_{1}\) is the first elastic modes natural frequencies, \(\upxi_{1}\) is their modal damping coefficients, and \(m_{22}\) is the corresponding elements of the mass matrix.

This gives the following modified dynamic model:

$$M\left( q \right)\ddot{q} + H_{d} \dot{q} + h\left( {q,\dot{q}} \right) + Kq = u(t)$$
(12)

2.3 State space representation

Further, (12) can be rewritten in the state space expression as follows:

$$\begin{aligned} \dot{x}_{1} & = x_{2} \\ \dot{x}_{2} & = f_{1} (x) + g_{1} (x)u(t) \\ \dot{x}_{3} & = x_{4} \\ \dot{x}_{4} & = f_{2} (x) + g_{2} (x)u(t) \\ \end{aligned}$$
(13)

The vector \(x\) defined by:

$$x = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & {x_{3} } & {x_{4} } \\ \end{array} } \right]^{T}$$
(14)

\(x_{1} = \theta\) and \(x_{3} = a_{1}\) are, respectively the joint angular of the beam, and elastic modal coordinates, \(x_{2}\) is the angular velocity of the beam, \(x_{4}\) is elastic modal coordinates velocity, \(u\left( t \right) = \tau\) is the control input, \(f_{i} \left( x \right)\) and \(g_{i} \left( x \right)\left( {i = 1,2} \right)\) are nonlinear function.

2.4 Model with uncertainties

Uncertainties can be classified into two categories: matched uncertainties and unmatched uncertainties. The uncertainties are matched if and only if the uncertainties are introduced into a dynamic system from the input control, in our study the uncertainties are considered to be unmatched.

The uncertain model of a single-link flexible manipulator can be described as:

$$\begin{aligned} \dot{x}_{1} & = x_{2} \\ \dot{x}_{2} & = f_{1} (x) + g_{1} (x)u(t) + d(t) \\ \dot{x}_{3} & = x_{4} \\ \dot{x}_{4} & = f_{2} (x) + g_{2} (x)u(t) + d(t) \\ \end{aligned}$$
(15)

The uncertain term \(d\left( t \right)\) represent, the time varying external disturbance.

3 Observer design

The aim of this section is to design SOSM observer to estimate the state space and to reconstruct the time varying external disturbance of a single link flexible manipulator.

3.1 State variables estimation

For the observation of flexible robots manipulators, we propose to use the second-order sliding observer [20] will be introduced as follows:

$$\begin{aligned} \dot{\hat{x}}_{1} & = \hat{x}_{2} + K_{1} (y - \hat{y}) \\ \dot{\hat{x}}_{2} & = f(\hat{x}) + g(x_{1} )u(t) + K_{2} (y - \hat{y}) + K_{3} (y - \hat{y}) \\ \end{aligned}$$
(16)

where \(\widehat{ \cdot }\) denotes estimation,\(\widehat{x}_{1}\) and \(\widehat{x}_{2}\) are the estimation of the states \(x_{1}\) and \(x_{2}\) respectively, whereas \(K_{1}\), \(K_{2}\) and \(K_{3}\) are the gains of the observer, they be definite positive diagonal matrices.

The design of the observer consist of an adequate gains that makes the estimation error converges to zero in finite time.

The observation error \(e_{i}\) is defined as follows:

$$e_{i} = x_{i} - \widehat{x}_{i} {\text{ for }}i = 1:2$$
(17)

The dynamics of the error observation are derived from Eq. (17)

$$\dot{e}_{i} = \dot{x}_{i} - \dot{\hat{x}}_{i}\,{\text{ for }}\,i = 1:2$$
(18)

By replacing Eq. (13) and (16) into (18) we obtain

$$\begin{aligned} \dot{e}_{1} & = e_{2} + K_{1} e_{1} \\ \dot{e}_{2} & = f(x) - f(x - e) + d(t) - K_{2} e_{1} + K_{3} {\text{sign}}(e_{1} ) \\ \end{aligned}$$
(19)

We introduce a new state vector \(\left[ {v_{1} v_{2} } \right]^{T}\), with the following equations \(\upupsilon_{1} = \text{e}_{1}\) and \(\upupsilon_{2} = \text{e}_{2} - \text{Ae}_{1}\). The dynamics of the system (19) can then be transformed into:

$$\begin{aligned} \dot{v}_{1} &= v_{2} \hfill \\ \quad \dot{v}_{2} &= - K_{1} v_{1} - K_{2} v_{2} + w(.) - K_{3} sign(v_{1} ) \hfill \\ \end{aligned}$$
(20)

where \(\omega \left( . \right) = f\left( x \right) - f\left( {x - e} \right) + d\left( . \right)\), \(K_{1}\) and \(K_{2}\) are positive constants.

Under the following conditions, the observer is globally asymptotic stable.

$$K_{3} > 2\lambda_{\hbox{max} } (P)\sqrt {\frac{{\lambda_{\hbox{max} } (P)}}{{\lambda_{\hbox{min} } (P)}}} \left( {\frac{{a\rho_{0} }}{\sigma }} \right)$$
(21)

For \(\rho_{0} > 0\), \(0 < \sigma < 1\) and \(P\) is the solution of the Lyapunov equation \(M^{T} P + PM = - I\) for the matrix \(M\).

$$M = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - K_{1} } & { - K_{2} } \\ \end{array} } \right]$$

3.2 External disturbance estimation

The equivalence output injection method is used in this section to give an estimate of the external disturbance

The single link manipulator can be represented in the state space form in the following form:

$$\dot{x} = f(x) + g(x)u(t) + d(t)$$
(22)

where \(x\) is the state vector,\(f\) and \(g\) are continuous functions, the disturbance \(d\left( t \right)\) is considered unknown but bounded.

The equivalent output injection term include the information about the external perturbations, and its presence on equilibrium point, which means that the states and their estimates are approximated in finite time \(x = \widehat{x}\)

Similarly;

$$e_{1} = e_{2} = 0$$

We can conclude that the dynamic of the error observation will converge to zero in finite time.

$$\dot{e}_{2} = f(x) - f(\hat{x}) + d(t) - K_{2} e_{1} - K_{3} {\text{sign}}(e_{1} )$$
(23)

The equivalent output injection term is then given by:

$$U_{eq} \equiv d(t) \equiv K_{3} {\text{sign}}(e_{1} )$$
(24)

The equivalent output injection is the result of an infinite switching frequency of the discontinuous term \(sign\left( {e_{1} } \right)\). Thus it is making necessary the application of a low-pass filter.

The external disturbance \(d\left( t \right)\) can be estimated directly from the equivalent output injection value.

$$\hat{d}(t) = \mathop {\lim }\limits_{t \to \infty } K_{3} sign(e_{1} )$$
(25)

A way to estimate the external disturbance is by filtering the discontinuous term. The diagram of the proposed observer connected to the plant and the filter is given in Fig. 2.

Fig. 2
figure 2

Block diagram to obtain the estimate of the disturbance

Full size image

4 Simulations results and discussion

In this section, simulation results are conducted using Matlab/Simulink to demonstrate the capability of the proposed observer. Numerical parameters of the system used for the simulation are given in Table 1, and the parameters of the proposed algorithm are set to \({\text{K}}_{1} = 1.2\),\({\text{K}}_{2} = 2.3\) and \({\text{K}}_{3} = 4.6\).

Table 1 Numerical parameters of the system
Full size table

The proposed observer is formulated to supply an accurate estimation of the flexible manipulator state vector: the angular position, the tip vibration, and their respective time derivatives. The observer is also meant to give an accurate estimation of a bounded external perturbation. The initial conditions for the nominal plant of the flexible manipulator are assumed zero, while the initial state supplied to the observer is:

$$\widehat{x}\left( 0 \right) = \left[ {\begin{array}{*{20}c} {\theta_{0} } & {\begin{array}{*{20}c} {q_{10} } & {\begin{array}{*{20}c} {\dot{\theta }_{0} } & {\dot{q}_{10} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} 0 & {\begin{array}{*{20}c} {0.5} & {\begin{array}{*{20}c} 5 & 2 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]^{T} .$$

The mechanical torque applied to the beam is depicted in Fig. 3.

Fig. 3
figure 3

Mechanical torque applied to the beam

Full size image

The simulation results are provided by Figs. 4, 5, 6, 7. In Fig. 4, the joint angle of the link and their estimate are illustrated. The matching is perfect since both initial conditions are zero.

Fig. 4
figure 4

Comparison of the actual and estimated: Joint angle θ(t)

Full size image
Fig. 5
figure 5

Comparison of the actual and estimated: Tip vibration a1(t)

Full size image
Fig. 6
figure 6

Comparison of the actual and estimated: Joint Angular velocity \({\dot{\theta }}\left( \text{t} \right)\)

Full size image
Fig. 7
figure 7

Comparison of the actual and estimated: Tip vibration velocity \({\dot{\text{a}}}_{1} \left( {\text{t}} \right)\)

Full size image

The tip vibration and its estimate are illustrated in Fig. 5. Although the initial conditions are different, the required time for the observer to provide an accurate estimation is less than one second.

The same performance is proven by the observer to give an accurate estimation of the angular velocity and the tip vibration velocity as illustrated in Figs. 6 and 7 respectively.

From Figs. 4, 5, 6 and 7, it can be observed that the proposed observer can estimate accurately and in finite time the full state based on the available outputs. The angular position can easily be measured using a high-precision potentiometer, and strain gauges can be used to supply the deflection of the link tip. Then the observer is able to provide a finite time accurate estimation of the unmeasured outputs.

The estimate of the flexible manipulator state is provided in the presence of an unmodeled bounded disturbance. Hence, the equivalent output injection method (Eq. 24) was used to identify this external disturbance through a Butterworth low pass filter. The estimation of a sinusoidal disturbance is illustrated in Fig. 8.

Fig. 8
figure 8

Sinusoidal perturbation signal and perturbation estimation

Full size image

It can be concluded that the error tends to vanish after a very short transient period. The discontinuous transient error is due to the discontinuous nature of the observer.

The Observer was implemented using a dSPACE DS1104 controller board with a fixed-point DSP TMS320F240. The observer is implemented using a sampling time of 0.001 s and a continuous solver Runge–Kutta O(4). The external perturbation was generated out using a Low frequency generator via the ADCs of DS 1104 board.

Two kinds of perturbation are generated to test the observer’s ability to estimate the external disturbance. These results are obtained in ControlDesk environment 4.2.

Figure 9 shows the square perturbation and its estimate, while the sinusoidal perturbation and its estimate are presented in Fig. 10.

Fig. 9
figure 9

square signal perturbation and estimated under controlDesk

Full size image
Fig. 10
figure 10

Sinusoidal perturbation signal and estimated under controlDesk

Full size image

The root mean square error (RMSE) is calculated for the square signal perturbation \(d_{square}\), and for sinusoidal perturbation signal \(d_{Sinusoidal}\), to quantify the perfermance of the observer, which is defined as:

$$RMSE = \sqrt {\frac{1}{Ns}\sum\nolimits_{i = 1}^{Ns} {(d_{i} - \widehat{d}_{i} )^{2} } } \begin{array}{*{20}c} {} & {} \\ \end{array}$$
(26)

The following table gives the value of RMSE for both perturbation signals

It can be seen that the average error between the actual disturbance and their estimate is equal to 0.130243 for square perturbation and 0.002458 for sinusoidal one. The quantified errors demonstarte the effectiveness of the SOSM when reconstructing the external disturbance (Table 2).

Table 2 RMSE values for signal perturbation
Full size table

The estimated disturbance is extracted from the DACs connector on the DS1104 R&D Controller Board and visualized on the oscilloscope. Figure 11 shows the actual and estimated Sinusoidal perturbation signal.

Fig. 11
figure 11

Sinusoidal external perturbation identification

Full size image

The major contribution of this work is the potential application of the proposed observer in experimental cases to decrease the number of sensors. Moreover, it also shows the importance of the dSPACE Controller Card for the implementation of observation and control laws for flexible manipulators. This is in good agreement with [21], which used Dspace Ds1104 to implement the active vibration control strategy based on the discrete variable control method with disturbance observer to suppress the vibrations of a flexible cantilever beam.

The main limitations of the proposed strategy are that its restriction to bounded unknown external disturbance and the discontinuous nature of the observer that can be avoided using higher order sliding mode observer.

5 Conclusion

The main contribution of this work is the design of a second order sliding mode observer to estimate both the state and the external perturbation for a nonlinear one-link flexible manipulator. The Lagrange’s equations of movement have been expressed, and the assumed modes method has been used to derive the dynamic model of the manipulator. The derived model carried unmatched uncertainties, and for simplicity sake, we considered, in this paper, only the dominant first mode of vibration. Nevertheless, other modes may be systematically added with minor revision to improve the accuracy of the model.

The advised observation scheme has been successfully implemented using the dSPACE Controller Card. The illustrated results, either of the conducted simulation or the experimental setting up, demonstrated the effectiveness of the proposed observer to give an accurate state estimation and a finite time external perturbation reconstruction. In future research, the proposed observer can be easily extended to a flexible manipulator of higher degrees of freedom. Moreover, could be integrated into the control schemes of a flexible manipulator that requires system states and disturbance feedback observation.