1 Introduction

The gas phase reaction of the hydroxyl radical with carbon monoxide is a crucial reaction in the combustion and atmospheric chemistry. This reaction is an important component of the hydrocarbon combustion models since it contributes to the propagation of hydrogen atom and constitutes the main source of CO2 [1]. Further, the OH + CO reaction plays a central role in the atmospheric chemistry. This reaction is one of the important mechanisms of loss for tropospheric carbon monoxide and a remarkable source of ozone and CO2 (through the HO2 radical formed by the product hydrogen and molecular oxygen) [2]. In the lower atmosphere, this reaction is also the key reaction to control the concentration of the important OH free radical, which is involved in the stratospheric cycles to produce ozone and NOx molecules.

Extensive experimental [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31] and theoretical [32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53] investigations have been carried out for the OH + CO → H + CO2 reaction. Thermal rate constants, k(T), have been determined experimentally in an extended temperature and pressure range [24]. The thermal rate constants values for this reaction show a strong non-Arrhenius dependence on temperature. They are nearly independent of T at low temperature (below 500 K). On the contrary, they sharply increase with T at temperatures higher than 500 K. The slope of the Arrhenius plot increases significantly at the higher temperatures than 500 K, which indicates that the actual energy barrier exists when the quantum mechanical tunnelling becomes less important. The unusual temperature dependence of the rate constant for this reaction could be explained if it proceeds via the formation of an energized intermediate, HOCO radical, which could then dissociate either back to the original reactants or to the reaction products, H + CO2, and could also be stabilized by collisions. The HOCO intermediate has been experimentally observed in several previous studies [10, 54,55,56,57,58]. Smith and Zellner [10] were the first to purpose that the reaction mechanism involved the formation of HOCO intermediate. Experiments have also determined the isotopic substitution of OD in OH [22, 28] and 17O, 18O and 13C for CO [28].

The reaction system is small enough to be applied for the accurate quantum mechanical methods. Therefore, it has become a benchmark for kinetics and dynamics calculations. Energies of the important points on the potential energy surface have been calculated at different levels of theory by many research groups [44, 45, 50, 51, 59,60,61,62,63,64,65,66,67,68,69]. Several ab initio potential energy surface (PES) studies report existence of two intermediates, HOCO and HCO2, which form in the reaction system. It is understood that, unlike ordinary bimolecular reactions, the reaction of CO with OH proceeds through the chemically activated intermediate HOCO. The RRKM rate constants have been calculated based on the results of these quantum mechanical calculations [24, 38, 40, 66, 68,69,70,71,72]. Zhu et al. [66] carried out an RRKM/master equation analysis using G2M potential energy surface and concluded that tunnelling may be responsible for the large values of rate constants at low tempratures. Senosian et al. [70] also calculated the RRKM/master equation rate constants by CCSD(T)/cc-pVTZ potential energy surface of Yu et al. [65]. In contrast to Zhu et al. [66], they concluded that tunnelling has < 10% contribution to reaction rate at 298 K and reproduced the experimental data over the temperature range 80–250 K but their results lower than experimental data, below 250 K. Rate constants have also been obtained using the methods of quantum reactive scattering [33, 34, 36, 37, 39, 53]. Further, quasiclassical trajectory calculations (QCT) have been carried out, usually on analytical surfaces derived from ab initio calculations [32, 41, 43, 49, 61, 73]. In general, thermal rate constant using QCT technique agree well with experimental data when the temperature is above 1000 K but are significantly underestimated below 1000 K, where the measured rate constant falls slowly with temperature. This defect may be attributed to the neglecting of tunnelling corrections.

For multichannel reactions consisting of deep potential wells, as the title reaction, it would be more accurate to look at the kinetics of each channel in the presence of other channels. Although the reaction has been the subject of many studies, to the best of our knowledge no theoretical data on the kinetics of the title multichannel multiwell reaction considered such a technique in calculating the rate constants for each individual channels of this reaction. The pre-reaction van der Waals complexes and energized intermediates along the reaction coordinate is detected and their effect on the dynamics of the title reaction is investigated. In the present study, the dynamics of the reaction is investigated using the chemical master equation which describes the evolution of a network of the chemical reactions as a stochastic process. Its solution yields the probabilities that the system has any given composition as a function of time. The calculated rate constants from CME modelling are compared with those obtained from the RRKM–SSA method [74], which is based on strong collision assumption and steady state approximation (SSA) for the formation of energized intermediates.

2 Computational methods

Gaussian09 program suite [75] was used to optimize the geometries of the stationary. The optimized geometries of the reactants, products, intermediates, and transition states were obtained using the M11 method in conjunction with the 6-311G** basis set. Grimme’s three-body dispersion correction (GD3) [76] was used with S8 = 0.0 and SR6 = 1.619 (the optimized values for a similar M06-2X functional) to include the long-range dispersion interactions. Masunov et al. [77] used M11+GD3/6-311G** to construct the potential energy surface (PES) for the title reaction and compared their results with some high-level ab initio values such as CCSD(T)-F12, CCSD(T) and MRCI//CAS. They found that the maximal deviation is approximately less than 3 kcal mol−1. Single point calculations on the optimised M11 geometries at the CCSD(T) level along with the aug-cc-pVTZ basis set was carried out. The energies of stationary points, predicted in this work at CCSD(T)/aug-cc-pVTZ//M11+GD3/6-311G**, is reported in Table 1. The high level ab initio and CBS-QM11 level of theory values from the literature are also shown for compression. In addition, we assessed the multireference character of the species using the corresponding T1 diagnostic values [78] at the CCSD(T)/aug-cc-pVTZ//M11+GD3/6-311G** level of theory. The T1 values for the all stationary points in the PES (the reactants, products and transition states) of the title reaction are given in Table 2. The T1 diagnostic value for all structures except HCO2 species, which according to our following discussion doesn’t play an important role in kinetics and dynamics of this system, was found to be less than 0.03, indicating that single-reference calculations can be used reliably to characterize the present reactive system [78, 79]. Therefore, this method is sufficient accuracy to use for this system. Harmonic vibrational frequencies were obtained at the M11+GD3/6-311G** level of theory to characterize the stationary points as local minima or first order saddle points by the absence or presence of an imaginary frequency, respectively, and to obtain zero-point vibration energy (ZPE). Some of thermodynamic properties of the stationary points such as ZPE, relative Gibbs free energies, enthalpies and entropies at the M11+GD3/6-311G** level of theory listed in the Table S1 to the Supplementary Information. Furthermore, the connection of each transition state to the corresponding minima along the reaction paths was validated using intrinsic reaction coordinate (IRC) calculations at the same level of theory.

Table 1 Relative energies (kJ mol−1) for the critical points of PES, predicted at different levels of theory
Full size table
Table 2 The values of T1 diagnostics test for all species at the CCSD(T)/aug-cc-pVTZ//M11+GD3/6-311G** level of theory
Full size table

The dynamics of the title reaction is studied by solving the chemical master equation. The CME is an equation which determines the probabilities that the system has any certain composition as a function of time. The MultiWell program suite [81] was used to solve the CME to describe the variation of the fractional population of different species of the system with time and calculate the rate constants and reaction yields. The Multiwell program employs Gillespie’s stochastic simulation algorithm [82, 83] to solve one-dimensional CME. The unimolecular microcanonical rate constants are calculated according to the VTST and RRKM theory in the MultiWell program suite [84,85,86,87].

In this work, the calculated rate constant from CEM are compared with the values obtained from the RRKM–SSA method [74], which is the multichannel RRKM-method along with the steady state assumption (SSA) for the formation and consumption of energized intermediates.

3 Results and discussion

The obtained PES and optimized geometries of all the stationary points at the CCSD(T)/aug-cc-pVTZ//M11+GD3/6-311G** level of theory are shown in Figs. 1 and 2, respectively. The proposed mechanism for the title reaction is displayed in Scheme 1, where w is the collisional rate coefficient for the stabilization processes and the energized species are marked with “*” character. The different reaction pathways are characterized by the different colors for clarity in each figure. The vibrational term values and the moments of inertia for all species are listed in Table 3.

Fig. 1
figure 1

The ZPE corrected relative energies for the reaction of CO(1Σ+) with OH(2Π) at CCSD(T)/Aug-cc-pVTZ//M11+GD3/6-311G** level of theory. Three different energy pathways are presented by different colors

Full size image
Fig. 2
figure 2

The optimized structures of the stationary points at the M11+GD3/6-311G** level. Bond lengths are in angstrom and angles are in degree. According to the PES, green, blue and red arrows are the lowest, intermediate and highest energy pathways of the reaction of CO(1Σ+) with OH(2Π), respectively

Full size image
Scheme 1
scheme 1

The suggested mechanism for the reaction of CO(1Σ+) with OH(2Π). The colors indicate the three different energy pathways of the reaction

Full size image
Table 3 The Harmonic vibrational wave numbers (cm−1) and moments of inertia (amu Å2) for the various species at the M11+GD3/6-311G** level of theory
Full size table

3.1 Some features of the potential energy surface and reaction mechanism

The lowest doublet PES for the reaction of CO(1Σ+) and OH(2Π) at the CCSD(T)/aug-cc-pVTZ//M11+GD3/6-311G** level (Fig. 1) indicates that there are two entrance channels for this system. The lowest energy pathway of the reaction (green color in Figs. 1, 2 and Scheme 1) consists the formation of a pre-reaction complex (vdw1), which is 8.3 kJ mol−1 more stable than the reactants. The vdw1 complex could undergo rearrangement process to form trans-HOCO intermediate, which is 132.1 kJ mol−1 more stable than the reactants by passing over a saddle point TS1 with low barrier height (4.4 kJ mol−1, reaction R1). Internal rotation about the O–C bond in the chemically activated trans-HOCO can proceed via the gauche transition state, TS3, with torsional barrier of 40.2 kJ mol−1 to form an energized intermediate, cis-HOCO conformer that is 127.0 kJ mol−1 more stable than reactants (reaction R3). cis-HOCO conformer can also be produced from another entrance channel, intermediate energy pathway (blue color in Figs. 1, 2 and Scheme 1), via the pre-reaction hydrogen-bond van der Waals complex vdw2, which is 6.0 kJ mol−1 more stable than the reactants by passing over a saddle point TS2 with 19.6 kJ mol−1 barrier height (reaction R2). The energized cis-HOCO can convert to CO2 molecule and hydrogen atom as the products, which are 102.0 kJ mol−1 more stable than the reactants by passing over or tunnelling through saddle point TS4 with 129.2 kJ mol−1 barrier height (reaction R4).

In case of having enough energy, trans-HOCO energized intermediate, via the highest energy pathway of this system (red color in Figs. 1, 2 and Scheme 1), can surmount or tunnel through transition state TS5 (160.3 kJ mol−1 barrier height) to form HCO2 intermediate (reaction R5) with 53.6 kJ mol−1 energy relative to the reactants that dissociate to CO2 and H products (reaction R6) by tunneling or surmounting through saddle point TS6 with 5.9 kJ mol−1 barrier height.

3.2 Calculations of the rate constants

MultiWell program by Barker et al. was used to estimate the population fractions of different species in this multichannel multiwell system with time and calculate the rate coefficients of different channels. The Multiwell program suite solves CME according to Gillespie’s stochastic simulation algorithm. The idea behind the Gillespie’s algorithm is to simulate a chain of Markov processes by sampling the probability distribution of the time elapsed since the last reaction, τ, and the probability that a specific reaction will occur at τ, such that any reaction occurring at τ has probability 1 [88]. A standard CME can be written as [89]

$$\frac{{d\rho_{i} }}{dt} = \omega \sum\limits_{j} {P_{ij} \rho_{j} - \omega \rho_{i} - k\rho_{i} + g_{i} }$$

where ω is the frequency of collision (the Lennard-Jones potential was used in this study), Pij is the transition probability of going from state j to i on collision and ki is the total microcanonical rate constant for the isomerization or dissociation of ith state. The function Pij should satisfy the detailed balance constraint and normalization. In the case of a multichannel process, ki will be the sum of the rate constants of the individual channels. gi is a value which shows the changing of the population of the given energy grain due to association from reactants or isomerization.

The MultiWell master equation code employs the Rice–Ramsperger–Kassel–Marcus (RRKM) theory to compute the energy-dependent microcanonical rate constants of the reactions with intrinsic energy barriers. This equation can be used to calculate the rate constants according to RRKM theoy

$$k(E) = \left[ {\frac{{m^{\# } }}{m}\frac{{\sigma_{ext} }}{{\sigma_{ext}^{\# } }}} \right]\frac{{g_{e}^{\# } }}{{g_{e} }}\frac{1}{h}\frac{{G^{\# } (E - E_{0} )}}{\rho (E)}$$

where m# and m are the number of the optical isomers, \(\sigma_{ext}^{\# }\) and \(\sigma_{ext}^{{}}\) are the external rotation symmetry numbers,\(g_{e}^{\# }\) and \(g_{e}\) are the electronic state degeneracies of the transition state and reactant, respectively, h is Planck’s constant, \(G^{\# } (E - E_{0} )\) is the transition state sum of states, E is the internal energy of the energized reactant molecule and E0 is the reaction threshold energy, the potential energy differences between reactant and activated complex of the reaction, and ρ(E) is the density of states of the reactant molecules. The canonical transition state theory (TST) and tunnelling correction through an unsymmetrical Eckart potential barrier [90,91,92], which was parametrized in terms of the energy barriers (forward and reverse directions) and the imaginary frequency, are routine in Multiwell package. The sums and densities of states were computed using the Stein-Rabinovitch extension [93] of the Beyer–Swinehart algorithm [94] by DenSum program, which is implemented in the MultiWell program suite.

The master equation calculations were carried out using reduced mechanism to simulate the reaction. According to the PES and Scheme 1, the mechanism of the reaction consisted of three intermediates (trans-HOCO, cis-HOCO and HCO2) and two set of products, which are connected by six reactions. The van der Waals complexes in the entrance channel (vdw1, vdw2) were neglected, because they are weakly bound and they have extremely short lifetimes. All isomerization reactions were treated as reversible, while the reactions to form bimolecular products were treated as irreversible.

The energy grain size of 10 cm−1 to a maximum 85,000 cm−1, and nitrogen as the bath gas were chosen to solve the master equation. The simulations were performed using ten million trials of 103 to 106 collisions. Lennard-Jones parameters for N2, collider gas, (σ = 3.75 Å and ε/kB = 82.0 K) and intermediates (σ = 4.1 Å and ε/kB = 210.0 K) were obtained by Hippler et al. [95] An exponential model with alpha (E) switching function was used for the collisions. It was assume that there is a statistical distribution of the energy inside the energized intermediates, because of the internal vibrational energy redistribution (IVR) in the energized species was faster than the unimolecular reactions.

The K-rotor is assumed to exchange energy freely with the other internal degrees of freedom when it was included in computing the sums and densities of states, while the degenerate two-dimensional external rotation is assumed to be inactive.

The rate constant for the recombination reaction at the high pressure limit can be calculated from detailed balance by using the equilibrium constant K(Ttrans) at translational temperature, Ttrans:

$$K(T_{trans} ) = {{k_{rec,\infty } (T_{trans} )} \mathord{\left/ {\vphantom {{k_{rec,\infty } (T_{trans} )} {k_{uni,\infty } }}} \right. \kern-0pt} {k_{uni,\infty } }}$$

where krec,∞(Ttrans) and kuni,∞ are the high pressure limiting recombination (reactants → trans-HOCO or reactants → cis-HOCO) and the unimolecular decompositions (trans-HOCO → reactants or cis-HOCO → reactants) rate constants, respectively. In this study, the total rate constant for the recombination reaction is sum of the recombination rate constants of each entrance channel. To obtain the overall rate constants for producing each species, the relative population (fraction) fi of that species at the end of the simulation is multiplied by krec,∞(Ttrans):

$$K(T_{trans} ) = f_{i} \times k_{rec,\infty } (T_{trans} )$$

The equilibrium constant K(Ttrans) is calculated using the Thermo program (part of the MultiWell program), which uses the standard statistical mechanics formulas for the partition functions of the reactants (CO and OH) and intermediates. kuni,∞ and the relative population (fraction) values, fi, were obtained using Multiwell program by solving the CME at the specific pressure and temperature.

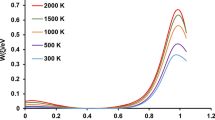
The population fractions of the different species in this reactive system at two different temperatures (298 and 2000 K) and reaction times (0.01−0.3 ps and 0.01–3 ns) are shown in Fig. 3 and 4. The feature of the PES along each particular channels is obviously determinant to judge about the importance of each pathway in a complex system, confirming the fractional yields. According to the PES, formation of HCO2 is the highest energy pathway of this system and it can be dissociated promptly to CO2 and H products over the small barrier. Therefore, HCO2 is a very short lifetime intermediate, which is only observed at the high temperatures at the early stages of the reaction, and it does not play an important role on the kinetics of this reaction. The decomposition of the HOCO intermediate competes with its stabilization at the moderate to high pressures. As shown in Figs. 3 and 4, because of the stabilization process at the higher temperatures is faster than low temperature, the population fraction of trans- and cis-HOCO are rapidly reached to Zero at 2000 K.

Fig. 3
figure 3

The population fraction of the different species as a function of time at two different temperatures

Full size image
Fig. 4
figure 4

The population fraction of the different species as a function of time at early stages of the reaction (0.01–0.3 ps)

Full size image

Owing the obtained results of the population fractions at different temperatures, the Arrhenius plots for different reaction channels at the early stages and long reaction times are shown in Figs. 5 and 6, respectively. Figure 5 shows that the rate constants of formation of the intermediates are notable at the early stages of the reaction times (less than 10−13 s), while the intermediates are converted to the products at the longer reaction times (up to 10−9 s; Fig. 6).

Fig. 5
figure 5

Arrhenius plot for each individual channel of the reaction of CO + OH calculated using Multiwell program at the early stages of the reaction at early stages of the reaction (0.01–0.3 ps)

Full size image
Fig. 6
figure 6

Arrhenius plot for each individual channel of the reaction CO + OH calculated using Multiwell program at the longer reaction time (0.01–3 ns) and the RRKM–SSA method

Full size image

The results indicate that in the long reaction time (about 3 ns), the population fractions of the energized intermediates are almost zero and products CO2 and H are formed (Figs. 3, 6).

On the other hand, as shown in Fig. 5, the fraction and rate constant of trans-HOCO is high and the fraction and rate constant of the products (CO2 + H) is low at the early stages of the reaction (up to 10−13 s). Meanwhile, in the time interval from 10−10 to 10−9 s, the fractional population of product is increased and the fraction of intermediates approach to zero.

According to the experimental results [24, 50, 96], the thermal rate constants measured for a wide range of temperatures show a significant non-Arrhenius behaviour and the total rate constant shows no significant temperature dependence at low temperatures, which indicates that the quantum mechanical tunnelling plays an important role. Therefore, we calculated the rate constants with tunnelling correction through an unsymmetrical Eckart potential barrier. As shown in Fig. 6, the obtained rate constants are in fairly good agreement with the experimental results. The following equation for the total rate expressions are obtained from fitting to the data in Fig. 6:

$$k_{{CO_{2} + H}} = 7.92 \times 10^{ - 19} T^{1.78} \exp \left( {\frac{{4.0\;{\text{kJ}}\;{\text{mol}}^{ - 1} }}{RT}} \right)$$
$$k_{trans - HOCO} = 1.64 \times 10^{ - 9} T^{ - 1.68} \exp \left( {\frac{{ - 1.4\;{\text{kJ}}\;{\text{mol}}^{ - 1} }}{RT}} \right)$$
$$k_{cis - HOCO} = 5.79 \times 10^{ - 10} T^{ - 1.60} \exp \left( {\frac{{ - 1.4\;{\text{kJ}}\;{\text{mol}}^{ - 1} }}{RT}} \right)$$

3.3 RRKM–SSA method

The rate of formation of the different reaction paths was also calculated using the RRKM–SSA method [74] according to a method suggested by Dean [97], which is based on a strong collision assumption. The results were then compared with those calculated by solving the CEM using Multiwell program.

The density of states of the reactant, the sum of states of the transition state along the reaction coordinates and the unimolecular rates for crossing various transition states were calculated using the RRKM program of Zhu and Hase [98]. In RRKM calculations, a step size of 0.4 kJ mol−1 (ΔE+) was used to calculate the available energy for the activated complexes, and the external rotations were treated as adiabatic. N2 was chosen as bath gas with a value of 0.5 for the collision [99]. To calculate the sums and densities of states, the semiclassical technique of Tardy, Whitten, and Rabinovitch [100], as implemented in the RRKM program, was used, in which the effective number of oscillators was adjusted as a function of the internal energy at each point along the reaction coordinate.

The individual rate constants for different channels and stabilization of each intermediate were calculated using the method based on the RRKM theory in conjugation with the steady state approximation (SSA) for energized intermediates [97]. The steady state approximation for the formation and consumption of the energized intermediates trans-HOCO, cis-HOCO and HCO2 leads to the following expressions for the second order rate constants of Rw1, Rw2, Rw3, R4 and R6 reactions in the lower energy entrance channel (through vdw1) of this system (Scheme 1):

$$k_{bi} (R4)_{path1} = \kappa \frac{{\sigma B_{e} Q_{a} }}{{hQ_{CO} Q_{OH} }}\sum\limits_{{E_{0} }}^{\infty } {\frac{{k_{3} (E)k_{4} (E)D^{''} \{ G(E^{ + } )\} \exp ({{ - E^{ + } } \mathord{\left/ {\vphantom {{ - E^{ + } } {RT)}}} \right. \kern-0pt} {RT)}}}}{F}}$$
$$k_{bi} (R6)_{path1} = \kappa \frac{{\sigma B_{e} Q_{a} }}{{hQ_{CO} Q_{OH} }}\sum\limits_{{E_{0} }}^{\infty } {\frac{{k_{5} (E)k_{6} (E)D^{'} \{ G(E^{ + } )\} \exp ({{ - E^{ + } } \mathord{\left/ {\vphantom {{ - E^{ + } } {RT)}}} \right. \kern-0pt} {RT)}}}}{F}}$$
$$k_{bi} (Rw1)_{path1} = \frac{{\sigma B_{e} Q_{a} }}{{hQ_{CO} Q_{OH} }}\sum\limits_{{E_{0} }}^{\infty } {\frac{{wD^{'} D^{''} \{ G(E^{ + } )\} \exp ({{ - E^{ + } } \mathord{\left/ {\vphantom {{ - E^{ + } } {RT)}}} \right. \kern-0pt} {RT)}}}}{F}}$$
$$k_{bi} (Rw2)_{path1} = \frac{{\sigma B_{e} Q_{a} }}{{hQ_{CO} Q_{OH} }}\sum\limits_{{E_{0} }}^{\infty } {\frac{{wk_{3} (E)D^{''} \{ G(E^{ + } )\} \exp ({{ - E^{ + } } \mathord{\left/ {\vphantom {{ - E^{ + } } {RT)}}} \right. \kern-0pt} {RT)}}}}{F}}$$
$$k_{bi} (Rw3)_{path1} = \frac{{\sigma B_{e} Q_{a} }}{{hQ_{CO} Q_{OH} }}\sum\limits_{{E_{0} }}^{\infty } {\frac{{wk_{5} (E)D^{'} \{ G(E^{ + } )\} \exp ({{ - E^{ + } } \mathord{\left/ {\vphantom {{ - E^{ + } } {RT)}}} \right. \kern-0pt} {RT)}}}}{F}}$$

and the following expressions for the second-order rate constants of the reactions in the higher energy entrance channel (through vdw2) of this system:

$$k_{bi} (R4)_{path2} = \kappa \frac{{\sigma B_{e} Q_{a}^{'} }}{{hQ_{CO} Q_{OH} }}\sum\limits_{{E_{0} }}^{\infty } {\frac{{k_{4} (E)F'\{ G(E^{ + } )\} \exp ({{ - E^{ + } } \mathord{\left/ {\vphantom {{ - E^{ + } } {RT)}}} \right. \kern-0pt} {RT)}}}}{D'F}}$$
$$k_{bi} (R6)_{path2} = \kappa \frac{{\sigma B_{e} Q_{a}^{'} }}{{hQ_{CO} Q_{OH} }}\sum\limits_{{E_{0} }}^{\infty } {\frac{{k_{5} (E)k_{6} (E)k_{ - 3} (E)\{ G(E^{ + } )\} \exp ({{ - E^{ + } } \mathord{\left/ {\vphantom {{ - E^{ + } } {RT)}}} \right. \kern-0pt} {RT)}}}}{F}}$$
$$k_{bi} (Rw1)_{path2} = \frac{{\sigma B_{e} Q_{a}^{'} }}{{hQ_{CO} Q_{OH} }}\sum\limits_{{E_{0} }}^{\infty } {\frac{{wk_{ - 3} (E)D^{''} \{ G(E^{ + } )\} \exp ({{ - E^{ + } } \mathord{\left/ {\vphantom {{ - E^{ + } } {RT)}}} \right. \kern-0pt} {RT)}}}}{F}}$$
$$k_{bi} (Rw2)_{path2} = \frac{{\sigma B_{e} Q_{q}^{'} }}{{hQ_{CO} Q_{OH} }}\sum\limits_{{E_{0} }}^{\infty } {\frac{{wF^{'} \{ G(E^{ + } )\} \exp ({{ - E^{ + } } \mathord{\left/ {\vphantom {{ - E^{ + } } {RT)}}} \right. \kern-0pt} {RT)}}}}{{D^{'} F}}}$$
$$k_{bi} (Rw3)_{path2} = \frac{{\sigma B_{e} Q_{a}^{'} }}{{hQ_{CO} Q_{OH} }}\sum\limits_{{E_{0} }}^{\infty } {\frac{{wk_{ - 3} (E)k_{5} (E)\{ G(E^{ + } )\} \exp ({{ - E^{ + } } \mathord{\left/ {\vphantom {{ - E^{ + } } {RT)}}} \right. \kern-0pt} {RT)}}}}{F}}$$

where

$$\begin{aligned} D & = w + k_{ - 1}^{'} (E) + k_{3} (E) + k_{5} (E) \\ D^{'} & = w + k_{ - 2}^{'} (E) + k_{ - 3} (E) + k_{4} (E) \\ D^{''} & = w + k_{ - 5}^{'} (E) + k_{6} (E) \\ F & = DD'D^{''} - D^{''} k_{ - 3}^{'} (E)k_{3} (E) - D'k_{5} (E)k_{ - 5} (E) \\ F^{'} & = DD'D^{''} - D^{'} k_{5} (E)k_{ - 5} (E) \\ \end{aligned}$$

where kbi(Rw1), kbi(Rw2) and kbi(Rw3) are the rate coefficients for the stabilization of energized intermediates trans-HOCO, cis-HOCO and HCO2 under collision at 1 atm N2, respectively. kbi(Rx)s are the rate constants of corresponding channels. h is Plank constant, σ is the reaction path degeneracy, Qa and Q′a are the products of translational and rotational partition functions of TS1 and TS2 respectively; QCO and QOH are the partition functions of the reactants. κ is the tunnelling factor according to a model suggested by Brown [101], where a hydrogen atom approaches to a one-dimensional unsymmetrical Eckart barrier. G(E+) is the sum of vibrational states of the corresponding transition states at internal energy E+, w (= Zβc[M]) is the collisional stabilization for energized intermediates, in which Z, βc and [M] are the collision frequency, the collision efficiency and the total bath gas density, respectively, and kx(E)s are the microcanonical rate constants for the corresponding steps in the energy range of E+ and E+ + dE, which is calculated from the quotient of the sum of states to density of states of the corresponding steps. Be is the ratio of the electronic partition functions for two association reactions of entrance channels that was calculated as:

$$B_{e} = \frac{2}{{2 + 2\exp ({{ - 1665.3} \mathord{\left/ {\vphantom {{ - 1665.3} {RT)}}} \right. \kern-0pt} {RT)}}}}$$

According of the PES of this reaction, there are two pre-reaction van der Waals complexes (vdw1 and vdw2) in the entrance channel of the reaction. It was recognized long age that there are different dynamical methods to account multiple reflections above the van der Waals complexes wells along the reaction coordinates on the rate constant of the reactions [102,103,104]. In this work, we used the method based on the canonical ensembles, to calculate the effect of the multiple reflections above the pre-reaction complexes (vdw1 and vdw2) in the entrance reaction channel, which is introduced by Garrett et al. [104]. The general expression of canonical unified statistical (CUS) rate is given by:

$$k^{CUS} = k^{CVT} (T)R^{CUS} (T)$$

with

$$R^{CUS} (T) = \left[ {1 + \frac{{k^{CVT} }}{{k^{\hbox{max} } }} + \frac{{k^{CVT} }}{{k^{\hbox{min} } }}} \right]^{ - 1}$$

where kCVT (rate constant of the canonical variational transition state theory), kmax and kmin are calculated at the highest maximum of ΔG (near the saddle point), the second highest maximum, and the minimum of ΔG (lowest minima between two maxima), with all free energies measured with respect to the reactants, respectively. Therefore, RCUS(T) indicates a degree of the multiple reflection or recrossing effect. In our study, the CVT and CUS thermal rate constants are calculated using the POLYRATE 2016-2A program suite [105]. Our results show that the recrossing or multiple reflections above two van der Waals complex (vdw1 and vdw2) have a slight effect on the rate constants (a decrease in the rate constants by a factor of 0.97 at 1000 K, and 0.98 at 2000 K). It is assumed that before further progress of the reaction, the microcanonical equilibrium between the reactants and vdw1 or vdw2 is rapidly established. Therefore, the role of formation of the pre-reaction complexes vdw1 and vdw2 could be assumed to be negligible.

For each reaction channel, sum of the calculated rate constants of the reaction path1 (via vdw1) and path2 (via vdw2) are the total bimolecular rate constants. The Arrhenius plots for the reactions R4, R6, Rw1, Rw2, and Rw3 and the total rate constant for the formation of the products, CO2 and H, (sum of the rate constants of the reactions R4 and R6) are shown in Fig. 7.

Fig. 7
figure 7

Arrhenius plot for the various channels of the reaction of CO + OH in N2 bath gas at 1 atm calculated using the RRKM–SSA method

Full size image

The following rate expressions are obtained from the non-linear least squares fitting the data in Fig. 7:

$$k_{4} = 5.15 \times 10^{ - 19} T^{1.72} \exp \left( {\frac{{4.6\;{\text{kJ}}\;{\text{mol}}^{ - 1} }}{RT}} \right)$$
$$k_{6} = 4.60 \times 10^{ - 22} T^{2.75} \exp \left( {\frac{{6.6\;{\text{kJ}}\;{\text{mol}}^{ - 1} }}{RT}} \right)$$
$$k_{{CO_{2} + H}} = 1.29 \times 10^{ - 20} T^{2.36} \exp \left( {\frac{{6.0\;{\text{kJ}}\;{\text{mol}}^{ - 1} }}{RT}} \right)$$
$$k_{Rw1} = 6.33 \times 10^{ - 10} T^{ - 2.08} \exp \left( {\frac{{ - 14.9\;{\text{kJ}}\;{\text{mol}}^{ - 1} }}{RT}} \right)$$
$$k_{Rw2} = 5.56 \times 10^{ - 11} T^{ - 1.81} \exp \left( {\frac{{ - 12.3\;{\text{kJ}}\;{\text{mol}}^{ - 1} }}{RT}} \right)$$
$$k_{Rw3} = 5.45 \times 10^{ - 10} T^{ - 2.35} \exp \left( {\frac{{ - 20.6\;{\text{kJ}}\;{\text{mol}}^{ - 1} }}{RT}} \right)$$

The calculated RRKM–SSA rate constant for the formation of CO2 and hydrogen atom products is compared with that is obtained by solving the CME and the expremental results in Fig. 6. As shown in Fig. 6, there is a good agreement between the results of the RRKM–SSA and the CME methos especially at higher temperatures (beyond 500 K). At lower temperatures, beacuse of the strong collision asomption in the calculated RRKM–SSA rate constant which assume that the lifetime of the energized intermediates is long enough to make the energy distribution statistical and therefore overestimates the calculated rate constants of collisional stabilisation of the intermediates, it was found to be twice of that obtained by Multiwell program which employ the Lenard-Jones potential to simulate the collisions. However, the MultiWell program is based on the one-dimensional master equation, in which the active (randomizable) internal energy (E) is considered and it does not include the angular momentum (J) (the two-dimensional master equation). In order to obtain the more accurate results by the CEM method, the additional studies will be needed to model the title reaction with E–J resolved two-dimensional multiwell master equation to account for the centrifugal effects. It is worth mentioning that although a simple collision energy transfer model (strong assumption) was used in the RRKM–SSA method, the rate constants were obtained by including the effect of tunnelling through transition states and multiple reflections above the pre-reaction complexes.

4 Conclusions

We have studied the kinetics and dynamics of the reaction between carbon monoxide molecule, CO(1Σ+), and hydroxyl radical, OH(2Π), by solving the stochastic CEM on the lowest doublet PES obtained at the CCSD(T)/aug-cc-pVTZ//M11+GD3/6-311G** level of theory. The suggested mechanism for the reaction consists of 9 different reactions with CO2 and H as the major products. The change of population fraction of the key species in the system with time was studied at the early stages of reactions, where the fraction of the energized intermediates start to decrease and convert to the products. Furthermore, the population fraction of the key species of the title reaction obtained at longer reaction times over the temperature range from 200 to 2000 K. The results indicated that HCO2 is an extremely short lifetime intermediate, which is form only at the early stages of the reaction at high temperatures. Therefore, it has not important role in the kinetics of the title reaction. The rate constants of each individual path is predicted by solving the chemical master equation and also RRKM–SSA method. Both methods predict the rate constant for the formation of the products of the title reaction in the reasonable agreement with the reported experimental data in the literature over the wide range of temperature (200–2000 K). The calculated rate constant by RRKM–SSA method with the strong collision assumption and therefore more effective energy transfer during the collisions, was compared with that obtained by solving the chemical master equation. According to strong collision assumption, it has been assume that the lifetime of the energized intermediates is long enough to make the energy distribution statistical. It should be note that this form of treatment in calculating the rate constants causes an overestimation of collisional stabilisation of the intermediates. Our results in this study are expected to have the costly modelling implication in the combustion and atmospheric chemistry.