1 Introduction

The boundary layer has a wide range of applications ranging from household to engineering practices such as aerodynamics (e.g. in separation and reattachment), species transport (e.g. blowing for cleaning the dust), heat transfer enhancement, mixing enhancement, golf ball aerodynamics etc. The similarity solution for flow and the heat transfer in/over different geometries considering constant surface temperature and convective surface boundary conditions has been reported by [1,2,3,4,5]. These authors demonstrated the possibility for the governing equations to have similarity solutions. Das [6] demonstrated that the plate temperature of a flat plate thermometer is less than one for a fluid whose Prantl number (Pr) is less than one and greater than one for a fluid whose Pr is greater than one. Furthermore, the plate temperature is approximately \(\Pr^{1/2}\) for Pr close to one. Some of the recent investigations on boundary layer include Khan et al. [7] who analysed the boundary layer flow of a nanofluid over a vertical wall. A comprehensive report on an empirical method of finding a Nusselt number in an enclosure with radiation effect has been present by Hagiwara et al. [8].

Thermal radiation is a process by which energy is emitted directly from the radiated surface in the form of an electromagnetic wave in all direction. From the engineering and physical point of view, thermal radiation effect has a pivotal role in the flow of different liquid and heat transfer. Thermal radiation is found to be useful in engineering processes which require high operating temperature. These include; the design of the nuclear plant, gas turbine, aircraft, space vehicle, reliable equipment, satellite etc. Satter and Hamid [9] analysed the significant impact of thermal radiation on unsteady free convection flow in a boundary layer. The role of thermal radiation on free convection boundary layer flow in a vertical parallel has been studied by [10,11,12,13]. Thermal radiation on magnetohydrodynamics (MHD) considering different geometries has been addressed [14,15,16,17,18]. These authors demonstrated that the temperature distribution enhanced with thermal radiation. The impact of the thermal radiation on the thermal boundary layer considering different geometry has been studied by [19,20,21]. The authors concluded that the temperature of the plate is enhanced as thermal radiation magnitude increases. Some recent work on the impact of thermal radiation on the fluid flow considering different geometries includes Cao and Baker [22] who examined heat transfer by radiation on boundary layer through optical fluid past a vertical wall. Aly and Ebaid [23] in their report presented on the role of thermal radiation and suction/injection on boundary layer nanofluid flow over a porous medium considering the induced magnetic field effect concluded that the velocity of the nanofluid flow decreases with volume fraction augment. Hayat et al. [24] also presented the role of radiation in a stagnation point flow of carbon nanofluid considering a stretching cylinder. Ghadikolaei et al. [25] numerically analysed the impact of the thermal radiation on boundary layer past a stretching surface. Tian et al. [26] analysed the significant effect of radiation properties on magnetohydrodynamics (MHD) boundary layer flow past a stretching surface. Shahid et al. [27] numerically analysed the effects of various slip and radiation on unsteady magnetohydrodynamics nanofluid flow past a stretching surface. Ymeli et al. [28] presented an analytic solution of Fourier and radiation conduction in an optical complex medium.

Following the work of Aziz [5], it appeared more appropriate to use convective surface boundary condition instead of the so-called constant surface boundary condition. Furthermore, several works carried out using constant surface boundary condition were revisited using the convective surface boundary condition. Makinde and Aziz [29] presented a report on MHD mixed convection flow from a vertical wall considering the convective boundary condition. Makinde and Olanrewaju [30] analysed the significant effect of thermal buoyancy on the boundary layer over a vertical wall with a convective boundary condition. Yao et al. [31] examined the heat transfer past a stretching/shrinking sheet considering convective surface boundary condition. Aljoufi and Ebaid [32] presented an exact solution of the significant impact of convective boundary condition on the boundary layer slip flow over a stretching surface. Lopez et al. [33] examined the significant role of thermal radiation with convective boundary condition on MHD nanofluid in a microchannel. Hassan and Salawu [34] analysed the convective surface boundary effect on buoyancy-driven flow in a parallel channel.

From the above literature, it is obvious that the impact of thermal radiation on the boundary layer considering convective surface boundary has not been given much attention. Therefore, the overall objective of the present paper is to examine the significant role of thermal radiation on the boundary layer considering a convective surface boundary condition. This is achieved by considering four different fluids namely; mercury, air, sulphur oxide and water, whose Pr are 0.044, 0.72, 2 and 7 respectively.

2 Problem statement

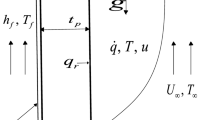
Consider the hydrodynamics and boundary layer over a flat plate in the presences of thermal radiation. Let the uniform velocity of the fluid moving on plate surface be \(U_{\infty }\), at the temperature \(T_{\infty }\) as illustrated in Fig. 1. Let x and y-axis be along and normal to the flat plate respectively. Then, governing equations can be written as;

$$\frac{\partial u}{\partial x} + \frac{\partial v}{dy} = 0,$$
(1)
$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{dy} = v\frac{{\partial^{2} u}}{{\partial y^{2} }},$$
(2)
$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha \left[ {\frac{{\partial^{2} T}}{{\partial y^{2} }} - \frac{1}{K}\frac{{\partial q_{r} }}{\partial y}} \right],$$
(3)

where T denote the dimensional temperature, K denotes the thermal conductivity, \(u\) and \(v\) denote the velocity component along and normal to the plate. The quantity \(q_{r}\) in Eq. (3) is the radiative heat flux in the y-direction. However, the radiative heat flux in the x-direction is assumed to be small in comparison to that in the y-direction. The radiative heat flux \(q_{r}\) can be simplified through Rosseland diffusion approximation for an optical thick fluid according to [35,36,37,38,39] as

$$q_{r} = \frac{{4\sigma \,\partial T^{4} }}{{3k^{*} \partial y}},$$
(4)

where \(\sigma\) and \(k^{*}\) represent the Stefan Boltzmann constant and mean absorption respectively. Furthermore, Rosseland approximation is only applicable for an optically thick fluid. However, regardless of these limitations, it has been adopted in several investigations ranging from the analysis of radiation effect on blast waves by the nuclear explosion to the transport of radiation through gases at low-density Ali Agha et al. [39].

Fig. 1
figure 1

Flow configuration and coordinate system

Full size image

The velocity boundary conditions can be expressed as

$$\begin{aligned} & u(x,y = 0) = v(x,y = 0) = 0 \\ & u(x,y \to \infty ) = U_{\infty } . \\ \end{aligned}$$
(5)

Regarding the temperature boundary condition, the base of the plate is assumed to be heated through convection from a hot fluid at a temperature \(T_{f}\) which provides a heat transfer coefficient \(h_{f}\). Therefore, the boundary conditions can be expressed as

$$\begin{aligned} & - k\frac{\partial T}{\partial y}(x,y = 0) = h_{f} \left[ {T_{f} - T(x,y = 0)} \right], \\ & T(x,y \to \infty ) = T_{\infty } . \\ \end{aligned}$$
(6)

We define the similarity variable \(\eta\) and a dimensionless temperature \(\theta (\eta )\) and a stream function \(f(\eta )\) as

$$\begin{aligned} \eta & = y\sqrt {\frac{{U_{\infty } }}{\nu x}} ,\;\;\;u = U_{\infty \,\,} f^{\prime } (\eta ), \\ v & = \frac{1}{2}\sqrt {\frac{{U_{\infty } \nu }}{x}} \left( {\eta f^{\prime } (\eta ) - f} \right),\;\;\;\theta = \frac{{T - T_{\infty } }}{{T_{f} - T_{\infty } }}. \\ \end{aligned}$$

Dimensionless parameters are defined as;

$$\Pr = \frac{{\mu C_{p} }}{K},$$
(7)
$$R = \frac{{4\sigma (T_{f}-T_{\infty})^{3} }}{k^{*}K},\,\,\,\,C_{T} = \frac{{T_{\infty } }}{{T_{f} - T_{\infty } }}.$$
(8)

Finally, the dimensionless equations can be written as;

$$2f^{\prime \prime \prime } (\eta ) + f(\eta )f^{\prime \prime } (\eta ) = 0,$$
(9)
$$\theta^{\prime \prime } (\eta )\left[ {1 + \frac{4R}{3}(\theta + C_{T} )^{3} } \right] + 4R[C_{T} + \theta ]^{2} [\theta^{\prime } (\eta )]^{2} + \frac{1}{2}\Pr \theta^{\prime } (\eta )f(\eta ) = 0.$$
(10)

Subject to;

$$f(0) = f^{\prime } (0) = 0,\,\,\,\,f^{\prime } (\eta \to \infty ) = 1,$$
(11)
$$\theta^{\prime } (0) = - a[1 - \theta (0)],\;\,\,\,\theta (\eta \to \infty ) = 0,$$
(12)

where \(C_{T}\), \(\Pr\) and R are temperature difference parameter, Prandtl number and thermal Radiation parameter respectively.

We define

$$a = \frac{{h_{f} }}{k}\sqrt {\frac{vx}{{U_{\infty } }}} .$$
(13)

Note that for the energy equation to have a similarity solution, the local convective heat transfer parameter \(a\) must be a constant and not function of x as it appeared in Eq. (13). This proposition is feasible if \(h_{f}\) is directly proportional to \(x^{ - 1/2}\). Hence we write

$$h_{f} = cx^{ - 1/2} ,$$
(14)

where c is constant.

Utilizing Eq. (14) in Eq. (13), we have

$$a = \frac{c}{k}\sqrt {\frac{v}{{U_{\infty } }}} .$$
(15)

Therefore, with a defined in Eq. (15), the solutions of Eqs. (9)–(12), gives the similarity solutions and the sets of solutions generated when a is defined as in Eq. (13) are called the local similarity solutions.

3 Results

3.1 Discussion

The thermal radiation effect on the thermal boundary layer past a flat plate considering the convective boundary condition is numerically studied. Maple software is used to solve Eqs. (9)–(12) using the RKF45 method. RKF45 is a default method in Maple due to its accuracy and robustness. Four different fluids considered are mercury, air, sulphur oxide and water whose Prandtl number (Pr) are 0.044, 0.72, 2 and 7 respectively. It is found that the solution converged when \(\eta \to 10\), hence \(\infty\) is replaced by 10 throughout the computation. The thermal radiation parameter (R) used are 0, 0.5, 1, 1.5, 2, 2.5, 3, 3.5 and 4. The local convective heat transfer parameter (a) used in the present numerical computation are 0.05, 0.10, 0.20, 0.40, 0.60, 0.80, 1, 5, 10, and 20. Also, the temperature difference parameter (\(C_{T}\)) used are 0, 0.2, 0.4, 0.6, 0.8 and 1. The present study is validated through comparison with Aziz [5] and Makinde and Olanrewaju [30]. Table 1 and Table 2 demonstrates the accuracy of the present solution of fluid whose Prandtl numbers are 0.72 and 10 for some selected values of \(a\) and it is observed that there is an excellent agreement in the absence of thermal radiation parameter (R).

Table 1 Comparison of the present results with Aziz [5] for R = 0 and \(C_{T}\) = 0.2
Full size table
Table 2 Comparison of the present results with Makinde [30] for Pr = 0.72, R = 0 and \(C_{T}\) = 0.2
Full size table

Figures 2, 3, 4 and 5 depict the temperature distribution of mercury, air, sulphur oxide and water for \(a = 1\) and \(C_{T}\) = 0.2 with various values of \(R\). It is evident that the temperature variation is proportional to R for all fluids under consideration. Figure 6 depicts the variation of temperature gradient for different values of R and fixed values of Pr, a and \(C_{T}\). This figure reveals that the temperature gradient of the fluid is inversely proportional to the R near the plate while the impact of the R is just reverse far away from the plate. Furthermore, an increase in Pr decreases boundary layer thickness as depicted in Fig. 7. In general, when Pr is unity, it means that the thermal and momentum diffusion are the same order of magnitude, which connote that the thermal and momentum boundary layer overlaps each other. Additionally, for Pr < 1, the thermal diffusivity is higher than viscous diffusivity which means, that the thermal boundary layer is thicker than the momentum boundary layer while the physical situation is just contrasted for Pr > 1. This can be observed in Fig. 7 where mercury has the largest thermal boundary layer thickness while water has the least thermal boundary layer thickness. Figure 8 illustrates the influence of temperature differences parameter (\(C_{T}\)) on the temperature distribution for air for fixed values of a and R. It is obvious from the figure that \(C_{T}\) plays a supporting role for temperature distribution. The role of the local convective heat transfer (a) is depicted in Fig. 9. It is obvious from the figure that increasing a, leads to an increase in the plate surface temperature. The numerical solution of the present work approaches the solution for constant temperature as \(a \to \infty\). This follows from Eq. (12) that the boundary condition reduces to \(\theta (0) = 1\) as \(a \to \infty\).

Fig. 2
figure 2

Impact of \(R\) variation on temperature distribution for mercury fluid \((a = 1,\;C_{T} = 0.2)\)

Full size image
Fig. 3
figure 3

Impact of \(R\) variation on temperature distribution for air fluid \((a = 1,\;C_{T} = 0.2)\)

Full size image
Fig. 4
figure 4

Impact of \(R\) variation on temperature distribution for sulphur oxide fluid \((a = 1,\;C_{T} = 0.2)\)

Full size image
Fig. 5
figure 5

Impact of \(R\) variation on temperature distribution for water fluid \((a = 1,\;C_{T} = 0.2)\)

Full size image
Fig. 6
figure 6

Impact of \(R\) variation on temperature gradient for air fluid (a = 1, \(C_{T}\) = 0.2)

Full size image
Fig. 7
figure 7

Variation of Pr on the boundary layer for (R = 1, a = 1)

Full size image
Fig. 8
figure 8

Variation of \(C_{T}\) on the temperature distribution for air fluid (R = 1, a = 1)

Full size image
Fig. 9
figure 9

Variation of \(a\) on the temperature distribution for air fluid (R = 1, \(C_{T}\) = 0.2)

Full size image

Table 3 demonstrates the significant effect of R on the surface temperature of the four fluids under consideration. The values of \(\theta (0)\) (plate temperature) enhance with R for all the four fluids under consideration while the opposite pattern is noticed for \(- \theta^{\prime } (0)\). It can also be seen that as Pr increases, the numerical values of \(\theta (0)\) decreases while the numerical value of \(- \theta^{\prime } (0)\) increases. Table 4 shows the effect of grid refinement on \(\theta (0)\) with R variation. It can be observed that the numerical values of \(\theta (0)\) increases with grid refinement until \(\eta\) approaches 10. This shows the validity for replacement of \(\eta \to \infty\) by \(\eta = 10\) in the present numerical computation which conforms with the customary practice in boundary layer theory.

Table 3 Effect of R on \(\theta (0)\) and \(-\, \theta^{\prime } (0)\) for \(a = 1\,\,{\text{and}}\,\,C_{T} = 0.2\)
Full size table
Table 4 Grid independency on \(\theta (0)\) for Pr = 0.72, \(a = 1\,\,{\text{and}}\,\,C_{T} = 0.2\)
Full size table

4 Conclusion

The numerical solution for impact of thermal radiation on thermal boundary layer formation on the flat plate with a convective boundary condition is discussed. The effects of R, \(C_{T}\), \(a\) and \(\Pr\) on temperature is analysed using line graphs and tables. The results indicated that:

  1. (i)

    Thermal radiation (R) has an increasing effect on the thermal boundary layer thickness and numerical values of \(\theta (0)\) while reverse impact on the temperature gradient \(- \theta^{\prime } (0)\).

  2. (ii)

    The thermal boundary layer thickness decreases as Pr increase.

  3. (iii)

    As temperature differences increases \((C_{T} )\), the temperature distribution increases.

  4. (iv)

    The numerical solution approaches contant surface temperature solution as \(a \to \infty\).

  5. (v)

    The temperature distribution enhanced with a augment.