Impact of Exponentially Decaying Internal Heat Generation on Mixed Convection Boundary Layer Slip Flow from a Thermally Radiated Vertical Plate

Abstract

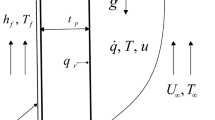
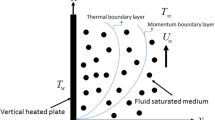
This study investigated the effects of thermal radiation and internal heat generation on mixed convection flow impacted by momentum and thermal partial slip boundary conditions. Using a similarity variable, the governing equations for the fluid flow are first converted to ordinary equations, which are then solved by the Runge–Kutta method in Maple 2022 after utilizing shooting procedures. Examined are the consequences of a some important parameters, including the momentum and thermal slip boundary conditions, internal heat generation parameter, nonlinear thermal radiation, mixed convection parameter, and nonlinear density variance with temperature. Some important discoveries include the fact that as the thermal partial slip parameter is raised, the thickness of the momentum and thermal boundary layers also substantially decreases. The mode of heat transfer for $\lambda_{x} < 1$ is from the porous surface into the fluid on the surface of right plate, and the surface temperature is less than 1 . The resultant heat does, however, flow back into the porous plate for $\lambda_{x} > 1$. Additionally, the presence of radiative heat influences the temperature distribution in the free stream which in turn enhances flow formation. Additionally, as the rate of injection rises, the thickness of the thermal and momentum boundary layers increases rapidly. With a weak buoyancy effect $Gr_{x} = 0.1$, the rate of particle suction/injection causes a reduction in the plate shear stress. Additionally, for particle suction/injection, as the fluid changes from air $\left( {\Pr = 0.72} \right)$ to water $\left( {\Pr = 7} \right)$, the reversible flow increases. For suction scenarios and some injection values $\left( {S > - 1} \right)$, the rate of heat flow accelerates. However, for mild particle injection $\left( {S < - 1} \right)$, the rate of mixed convection  decreases.